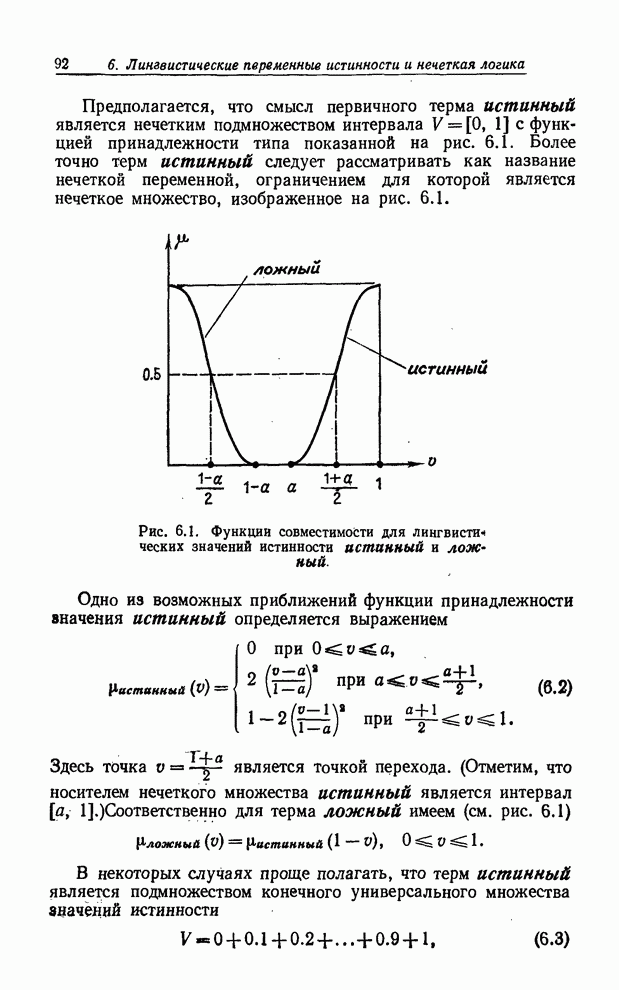
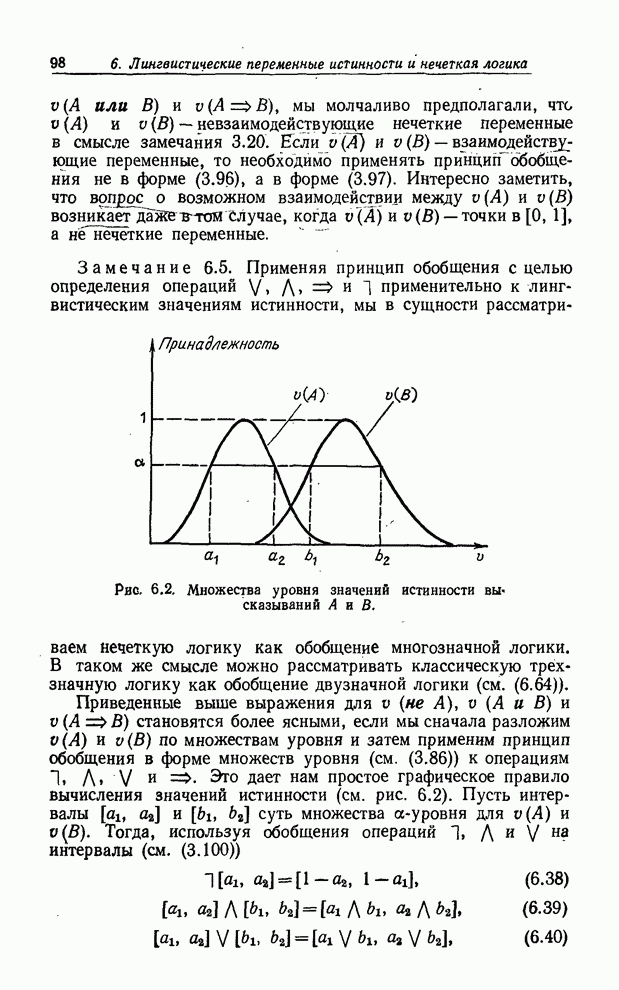
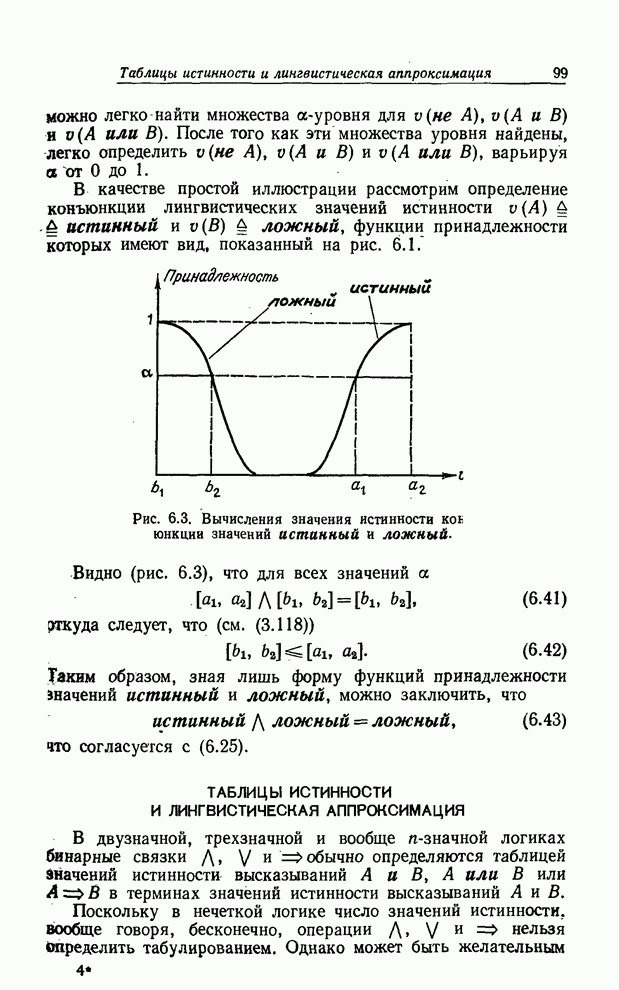
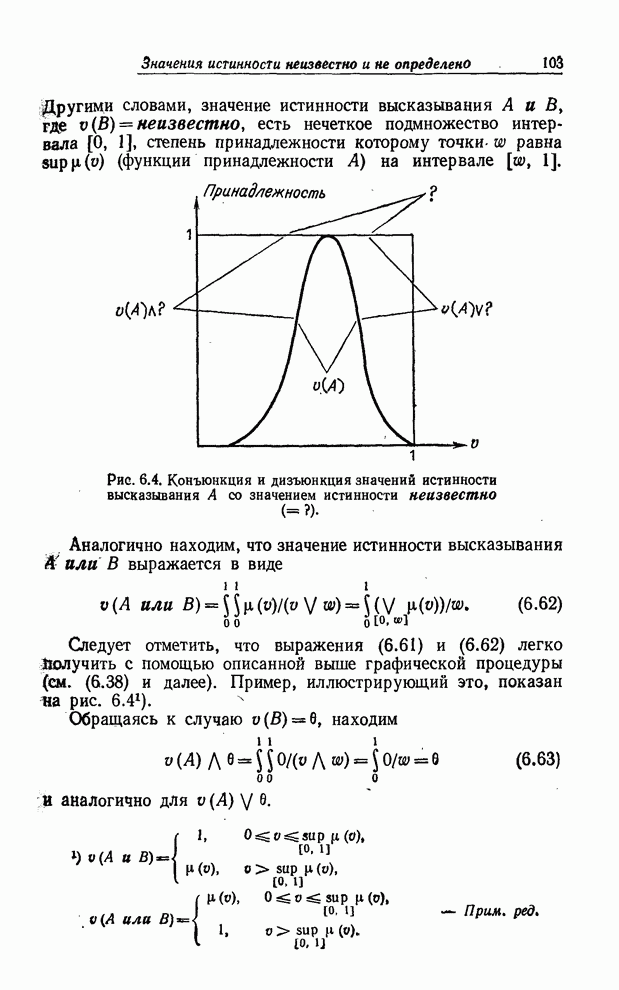
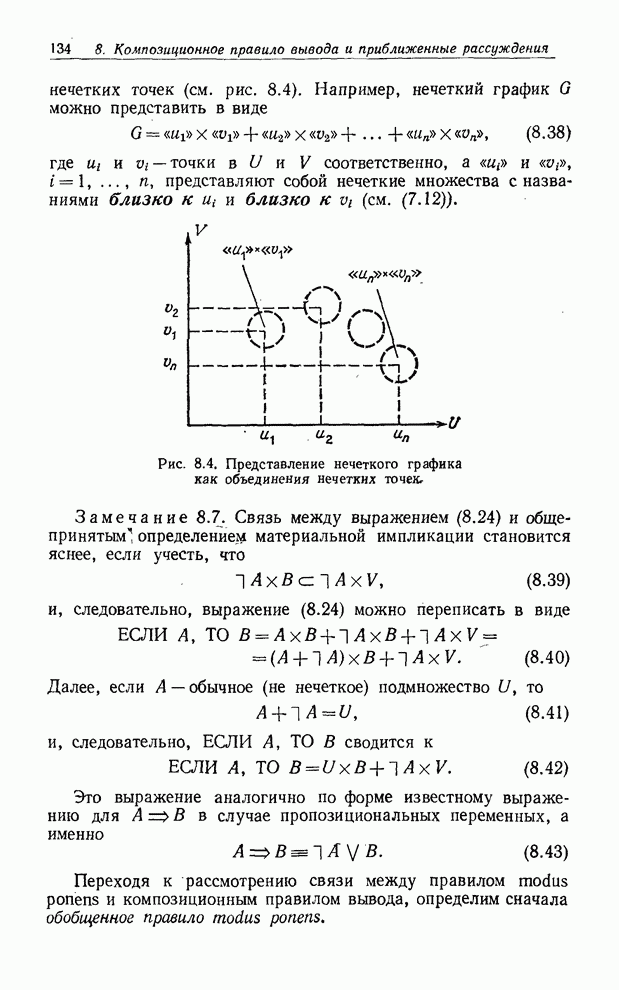
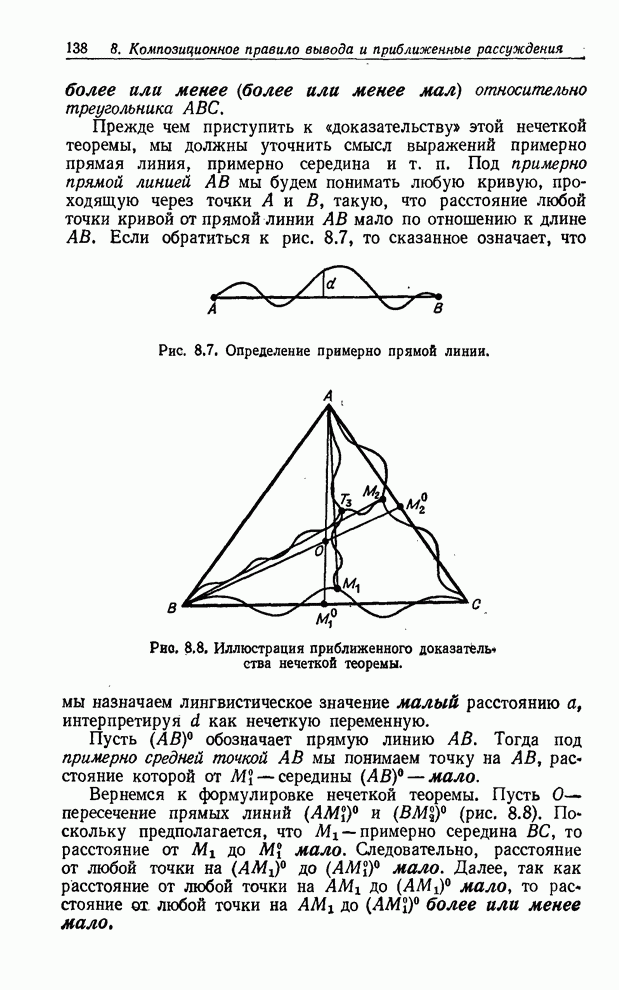
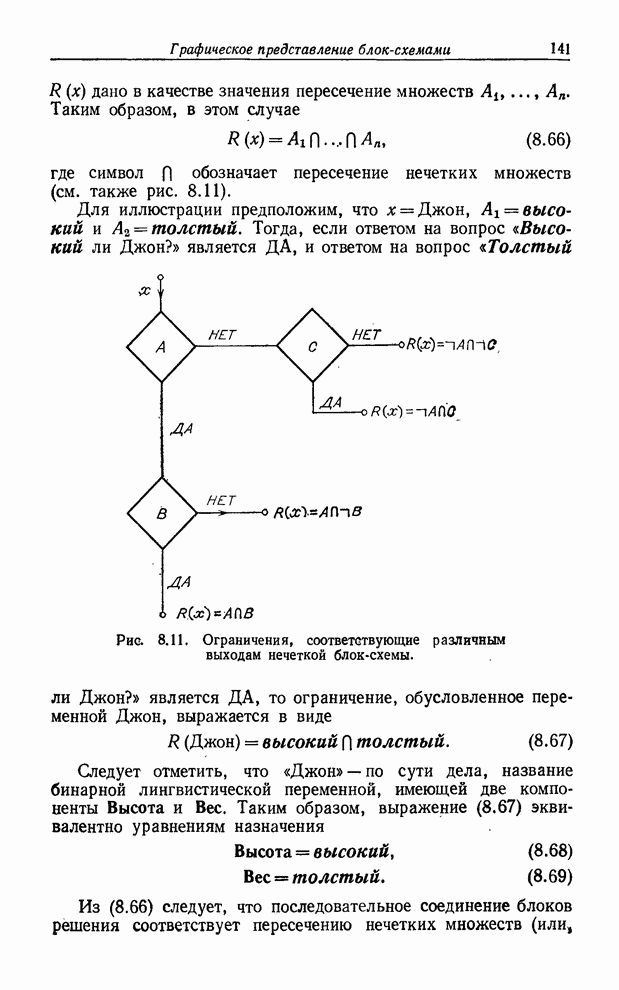
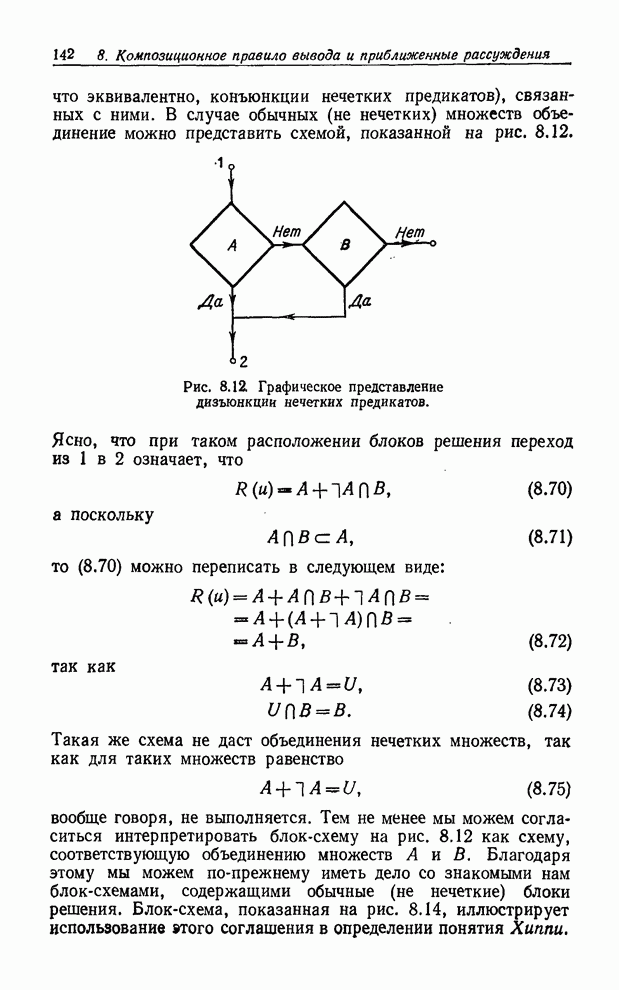
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
Во многих приложениях теории вероятностей, например, при
вычислении средних значений, дисперсий и т. п., часто встречаются линейные
комбинации вида (![]() арифметическая сумма)
арифметическая сумма)
![]() ,
(7.26)
,
(7.26)
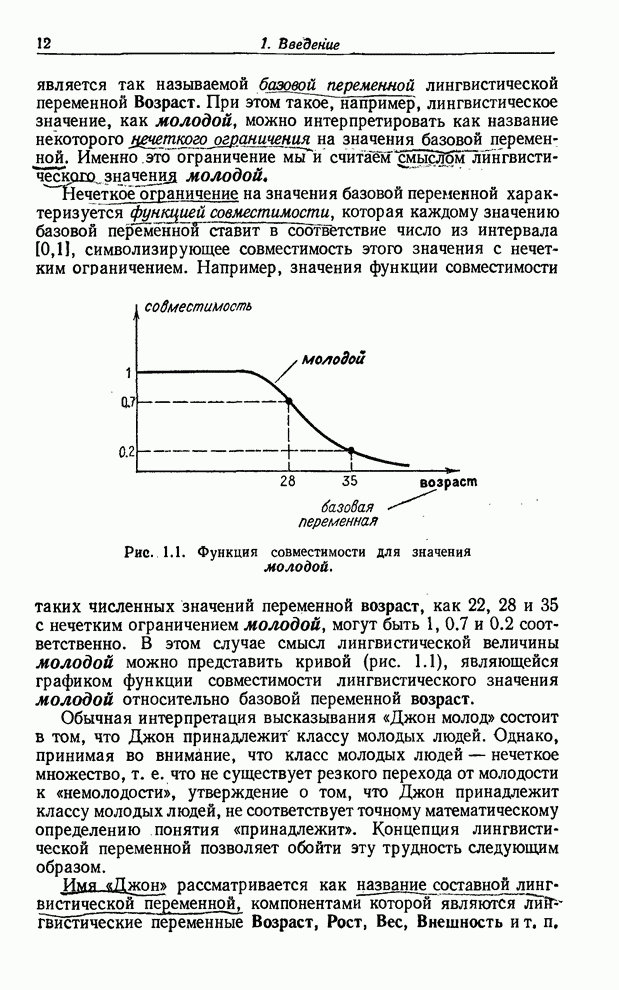
где ![]() —
действительные числа, а
—
действительные числа, а ![]() — значения вероятностей из
интервала [0, 1]. Если
— значения вероятностей из
интервала [0, 1]. Если ![]() — числа из интервала [0, 1], то
вычисление значения комбинации
— числа из интервала [0, 1], то
вычисление значения комбинации ![]() при заданных
при заданных ![]() и
и ![]() не представляет труда. Однако
оно становится нетривиальным, когда рассматриваемые вероятности являются
лингвистическими по своей природе, т. е. когда
не представляет труда. Однако
оно становится нетривиальным, когда рассматриваемые вероятности являются
лингвистическими по своей природе, т. е. когда
![]() ,
(7.27)
,
(7.27)
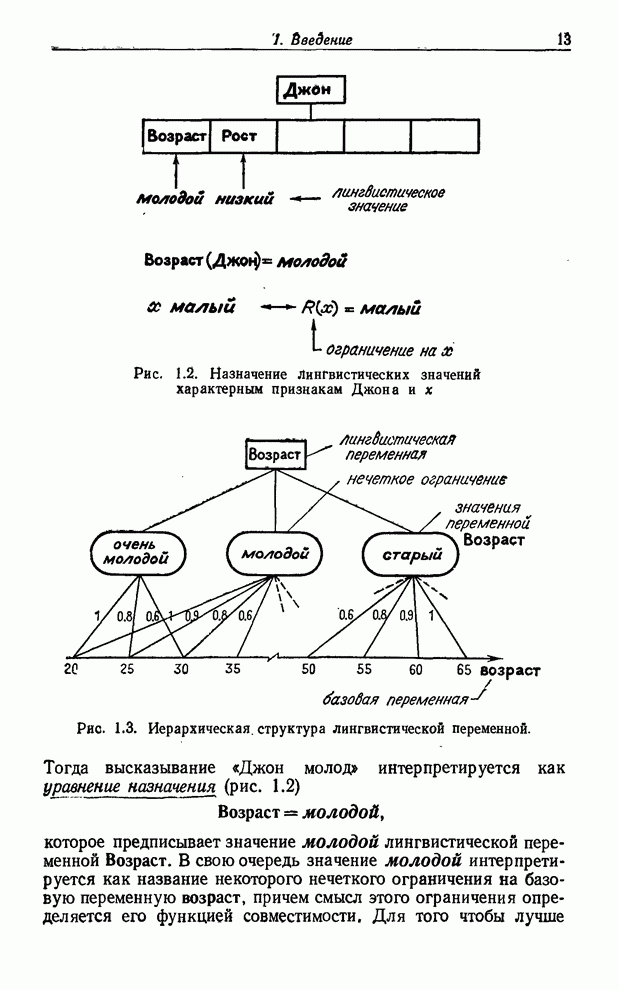
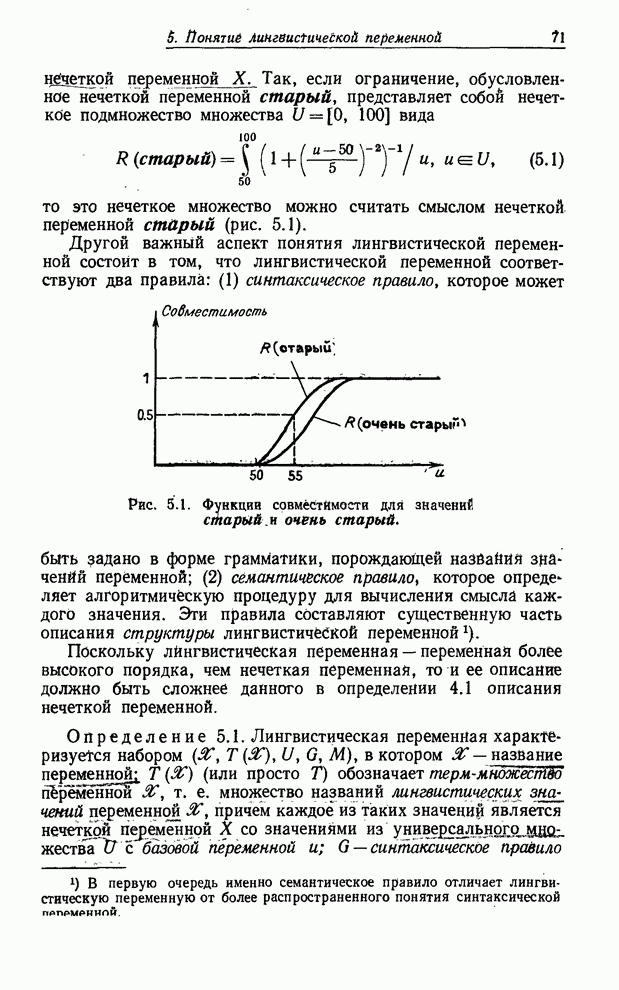
где ![]() —
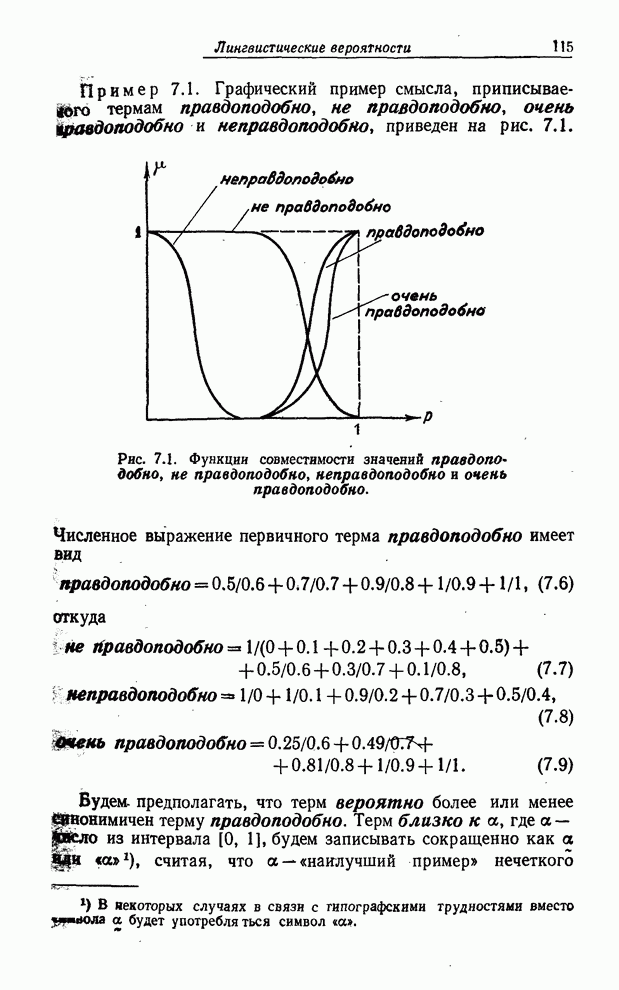
такие лингвистические значения вероятностей, как правдоподобно, неправдоподобно,
очень правдоподобно, близко к
—
такие лингвистические значения вероятностей, как правдоподобно, неправдоподобно,
очень правдоподобно, близко к ![]() и т. п. Соответственно
и т. п. Соответственно ![]() —недействительное число, как в (7.26), а
нечеткое подмножество действительной оси
—недействительное число, как в (7.26), а
нечеткое подмножество действительной оси![]() , причем функция принадлежности
подмножества
, причем функция принадлежности
подмножества ![]() зависит
от функций принадлежности
зависит
от функций принадлежности ![]() .
.
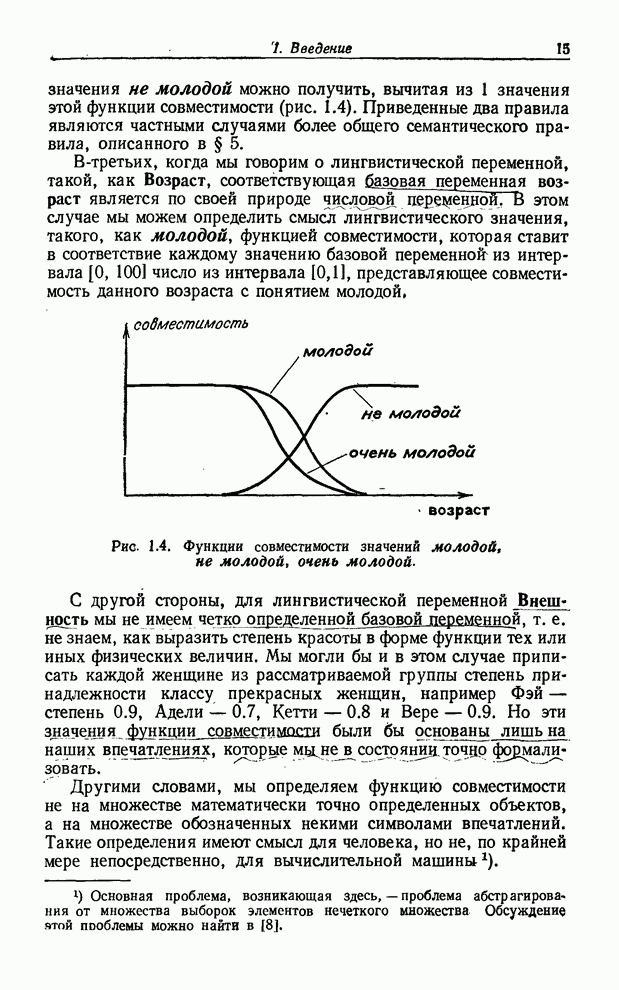
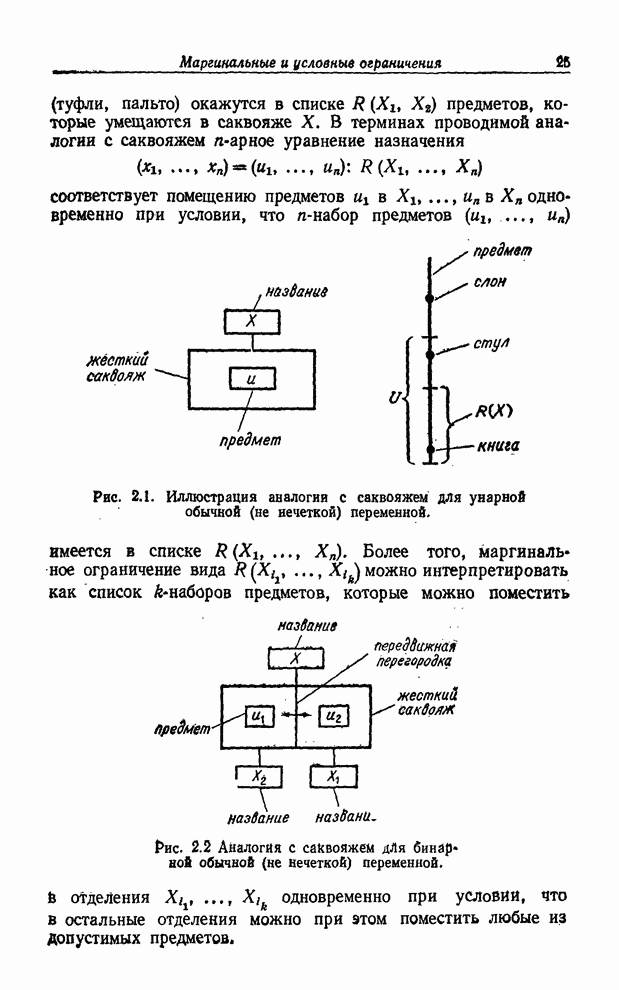
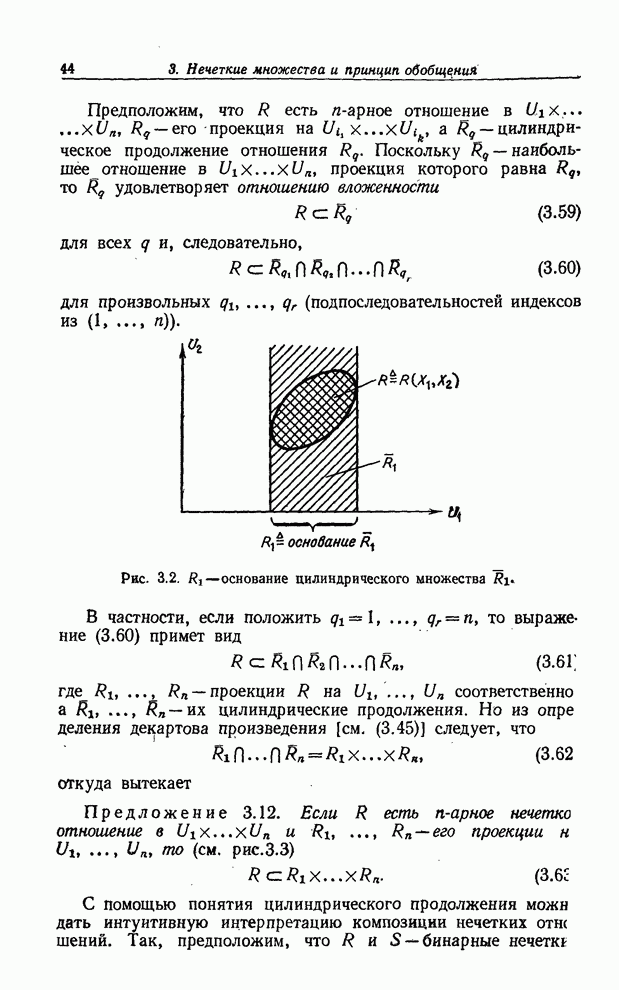
В предположении, что нечеткие переменные ![]() - невзаимодействующие (не
считая ограничения (7.15)), ограничение, обусловленное набором
- невзаимодействующие (не
считая ограничения (7.15)), ограничение, обусловленное набором ![]() , принимает вид
(см. (7.16))
, принимает вид
(см. (7.16))
![]() . (7.28)
. (7.28)
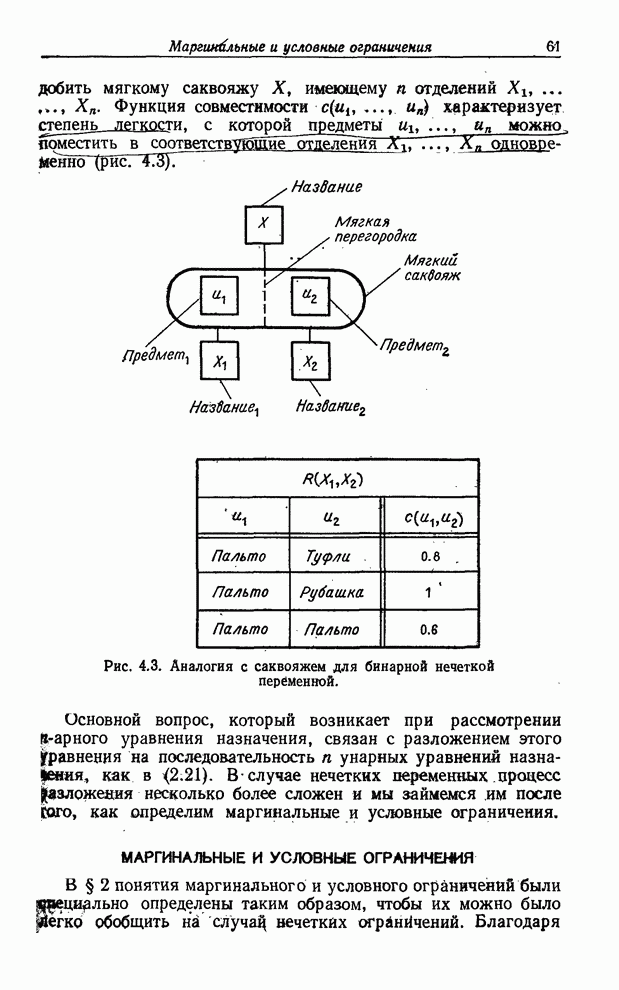
Пусть ![]() - функция принадлежности ограничения
- функция принадлежности ограничения
![]() и пусть
и пусть ![]() — функция
принадлежности ограничения
— функция
принадлежности ограничения ![]() . Тогда, применяя принцип обобщения
(3.90) к (7.26), можно выразить
. Тогда, применяя принцип обобщения
(3.90) к (7.26), можно выразить ![]() в виде нечеткого множества (
в виде нечеткого множества (![]() арифметическая
сумма)
арифметическая
сумма)
![]() , (7.29)
, (7.29)
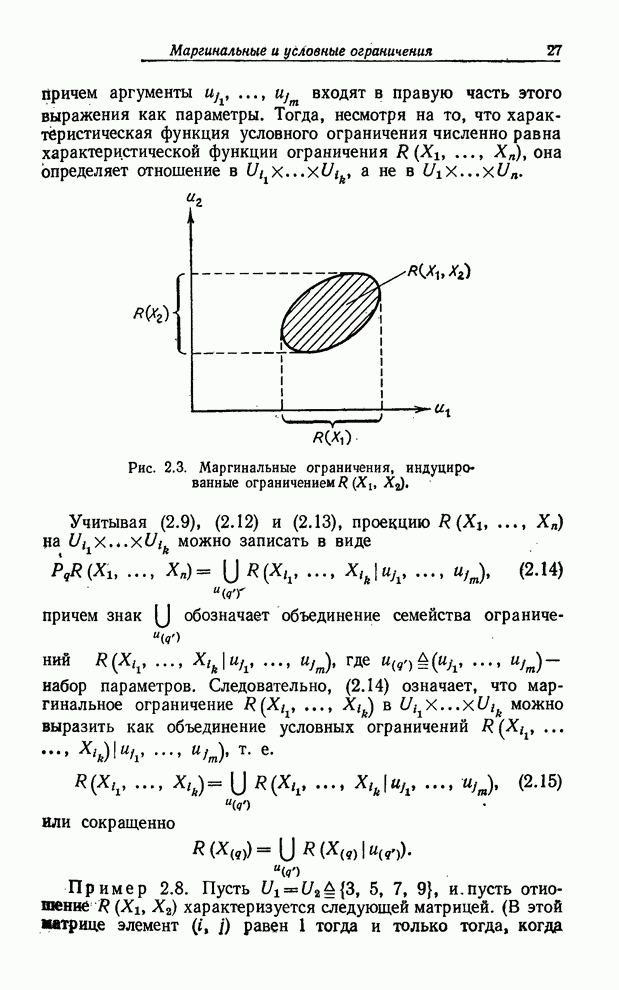
которое с учетом (7.28) можно записать как
![]() , (7.30)
, (7.30)
понимая при этом, что ![]() в (7.30) удовлетворяют ограничению
в (7.30) удовлетворяют ограничению
![]() . (7.31)
. (7.31)
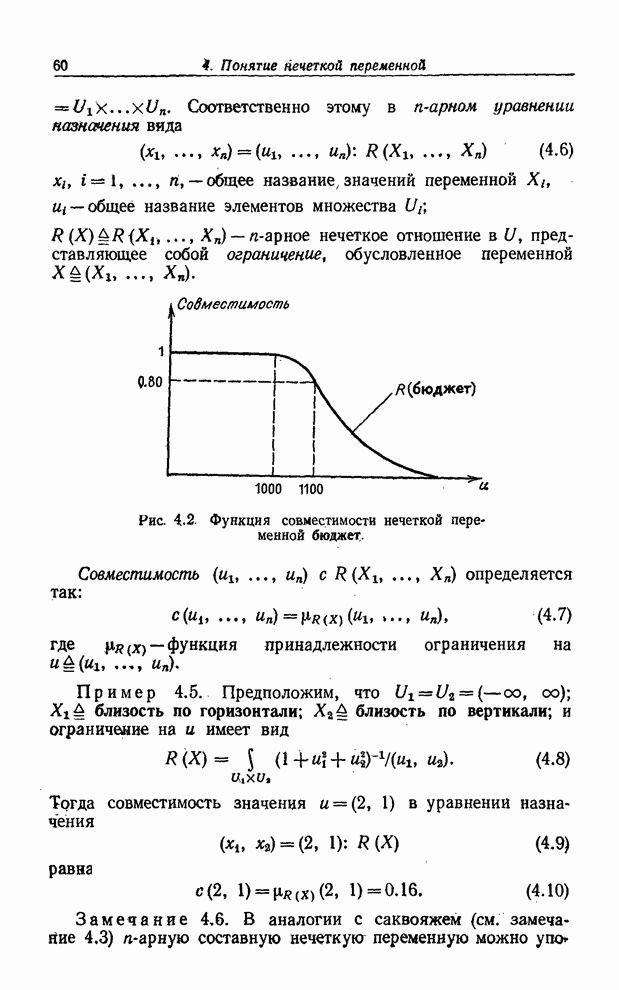
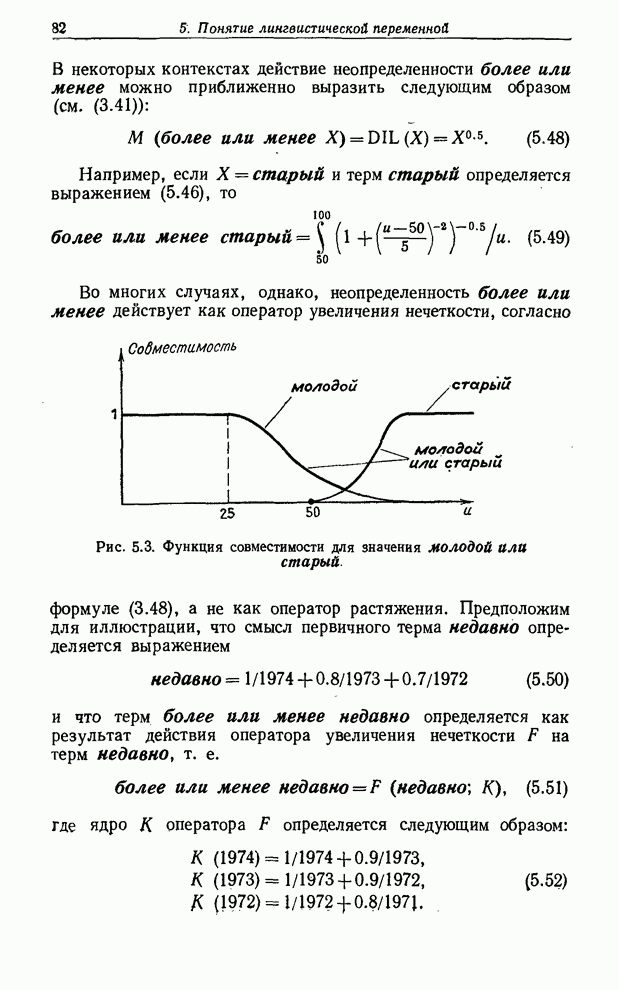
Таким образом мы можем представить линейную комбинацию значений лингвистических вероятностей нечетким подмножеством действительной оси.
Выражение для ![]() можно записать другим более удобным для
вычислений способом. Так, пусть
можно записать другим более удобным для
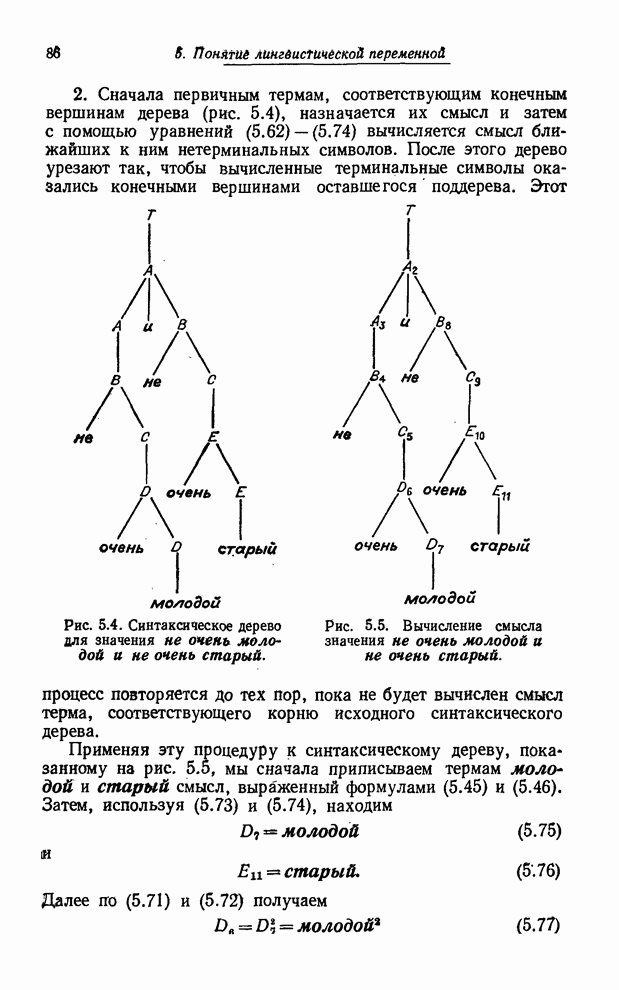
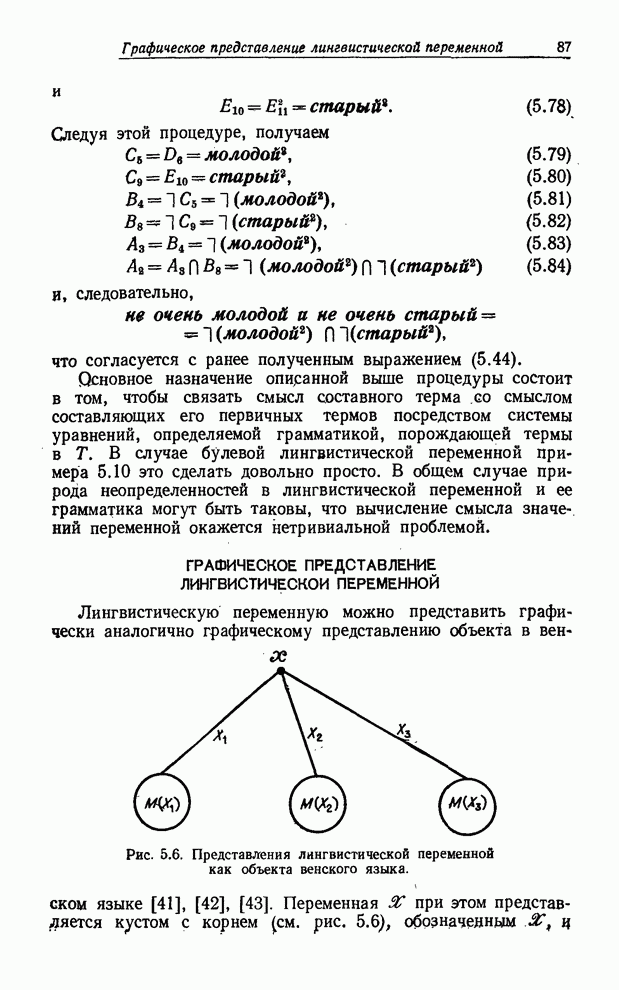
вычислений способом. Так, пусть ![]() обозначает функцию принадлежности
множества
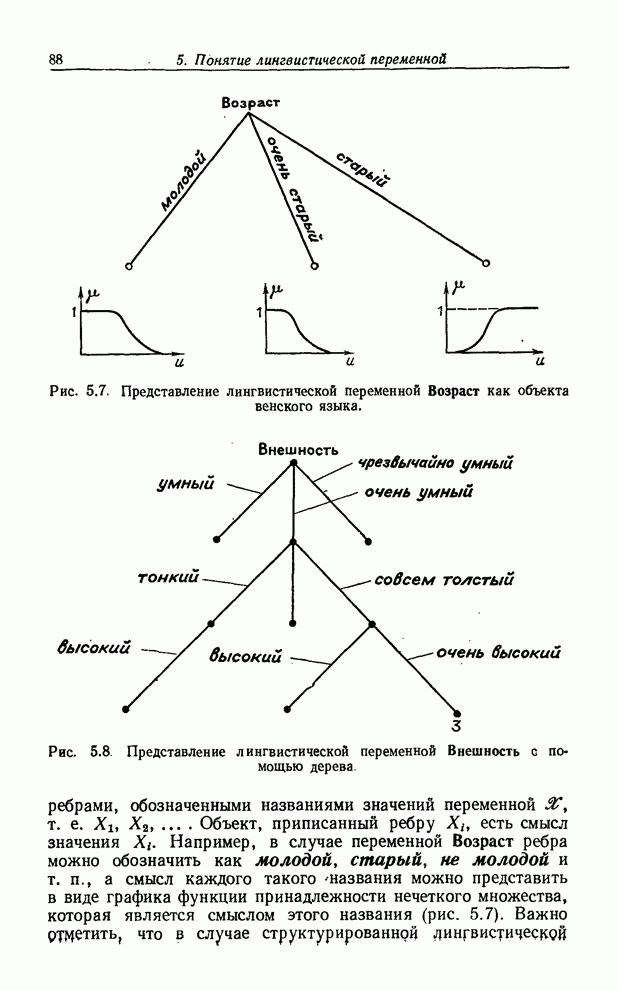
обозначает функцию принадлежности
множества ![]() ,
причем
,
причем ![]() .
Тогда из (7.30)
следует, что
.
Тогда из (7.30)
следует, что
![]() (7.32)
(7.32)
при ограничениях
![]() ,
(7.33)
,
(7.33)
![]() .
(7.34)
.
(7.34)
В этом случае вычисление ![]() сводится к решению задачи нелинейного
программирования с линейными ограничениями. Более точно эту задачу можно
сформулировать следующим образом: максимизировать
сводится к решению задачи нелинейного
программирования с линейными ограничениями. Более точно эту задачу можно
сформулировать следующим образом: максимизировать ![]() при следующих ограничениях (
при следующих ограничениях (![]() арифметическая
сумма):
арифметическая
сумма):
 (7.35)
(7.35)
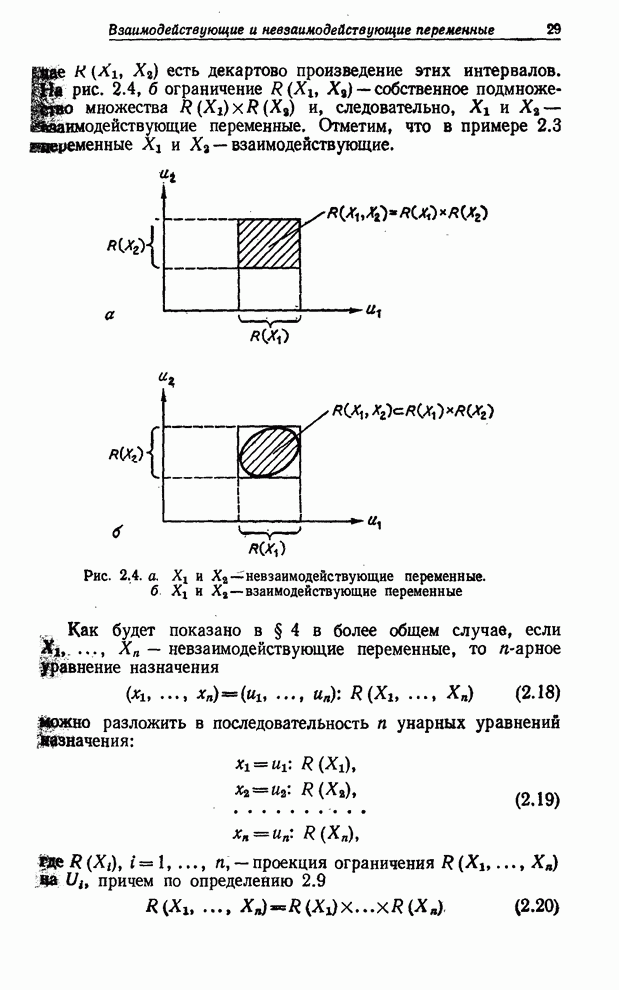
Пример 7.4. Проиллюстрируем изложенное следующим очень простым примером. Предположим, что
![]() ,
(7.36)
,
(7.36)
![]() , (7.37)
, (7.37)
где
 (7.38)
(7.38)
![]() .
(7.39)
.
(7.39)
тогда [см. (7.5)]
![]() . (7.40)
. (7.40)
Предположим, что мы хотим вычислить математическое ожидание (![]() арифметическая
сумма) вида
арифметическая
сумма) вида
![]() . (7.41)
. (7.41)
используя (7.23), получаем
![]() (7.42)
(7.42)
при ограничениях
![]() (7.43)
(7.43)
Теперь с учетом (7.40), если ![]() , имеем
, имеем
![]() , (7.44)
, (7.44)
и, следовательно, (7.42) сводится к
 (7.45)
(7.45)
или, в более явной форме,
 .
(7.46)
.
(7.46)
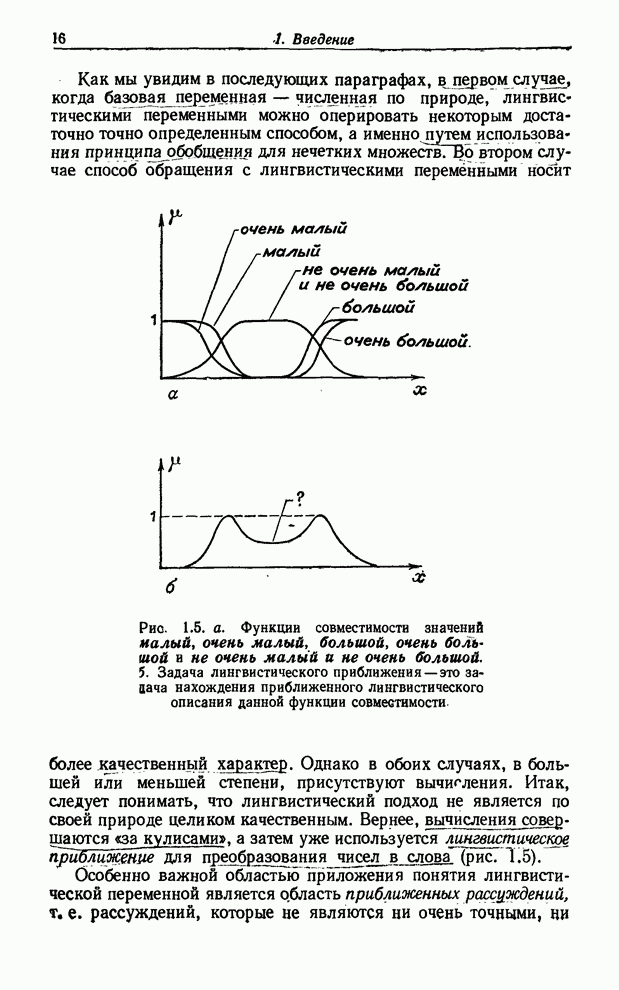
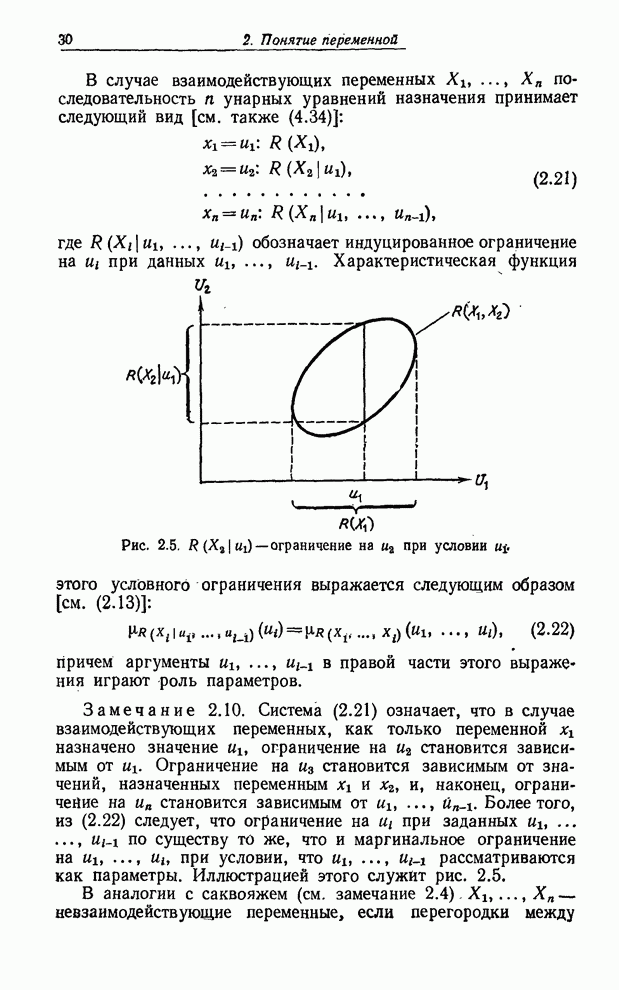
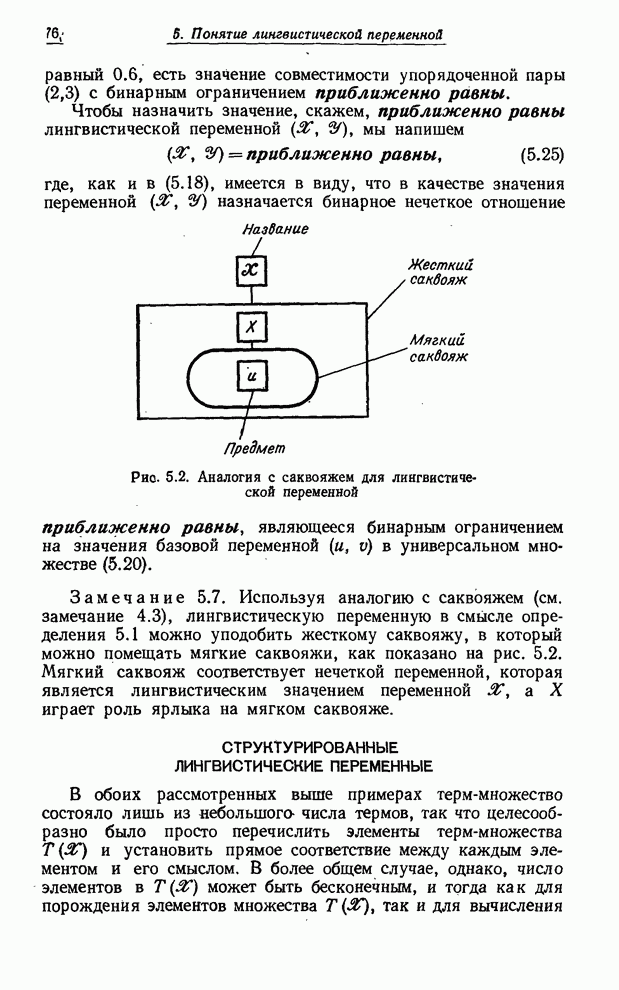
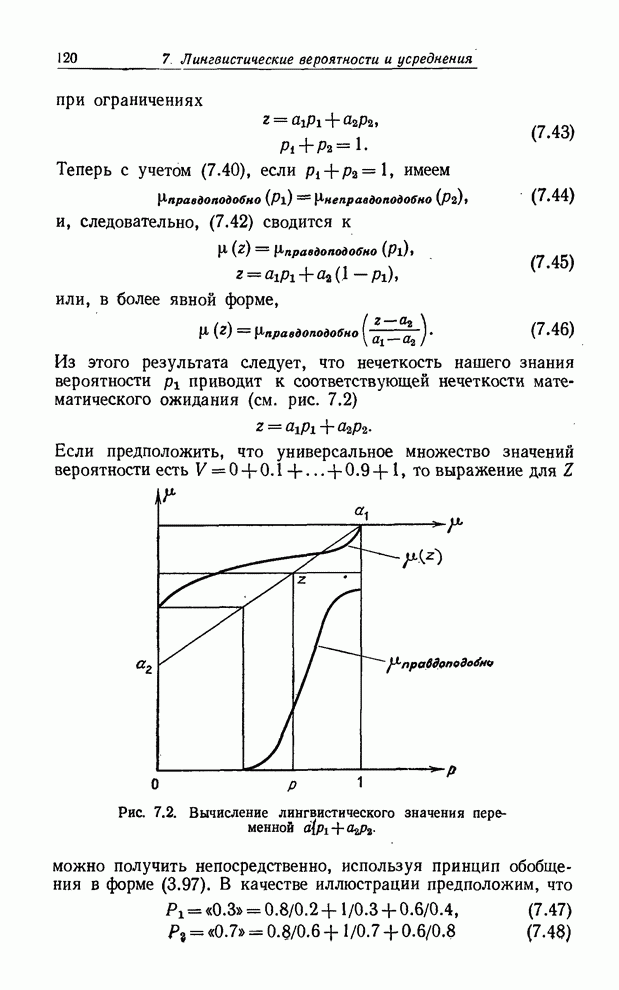
Из этого результата следует, что нечеткость нашего знания
вероятности ![]() приводит
к соответствующей нечеткости математического ожидания (см. рис. 7.2)
приводит
к соответствующей нечеткости математического ожидания (см. рис. 7.2)
![]() .
.

Рис. 7.2. Вычисление лингвистического
значения переменной ![]() .
.
Если предположить, что универсальное множество значений
вероятности есть, то есть выражение для ![]() можно получить
непосредственно, используя принцип обобщения в форме (3.97). В качестве
иллюстрации предположим, что
можно получить
непосредственно, используя принцип обобщения в форме (3.97). В качестве
иллюстрации предположим, что
![]() ,
(7.47)
,
(7.47)
![]() (7.48)
(7.48)
(![]() арифметическая сумма)
арифметическая сумма)
![]() , (7.49)
, (7.49)
где символ ![]() используется во избежание путаницы со
знаком объединения.
используется во избежание путаницы со
знаком объединения.
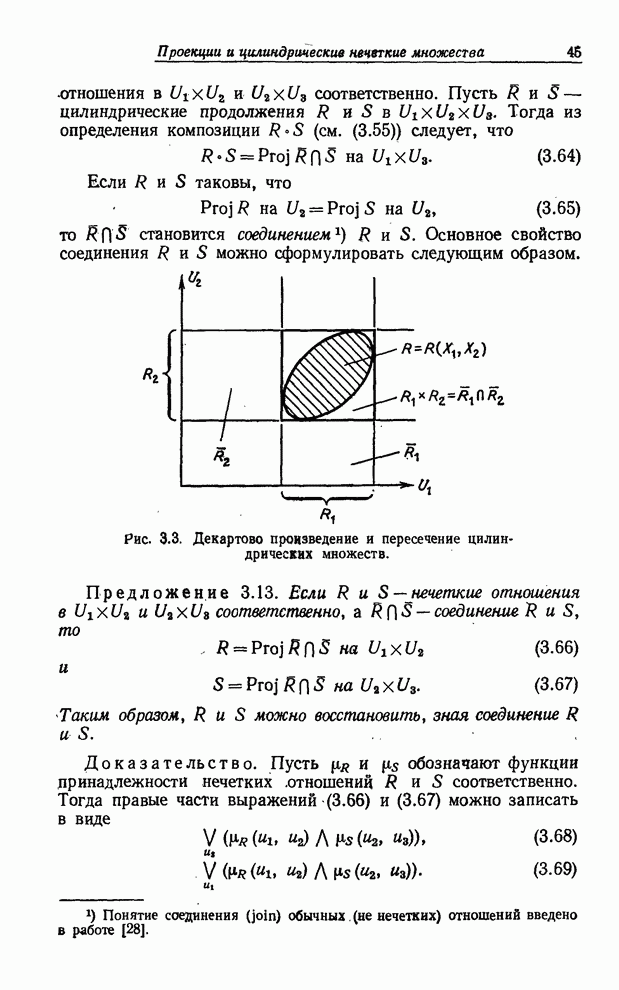
Подставляя (7.47) и (7.48) в (7.49), получаем
![]() (7.50)
(7.50)
Раскрывая скобки в правой части (7.50), следует иметь в виду
ограничение ![]() ,
которое означает, что член вида
,
которое означает, что член вида
![]() (7.51)
(7.51)
сводится к
 (7.52)
(7.52)
Таким образом, мы получаем
![]() , (7.53)
, (7.53)
т. е. выражение для ![]() как нечеткого подмножества
действительной оси
как нечеткого подмножества
действительной оси ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
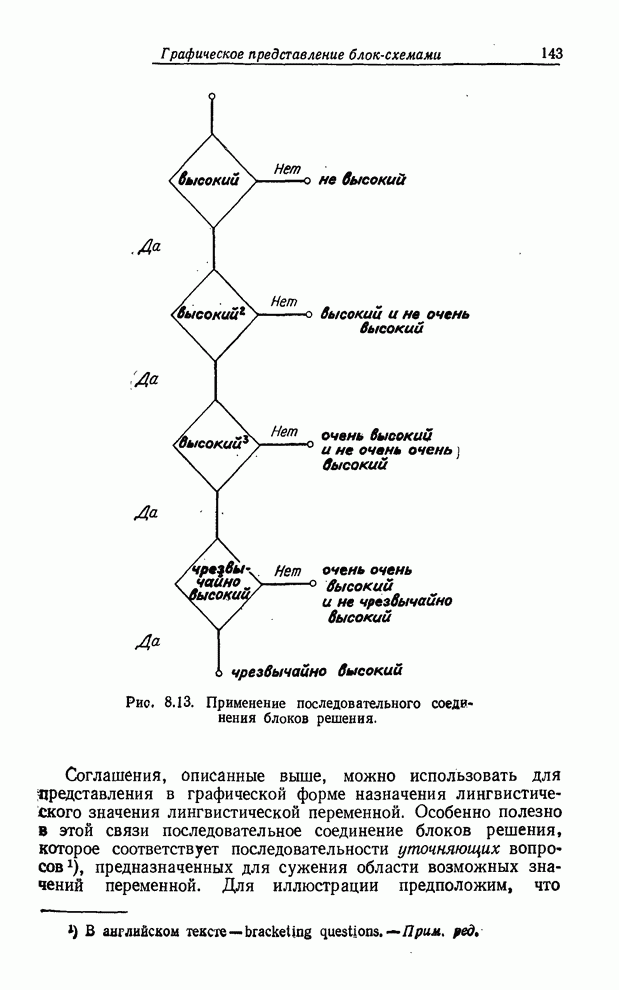
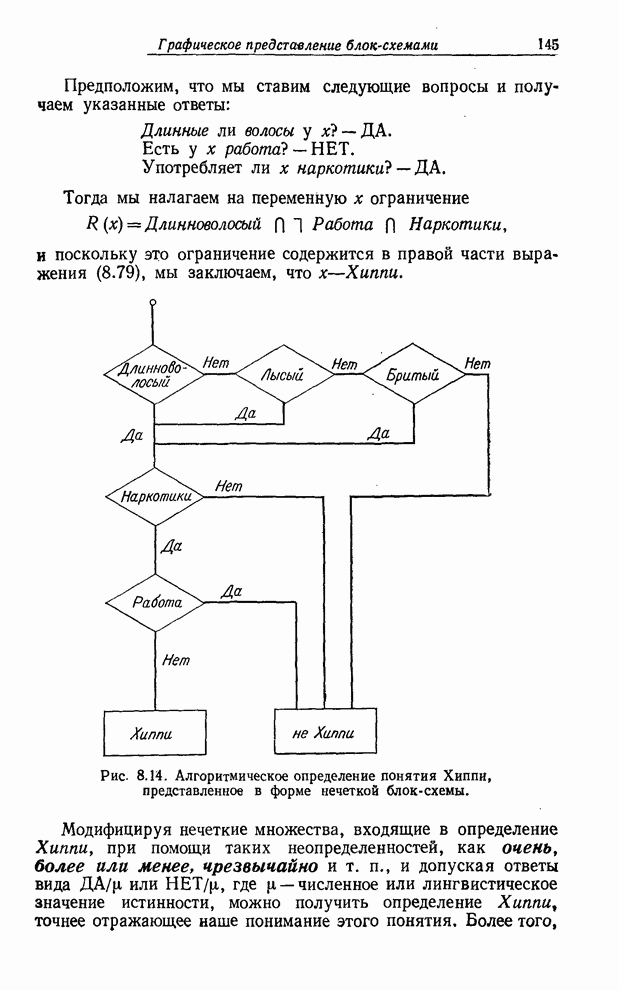
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ