| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
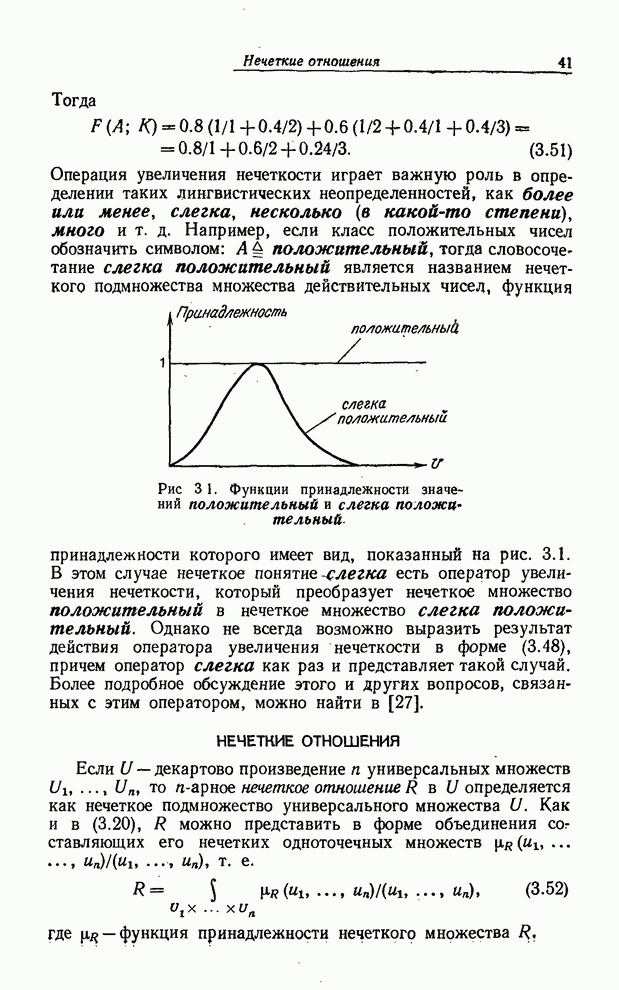
Правило modus ponens как частный случай композиционного правила вывода
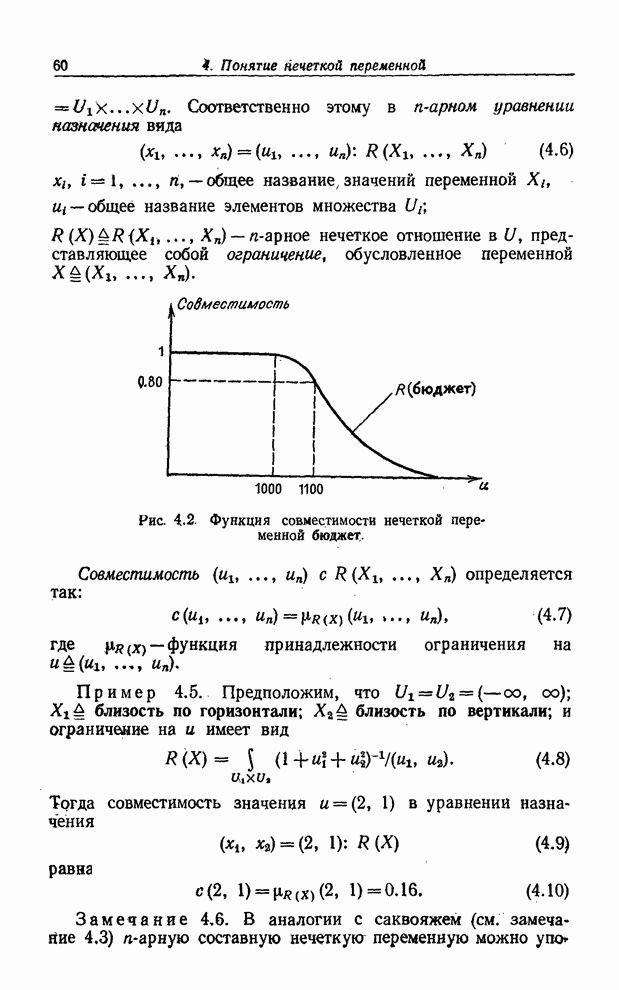
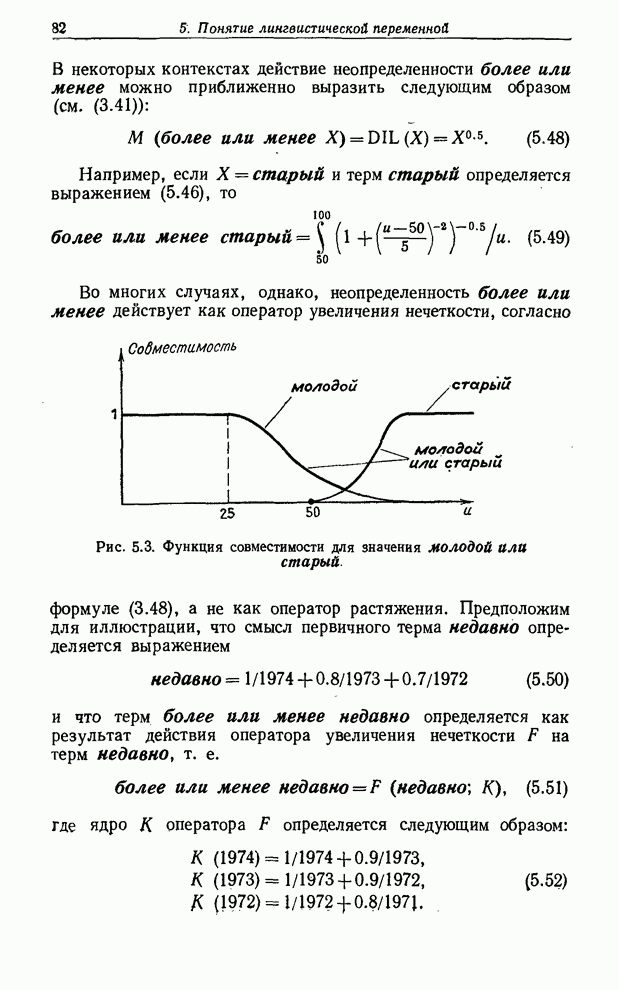
Как мы увидим ниже, правило modus ponens можно рассматривать как частный случай композиционного правила вывода. Чтобы установить эту связь, мы сначала обобщим понятие материальной импликации с пропозициональных переменных на нечеткие множества.
В
традиционной логике материальная импликация определяется как логическая связка
для пропозициональных переменных. Так, если ![]() и
и ![]() - пропозициональные переменные, то
таблица истинности для
- пропозициональные переменные, то
таблица истинности для ![]() , или, что эквивалентно, ЕСЛИ
, или, что эквивалентно, ЕСЛИ ![]() , ТО
, ТО ![]() , записывается в
таком виде (см. табл. 6.8):
, записывается в
таком виде (см. табл. 6.8):
Таблица 8.4
|
|
|
|
|
|
|
|
|
|
|
|
В
обычных рассуждениях, однако, выражение ЕСЛИ ![]() , ТО
, ТО ![]() употребляется в ситуациях, в которых
употребляется в ситуациях, в которых ![]() и
и ![]() - нечеткие множества
(или нечеткие предикаты), а не пропозициональные переменные. Например, в случае
высказывания ЕСЛИ Джон болен, ТО Джон капризен, которое можно сокращенно
записать как болен
- нечеткие множества
(или нечеткие предикаты), а не пропозициональные переменные. Например, в случае
высказывания ЕСЛИ Джон болен, ТО Джон капризен, которое можно сокращенно
записать как болен![]() капризен,
болен и капризен в сущности - названия нечетких множеств.
капризен,
болен и капризен в сущности - названия нечетких множеств.
То же самое справедливо по отношению к высказыванию ЕСЛИ яблоко красное, ТО яблоко спелое, где красное и спелое играют роль нечетких множеств.
Чтобы
обобщить понятие материальной импликации на нечеткие множества, предположим,
что ![]() и
и ![]() - два возможно
различных универсальных множества, а
- два возможно
различных универсальных множества, а ![]() ,
, ![]() и
и ![]() - нечеткие подмножества
- нечеткие подмножества ![]() ,
, ![]() и
и ![]() соответственно. Сначала
определим смысл высказывания ЕСЛИ
соответственно. Сначала
определим смысл высказывания ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() и затем определим ЕСЛИ
и затем определим ЕСЛИ ![]() , ТО
, ТО ![]() как частный случай
высказывания ЕСЛИ
как частный случай
высказывания ЕСЛИ ![]() ,
ТО
,
ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() .
.
Определение
8.3. Высказывание ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() есть бинарное нечеткое отношение в
есть бинарное нечеткое отношение в ![]() , определяемое
следующим образом:
, определяемое
следующим образом:
ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() . (8.23)
. (8.23)
То
есть если ![]() ,
,
![]() и
и ![]() - унарные нечеткие
отношения в
- унарные нечеткие
отношения в ![]() ,
,
![]() и
и ![]() , тогда ЕСЛИ
, тогда ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() - бинарное нечеткое
отношение в
- бинарное нечеткое
отношение в ![]() ,
которое является объединением декартова произведения
,
которое является объединением декартова произведения ![]() и
и ![]() (см. (3.45)) и декартова
произведения отрицания
(см. (3.45)) и декартова
произведения отрицания ![]() и
и ![]() .
.
Далее
высказывание ЕСЛИ ![]() ,
ТО
,
ТО ![]() можно
рассматривать как частный случай высказывания ЕСЛИ
можно
рассматривать как частный случай высказывания ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() при допущении, что
при допущении, что ![]() - полное множество
- полное множество ![]() . Таким образом,
. Таким образом,
ЕСЛИ ![]() , ТО
, ТО ![]() ЕСЛИ
ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() . (8.24)
. (8.24)
В
сущности это равнозначно интерпретации высказывания ЕСЛИ ![]() , ТО
, ТО ![]() высказыванием ЕСЛИ
высказыванием ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ безразлично.
, ИНАЧЕ безразлично.
Полезно
заметить, что в терминах матриц отношения ![]() ,
, ![]() и
и ![]() равенство (8.23) можно выразить как
сумму попарных произведений, содержащих
равенство (8.23) можно выразить как
сумму попарных произведений, содержащих ![]() и
и ![]() (и
(и ![]() и
и ![]() )в виде вектор-столбца и вектор-строки
соответственно. Так,
)в виде вектор-столбца и вектор-строки
соответственно. Так,
ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() . (8.25)
. (8.25)
Пример 8.4. Проиллюстрируем (8.23) и (8.24) следующим примером. Предположим, что
![]() , (8.26)
, (8.26)
![]() , (8.27)
, (8.27)
![]() , (8.28)
, (8.28)
![]() . (8.29)
. (8.29)
Тогда
 , (8.30)
, (8.30)
что можно представить в виде матрицы отношения
ЕСЛИ ![]() , ТО
, ТО ![]() , ИНАЧЕ
, ИНАЧЕ  . (8.31)
. (8.31)
Аналогично

или, эквивалентно,
ЕСЛИ ![]() , ТО
, ТО  . (8.32)
. (8.32)
Замечание
8.5. Следует отметить, что в определении высказывания ЕСЛИ ![]() , ТО
, ТО ![]() мы неявно предполагали, что
мы неявно предполагали, что ![]() и
и ![]() -
невзаимодействующие в том смысле, что не существует ограничения, содержащего
одновременно базовые переменные
-
невзаимодействующие в том смысле, что не существует ограничения, содержащего
одновременно базовые переменные ![]() и
и ![]() . Этого не будет в случае обычного (не
нечеткого) высказывания ЕСЛИ
. Этого не будет в случае обычного (не
нечеткого) высказывания ЕСЛИ ![]() , ТО
, ТО ![]() , которое можно выразить как ЕСЛИ
, которое можно выразить как ЕСЛИ ![]() , ТО
, ТО ![]() при выполнении
ограничения
при выполнении
ограничения ![]() .
Если обозначить это ограничение через
.
Если обозначить это ограничение через ![]() , отношение, представляющее
рассматриваемое высказывание, будет иметь вид
, отношение, представляющее
рассматриваемое высказывание, будет иметь вид
ЕСЛИ ![]() , ТО
, ТО ![]() . (8.33)
. (8.33)
Замечание
8.6. В определении отношения ![]() мы полагали, что ЕСЛИ
мы полагали, что ЕСЛИ ![]() , ТО
, ТО ![]() есть частный случай
высказывания ЕСЛИ
есть частный случай
высказывания ЕСЛИ ![]() ,
ТО
,
ТО ![]() , ИНАЧЕ
, ИНАЧЕ ![]() при
при ![]() . Если мы положим
. Если мы положим ![]() равным
равным ![]() (пустое множество),
а не
(пустое множество),
а не ![]() , то
правая часть (8.23) сведется к декартову произведению
, то
правая часть (8.23) сведется к декартову произведению ![]() , которое можно
интерпретировать как
, которое можно
интерпретировать как ![]() СПАРЕННОЕ С
СПАРЕННОЕ С ![]() (а не
(а не ![]() ВЛЕЧЕТ
ВЛЕЧЕТ ![]() ).
).
Так, по определению
![]() СПАРЕННОЕ С
СПАРЕННОЕ С ![]() (8.34)
(8.34)
и, следовательно,
![]() СПАРЕННОЕ С
СПАРЕННОЕ С ![]() плюс
плюс ![]() СПАРЕННОЕ С
СПАРЕННОЕ С ![]() (8.35)
(8.35)
В общем случае выражение вида
![]() (8.36)
(8.36)
описывается словами следующим образом:
![]() СПАРЕННОЕ С
СПАРЕННОЕ С ![]() , плюс ... плюс
, плюс ... плюс ![]() СПАРЕННОЕ С
СПАРЕННОЕ С ![]() . (8.37)
. (8.37)
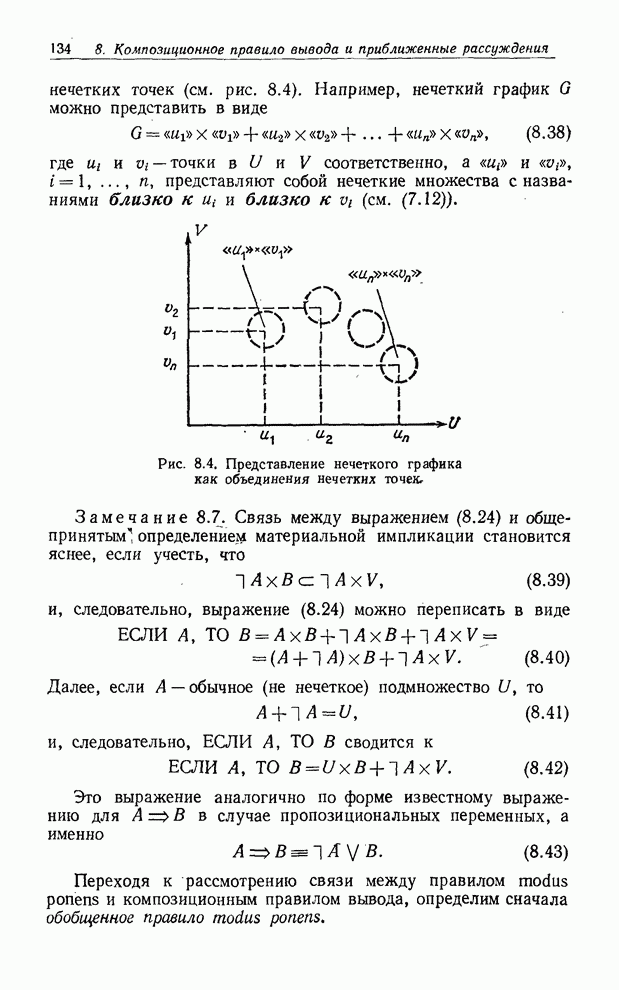
Следует
заметить, что выражение типа (8.37) можно использовать для представления
нечеткого графика как объединения нечетких точек (см. рис. 8.4). Например,
нечеткий график ![]() можно
представить в виде
можно
представить в виде
![]() , (8.38)
, (8.38)
где
![]() и
и ![]() - точки в
- точки в ![]() и
и ![]() соответственно, а «
соответственно, а «![]() » и «
» и «![]() »,
», ![]() , представляют собой
нечеткие множества с названиями близко к
, представляют собой
нечеткие множества с названиями близко к ![]() и близко к
и близко к ![]() (см. (7.12)).
(см. (7.12)).

Рис. 8.4. Представление нечеткого графика как объединения нечетких точек.
Замечание 8.7. Связь между выражением (8.24) и общепринятым определением материальной импликации становится яснее, если учесть, что
![]() , (8.39)
, (8.39)
и, следовательно, выражение (8.24) можно переписать в виде
ЕСЛИ ![]() , ТО
, ТО ![]() . (8.40)
. (8.40)
Далее,
если ![]() -
обычное (не нечеткое) подмножество
-
обычное (не нечеткое) подмножество ![]() , то
, то
![]() , (8.41)
, (8.41)
и,
следовательно, ЕСЛИ ![]() , ТО
, ТО ![]() сводится к
сводится к
ЕСЛИ ![]() , ТО
, ТО ![]() . (8.42)
. (8.42)
Это
выражение аналогично по форме известному выражению для ![]() в случае пропозициональных
переменных, а именно
в случае пропозициональных
переменных, а именно
![]() . (8.43)
. (8.43)
Переходя к рассмотрению связи между правилом modus ponens и композиционным правилом вывода, определим сначала обобщенное правило modus ponens.
Определение
8.8. Пусть ![]() ,
,
![]() и
и ![]() - нечеткие
подмножества множеств
- нечеткие
подмножества множеств ![]() ,
, ![]() и
и ![]() соответственно. Предположим, что
значение
соответственно. Предположим, что
значение ![]() назначено
ограничению
назначено
ограничению ![]() ,
а отношение
,
а отношение ![]() (определенное
по формуле (8.24)) назначено ограничению
(определенное
по формуле (8.24)) назначено ограничению ![]() , т. е.
, т. е.
![]() , (8.44)
, (8.44)
![]() . (8.45)
. (8.45)
Как
было показано раньше, эти уравнения назначения в отношениях можно разрешить
относительно ограничения на ![]() следующим образом:
следующим образом:
![]() . (8.46)
. (8.46)
Выражение этого вывода в форме

и составляет формулировку обобщенного правила modus ponens.
Замечание
8.9. Приведенная формулировка отличается от традиционной формулировки правила
modus ponens в двух отношениях: во-первых, здесь допускается, что ![]() ,
, ![]() и
и ![]() - нечеткие множества, и,
во-вторых,
- нечеткие множества, и,
во-вторых, ![]() необязательно
идентично
необязательно
идентично ![]() .
Чтобы рассмотреть случай, когда
.
Чтобы рассмотреть случай, когда ![]() и
и ![]() - не нечеткое множество, подставим
выражение для
- не нечеткое множество, подставим
выражение для ![]() в
уравнение (8.46). В результате получим
в
уравнение (8.46). В результате получим
![]() , (8.50)
, (8.50)
где
вместо обозначений строка и столбец употребляются обозначения ![]() и
и ![]() соответственно;
соответственно; ![]() и
и ![]() обозначают матрицы
отношения для
обозначают матрицы
отношения для ![]() ,
имеющие вид вектор-строки и вектор-столбца соответственно; произведение матриц
понимается как максминное произведение.
,
имеющие вид вектор-строки и вектор-столбца соответственно; произведение матриц
понимается как максминное произведение.
Далее,
поскольку ![]() -
обычное (не нечеткое) множество, то
-
обычное (не нечеткое) множество, то
![]() , (8.51)
, (8.51)
и
поскольку ![]() -
нормальное множество (см. (3.23)),
-
нормальное множество (см. (3.23)),
![]() . (8.52)
. (8.52)
Следовательно,
![]() , (8.53)
, (8.53)
что находится в соответствии с выводом, который получается по правилу modus ponens.
Пример 8.10. Проиллюстрируем (8.49) простым примером. Предположим, что
![]() , (8.54)
, (8.54)
![]() , (8.55)
, (8.55)
![]() , (8.56)
, (8.56)
![]() . (8.57)
. (8.57)
Тогда (см. (2.32))
 (8.58)
(8.58)
и
 (8.59)
(8.59)
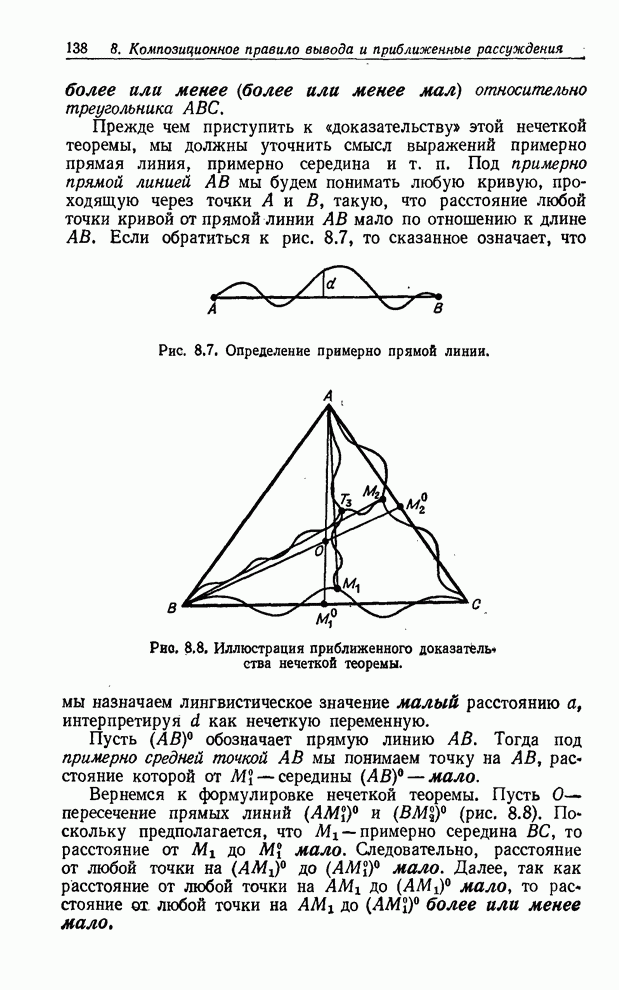
грубым приближением которого может быть более или менее большой. Таким образом, в рассматриваемом случае обобщенное правило modus ponens дает
 (8.60)
(8.60)
Замечание
8.11. Вследствие определения ![]() в виде
в виде
![]()
степень
принадлежности точки ![]() нечеткому множеству
нечеткому множеству ![]() будет высокой, если мала
степень принадлежности
будет высокой, если мала
степень принадлежности ![]() множеству
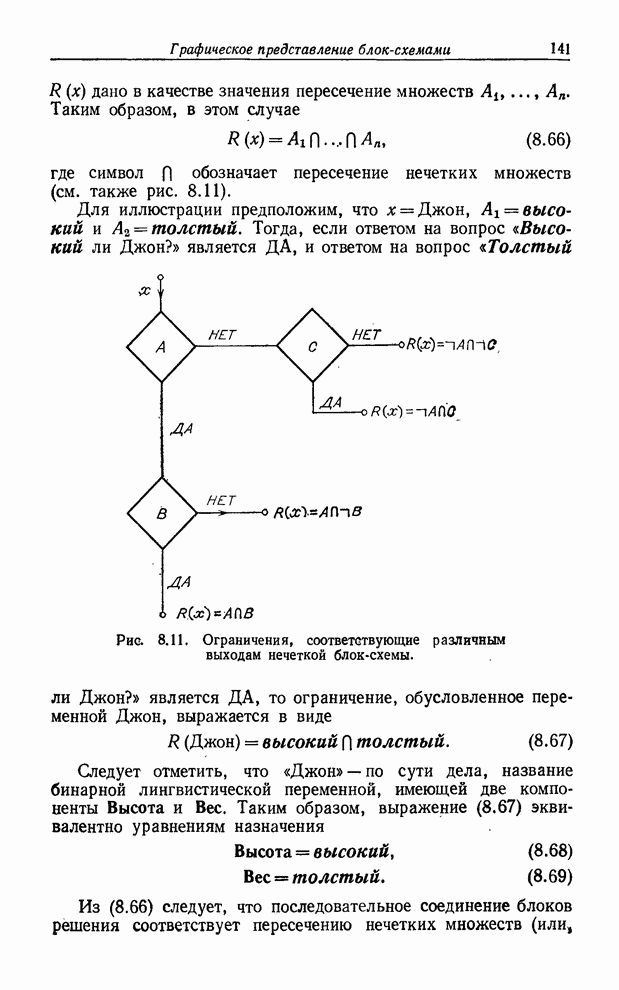
множеству ![]() . Это приводит к тому, что если
. Это приводит к тому, что если ![]() - нечеткое
множество, то множества
- нечеткое
множество, то множества ![]() и
и ![]() перекрываются, причем вывод из
предпосылок
перекрываются, причем вывод из
предпосылок ![]() и
и
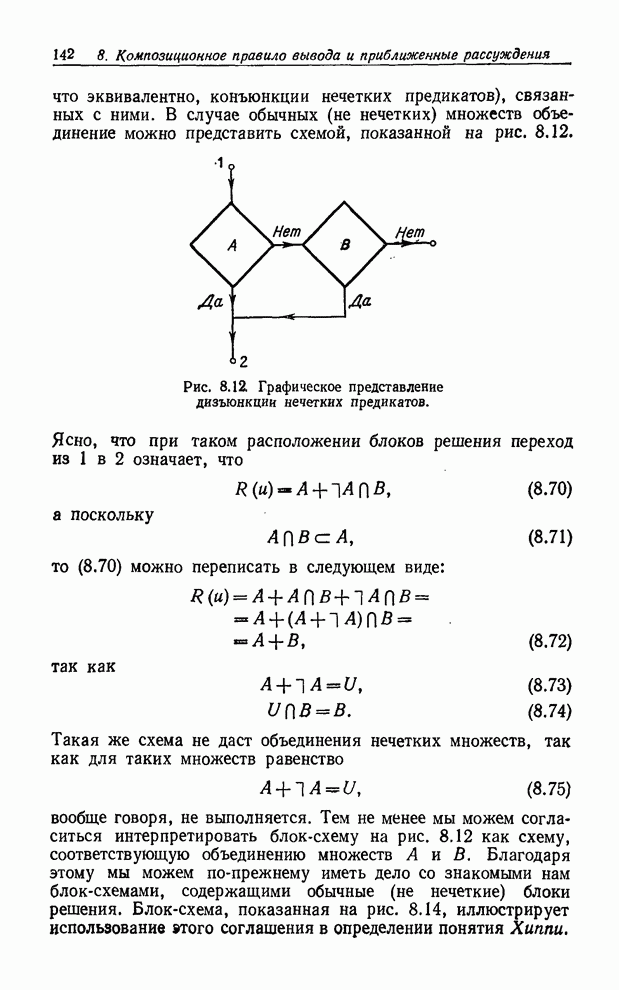
![]() есть не
есть не ![]() , а
, а
![]() , (8.61)
, (8.61)
где
член ![]() появляется
в связи с этим перекрытием.
появляется
в связи с этим перекрытием.
Чтобы
избежать этого явления, возможно придется определить ![]() способом, при котором
различаются численные значения истинности из интервала
способом, при котором
различаются численные значения истинности из интервала ![]() и такое значение истинности,
как неизвестно (см. (6.52)). Следует отметить также, что для высказывания
и такое значение истинности,
как неизвестно (см. (6.52)). Следует отметить также, что для высказывания ![]() СПАРЕННЫЙ С
СПАРЕННЫЙ С ![]() (см. 8.34)), мы
имеем
(см. 8.34)), мы
имеем
![]() , (8.62)
, (8.62)
если
![]() -
нормальное нечеткое множество.
-
нормальное нечеткое множество.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ