| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
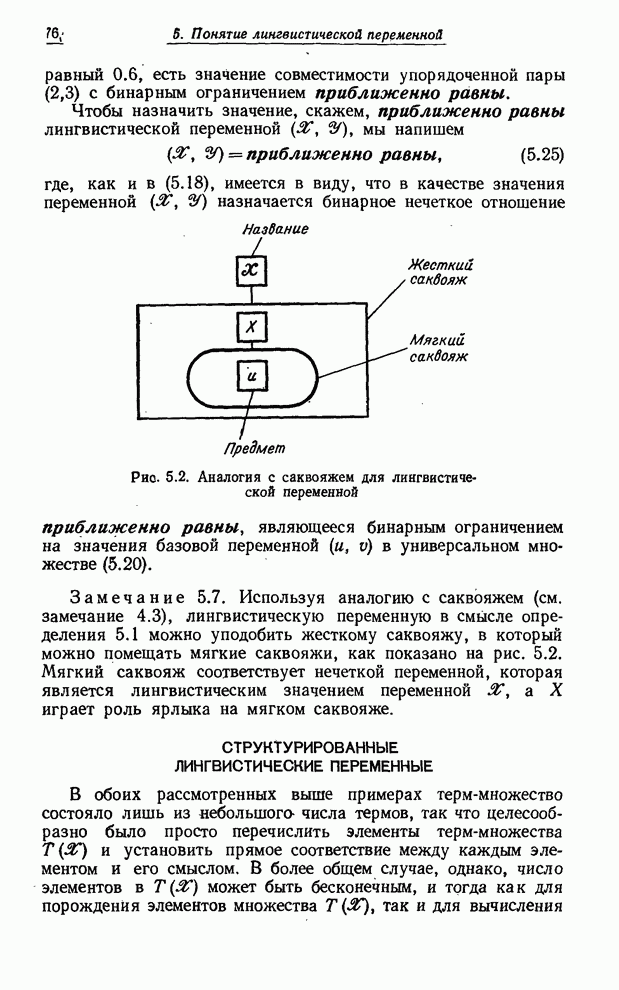
СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
В
обоих рассмотренных выше примерах терм-множество состояло лишь из небольшого
числа термов, так что целесообразно было просто перечислить элементы
терм-множества ![]() и
установить прямое соответствие между каждым элементом и его смыслом, В более
общем случае, однако, число элементов в
и
установить прямое соответствие между каждым элементом и его смыслом, В более
общем случае, однако, число элементов в ![]() может быть бесконечным, и тогда как для
порождения элементов множества
может быть бесконечным, и тогда как для
порождения элементов множества ![]() , так и для вычисления их смысла
необходимо применять алгоритм, а не просто процедуру просмотра элементов
терм-множества.
, так и для вычисления их смысла
необходимо применять алгоритм, а не просто процедуру просмотра элементов
терм-множества.
Будем
говорить, что лингвистическая переменная ![]() структурирована, если
ее терм-множество
структурирована, если
ее терм-множество ![]() и
функцию
и
функцию ![]() ,
которая ставит в соответствие каждому элементу терм- множества его смысл, можно
задать алгоритмически. Из этих соображений синтаксическое и семантическое
правила, связанные со структурированной лингвистической переменной, можно
рассматривать как алгоритмические процедуры для порождения элементов множества
,
которая ставит в соответствие каждому элементу терм- множества его смысл, можно
задать алгоритмически. Из этих соображений синтаксическое и семантическое
правила, связанные со структурированной лингвистической переменной, можно
рассматривать как алгоритмические процедуры для порождения элементов множества ![]() и вычисления смысла
каждого терма в
и вычисления смысла
каждого терма в ![]() соответственно.
В дальнейшем, если не оговорено противное, будем считать, что рассматриваемые
лингвистические переменные являются структурированными.
соответственно.
В дальнейшем, если не оговорено противное, будем считать, что рассматриваемые
лингвистические переменные являются структурированными.
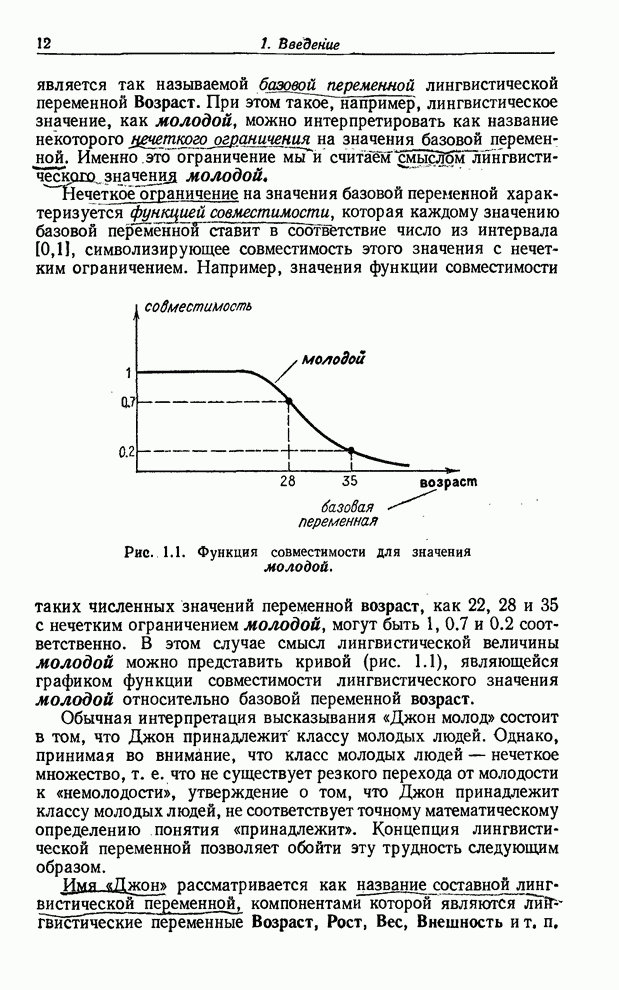
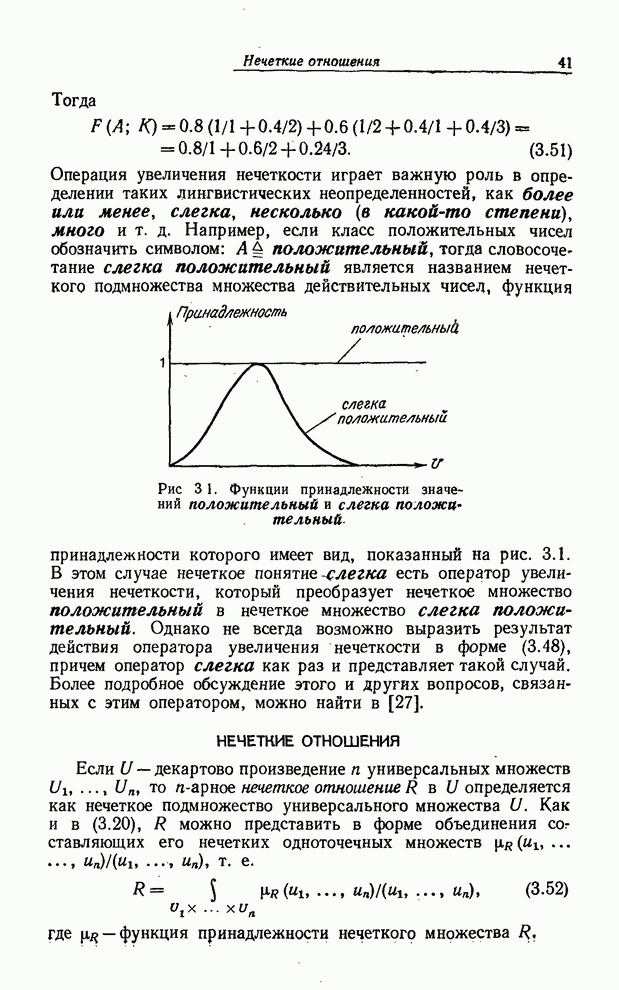
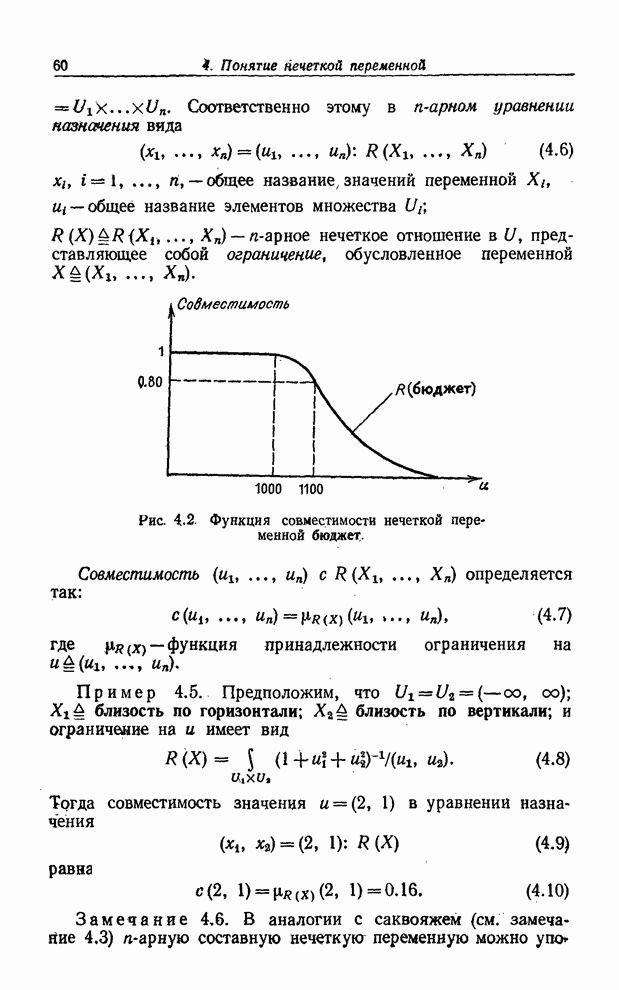
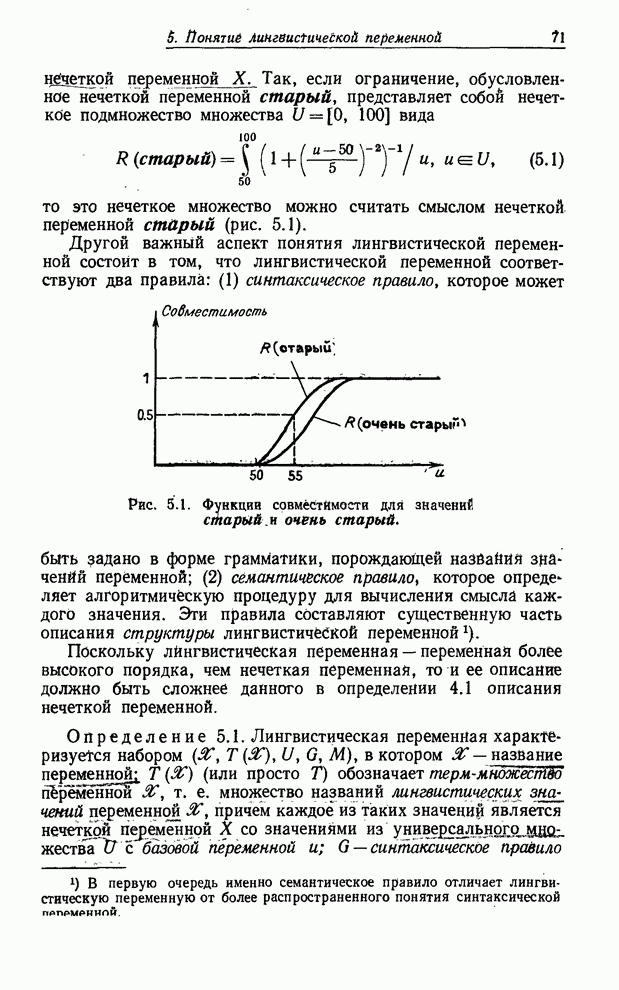
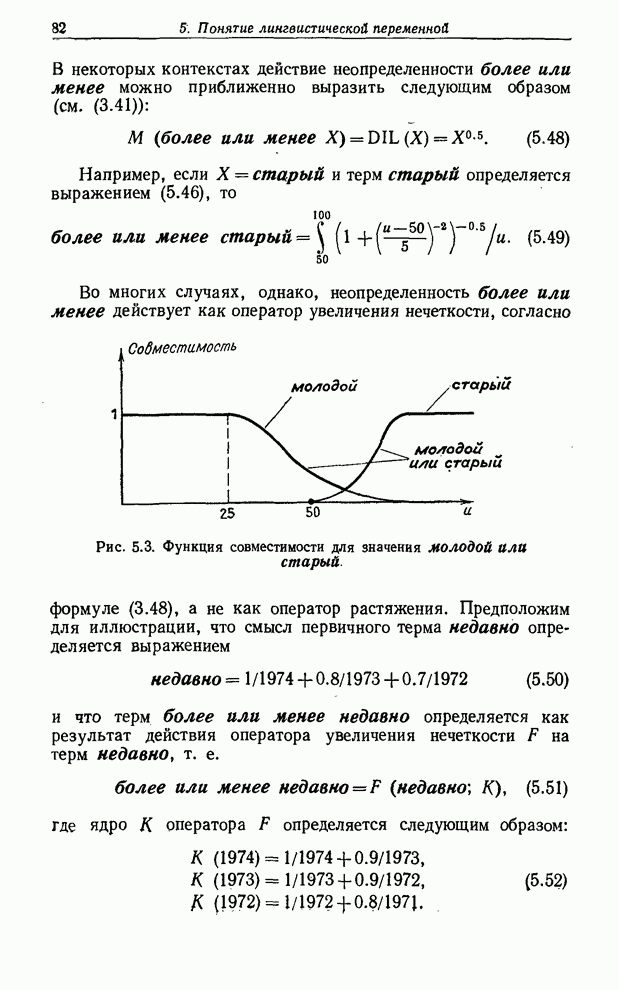
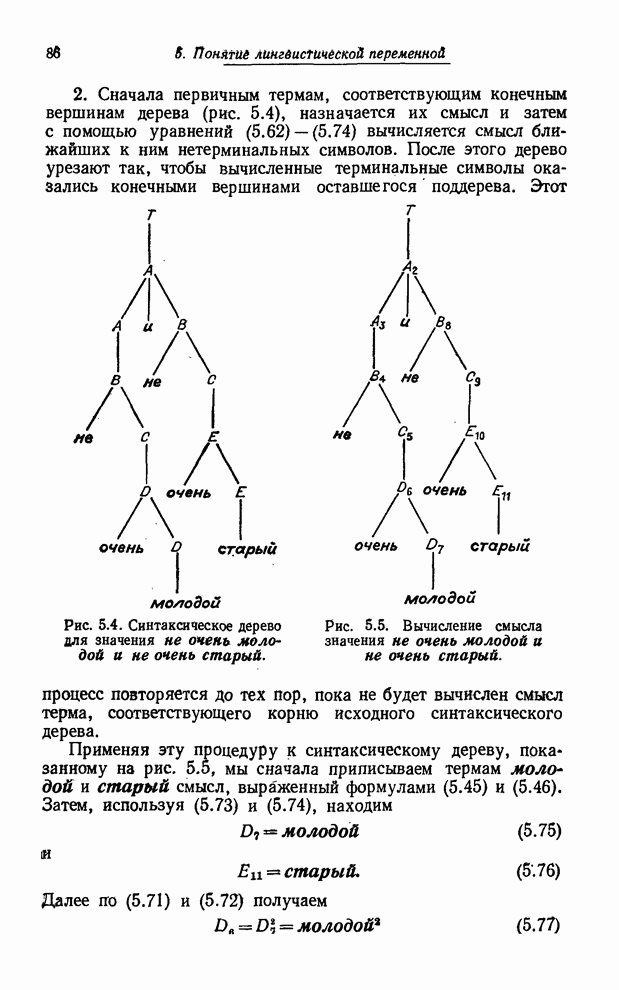
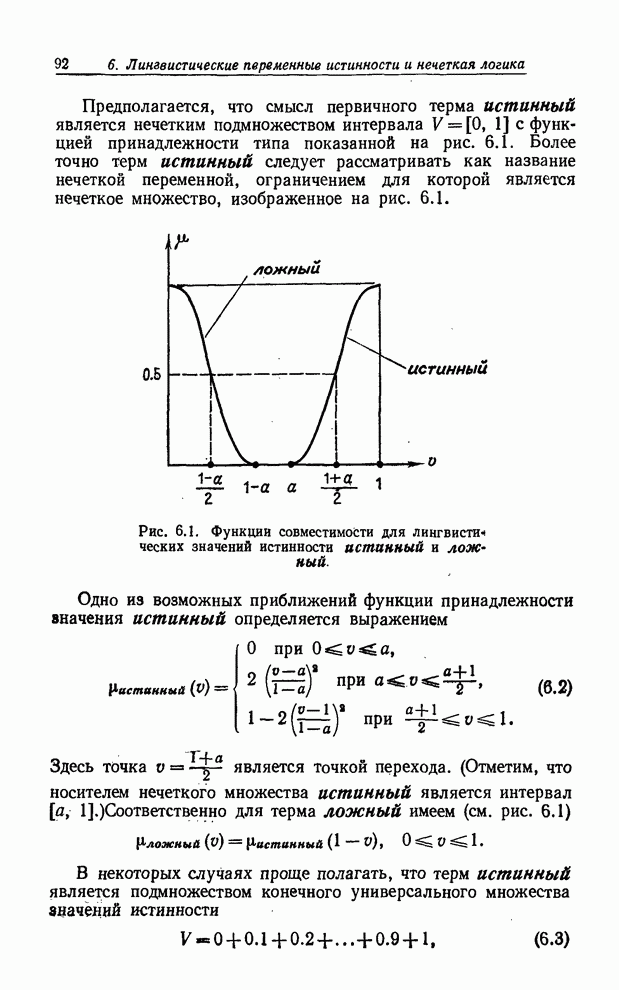
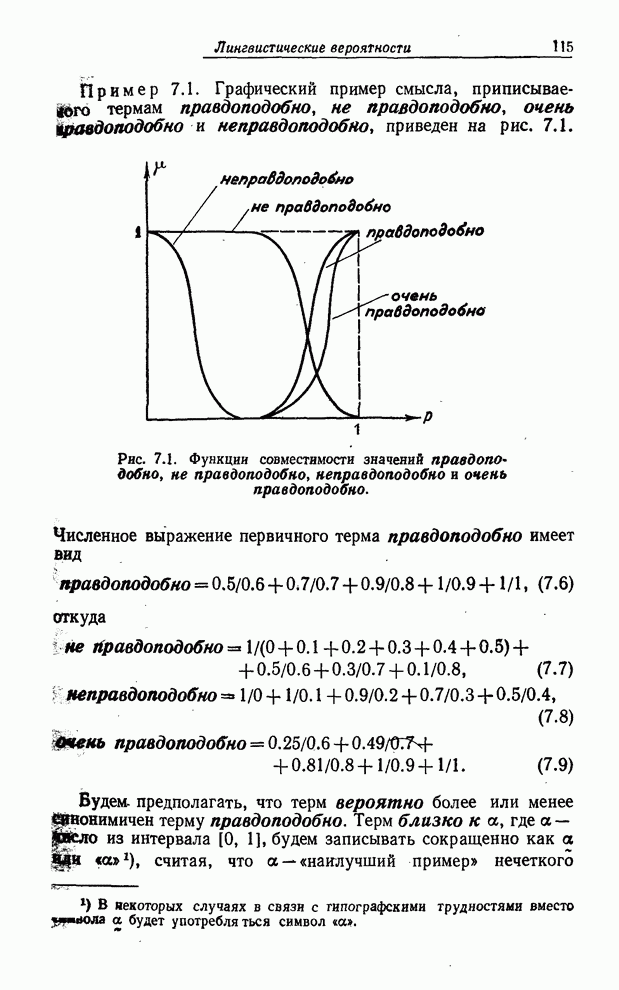
Пример 5.8. В качестве очень простой иллюстрации той роли, которую играют синтаксическое и семантическое правила в случае структурированной лингвистической переменной, рассмотрим переменную Возраст, элементами терм-множества которой являются термы типа старый, очень старый, очень очень старый, очень очень очень старый и т. п. Таким образом, терм-множество переменной Возраст можно записать в виде
 (5.26)
(5.26)
В
этом простом случае легко проверить, что каждый терм множества ![]() имеет вид старый
или очень очень … очень. Чтобы вывести это правило в более общем виде,
поступим следующим образом.
имеет вид старый
или очень очень … очень. Чтобы вывести это правило в более общем виде,
поступим следующим образом.
Пусть
![]() обозначает
конкатенацию символьных цепочек
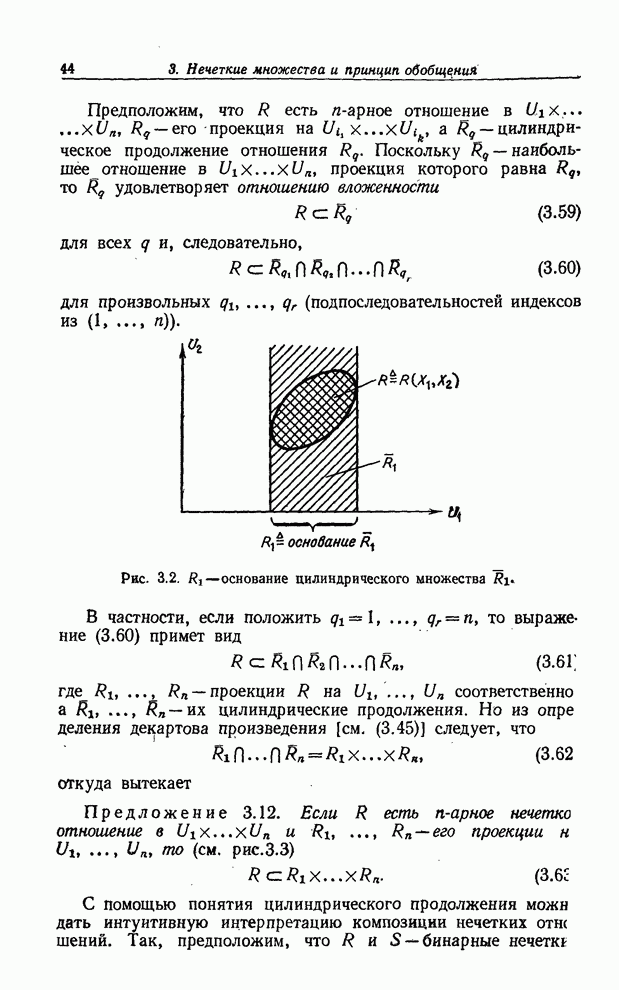
обозначает
конкатенацию символьных цепочек ![]() и
и ![]() , например,
, например, ![]() ,
, ![]() ,
, ![]() . Если
. Если ![]() и
и ![]() — множества цепочек, например
— множества цепочек, например
![]() , (5.27)
, (5.27)
![]() , (5.28)
, (5.28)
где
![]() и
и ![]() — символьные
цепочки, то конкатенация
— символьные
цепочки, то конкатенация![]() и
и ![]() обозначается
обозначается ![]() и определяется как
множество цепочек вида
и определяется как
множество цепочек вида
![]() . (5.29)
. (5.29)
Например,
если ![]() и
и ![]() , то
, то
![]() (5.30)
(5.30)
Используя
эти обозначения, данное представление для ![]() можно рассматривать как решение
уравнения
можно рассматривать как решение
уравнения
![]() , (5.31)
, (5.31)
которое
означает, что множество ![]() состоит из терма старый
и термов, состоящих из слова очень и некоторого терма из
состоит из терма старый
и термов, состоящих из слова очень и некоторого терма из ![]() .
.
Уравнение (5.31) можно решать итеративным способом, используя рекуррентное соотношение
![]() (5.32)
(5.32)
и
взяв пустое множество ![]() в качестве начального
значения
в качестве начального
значения ![]() . Тогда
. Тогда
 (5.33)
(5.33)
и решение уравнения (5.31) имеет вид
 (5.34)
(5.34)
Для рассматриваемого примера синтаксическое правило выражается уравнением (5.31) и его решением (5.34). Эквивалентным образом синтаксическое правило можно охарактеризовать следующей системой подстановок:
![]() , (5.35)
, (5.35)
![]() (5.36)
(5.36)
для
которой (5.31) играет роль алгебраического представления. В этом случае терм в ![]() может
быть порожден при помощи стандартной процедуры ([36], [37]), включающей в себя
последовательное применение правил (5.35) и (5.36), начиная с символа
может
быть порожден при помощи стандартной процедуры ([36], [37]), включающей в себя
последовательное применение правил (5.35) и (5.36), начиная с символа ![]() . Таким образом, если
. Таким образом, если
![]() заменить
на
заменить
на ![]() и
затем
и
затем ![]() в
в ![]() заменить на
заменить на ![]() , мы получаем терм
очень старый. Аналогично терм очень очень очень старый
можно получить из
, мы получаем терм
очень старый. Аналогично терм очень очень очень старый
можно получить из ![]() по
следующей цепочке подстановок:
по
следующей цепочке подстановок:
![]() (5.37)
(5.37)
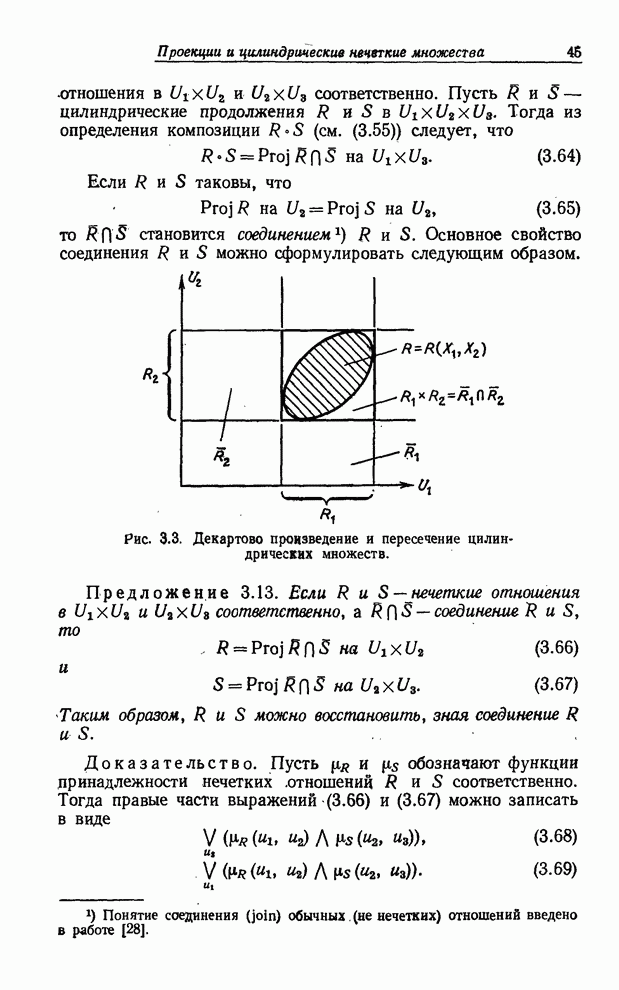
Возвращаясь
к семантическому правилу для переменной Возраст, отметим, что
для вычисления смысла такого терма, как очень…очень старый
требуется знать смысл терма старый и модификатора очень.
Терм старый играет роль первичного терма, т. е. терма, смысл
которого должен быть задан заранее с тем, чтобы можно было вычислять смысл
составных термов в ![]() .
Что касается модификатора очень, то он действует как лингвистическая
неопределенность, т. е. как модификатор смысла следующего за ним терма.
Если в качестве очень простого приближения мы предположим, что модификатор очень
действует как оператор концентрирования (см. (3.40)), то
.
Что касается модификатора очень, то он действует как лингвистическая
неопределенность, т. е. как модификатор смысла следующего за ним терма.
Если в качестве очень простого приближения мы предположим, что модификатор очень
действует как оператор концентрирования (см. (3.40)), то
![]() . (5.58)
. (5.58)
Следовательно, семантическое правило для переменной Возраст можно записать в виде
![]() , (5.39)
, (5.39)
где
![]() — число
вхождений слова очень в терм очень…очень старый,
— число
вхождений слова очень в терм очень…очень старый,
![]() — смысл
терма очень…очень старый. Далее, если определить первичный
терм старый по формуле
— смысл
терма очень…очень старый. Далее, если определить первичный
терм старый по формуле
 , (5.40)
, (5.40)
то получим
 (5.41)
(5.41)
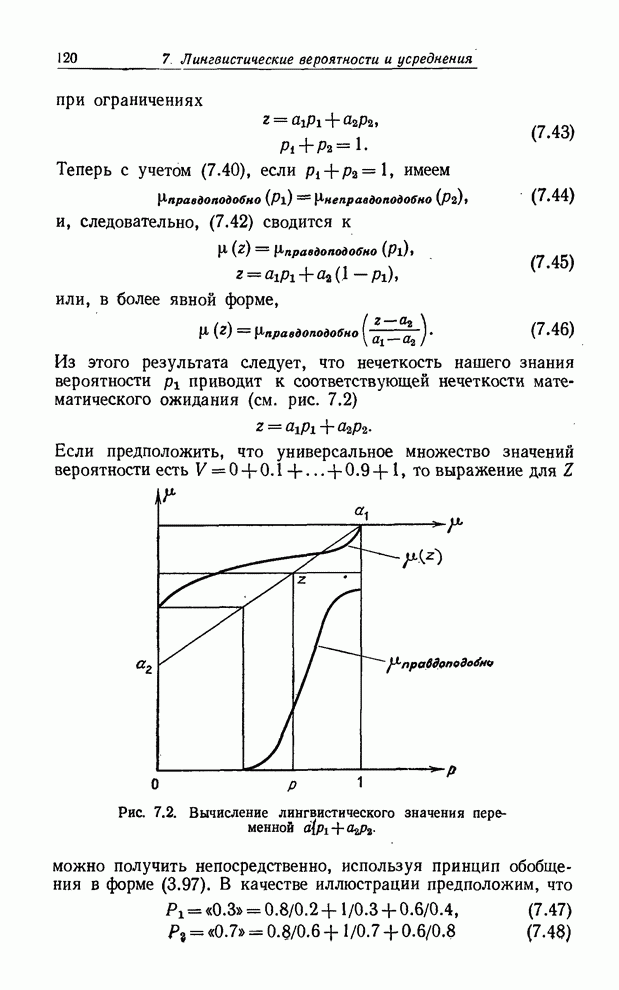
Это уравнение выражает в явном виде семантическое правило для вычисления смысла составных термов, образованных по формуле (5.31), если известны смысл первичного терма старый и смысл неопределенности очень.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
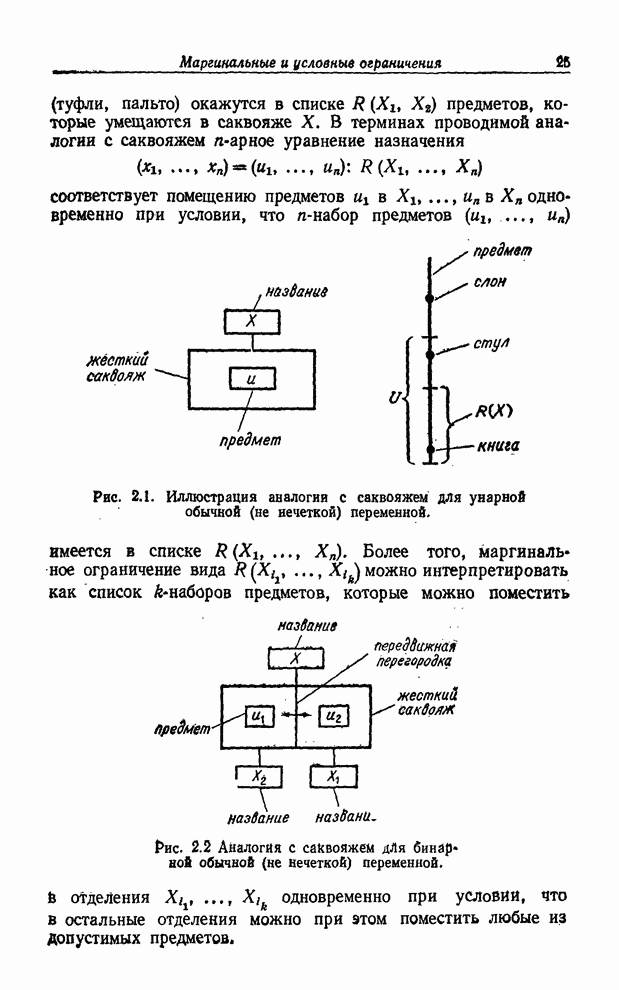
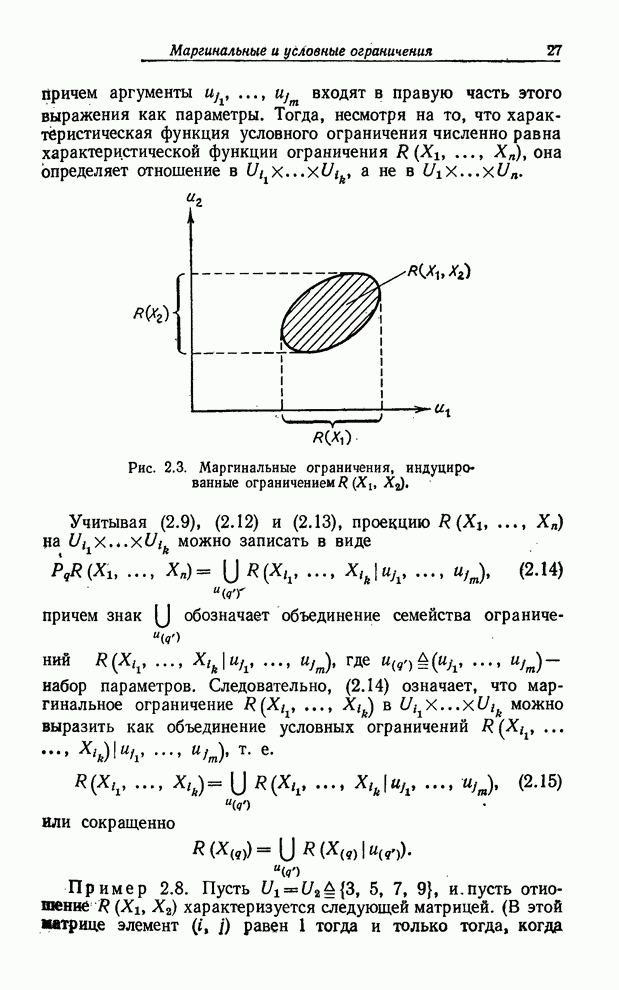
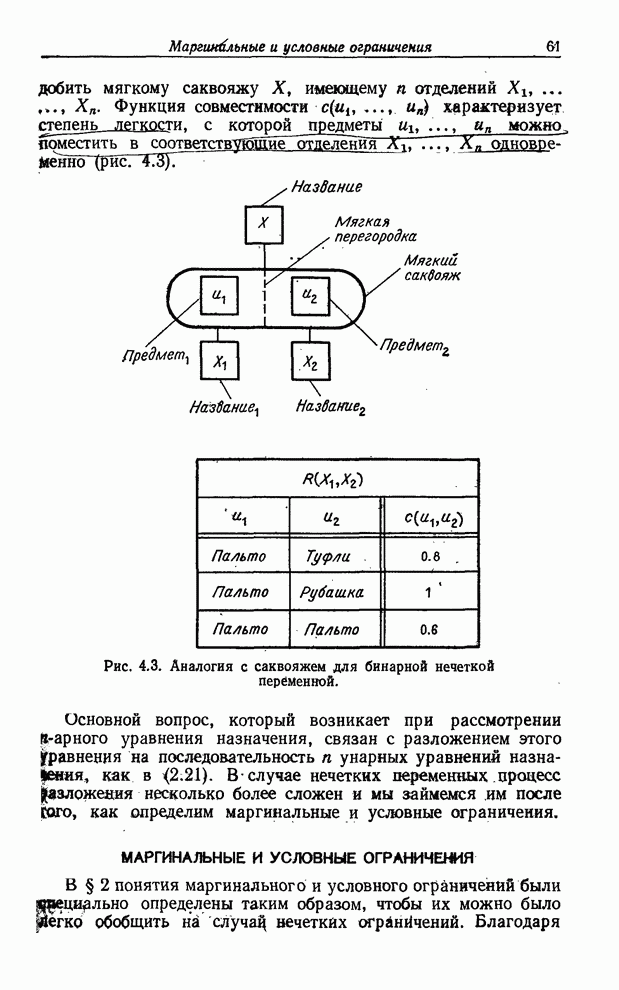
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
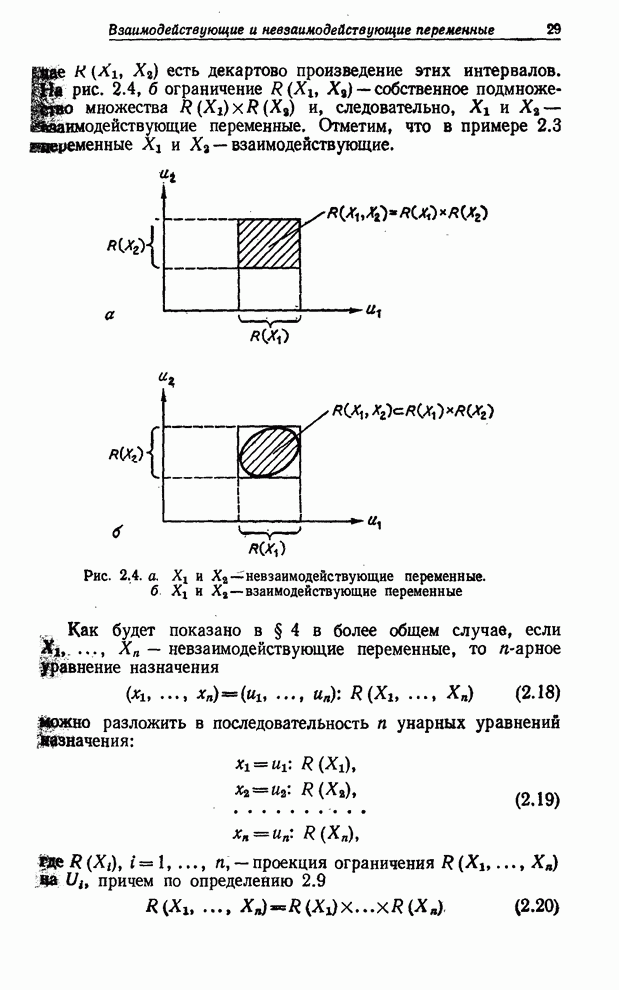
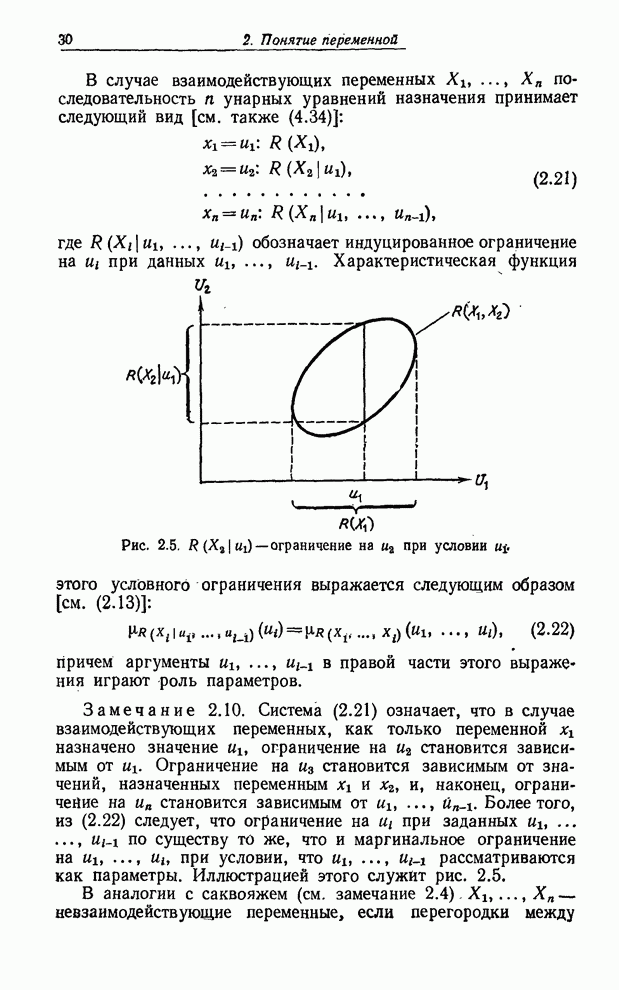
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
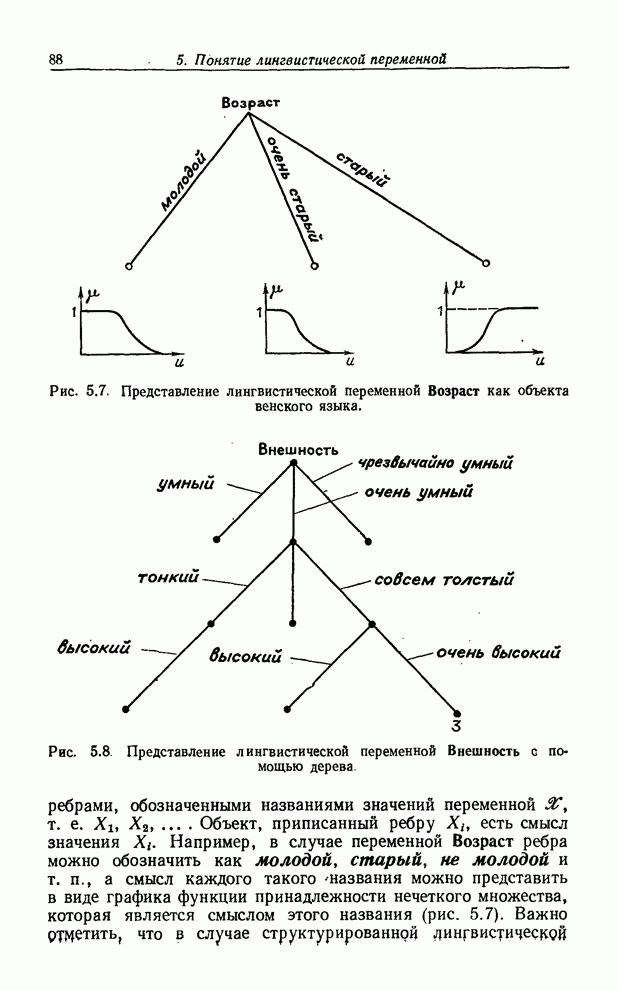
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ