| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
Определение
4.16.
![]() -арное
ограничение
-арное
ограничение ![]() сепарабельно тогда и только
тогда, когда его можно представить в виде декартова произведения унарных
ограничений:
сепарабельно тогда и только
тогда, когда его можно представить в виде декартова произведения унарных
ограничений:
![]() , (4.25)
, (4.25)
или, что то же самое, как пересечение цилиндрических продолжений [см. (3.62)]:
![]() . (4.26)
. (4.26)
Следует
отметить, что если ![]() —
нормально, то нормальны и соответствующие маргинальные ограничения (см.
предложение 3.14). Отсюда вытекает, что множества
—
нормально, то нормальны и соответствующие маргинальные ограничения (см.
предложение 3.14). Отсюда вытекает, что множества ![]() в выражении (4.25) — маргинальные
ограничения, индуцированные ограничением
в выражении (4.25) — маргинальные
ограничения, индуцированные ограничением ![]() . Действительно, из (4.25) следует, что
. Действительно, из (4.25) следует, что
![]() , (4.27)
, (4.27)
и поэтому, используя (3.57), получаем
![]() . (4.28)
. (4.28)
В
дальнейшем, если не оговорено противное, будем предполагать, что ограничение ![]() нормально.
нормально.
Пример 4.17. Матрицу отношения ограничения, приведенную ниже, можно представить как максминное произведение вектор-столбца (унарное отношение) и вектор-строки(унарное отношение). Отсюда следует, что ограничение, о котором идет речь, сепарабельно:

Пример 4.18. Ограничения, определенные в примерах 4.8 и 4.9, не сепарабельны.
Прямым следствием сепарабельности является.
Предложение
4.19.
Если ![]() сепарабельно,
то сепарабельно и любое маргинальное ограничение, индуцированное ограничением
сепарабельно,
то сепарабельно и любое маргинальное ограничение, индуцированное ограничением ![]() .
.
Следствием соотношения (4.25) является также.
Предложение
4.20.
Сепарабельное ограничение ![]() – наибольшее из ограничений, которым
соответствуют маргинальные ограничения
– наибольшее из ограничений, которым
соответствуют маргинальные ограничения ![]() .
.
Понятие сепарабельности тесно связано с понятием невзаимодействия нечетких переменных:
Определение
4.21.
Нечеткие переменные ![]() являются невзаимодействующими тогда и
только тогда, когда ограничение
являются невзаимодействующими тогда и
только тогда, когда ограничение ![]() сепарабельно.
сепарабельно.
Напомним,
что обычные (не нечеткие) переменные ![]() мы называем невзаимодействующими потому
(см. (2.18)), что при выполнении равенства
мы называем невзаимодействующими потому
(см. (2.18)), что при выполнении равенства
![]() (4.29)
(4.29)
![]() -арное уравнение назначения
-арное уравнение назначения
![]() (4.30)
(4.30)
можно
представить в виде последовательности ![]() унарных уравнений назначения
унарных уравнений назначения
 (4.31)
(4.31)
Приведем основное следствие невзаимодействия нечетких переменных, частным случаем которого является разложение (2.19).
Предложение
4.22.
Если нечеткие переменные невзаимодействующие, то ![]() -арное уравнение назначения (4.30) можно
представить в виде последовательности
-арное уравнение назначения (4.30) можно
представить в виде последовательности ![]() унарных уравнений назначения (4.31),
имея в виду, что если
унарных уравнений назначения (4.31),
имея в виду, что если ![]() — совместимость
— совместимость ![]() с
с ![]() , а
, а ![]() ,
, ![]() — совместимость
— совместимость ![]() с
с ![]() , то
, то
![]() . (4.32)
. (4.32)
Доказательство. Из определений совместимости, невзаимодействия и сепарабельности сразу получаем
 (4.33)
(4.33)
Предложение доказано.
Замечание
4.23.
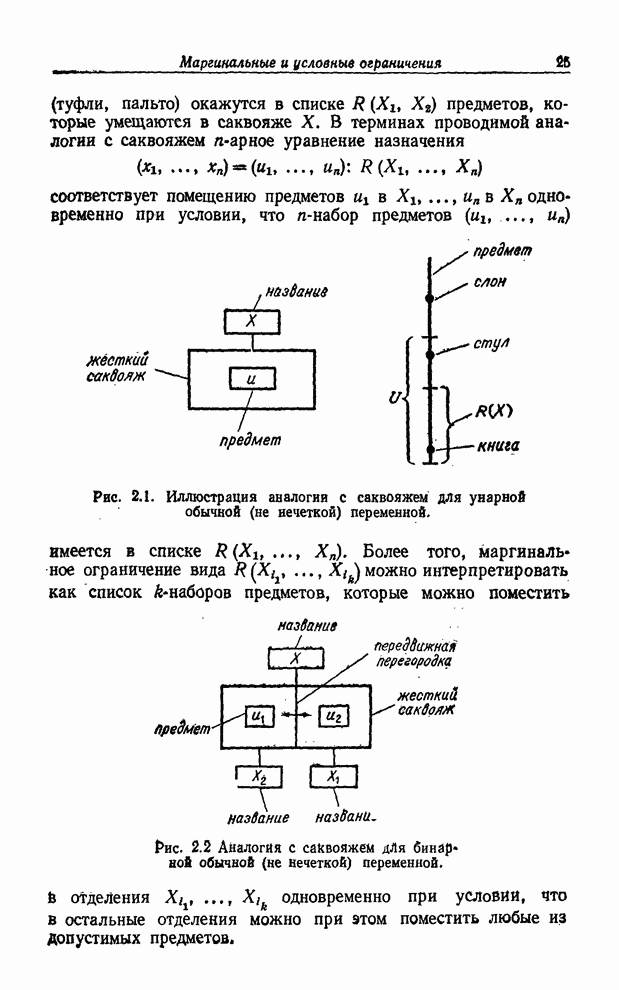
Продолжая аналогию с саквояжем (см. замечание 4.6), невзаимодействующие
нечеткие переменные ![]() можно уподобить
можно уподобить ![]() отдельным
мягким саквояжам с ярлыками
отдельным
мягким саквояжам с ярлыками ![]() . Ограничение, связанное с саквояжем
. Ограничение, связанное с саквояжем ![]() характеризуется
функцией совместимости
характеризуется
функцией совместимости ![]() . Тогда полная функция совместимости для
саквояжей
. Тогда полная функция совместимости для
саквояжей ![]() записывается
в виде (4.32) (рис. 4.4).
записывается
в виде (4.32) (рис. 4.4).

Рис. 4.4. Аналогия с саквояжем для невзаимодействующих нечетких переменных.
Замечание
4.24.
(См. определение 4.1.) Невзаимодействие переменных ![]() подразумевает отсутствие каких
бы то ни было ограничений, в которых присутствуют все величины
подразумевает отсутствие каких
бы то ни было ограничений, в которых присутствуют все величины ![]() , где
, где ![]() — базовая переменная
для
— базовая переменная
для ![]() ,
, ![]() . Например, если
. Например, если ![]() связаны ограничением
связаны ограничением
![]() ,
,
то
![]() — взаимодействующие
переменные, т. е. переменные, не являющиеся невзаимодействующими (см. замечание
3.20).
— взаимодействующие
переменные, т. е. переменные, не являющиеся невзаимодействующими (см. замечание
3.20).
Если
![]() —
взаимодействующие переменные, то по-прежнему можно представить
—
взаимодействующие переменные, то по-прежнему можно представить ![]() -арное уравнение
назначения в виде последовательности
-арное уравнение
назначения в виде последовательности ![]() унарных уравнений назначения. Однако в
этом случае ограничение на
унарных уравнений назначения. Однако в
этом случае ограничение на ![]() как правило, зависит от значений
переменных
как правило, зависит от значений
переменных![]() .
Поэтому
.
Поэтому ![]() уравнений
назначения принимают вид (см. (2.21))
уравнений
назначения принимают вид (см. (2.21))
 (4.84)
(4.84)
где
![]() —
ограничение на
—
ограничение на ![]() при
фиксированных
при
фиксированных ![]() (см.
определение 4.11).
(см.
определение 4.11).
Пример
4.25.
Рассмотрим пример 4.10 и положим ![]() ,
, ![]() и
и ![]() . Тогда
. Тогда
 (4.35)
(4.35)
так что
 (4.36)
(4.36)
Как и в случае системы (4.31), справедливость системы (4.34) подтверждает
Предложение
4.26.
Если ![]() —
взаимодействующие нечеткие переменные при ограничении
—
взаимодействующие нечеткие переменные при ограничении ![]() , а
, а ![]() ,
, ![]() — совместимость
— совместимость ![]() с условным
ограничением
с условным
ограничением ![]() в
(4.34), то
в
(4.34), то
![]() , (4.37)
, (4.37)
где
![]() —
совместимость
—
совместимость ![]() с
с
![]() .
.
Доказательство.
По определению условного ограничения [см. (4.20)] имеем для всех ![]() ,
,![]() ,
,
![]() . (4.38)
. (4.38)
С
другой стороны, из определения маргинального ограничения (см. (4.16)) следует,
что для всех ![]() и
всех
и
всех ![]() выполнено
выполнено
![]() (4.39)
(4.39)
откуда следует, что
![]() (4.40)
(4.40)
Объединяя (4.40) с определением
![]() , (4.41)
, (4.41)
получаем
![]() . (4.42)
. (4.42)
Предложение доказано.
На этом мы заканчиваем обсуждение некоторых свойств нечетких переменных, имеющих отношение к понятию лингвистической переменной. В следующем параграфе мы сформулируем понятие лингвистической переменной и рассмотрим некоторые ее свойства.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
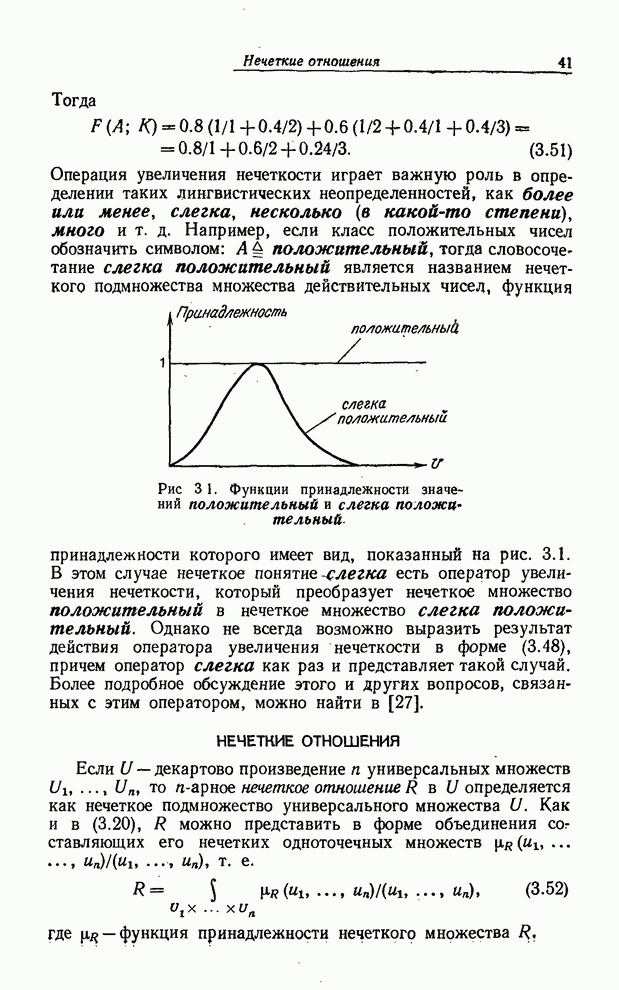
- НЕЧЕТКИЕ ОТНОШЕНИЯ
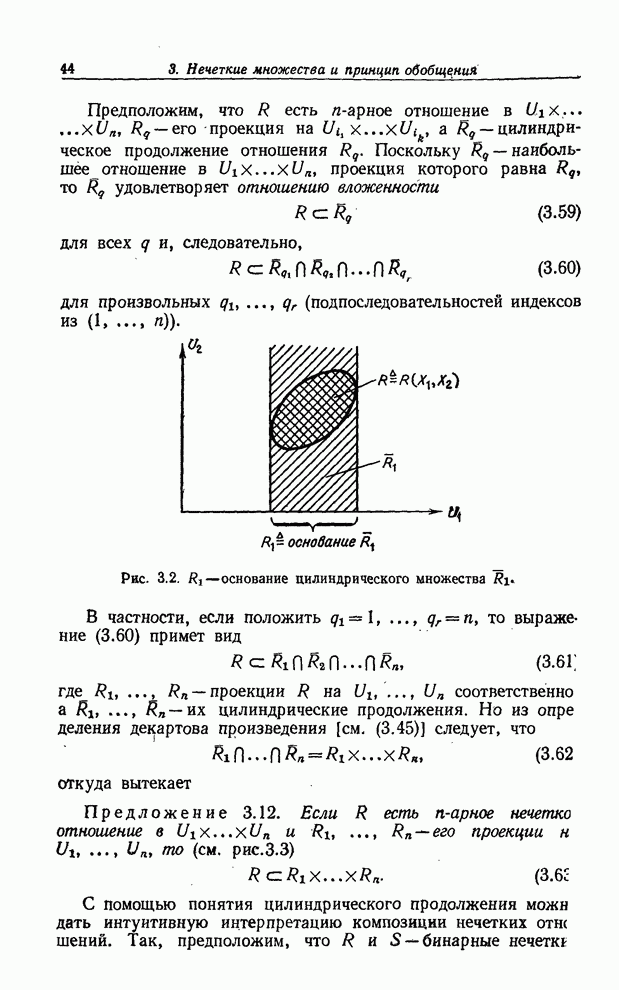
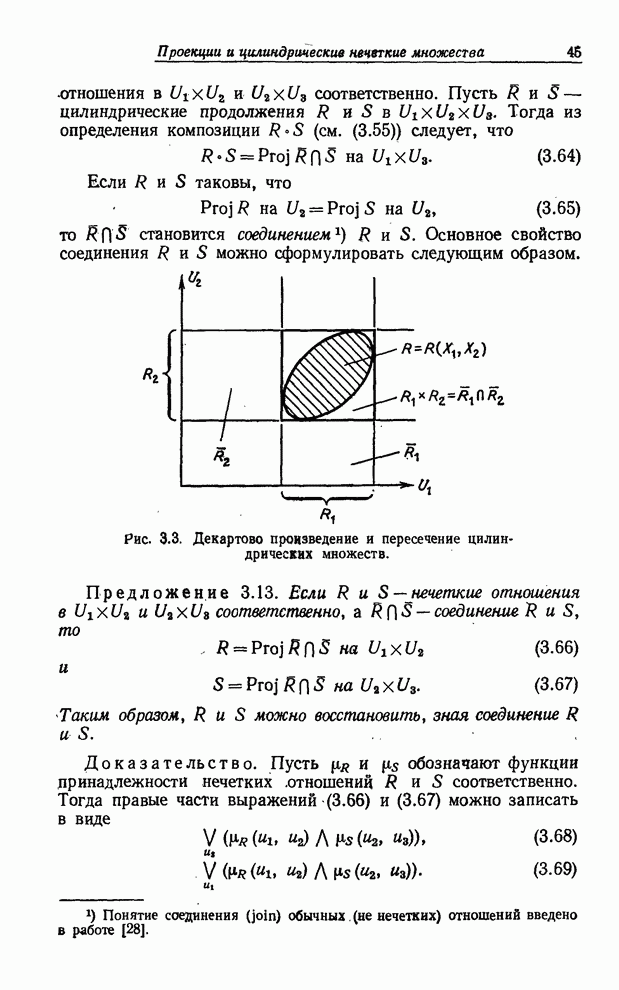
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
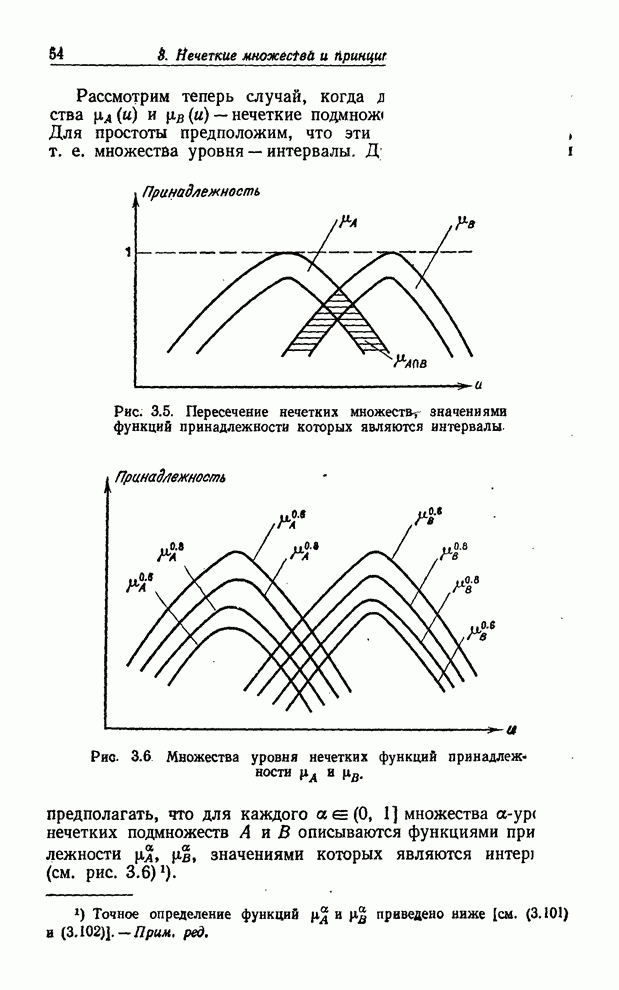
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
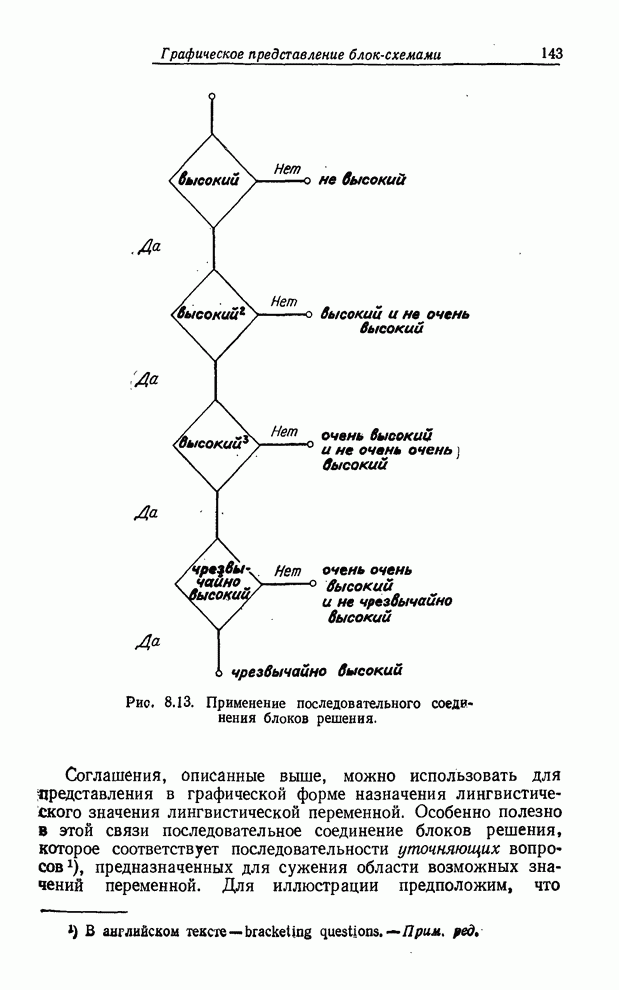
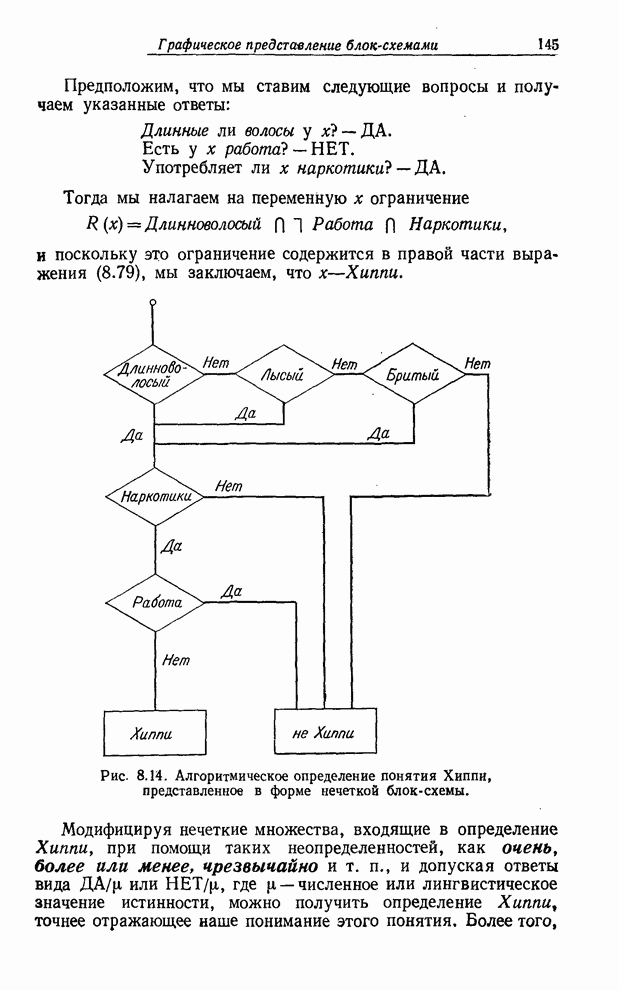
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ