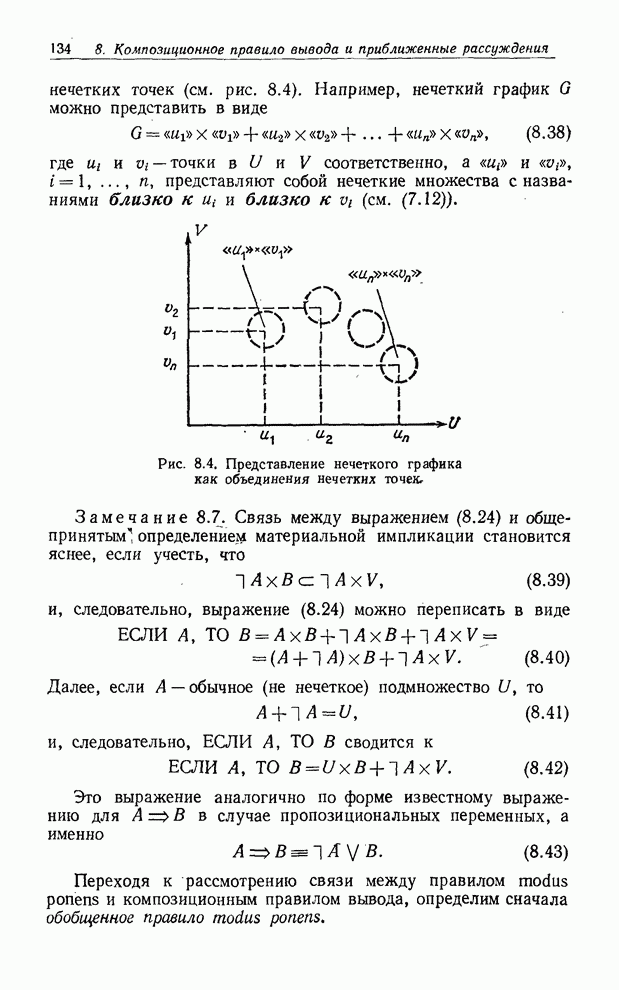
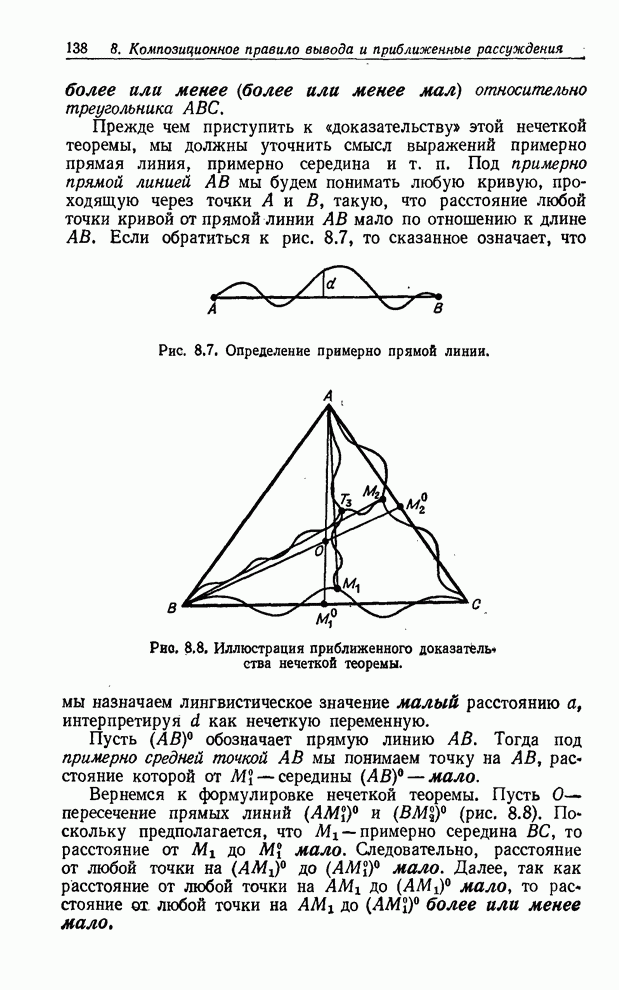
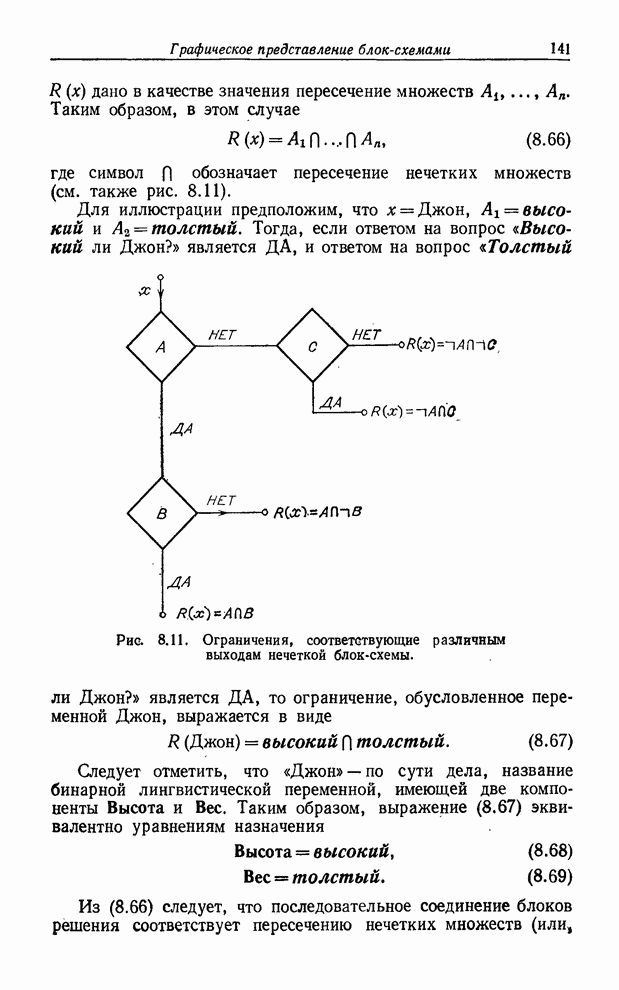
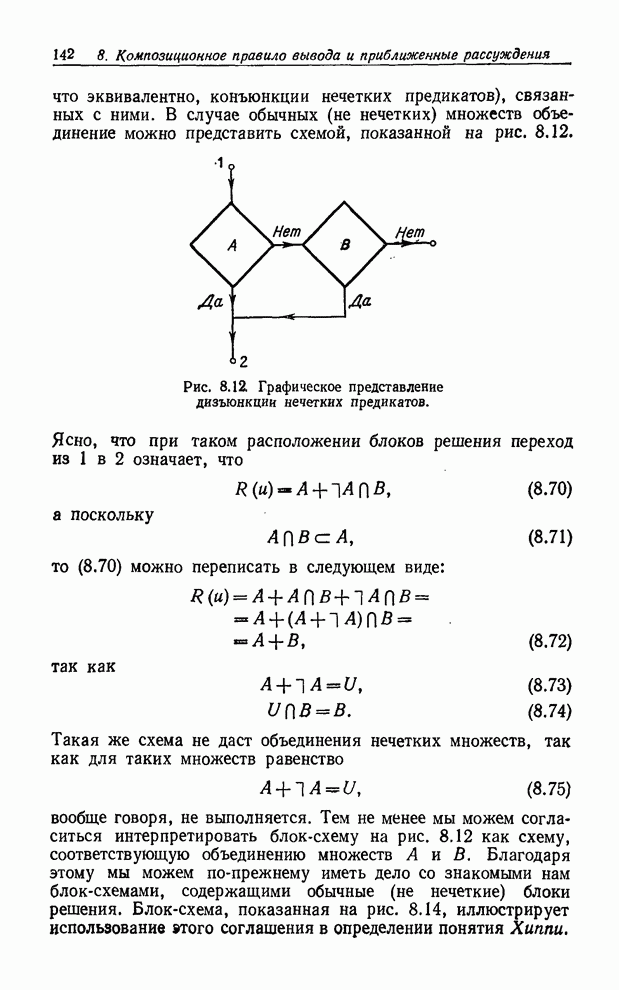
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1. ВВЕДЕНИЕ
Один из фундаментальных принципов современной науки состоит в том, что явление нельзя считать хорошо понятым до тех пор, пока оно не описано посредством количественных характеристик.
С этой точки зрения многое из того, что составляет сущность научного знания, можно рассматривать как совокупность принципов и методов, необходимых для конструирования математических моделей различных систем, позволяющих получать количественную информацию об их поведении. При существующем уважении ко всему точному, строгому и количественному и пренебрежении ко всему неточному, нестрогому и качественному неудивительно, что появление вычислительных машин вызвало широкое распространение количественных методов во многих областях человеческого знания. Несомненно, вычислительные машины оказались высокоэффективными при работе с механистическими системами, т. е. с системами, поведение которых определяется законами механики, физики, химии и электромагнетизма. К сожалению, то же самое нельзя сказать о гуманистических системах, которые, по крайней мере до сих пор, оказывали весьма стойкое сопротивление математическому анализу и моделированию с применением ЭВМ. В самом деле, многими признается, что использование вычислительных машин не пролило много света на основные проблемы, возникающие в философии, психологии, литературе, праве, политике, социологии и в других гуманитарных областях знаний. Вычислительные машины не продвинули нас сколько-нибудь значительно в понимании процесса мышления, за исключением, быть может, некоторых примеров из области искусственного интеллекта и смежных областей.
Можно утверждать, как мы делали в работах [6] и [7], что неэффективность вычислительных машин в изучении гуманистических систем является подтверждением того, что может быть названо принципом несовместимости - принципом, утверждающим, что высокая точность несовместима с большой сложностью системы. Таким образом, быть может именно по этой причине обычные методы анализа систем и моделирования на ЭВМ, основанные на точной обработке численных данных, по существу не способны охватить огромную сложность процессов человеческого мышления и принятия решений. Отсюда напрашивается вывод о том, что для получения существенных выводов о поведении гуманистически систем придется, по-видимому, отказаться от высоких стандартов точности и строгости, которые мы, как правило, ожидаем при математическом анализе четко определенных механистических систем, и относиться более терпимо к иным подходам, которые являются приближенными по своей природе. Вполне возможно, что лишь при использовании таких подходов моделирование на ЭВМ станет действительно эффективным методом анализа систем, которые настолько сложны или некорректно определены, что не поддаются обычному количественному анализу.
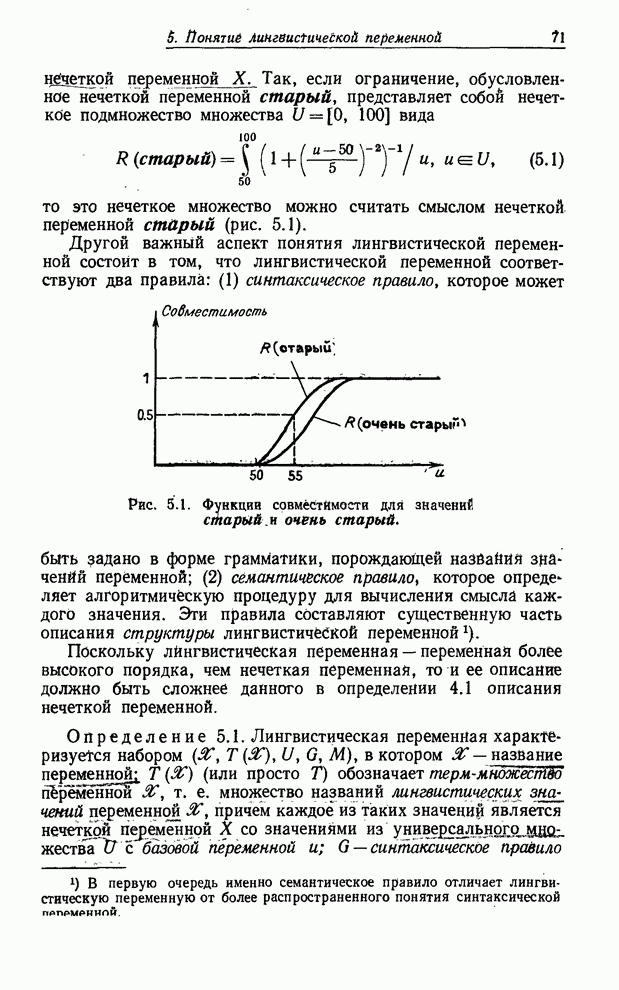
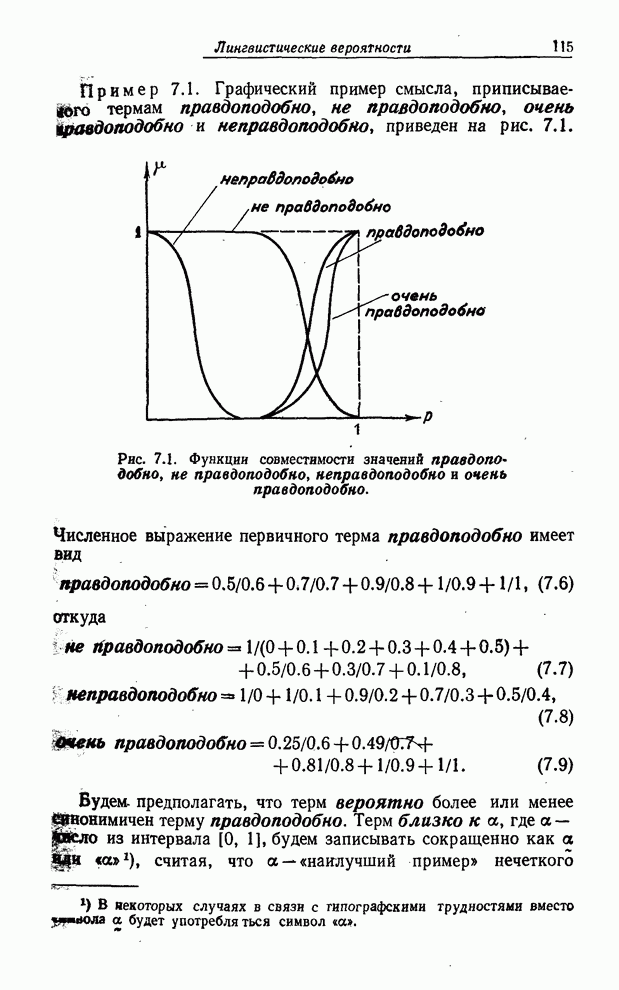
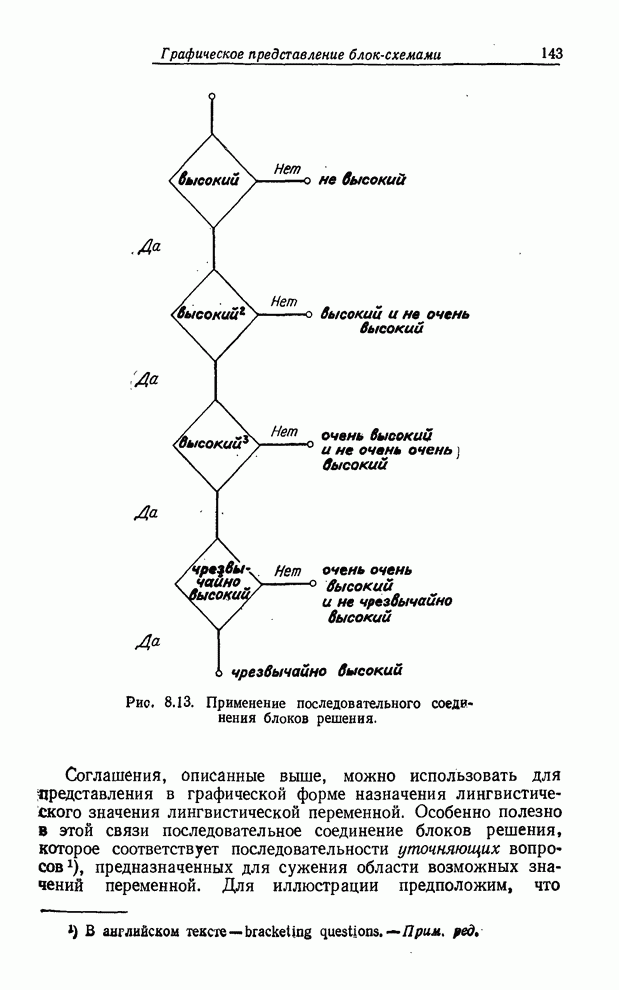
Жертвуя точностью перед лицом ошеломляющей сложности, естественно изучить возможность использования так называемых лингвистических переменных, т. е. переменных, значениями которых являются не числа, а слова или предложения в естественном или формальном языке.
Использование слов и предложений, а не чисел, мотивировано тем, что лингвистическое описание, как правило, менее конкретно, чем описание числами. Например, фраза «Джон молод» менее конкретна, чем фраза «Джону 25 лет». В этом смысле слово молодой можно рассматривать как лингвистическое значение переменной Возраст, имея в виду при этом, что лингвистическое значение играет такую же роль, как и численное значение 25, но является менее точным и, следовательно, менее информативным. То же самое можно сказать о лингвистических значениях очень молодой, не молодой, чрезвычайно молодой, не очень молодой и т. д. если их сопоставить с численными значениями 20, 21, 22, 23.
Если значения численной переменной изображают графически точками на плоскости, то значения лингвистической переменной можно изобразить графически как площадки с нечетко очерченными границами. Именно благодаря такой интерпретации - использованию площадок, а не точек - лингвистические переменные могут служить средством приближенного описания явлений, которые настолько сложны или некорректно определены, что не поддаются точному описанию.
Следует отметить также, что благодаря использованию так называемого принципа обобщения большая часть существующего математического аппарата, применяющегося для анализа систем, может быть приспособлена к лингвистическим переменным. Таким образом, имеется возможность развивать приближенное исчисление лингвистических переменных, которое, по-видимому, найдет широкое практическое применение.
Совокупность значений лингвистической переменной составляет терм-множество этой переменной. Это множество может иметь, вообще говоря, бесконечное число элементов. Например, терм-множество лингвистической переменной Возраст можно записать так:
![]() (Возраст)
= молодой + не молодой + очень молодой + не очень молодой + очень очень молодой
+ ... + старый + не старый + очень старый + не очень старый + не очень молодой
и не очень старый + ... ... + среднего возрастание среднего возраста + ... + не
старый и не среднего возраста + чрезвычайно старый.
(Возраст)
= молодой + не молодой + очень молодой + не очень молодой + очень очень молодой
+ ... + старый + не старый + очень старый + не очень старый + не очень молодой
и не очень старый + ... ... + среднего возрастание среднего возраста + ... + не
старый и не среднего возраста + чрезвычайно старый.
Знак
![]() обозначает
здесь объединение, а не арифметическое суммирование. Аналогично, терм-множество
лингвистической переменной Наружность можно записать следующим образом:
обозначает
здесь объединение, а не арифметическое суммирование. Аналогично, терм-множество
лингвистической переменной Наружность можно записать следующим образом:
![]() (Наружность)
= прекрасная + хорошенькая + миловидная + красивая + привлекательная + не
прекрасная + очень хорошенькая + очень очень красивая + более или менее
хорошенькая + довольно хорошенькая + довольно красивая + безусловно красивая + не
очень привлекательная, но и не очень непривлекательная + ...
(Наружность)
= прекрасная + хорошенькая + миловидная + красивая + привлекательная + не
прекрасная + очень хорошенькая + очень очень красивая + более или менее
хорошенькая + довольно хорошенькая + довольно красивая + безусловно красивая + не
очень привлекательная, но и не очень непривлекательная + ...
В случае лингвистической переменной Возраст числовая переменная возраст,
принимающая значения 0, 1, 2, 3, …, 100, является так называемой базовой
переменной лингвистической переменной Возраст. При этом такое, например,
лингвистическое значение, как молодой, можно интерпретировать как название
некоторого нечеткого ограничения на значения базовой переменной. Именно это
ограничение мы и считаем смыслом лингвистического значения молодой.
Нечеткое
ограничение на значения базовой переменной характеризуется функцией
совместимости, которая каждому значению базовой переменной ставит в
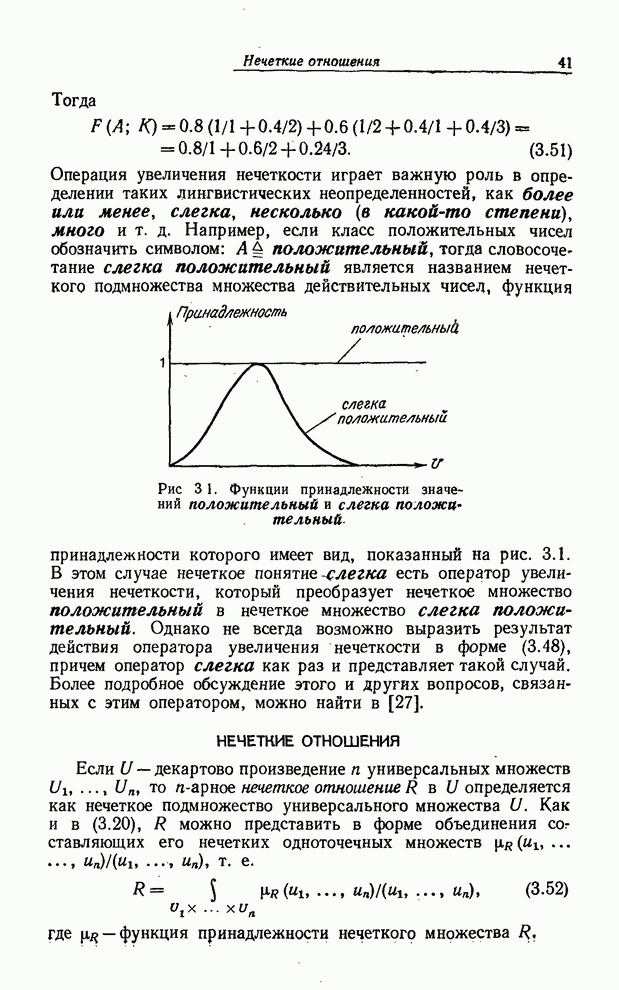
соответствие число из интервала ![]() , символизирующее совместимость этого
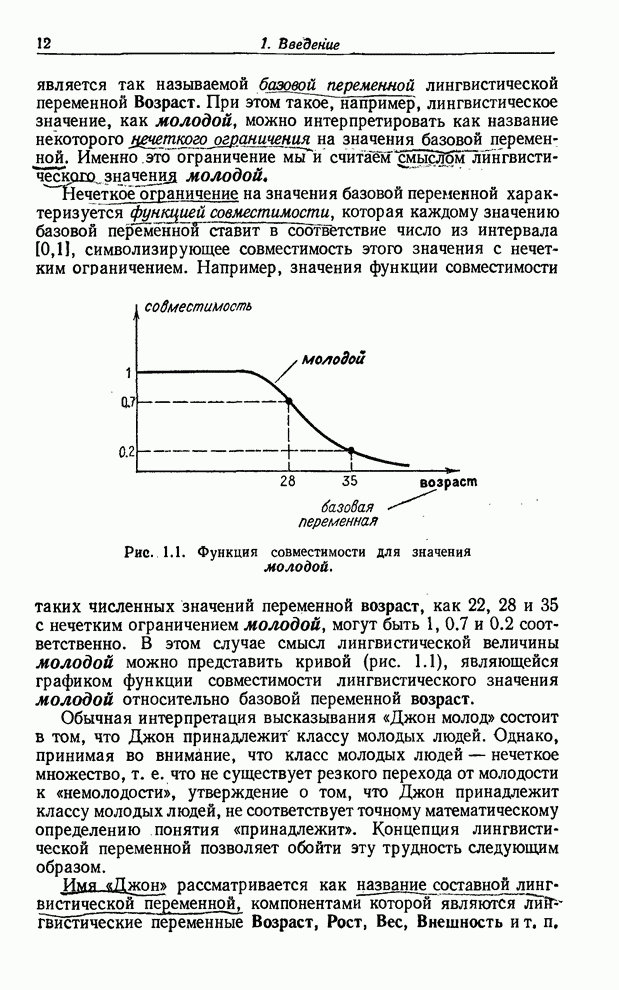
значения с нечетким ограничением. Например, значения функции совместимости таких
численных значений переменной возраст, как 22, 28 и 35 с нечетким ограничением
молодой, могут быть 1, 0.7 и 0.2 соответственно. В этом случае смысл
лингвистической величины молодой можно представить кривой (рис. 1.1),
являющейся графиком функции совместимости лингвистического значения молодой
относительно базовой переменной возраст.
, символизирующее совместимость этого
значения с нечетким ограничением. Например, значения функции совместимости таких
численных значений переменной возраст, как 22, 28 и 35 с нечетким ограничением
молодой, могут быть 1, 0.7 и 0.2 соответственно. В этом случае смысл
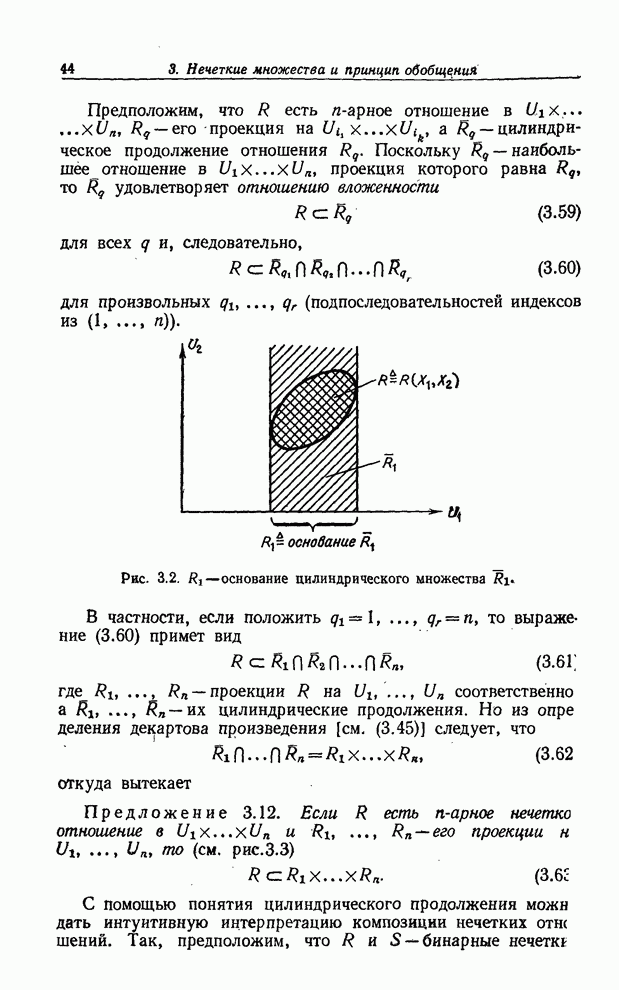
лингвистической величины молодой можно представить кривой (рис. 1.1),
являющейся графиком функции совместимости лингвистического значения молодой
относительно базовой переменной возраст.

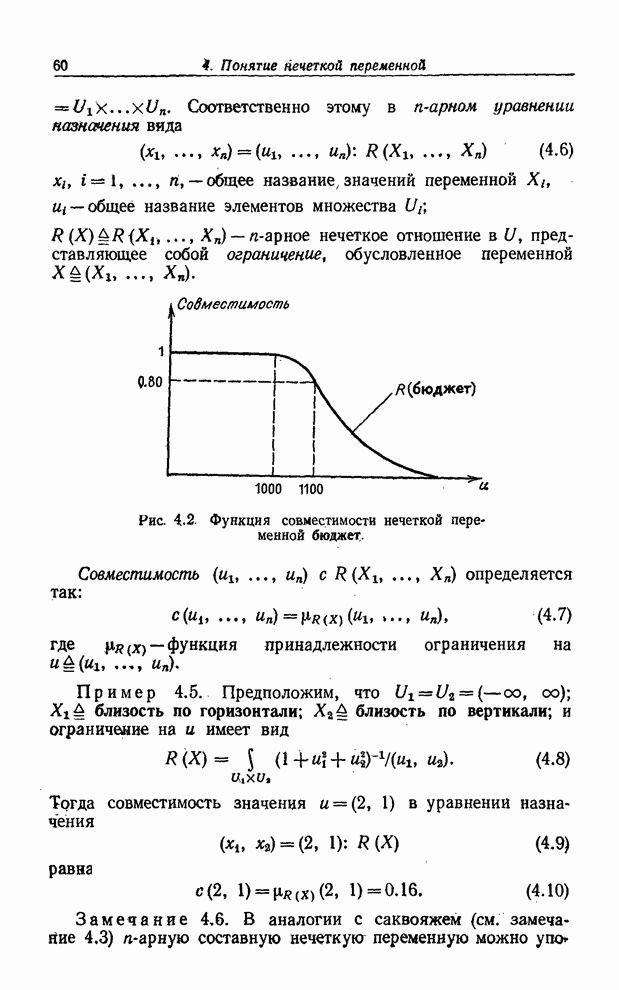
Рис. 1.1. Функция совместимости для значения молодой.
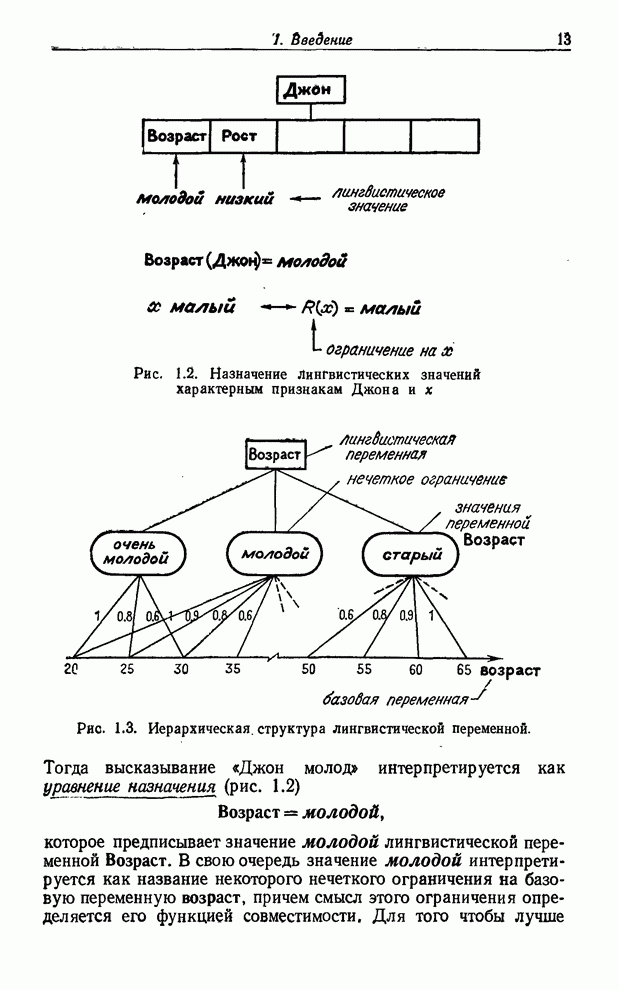
Обычная интерпретация высказывания «Джон молод» состоит в том, что Джон принадлежит классу молодых людей. Однако, принимая во внимание, что класс молодых людей - нечеткое множество, т. е. что не существует резкого перехода от молодости к «немолодости», утверждение о том, что Джон принадлежит классу молодых людей, не соответствует точному математическому определению понятия «принадлежит». Концепция лингвистической переменной позволяет обойти эту трудность следующим образом.
Имя «Джон» рассматривается как название составной лингвистической переменной, компонентами которой являются лингвистические переменные Возраст, Рост, Вес, Внешность и т. п. Тогда высказывание «Джон молод» интерпретируется как уравнение назначения (рис. 1.2)
Возраст = молодой,
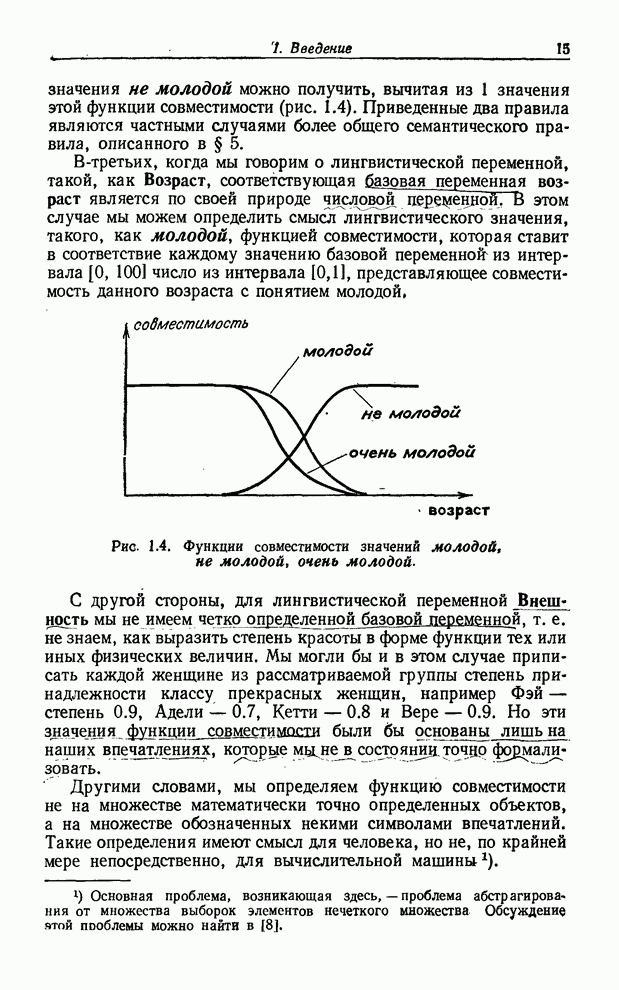
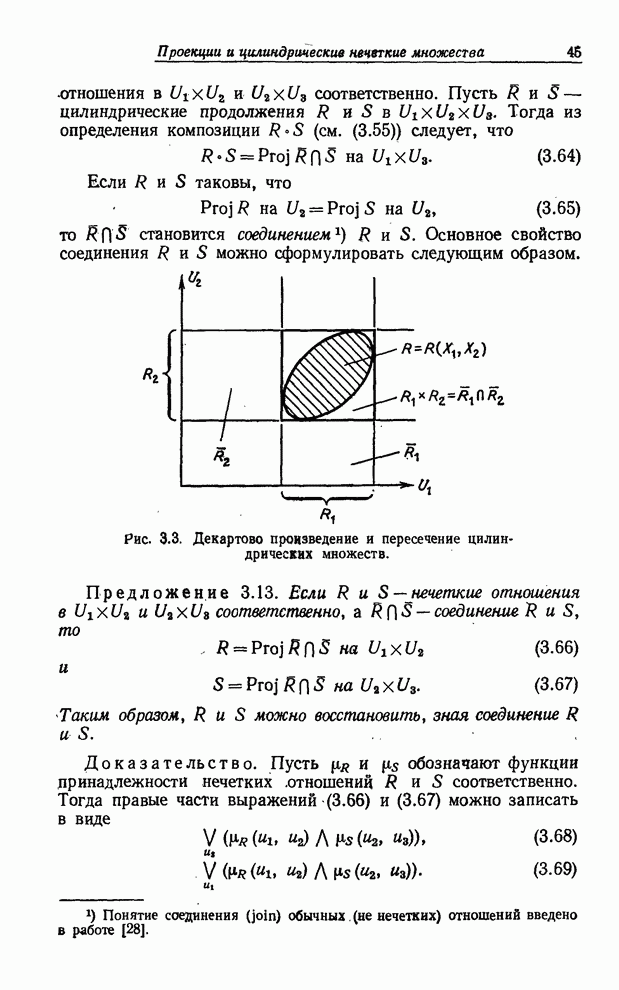
которое предписывает значение молодой лингвистической переменной Возраст. В свою очередь значение молодой интерпретируется как название некоторого нечеткого ограничения на базовую переменную возраст, причем смысл этого ограничения определяется его функцией совместимости. Для того чтобы лучше понять, что такое лингвистическая переменная, можно обратиться к рис. 1.3, на котором изображена иерархическая структура связи между лингвистической переменной Возраст, нечеткими ограничениями, представляющими смысл ее значений, и значениями базовой переменной возраст.

Рис. 1.2. Назначение
лингвистических значений характерным признакам Джона и ![]()

Рис. 1.3. Иерархическая, структура лингвистической переменной.
Существует несколько основных аспектов понятия лингвистической переменной, которые нуждаются в уточнении.
Во-первых, важно уяснить, что понятие совместимости отлично от понятия вероятности. Так, высказывание о том, что совместимость, скажем, численного значения 28 с лингвистическим значением молодой равна 0.7, не имеет никакого отношения к вероятности того, что значение переменной возраст равно 28. Правильная интерпретация значения совместимости, равного 0.7, состоит в том, что оно есть лишь субъективная мера того, насколько возраст 28 лет соответствует в представлении субъекта слову «молодой». Как мы увидим в последующих параграфах, математические операции, применяемые к значениям совместимости, отличны от операций, применяемых к значениям вероятностей, хотя между ними и существует некоторая аналогия.
Во-вторых, мы будем обычно предполагать, что лингвистическая переменная имеет структуру в том смысле, что она связана с двумя правилами: первое - синтаксическое правило - определяет способ порождения лингвистических значений, принадлежащих терм-множеству этой переменной. При этом мы будем обычно предполагать, что элементы терм-множества порождаются бесконтекстной грамматикой.
Второе - семантическое правило - определяет способ вычисления смысла любой лингвистической переменной. Отметим в связи с этим, что типичное значение лингвистической переменной, например не очень молодой и не очень старый, включает в себя то, что можно было бы назвать первичными термами, например молодой и старый, смысл которых субъективен и зависит от контекста. Предполагается, что смысл таких термов определен заранее.
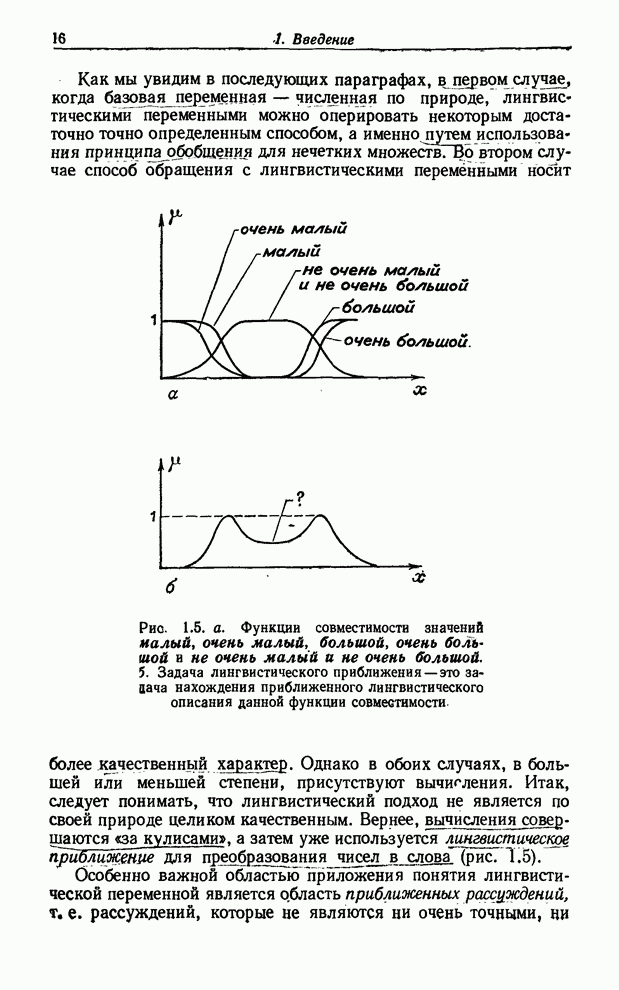
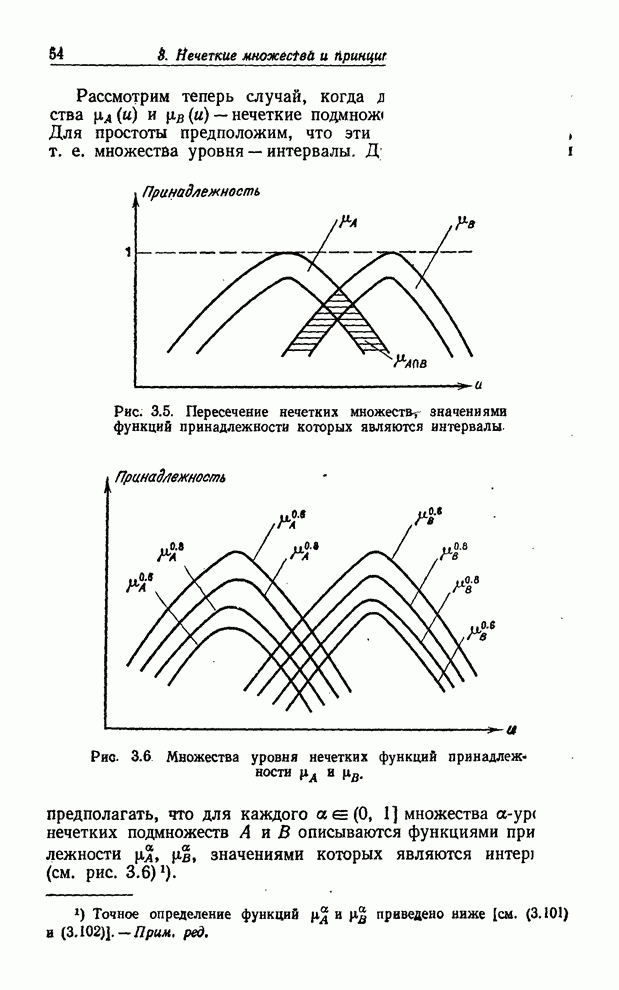
Кроме первичных термов лингвистическое значение может включать в себя связки, такие, как и, или, ..., ни и т. п.; отрицание не, такие неопределенности, как очень, более или менее, совершенно, совсем, безусловно, чрезвычайно, отчасти и т. п. Как мы увидим далее, связки, неопределенности и отрицание можно трактовать как операторы, которые видоизменяют смысл первичных термов особым, независимым от контекста образом. Так, если функция совместимости лингвистического значения молодой изображается кривой, показанной на рис. 1.1, то смысл лингвистического значения очень молодой может быть получен возведением в квадрат значений функции совместимости лингвистического значения молодой. Смысл лингвистического значения не молодой можно получить, вычитая из 1 значения этой функции совместимости (рис. 1.4). Приведенные два правила являются частными случаями более общего семантического правила, описанного в § 5.

Рис. 1.4. Функции совместимости значений молодой, не молодой, очень молодой.
В-третьих,
когда мы говорим о лингвистической переменной, такой, как Возраст,
соответствующая базовая переменная возраст является по своей природе числовой
переменной. В этом случае мы можем определить смысл лингвистического значения,
такого, как молодой, функцией совместимости, которая ставит в соответствие
каждому значению базовой переменной из интервала ![]() число из интервала
число из интервала ![]() , представляющее совместимость
данного возраста с понятием молодой.
, представляющее совместимость
данного возраста с понятием молодой.
С другой стороны, для лингвистической переменной Внешность мы не имеем четко определенной базовой переменной, т. е. не знаем, как выразить степень красоты в форме функции тех или иных физических величин. Мы могли бы и в этом случае приписать каждой женщине из рассматриваемой группы степень принадлежности классу прекрасных женщин, например Фэй - степень 0.9, Адели - 0.7, Кетти - 0.8 и Вере - 0.9. Но эти значения функции совместимости были бы основаны лишь на наших впечатлениях, которые мы не в состоянии точно формализовать.
Другими словами, мы определяем функцию совместимости не на множестве математически точно определенных объектов, а на множестве обозначенных некими символами впечатлений. Такие определения имеют смысл для человека, но не, по крайней мере непосредственно, для вычислительной машины.
Как мы увидим в последующих параграфах, в первом случае, когда базовая переменная - численная по природе, лингвистическими переменными можно оперировать некоторым достаточно точно определенным способом, а именно путем использования принципа обобщения для нечетких множеств. Во втором случае способ обращения с лингвистическими переменными носит более качественный характер. Однако в обоих случаях, в большей или меньшей степени, присутствуют вычисления. Итак, следует понимать, что лингвистический подход не является по своей природе целиком качественным. Вернее, вычисления совершаются «за кулисами», а затем уже используется лингвистическое приближение для преобразования чисел (рис. 1.5).

Рис. 1.5. а. Функции совместимости значений малый, очень малый, большой, очень большой и не очень малый и не очень большой. б. Задача лингвистического приближения - это задача нахождения приближенного лингвистического описания данной функции совместимости.
Особенно важной областью приложения понятия лингвистической переменной является область приближенных рассуждений, т. е. рассуждений, которые не являются ни очень точными, ни очень неточными. В качестве иллюстрации приведем следующую цепочку приближенных рассуждений:
![]() мало,
мало,
![]() и
и
![]() примерно
равны.
примерно
равны.
Следовательно,
![]() более
или менее мало.
более
или менее мало.
Понятие лингвистической переменной появляется в приближенных рассуждениях в результате толкования понятия Истинность как лингвистической переменной, значения которой образуют такое терм-множество:
![]() (Истинность)
= истинный + не истинный + очень истинный + полностью истинный + более или
менее истинный + совершенно истинный + существенно истинный + ... +ложный +
очень ложный + ни истинный, ни ложный + …
(Истинность)
= истинный + не истинный + очень истинный + полностью истинный + более или
менее истинный + совершенно истинный + существенно истинный + ... +ложный +
очень ложный + ни истинный, ни ложный + …
Предполагается,
что соответствующая базовая переменная, является числом из интервала ![]() , а смысл первичного
терма, такого, как истинный, отождествляется с нечетким ограничением на
значения базовой переменной. Как обычно, такое ограничение характеризуется
функцией совместимости, которая каждому численному значению истинности ставит в
соответствие число из интервала
, а смысл первичного
терма, такого, как истинный, отождествляется с нечетким ограничением на
значения базовой переменной. Как обычно, такое ограничение характеризуется
функцией совместимости, которая каждому численному значению истинности ставит в
соответствие число из интервала ![]() . Например, совместимость численного
значения истинности 0.7 с лингвистическим значением истинности очень истинный
может быть равна 0.6. Таким образом, в случае значений истинности функция
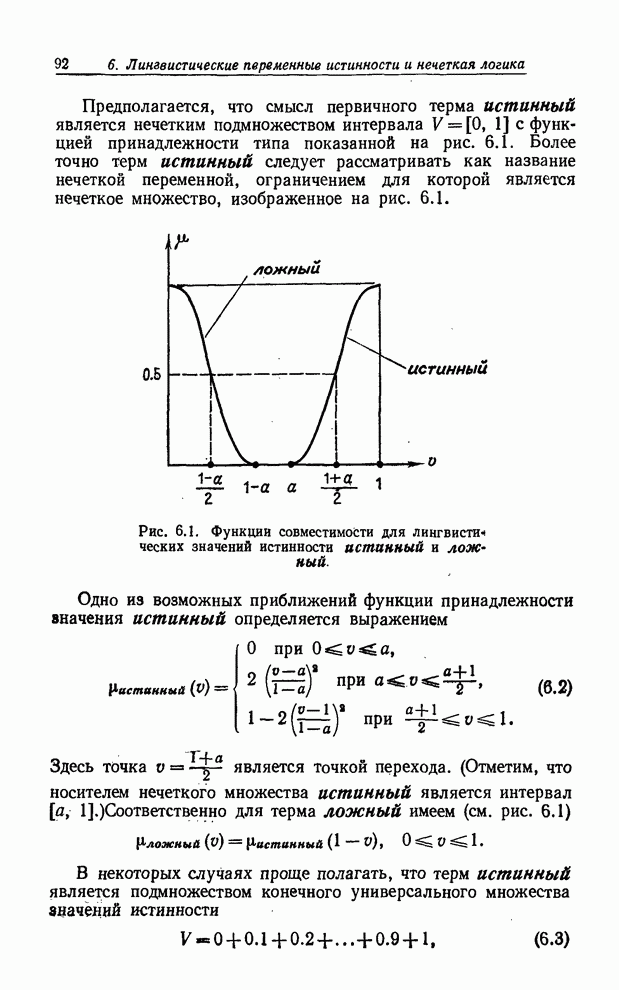
совместимости является отображением единичного интервала в себя (рис. 6.1).
. Например, совместимость численного
значения истинности 0.7 с лингвистическим значением истинности очень истинный
может быть равна 0.6. Таким образом, в случае значений истинности функция
совместимости является отображением единичного интервала в себя (рис. 6.1).
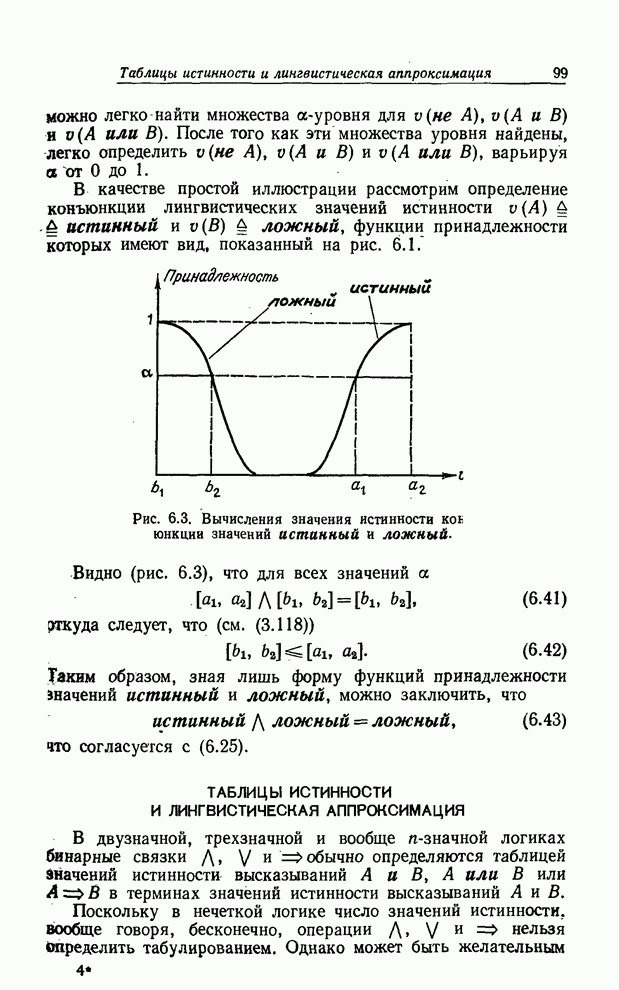
Трактование истинности как лингвистической переменной приводит к нечеткой логике, которая вполне может оказаться лучшим приближением к логике, управляющей принятием решений человеком, чем классическая двузначная логика. В нечеткой логике вполне может иметь смысл то, что в классической логике является недопустимо неопределенным, например:
значением истинности высказывания «Беркли близок к Сан-Франциско» является совершенно истинно,
значением истинности высказывания «Поло Алто близок к Сан-Франциско» является весьма истинно.
Следовательно, значением истинности высказывания «Поло Алто более или менее близок к Беркли» является более или менее истинно.
Другая важная область приложения понятия лингвистической переменной - теория вероятностей. Если вероятность рассматривать как лингвистическую переменную, то ее терм-множество могло бы, например, иметь следующий вид:
![]() (Вероятность)
= правдоподобно + очень правдоподобно + неправдоподобно + чрезвычайно
правдоподобно + весьма правдоподобно + ... + вероятно + невероятно + более или
менее вероятно + …
(Вероятность)
= правдоподобно + очень правдоподобно + неправдоподобно + чрезвычайно
правдоподобно + весьма правдоподобно + ... + вероятно + невероятно + более или
менее вероятно + …
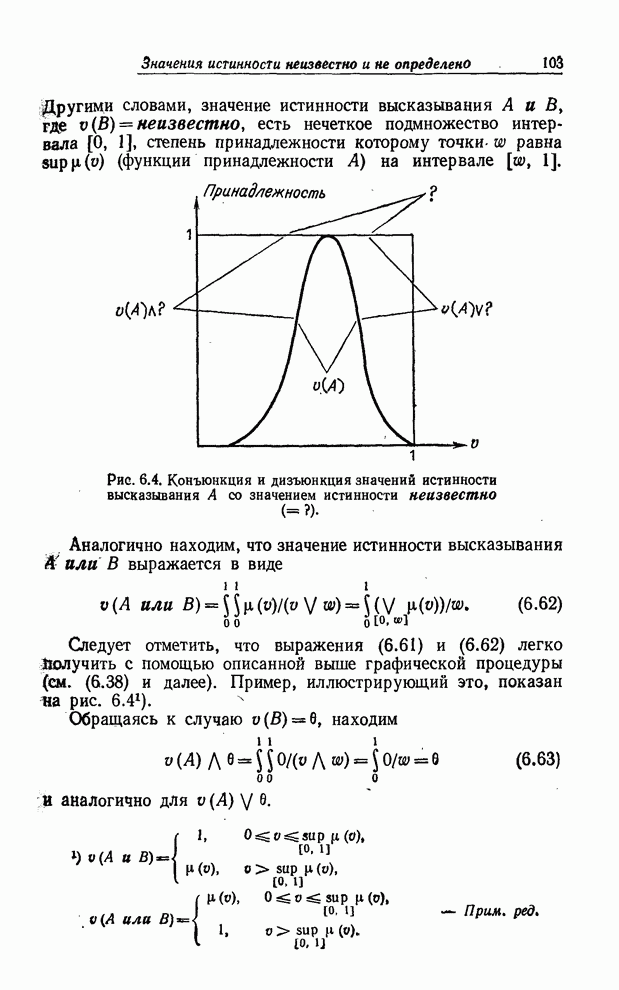
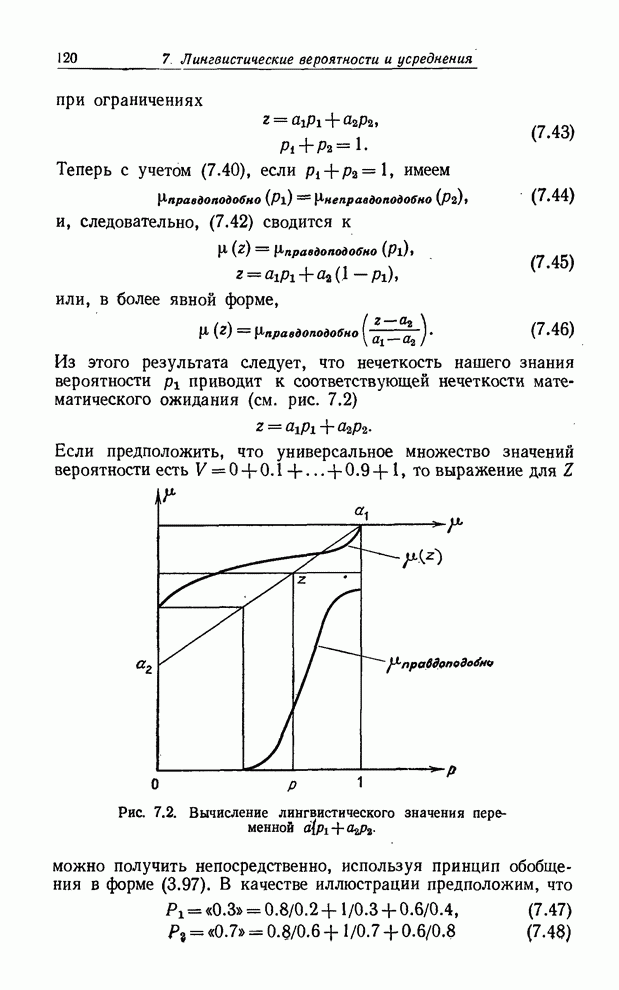
Допустив использование лингвистических значений вероятности, мы получаем возможность на вопрос: «Какова вероятность того, что ровно через неделю будет теплый день?» ответить следующим образом: «весьма высокая» вместо, например, «0.8». Лингвистический ответ, вообще говоря, более реалистичен, принимая во внимание, во-первых, что теплый день - нечеткое событие, и, во-вторых, что мы еще недостаточно понимаем динамику погоды и не можем делать определенных выводов о значениях вероятностей подобных событий.
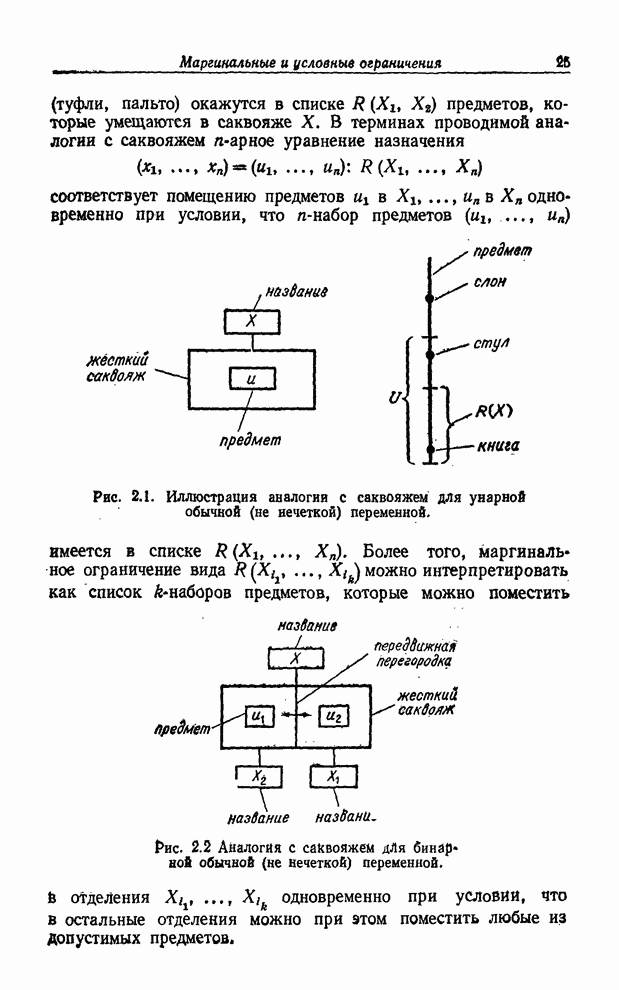
Более подробно понятие лингвистической переменной и ее приложения обсуждаются в последующих параграфах. Чтобы представить понятие лингвистической переменной в должной перспективе, мы начнем изложение с формализации понятия обычной (не нечеткой) переменной. Нам будет полезно уподобить такую переменную саквояжу с жесткими стенками (рис. 2.1) с прикрепленным к нему ярлыком. Поместить некоторый предмет в саквояж означает приписать соответствующей переменной определенное значение, а ограниченное множество предметов, которые можно поместить в саквояж, соответствует подмножеству полного множества, содержащему те элементы, которые могут быть использованы в качестве значений данной переменной.
Аналогично
нечеткую переменную, определение которой дано в § 4, можно уподобить саквояжу
не с твердыми, а мягкими стенками (рис. 4.1). В этом случае множество предметов,
которые можно поместить в этот саквояж, является нечетким по своей природе и определяется
функцией совместимости, которая ставит в соответствие каждому предмету число из
интервала ![]() ,
символизирующее степень легкости, с которой этот предмет можно поместить в
саквояж. Пусть, например, имеется саквояж
,
символизирующее степень легкости, с которой этот предмет можно поместить в
саквояж. Пусть, например, имеется саквояж ![]() ; совместимость пальто с
; совместимость пальто с ![]() может быть равна 1,
тогда как совместимость проигрывателя с
может быть равна 1,
тогда как совместимость проигрывателя с ![]() может быть равна 0.7.
может быть равна 0.7.
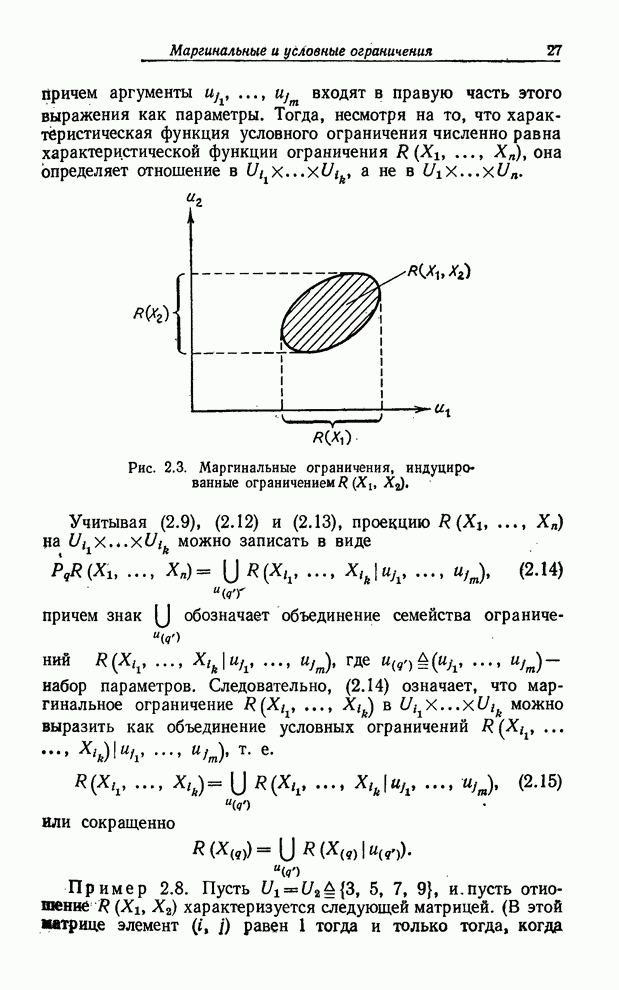
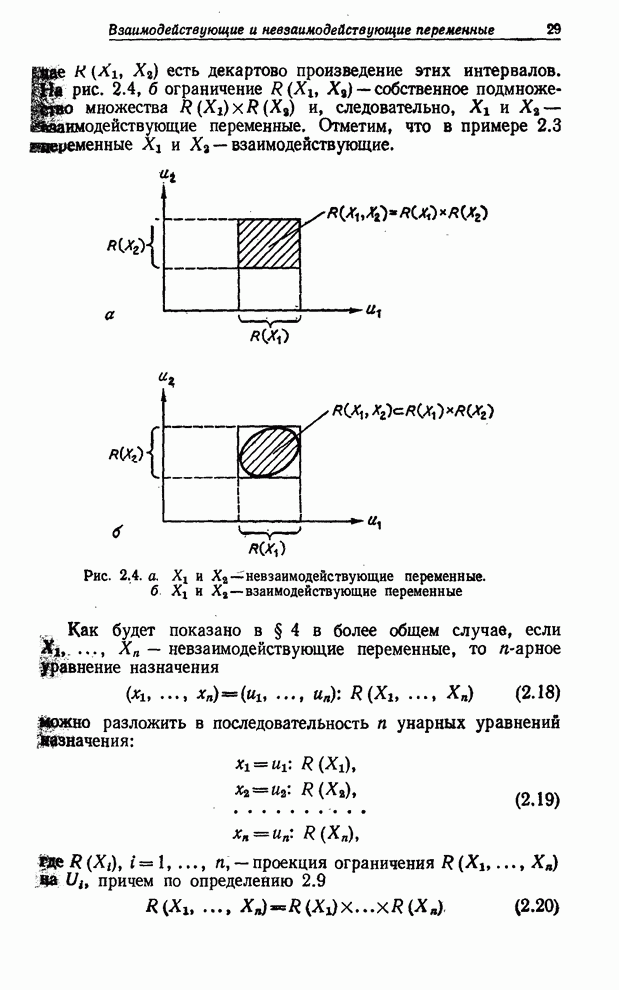
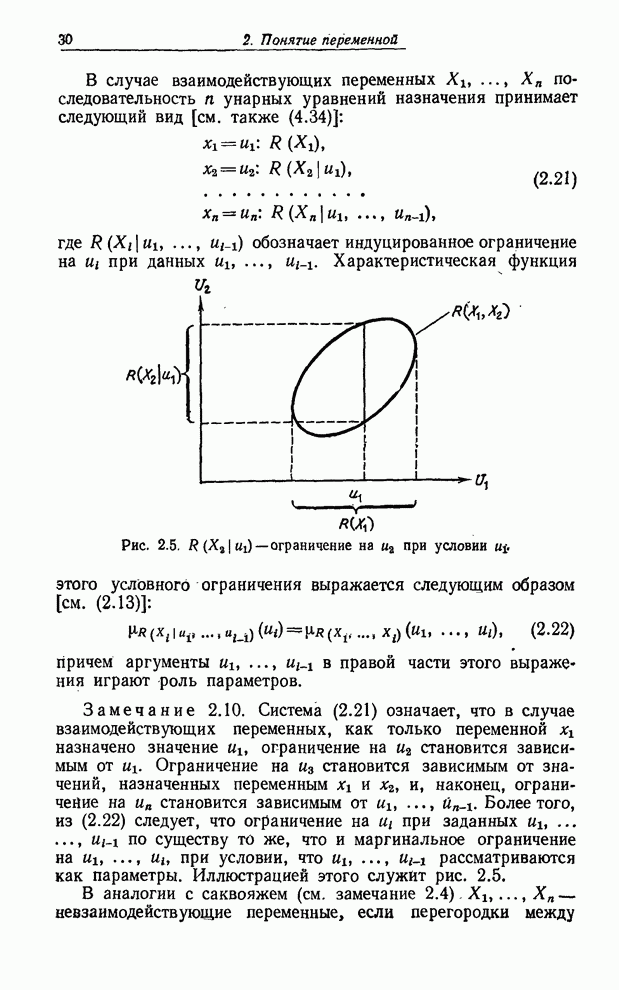
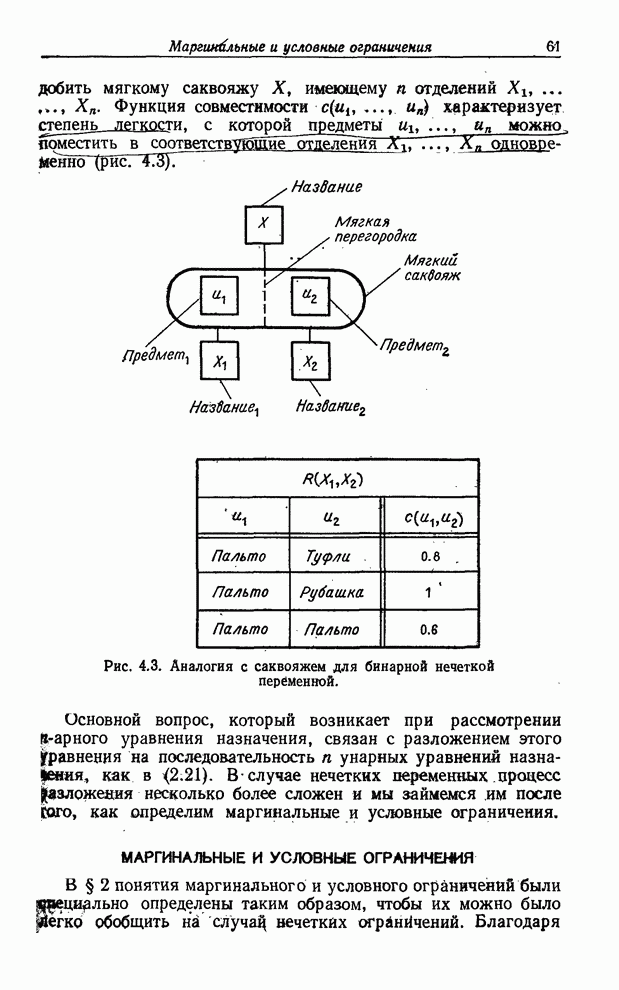
Как будет показано в § 4, существенным при рассмотрении нечетких переменных является понятие невзаимодействия, аналогичное понятию независимости для случайных переменных. Необходимость в этом понятии возникает, когда мы имеем дело с двумя или большим числом нечетких переменных, каждую из которых можно уподобить отделению в мягком саквояже. Нечеткие переменные являются взаимодействующими, если присвоение значения одной из них влияет на нечеткие ограничения, налагаемые на другие переменные. Этот случай можно уподобить взаимодействию между предметами, помещенными в различные отделения саквояжа (рис. 4.3).
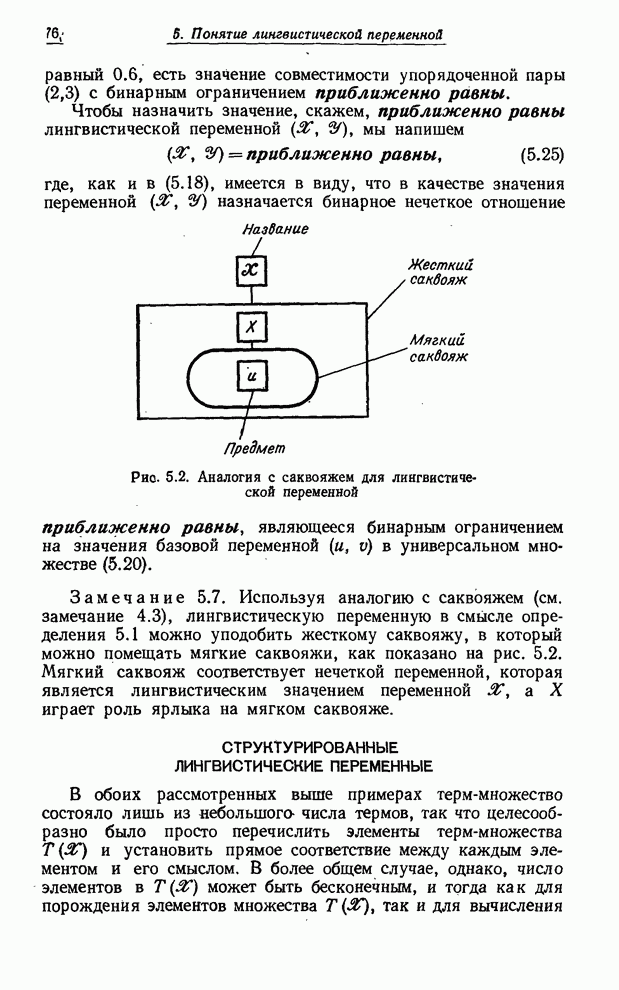
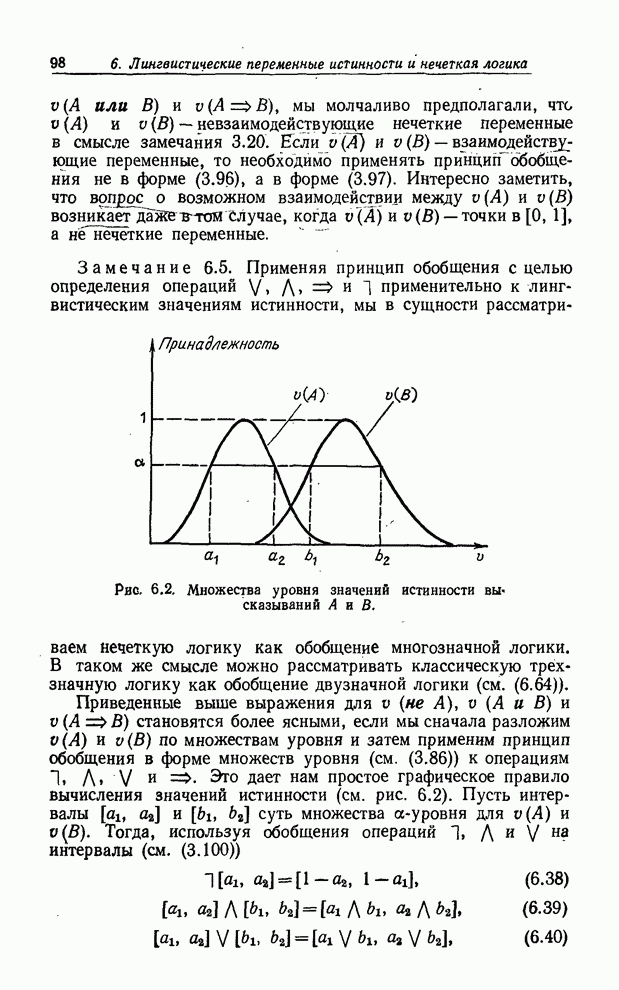
Лингвистическая переменная определяется в § 5 как переменная, значениями которой являются нечеткие переменные. Пользуясь все той же аналогией, уподобим лингвистическую переменную твердому саквояжу, в который можно поместить мягкие саквояжи с ярлыками. На каждом из этих ярлыков приведено описание нечеткого ограничения на множество предметов, которые можно поместить в соответствующий мягкий саквояж (рис. 5.2).
Применение понятия лингвистической переменной для описания «истинности» обсуждается в § 6. Описываются методы вычисления лингвистических значений истинности для конъюнкций, дизъюнкций и отрицаний и закладываются основы нечеткой логики.
В § 7 понятие лингвистической переменной применяется к вероятностям и показывается, что с лингвистическими вероятностями можно производить вычисления. Однако из-за того, что численные значения вероятностей в сумме должны давать 1, вычисления с лингвистическими переменными связаны с решением задач нелинейного программирования и, следовательно, не так просты, как вычисления с численными значениями вероятностей.
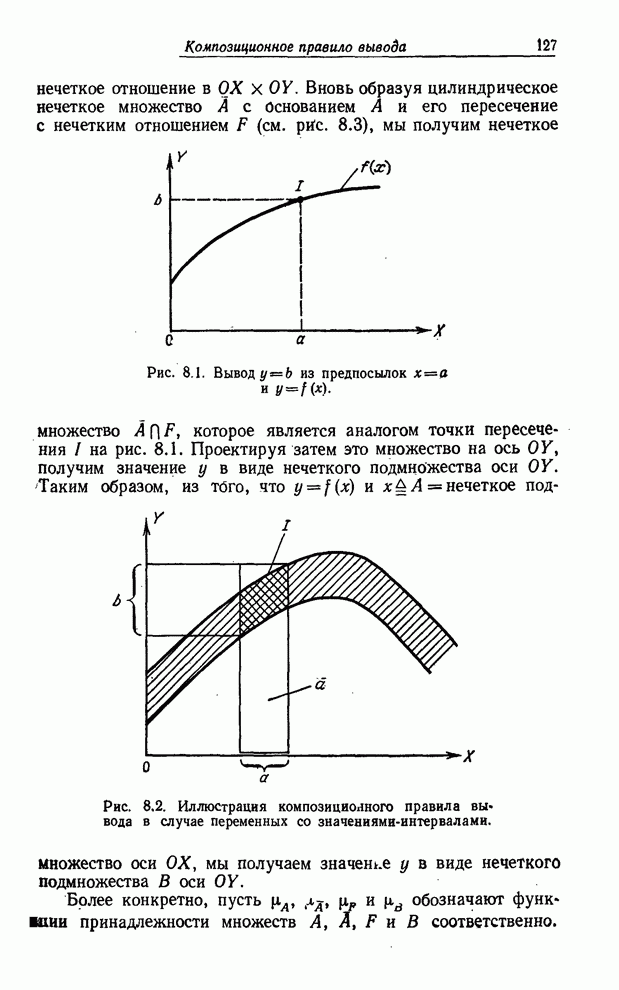
Последний
параграф посвящен обсуждению так называемого композиционного правила вывода и
его применения в приближенных рассуждениях. Это правило вывода интерпретируется
как процесс решения системы уравнений назначения в отношениях, в которых
нечетким ограничениям назначаются лингвистические значения. Так, если
высказывание «![]() - малый» интерпретируется как назначение лингвистического значения малый
нечеткому ограничению на
- малый» интерпретируется как назначение лингвистического значения малый
нечеткому ограничению на ![]() , а высказывание «
, а высказывание «![]() и
и ![]() приближенно равны»
интерпретируется как назначение нечеткого отношения приближенно равны нечеткому
ограничению на упорядоченную пару
приближенно равны»
интерпретируется как назначение нечеткого отношения приближенно равны нечеткому
ограничению на упорядоченную пару ![]() , то вывод «
, то вывод «![]() более или менее малый» можно
рассматривать как лингвистическое приближение решения следующей системы
уравнений:
более или менее малый» можно
рассматривать как лингвистическое приближение решения следующей системы
уравнений:
![]() =
малый,
=
малый,
![]() =
приближенно равны,
=
приближенно равны,
в
которой ![]() и
и ![]() обозначают
ограничения на
обозначают
ограничения на ![]() и
и
![]() соответственно
(рис. 8.3).
соответственно
(рис. 8.3).
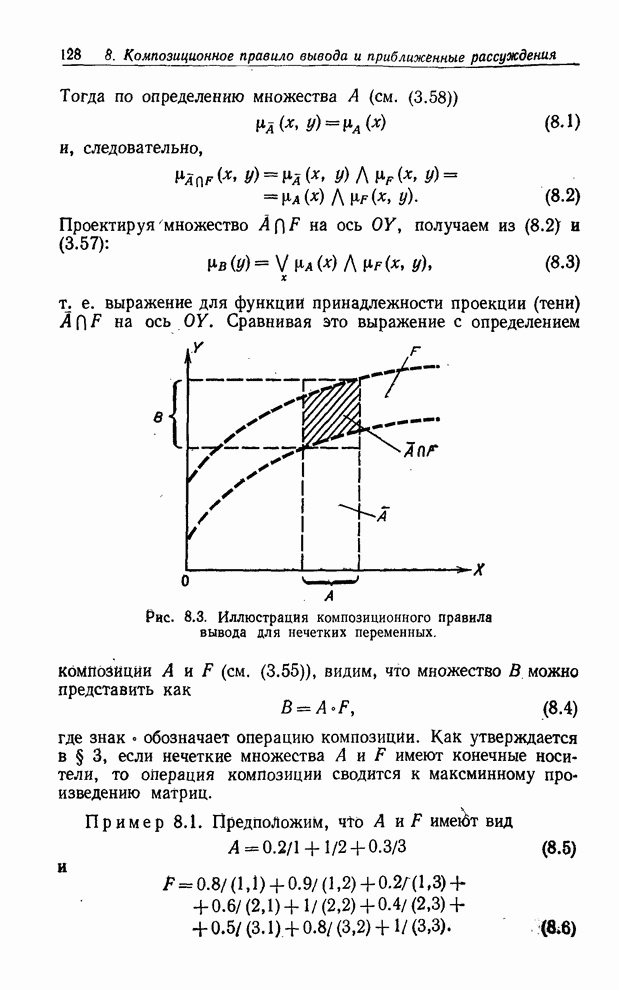
Композиционное
правило вывода приводит к обобщенному правилу modus ponens, причем его можно
рассматривать как обобщение известного правила вывода: если ![]() истинно и
истинно и ![]() влечёт
влечёт ![]() , то
, то ![]() истинно. Параграф
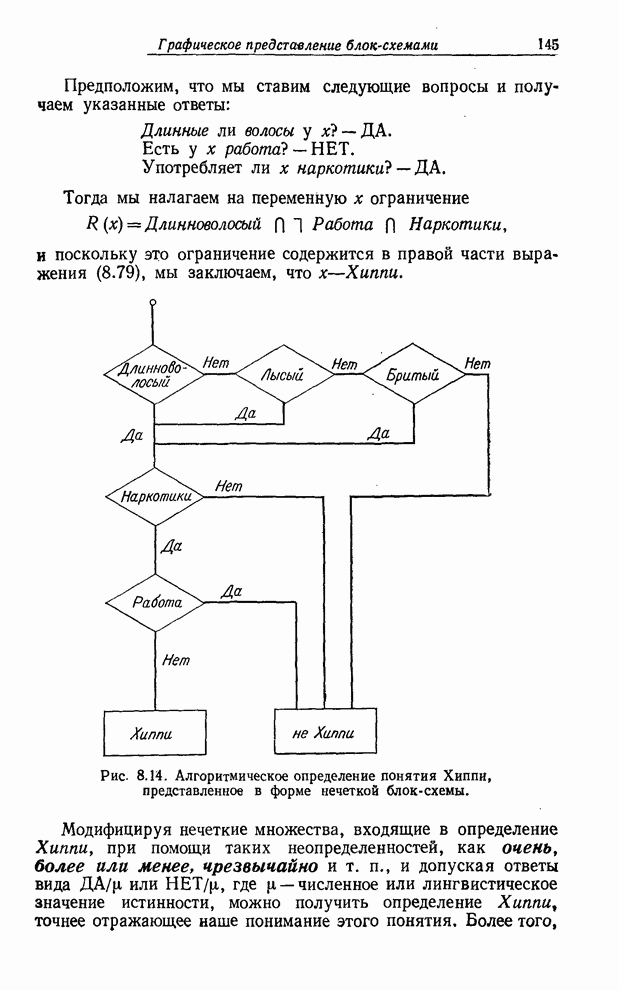
заканчивается примером нечеткой теоремы из элементарной геометрии и коротким
обсуждением использования нечетких блок-схем для представления нечетких
алгоритмов определения.
истинно. Параграф
заканчивается примером нечеткой теоремы из элементарной геометрии и коротким
обсуждением использования нечетких блок-схем для представления нечетких
алгоритмов определения.
Материал § 2-4 предназначен для того, чтобы заложить математическую основу понятия лингвистической переменой, вводимого в § 5.
Те читатели, которых, возможно, не интересуют математические аспекты этой теории, могут сразу перейти к § 5 и по мере надобности обращаться к предыдущим параграфам за необходимыми определениями и результатами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ