| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
Чтобы
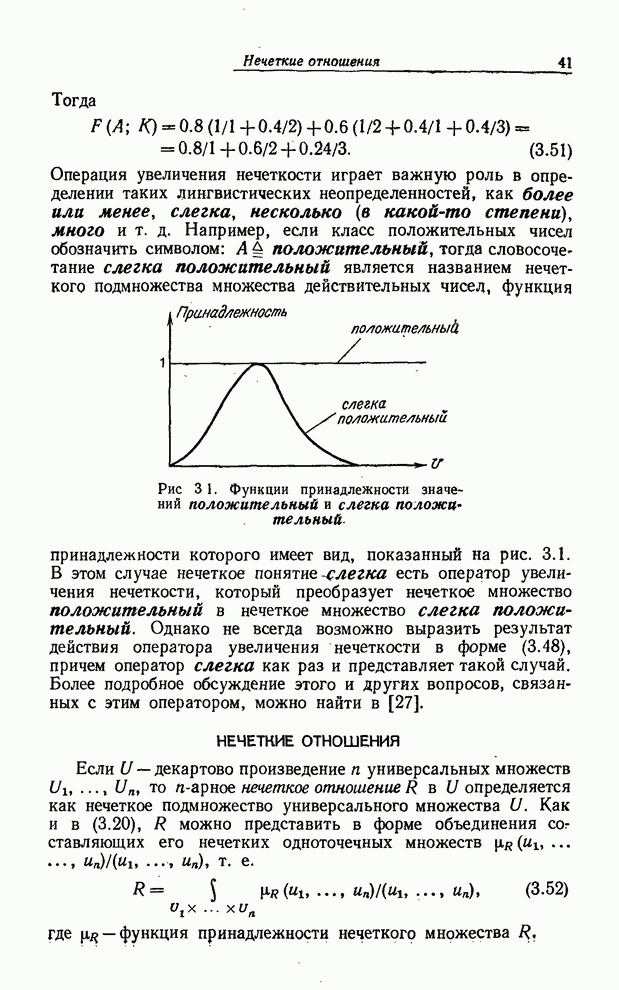
заложить основу для нечеткой логики, необходимо расширить содержание таких
логических операций, как отрицание, дизъюнкция, конъюнкция и импликация
применительно к высказываниям, которые имеют не числовые, а лингвистические
значения истинности. Другими словами, мы должны уметь вычислять значение
истинности высказывания ![]() и
и ![]() , зная лингвистические значения
истинности высказываний
, зная лингвистические значения
истинности высказываний ![]() и
и ![]() . При рассмотрении этой проблемы
полезно иметь в виду, что если
. При рассмотрении этой проблемы
полезно иметь в виду, что если ![]() — нечеткое подмножество универсального
множества
— нечеткое подмножество универсального
множества ![]() и
и
![]() , то два
следующих утверждения эквивалентны:
, то два
следующих утверждения эквивалентны:
 (6.6)
(6.6)
Таким
образом, вопрос «Что является значением истинности высказывания ![]() и
и ![]() , если заданы
лингвистические значения истинности
, если заданы
лингвистические значения истинности![]() и
и ![]() ?» аналогичен вопросу, который мы
поставили в § 3: «Какова степень принадлежности элемента
?» аналогичен вопросу, который мы
поставили в § 3: «Какова степень принадлежности элемента![]() множеству
множеству![]() , если заданы степени
принадлежности элемента
, если заданы степени
принадлежности элемента ![]() множествам
множествам ![]() и
и ![]() ?»
?»
Чтобы ответить на последний вопрос, мы использовали принцип обобщения. Будем придерживаться той же процедуры для обобщения смысла отрицания не, а также связок и, или и влечет применительно к лингвистическим значениям истинности.
В
частности, если ![]() —
точка в
—
точка в ![]() ,
представляющая значение истинности высказывания «
,
представляющая значение истинности высказывания «![]() » (или просто
» (или просто ![]() ), где
), где ![]() — элемент универсального
множества
— элемент универсального
множества ![]() ,
то значение истинности высказывания не
,
то значение истинности высказывания не![]() (или
(или![]() ) определяется выражением
) определяется выражением
![]() . (6.7)
. (6.7)
Предположим
теперь, что ![]() —
не точка в
—
не точка в ![]() ,
а нечеткое подмножество интервала
,
а нечеткое подмножество интервала ![]() , представленное в виде
, представленное в виде
![]() , (6.8)
, (6.8)
где
![]() — точки в
— точки в ![]() , а
, а ![]() — их степени
принадлежности множеству
— их степени
принадлежности множеству ![]() . Тогда, применяя принцип обобщения
(3.80) к (6.7), получим выражения для
. Тогда, применяя принцип обобщения
(3.80) к (6.7), получим выражения для ![]() как нечеткого подмножества интервала
как нечеткого подмножества интервала ![]() , т. е.
, т. е.
![]() . (6.9)
. (6.9)
В
частности, если значение истинности ![]() есть истинно, т.
е.
есть истинно, т.
е.
![]() , (6.10)
, (6.10)
то значение истинности ложно можно записать в виде
![]() . (6.11)
. (6.11)
Например, если
![]() , (6.12)
, (6.12)
то
значение истинности высказывания не ![]() имеет вид
имеет вид
![]() .
.
Замечание 6.1. Следует отметить, что если
![]() , (6.13)
, (6.13)
то согласно (3.33), имеем
![]() , (6.14)
, (6.14)
Однако если
![]() , (6.15)
, (6.15)
то
![]() . (6.16)
. (6.16)
То же самое относится и к лингвистическим неопределенностям. Например, согласно определению неопределенности очень (см. (5.38)),
![]() . (6.17)
. (6.17)
С
другой стороны, значение истинности высказывания очень ![]() равно
равно
![]() . (6.18)
. (6.18)
Перейдем
к бинарным связкам. Пусть ![]() и
и ![]() — лингвистические значения истинности
высказываний
— лингвистические значения истинности
высказываний ![]() и
и
![]() соответственно.
Для простоты будем пользоваться теми же обозначениями, что и в случае, когда
соответственно.
Для простоты будем пользоваться теми же обозначениями, что и в случае, когда ![]() и
и ![]() – точки в
– точки в![]() :
:
![]() , (6.19)
, (6.19)
![]() , (6.20)
, (6.20)
![]() , (6.21)
, (6.21)
![]() , (6.22)
, (6.22)
имея
при этом в виду, что в случае, когда ![]() и
и ![]() — точки в
— точки в ![]() , операции
, операции ![]() ,
, ![]() и
и ![]() сводятся к операциям min (конъюнкция), max (дизъюнкция) и
вычитания из единицы соответственно.
сводятся к операциям min (конъюнкция), max (дизъюнкция) и
вычитания из единицы соответственно.
Далее,
если ![]() и
и ![]() — лингвистические
значения истинности, заданные выражениями
— лингвистические
значения истинности, заданные выражениями
![]() , (6.23)
, (6.23)
![]() , (6.24)
, (6.24)
где
![]() и
и ![]() — точки в
— точки в ![]() , а
, а ![]() и
и ![]() — соответствующие им
степени принадлежности множествам
— соответствующие им
степени принадлежности множествам ![]() и
и ![]() , то, применяя принцип обобщения к
, то, применяя принцип обобщения к ![]() , получим
, получим
 (6.25)
(6.25)
Таким
образом, значение истинности высказывания ![]() и
и ![]() есть нечеткое подмножество
интервала
есть нечеткое подмножество
интервала ![]() ,
носитель которого состоит из точек вида
,
носитель которого состоит из точек вида
![]() ,
,
с
соответствующими степенями принадлежности ![]() . Отметим, что выражение (6.25)
эквивалентно выражению (3.107) для функции принадлежности пересечения нечетких
множеств, имеющих нечеткие функции принадлежности.
. Отметим, что выражение (6.25)
эквивалентно выражению (3.107) для функции принадлежности пересечения нечетких
множеств, имеющих нечеткие функции принадлежности.
Пример 6.2. Предположим, что
![]() (6.26)
(6.26)
и
 (6.27)
(6.27)
Тогда, используя (6.25), получаем
 (6.28)
(6.28)
Аналогично,
для значения истинности высказывания ![]() или
или ![]() получим
получим
 (6.29)
(6.29)
Значение
истинности высказывания ![]() зависит от того, как определена связка
зависит от того, как определена связка ![]() для числовых
значений истинности. Так, если для случая, когда
для числовых
значений истинности. Так, если для случая, когда ![]() и
и ![]() — точки в
— точки в ![]() , мы положим (см. (8.24))
, мы положим (см. (8.24))
![]() , (6.30)
, (6.30)
то, применив принцип обобщения, получим (см. замечание 3.20)
 (6.31)
(6.31)
для
случая, когда ![]() и
и
![]() — нечеткие
подмножества интервала
— нечеткие
подмножества интервала ![]() .
.
Замечание
6.3. Важно четко понимать разницу между связкой и в терме,
скажем, истинный и не очень истинный и символом ![]() в высказывании истинный
в высказывании истинный
![]() не
истинный. В первом случае нас интересует смысл терма истинный и
не истинный, и связка и определяется отношением
не
истинный. В первом случае нас интересует смысл терма истинный и
не истинный, и связка и определяется отношением
 (6.32)
(6.32)
где
![]() — смысл
терма
— смысл
терма ![]() (см.
определение 5.1). Напротив, в случае терма истинный
(см.
определение 5.1). Напротив, в случае терма истинный![]() не истинный нас в
основном интересует значение истинности высказывания истинный
не истинный нас в
основном интересует значение истинности высказывания истинный ![]() не истинный,
которое получается из равенства (см. (6.19))
не истинный,
которое получается из равенства (см. (6.19))
![]() . (6.33)
. (6.33)
Таким
образом, в (6.32)символ ![]() обозначает операцию пересечения
нечетких множеств, а в (6.33) символ
обозначает операцию пересечения
нечетких множеств, а в (6.33) символ ![]() обозначает операцию конъюнкции.
Проиллюстрируем это различие на простом примере. Пусть
обозначает операцию конъюнкции.
Проиллюстрируем это различие на простом примере. Пусть ![]() , а
, а ![]() и
и ![]() — нечеткие подмножества
множества
— нечеткие подмножества
множества ![]() ,
определяемые следующим образом:
,
определяемые следующим образом:
![]() , (6.34)
, (6.34)
![]() . (6.35)
. (6.35)
Тогда
![]() , (6.36)
, (6.36)
в то время как
![]() . (6.37)
. (6.37)
Отметим,
что такое же различие имеет место и в случае отрицания не и
операции ![]() ,
как указывалось в замечании 6.1.
,
как указывалось в замечании 6.1.
Замечание
6.4. Следует отметить, что, применяя принцип обобщения (3.96) к вычислению
значений ![]() ,
, ![]() и
и ![]() , мы молчаливо
предполагали, что
, мы молчаливо
предполагали, что ![]() и
и
![]() —
невзаимодействующие нечеткие переменные в смысле замечания 3.20. Если
—
невзаимодействующие нечеткие переменные в смысле замечания 3.20. Если ![]() и
и ![]() — взаимодействующие
переменные, то необходимо применять принцип обобщения не в форме (3.96), а в
форме (3.97). Интересно заметить, что вопрос о возможном взаимодействии между
— взаимодействующие
переменные, то необходимо применять принцип обобщения не в форме (3.96), а в
форме (3.97). Интересно заметить, что вопрос о возможном взаимодействии между ![]() и
и ![]() возникает даже в том
случае, когда
возникает даже в том
случае, когда ![]() и
и
![]() — точки в
— точки в ![]() , а не нечеткие
переменные.
, а не нечеткие
переменные.
Замечание
6.5. Применяя принцип обобщения с целью определения операций ![]() ,
, ![]() ,
, ![]() и
и ![]() применительно к
лингвистическим значениям истинности, мы в сущности рассматриваем нечеткую
логику как обобщение многозначной логики. В таком же смысле можно рассматривать
классическую трёхзначную логику как обобщение двузначной логики (см. (6.64)).
применительно к
лингвистическим значениям истинности, мы в сущности рассматриваем нечеткую
логику как обобщение многозначной логики. В таком же смысле можно рассматривать
классическую трёхзначную логику как обобщение двузначной логики (см. (6.64)).

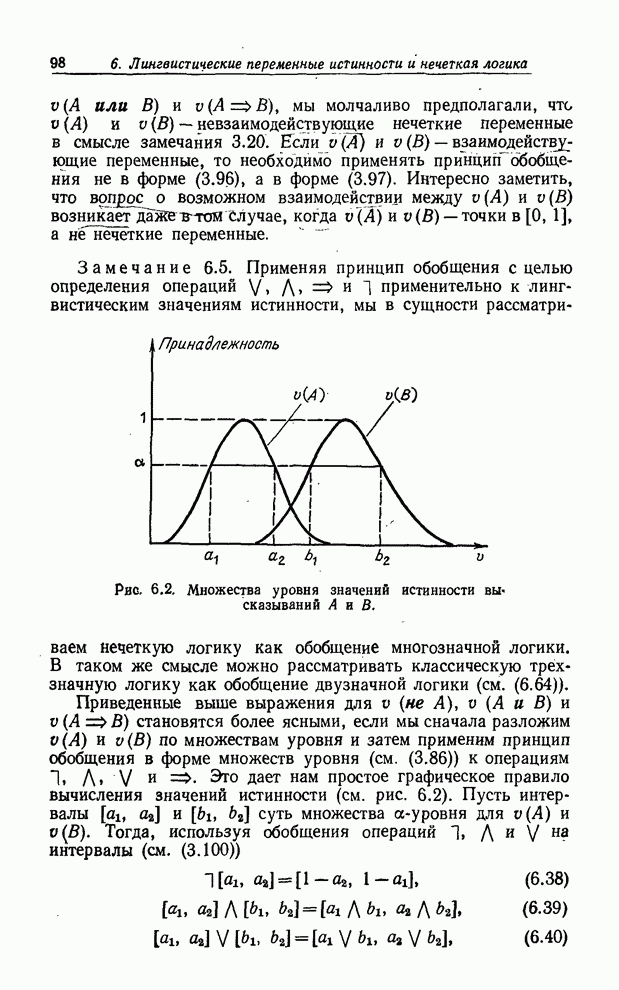
Рис. 6.2. Множества уровня значений истинности
высказываний ![]() и
и
![]() .
.
Приведенные
выше выражения для ![]() ,
,
![]() и
и ![]() становятся более
ясными, если мы сначала разложим
становятся более
ясными, если мы сначала разложим ![]() и
и ![]() по множествам уровня и затем применим
принцип обобщения в форме множеств уровня (см. (3.86)) к операциям
по множествам уровня и затем применим
принцип обобщения в форме множеств уровня (см. (3.86)) к операциям ![]() ,
, ![]() ,
, ![]() и
и ![]() . Это дает нам простое графическое
правило вычисления значений истинности (см. рис. 6.2). Пусть интервалы
. Это дает нам простое графическое
правило вычисления значений истинности (см. рис. 6.2). Пусть интервалы ![]() и
и ![]() суть множества
суть множества ![]() -уровня для
-уровня для ![]() и
и ![]() . Тогда, используя
обобщения операций
. Тогда, используя
обобщения операций ![]() ,
,
![]() и
и ![]() на интервалы (см.
(3.100))
на интервалы (см.
(3.100))
![]() , (6.38)
, (6.38)
![]() , (6.39)
, (6.39)
![]() , (6.40)
, (6.40)
можно
легко найти множества ![]() -уровня для
-уровня для ![]() ,
, ![]() и
и ![]() . После того как эти множества
уровня найдены, легко определить
. После того как эти множества
уровня найдены, легко определить ![]() ,
, ![]() и
и ![]() , варьируя
, варьируя ![]() от 0 до 1.
от 0 до 1.
В
качестве простой иллюстрации рассмотрим определение конъюнкции лингвистических
значений истинности ![]() и
и ![]() , функции принадлежности которых имеют
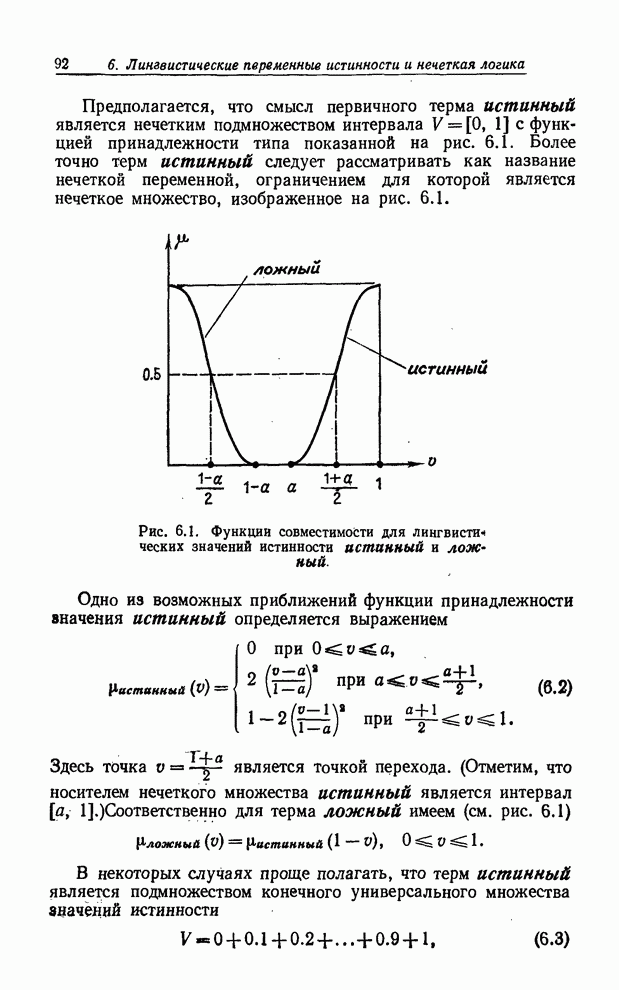
вид, показанный на рис. 6.1.
, функции принадлежности которых имеют
вид, показанный на рис. 6.1.

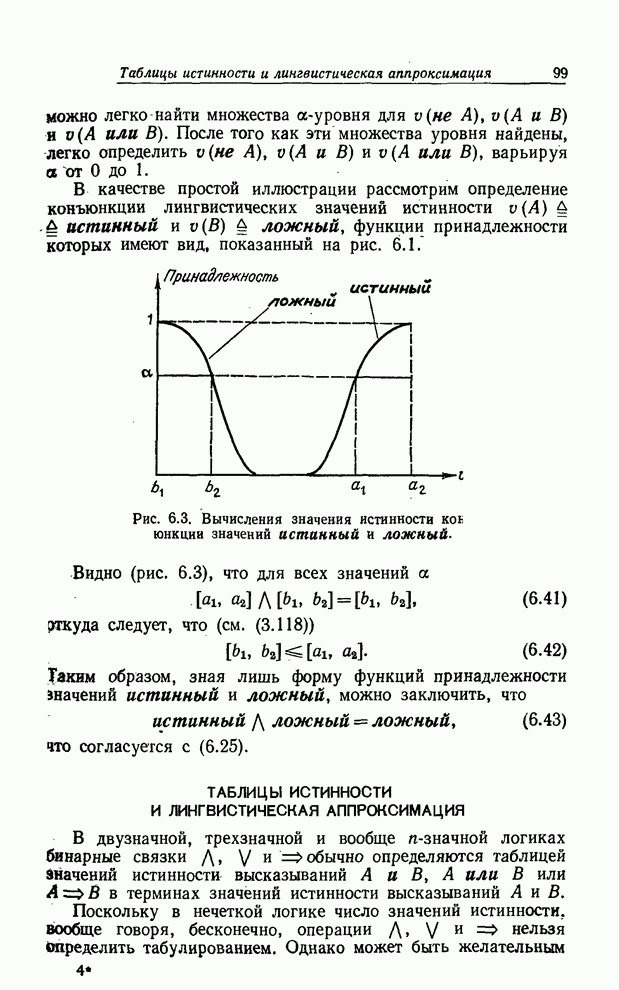
Рис. 6.3. Вычисления значения истинности конъюнкции значений истинный и ложный.
Видно
(рис. 6.3), что для всех значений ![]()
![]() , (6.41)
, (6.41)
откуда следует, что (см. (3.118))
![]() . (6.42)
. (6.42)
Таким образом, зная лишь форму функций принадлежности значений истинный и ложный, можно заключить, что
![]() , (6.43)
, (6.43)
что согласуется с (6.25).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
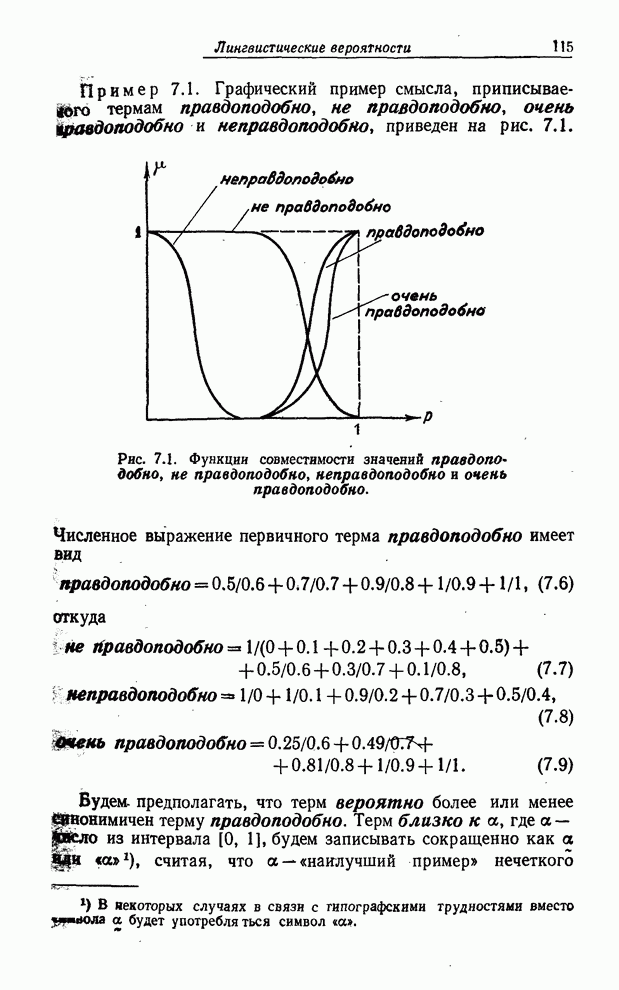
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
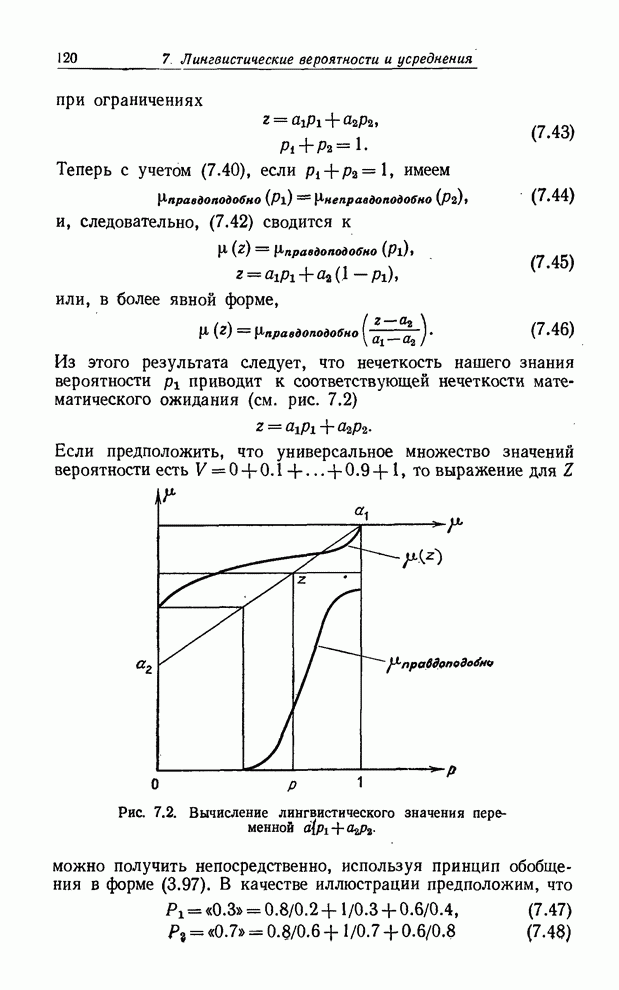
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
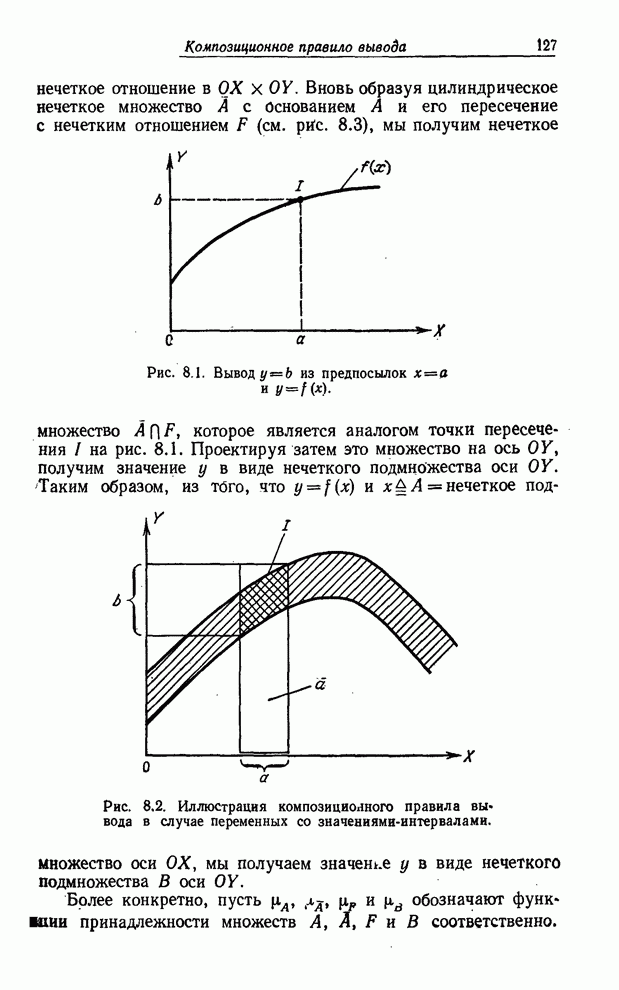
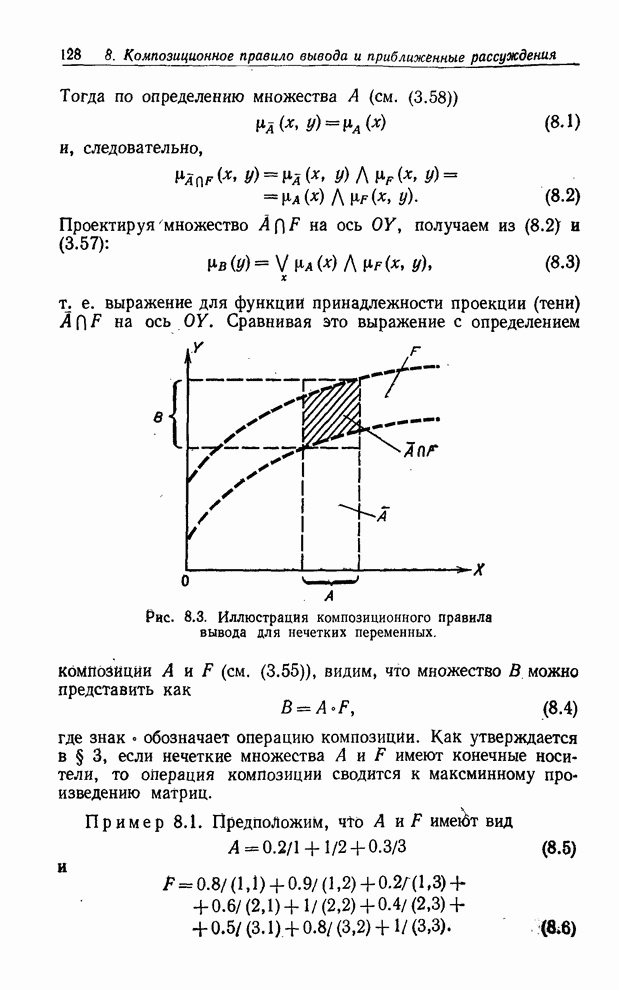
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
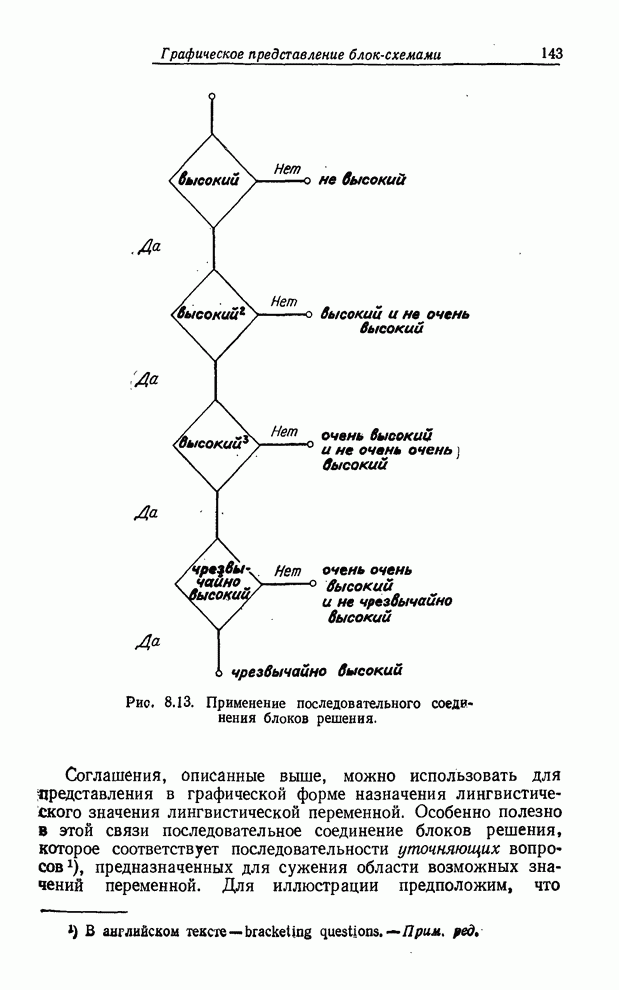
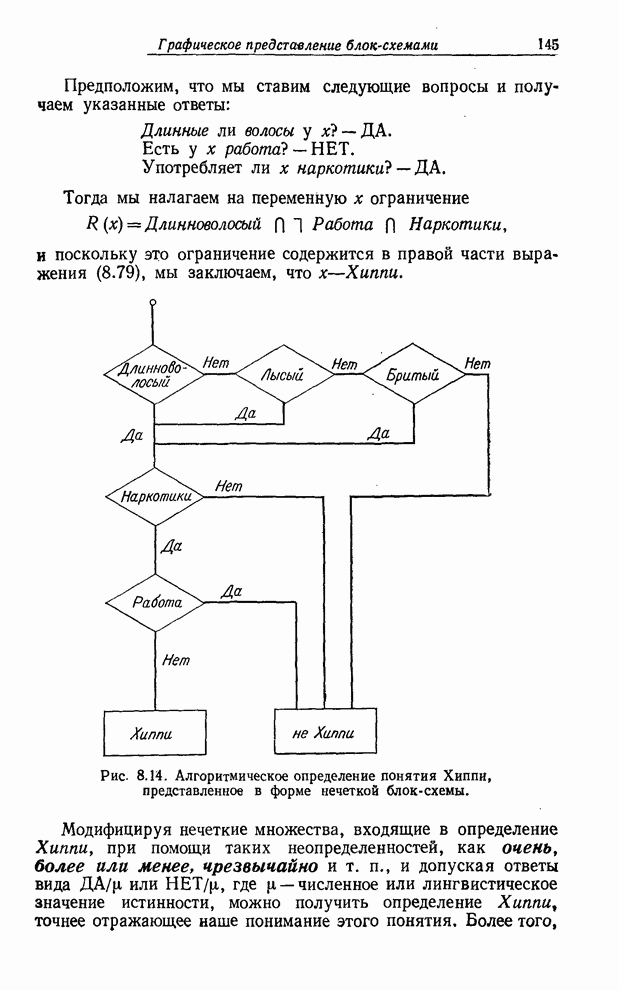
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ