| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
Теперь мы можем обобщить понятия, введенные в § 2, на так называемые нечеткие переменные. Нам будет удобно формализовать понятие нечеткой переменной аналогично тому, как это было сделано в определении 2.1 понятия обычной (не нечеткой) переменной.
Определение
4.1.
Нечеткая переменная характеризуется тройкой ![]() , где
, где ![]() — название переменной,
— название переменной, ![]() — универсальное
множество (конечное или бесконечное),
— универсальное
множество (конечное или бесконечное), ![]() — общее название элементов множества
— общее название элементов множества ![]() ,
, ![]() — нечеткое
подмножество множества
— нечеткое
подмножество множества ![]() , представляющее собой нечеткое ограничение
на значения переменной
, представляющее собой нечеткое ограничение
на значения переменной ![]() , обусловленное
, обусловленное![]() . [Как и в случае обычных (не
нечетких) переменных, вместо
. [Как и в случае обычных (не
нечетких) переменных, вместо ![]() мы будем, как правило,
писать сокращенно
мы будем, как правило,
писать сокращенно![]() ,
,![]() или
или ![]() , где
, где ![]() — общее
название значений переменной
— общее
название значений переменной ![]() , и будем называть
, и будем называть ![]() ограничением на
ограничением на ![]() или
ограничением, обусловленным
или
ограничением, обусловленным ![]() .] Неограниченная обычная (не нечеткая)
переменная
.] Неограниченная обычная (не нечеткая)
переменная ![]() является
для
является
для ![]() базовой
переменной.
базовой
переменной.
Уравнение
назначения для
![]() имеет вид
имеет вид
![]() (4.1)
(4.1)
и
отражает то, что элементу ![]() назначается значение
назначается значение ![]() с учетом ограничения
с учетом ограничения
![]() .
.
Ту
степень, с которой удовлетворяется это равенство, будем называть
совместимостью значения ![]() с
с ![]() и обозначать
ее через
и обозначать
ее через ![]() .
По определению
.
По определению
![]() , (4.2)
, (4.2)
где
![]() —
степень принадлежности
—
степень принадлежности![]() ограничению
ограничению![]() .
.
Замечание
4.2.
Важно отметить, что совместимость значения ![]() не есть то же самое, что вероятность
значения
не есть то же самое, что вероятность
значения ![]() . Совместимость
. Совместимость
![]() с
с ![]() — это
лишь мера того, насколько значение
— это
лишь мера того, насколько значение ![]() удовлетворяет ограничению
удовлетворяет ограничению ![]() ; она не имеет
никакого отношения к тому, насколько вероятно или невероятно это значение.
; она не имеет
никакого отношения к тому, насколько вероятно или невероятно это значение.
Замечание
4.3.
Используя аналогию с саквояжем (см. замечание 2.4), нечеткую переменную можно
уподобить саквояжу с ярлыком, имеющему мягкие стенки. Тогда ![]() — надпись на ярлыке
(название саквояжа),
— надпись на ярлыке
(название саквояжа), ![]() — список предметов, которые в принципе
можно поместить в саквояж, а
— список предметов, которые в принципе
можно поместить в саквояж, а ![]() — часть этого списка, в которой для
каждого предмета
— часть этого списка, в которой для
каждого предмета ![]() указано
число
указано
число![]() ,
характеризующее степень легкости, с которой предмет
,
характеризующее степень легкости, с которой предмет ![]() можно поместить в саквояж
можно поместить в саквояж ![]() (рис. 4.1).
(рис. 4.1).

Рис. 4.1. Аналогия с саквояжем для унарной нечеткой переменной
Чтобы
упростить обозначения, удобно использовать один и тот же символ для ![]() и
и ![]() и
положиться на контекст для разрешения возможных неопределенностей. Покажем это
на следующем примере.
и
положиться на контекст для разрешения возможных неопределенностей. Покажем это
на следующем примере.
Пример
4.4.
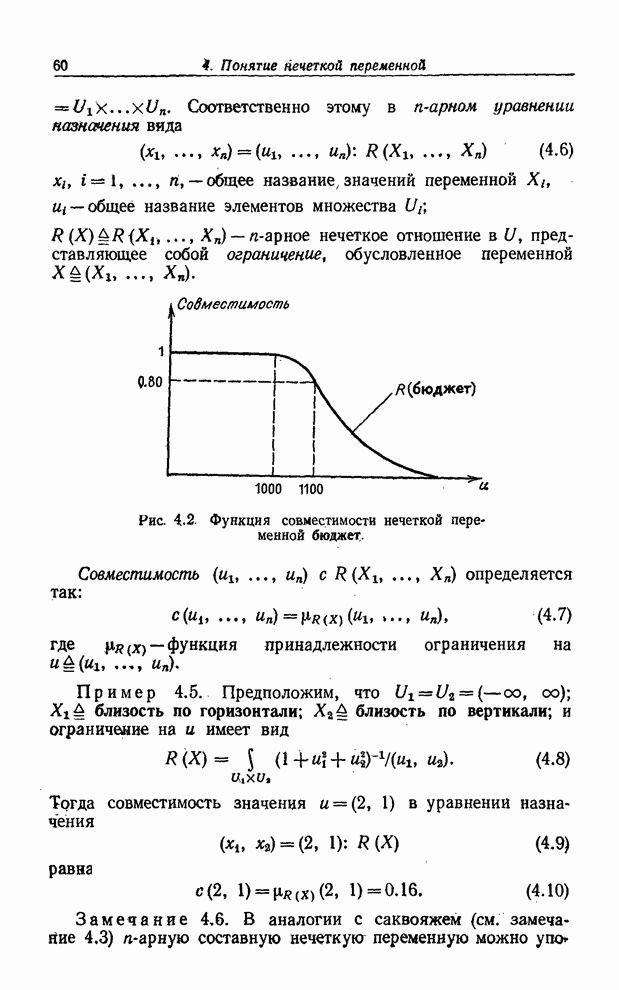
Рассмотрим нечеткую переменную, именуемую бюджет. Пусть ![]() , а
, а![]() определяется
следующим образом (см. рис. 4.2):
определяется
следующим образом (см. рис. 4.2):
 . (4.3)
. (4.3)
Тогда в уравнении назначения
![]() (4.4)
(4.4)
совместимость
значения ![]() с
ограничением
с
ограничением![]() равна
равна
![]() . (4.5)
. (4.5)
Как
и в случае обычных (не нечетких) переменных, если ![]() — нечеткие переменные в
— нечеткие переменные в ![]() соответственно, то
соответственно, то ![]() есть
есть ![]() -арная составная
переменная в
-арная составная
переменная в ![]() .
Соответственно этому в
.
Соответственно этому в ![]() -арном уравнении назначения вида
-арном уравнении назначения вида
![]() (4.6)
(4.6)
![]() , – общее название значений переменной
, – общее название значений переменной![]() ,
, ![]() — общее название
элементов множества
— общее название
элементов множества ![]() ;
; ![]() –
– ![]() -арное нечеткое отношение в
-арное нечеткое отношение в ![]() , представляющее
собой ограничение, обусловленное переменной
, представляющее
собой ограничение, обусловленное переменной ![]() .
.

Рис. 4.2. Функция совместимости нечеткой переменной бюджет.
Совместимость
![]() с
с ![]() определяется
так:
определяется
так:
![]() , (4.7)
, (4.7)
где
![]() — функция
принадлежности ограничения на
— функция
принадлежности ограничения на ![]() .
.
Пример
4.5.
Предположим, что ![]() ;
;
![]() близость
по горизонтали;
близость
по горизонтали; ![]() близость по вертикали; и ограничение
на
близость по вертикали; и ограничение
на ![]() имеет
вид
имеет
вид
 . (4.8)
. (4.8)
Тогда
совместимость значения ![]() в уравнении назначения
в уравнении назначения
![]() (4.9)
(4.9)
равна
![]() . (4.10)
. (4.10)
Замечание
4.6.
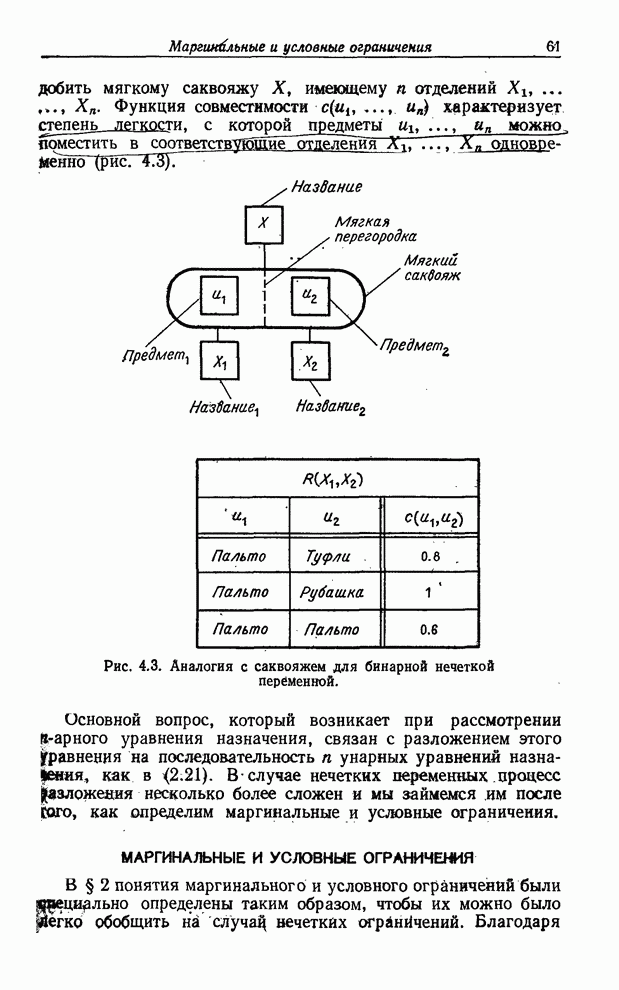
В аналогии с саквояжем (см. замечание 4.3) ![]() -арную составную нечеткую переменную
можно уподобить мягкому саквояжу
-арную составную нечеткую переменную
можно уподобить мягкому саквояжу ![]() , имеющему
, имеющему ![]() отделений
отделений ![]() . Функция совместимости
. Функция совместимости ![]() характеризует степень
легкости, с которой предметы
характеризует степень
легкости, с которой предметы ![]() можно поместить в
соответствующие отделения
можно поместить в
соответствующие отделения ![]() одновременно (рис. 4.3).
одновременно (рис. 4.3).

Рис. 4.3. Аналогия с саквояжем для бинарной нечеткой переменной.
Основной
вопрос, который возникает при рассмотрении ![]() -арного уравнения назначения, связан с
разложением этого уравнения на последовательность
-арного уравнения назначения, связан с
разложением этого уравнения на последовательность ![]() унарных уравнений назначения, как в
(2.21). В случае нечетких переменных процесс разложения несколько более сложен
и мы займемся им после того, как определим маргинальные и условные ограничения.
унарных уравнений назначения, как в
(2.21). В случае нечетких переменных процесс разложения несколько более сложен
и мы займемся им после того, как определим маргинальные и условные ограничения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
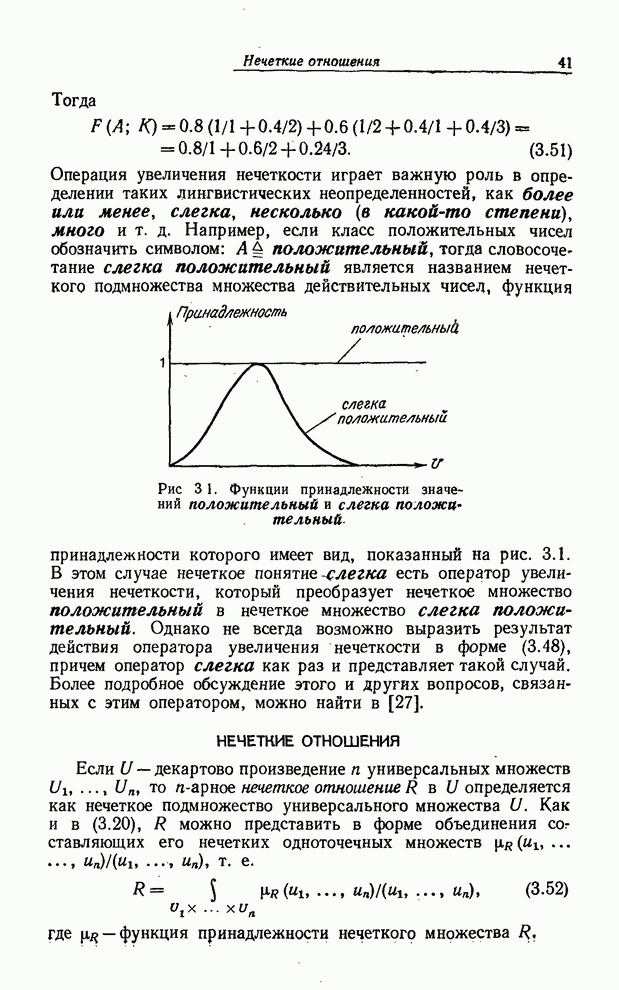
- НЕЧЕТКИЕ ОТНОШЕНИЯ
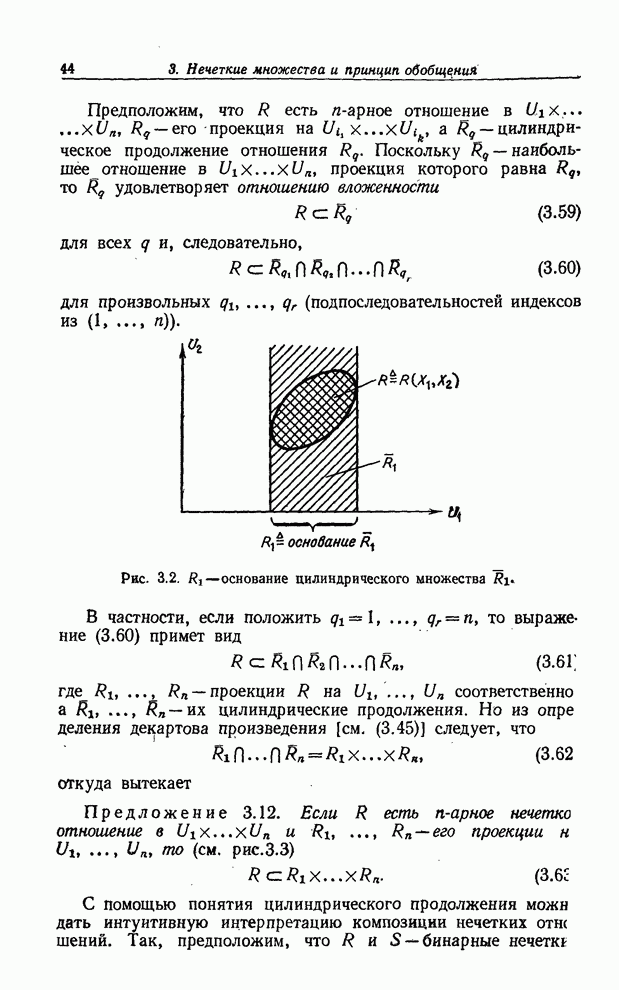
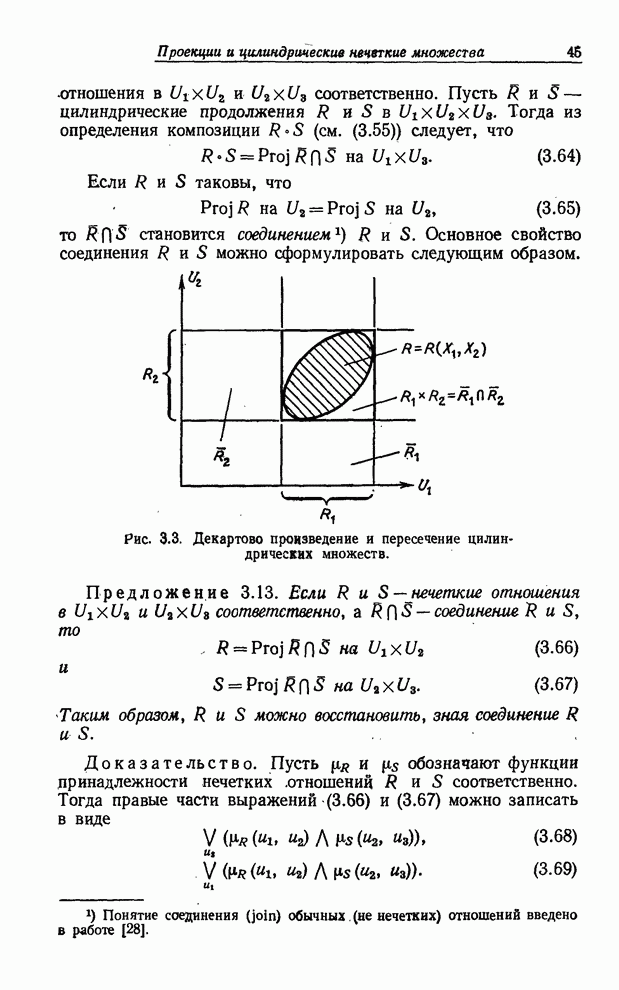
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
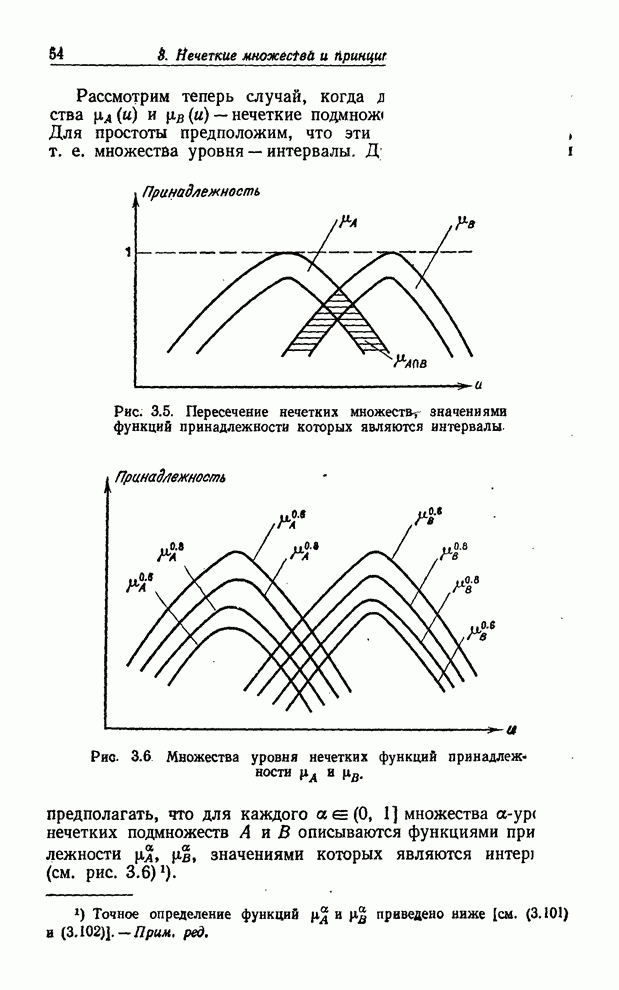
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
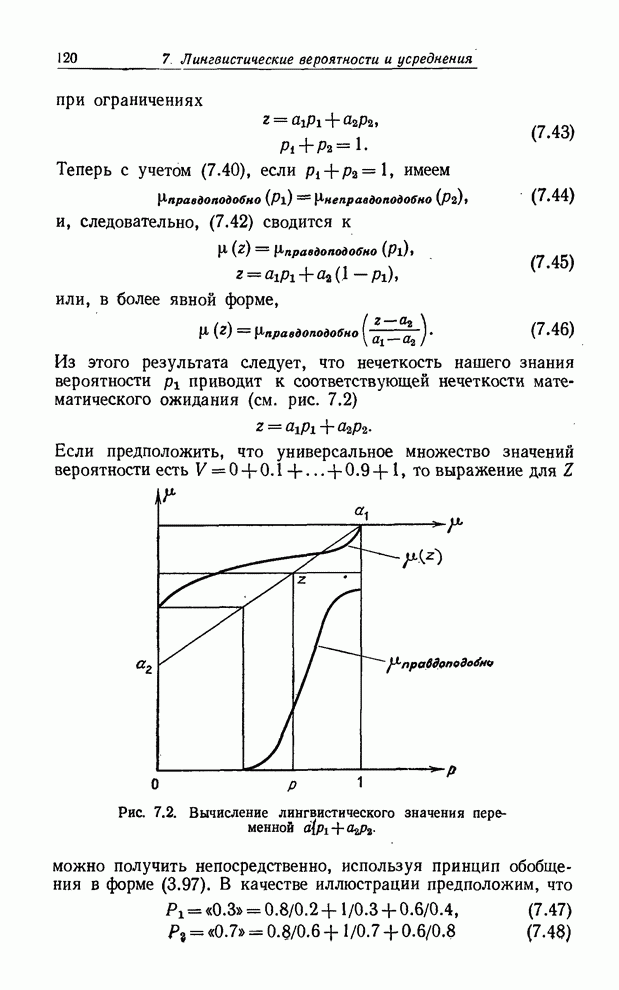
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
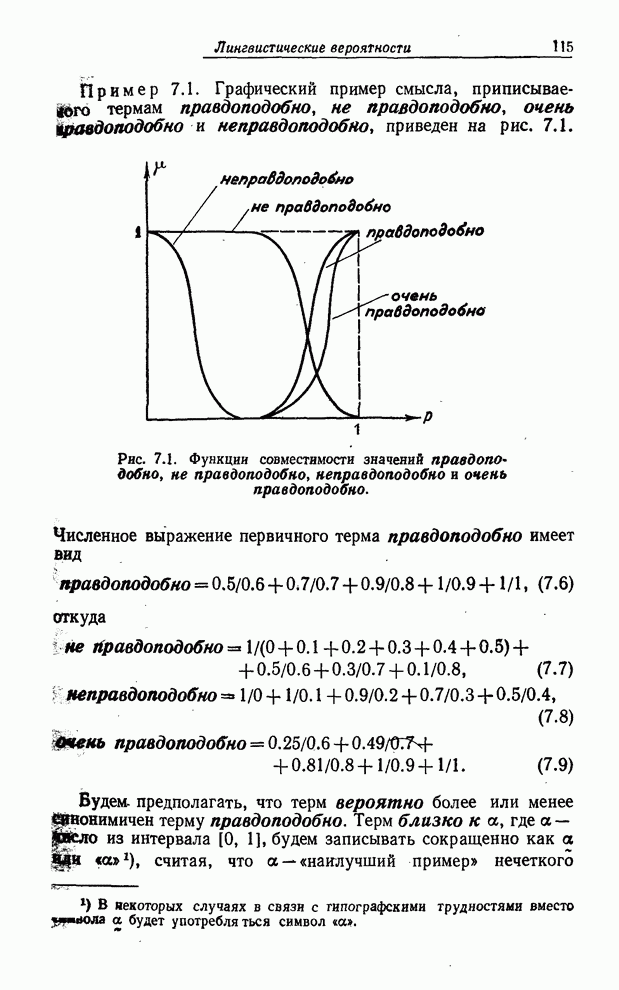
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
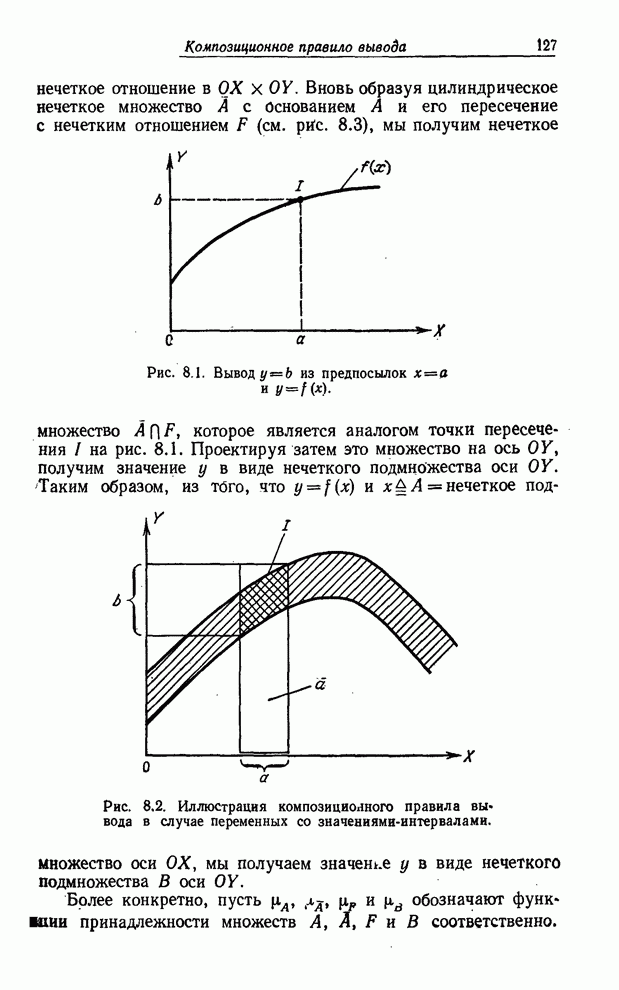
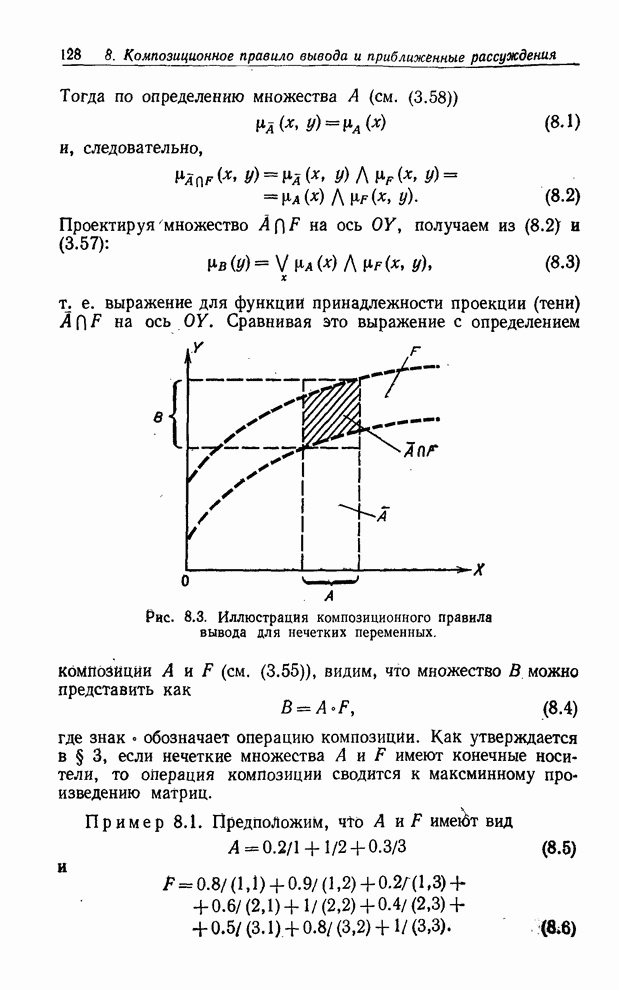
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
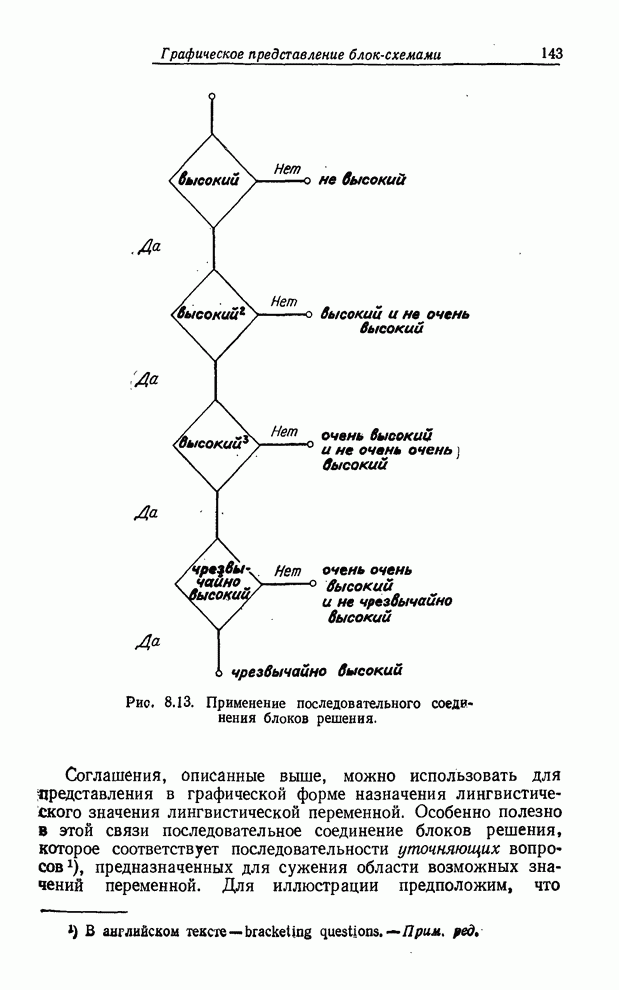
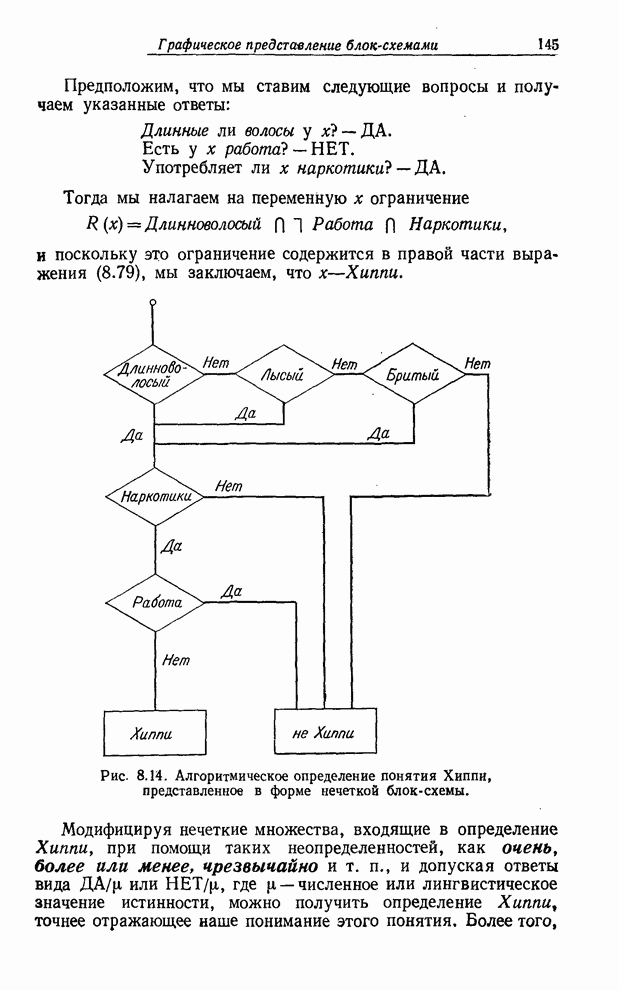
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ