| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
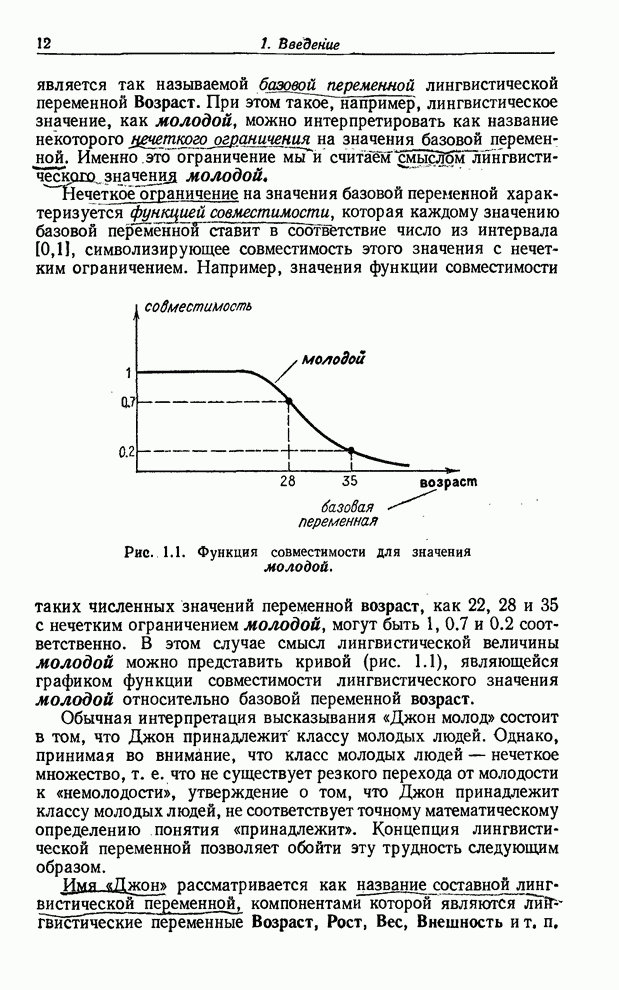
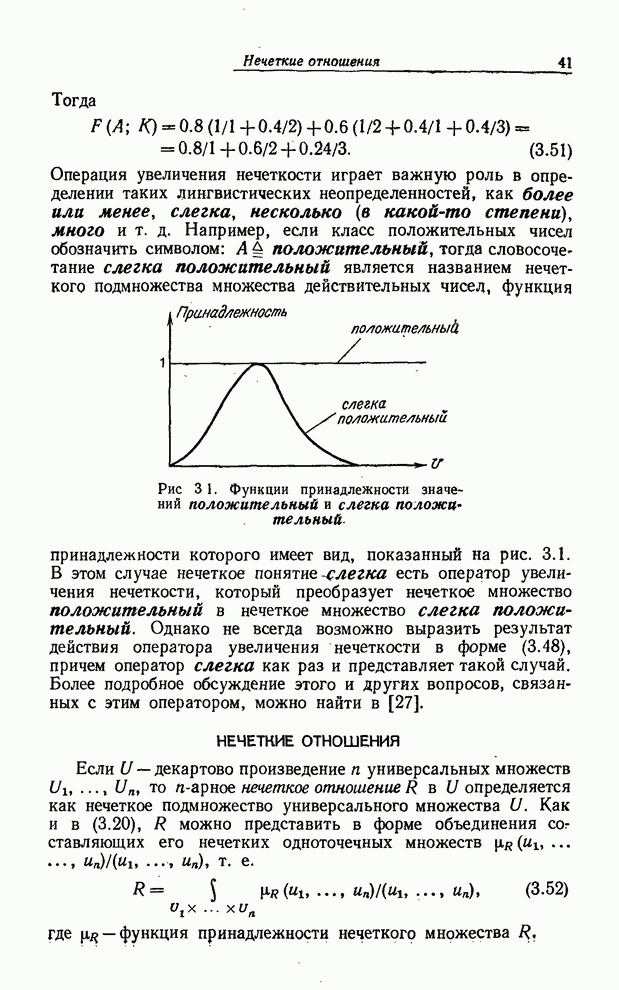
ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
Чтобы упростить изложение, будем рассматривать переменную ![]() с конечным
универсальным множеством
с конечным
универсальным множеством
![]() . (7.1)
. (7.1)
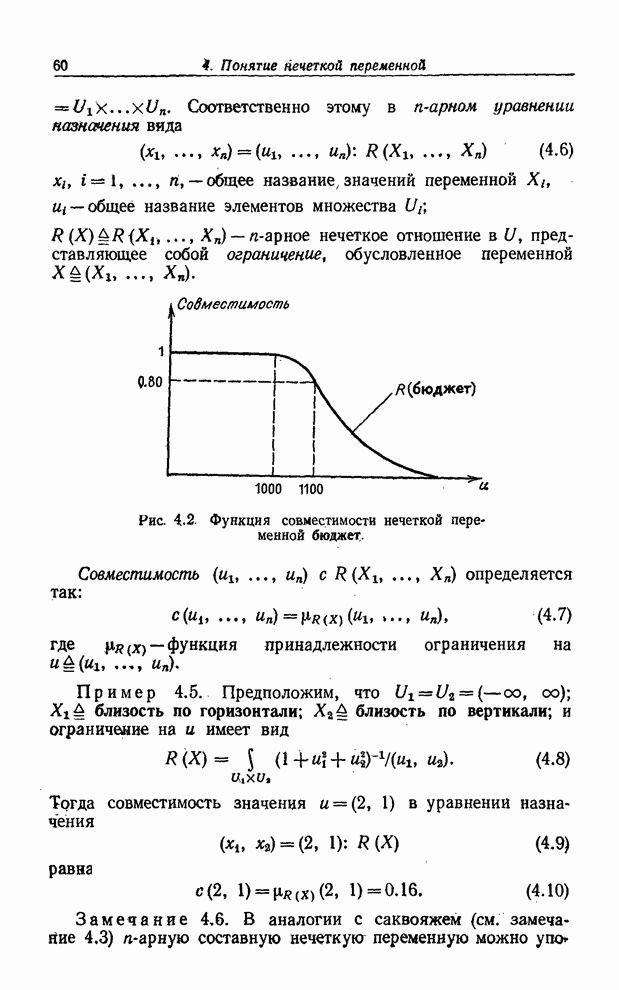
Кроме того, будем предполагать, что ограничение, обусловленное ![]() , совпадает с
, совпадает с ![]() . Иными словами,
любая точка в
. Иными словами,
любая точка в ![]() может
быть выбрана в качестве значения переменной
может
быть выбрана в качестве значения переменной ![]() .
.
Каждому элементу ![]() мы поставим в соответствие
лингвистическую вероятность
мы поставим в соответствие
лингвистическую вероятность ![]() , которая является булевой
лингвистической переменной в смысле определения 5.9;
, которая является булевой
лингвистической переменной в смысле определения 5.9; ![]() , — базовая переменная для
, — базовая переменная для ![]() . Для определенности
предположим, что универсальное множество
. Для определенности
предположим, что универсальное множество ![]() , соответствующее
, соответствующее ![]() , представляет собой либо
единичный интервал [0, 1], либо конечное множество
, представляет собой либо
единичный интервал [0, 1], либо конечное множество
![]() . (7.2)
. (7.2)
Будем употреблять ![]() в качестве общего названия переменных
в качестве общего названия переменных ![]() ; типичное
терм-множество для
; типичное
терм-множество для ![]() имеет
такой вид:
имеет
такой вид:
 (7.3)
(7.3)
где термы правдоподобно, вероятно и близко к играют роль первичных термов.
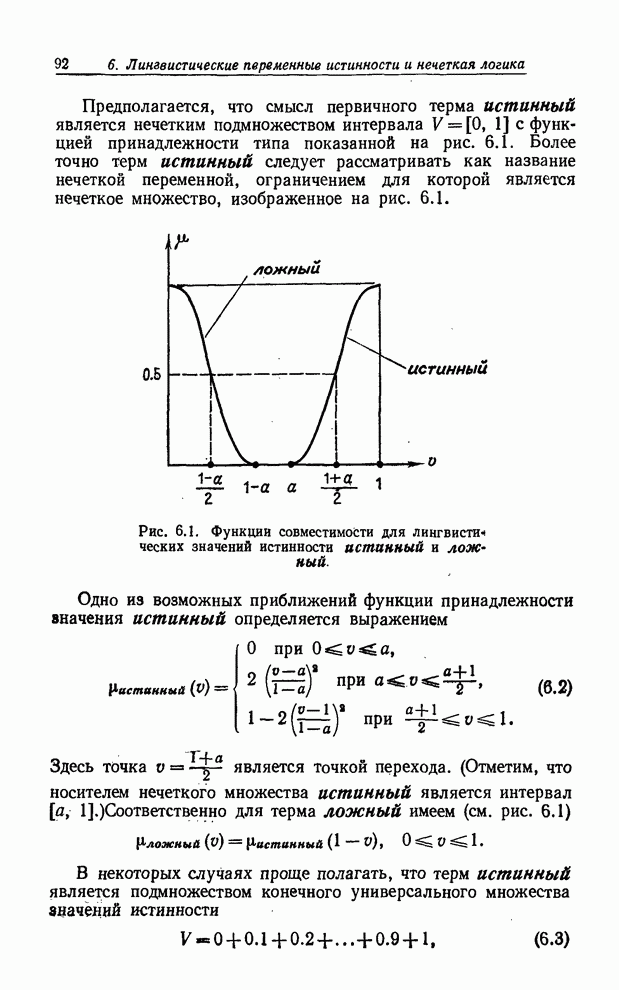
Будем считать, что функция принадлежности нечеткого множества правдоподобно имеет тот же вид, что и функция принадлежности нечеткого множества истинно (см. (6.2)), а функции принадлежности нечетких множеств не правдоподобно и неправдоподобно определим следующим образом:
![]() ,
(7.4)
,
(7.4)
![]() ,
(7.5)
,
(7.5)
где ![]() —
общее название переменных
—
общее название переменных ![]() .
.
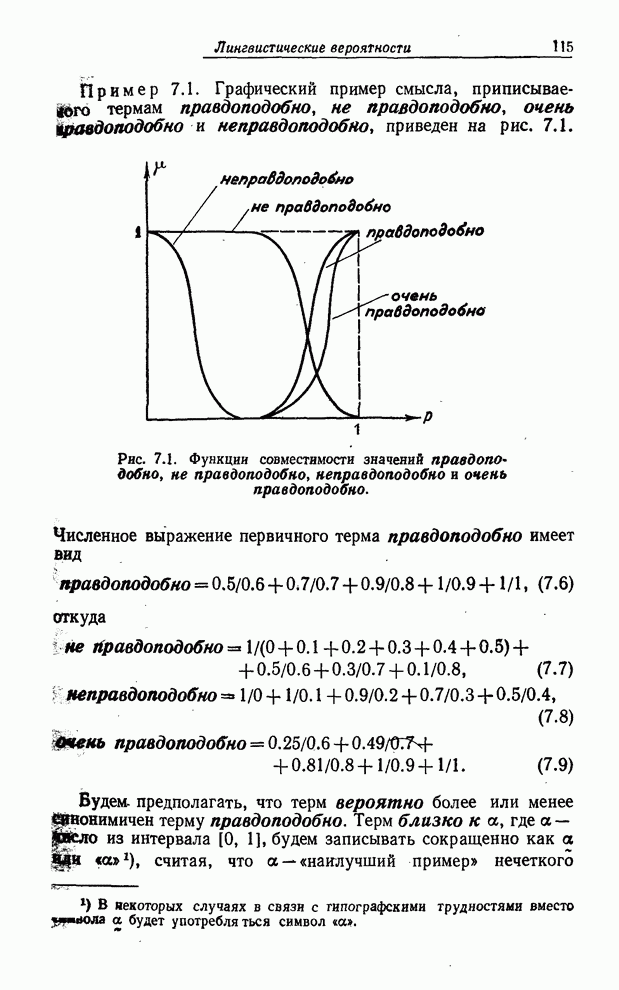
Пример 7.1. Графический пример смысла, приписываемого термам правдоподобно, не правдоподобно, очень правдоподобно и неправдоподобно, приведен на рис.7.1.

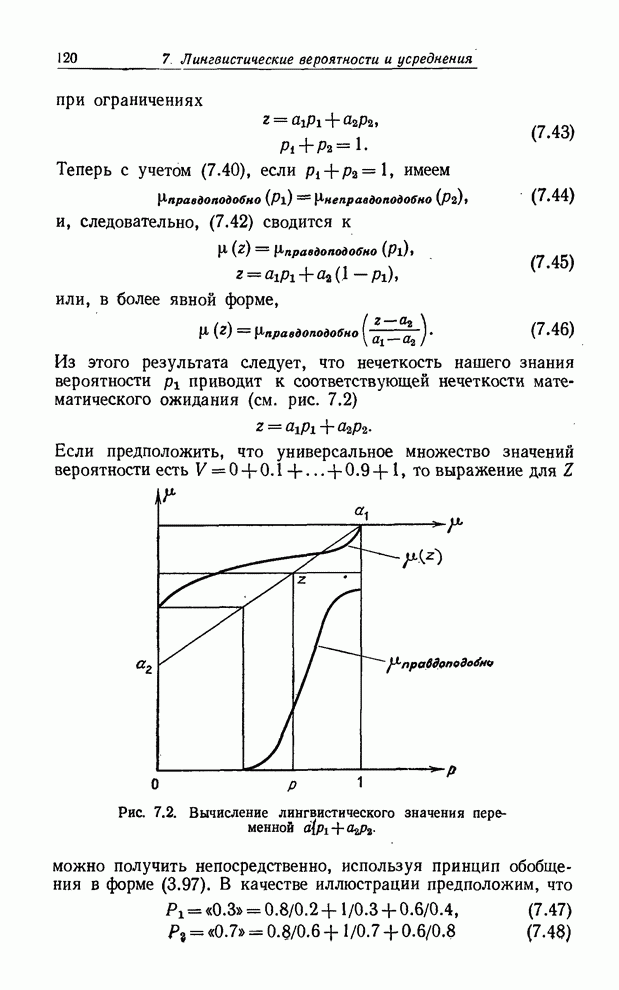
Рис. 7.1. Функции совместимости значений правдоподобно, не правдоподобно, неправдоподобно и очень правдоподобно.
Численное выражение первичного терма правдоподобно имеет вид
![]() , (7.6)
, (7.6)
откуда
![]() (7.7)
(7.7)
![]() , (7.8)
, (7.8)
![]() . (7.9)
. (7.9)
Будем предполагать, что терм вероятно более или
менее синонимичен терму правдоподобно. Терм близко к ![]() , где
, где ![]() — число из интервала
[0, 1], будем записывать сокращенно как
— число из интервала
[0, 1], будем записывать сокращенно как ![]() или
или ![]() ), считая, что
), считая, что ![]() — «наилучший пример»
нечеткого множества «
— «наилучший пример»
нечеткого множества «![]() ». Имея это в виду, можно записать
». Имея это в виду, можно записать
![]() ,
(7.10)
,
(7.10)
![]() ,
(7.11)
,
(7.11)
![]() , (7.12)
, (7.12)
отсюда следует, что
![]()
Терм в ![]() будем обозначать через
будем обозначать через ![]() или
или ![]() в случае, когда
двойной индекс необходим. Так, если
в случае, когда
двойной индекс необходим. Так, если ![]() очень правдоподобно, то
очень правдоподобно, то ![]() обозначает, что терм
очень правдоподобно назначен в качестве значения лингвистической
переменной
обозначает, что терм
очень правдоподобно назначен в качестве значения лингвистической
переменной ![]() .
.
Введем ![]() -арную лингвистическую переменную
-арную лингвистическую переменную ![]() , которая
представляет собой список значений лингвистических вероятностей,
соответствующий
, которая
представляет собой список значений лингвистических вероятностей,
соответствующий ![]() .
Саму переменную
.
Саму переменную ![]() будем
называть при этом лингвистической случайной переменной. По аналогии с
распределениями значений истинности (см. (6.74)) совокупность списков значений
лингвистических вероятностей будем называть распределением лингвистических
вероятностей.
будем
называть при этом лингвистической случайной переменной. По аналогии с
распределениями значений истинности (см. (6.74)) совокупность списков значений
лингвистических вероятностей будем называть распределением лингвистических
вероятностей.
Назначение переменной ![]() значения
значения ![]() можно выразить равенством
можно выразить равенством
![]() (7.13)
(7.13)
где ![]() используется
как общее название нечетких переменных, составляющих
используется
как общее название нечетких переменных, составляющих ![]() . Например, можно писать
. Например, можно писать
![]() , (7.14)
, (7.14)
где очень правдоподобно можно отождествить с ![]() (т. е. со значением
(т. е. со значением ![]() , назначенным
переменной
, назначенным
переменной ![]() ).
).
Важное свойство лингвистических вероятностей ![]() состоит в том, что
они являются
состоит в том, что
они являются ![]() -взаимодействующими
в смысле определения 6.8. Взаимодействие между
-взаимодействующими
в смысле определения 6.8. Взаимодействие между ![]() есть следствие ограничения (
есть следствие ограничения (![]() арифметическая
сумма)
арифметическая
сумма)
![]() , (7.15)
, (7.15)
в котором ![]() — базовые переменные (т. е. числовые
вероятности), связанные с
— базовые переменные (т. е. числовые
вероятности), связанные с ![]() .
.
Более конкретно, пусть ![]() обозначает нечеткое
обозначает нечеткое ![]() -арное отношение в
-арное отношение в
![]() ,
представляющее (7.15). Пусть, кроме того,
,
представляющее (7.15). Пусть, кроме того, ![]() обозначает ограничение на значения
переменной
обозначает ограничение на значения
переменной ![]() .
Тогда ограничение, обусловленное
.
Тогда ограничение, обусловленное ![]() -арной нечеткой переменной
-арной нечеткой переменной ![]() , можно записать в
виде
, можно записать в
виде
![]() . (7.16)
. (7.16)
Откуда следует, что без ограничения (7.15) нечеткие переменные ![]() были бы
невзаимодействующими.
были бы
невзаимодействующими.
Пример 7.2. Допустим, что
![]() , (7.17)
, (7.17)
![]() . (7.18)
. (7.18)
Тогда
 (7.19)
(7.19)
Что касается отношения ![]() , то его можно выразить в виде
, то его можно выразить в виде
![]() , (7.20)
, (7.20)
и, образуя пересечение (7.19) и (7.20), получаем
![]() , (7.21)
, (7.21)
т.е. выражение для ограничения, обусловленного составной
переменной ![]() .
Ясно, что
.
Ясно, что ![]() состоит
из тех членов выражения для
состоит
из тех членов выражения для ![]() , которые удовлетворяют ограничению
(7.15).
, которые удовлетворяют ограничению
(7.15).
Замечание 7.3. Следует отметить, что
ограничение ![]() вида
(7.21) является нормальным ограничением (см 3.23)). Это справедливо также и в
более общем случае, когда
вида
(7.21) является нормальным ограничением (см 3.23)). Это справедливо также и в
более общем случае, когда![]() имеют вид
имеют вид
![]() , (7.22)
, (7.22)
и ![]() Заметим,
что в примере 7.2 мы имеем
Заметим,
что в примере 7.2 мы имеем
![]() , (7.23)
, (7.23)
![]() , (7.24)
, (7.24)
![]() . (7.25)
. (7.25)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
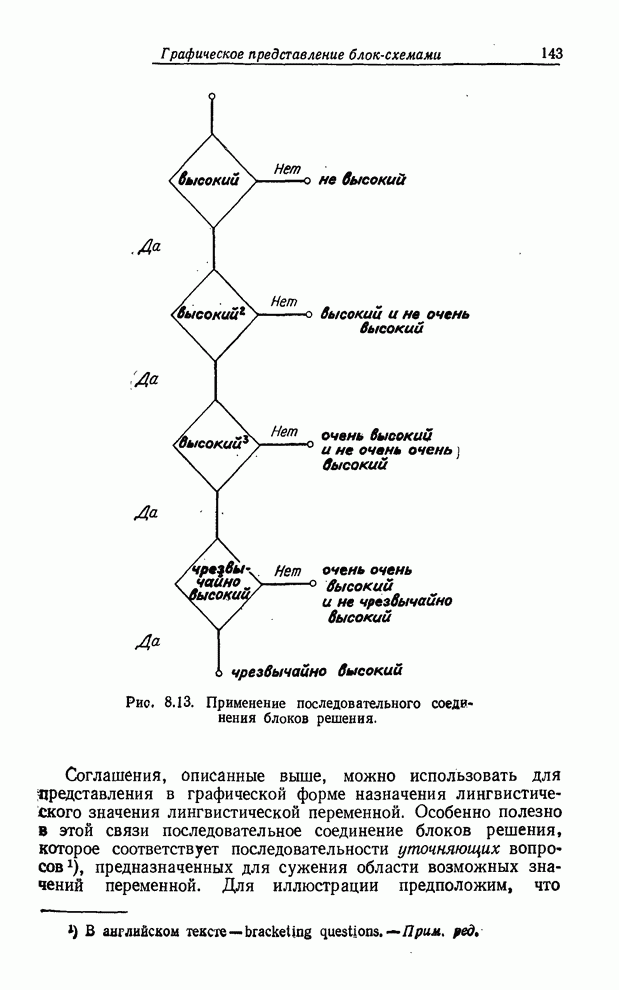
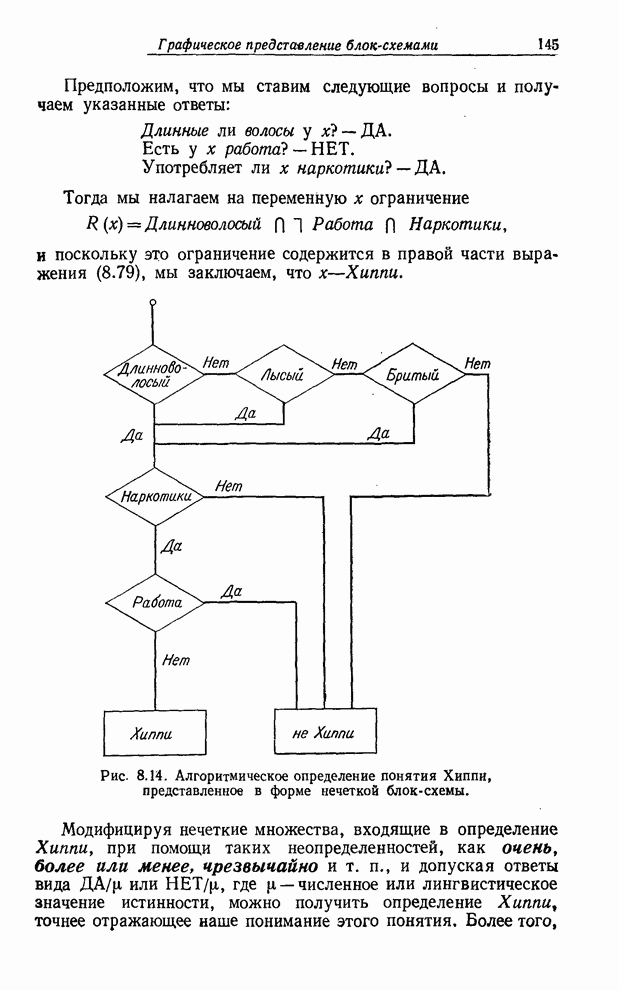
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ