| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
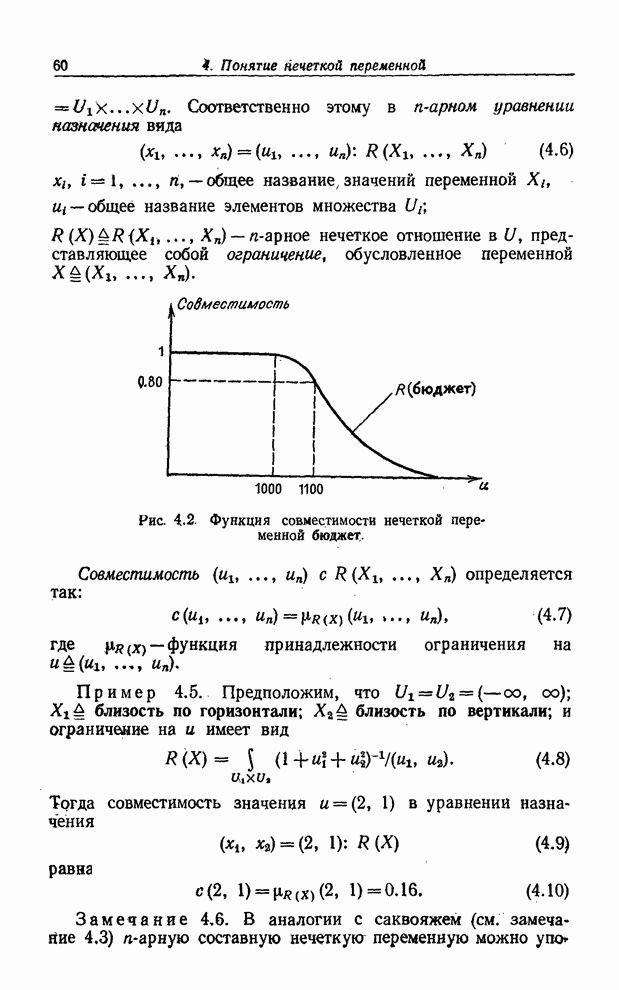
ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
Основным
понятием, которое нам понадобится в дальнейшем, является понятие взаимодействия
двух или большего числа переменных - понятие, аналогичное понятию зависимости
случайных величин. Пусть переменная ![]() связана с ограничением
связана с ограничением ![]() , которое индуцирует
ограничения
, которое индуцирует
ограничения ![]() на
на
![]() соответственно.
Введем
соответственно.
Введем
Определение
2.9. Переменные ![]() называются
невзаимодействующими при ограничении
называются
невзаимодействующими при ограничении ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() сепарабельно, т. е.
сепарабельно, т. е.
![]() , (2.16)
, (2.16)
где
для ![]()
![]() на
на
 ; (2.17)
; (2.17)
здесь
![]() и
и ![]() дополнение
дополнение ![]() в
в ![]() .
.
Пример
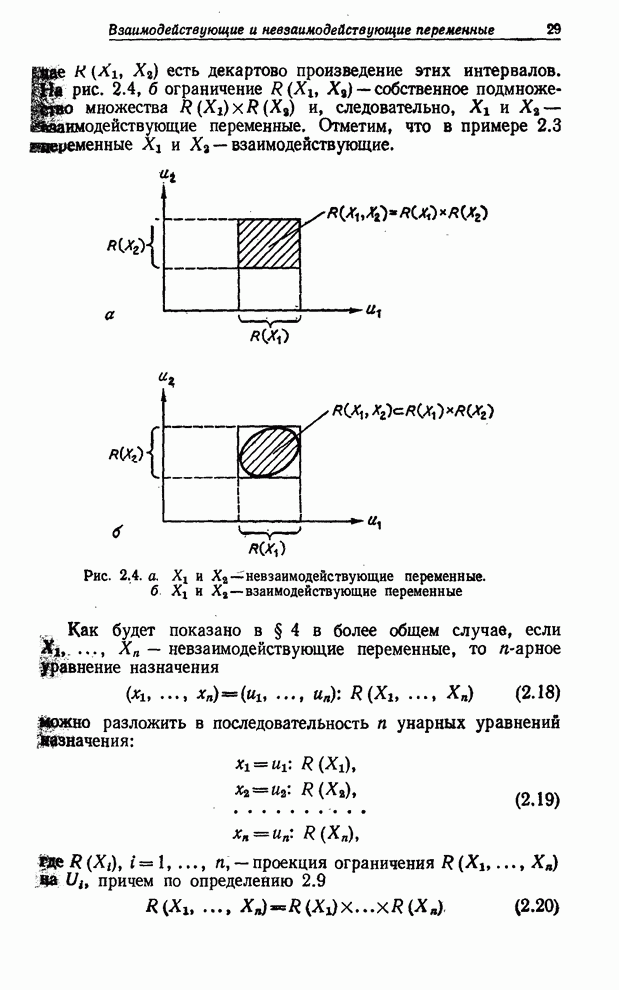
2.10. На рис.
2.4,а представлены графически две невзаимодействующие переменные ![]() и
и ![]() , ограничениями
, ограничениями ![]() и
и ![]() для которых являются
интервалы; в этом случае
для которых являются
интервалы; в этом случае ![]() есть декартово произведение этих
интервалов. На рис. 2.4,б ограничение
есть декартово произведение этих
интервалов. На рис. 2.4,б ограничение ![]() - собственное подмножество множества
- собственное подмножество множества ![]() и, следовательно,
и, следовательно, ![]() и
и ![]() - взаимодействующие
переменные. Отметим, что в примере 2.3 переменные
- взаимодействующие
переменные. Отметим, что в примере 2.3 переменные ![]() и
и ![]() - взаимодействующие.
- взаимодействующие.

Рис. 2.4.а. ![]() и
и ![]() - невзаимодействующие
переменные. б.
- невзаимодействующие
переменные. б. ![]() и
и
![]() - взаимодействующие
переменные
- взаимодействующие
переменные
Как
будет показано в § 4 в более общем случае, если ![]() - невзаимодействующие переменные, то
- невзаимодействующие переменные, то ![]() -арное уравнение
назначения
-арное уравнение
назначения
![]() (2.18)
(2.18)
можно
разложить в последовательность ![]() унарных уравнений назначения:
унарных уравнений назначения:
 (2.19)
(2.19)
где
![]() ,
, ![]() - проекция
ограничения
- проекция
ограничения ![]() на
на
![]() , причем по
определению 2.9
, причем по
определению 2.9
![]() (2.20)
(2.20)
В
случае взаимодействующих переменных ![]() последовательность
последовательность ![]() унарных уравнений назначения
принимает следующий вид [см. также (4.34)]:
унарных уравнений назначения
принимает следующий вид [см. также (4.34)]:
 (2.21)
(2.21)
где
![]() обозначает
индуцированное ограничение на
обозначает
индуцированное ограничение на ![]() при данных
при данных ![]() . Характеристическая функция этого
условного ограничения выражается следующим образом[см. (2.13)]:
. Характеристическая функция этого
условного ограничения выражается следующим образом[см. (2.13)]:
![]() (2.22)
(2.22)
причем
аргументы ![]() в
правой части этого выражения играют роль параметров.
в
правой части этого выражения играют роль параметров.

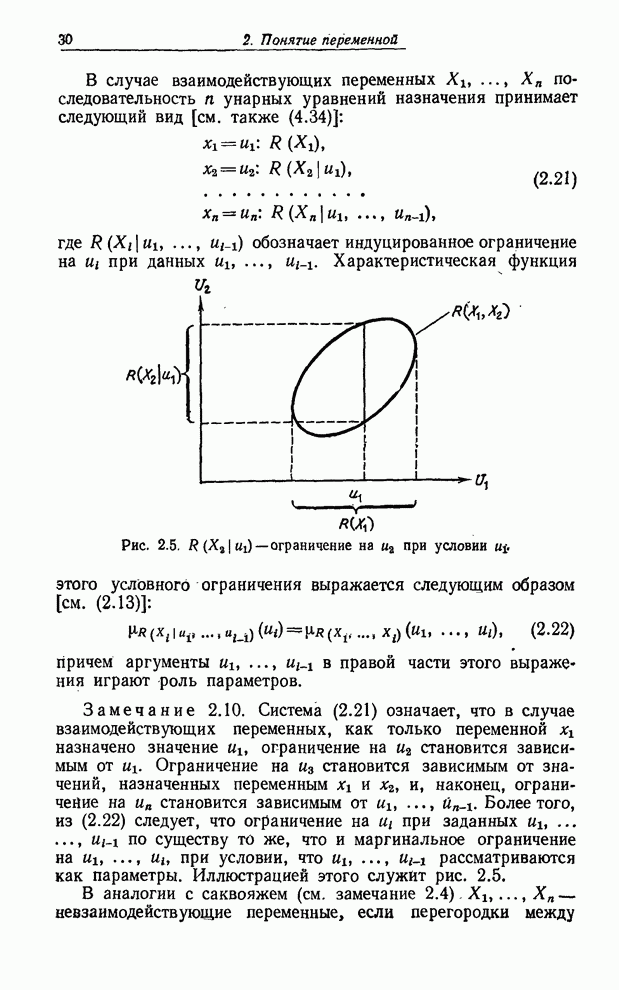
Рис. 2.5. ![]() - ограничение на
- ограничение на ![]() при условии
при условии ![]() .
.
Замечание
2.10.
Система (2.21) означает, что в случае взаимодействующих переменных, как только
переменной ![]() назначено
значение
назначено
значение ![]() , ограничение
на
, ограничение
на ![]() становится
зависимым от
становится
зависимым от ![]() .
Ограничение на
.
Ограничение на ![]() становится
зависимым от значений, назначенных переменным
становится
зависимым от значений, назначенных переменным ![]() и
и ![]() , и, наконец, ограничение на
, и, наконец, ограничение на ![]() становится зависимым
от
становится зависимым
от ![]() . Более
того, из (2.22) следует, что ограничение на
. Более
того, из (2.22) следует, что ограничение на ![]() при заданных
при заданных ![]() по существу то же,
что и маргинальное ограничение на
по существу то же,
что и маргинальное ограничение на ![]() , при условии, что
, при условии, что ![]() рассматриваются как параметры.
Иллюстрацией этого служит рис. 2.5.
рассматриваются как параметры.
Иллюстрацией этого служит рис. 2.5.
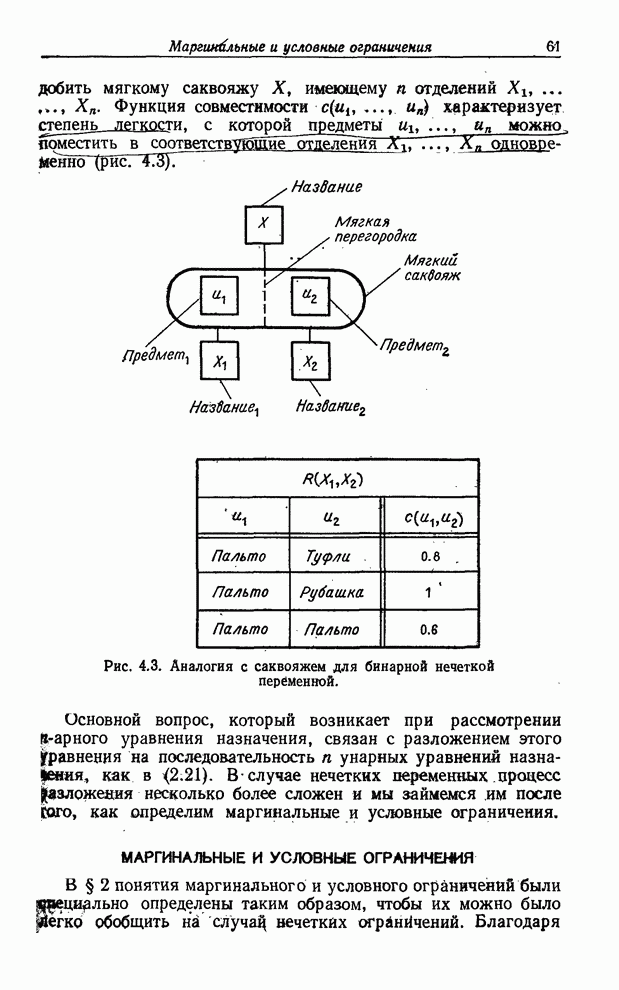
В
аналогии с саквояжем (см. замечание 2.4) ![]() — невзаимодействующие
переменные, если перегородки между отделениями саквояжа, обозначенными через
— невзаимодействующие
переменные, если перегородки между отделениями саквояжа, обозначенными через ![]() , не податливые. В
этом случае то, что помещено в одном отделении, не влияет на предметы, которые
можно поместить в другие отделения.
, не податливые. В
этом случае то, что помещено в одном отделении, не влияет на предметы, которые
можно поместить в другие отделения.
Если
же перегородки между отделениями податливые, то переменные ![]() становятся взаимодействующими
в том смысле, что помещение какого-либо предмета, скажем
становятся взаимодействующими
в том смысле, что помещение какого-либо предмета, скажем ![]() , в
, в ![]() влияет на то, что можно
поместить в остальные отделения. С этой точки зрения последовательность унарных
уравнений (2.21) есть описание того, каким образом помещение предметов
влияет на то, что можно
поместить в остальные отделения. С этой точки зрения последовательность унарных
уравнений (2.21) есть описание того, каким образом помещение предметов ![]() в отделения
в отделения ![]() влияет на ограничение
для отделения
влияет на ограничение
для отделения ![]() .
.
Определяя понятия невзаимодействия, маргинального ограничения, условного ограничения и т. п. для обычных (не нечетких) переменных, мы ставили своей целью а) показать, что понятия, аналогичные понятиям статистической независимости, маргинального распределения, условного распределения и т. п. применимы также к неслучайным, не нечетким переменным; и б) получить основу для введения подобных понятий в случае нечетких переменных.
Прежде чем перейти к этим понятиям, мы рассмотрим некоторые свойства нечетких множеств и сформулируем принцип обобщения, который будет играть важную роль в дальнейшем изложении.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
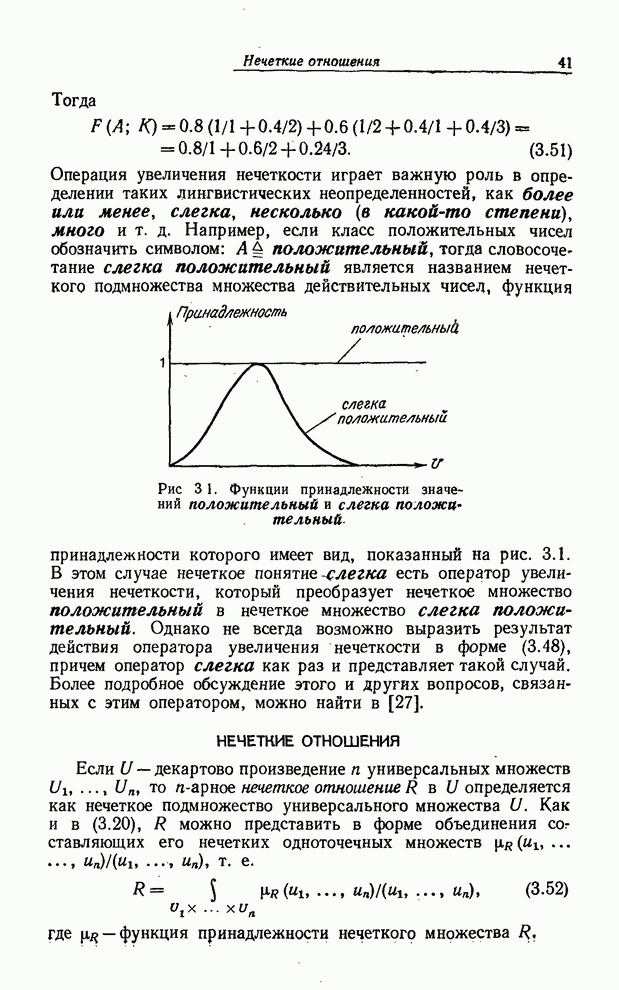
- НЕЧЕТКИЕ ОТНОШЕНИЯ
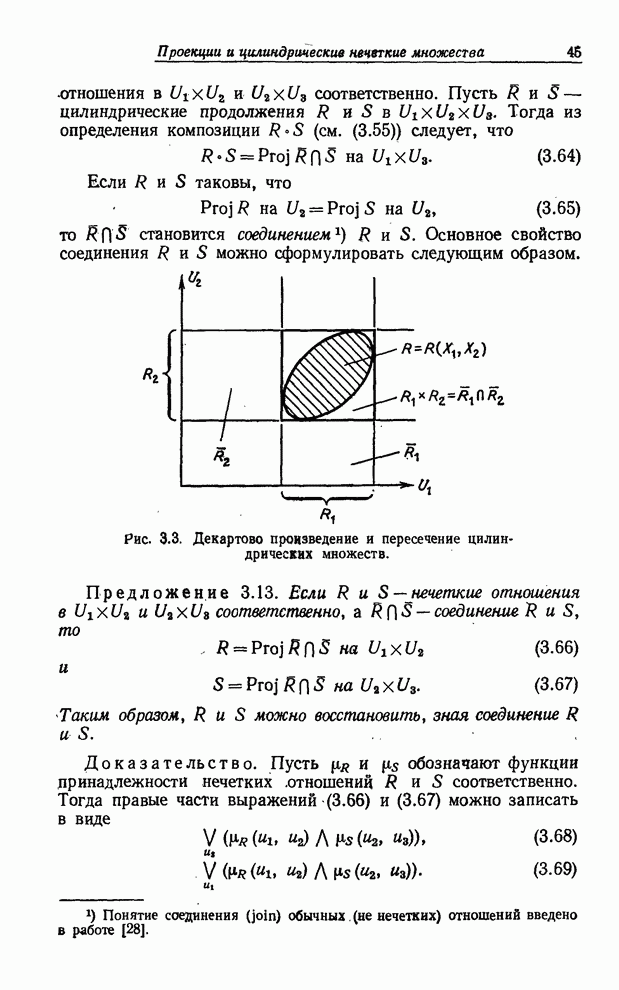
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
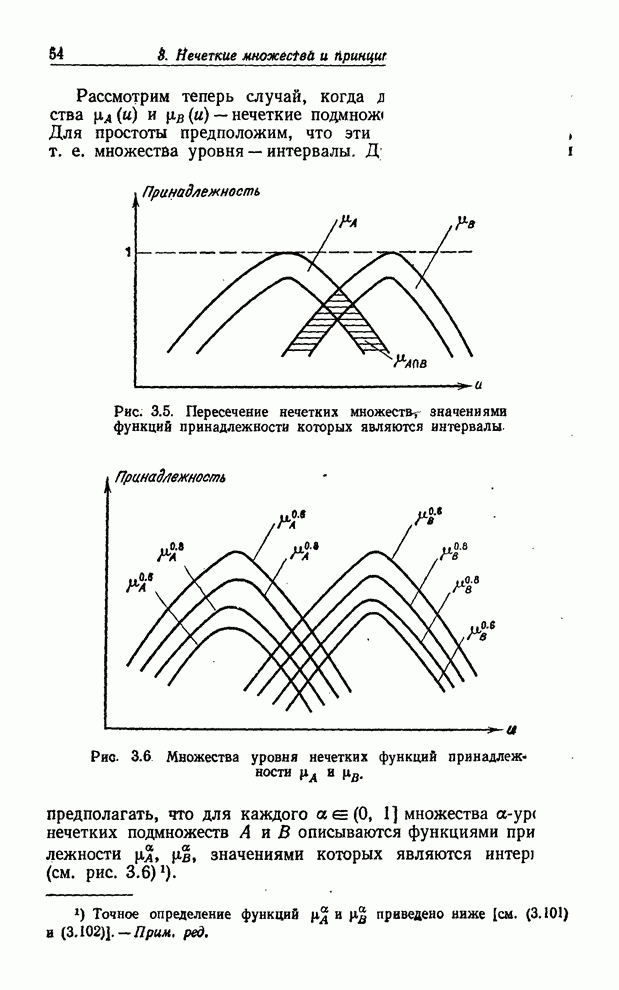
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
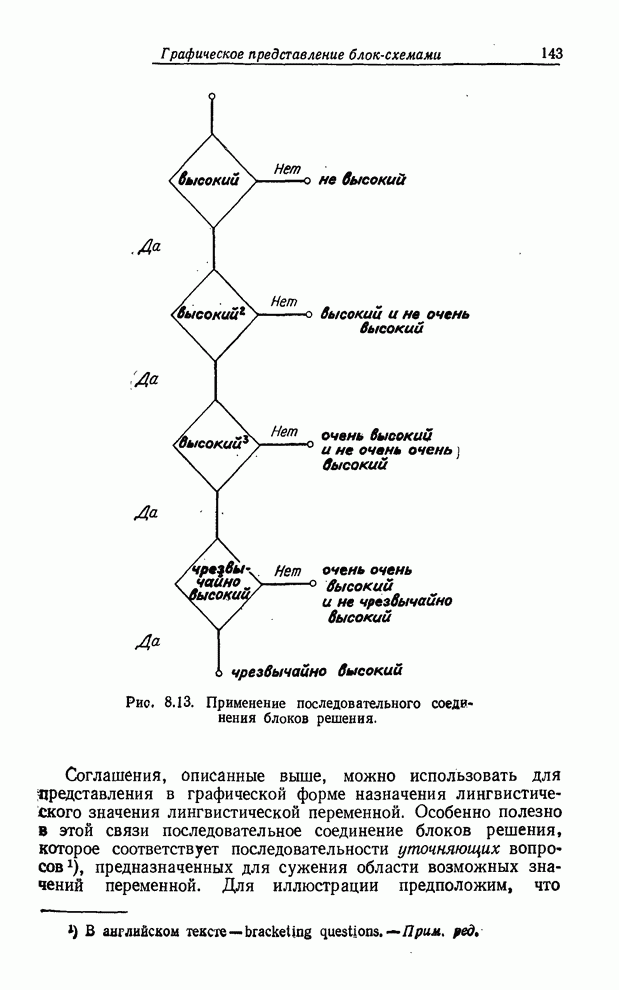
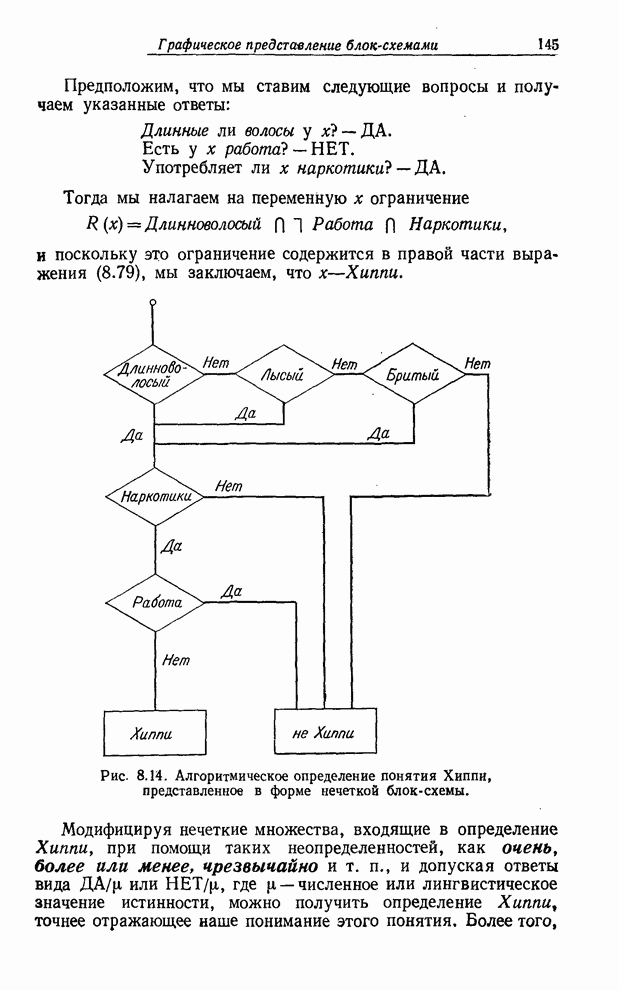
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ