| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
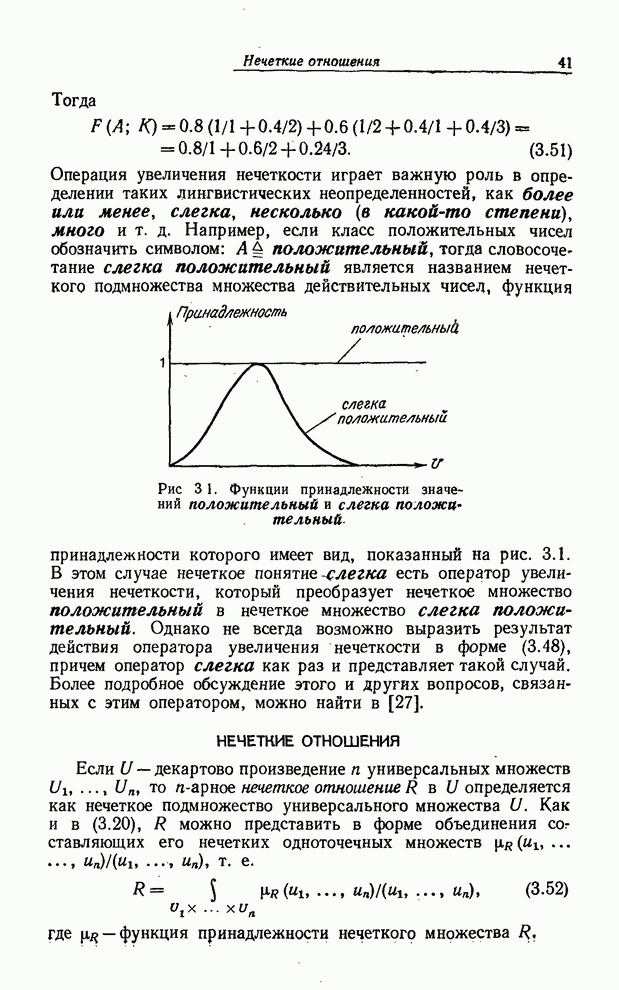
КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
Композиционное правило вывода — это всего лишь обобщение следующей
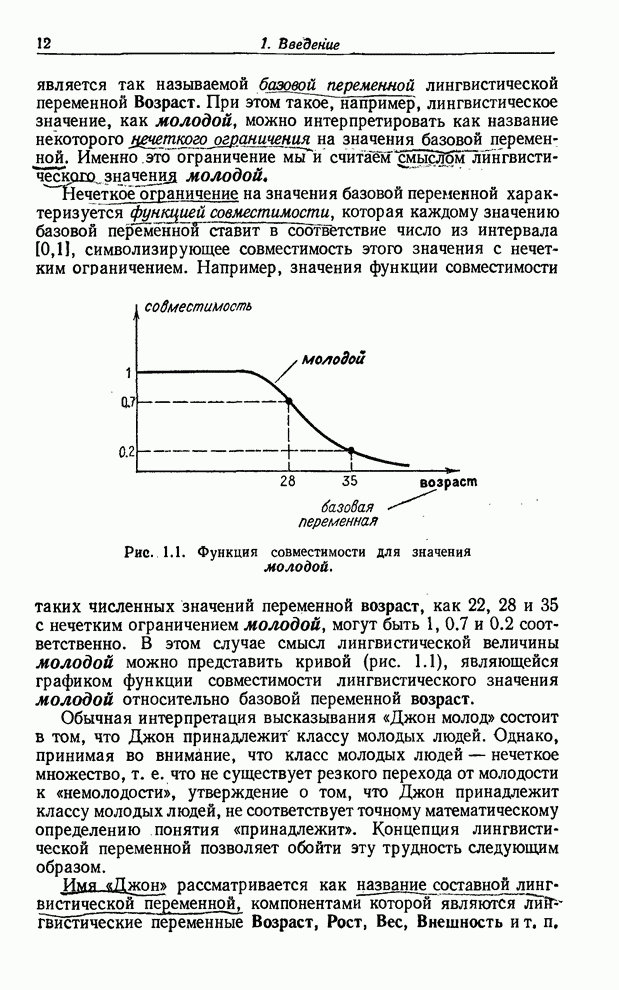
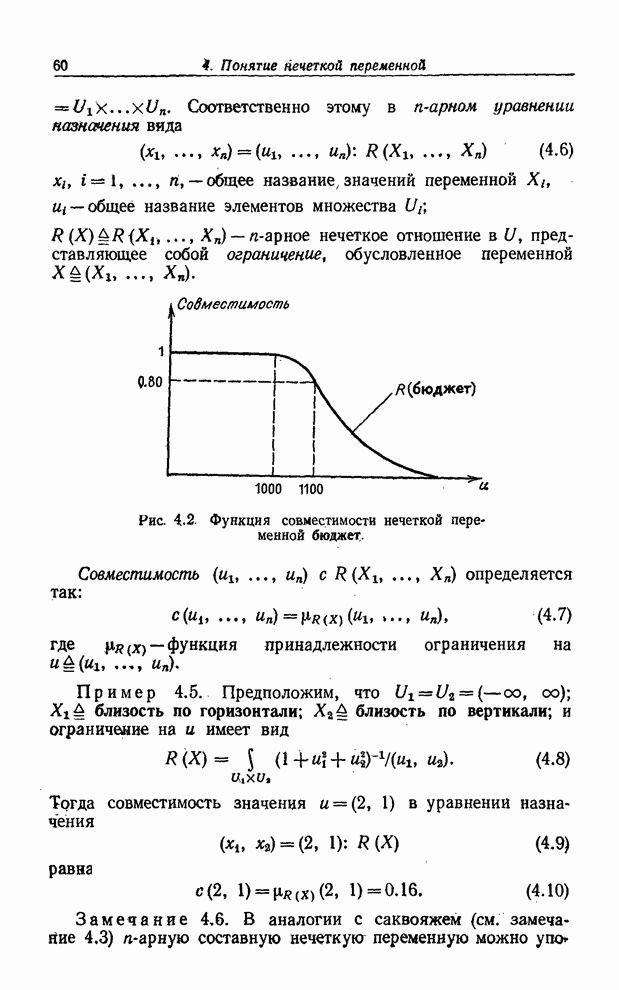
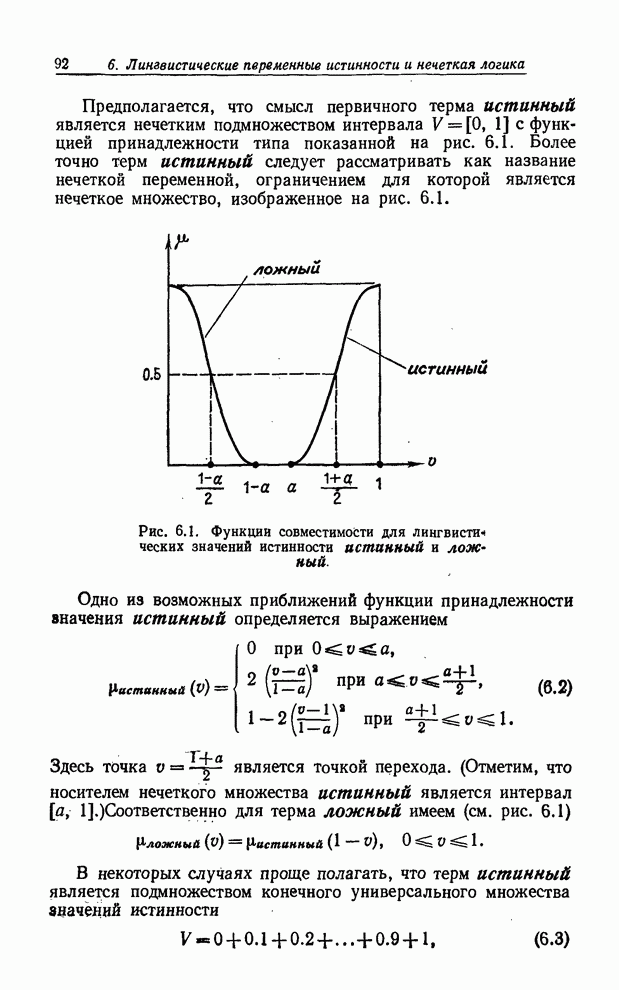
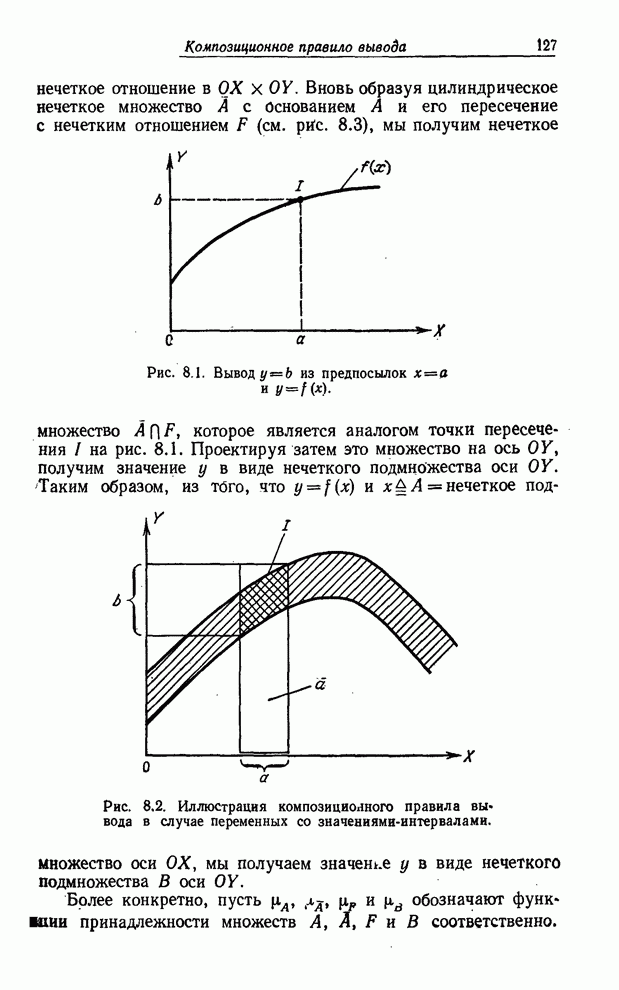
знакомой процедуры. Обращаясь к рис. 8.1, предположим, что имеется кривая ![]() и задано значение
и задано значение ![]() . Тогда из того, что
. Тогда из того, что ![]() и
и ![]() , мы можем заключить,
что
, мы можем заключить,
что ![]() .
.
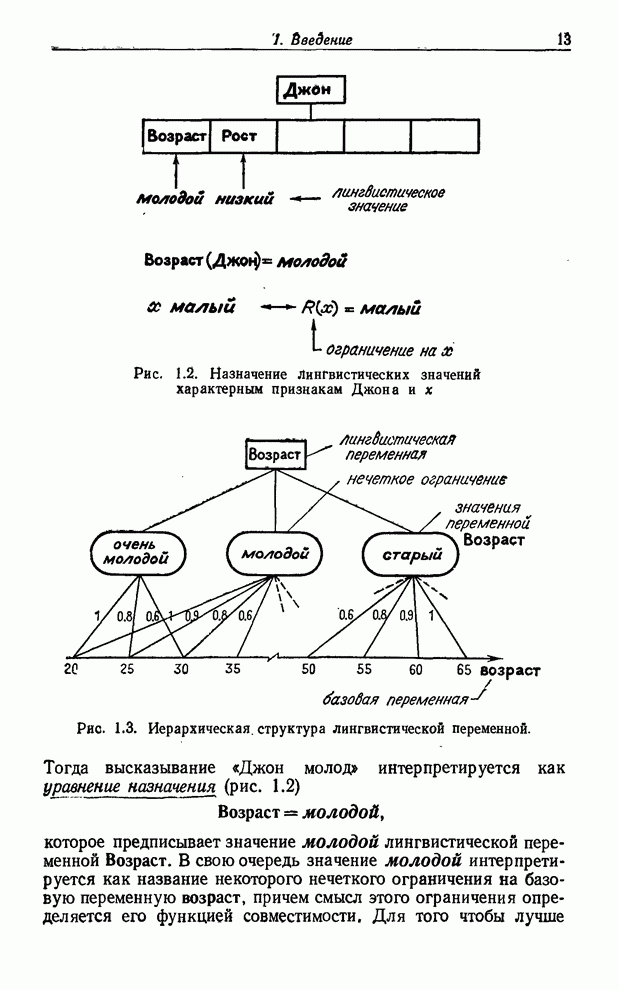
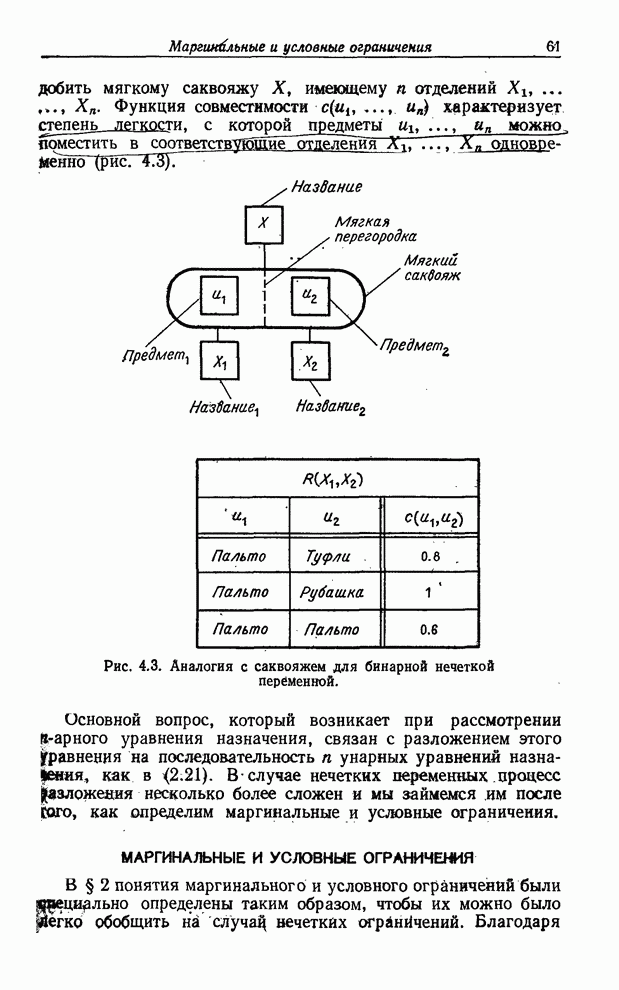
Обобщим теперь этот процесс, предположив, что ![]() — интервал, а
— интервал, а ![]() — функция, значения
которой суть интервалы, как на рис. 8.2. В этом случае, чтобы найти интервал
— функция, значения
которой суть интервалы, как на рис. 8.2. В этом случае, чтобы найти интервал
![]() , соответствующий интервалу
, соответствующий интервалу ![]() , мы сначала построим
цилиндрическое множество
, мы сначала построим
цилиндрическое множество ![]() с основанием
с основанием ![]() (см. (3.58)) и найдем его
пересечение
(см. (3.58)) и найдем его
пересечение ![]() с
кривой, значения которой суть интервалы. Затем спроектируем это пересечение на
ось
с
кривой, значения которой суть интервалы. Затем спроектируем это пересечение на
ось ![]() и
получим желаемое значение
и
получим желаемое значение ![]() в виде интервала
в виде интервала ![]() .
.
Чтобы продвинуться еще на один шаг по пути обобщения, предположим,
что ![]() —
нечеткое подмножество оси
—
нечеткое подмножество оси ![]() , а
, а ![]() — нечеткое отношение в
— нечеткое отношение в ![]() . Вновь образуя цилиндрическое
нечеткое множество
. Вновь образуя цилиндрическое
нечеткое множество ![]() с
основанием
с
основанием ![]() и
его пересечение с нечетким отношением
и
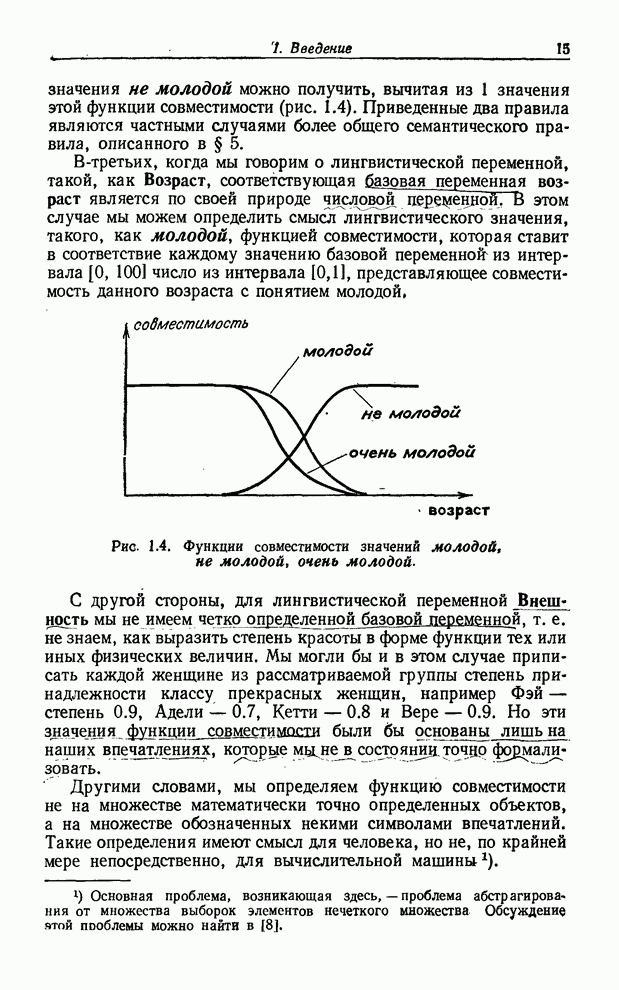
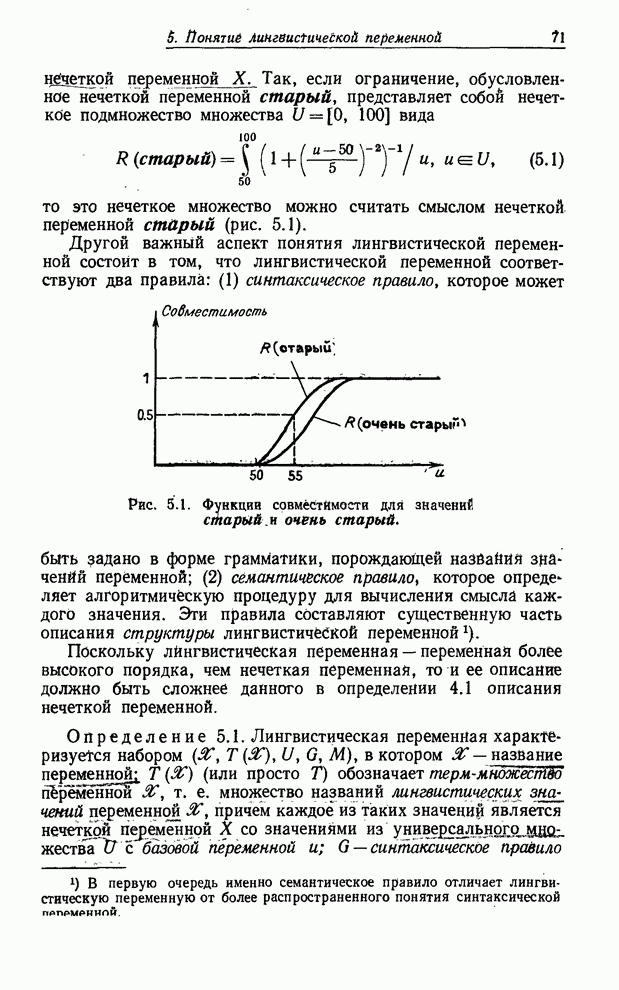
его пересечение с нечетким отношением ![]() (см. рис. 8.3), мы получим нечеткое множество
(см. рис. 8.3), мы получим нечеткое множество
![]() , которое
является аналогом точки пересечения
, которое
является аналогом точки пересечения ![]() на рис. 8.1. Проектируя затем это
множество на ось
на рис. 8.1. Проектируя затем это
множество на ось ![]() ,
получим значение
,
получим значение![]() в виде нечеткого подмножества оси
в виде нечеткого подмножества оси ![]() . Таким образом, из того, что
. Таким образом, из того, что ![]() и
и ![]() - нечеткое подмножество
оси
- нечеткое подмножество
оси ![]() , мы
получаем значение
, мы
получаем значение ![]() в
виде нечеткого подмножества
в
виде нечеткого подмножества![]() оси
оси ![]() .
.

Рис. 8.1. Вывод![]() из предпосылок
из предпосылок ![]() и
и ![]() .
.

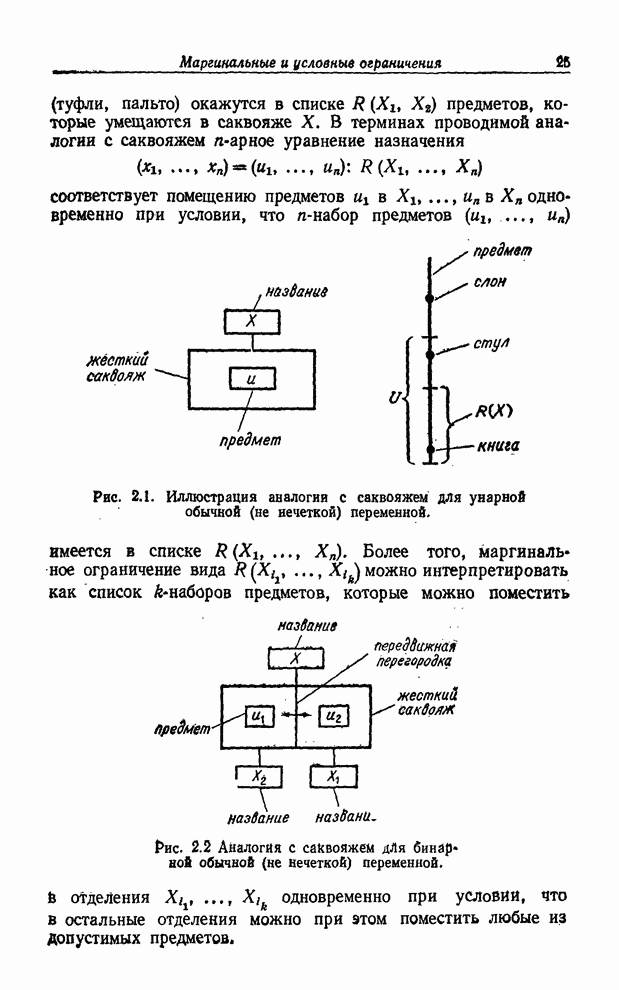
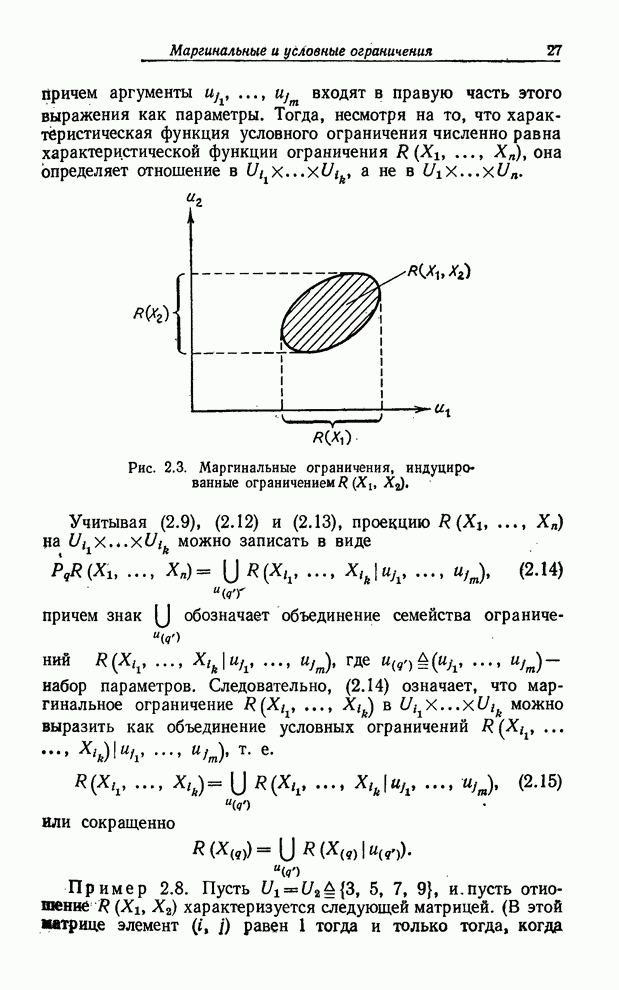
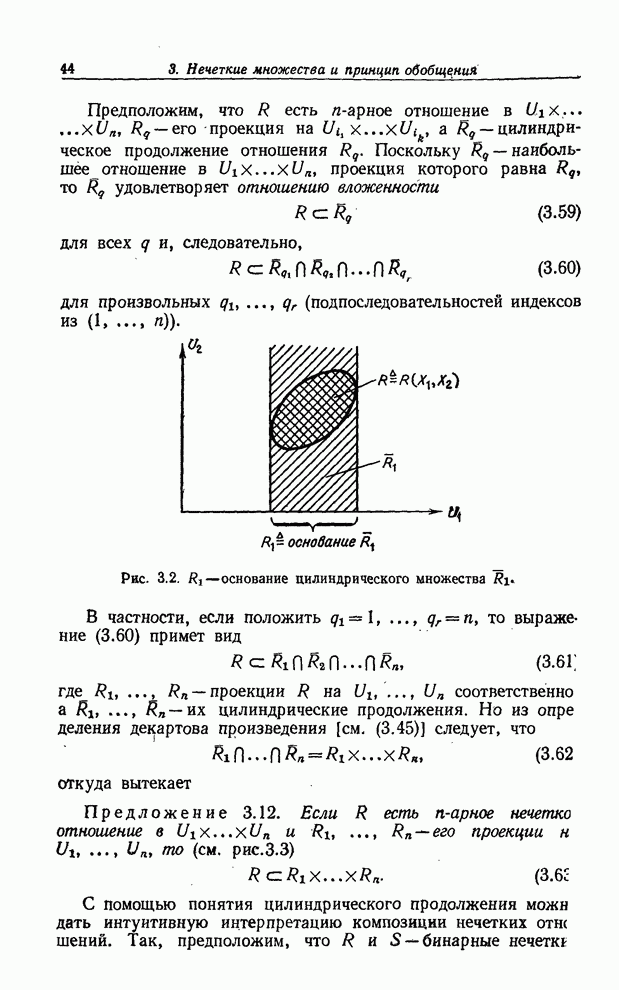
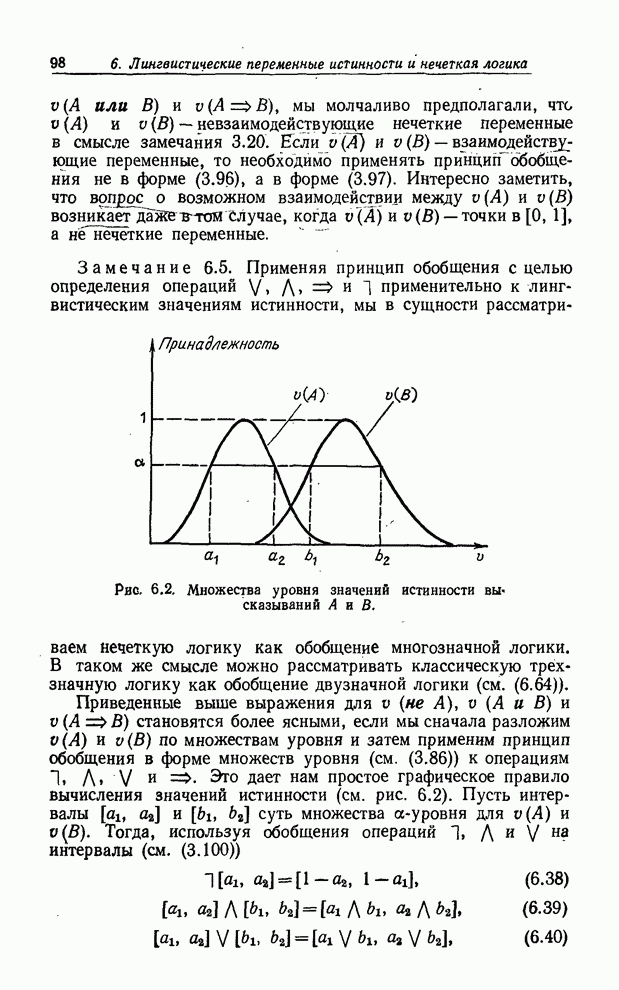
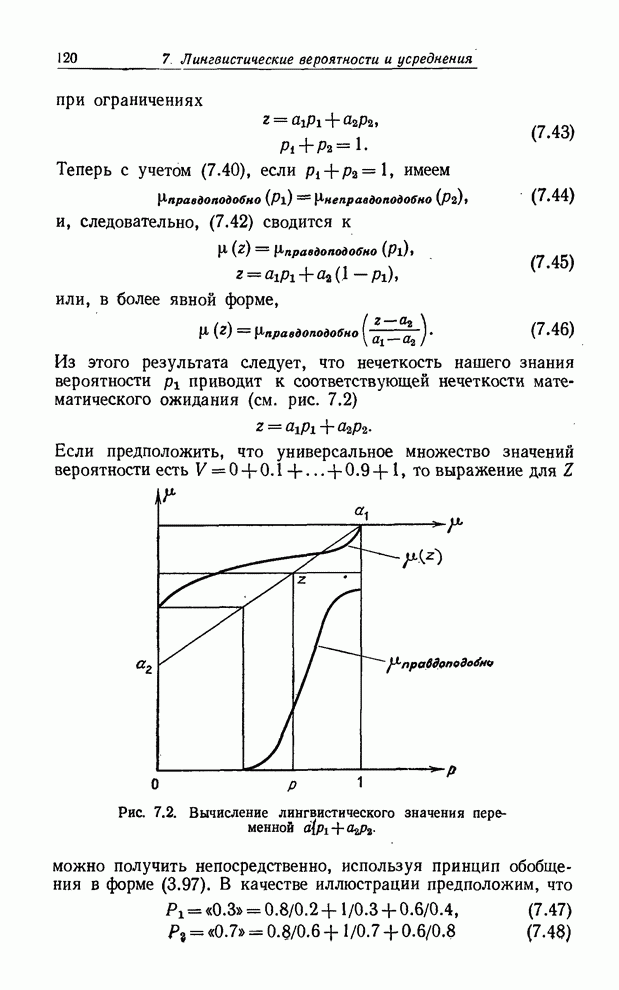
Рис. 8.2. Иллюстрация композиционного правила вывода в случае переменных со значениями-интервалами.
Более конкретно, пусть ![]() и
и ![]() обозначают функции принадлежности
множеств
обозначают функции принадлежности
множеств![]() и
и ![]() соответственно.
Тогда по определению множества
соответственно.
Тогда по определению множества ![]() (см. (3.58))
(см. (3.58))
![]() (8.1)
(8.1)
и, следовательно,
![]() . (8.2)
. (8.2)
Проектируя множество ![]() на ось
на ось ![]() , получаем из (8.2) и (3.57):
, получаем из (8.2) и (3.57):
![]() , (8.3)
, (8.3)
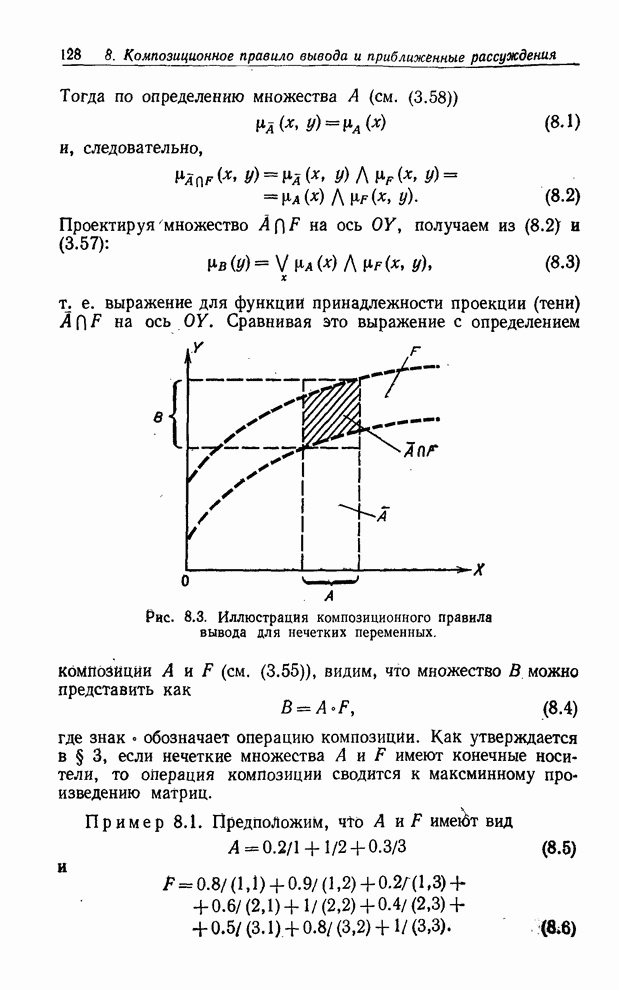
т. е. выражение для функций принадлежности проекции (тени) ![]() на ось
на ось ![]() . Сравнивая это
выражение с определением композиции
. Сравнивая это
выражение с определением композиции
![]() и
и ![]() (см. (3.55)), видим, что множество
(см. (3.55)), видим, что множество ![]() можно представить как
можно представить как
![]() ,
(8.4)
,
(8.4)
где знак ![]() обозначает операцию композиции. Как
утверждается в § 3, если нечеткие множества
обозначает операцию композиции. Как
утверждается в § 3, если нечеткие множества ![]() и
и![]() имеют конечные носители, то операция композиции сводится к максминному
произведению матриц.
имеют конечные носители, то операция композиции сводится к максминному
произведению матриц.

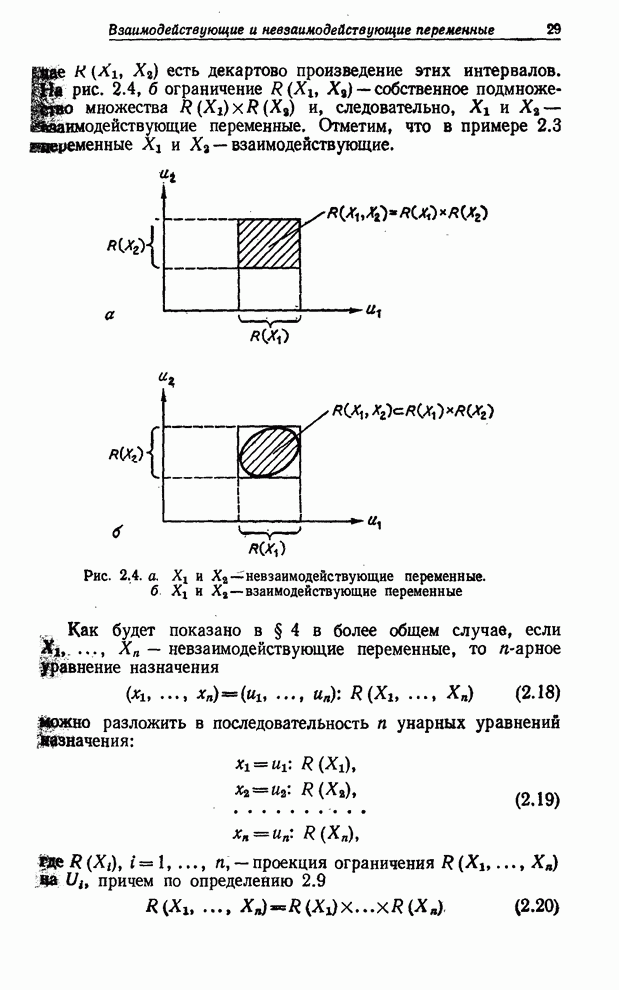
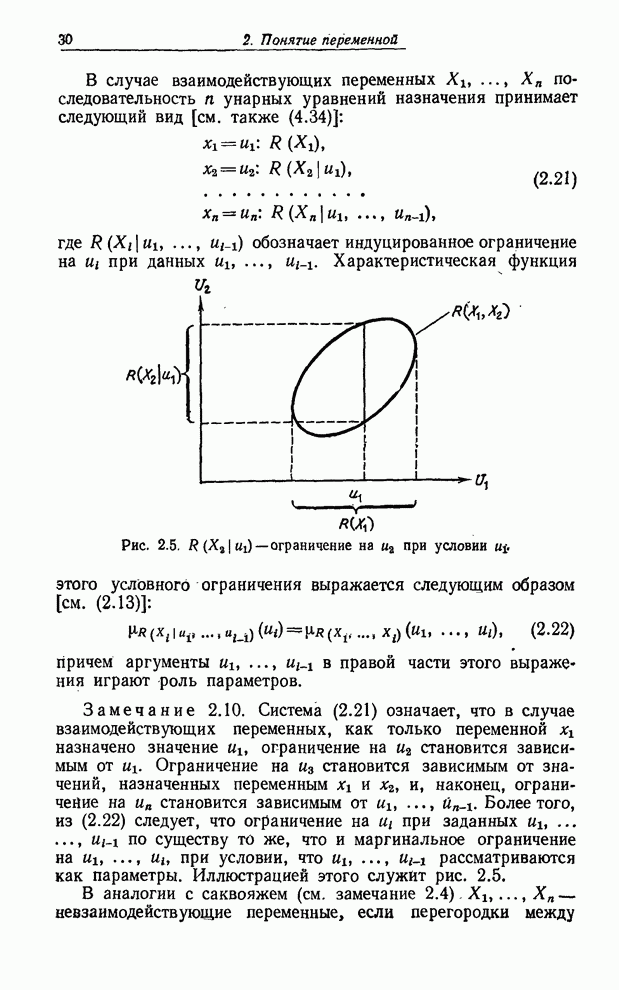
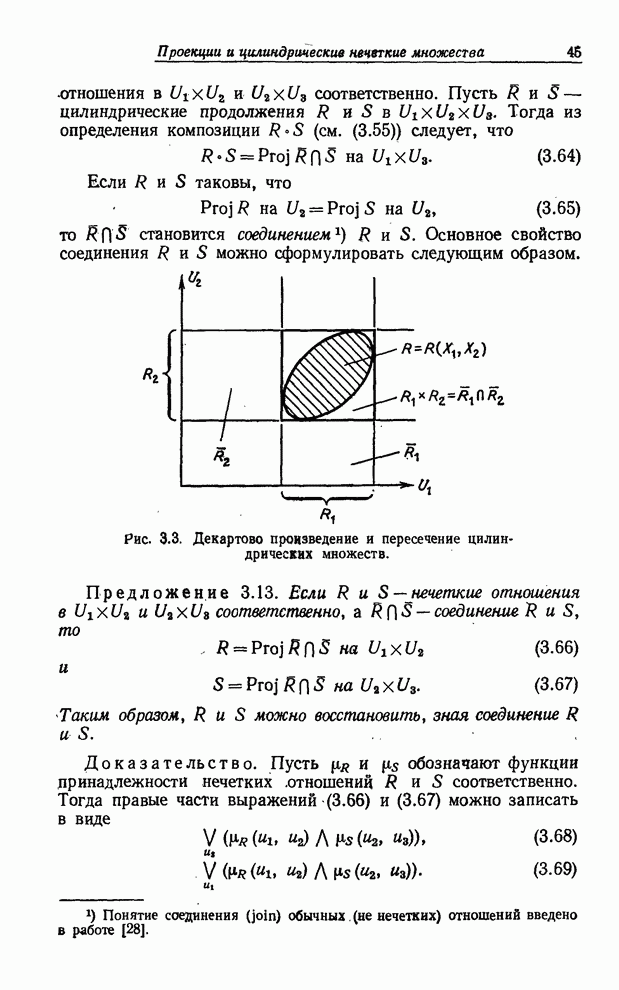
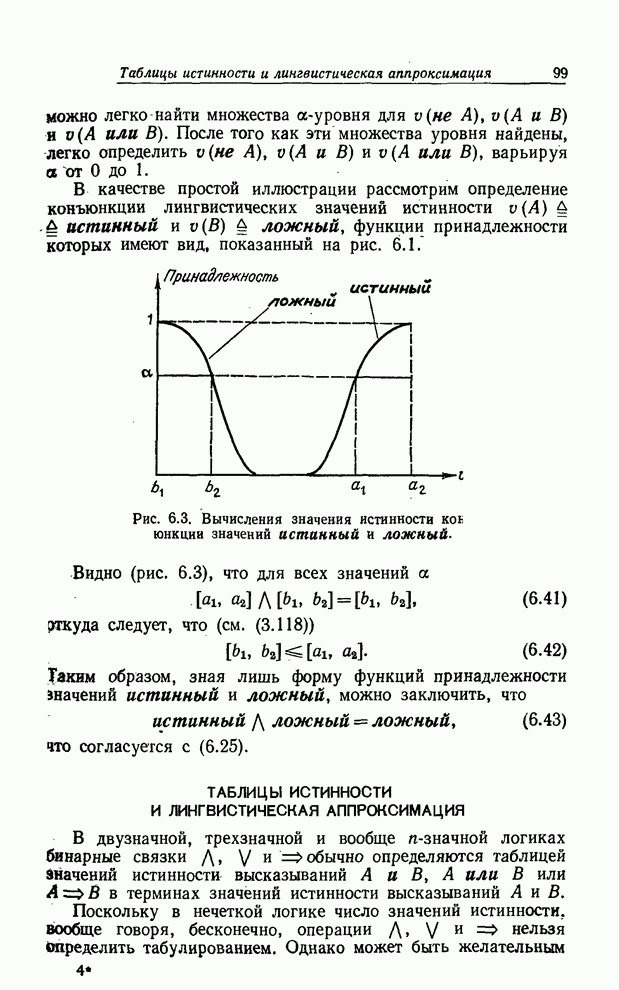
Рис. 8.3. Иллюстрация композиционного правила вывода для нечетких переменных.
Пример 8.1.
Предположим, что ![]() и
и
![]() имеют вид
имеют вид
![]() (8.5)
(8.5)
и
![]() (8.6)
(8.6)
Выражая ![]() и
и ![]() с помощью матриц и образуя матричное
произведение (8.4), получаем
с помощью матриц и образуя матричное
произведение (8.4), получаем
 (8.7)
(8.7)
Вышеизложенные замечания и примеры помогают обосновать следующее правило вывода.
Правило 8.2.
Пусть ![]() и
и ![]() — два
универсальных множества с базовыми переменными
— два
универсальных множества с базовыми переменными ![]() и
и ![]() соответственно. Пусть
соответственно. Пусть ![]() обозначают
ограничения на
обозначают
ограничения на ![]() и
и
![]() соответственно
и представляют собой нечеткие отношения в
соответственно
и представляют собой нечеткие отношения в ![]() . Пусть
. Пусть ![]() и
и ![]() — нечеткие
подмножества множеств
— нечеткие
подмножества множеств ![]() . Тогда композиционное правило
вывода утверждает, что решение уравнений назначения
. Тогда композиционное правило
вывода утверждает, что решение уравнений назначения
![]() , (8.8)
, (8.8)
![]() (8.9)
(8.9)
имеет вид
![]() , (8.10)
, (8.10)
где
![]() —
композиция
—
композиция ![]() и
и
![]() . В этом
смысле мы можем делать вывод
. В этом
смысле мы можем делать вывод ![]() из того, что
из того, что![]() и
и ![]() .
.
В качестве простой иллюстрации применения этого правила предположим, что
![]() ,
(8.11)
,
(8.11)
![]() (8.12)
(8.12)
и
 (8.13)
(8.13)
Другими словами, ![]() — унарное нечеткое отношение в
— унарное нечеткое отношение в ![]() , названное малый,
, названное малый,
![]() —
бинарное нечеткое отношение в
—
бинарное нечеткое отношение в ![]() , названное
примерно равны.
, названное
примерно равны.
Уравнения назначения в этом случае имеют вид
![]() , (8.14)
, (8.14)
![]() , (8.15)
, (8.15)
и, следовательно,
 (8.16)
(8.16)
что можно аппроксимировать следующим образом:
![]() , (8.17)
, (8.17)
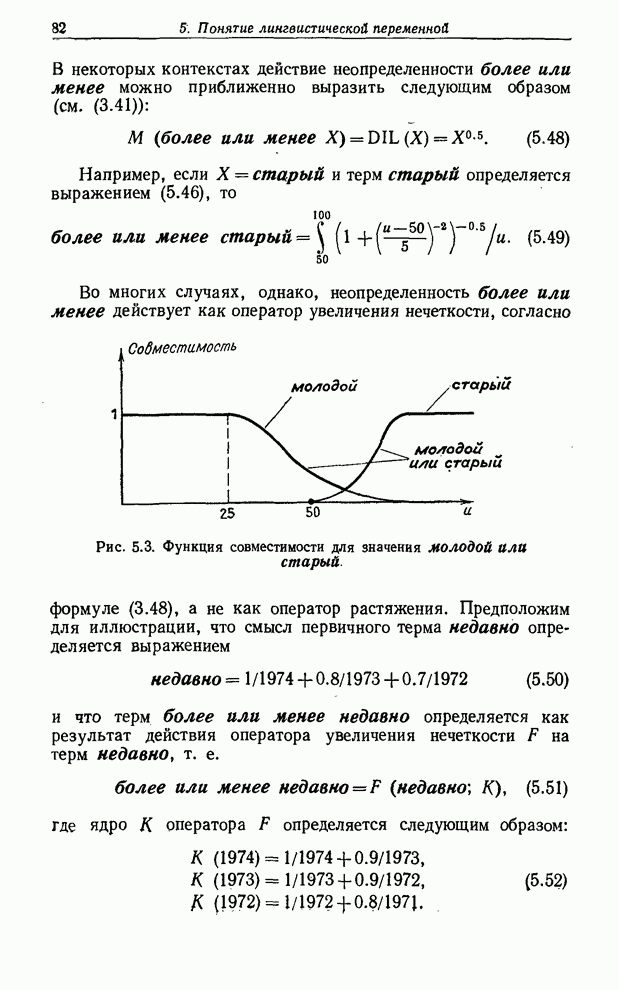
если терм более или менее определяется как оператор увеличения нечеткости (см. (3.48)), где
 (8.18)
(8.18)
Заметим,
что применение этого оператора к ![]() дает
дает
![]() (8.19)
(8.19)
в
качестве аппроксимации набора ![]() .
.
Итак,
используя композиционное правило вывода, из того, что ![]() и
и ![]() , мы вывели, что
, мы вывели, что
![]() точно (8.20)
точно (8.20)
и
![]() - в качестве лингвистического
приближения. (8.21)
- в качестве лингвистического
приближения. (8.21)
Словами этот приближенный вывод можно записать в виде
 (8.22)
(8.22)
Основная идея этого схематически описанного метода состоит в следующем. Каждый факт или предпосылка записывается в виде уравнения назначения в отношениях, содержащего одно или большее число ограничений на базовые переменные. Эти уравнения решаются относительно желаемых ограничений при помощи композиции нечетких отношений. Получаемые решения и представляют собой вывод из данного набора предпосылок.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
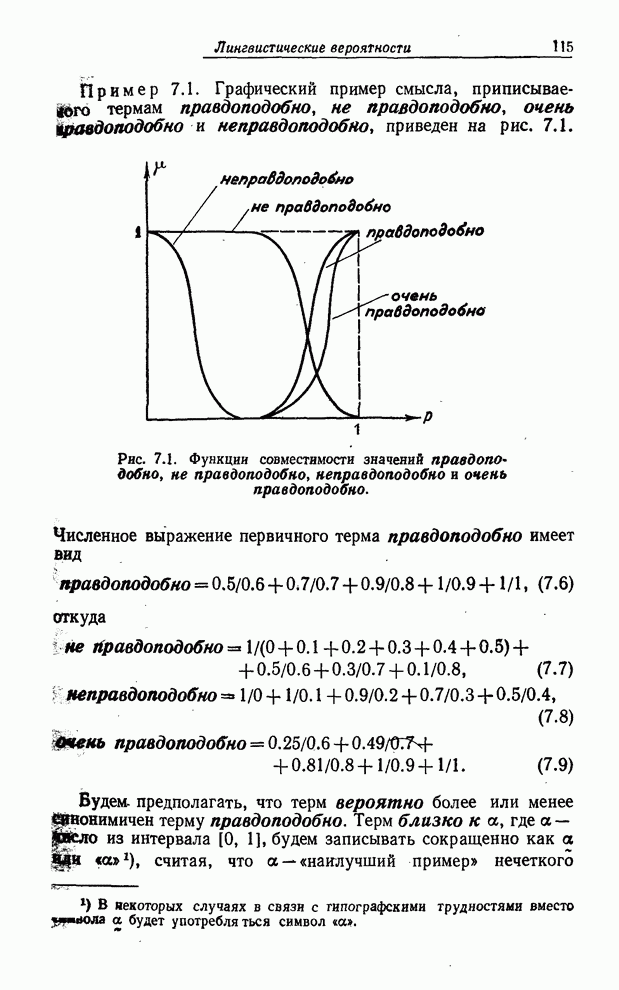
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
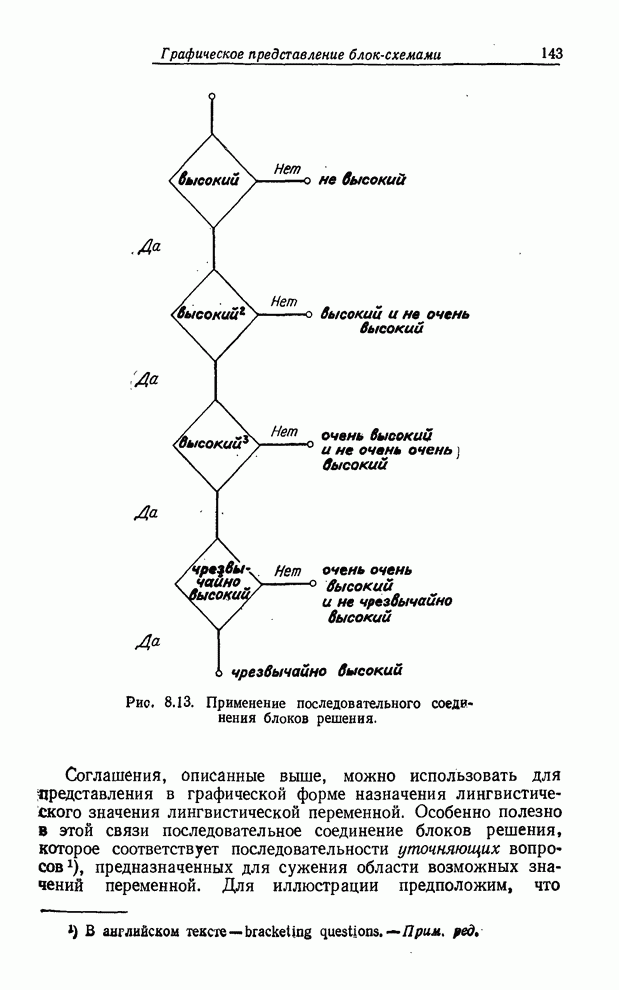
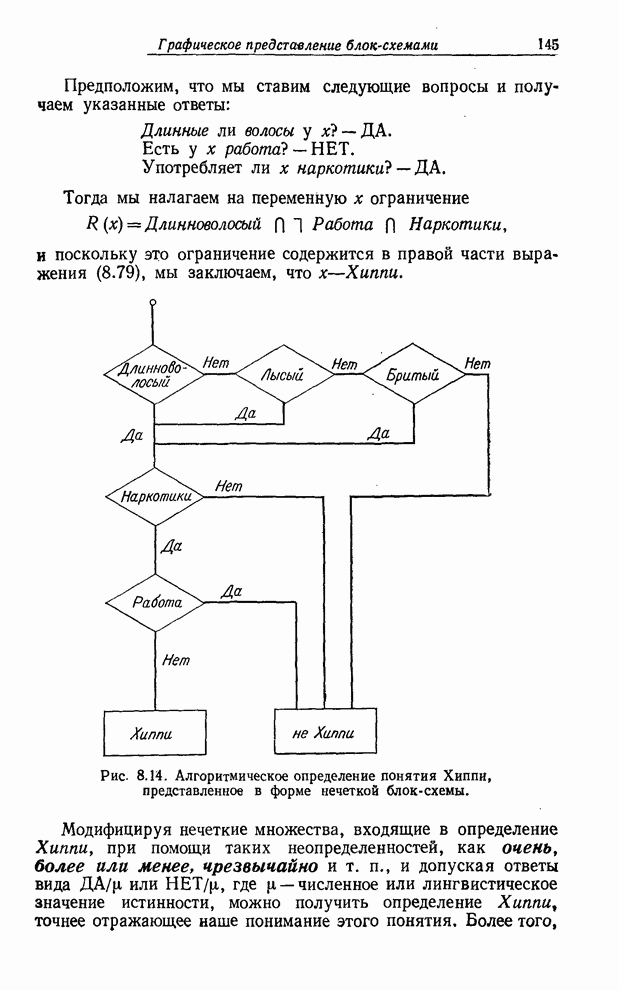
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ