| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
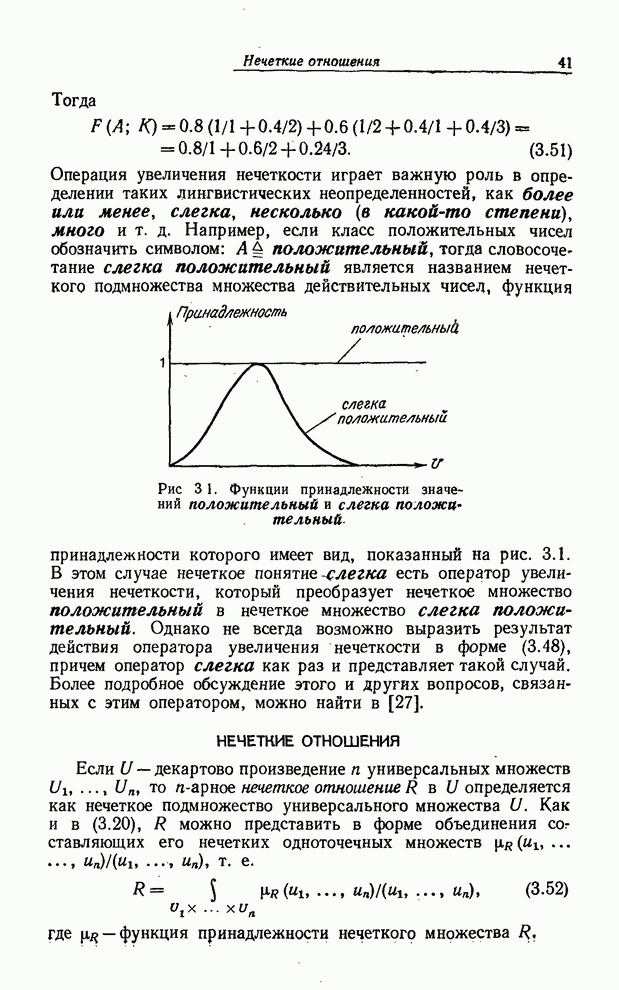
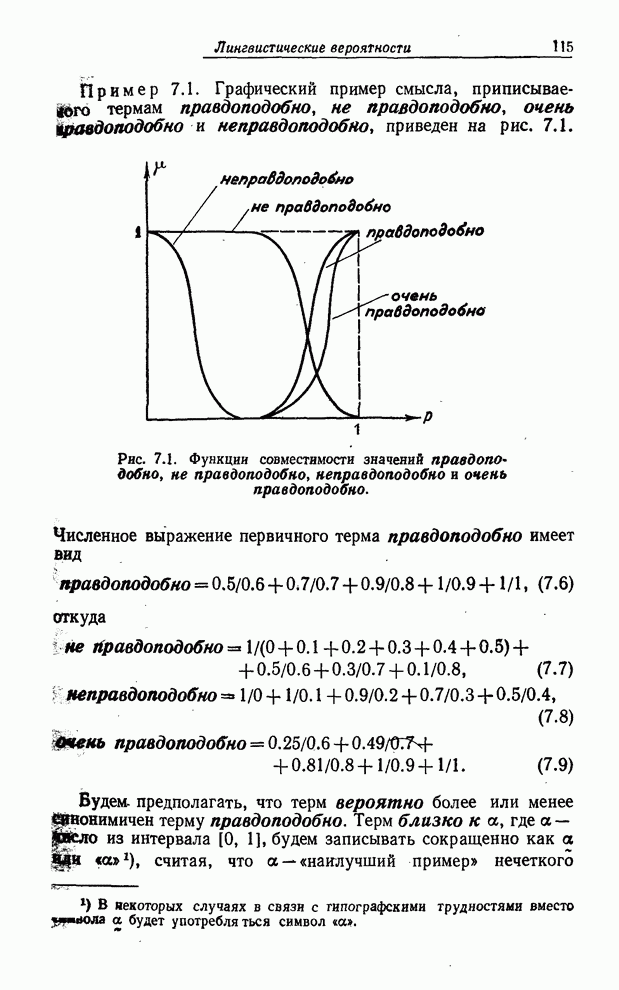
ПРИНЦИП ОБОБЩЕНИЯ
Принцип обобщения для нечетких
множеств представляет собой в сущности основное равенство, позволяющее расширить
область определения ![]() отображения или отношения, включив в
нее наряду с точками произвольные нечеткие подмножества множества
отображения или отношения, включив в
нее наряду с точками произвольные нечеткие подмножества множества ![]() . Более конкретно,
предположим, что
. Более конкретно,
предположим, что ![]() —
отображение
—
отображение ![]() ,
а
,
а ![]() — нечеткое
подмножество вида
— нечеткое
подмножество вида
![]() . (3.79)
. (3.79)
Тогда принцип обобщения утверждает, что
![]() . (3.80)
. (3.80)
Итак,
образ множества ![]() при
отображении
при
отображении ![]() можно
получить, зная образы элементов
можно
получить, зная образы элементов ![]() при этом отображении.
при этом отображении.
Пример 3.15. Пусть
![]() ,
,
и
пусть ![]() —
операция возведения в квадрат. Пусть малый — нечеткое
подмножество множества
—
операция возведения в квадрат. Пусть малый — нечеткое
подмножество множества ![]() вида
вида
![]() . (3.81)
. (3.81)
Тогда, учитывая (3.80), имеем
![]() . (3.82)
. (3.82)
Если
носитель подмножества ![]() имеет мощность континуума, т. е.
имеет мощность континуума, т. е.
![]() , (3.83)
, (3.83)
то принцип обобщения принимает следующий вид
 ; (3.84)
; (3.84)
при
этом необходимо учитывать, что ![]() — точка множества
— точка множества ![]() , а
, а ![]() — степень
принадлежности
— степень
принадлежности ![]() нечеткому
подмножеству
нечеткому
подмножеству ![]() множества
множества
![]() .
.
В
некоторых случаях удобно использовать принцип обобщения в другой форме, которая
получается из выражения (3.84) путем разложения ![]() не на одноточечные нечеткие множества,
а на соответствующие ему множества уровня [см. разложение (3.28)]. Таким
образом, написав
не на одноточечные нечеткие множества,
а на соответствующие ему множества уровня [см. разложение (3.28)]. Таким
образом, написав
 , (3.85)
, (3.85)
где
![]() —
соответствующее
—
соответствующее ![]() множество
множество
![]() -уровня,
получим принцип обобщения в следующей форме:
-уровня,
получим принцип обобщения в следующей форме:
 , (3.86)
, (3.86)
если
носитель ![]() —
континуум, или
—
континуум, или
 , (3.87)
, (3.87)
если
либо носитель множества ![]() — счетное множество, либо множества
уровня, соответствующие
— счетное множество, либо множества
уровня, соответствующие ![]() , образуют счетное семейство.
, образуют счетное семейство.
Замечание
3.16.
Принцип обобщения в форме (3.84) позволяет расширить область определения ![]() отображения
отображения ![]() , включив в нее
наряду с точками произвольные нечеткие подмножества множества
, включив в нее
наряду с точками произвольные нечеткие подмножества множества ![]() . Принцип обобщения в
форме (3.86) позволяет расширить область определения отображения
. Принцип обобщения в
форме (3.86) позволяет расширить область определения отображения ![]() , включив в нее
наряду с обычными (не нечеткими) подмножествами
, включив в нее
наряду с обычными (не нечеткими) подмножествами ![]() произвольные нечеткие подмножества
произвольные нечеткие подмножества ![]() . Следует подчеркнуть,
что выражения (3.84) и (3.86) эквивалентны, поскольку (3.86) вытекает из
(3.84), если перегруппировать члены в разложении множества
. Следует подчеркнуть,
что выражения (3.84) и (3.86) эквивалентны, поскольку (3.86) вытекает из
(3.84), если перегруппировать члены в разложении множества ![]() .
.
Замечание
3.17.
Принцип обобщения аналогичен принципу суперпозиции для линейных систем.
Согласно последнему, если ![]() — линейная система и
— линейная система и ![]() — входные
сигналы, то откликом системы
— входные
сигналы, то откликом системы ![]() на любую линейную комбинацию
на любую линейную комбинацию
![]() , (3.88)
, (3.88)
где
![]() — постоянные
коэффициенты, является
— постоянные
коэффициенты, является
![]() . (3.89)
. (3.89)
Существенное
различие между (3.89) и (3.80) состоит в том, что в (3.80) знак ![]() обозначает
объединение, а не арифметическую сумму, и
обозначает
объединение, а не арифметическую сумму, и ![]() не ограничивается только линейными отображениями.
не ограничивается только линейными отображениями.


Рис. 3.4. Обобщение таблицы умножения на множества целых
чисел; ![]() обозначает
1 или 2.
обозначает
1 или 2.
Замечание
3.18.
Следует заметить, что, когда ![]() , результат применения принципа
обобщения аналогичен результату образования
, результат применения принципа
обобщения аналогичен результату образования ![]() -кратного декартова произведения
алгебраической системы
-кратного декартова произведения
алгебраической системы ![]() самой на себя. Обобщение
таблицы умножения на подмножества чисел показано на рис. 3.4.
самой на себя. Обобщение
таблицы умножения на подмножества чисел показано на рис. 3.4.
Во
многих приложениях принципа обобщения возникает следующая проблема. Имеется
функция ![]() переменных
переменных
![]() и
нечеткое множество (отношение)
и
нечеткое множество (отношение) ![]() в
в ![]() , характеризующееся функцией
принадлежности
, характеризующееся функцией
принадлежности ![]() ,
где
,
где![]() .
Непосредственное применение принципа обобщения (3.84) в этом случае дает
.
Непосредственное применение принципа обобщения (3.84) в этом случае дает
 ; (3.90)
; (3.90)
однако
во многих случаях нам известно не само множество ![]() , а его проекции
, а его проекции ![]() на
на![]() соответственно (см.
(3.57)). В связи с этим возникает вопрос: какое выражение для
соответственно (см.
(3.57)). В связи с этим возникает вопрос: какое выражение для![]() следует использовать
в (3.90)?
следует использовать
в (3.90)?
В
таких случаях, если особо не оговорено, будем предполагать, что функция
принадлежности отношения ![]() имеет вид
имеет вид
![]() , (3.91)
, (3.91)
где
![]() ,
, ![]() — функция принадлежности
отношения
— функция принадлежности
отношения ![]() .
Если учесть равенство (3.45), то (3.91) эквивалентно предположению о том, что
.
Если учесть равенство (3.45), то (3.91) эквивалентно предположению о том, что ![]() — декартово
произведение своих проекций, т. е.
— декартово
произведение своих проекций, т. е.
![]() ,
,
откуда
в свою очередь следует, что ![]() — наибольшее множество, проекции
которого на
— наибольшее множество, проекции
которого на ![]() суть
суть
![]() соответственно
(см. (3.63)).
соответственно
(см. (3.63)).
Пример 3.19. Предположим, что, как и в примере 3.15,
![]()
и
![]() , (3.92)
, (3.92)
![]() , (3.93)
, (3.93)
![]() арифметическое произведение
арифметическое произведение ![]() и
и ![]() .
.
Используя (3.91) и применяя принцип обобщения в форме (3.90), имеем
 (3.94)
(3.94)
Таким образом, арифметическое произведение нечетких чисел примерно 2 и примерно 6 есть нечеткое число, выраженное формулой (3.94).
Вообще
пусть символ ![]() обозначает
некоторую бинарную операцию, определенную на
обозначает
некоторую бинарную операцию, определенную на ![]() , со значениями в
, со значениями в ![]() . Так, если
. Так, если ![]() и
и ![]() , то
, то
![]()
Предположим
теперь, что ![]() и
и
![]() — нечеткие
подмножества множеств
— нечеткие
подмножества множеств ![]() и
и ![]() соответственно, причем
соответственно, причем
![]()
и
![]() (3.95)
(3.95)
Используя
принцип обобщения и предполагая, что выполняется равенство (3.91), операцию ![]() можно обобщить на
нечеткие подмножества множеств
можно обобщить на
нечеткие подмножества множеств ![]() и
и ![]() , определив отношение
, определив отношение
 . (3.96)
. (3.96)
Легко
проверить, что в случае, когда ![]() ,
, ![]() и
и ![]() , как в примере 3.19, применение
выражения (3.96) приводит к выражению для
, как в примере 3.19, применение
выражения (3.96) приводит к выражению для ![]() .
.
Замечание 3.20. Важно отметить, что применимость (3.96) зависит существенным образом от предположения (3.91), т. е. от того, верно ли равенство
![]() .
.
Следствием
этого равенства является то, что ![]() и
и ![]() — невзаимодействующие переменные в
смысле определения 2.9. Если же существует ограничение на
— невзаимодействующие переменные в
смысле определения 2.9. Если же существует ограничение на ![]() , которое выражается отношением
, которое выражается отношением
![]() с функцией
принадлежности
с функцией
принадлежности ![]() ,
то выражение для
,
то выражение для ![]() имеет
вид
имеет
вид
 (3.97)
(3.97)
Заметим,
что если ![]() —
обычное (не нечеткое) отношение, то правая часть (3.97) будет содержать только
те члены, которые удовлетворяют ограничению
—
обычное (не нечеткое) отношение, то правая часть (3.97) будет содержать только
те члены, которые удовлетворяют ограничению ![]() .
.
Простой
иллюстрацией случая, в котором ![]() и
и ![]() — взаимодействующие
переменные, служит выражение
— взаимодействующие
переменные, служит выражение
![]() , (3.98)
, (3.98)
в
котором арифметическое суммирование обозначено знаком ![]() , а арифметическое
произведение — знаком
, а арифметическое
произведение — знаком ![]() . Если
. Если ![]() ,
, ![]() и
и ![]() — невзаимодействующие, то мы можем
применить принцип обобщения в форме (3.96) для вычисления
— невзаимодействующие, то мы можем
применить принцип обобщения в форме (3.96) для вычисления ![]() , где
, где ![]() ,
, ![]() и
и ![]() —
нечеткие подмножества действительной прямой. С другой стороны, если (3.98)
переписать в виде
—
нечеткие подмножества действительной прямой. С другой стороны, если (3.98)
переписать в виде
![]() ,
,
то
члены ![]() и
и ![]() — взаимодействующие
благодаря наличию в них общего множителя
— взаимодействующие
благодаря наличию в них общего множителя ![]() и, следовательно,
и, следовательно,
![]() . (3.99)
. (3.99)
Из этого факта можно сделать важный вывод о том, что произведение нечетких чисел не дистрибутивно, если оно вычисляется по формуле (3.96). Чтобы получить равенство в (3.99), мы можем применить принцип обобщения в форме (3.96) к левой части (3.99) и должны применить его обязательно в форме (3.97) к правой части (3.99).
Замечание 3.21. Принцип обобщения можно применять не только к функциям, но также и к отношениям, или, что эквивалентно, к предикатам. Мы не будем останавливаться здесь на этом вопросе, так как применение принципа обобщения к отношениям не играет значительной роли в этой работе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
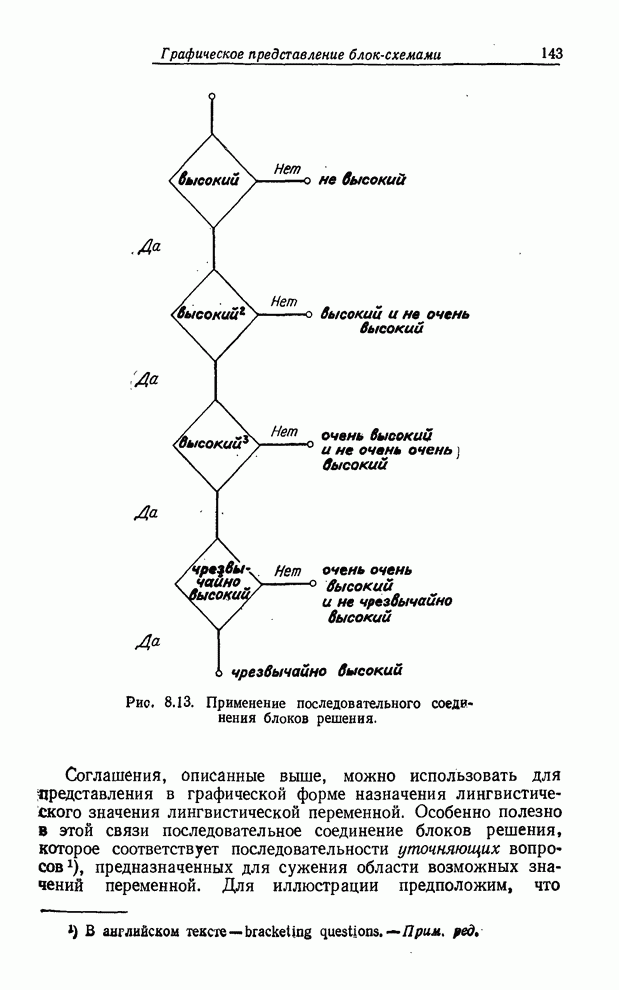
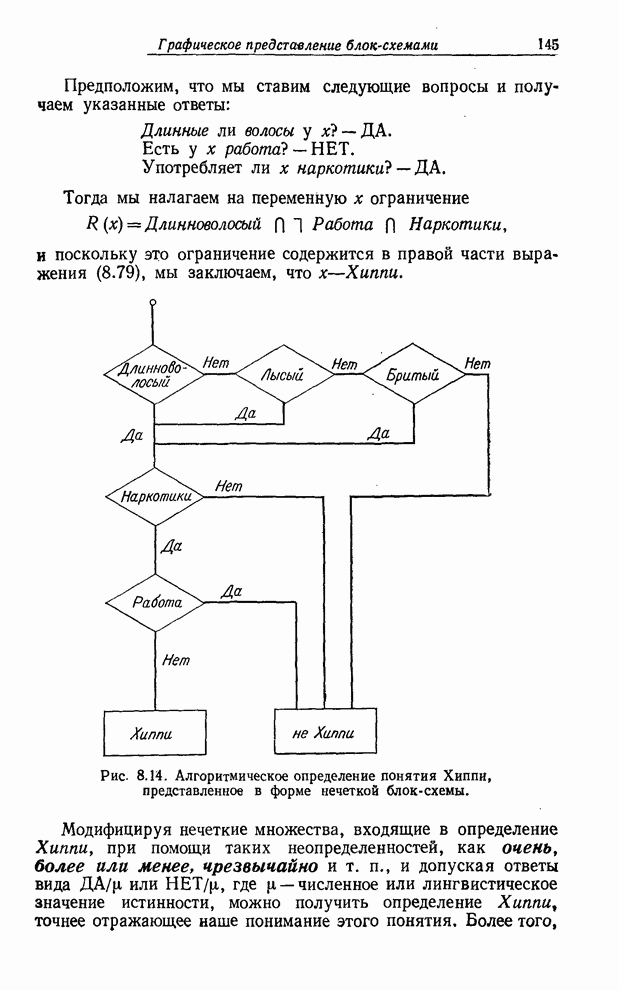
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ