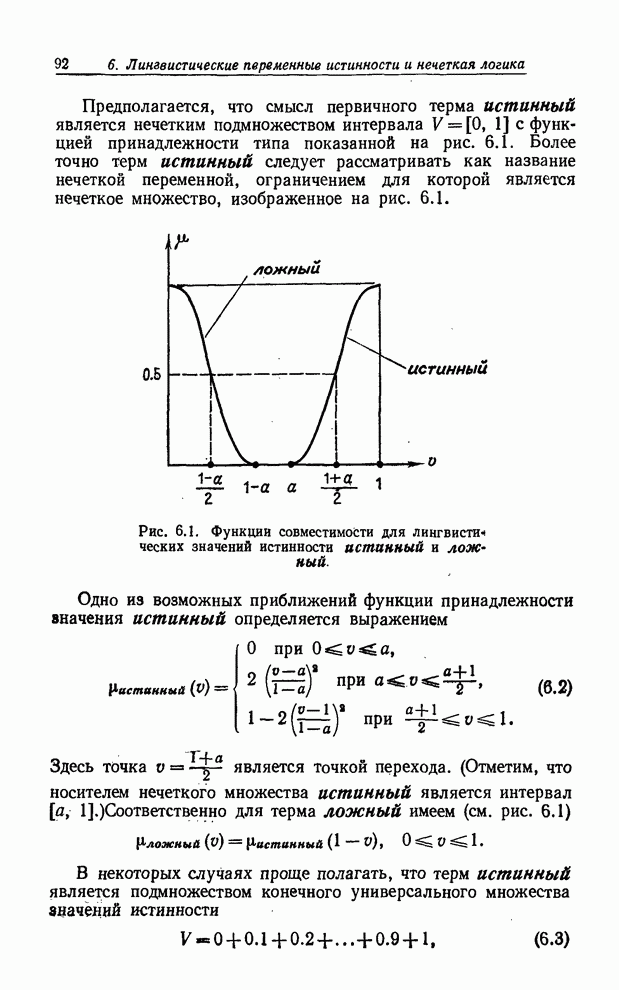
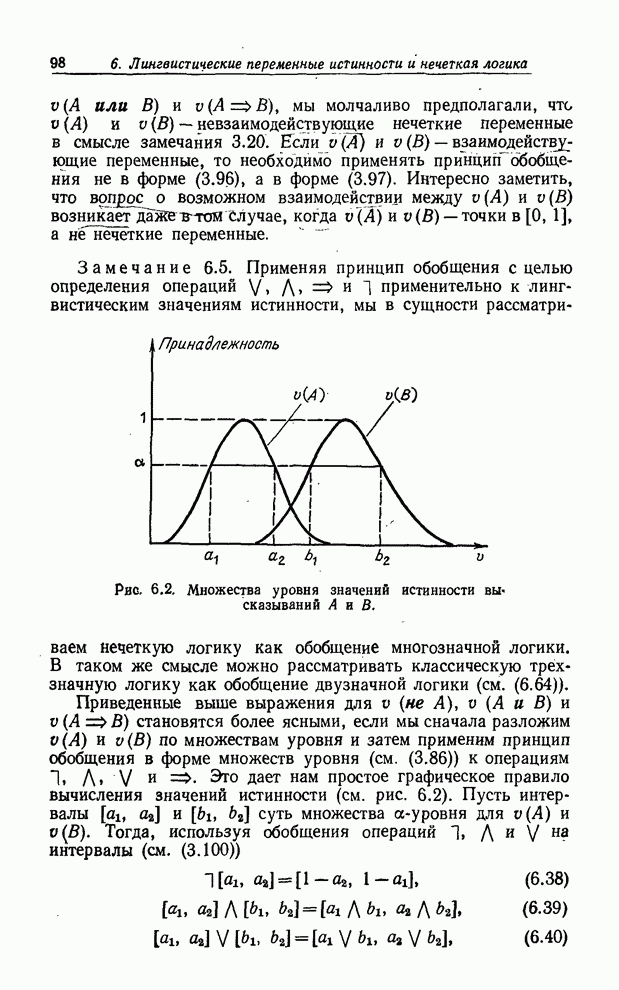
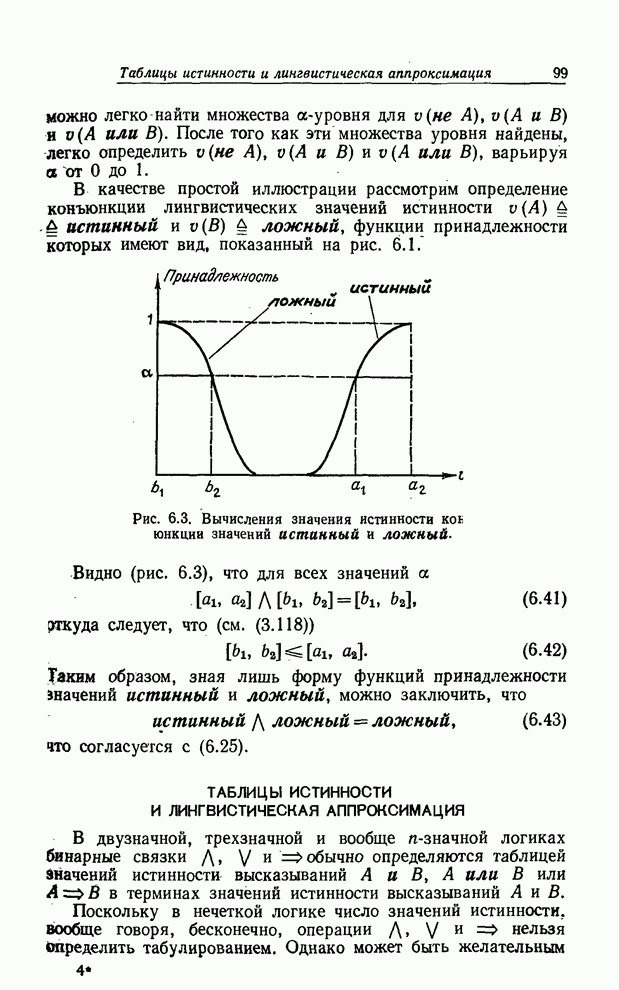
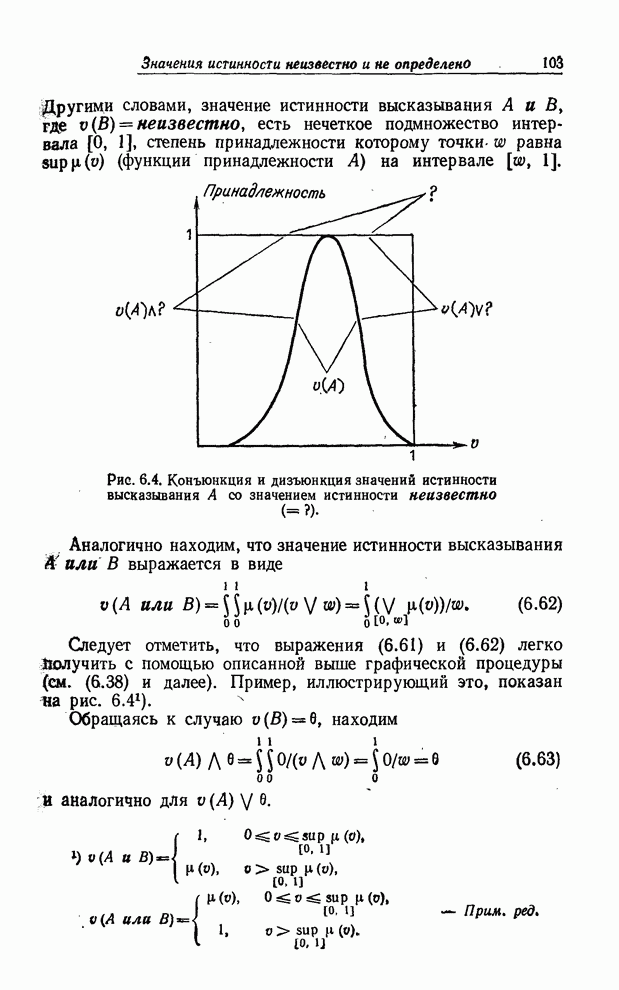
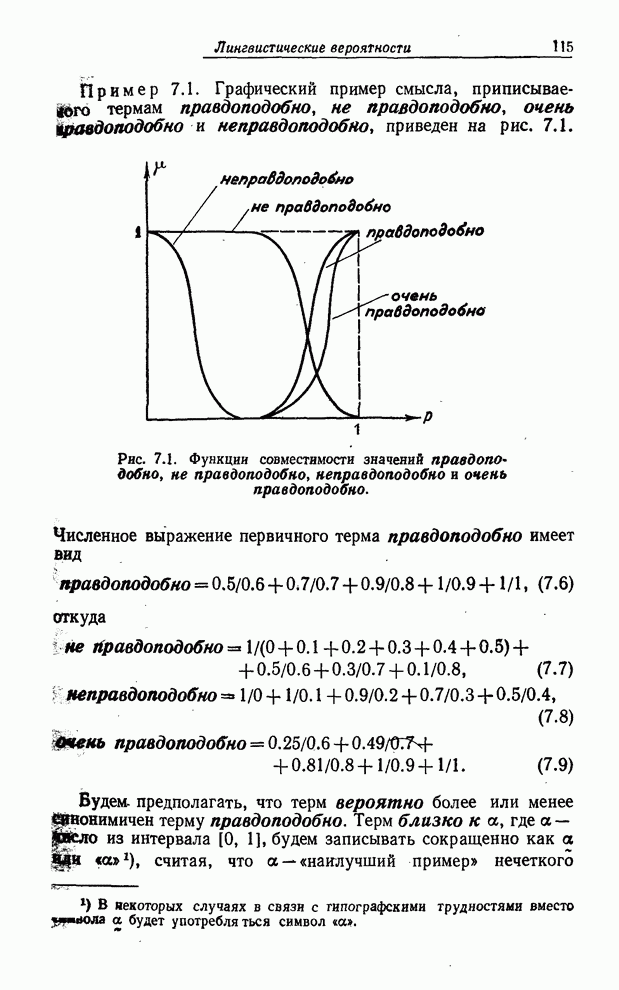
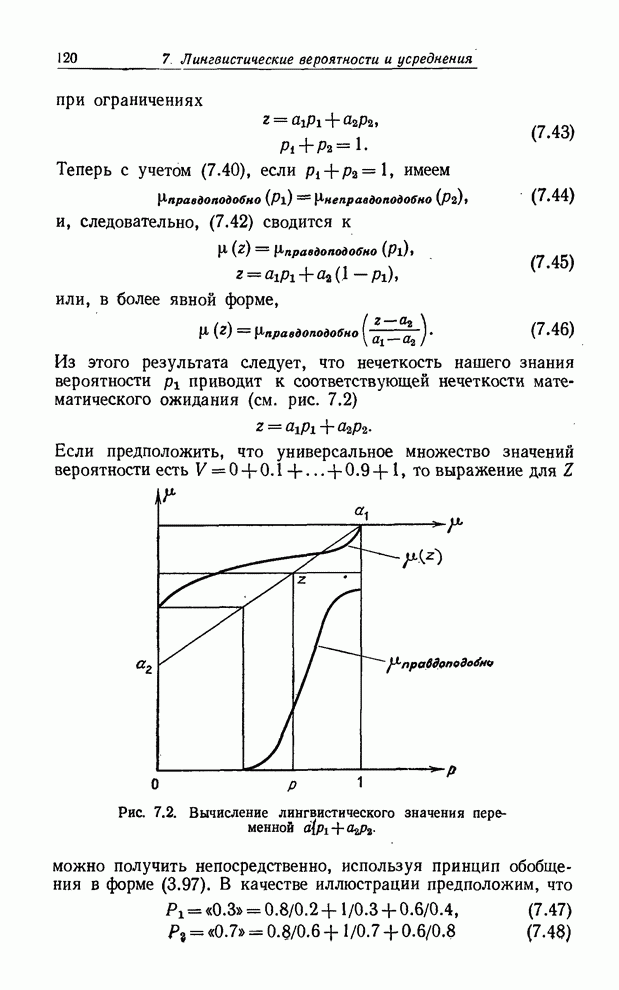
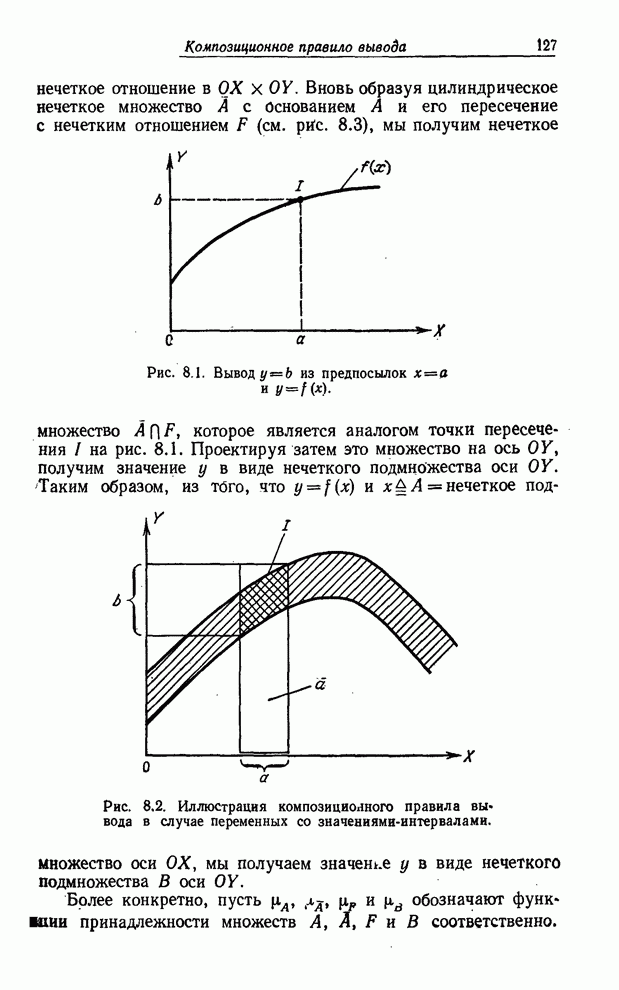
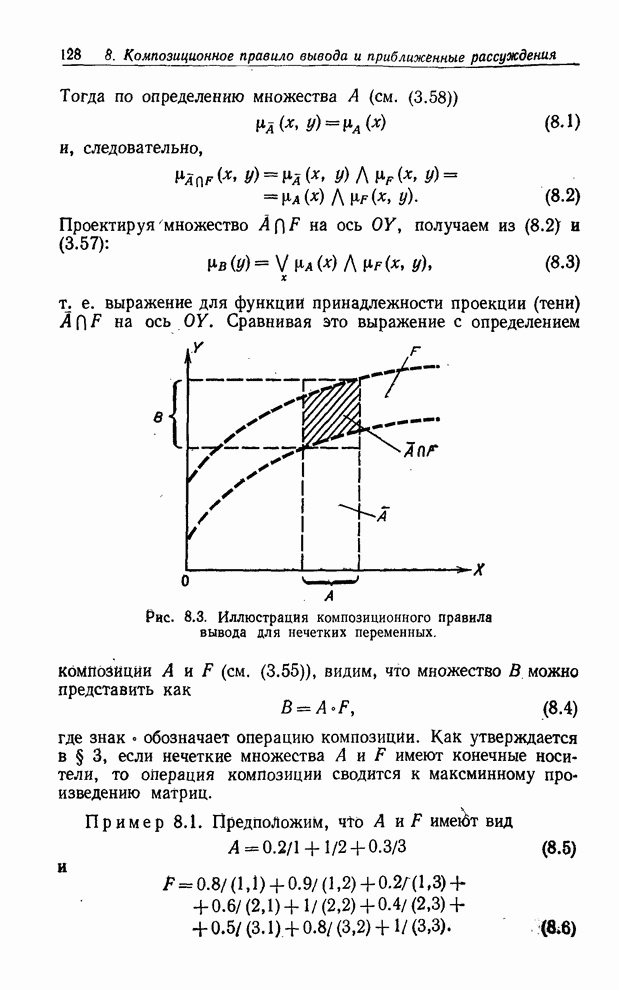
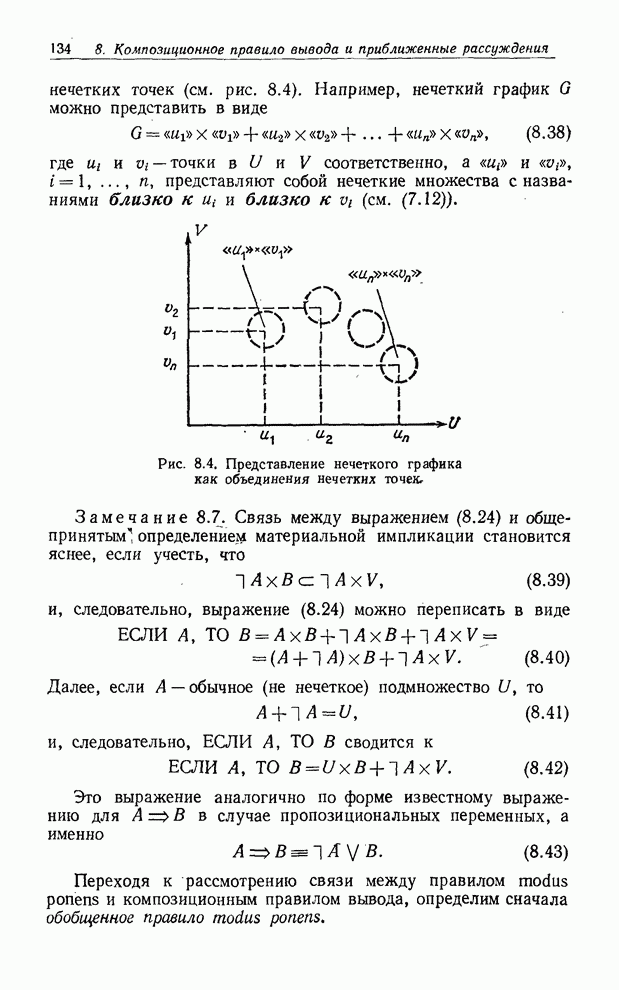
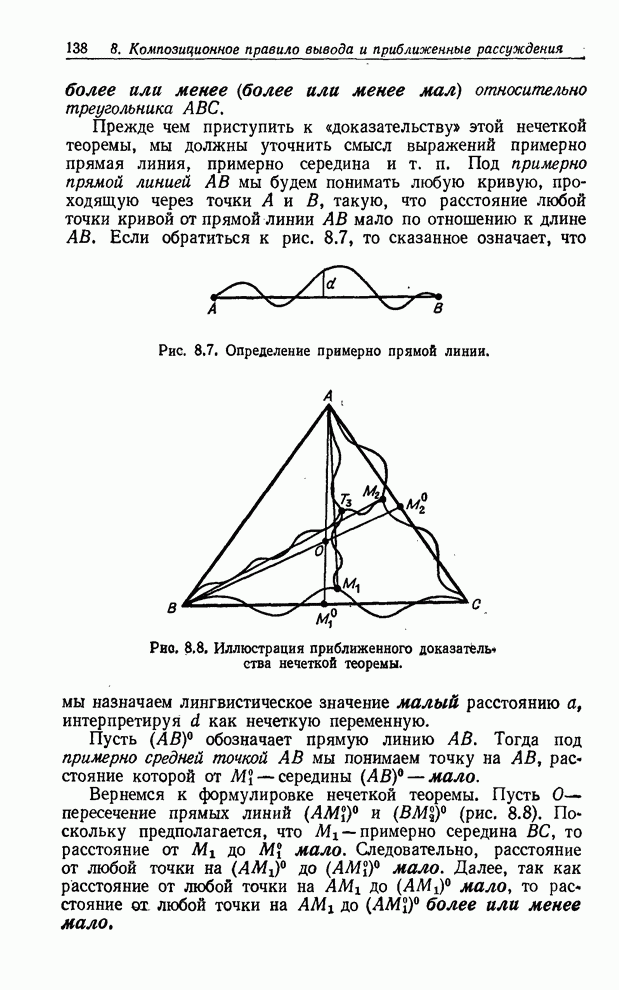
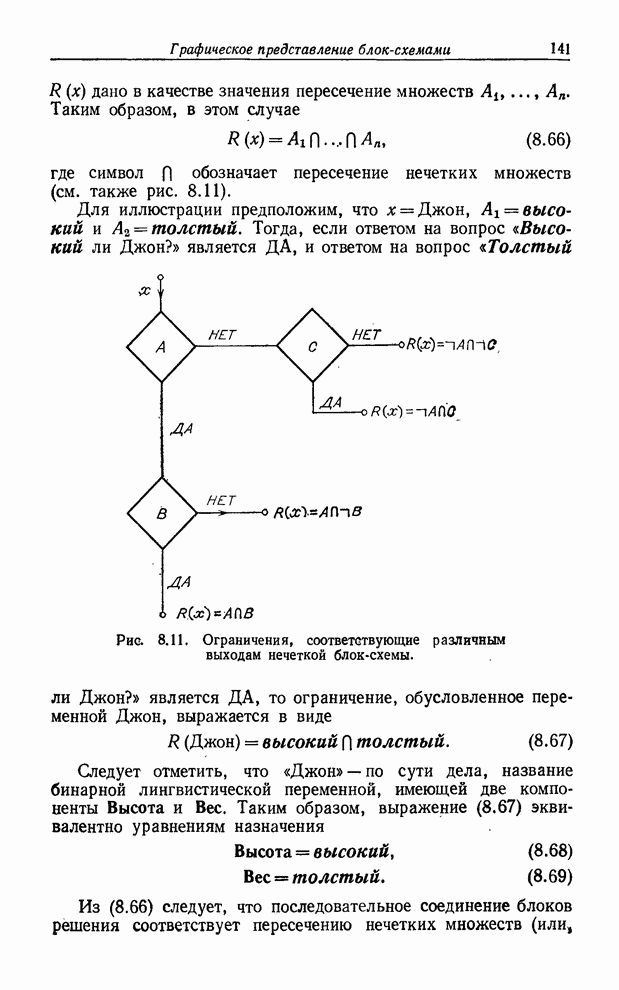
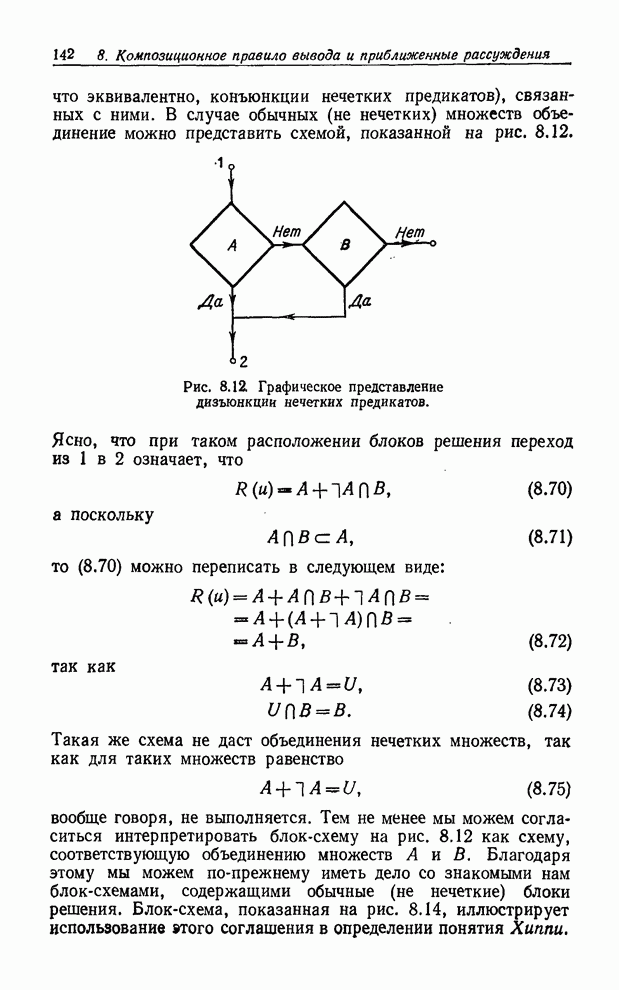
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
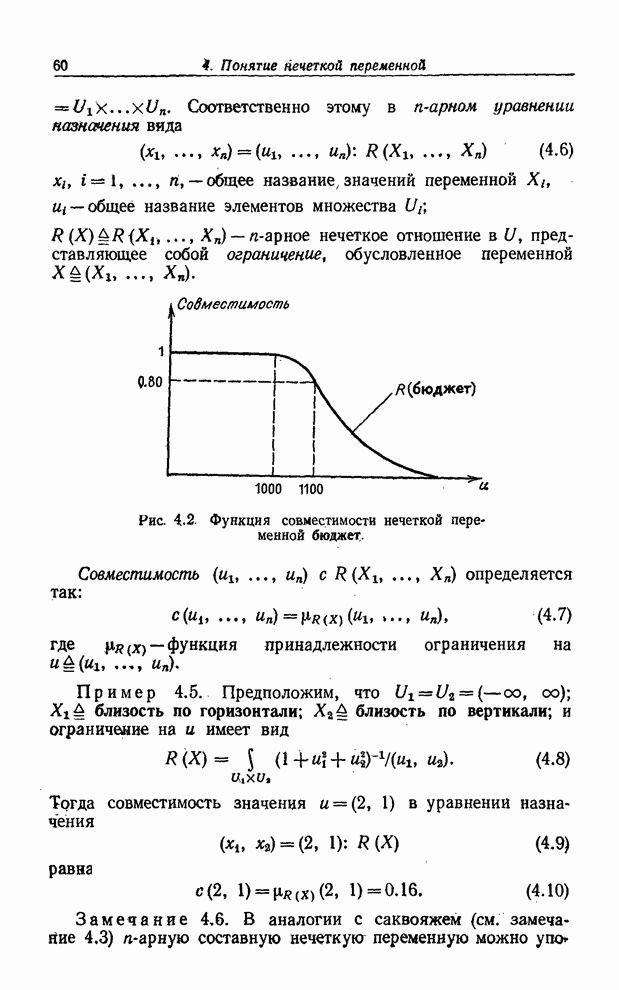
В классическом теоретико-вероятностном подходе событие ![]() определяется
как элемент
определяется
как элемент ![]() -поля
-поля
![]() подмножеств
пространства элементарных событий
подмножеств
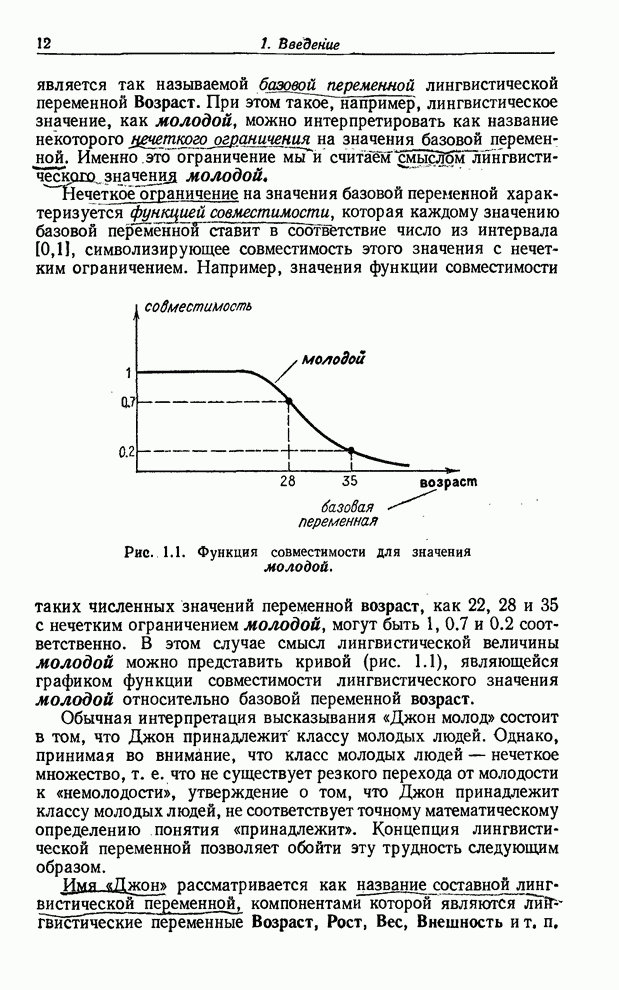
пространства элементарных событий ![]() . Так, если
. Так, если ![]() — нормированная мера над
измеримым пространством
— нормированная мера над
измеримым пространством ![]() , то вероятность
, то вероятность ![]() события
события ![]() определяется как мера
множества
определяется как мера
множества![]() и
является числом из интервала [0, 1].
и
является числом из интервала [0, 1].
Существует много реальных проблем, в которых нарушается одно или
больше предположений, неявно присутствующих в приведенном выше определении.
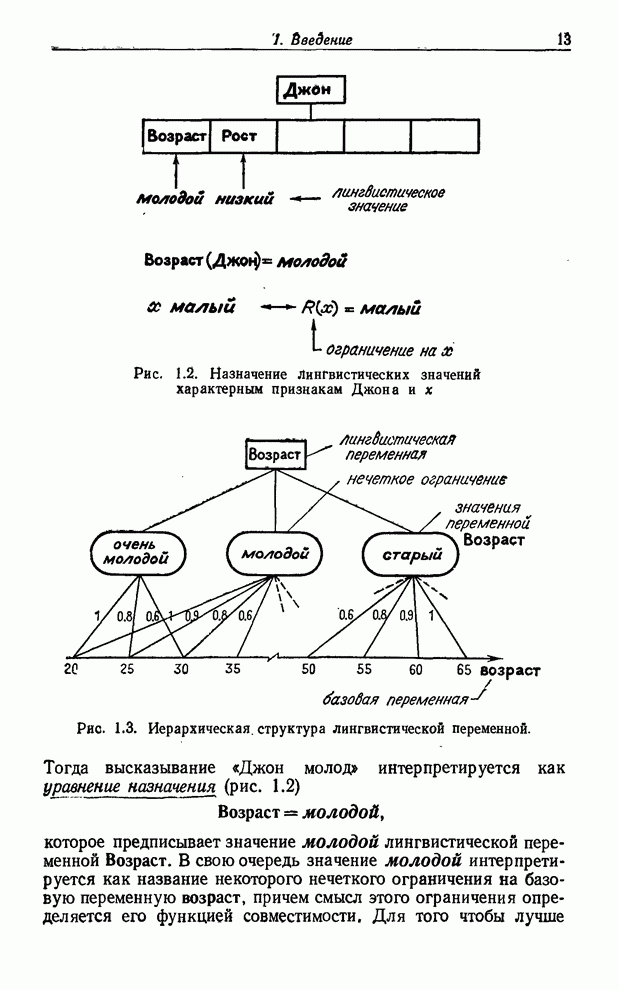
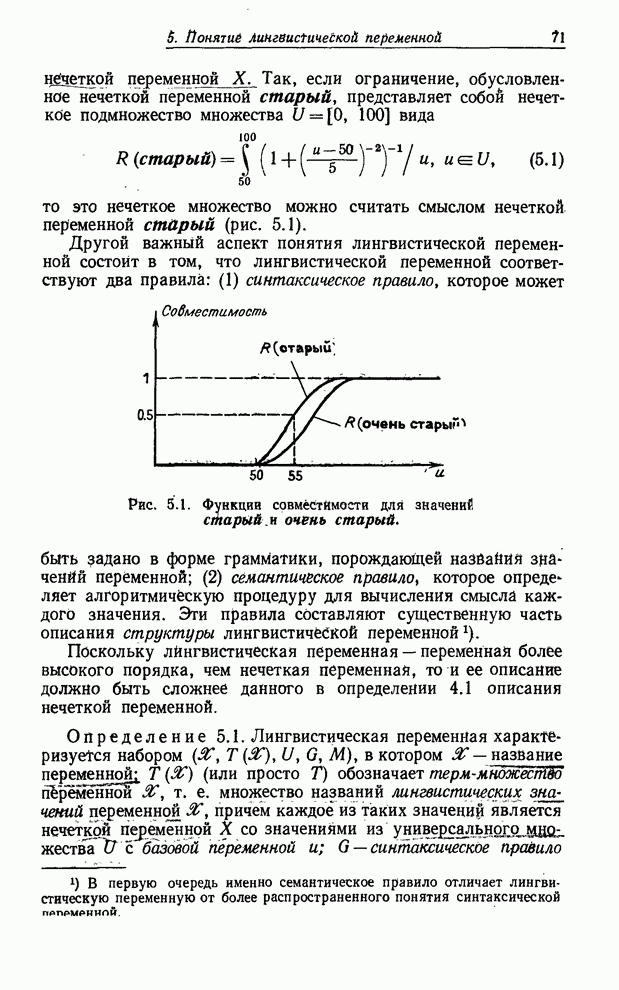
Во-первых, часто бывает плохо определено само событие ![]() , как, например, в вопросе
«Какова вероятность того, что завтра будет теплый день?» В этом
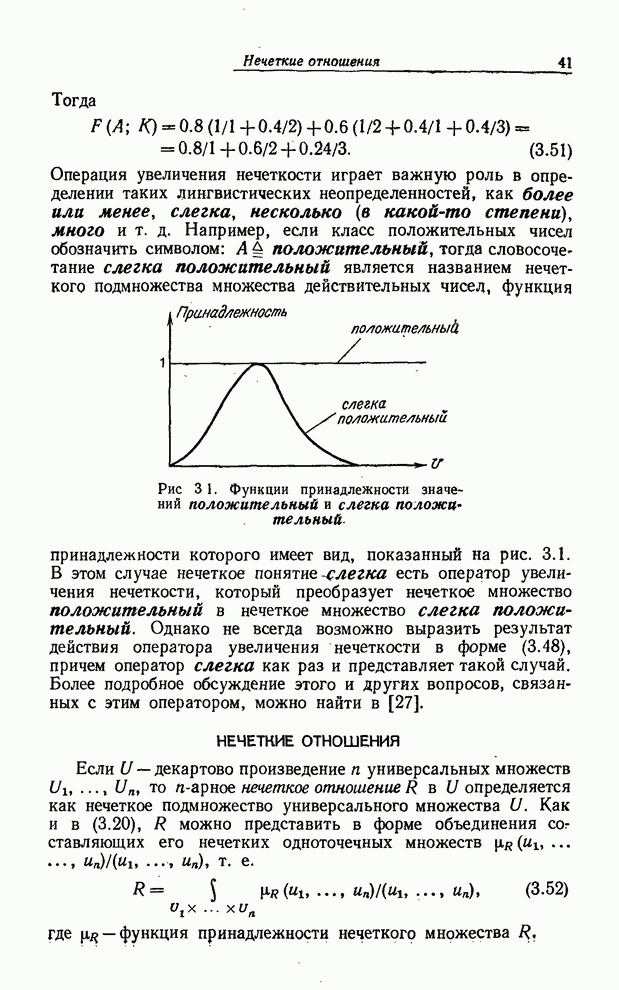
случае событие теплый день — нечеткое событие в том
смысле, что не существует резкой грани между его появлением и непоявлением. Как
показано в [48], такое событие можно охарактеризовать как нечеткое подмножество
, как, например, в вопросе
«Какова вероятность того, что завтра будет теплый день?» В этом
случае событие теплый день — нечеткое событие в том
смысле, что не существует резкой грани между его появлением и непоявлением. Как
показано в [48], такое событие можно охарактеризовать как нечеткое подмножество
![]() пространства
элементарных событий
пространства
элементарных событий ![]() с измеримой функцией принадлежности
с измеримой функцией принадлежности ![]() .
.
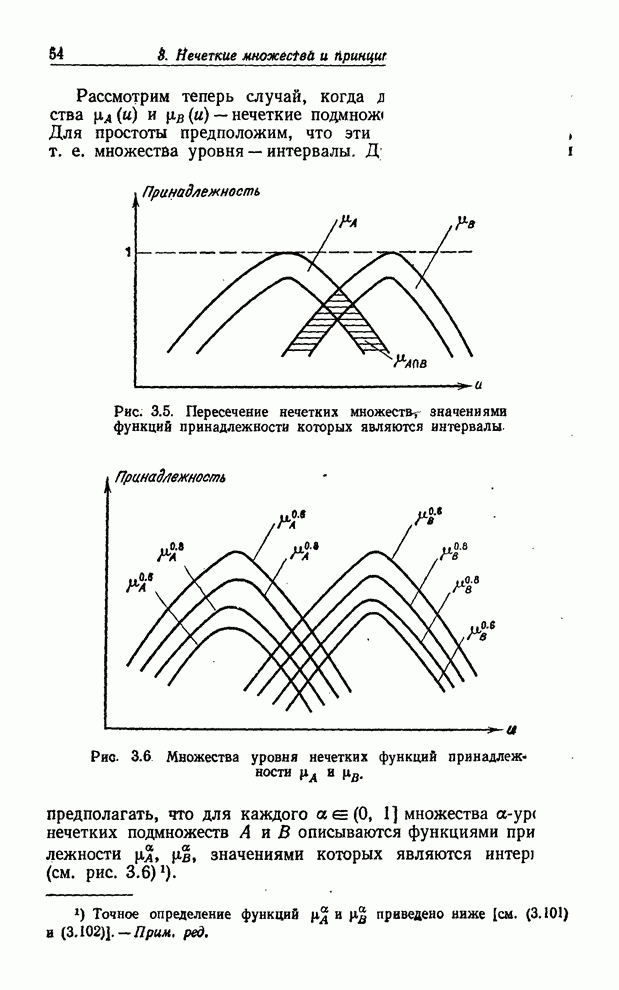
Во-вторых, даже если ![]() — вполне определенное обычное (не
нечеткое) событие, его вероятность
— вполне определенное обычное (не
нечеткое) событие, его вероятность ![]() может быть определена плохо.
Например, на вопрос «Какова вероятность того, что через месяц средняя цена на
акции фирмы «Доу-Джонс» будет выше?» было бы, по-видимому, неразумно однозначно
отвечать числом, например 0.7. В этом случае неопределенный ответ типа «вполне
вероятно» более соответствовал бы нашему нечеткому пониманию динамики цен на
акции и, следовательно, более реалистично, хотя и менее точно, характеризовал
бы рассматриваемую вероятность.
может быть определена плохо.
Например, на вопрос «Какова вероятность того, что через месяц средняя цена на
акции фирмы «Доу-Джонс» будет выше?» было бы, по-видимому, неразумно однозначно
отвечать числом, например 0.7. В этом случае неопределенный ответ типа «вполне
вероятно» более соответствовал бы нашему нечеткому пониманию динамики цен на
акции и, следовательно, более реалистично, хотя и менее точно, характеризовал
бы рассматриваемую вероятность.
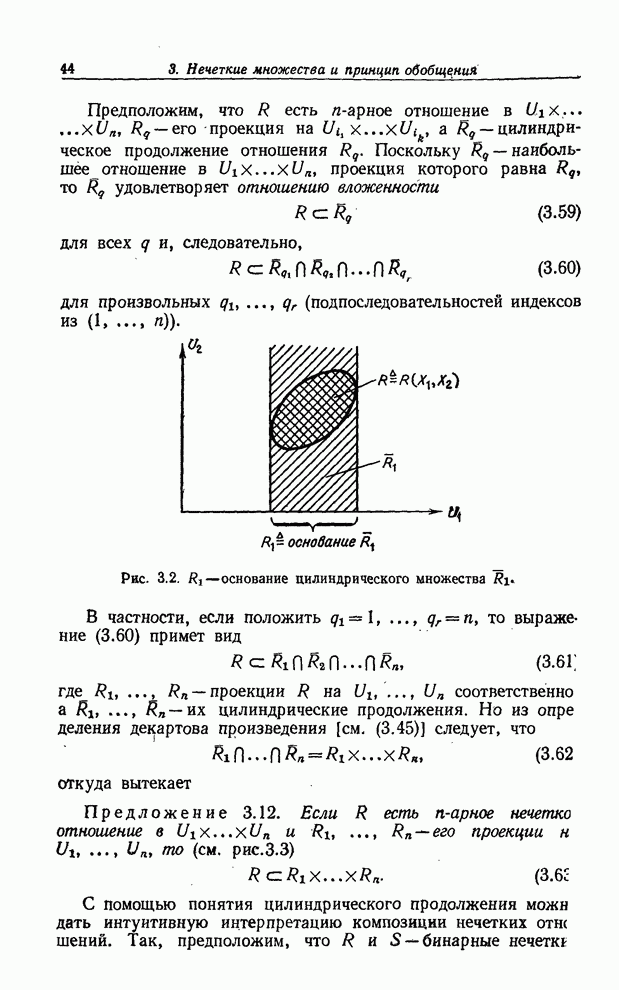
Ограничения, обусловленные предположением о том, что ![]() — вполне
определенное событие, можно устранить по крайней мере частично, если допустить,
что
— вполне
определенное событие, можно устранить по крайней мере частично, если допустить,
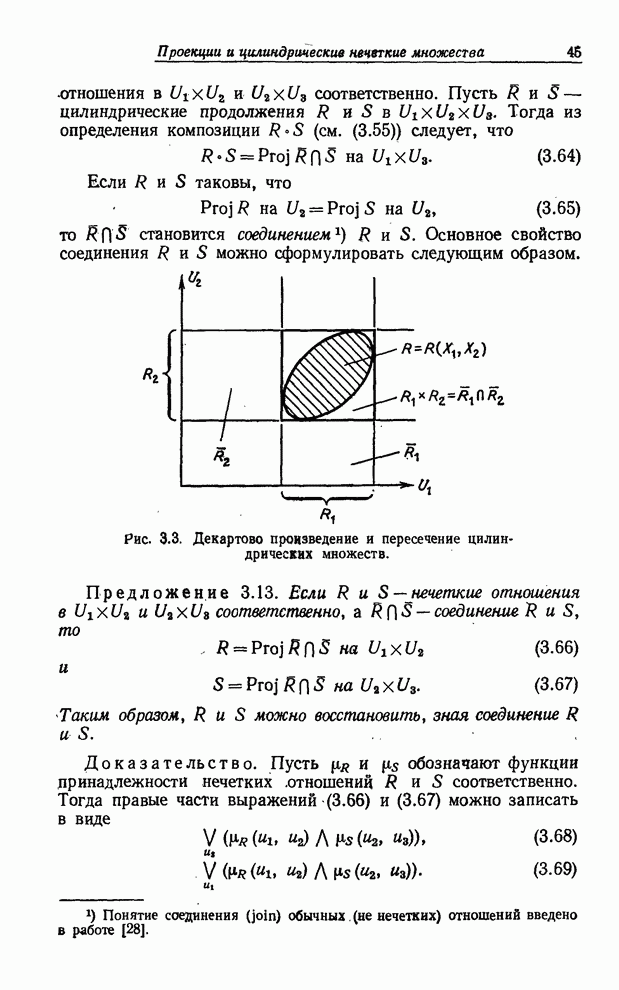
что ![]() может
быть нечетким событием, как это было сделано в [48]. Другой и, возможно,
более важный шаг, который можно предпринять с целью сделать теорию вероятностей
применимой к плохо определенным ситуациям, состоит в допущении того, что
вероятность
может
быть нечетким событием, как это было сделано в [48]. Другой и, возможно,
более важный шаг, который можно предпринять с целью сделать теорию вероятностей
применимой к плохо определенным ситуациям, состоит в допущении того, что
вероятность ![]() может
быть лингвистической переменной в смысле определения, данного в § 6.
Ниже мы изложим в общих чертах, каким образом это можно сделать, и исследуем
некоторые элементарные следствия, вытекающие из того, что вероятность
может
быть лингвистической переменной в смысле определения, данного в § 6.
Ниже мы изложим в общих чертах, каким образом это можно сделать, и исследуем
некоторые элементарные следствия, вытекающие из того, что вероятность ![]() — лингвистическая
переменная.
— лингвистическая
переменная.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
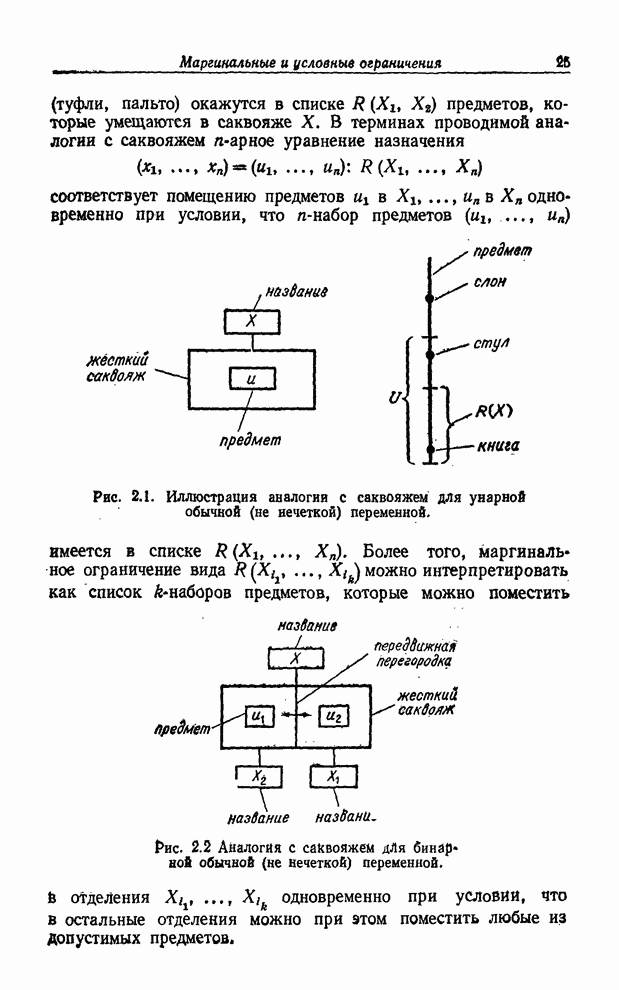
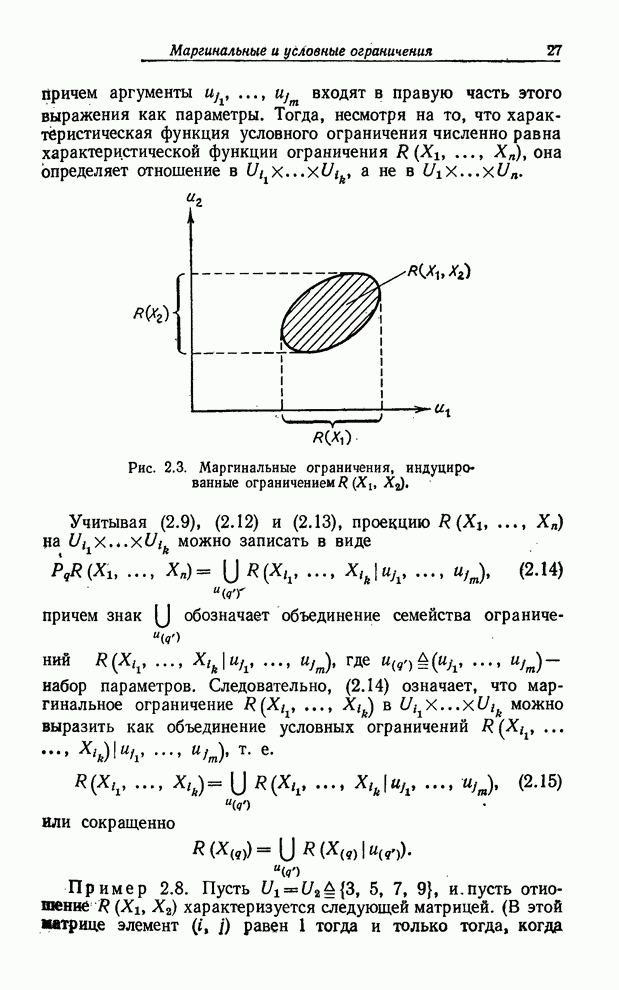
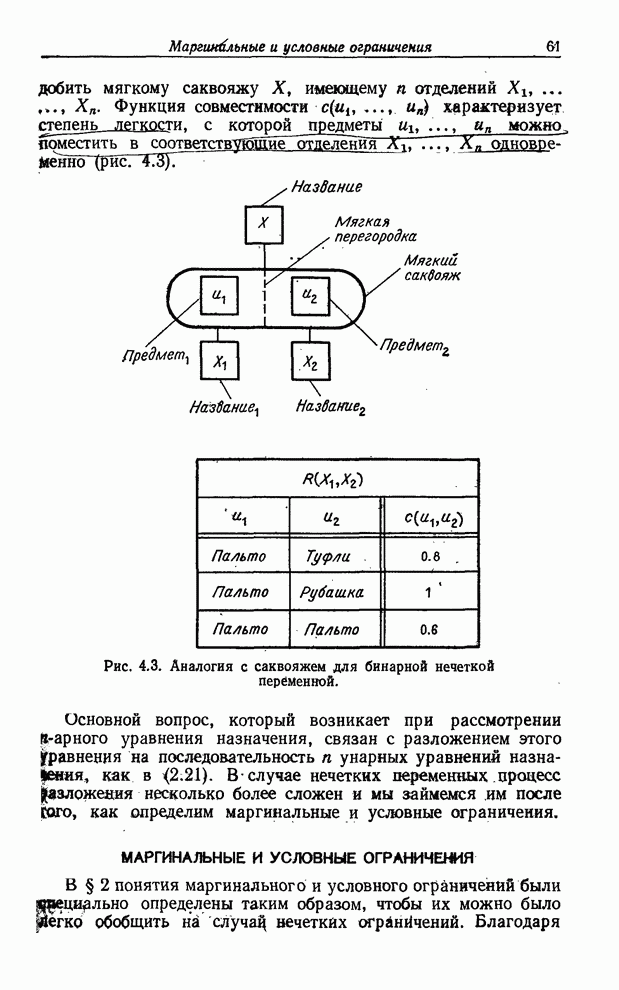
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
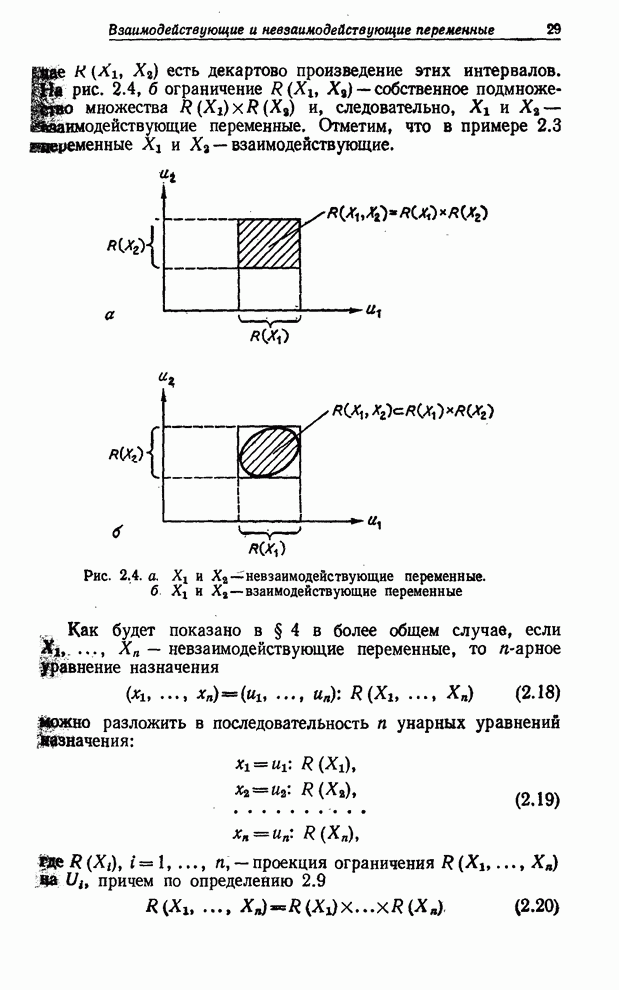
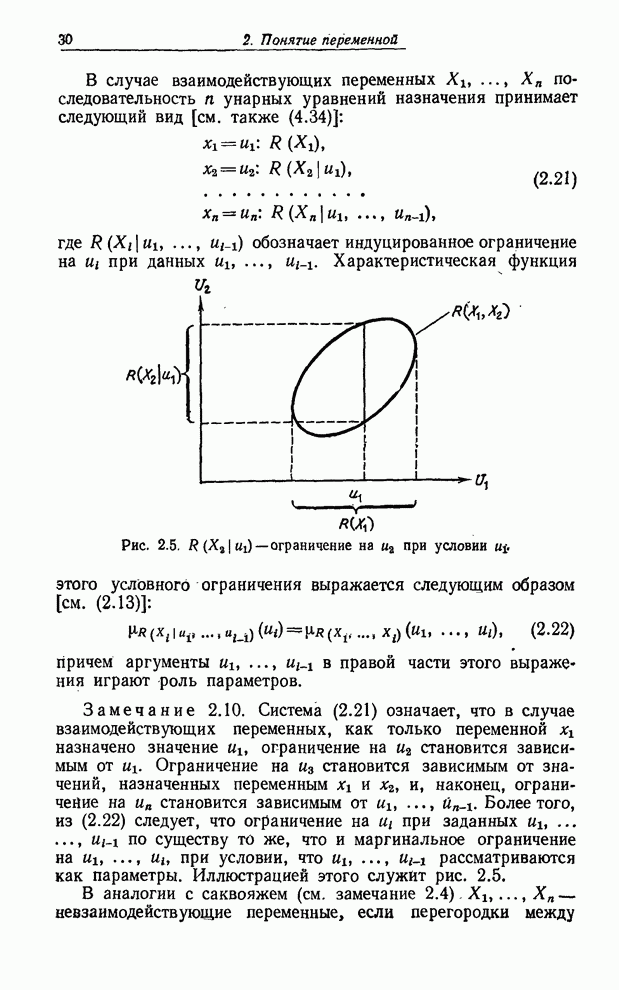
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
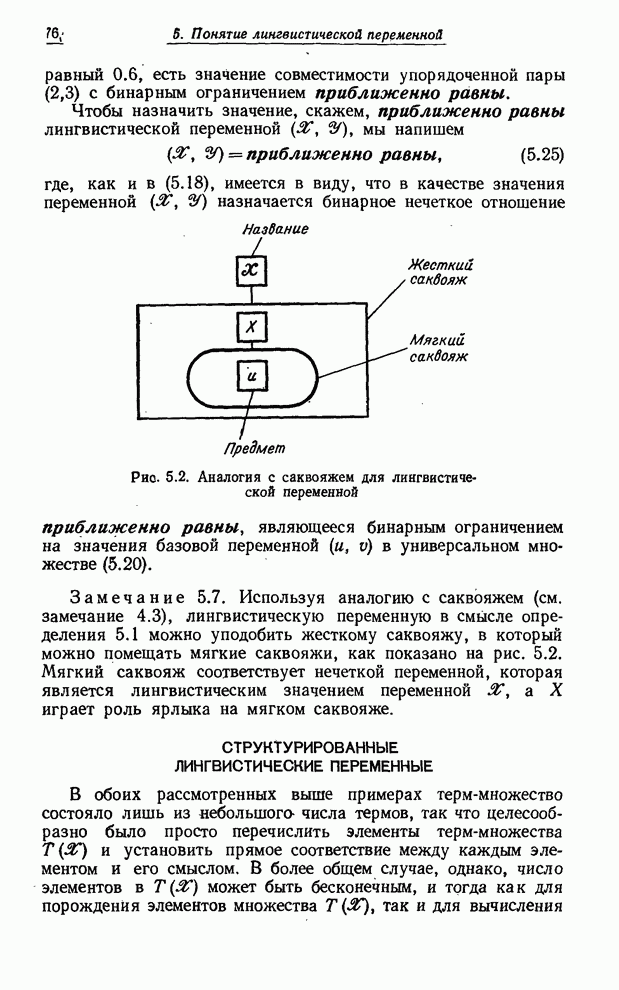
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
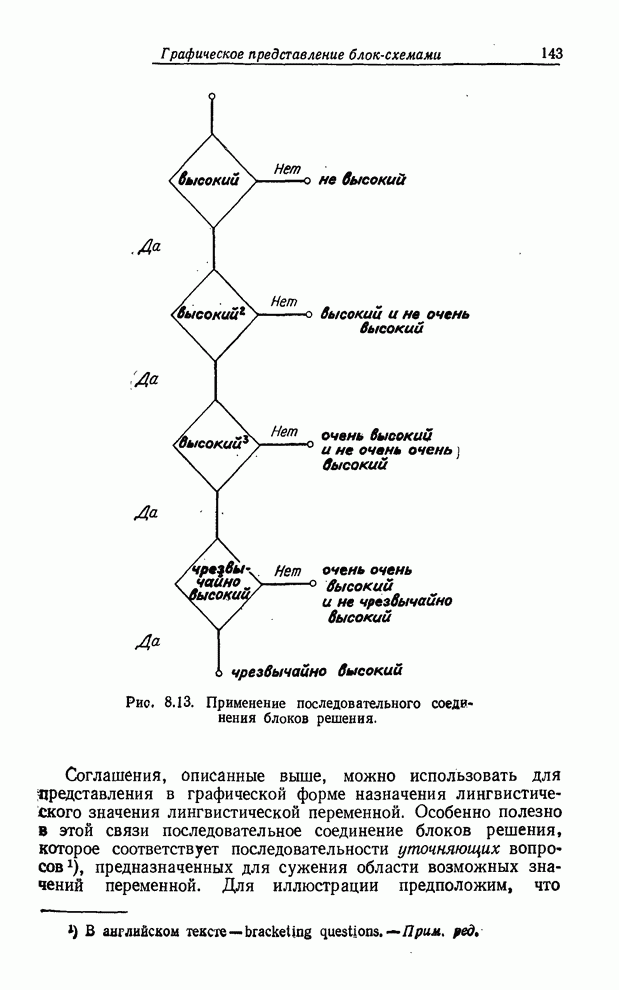
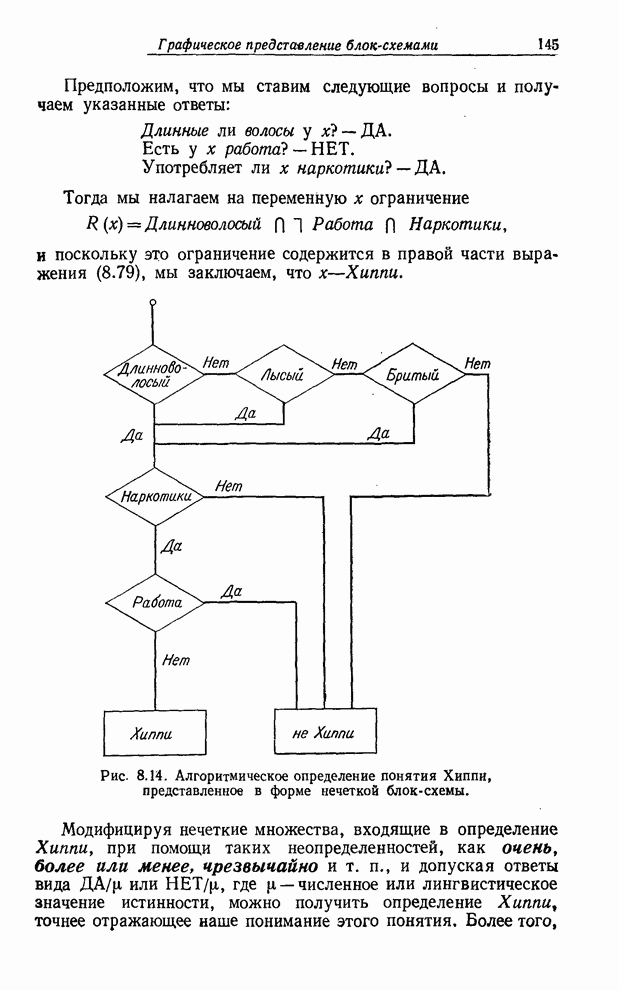
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ