| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
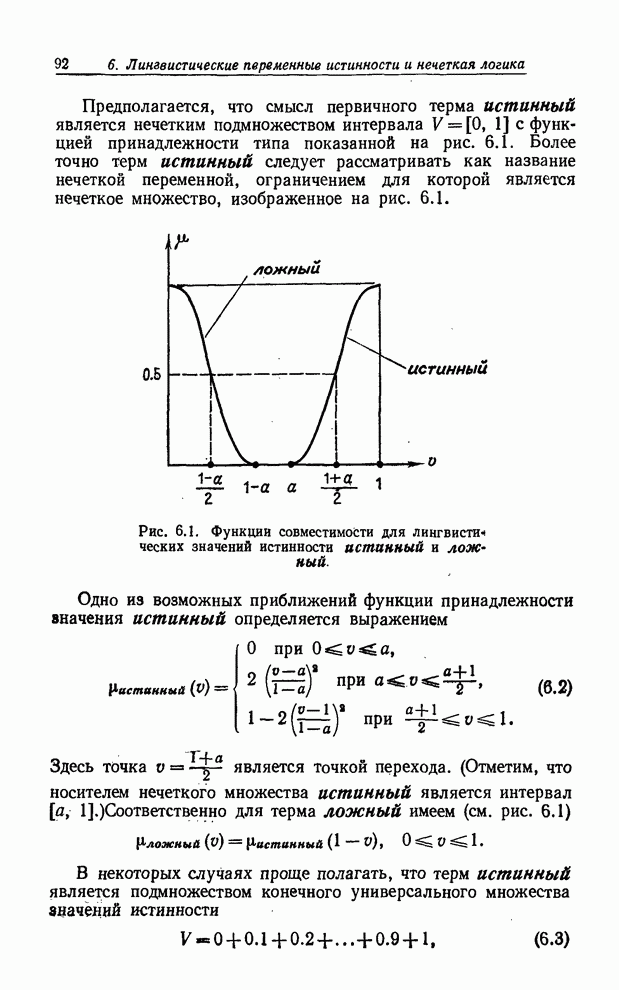
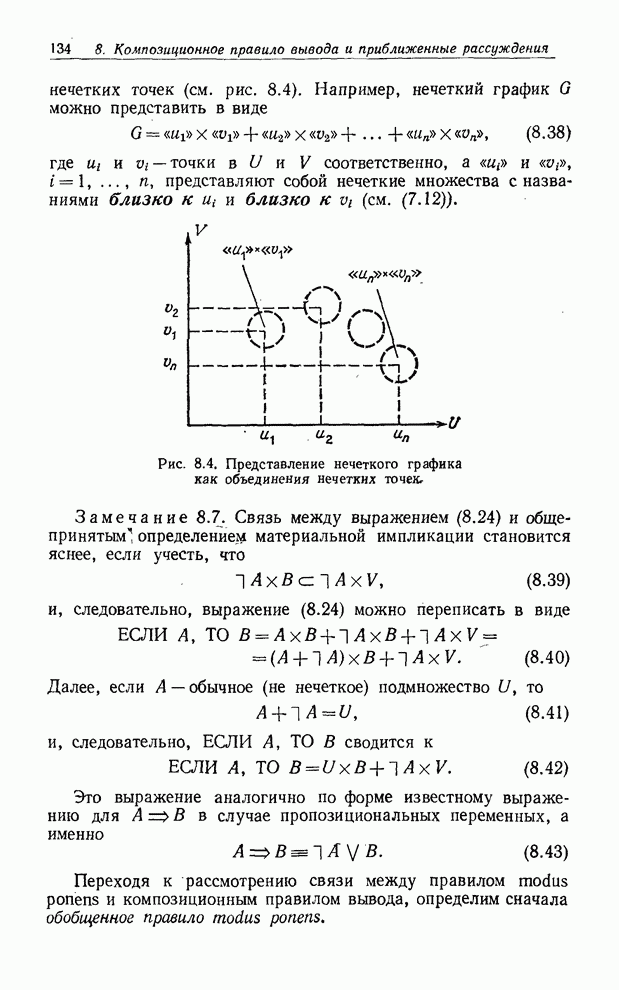
Как отмечалось в работе [7], при описании и реализации нечетких алгоритмов часто бывает очень удобно определять отношения между переменными и присваивать им конкретные значения с помощью блок-схем.
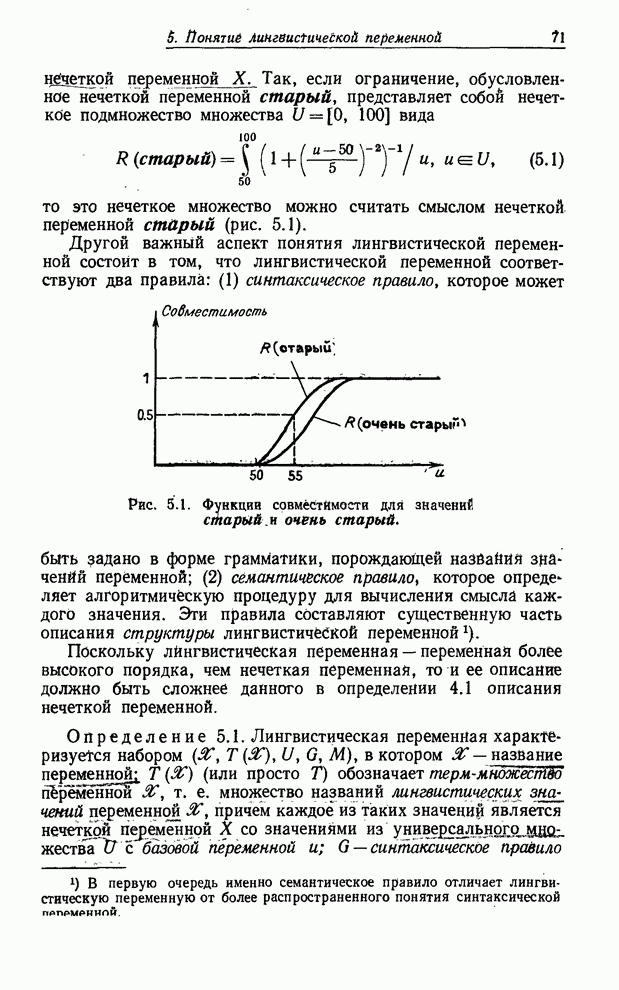
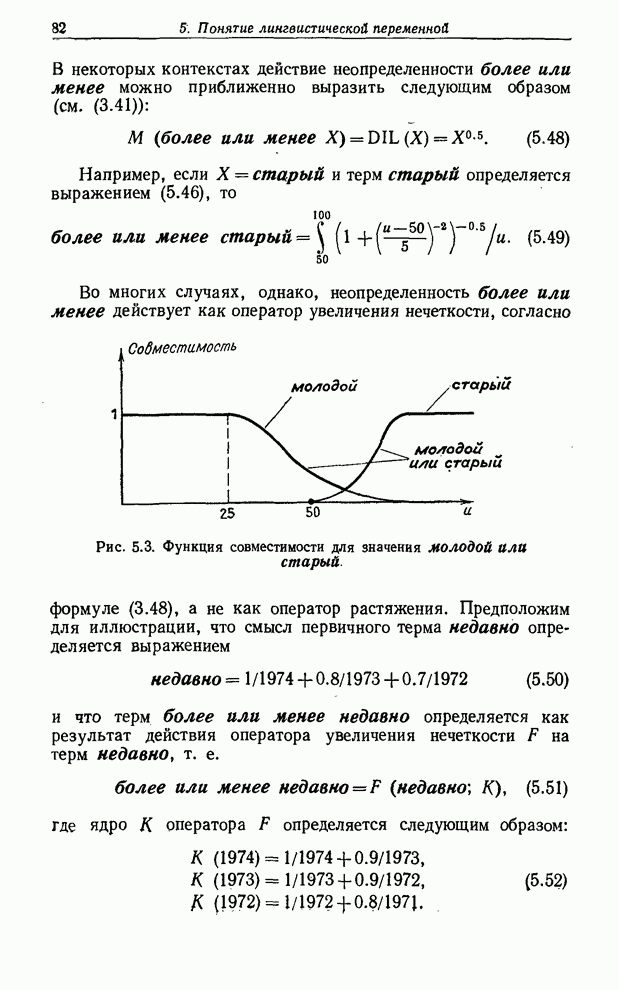
В дальнейшем мы не будем касаться многих сложных вопросов, связанных с описанием и реализацией нечетких алгоритмов. Наша цель - лишь уяснить роль, которую играют блоки решений применительно не к обычным (не нечетким), а нечетким предикатам, связав их с назначением ограничений на базовые переменные.
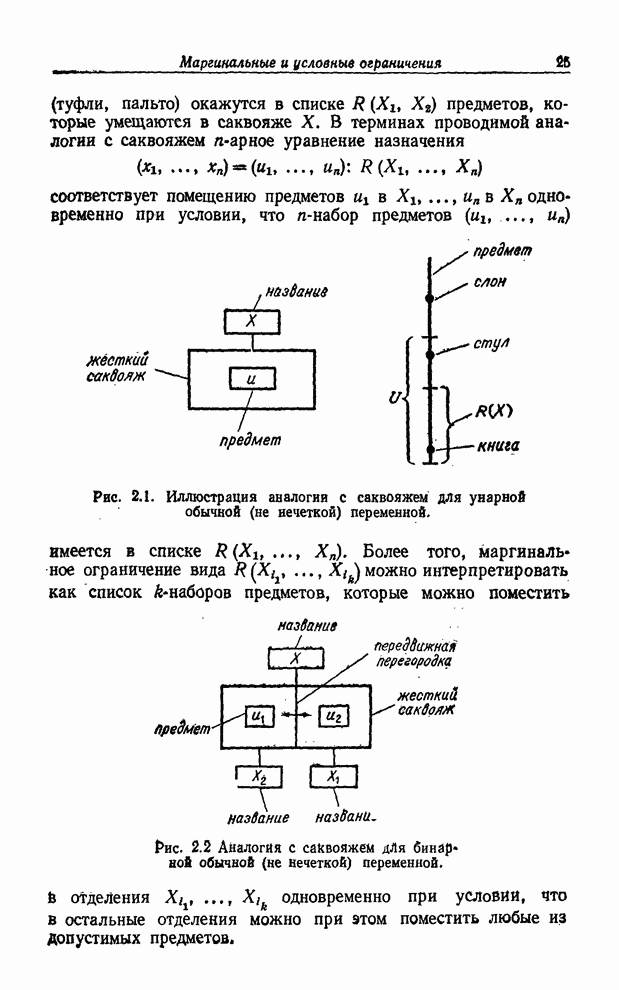
В
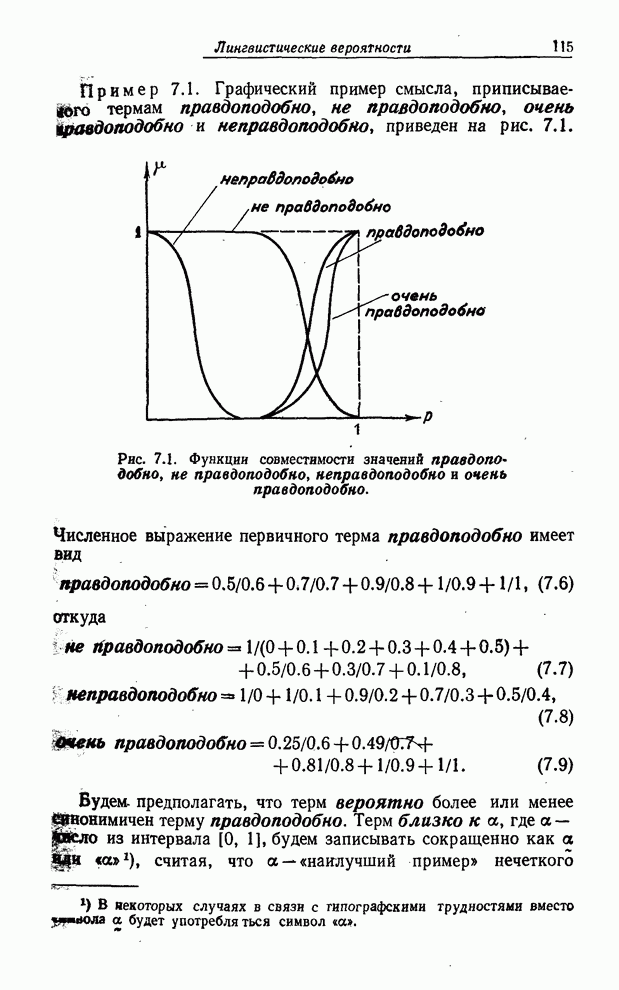
обычной блок-схеме блок решения типа блока ![]() на рис. 8.9 соответствует одноместному
предикату
на рис. 8.9 соответствует одноместному
предикату ![]() .
Так, переход из точки 1 в точку 2 означает, что
.
Так, переход из точки 1 в точку 2 означает, что ![]() - истинно, в то время как переход из
точки 1 в точку 3 означает, что
- истинно, в то время как переход из
точки 1 в точку 3 означает, что ![]() - ложно.
- ложно.

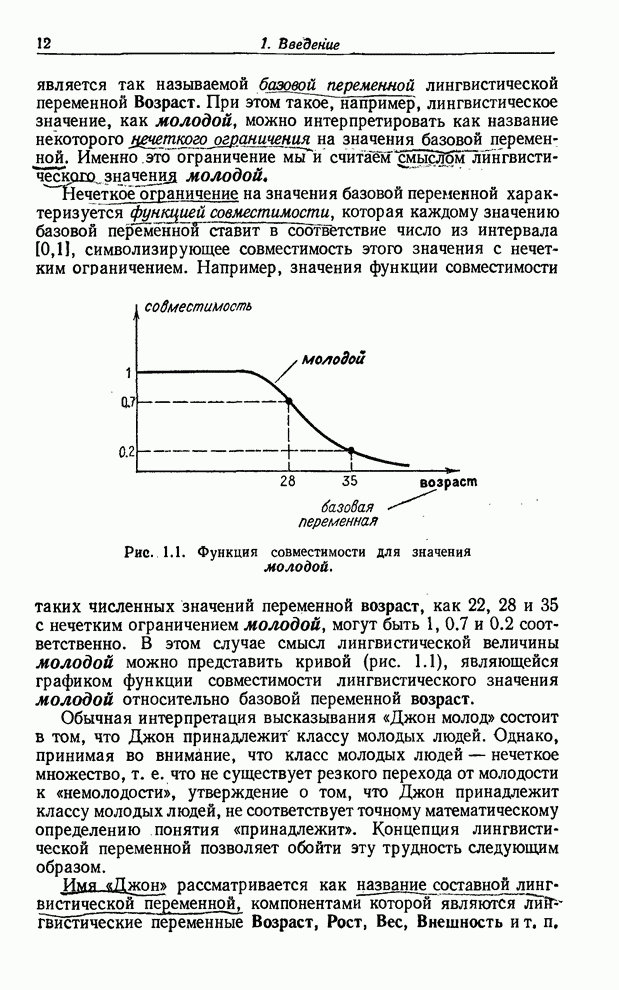
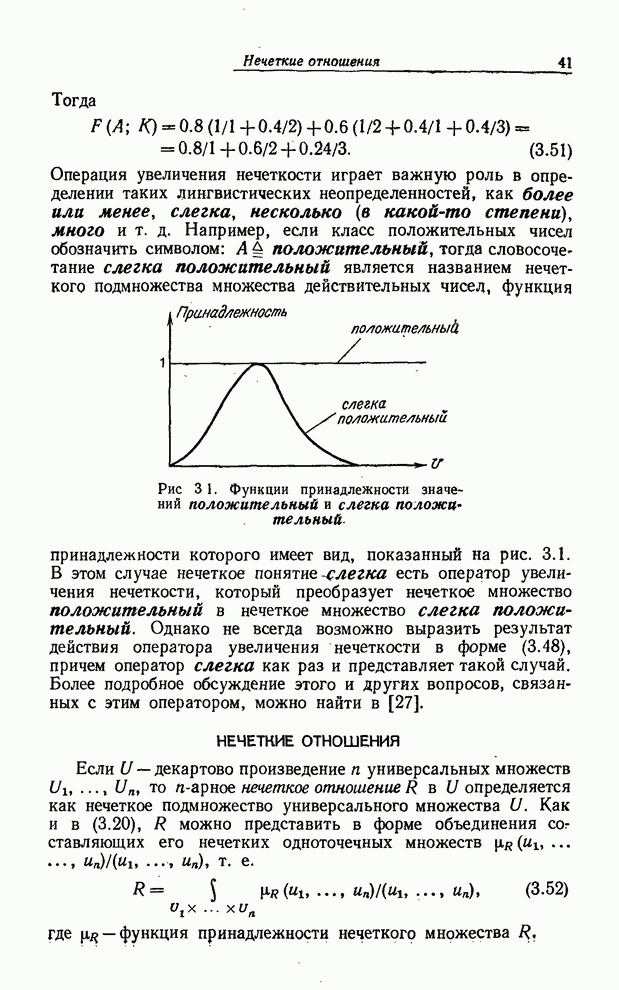
Рис. 8.9. Нечеткий блок решения.
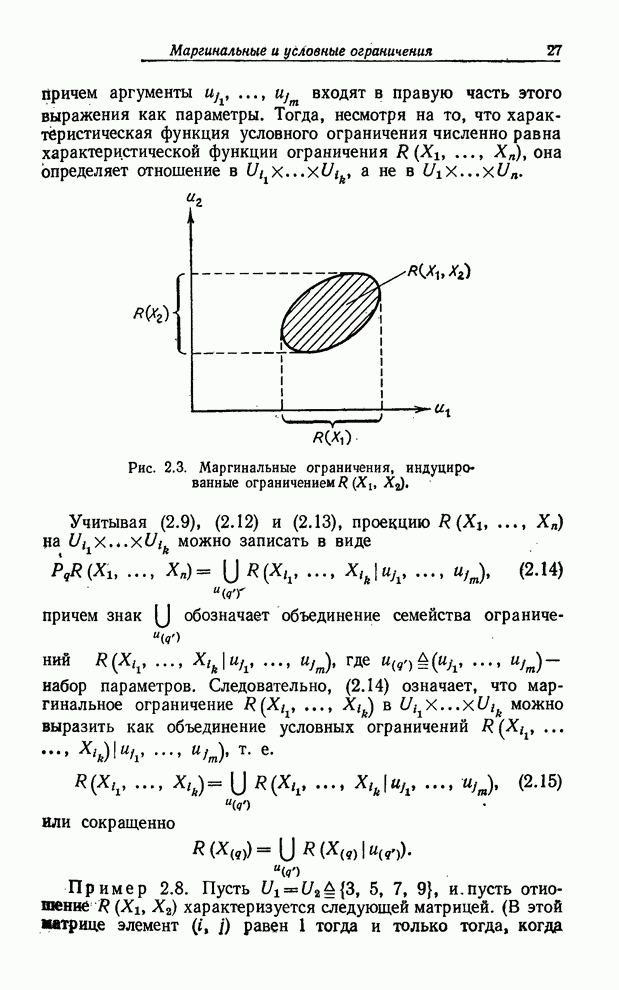
Понятия,
введенные в предыдущих параграфах, лежат в основе обобщения понятия блока
решений применительно к нечетким множествам (или предикатам). В частности, имея
в виду рис. 8.9, предположим, что ![]() - нечеткое подмножество множества
- нечеткое подмножество множества ![]() и что вопрос,
соответствующий блоку решения, имеет вид: «Является ли
и что вопрос,
соответствующий блоку решения, имеет вид: «Является ли ![]()
![]() ?», например «является ли
?», например «является ли ![]() малым?», где
малым?», где ![]() - общее название
входной переменной. Блок-схемы с блоками решения такого типа будем называть
нечеткими блок-схемами.
- общее название
входной переменной. Блок-схемы с блоками решения такого типа будем называть
нечеткими блок-схемами.
Если
ответом является просто ДА, то мы назначаем ограничению на ![]() значение
значение ![]() , т. е. полагаем
, т. е. полагаем
![]() , (8.63)
, (8.63)
и
переводим ![]() из
1 в 2.
из
1 в 2.
С другой стороны, если ответом является НЕТ, мы полагаем
![]() (8.64)
(8.64)
и
переводим ![]() из
1 в 3.
из
1 в 3.
Если,
например, ![]() малый,
то уравнение (8.63) примет вид
малый,
то уравнение (8.63) примет вид
![]() малый. (8.65)
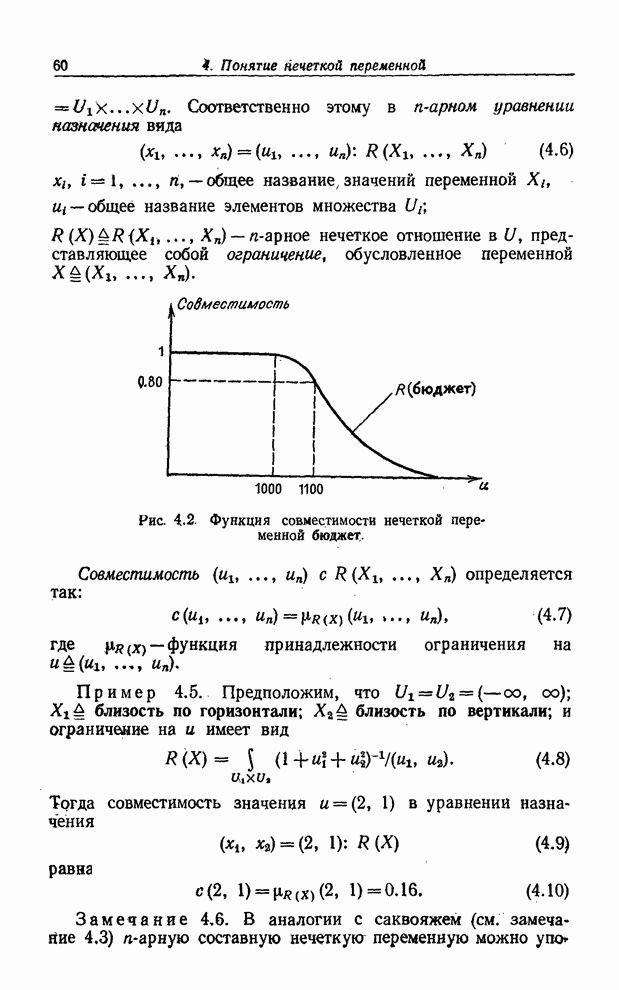
малый. (8.65)
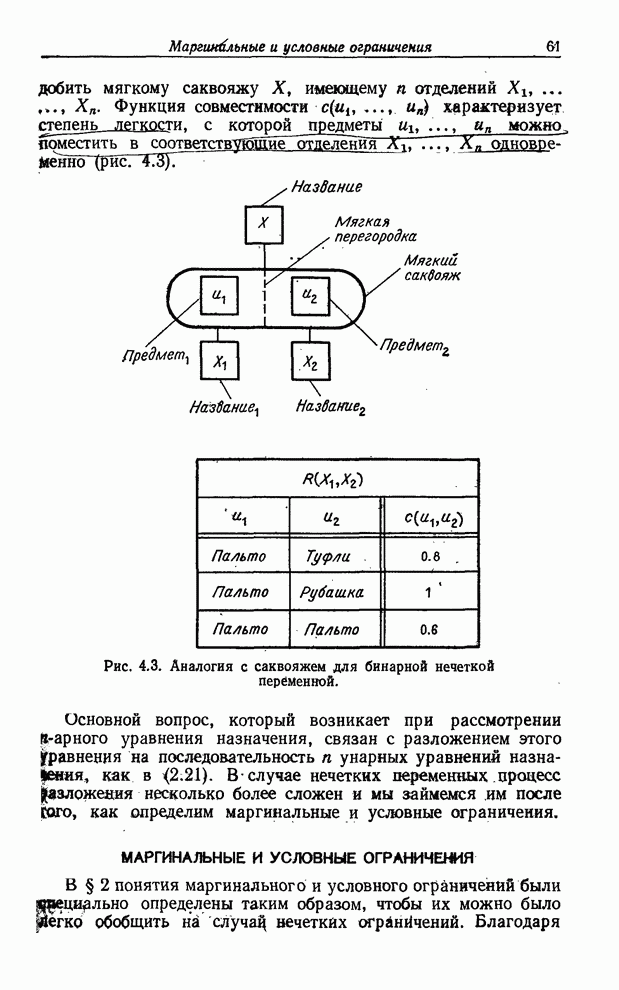
Если
ответом является ![]() ,
где
,
где ![]() , то мы
переводим
, то мы
переводим ![]() в
точку 2, заключив, что степень принадлежности
в
точку 2, заключив, что степень принадлежности ![]() множеству
множеству ![]() равна
равна ![]() . Кроме того, мы переводим
. Кроме того, мы переводим ![]() в точку 3, заключив,
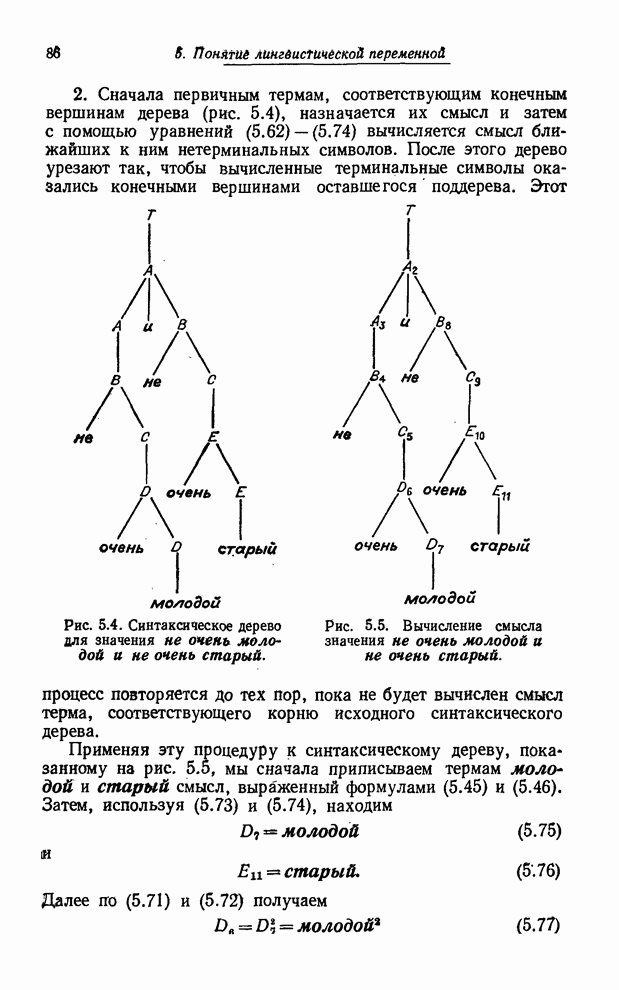
что степень принадлежности
в точку 3, заключив,
что степень принадлежности ![]() множеству
множеству ![]() равна
равна ![]() .
.
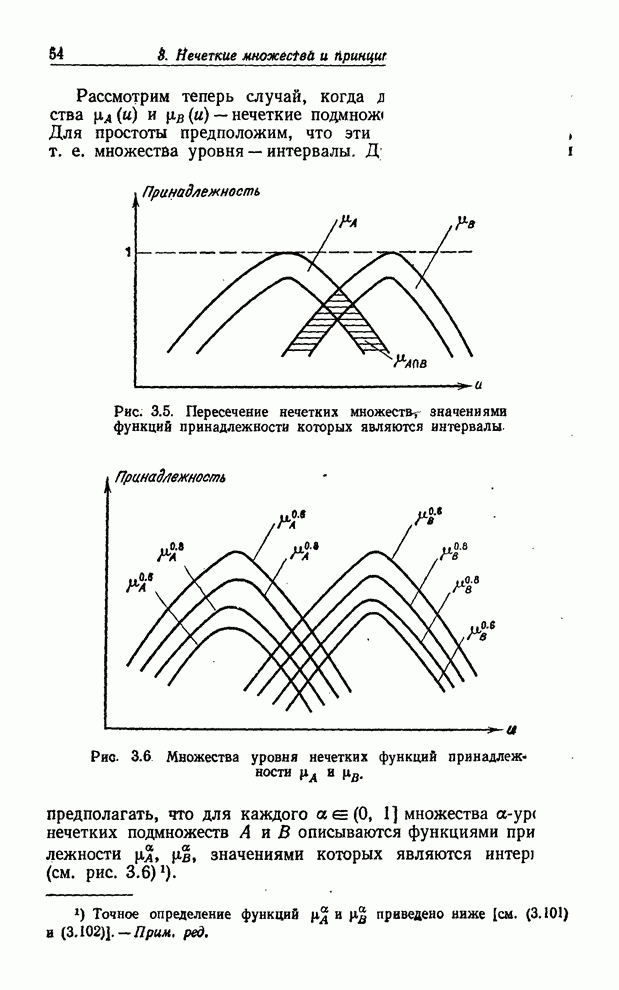
Если
степень принадлежности ![]() принимает лингвистические, а не
числовые значения, то мы представляем эти значения как лингвистические значения
истинности. В этих случаях типичными будут ответы типа ДА/истинно, ДA/очень
истинно, ДА/более или менее истинно и т. п. Как и раньше, мы будем полагать,
что степень принадлежности
принимает лингвистические, а не
числовые значения, то мы представляем эти значения как лингвистические значения
истинности. В этих случаях типичными будут ответы типа ДА/истинно, ДA/очень
истинно, ДА/более или менее истинно и т. п. Как и раньше, мы будем полагать,
что степень принадлежности ![]() множеству
множеству ![]() равна
равна ![]() , где
, где ![]() - лингвистическое значение истинности,
и переводить
- лингвистическое значение истинности,
и переводить ![]() в
точку 3, заключив, что степень принадлежности
в
точку 3, заключив, что степень принадлежности ![]() множеству
множеству ![]() равна
равна ![]() .
.
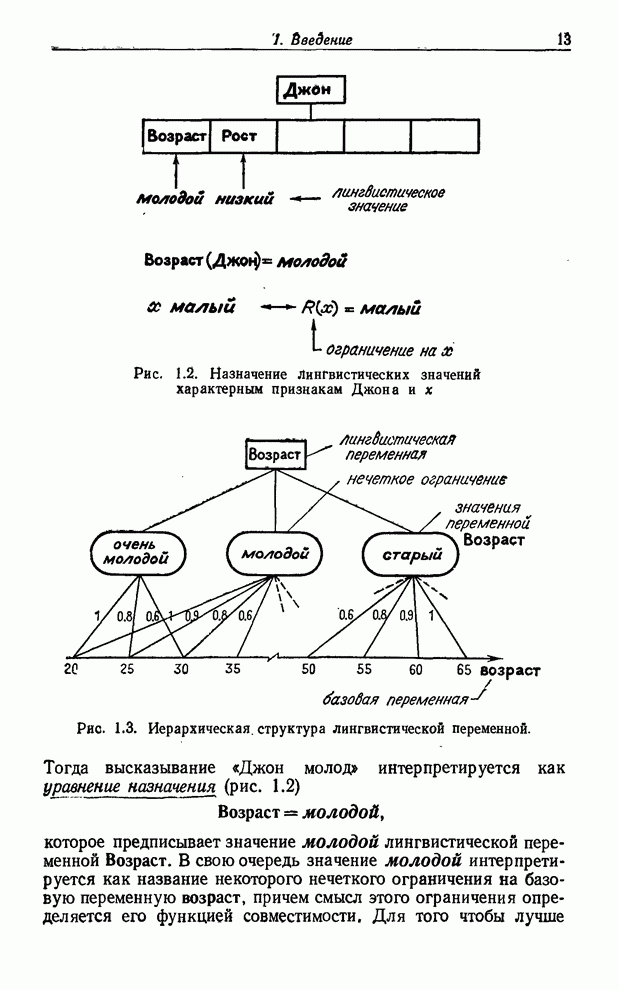
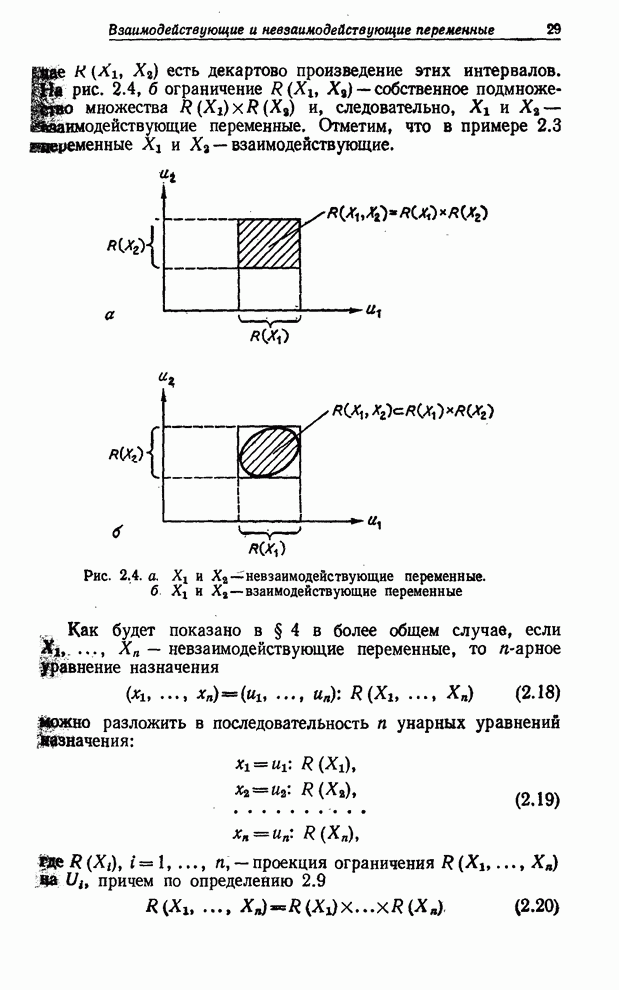
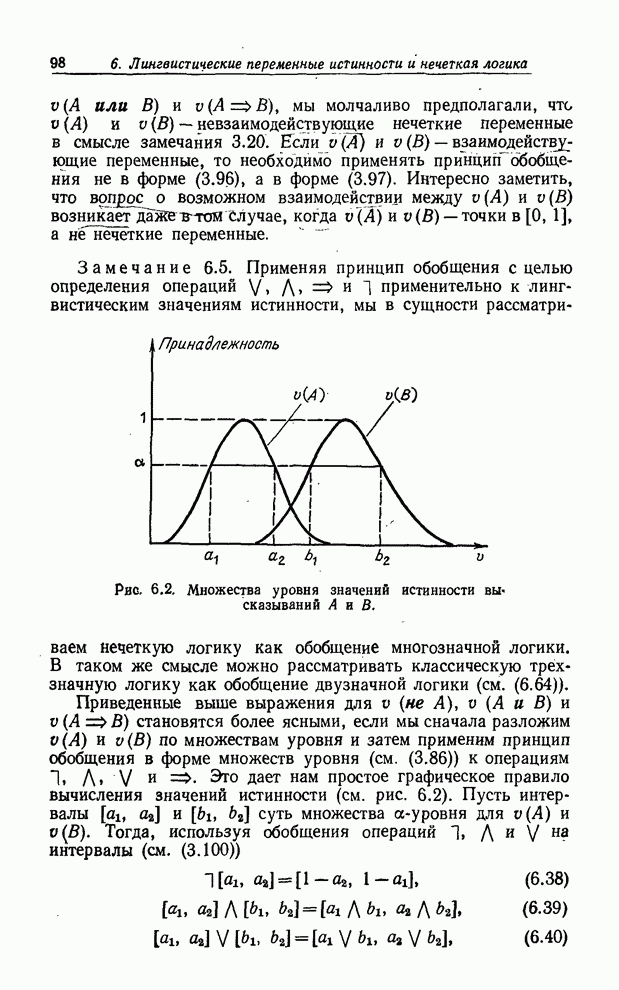
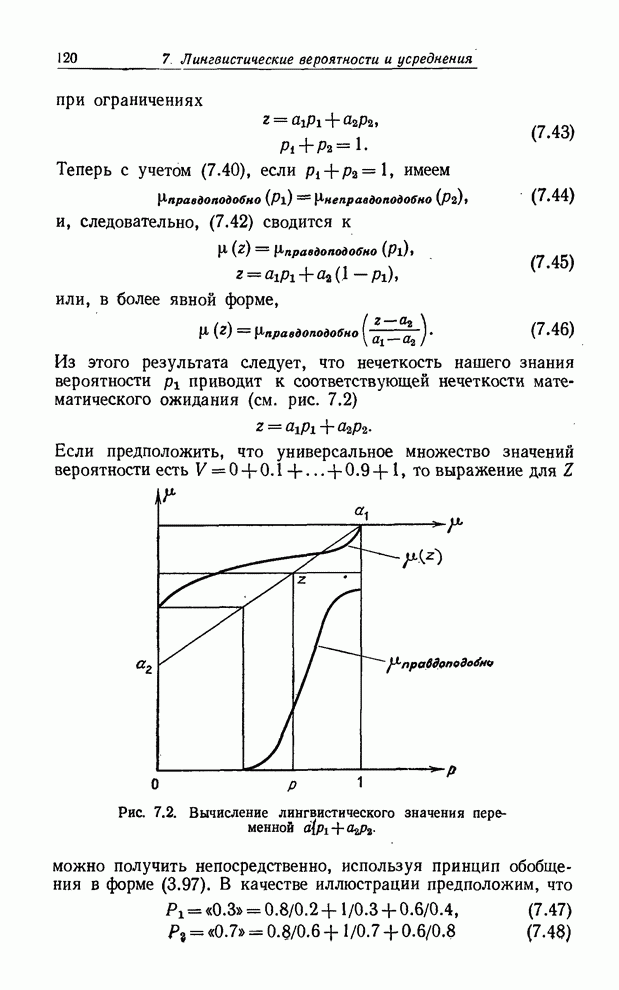
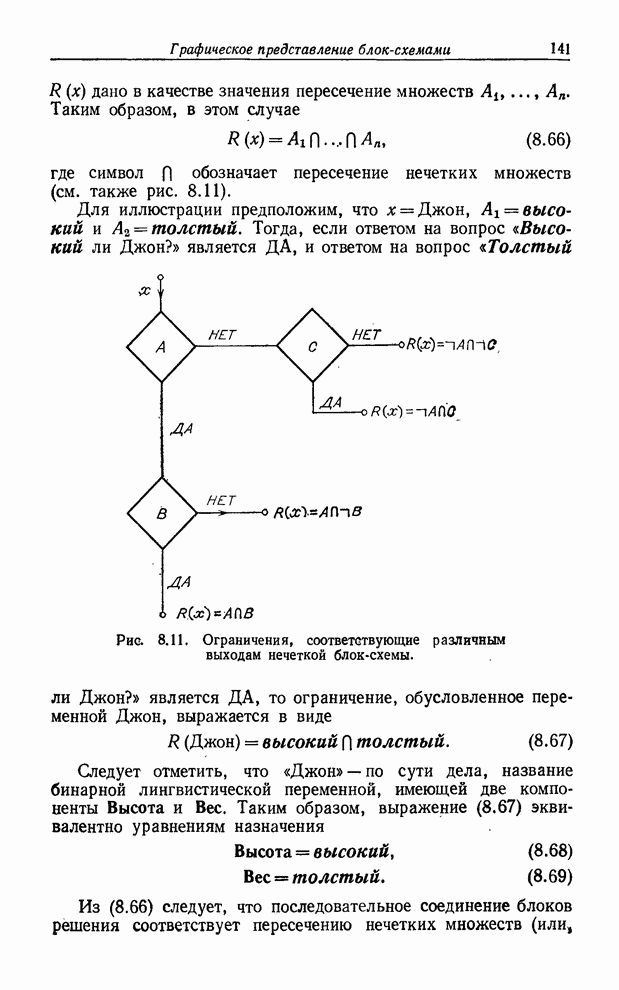
Если
имеется цепочка блоков решений, как на рис. 8.10, то последовательность ответов
ДА переведет ![]() из
точки 1 в точку
из
точки 1 в точку ![]() и
результатом ее будет то, что ограничению
и
результатом ее будет то, что ограничению ![]() дано в качестве значения пересечение
множеств
дано в качестве значения пересечение
множеств ![]() .
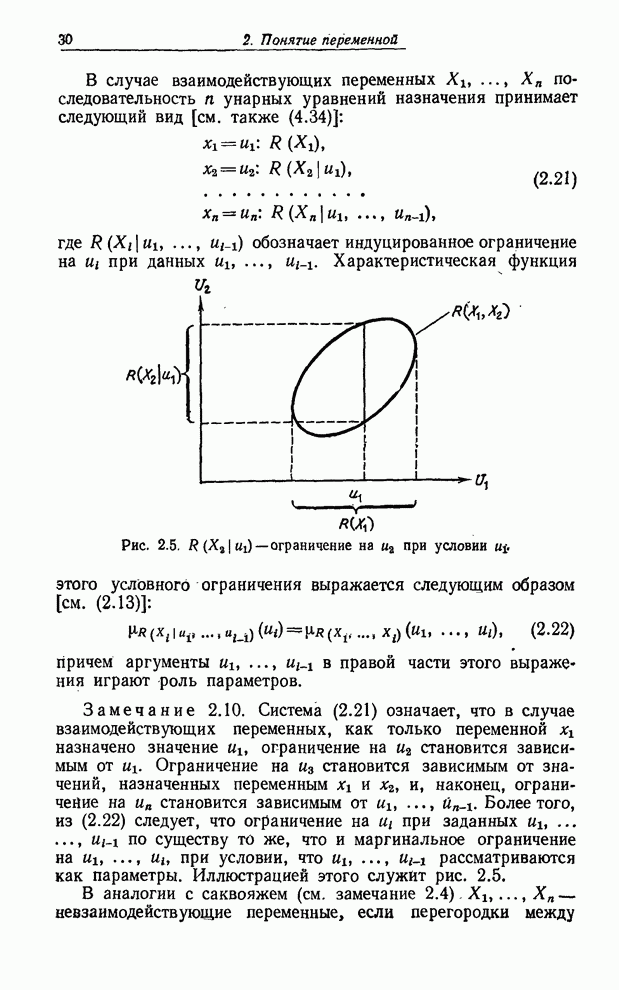
Таким образом, в этом случае
.
Таким образом, в этом случае
![]() , (8.66)
, (8.66)
где
символ ![]() обозначает
пересечение нечетких множеств (см. также рис. 8.11).
обозначает
пересечение нечетких множеств (см. также рис. 8.11).

Рис. 8.10. Последовательное соединение блоков решения.

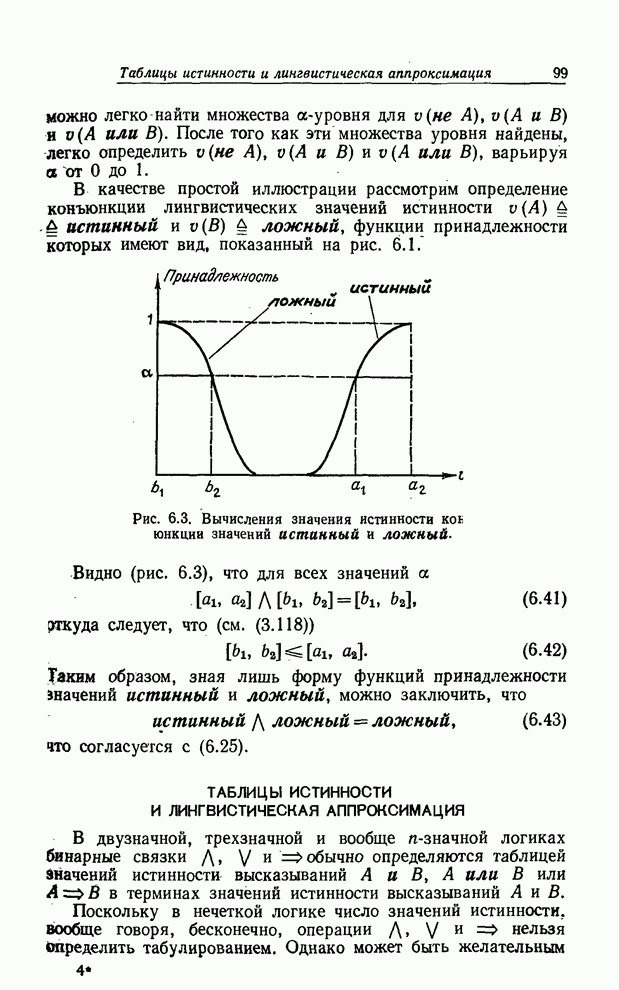
Рис. 8.11. Ограничения, соответствующие различным выходам нечеткой блок-схемы
Для
иллюстрации предположим, что ![]() Джон,
Джон, ![]() высокий и
высокий и ![]() толстый. Тогда, если ответом на вопрос
«Высокий ли Джон?» является ДА, и ответом на вопрос «Толстый ли Джон?» является
ДА, то ограничение, обусловленное переменной Джон, выражается в виде
толстый. Тогда, если ответом на вопрос
«Высокий ли Джон?» является ДА, и ответом на вопрос «Толстый ли Джон?» является
ДА, то ограничение, обусловленное переменной Джон, выражается в виде
![]() . (8.67)
. (8.67)
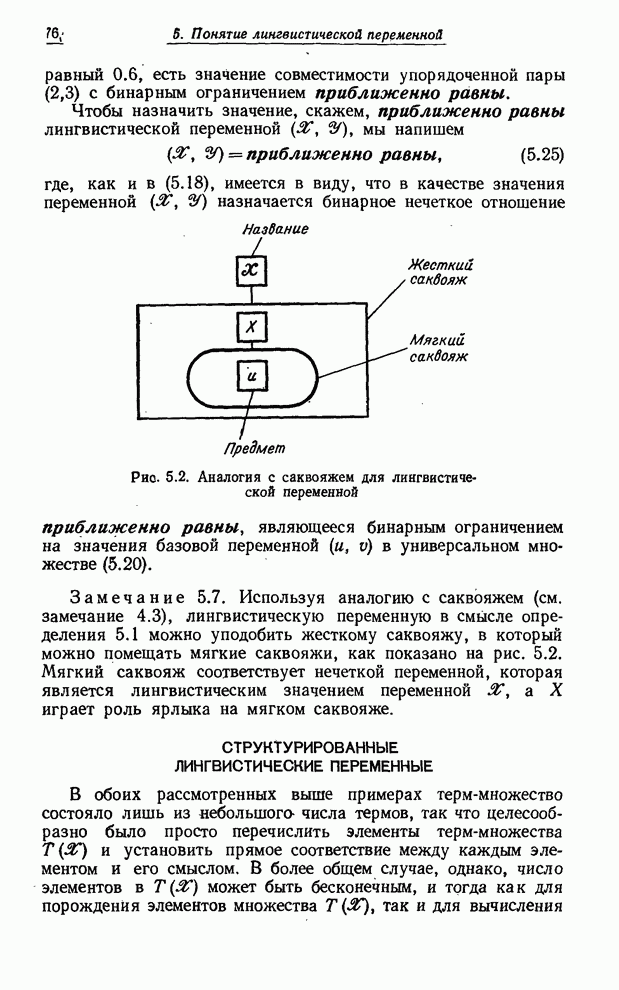
Следует отметить, что «Джон» - по сути дела, название бинарной лингвистической переменной, имеющей две компоненты Высота и Вес. Таким образом, выражение (8.67) эквивалентно уравнениям назначения
Высота = высокий, (8.68)
Вес = толстый. (8.69)
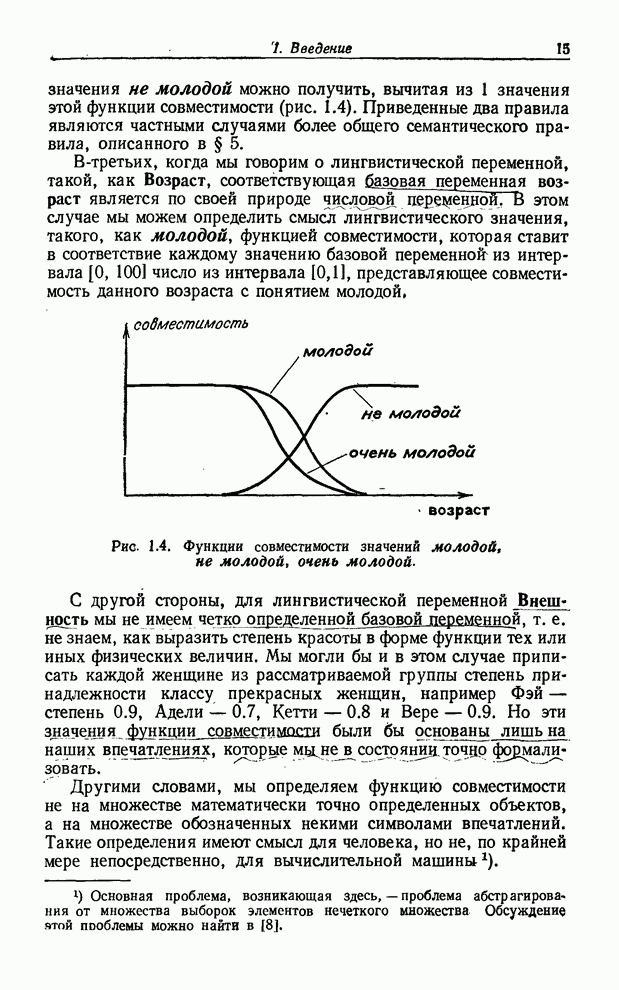
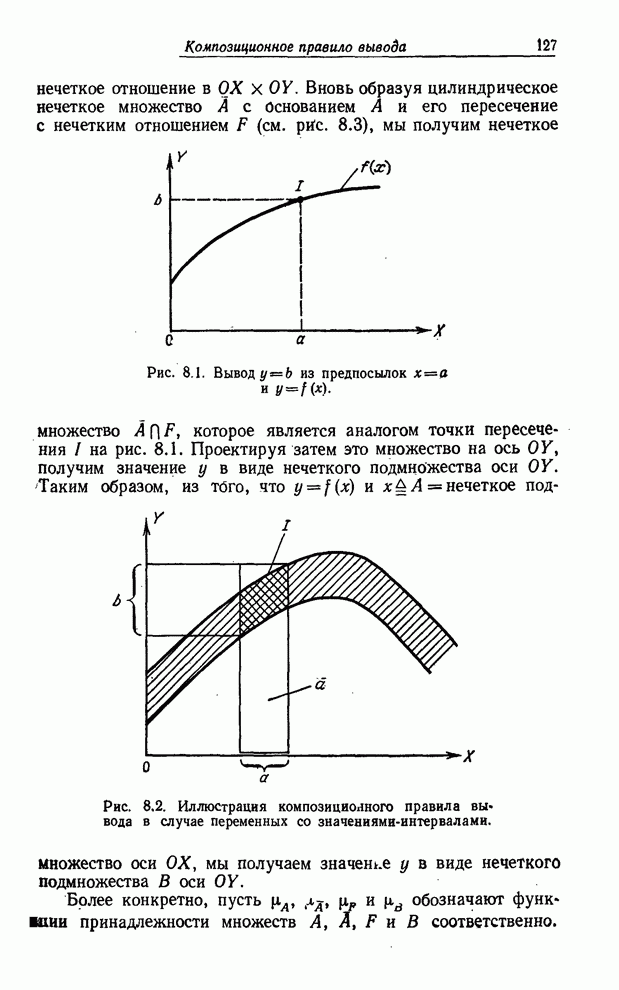
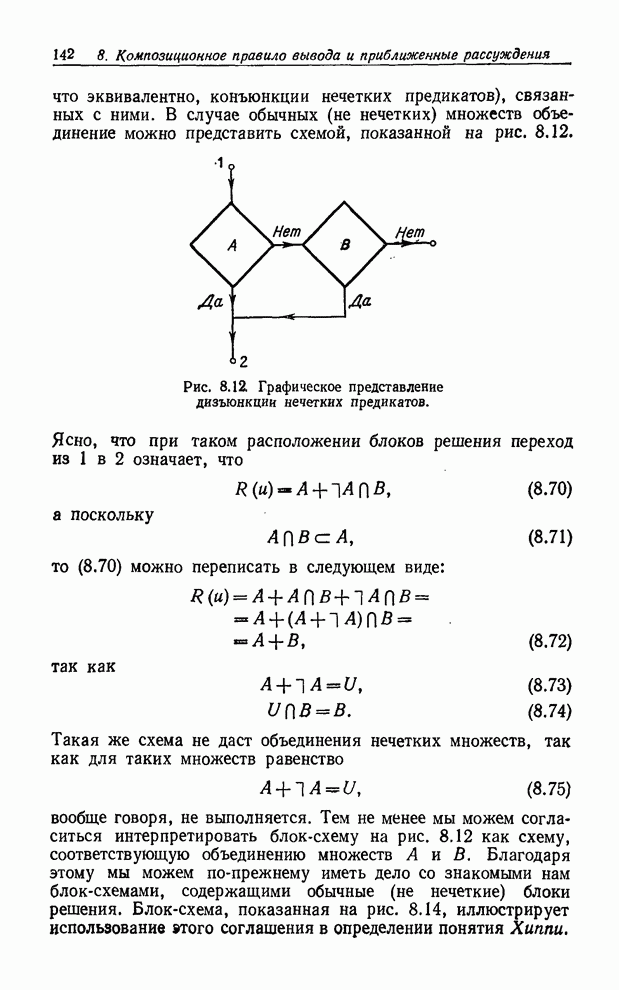
Из (8.66) следует, что последовательное соединение блоков решения соответствует пересечению нечетких множеств (или, что эквивалентно, конъюнкции нечетких предикатов), связанных с ними. В случае обычных (не нечетких) множеств объединение можно представить схемой, показанной на рис. 8.12.

Рис. 8.12. Графическое представление дизъюнкции нечетких предикатов.
Ясно, что при таком расположении блоков решения переход из 1 в 2 означает, что
![]() , (8.70)
, (8.70)
а поскольку
![]() , (8.71)
, (8.71)
то (8.70) можно переписать в следующем виде:
![]() , (8.72)
, (8.72)
так как
![]() , (8.73)
, (8.73)
![]() . (8.74)
. (8.74)
Такая же схема не даст объединения нечетких множеств, так как для таких множеств равенство
![]() , (8.75)
, (8.75)
вообще
говоря, не выполняется. Тем не менее мы можем согласиться интерпретировать
блок-схему на рис. 8.12 как схему, соответствующую объединению множеств ![]() и
и ![]() . Благодаря этому мы
можем по-прежнему иметь дело со знакомыми нам блок-схемами, содержащими обычные
(не нечеткие) блоки решения. Блок-схема, показанная на рис. 8.14, иллюстрирует
использование этого соглашения в определении понятия Хиппи.
. Благодаря этому мы
можем по-прежнему иметь дело со знакомыми нам блок-схемами, содержащими обычные
(не нечеткие) блоки решения. Блок-схема, показанная на рис. 8.14, иллюстрирует
использование этого соглашения в определении понятия Хиппи.

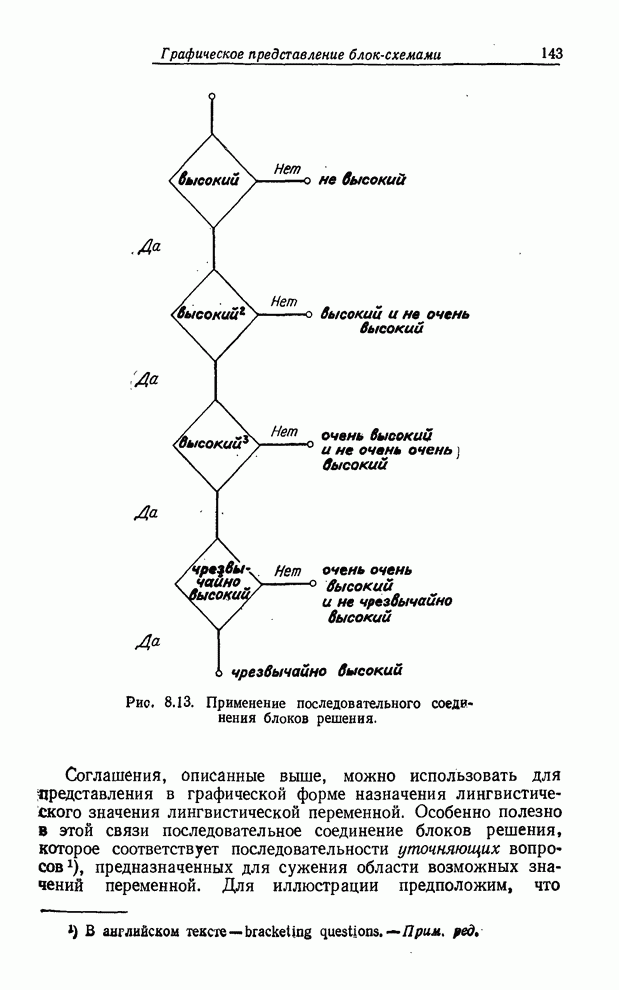
Рис. 8.13. Применение последовательного соединения блоков решения.
Соглашения,
описанные выше, можно использовать для представления в графической форме
назначения лингвистического значения лингвистической переменной. Особенно
полезно в этой связи последовательное соединение блоков решения, которое
соответствует последовательности уточняющих вопросов, предназначенных для
сужения области возможных значений переменной. Для иллюстрации предположим, что
![]() Джон и (см.
рис. 8.13)
Джон и (см.
рис. 8.13)
 (8.76)
(8.76)
Если ответ на первый вопрос - ДА, то
![]() высокий. (8.77)
высокий. (8.77)
Если ответ на второй вопрос - ДА, а на третий вопрос - НЕТ, то
![]() очень высокий и
не очень очень высокий, (8.78)
очень высокий и
не очень очень высокий, (8.78)
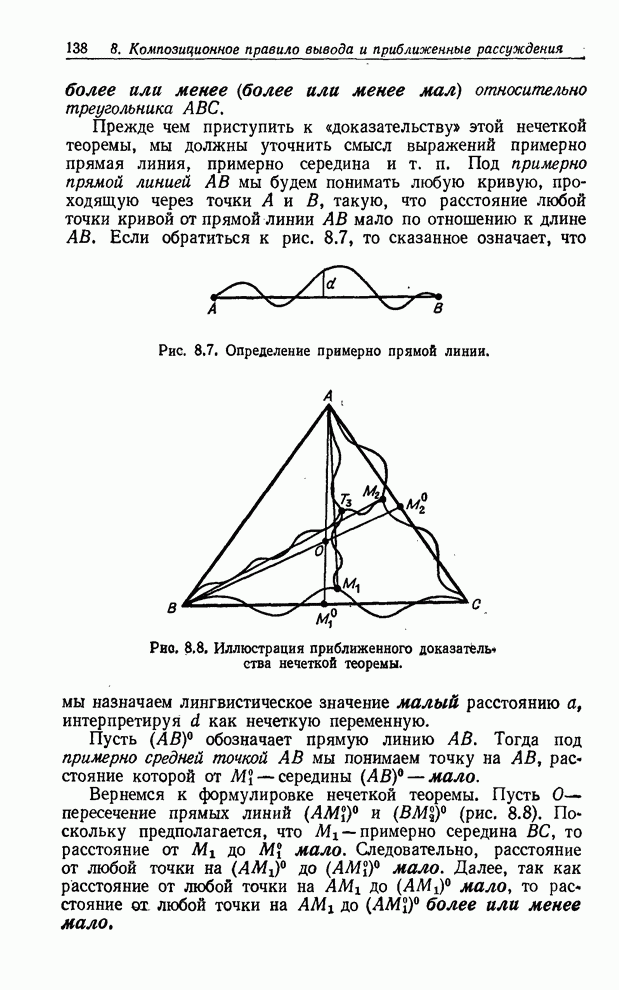
т. е. значение высоты Джона заключено между значениями очень высокий и не очень очень высокий.
При наличии механизма, такого, как в случае уточняющих вопросов, для назначения переменным лингвистических значений поэтапно, а не за один шаг нечеткие блок-схемы могут оказаться весьма полезными для алгоритмических определений нечетких понятий.
Основная идея при этом состоит в том, чтобы определить сложное или новое нечеткое понятие посредством более простых или более знакомых понятий. Поскольку нечеткое понятие можно рассматривать как название некоторого нечеткого множества, то эта идея означает фактически разложение нечеткого множества на комбинацию более простых нечетких множеств.
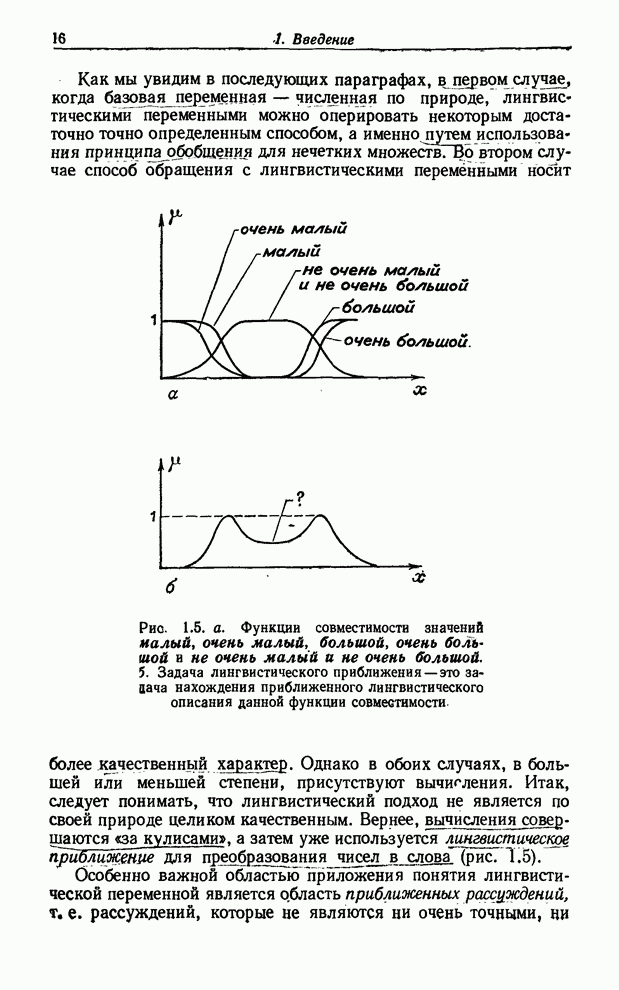
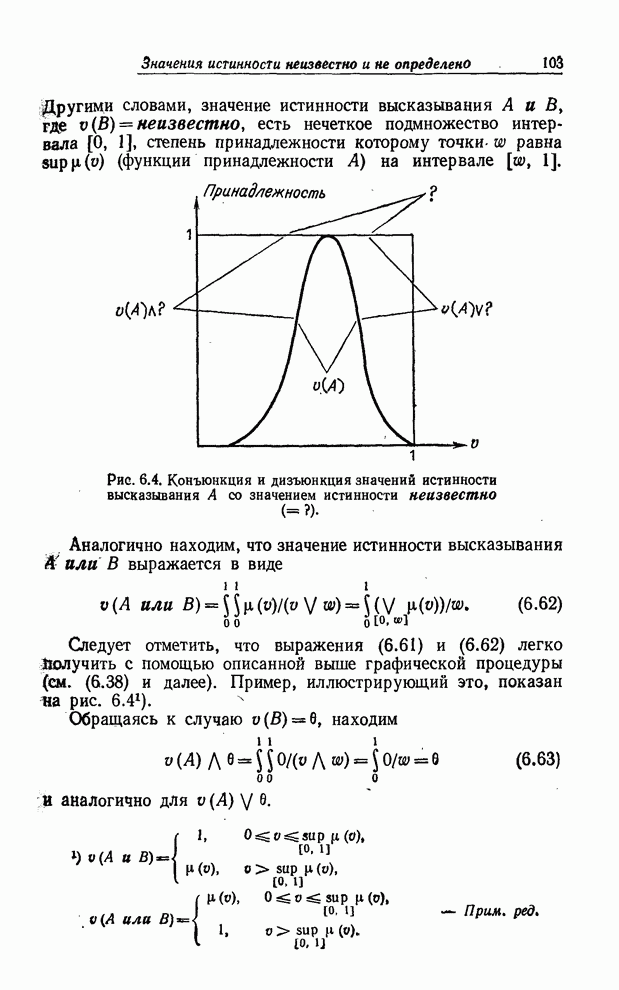
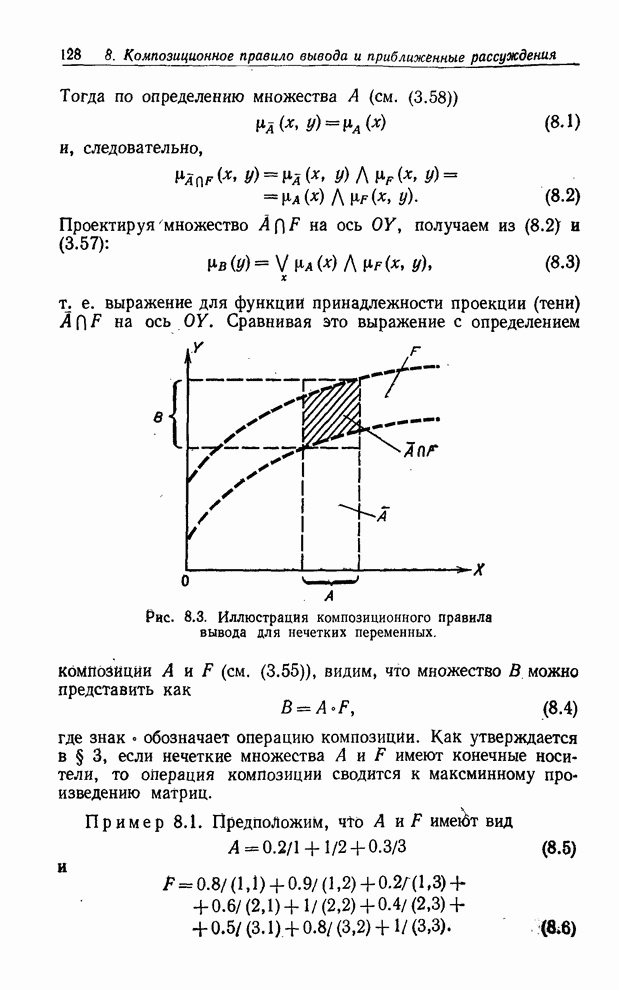
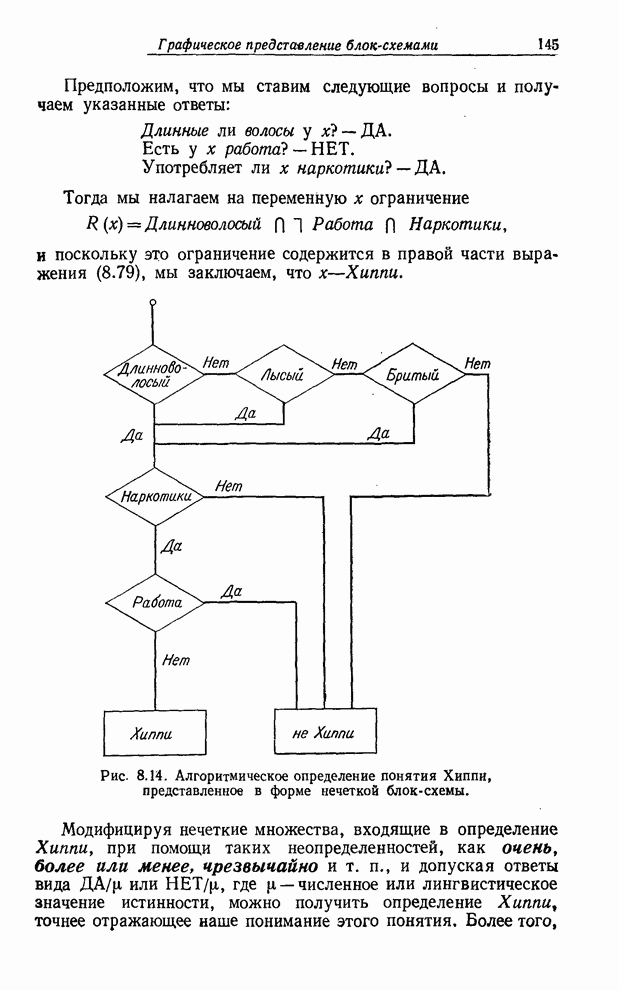
Проиллюстрируем
это следующим примером. Предположим для иллюстрации, что мы хотим определить
термин Хиппи, который можно рассматривать как название нечеткого подмножества
полного множества людей. Для этого мы воспользуемся нечеткой блок-схемой,
приведенной на рис. 8.14. В сущности эта схема определяет нечеткое множество
Хиппи в терминах нечетких множеств, имеющих названия Длинноволосый, Лысый,
Бритый, Работа и Наркотики. Более точно оно определяет нечеткое множество Хиппи
как (![]() объединение).
объединение).
![]() . (8.79)
. (8.79)

Рис. 8.14. Алгоритмическое определение понятия Хиппи, представленное в форме нечеткой блок-схемы.
Предположим, что мы ставим следующие вопросы и получаем указанные ответы:
Длинные ли волосы у ![]() ? - ДА.
? - ДА.
Есть у ![]() работа? - НЕТ.
работа? - НЕТ.
Употребляет ли ![]() наркотики? - ДА.
наркотики? - ДА.
Тогда
мы налагаем на переменную ![]() ограничение
ограничение
![]() ,
,
и
поскольку это ограничение содержится в правой части выражения (8.79), мы
заключаем, что ![]() -
Хиппи.
-
Хиппи.
Модифицируя
нечеткие множества, входящие в определение Хиппи, при помощи таких
неопределенностей, как очень, более или менее, чрезвычайно и т. п., и допуская
ответы вида ДА/![]() или НЕТ/
или НЕТ/![]() ,
где
,
где ![]() -
численное или лингвистическое значение истинности, можно получить определение
Хиппи, точнее отражающее наше понимание этого понятия. Более того, мы можем
использовать мягкое
-
численное или лингвистическое значение истинности, можно получить определение
Хиппи, точнее отражающее наше понимание этого понятия. Более того, мы можем
использовать мягкое ![]() (см. замечание 3.7) и допустить тем
самым некоторое взаимодействие между характеристиками, которые определяют
Хиппи. И наконец, мы можем рассматривать блоки решения со многими входами и
выходами. Таким образом, понятие, такое, как Хиппи, можно определить как угодно
полно в терминах составляющих понятий, каждое из которых в свою очередь можно
определить алгоритмически. Используя нечеткую блок-схему для определения такого
нечеткого понятия, как Хиппи, мы в сущности разлагаем высказывания общего вида
(см. замечание 3.7) и допустить тем
самым некоторое взаимодействие между характеристиками, которые определяют
Хиппи. И наконец, мы можем рассматривать блоки решения со многими входами и
выходами. Таким образом, понятие, такое, как Хиппи, можно определить как угодно
полно в терминах составляющих понятий, каждое из которых в свою очередь можно
определить алгоритмически. Используя нечеткую блок-схему для определения такого
нечеткого понятия, как Хиппи, мы в сущности разлагаем высказывания общего вида
![]() (8.80)
(8.80)
на уравнения назначения значений истинности такого же вида, но содержащие более простые или более знакомые переменные в левой части.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
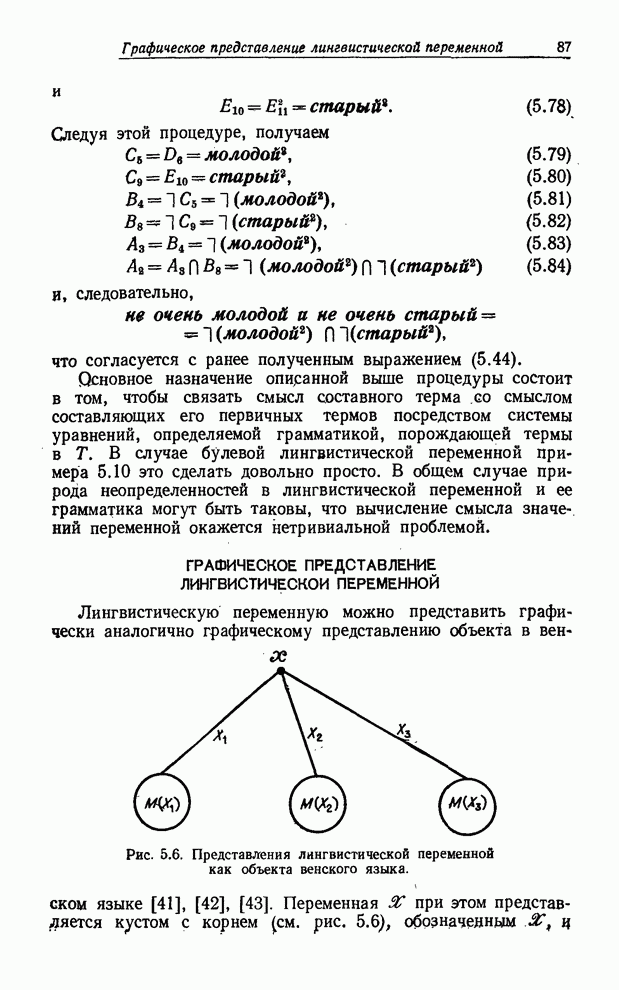
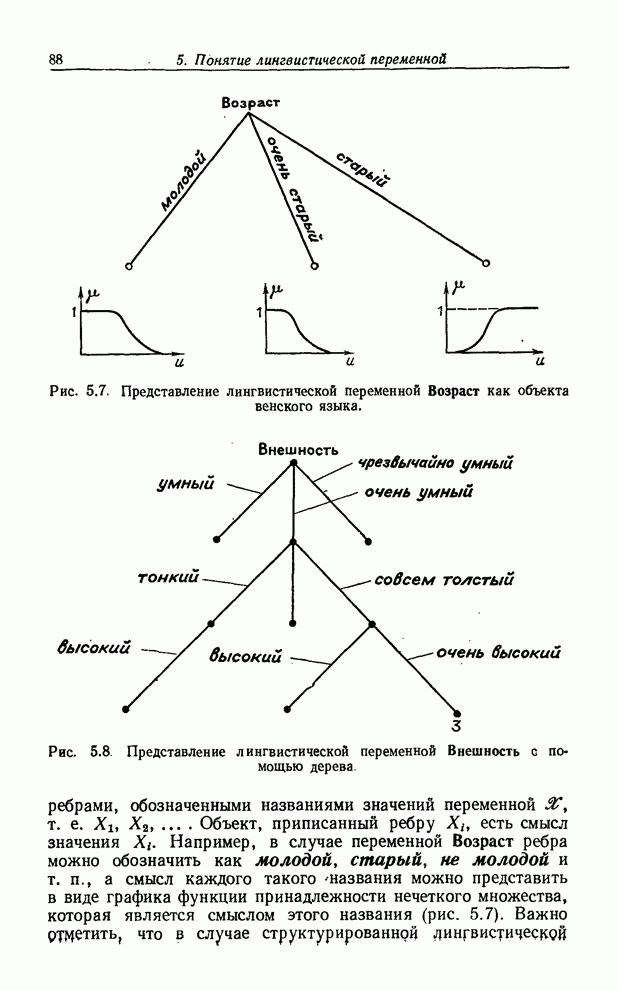
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ