| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
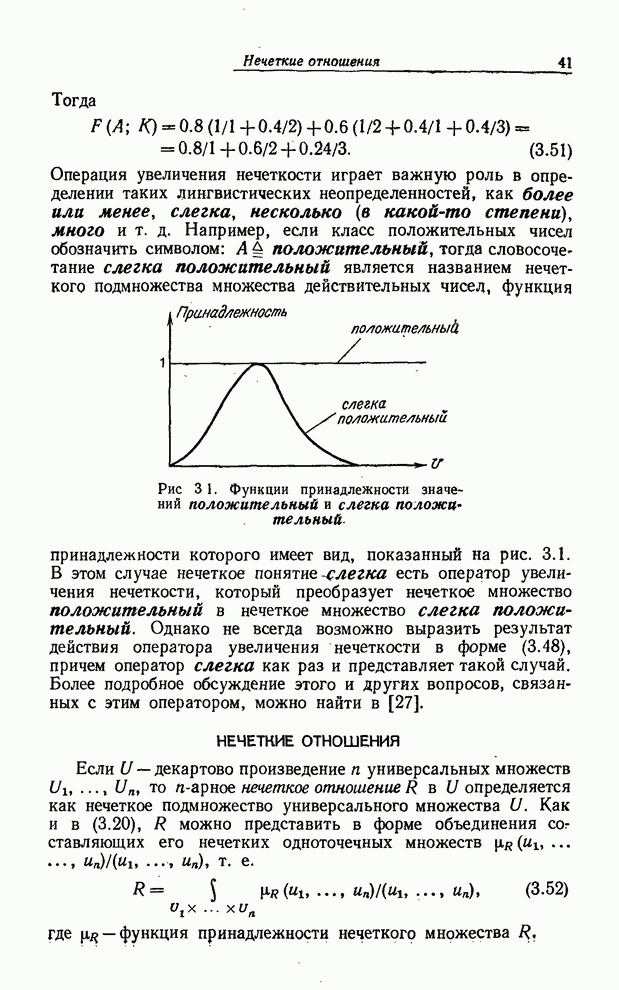
НЕЧЕТКИЕ ОТНОШЕНИЯ
Если
![]() — декартово
произведение
— декартово
произведение ![]() универсальных
множеств
универсальных
множеств ![]() ,
то
,
то ![]() -арное нечеткое
отношение
-арное нечеткое
отношение ![]() в
в
![]() определяется
как нечеткое подмножество универсального множества
определяется
как нечеткое подмножество универсального множества ![]() . Как и в (3.20),
. Как и в (3.20), ![]() можно
представить в форме объединения составляющих его нечетких одноточечных множеств
можно
представить в форме объединения составляющих его нечетких одноточечных множеств
![]() , т. е.
, т. е.
![]() (3.52)
(3.52)
где
![]() —
функция принадлежности нечеткого множества
—
функция принадлежности нечеткого множества ![]() .
.
Распространенными
примерами (бинарных) нечетких отношений являются много больше
чем, имеет сходство, имеет отношение, близко к и т. д. Например, если ![]() , то отношение
близко к можно определить следующим образом:
, то отношение
близко к можно определить следующим образом:
 (3.53)
(3.53)
где
![]() —
масштабный коэффициент. Аналогично, если
—
масштабный коэффициент. Аналогично, если ![]() , то отношение много больше чем
можно определить матрицей отношения
, то отношение много больше чем
можно определить матрицей отношения
 (3.54)
(3.54)
![]() -й элемент которой есть значение
-й элемент которой есть значение ![]() для
для ![]() -го значения
-го значения ![]() и
и ![]() -го значения
-го значения ![]() .
.
Если
![]() —
отношение
—
отношение ![]() (или,
что то же самое, отношение в
(или,
что то же самое, отношение в ![]() ), а
), а ![]() — отношение
— отношение ![]() , то композицией
, то композицией ![]() и
и ![]() является нечеткое
отношение
является нечеткое
отношение ![]() , обозначаемое
, обозначаемое
![]() и определяемое
формулой
и определяемое
формулой
![]() (3.55)
(3.55)
Если
![]() ,
, ![]() и
и ![]() — конечные множества, то
матрица отношения
— конечные множества, то
матрица отношения ![]() есть
максминное произведение матриц отношений
есть
максминное произведение матриц отношений ![]() и
и ![]() . Пример такого максминного произведения:
. Пример такого максминного произведения:
 (3.56)
(3.56)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
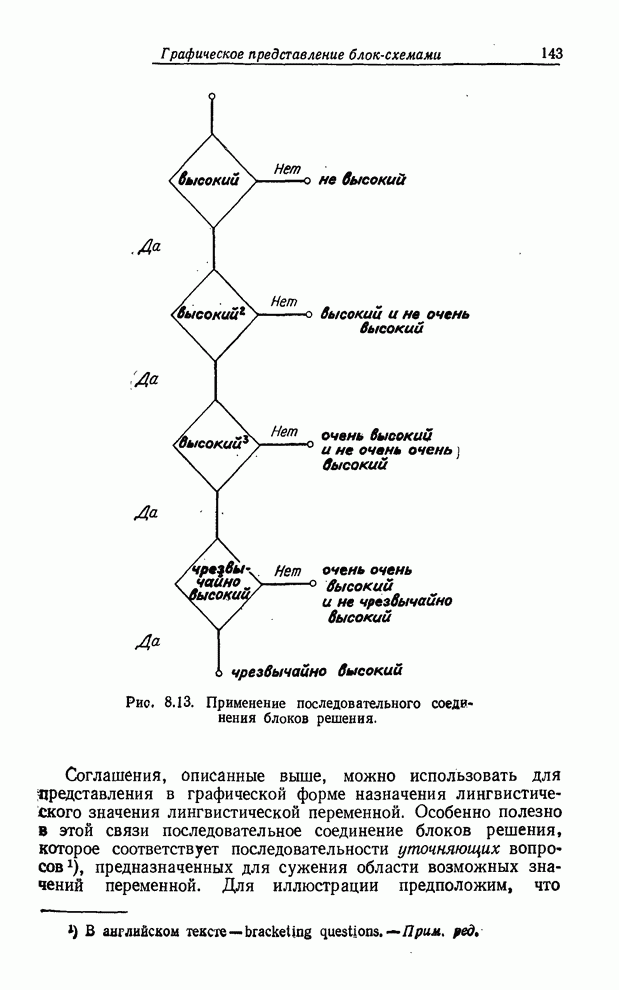
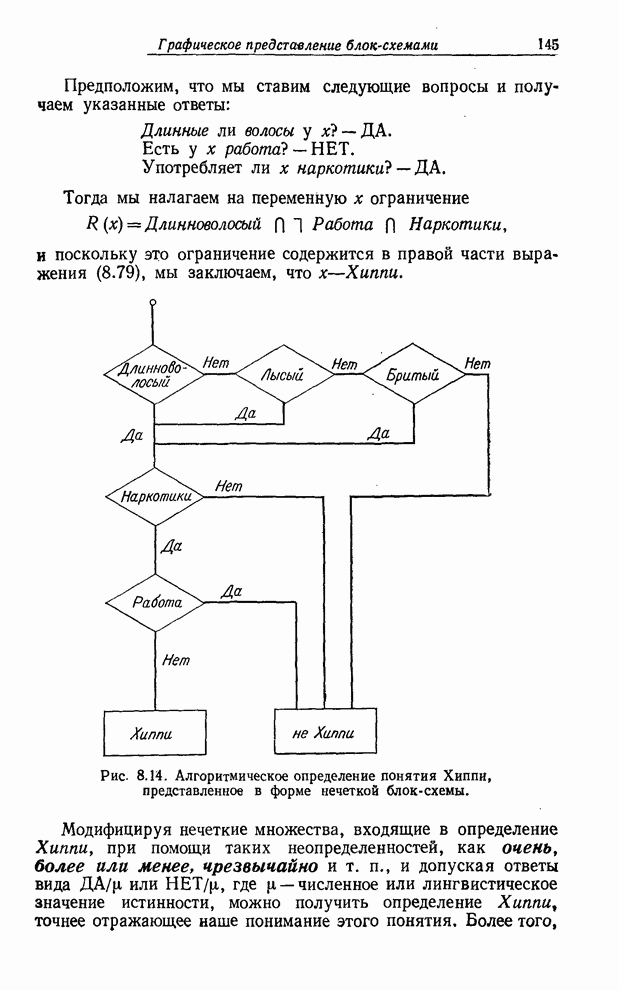
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ