| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
Отправной точкой предшествующего изложения было предположение о
том, что каждому элементу ![]() конечного универсального множества
конечного универсального множества ![]() ставится в
соответствие значение
ставится в
соответствие значение ![]() лингвистической вероятности, являющееся
компонентой списка значений лингвистических вероятностей
лингвистической вероятности, являющееся
компонентой списка значений лингвистических вероятностей ![]() .
.
В данном контексте нечеткое подмножество ![]() множества
множества ![]() играет роль
нечеткого события. Пусть
играет роль
нечеткого события. Пусть ![]() - степень принадлежности
- степень принадлежности ![]() подмножеству
подмножеству![]() . Тогда если
. Тогда если ![]() — обычные
вероятности
— обычные
вероятности ![]() ,
то вероятность
,
то вероятность ![]() события
события
![]() определяется
как (см. [48]) (
определяется
как (см. [48]) (![]() арифметическая сумма)
арифметическая сумма)
![]() . (7.54)
. (7.54)
Естественно обобщить это определение на лингвистические вероятности,
определив лингвистическую вероятность события ![]() как
как
![]() , (7.55)
, (7.55)
понимая при этом правую часть выражения (7.55) как линейную форму типа (7.27). В связи с выражением (7.55) необходимо отметить, что из ограничения
![]() (7.56)
(7.56)
на рассматриваемые вероятности и того, что
![]()
следует, что![]() — нечеткое подмножество интервала [0,
1].
— нечеткое подмножество интервала [0,
1].
Пример 7.5. Проиллюстрируем сказанное очень простым примером. Предположим, что
![]() ,
(7.57)
,
(7.57)
![]() ,
(7.58)
,
(7.58)
![]() , (7.59)
, (7.59)
![]() , (7.60)
, (7.60)
![]() . (7.61)
. (7.61)
Тогда (![]() арифметическая сумма)
арифметическая сумма)
![]() (7.62)
(7.62)
при ограничении
![]() . (7.63)
. (7.63)
Выбирая такие члены в (7.62), которые удовлетворяют (7.63), получаем
 (7.64)
(7.64)
откуда
![]() . (7.65)
. (7.65)
выражение (7.65) можно грубо аппроксимировать равенством
![]() . (7.66)
. (7.66)
Лингвистическую вероятность нечеткого события, выраженную формулой
(7.55), можно рассматривать как частный случай более общего понятия, а именно
лингвистического среднего, или, что то же самое, лингвистического
математического ожидания функции (определенной на ![]() ) по нечеткому подмножеству
множества
) по нечеткому подмножеству
множества ![]() .
Более конкретно, пусть
.
Более конкретно, пусть ![]() — определенная на
— определенная на ![]() функция, принимающая
действительные значения; пусть
функция, принимающая
действительные значения; пусть ![]() — нечеткое подмножество множества
— нечеткое подмножество множества ![]() , и пусть
, и пусть ![]() — лингвистические
вероятности, соответствующие
— лингвистические
вероятности, соответствующие ![]() . Тогда лингвистическое среднее
функции
. Тогда лингвистическое среднее
функции ![]() по
по
![]() обозначается
как
обозначается
как ![]() и
определяется следующим образом (
и
определяется следующим образом (![]() арифметическая сумма):
арифметическая сумма):
![]() . (7.67)
. (7.67)
Рассмотрим следующий конкретный пример выражения (7.67).
Предположим, что люди с именами ![]() выбираются в соответствии с
лингвистическими вероятностями
выбираются в соответствии с
лингвистическими вероятностями![]() , где
, где ![]() - ограничение
на
- ограничение
на ![]() . Предположим,
что на
. Предположим,
что на ![]() накладывается
штраф в размере
накладывается
штраф в размере ![]() ,
уменьшенном пропорционально степени принадлежности
,
уменьшенном пропорционально степени принадлежности ![]() классу
классу ![]() . Тогда лингвистический
средний (ожидаемый) размер штрафа выражается формулой (7.67).
. Тогда лингвистический
средний (ожидаемый) размер штрафа выражается формулой (7.67).
Замечание 7.6. Отметим, что (7.67) по существу является линейной комбинацией вида (7.27), где
![]() . (7.68)
. (7.68)
|
Т |
аким образом, чтобы вычислить (7.67), можно использовать метод,
описанный ранее для вычисления линейных форм в лингвистических вероятностях. В
частности, следует отметить, что, когда ![]() , правая часть (7.67) имеет вид
, правая часть (7.67) имеет вид
![]() . (7.69)
. (7.69)
![]() сводится к
сводится к![]() .
.
Кроме выражения для ![]() выражение (7.67) содержит в себе в
качестве частных случаев и выражения для других средних, встречающихся в
различных приложениях. Среди них существуют два типа, которые можно
рассматривать как вырожденные формы (7.67) и которые часто встречаются во многих
задачах, представляющих практический интерес. Мы кратко остановимся на этих
типах средних и для удобства сформулируем их определения в форме ответов на
вопросы.
выражение (7.67) содержит в себе в
качестве частных случаев и выражения для других средних, встречающихся в
различных приложениях. Среди них существуют два типа, которые можно
рассматривать как вырожденные формы (7.67) и которые часто встречаются во многих
задачах, представляющих практический интерес. Мы кратко остановимся на этих
типах средних и для удобства сформулируем их определения в форме ответов на
вопросы.
Вопрос 7.7.
Каково число элементов в данном нечетком множестве ![]() ? Очевидно, этот вопрос
поставлен некорректно, поскольку в случае нечеткого множества не существует
четкой границы между принадлежностью и непринадлежностью элемента множеству.
Тем не менее понятие мощности нечеткого множества [49], определяемое как
? Очевидно, этот вопрос
поставлен некорректно, поскольку в случае нечеткого множества не существует
четкой границы между принадлежностью и непринадлежностью элемента множеству.
Тем не менее понятие мощности нечеткого множества [49], определяемое как
![]() , (7.70)
, (7.70)
является естественным обобщением понятия числа элементов ![]() .
.
Для иллюстрации предположим, что ![]() — универсальное множество жителей в
городе, а
— универсальное множество жителей в
городе, а ![]() —
нечеткое множество безработных в этом городе. Если интерпретировать
—
нечеткое множество безработных в этом городе. Если интерпретировать ![]() как степень
принадлежности человека
как степень
принадлежности человека ![]() классу безработных (например,
классу безработных (например, ![]() =0.5, если
=0.5, если ![]() занял половину
рабочего времени и ищет работу с полным рабочим днем), то
занял половину
рабочего времени и ищет работу с полным рабочим днем), то ![]() можно интерпретировать как
эквивалентное число полностью безработных.
можно интерпретировать как
эквивалентное число полностью безработных.
Вопрос 7.8.
Предположим, что ![]() —
функция, принимающая действительные значения и определенная на
—
функция, принимающая действительные значения и определенная на ![]() . Каково среднее
значение
. Каково среднее
значение ![]() на
нечетком подмножестве
на
нечетком подмножестве ![]() множества
множества ![]() ?
?
Будем пользоваться теми же обозначениями, что и в выражении
(7.67). Пусть ![]() (обозначает
среднее значение функции
(обозначает
среднее значение функции ![]() на
на ![]() . Если бы
. Если бы ![]() было обычным (не нечетким) множеством,
то
было обычным (не нечетким) множеством,
то ![]() выражалось
бы формулой
выражалось
бы формулой
 , (7.71)
, (7.71)
где ![]() обозначает
суммирование по тем
обозначает
суммирование по тем ![]() , которые принадлежат
, которые принадлежат ![]() , а
, а ![]() — число этих
элементов. Чтобы обобщить (7.71) на нечеткие множества, заметим, что (7.71)
можно переписать так:
— число этих
элементов. Чтобы обобщить (7.71) на нечеткие множества, заметим, что (7.71)
можно переписать так:
 , (7.72)
, (7.72)
где ![]() —
характеристическая функция множества
—
характеристическая функция множества ![]() . Тогда (7.72) можно принять в качестве
определения
. Тогда (7.72) можно принять в качестве
определения ![]() для
нечеткого множества
для
нечеткого множества ![]() , если интерпретировать
, если интерпретировать ![]() как степень
принадлежности
как степень
принадлежности ![]() множеству
множеству
![]() . При этом
мы приходим к выражению для
. При этом
мы приходим к выражению для![]() , которое можно рассматривать как
частный случай выражения (7.67).
, которое можно рассматривать как
частный случай выражения (7.67).
Проиллюстрируем (7.72) следующим примером. Предположим, что ![]() — полное множество
жителей в городе и
— полное множество
жителей в городе и![]() — нечеткое подмножество молодых жителей; кроме того, предположим, что
— нечеткое подмножество молодых жителей; кроме того, предположим, что ![]() — заработок жителя
— заработок жителя ![]() . Тогда средний
заработок молодых жителей города выражается формулой (7.72).
. Тогда средний
заработок молодых жителей города выражается формулой (7.72).
Замечание 7.9. Поскольку выражение для
![]() есть
линейная форма переменных
есть
линейная форма переменных ![]() мощность нечеткого множества типа 2
(см. определение 3.22) можно легко подсчитать методом, которым мы пользовались
ранее для вычисления
мощность нечеткого множества типа 2
(см. определение 3.22) можно легко подсчитать методом, которым мы пользовались
ранее для вычисления ![]() .
.
В случае ![]() , однако, мы имеем дело с отношением
линейных форм, и, следовательно, вычисление
, однако, мы имеем дело с отношением
линейных форм, и, следовательно, вычисление ![]() для нечетких множеств типа 2
представляет собой более трудную отдачу.
для нечетких множеств типа 2
представляет собой более трудную отдачу.
Целью предыдущего изложения было показать, что понятие лингвистической переменной служит основой для определения вероятностей и в сочетании с принципом обобщения может быть использовано для вычисления линейных комбинаций разных вероятностей. Мы не будем больше останавливаться в этом вопросе и в последующем изложении обратим внимание на основное правило вывода в нечеткой логике.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
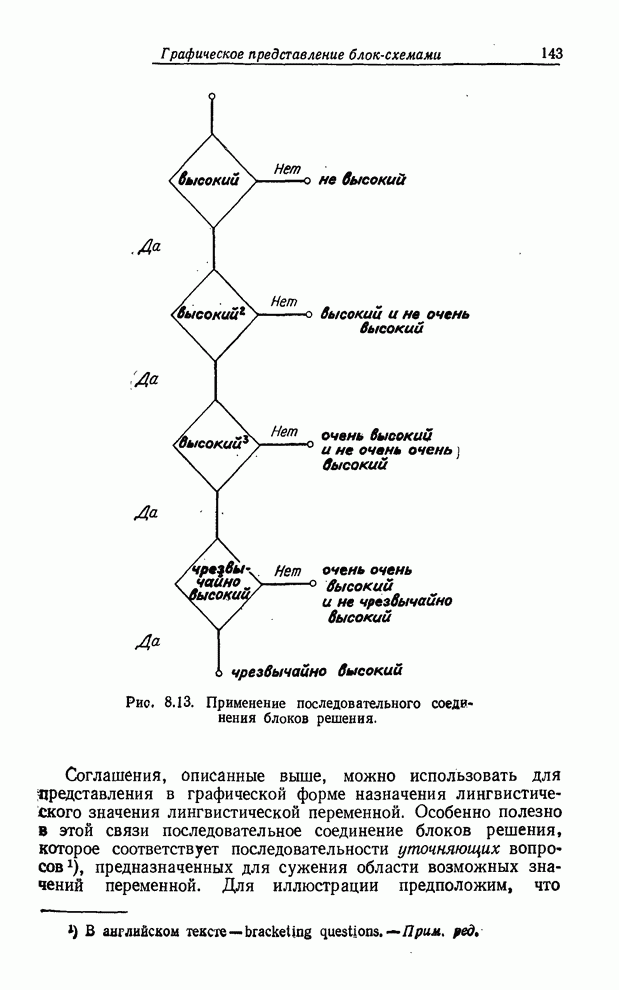
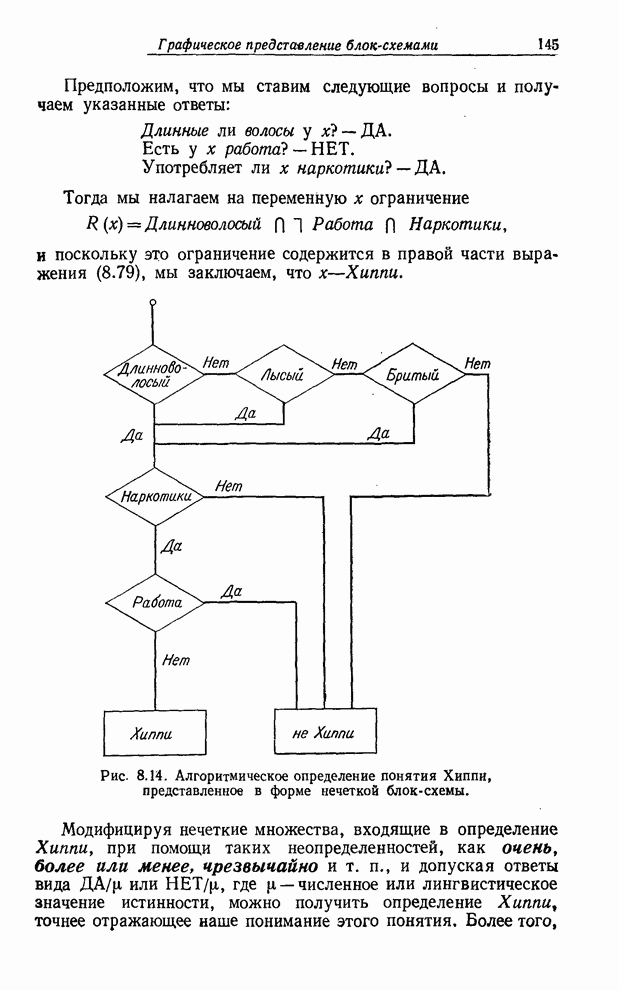
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ