| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
В § 2 понятия маргинального и условного ограничений были специально определены таким образом, чтобы их можно было легко обобщить на случай нечетких ограничений. Благодаря этому в более общем случае нечетких переменных эти понятия можно сформулировать почти так же, как это было сделано в § 2.
Замечание 4.7. Как мы уже видели в наших прежних обсуждениях понятий маргинального и условного ограничений, в целях упрощения удобно пользоваться следующими обозначениями.
Пусть
![]() (4.11)
(4.11)
—
упорядоченная подпоследовательность последовательности индексов ![]() . Например,
. Например, ![]() при
при ![]() . Упорядоченное дополнение
подпоследовательности
. Упорядоченное дополнение
подпоследовательности ![]() обозначается через
обозначается через
![]() . (4.12)
. (4.12)
Например,
для ![]() имеем
имеем ![]() .
.
Набор
![]() переменных
переменных
![]() обозначается
через
обозначается
через ![]() :
:
![]() (4.13)
(4.13)
и аналогично
![]() (4.14)
(4.14)
Например, если
![]() ,
,
то
![]() .
.
Если
![]() , то будем
писать просто
, то будем
писать просто
![]() . (4.15)
. (4.15)
В дальнейшем эти обозначения применяются без специальных пояснений.
Определение
4.8.
![]() -арное
ограничение
-арное
ограничение ![]() в
в ![]() индуцирует
индуцирует ![]() -арное
маргинальное ограничение
-арное
маргинальное ограничение ![]() , которое определяется как проекция
(тень)
, которое определяется как проекция
(тень) ![]() на
на ![]() . Используя
определение проекции (см. (3.57)) и применяя обозначения, введенные в замечании
4.7, функцию принадлежности маргинального ограничения
. Используя
определение проекции (см. (3.57)) и применяя обозначения, введенные в замечании
4.7, функцию принадлежности маргинального ограничения ![]() можно
записать в виде
можно
записать в виде
![]() (4.16)
(4.16)
Пример 4.9. Для нечеткой бинарной переменной, определенной в примере 4.5, получаем

Пример 4.10. Предположим, что
![]()
и
![]() —
тернарное нечеткое отношение в
—
тернарное нечеткое отношение в ![]() вида
вида
 (4.17)
(4.17)
Применяя (4.16) к (4.17), получаем
 (4.18)
(4.18)
и
 (4.19)
(4.19)
Определение
4.11.
Пусть ![]() — ограничение на
— ограничение на
![]() , и пусть
, и пусть ![]() –
некоторые значения переменных
–
некоторые значения переменных ![]() соответственно. Если в функции
принадлежности ограничения
соответственно. Если в функции
принадлежности ограничения ![]() значения
переменных
значения
переменных ![]() положить
равными
положить
равными ![]() ,
то результирующая функция аргументов
,
то результирующая функция аргументов ![]() , где последовательность индексов
, где последовательность индексов ![]() является
дополнением последовательности
является
дополнением последовательности ![]() , определяется как функция
принадлежности условного ограничения
, определяется как функция
принадлежности условного ограничения![]() , или сокращенно
, или сокращенно![]() .
.
Таким образом,
![]()
или сокращенно
![]() . (4.20)
. (4.20)
Простота
связи между условным и безусловным ограничениями становится более ясной, если ![]() записывать без
верхнего индекса. При этом выражение (4.20) примет вид
записывать без
верхнего индекса. При этом выражение (4.20) примет вид
![]()
или сокращенно
![]() . (4.21)
. (4.21)
Замечание
4.12.
В некоторых случаях предпочтительно использовать другое обозначение для
условных ограничений. Например, если ![]() ,
, ![]() и
и ![]() , то может оказаться проще писать
, то может оказаться проще писать ![]() вместо
вместо ![]() . Это особенно
существенно, когда в качестве аргументов с верхними индексами используются
числовые значения, например
. Это особенно
существенно, когда в качестве аргументов с верхними индексами используются
числовые значения, например ![]() и
и ![]() вместо
вместо ![]() и
и ![]() . В таких случаях,
для того чтобы избежать разночтений, приходится писать более подробно:
. В таких случаях,
для того чтобы избежать разночтений, приходится писать более подробно:
![]() , или проще
, или проще ![]() .
.
Пример 4.13. В примере 4.10 имеем
 (4.22)
(4.22)
а, используя (4.16),
 (4.23)
(4.23)
Полезно отметить, что из определений маргинального и условного ограничений немедленно вытекает
Предложение
4.14.
Пусть ![]() —
маргинальное ограничение, индуцированное ограничением
—
маргинальное ограничение, индуцированное ограничением ![]() и пусть
и пусть ![]() или, более
просто
или, более
просто ![]() —
условное ограничение при фиксированных
—
условное ограничение при фиксированных ![]() , где
, где ![]() и
и ![]() — взаимно дополнительные
последовательности индексов. Тогда из (4.16), (4.21) и из определения
объединения (см. (3.34)) следует, что
— взаимно дополнительные
последовательности индексов. Тогда из (4.16), (4.21) и из определения
объединения (см. (3.34)) следует, что
 ,
,
где
символ ![]() обозначает
объединение (а не арифметическую сумму) по значениям
обозначает
объединение (а не арифметическую сумму) по значениям![]() .
.
Пример 4.15. Принимая во внимание примеры 4.9 и 4.12, легко проверить, что
![]()
и
![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
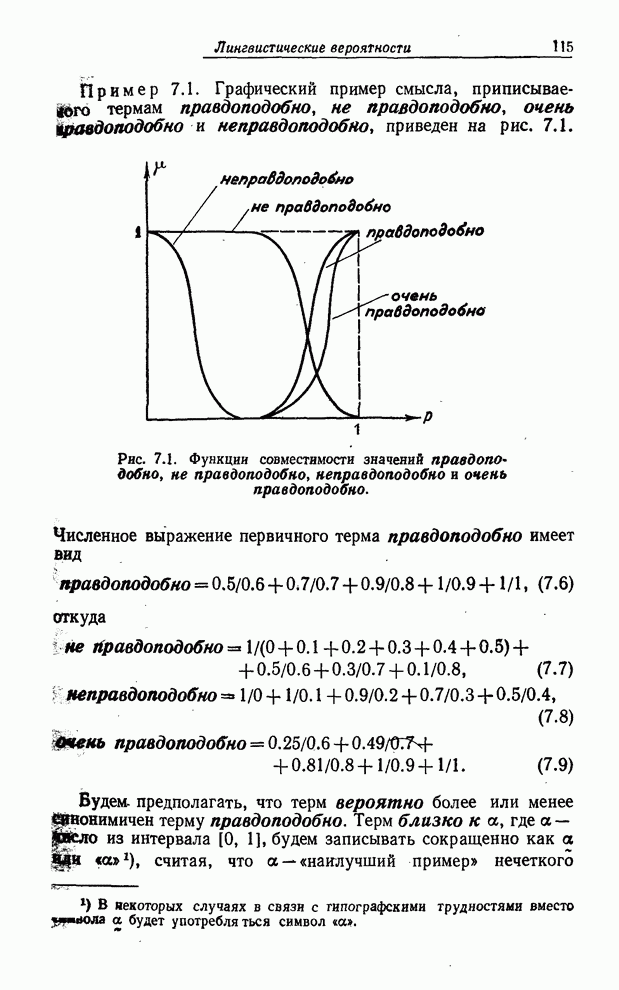
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
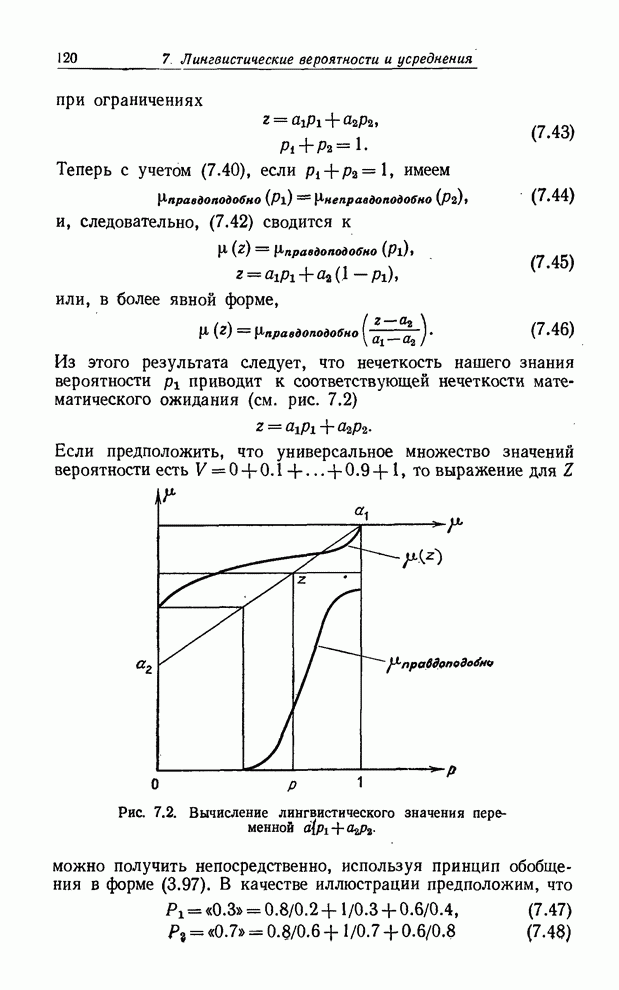
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
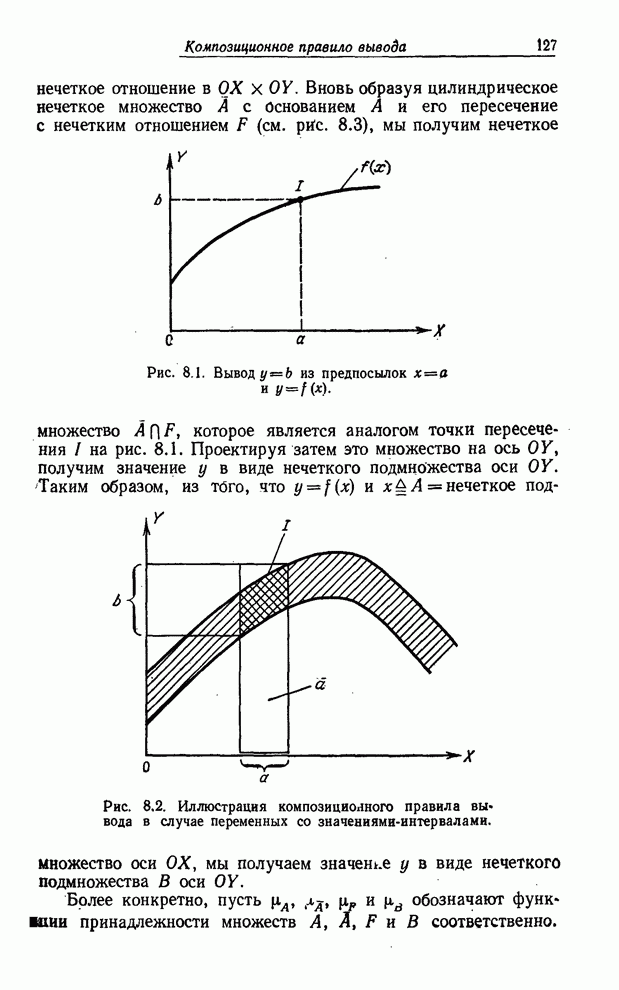
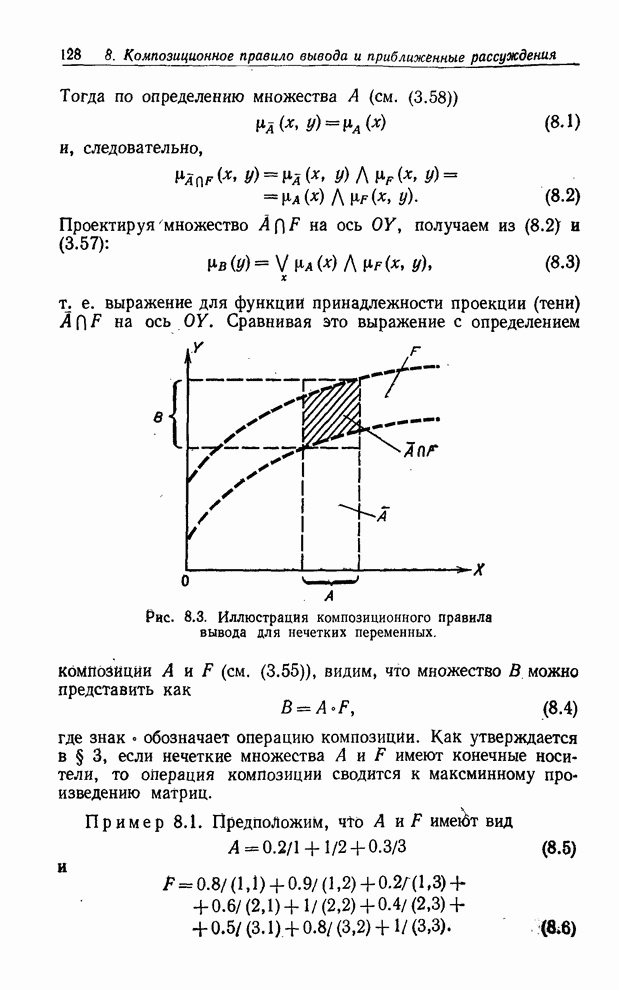
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
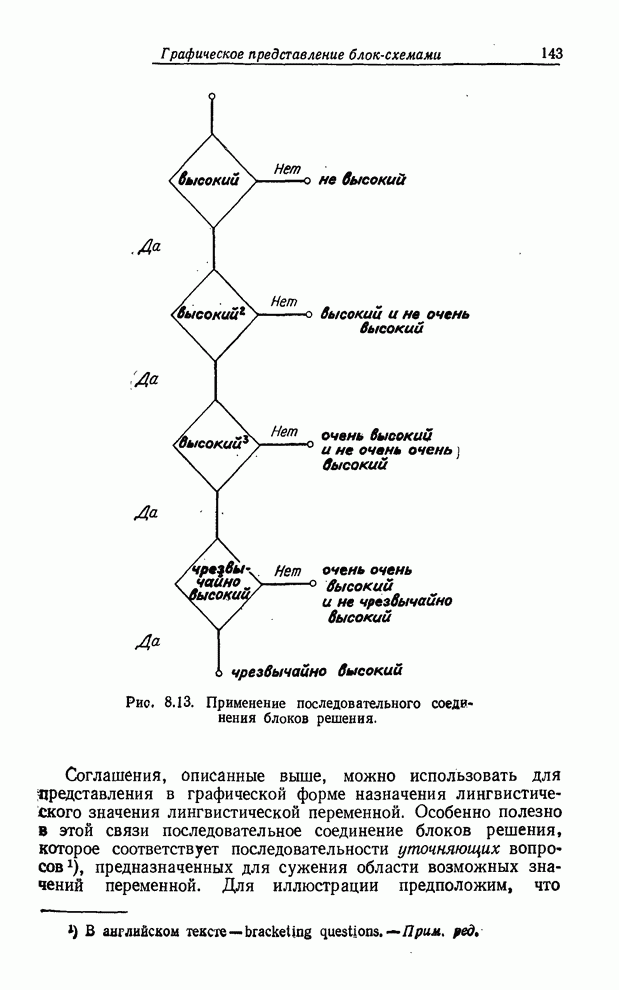
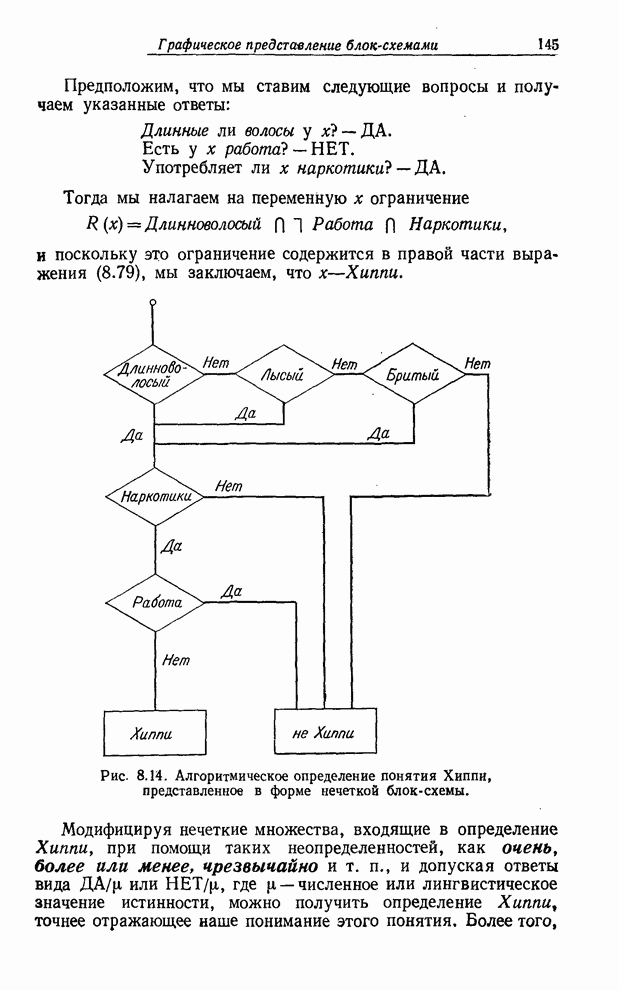
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ