| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
Сначала, имея в виду применения в гл. 6, мы рассмотрим ненулевой случай, по существу, модель (1.3.4), для которой

Совместное распределение очков
Пусть  число случаев, в которых
число случаев, в которых  предпочтительнее, чем
предпочтительнее, чем  сравнениях. Совместное распределение этих независимых переменных дается выражением
сравнениях. Совместное распределение этих независимых переменных дается выражением

Результаты можно записать в виде

Следовательно, совместное распределение любых  значений получается суммированием (2.4.1) с учетом ограничений на
значений получается суммированием (2.4.1) с учетом ограничений на  значений, которые накладываются (2.4.2); в частности, если
значений, которые накладываются (2.4.2); в частности, если  распределение вероятностей вектора значений имеет вид
распределение вероятностей вектора значений имеет вид

где  обозначает набор вероятностей предпочтения
обозначает набор вероятностей предпочтения  а
а  ограничения (2.4.2). Если все обтекты эквивалентны, (2.4.3) дает
ограничения (2.4.2). Если все обтекты эквивалентны, (2.4.3) дает

Так как  должна быть симметричной функцией значений, мы имеем, между прочим, что
должна быть симметричной функцией значений, мы имеем, между прочим, что

симметрична относительно  Функция
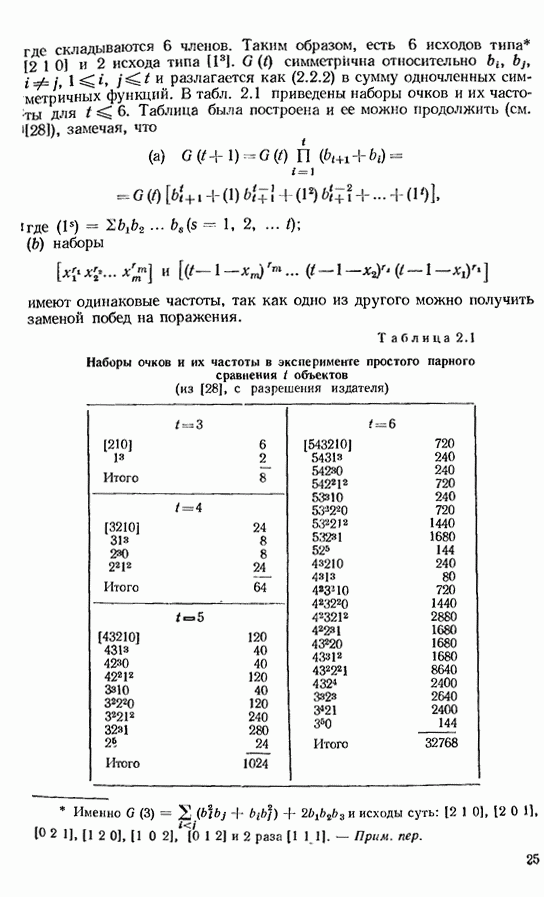
Функция  дает число путей, которые приводят к а, и тесно связана с частотами наборов из § 2.2. Последние дают число возможных наборов
дает число путей, которые приводят к а, и тесно связана с частотами наборов из § 2.2. Последние дают число возможных наборов  при
при  очках
очках  независимо от порядка, и его можно обозначить
независимо от порядка, и его можно обозначить  Из соображений симметрии
Из соображений симметрии  мы имеем
мы имеем

где  число всех данных со значением
число всех данных со значением 
Средние, дисперсии и ковариации значений
Если  число очков, полученных объектом
число очков, полученных объектом  повторении (реплике), мы сразу же имеем
повторении (реплике), мы сразу же имеем

Для нахождения  ковариации
ковариации  рассмотрим дисперсию
рассмотрим дисперсию  для удобства полагая
для удобства полагая  Тогда
Тогда

Отсюда  Из независимости повторных сравнений следует, что
Из независимости повторных сравнений следует, что

Разности значений
Особый интерес для последующей работы представляет распределение вектора разностей

Случайная величина  имеет среднее
имеет среднее

и дисперсию

Так же получается ковариация 

Теперь

имеют для любого заданного у средние, дисперсии и ковариации  и об
и об  соответственно. Из независимости реплик (повтсров) и многомерной центральной предельной теоремы (например, [3]) следует, что предельное распределение при
соответственно. Из независимости реплик (повтсров) и многомерной центральной предельной теоремы (например, [3]) следует, что предельное распределение при  вектора
вектора  будет многомерным нормальным
будет многомерным нормальным  , где
, где  - матрица
- матрица 
Замечания
Предположим, что в двух множествах попарных сравнений пяти объектов  мы имеем
мы имеем  для
для  за исключением того, что в первом множестве
за исключением того, что в первом множестве  и во втором множестве
и во втором множестве  В обоих случаях есть единственная несовместимость по срявненню с ранжировкой
В обоих случаях есть единственная несовместимость по срявненню с ранжировкой  С другой сторны эти множества имеют возрастание своих исходов экспериментое [3310], [32212] с различным числом циклических триад, а именно
С другой сторны эти множества имеют возрастание своих исходов экспериментое [3310], [32212] с различным числом циклических триад, а именно  . Распределение числа несовместимостей с ближайшей ранжировкой было
. Распределение числа несовместимостей с ближайшей ранжировкой было  Слейтером [127], который пропагандировал использование несовместимостей, отличных от циклических триад, как критерия
Слейтером [127], который пропагандировал использование несовместимостей, отличных от циклических триад, как критерия  гипотезы
гипотезы  о случайности Он доказывает, что каждой несовместимости должен приписываться равный вес, пока
о случайности Он доказывает, что каждой несовместимости должен приписываться равный вес, пока  не отвергнута. Представляется, что эта точкг зрения пренебрегает тем, что более разумной альтернативой
не отвергнута. Представляется, что эта точкг зрения пренебрегает тем, что более разумной альтернативой  против случайности (отличной от ляпсусов и случайных ошибок) служит предположение, что непоследовательность
против случайности (отличной от ляпсусов и случайных ошибок) служит предположение, что непоследовательность  более правдоподобна, чем 4] Поэтому первое множество сравнений более согласовано с На, чем второе, менее совместимое с
более правдоподобна, чем 4] Поэтому первое множество сравнений более согласовано с На, чем второе, менее совместимое с  что отражено его более низким с-значением.
что отражено его более низким с-значением.
Упражнения
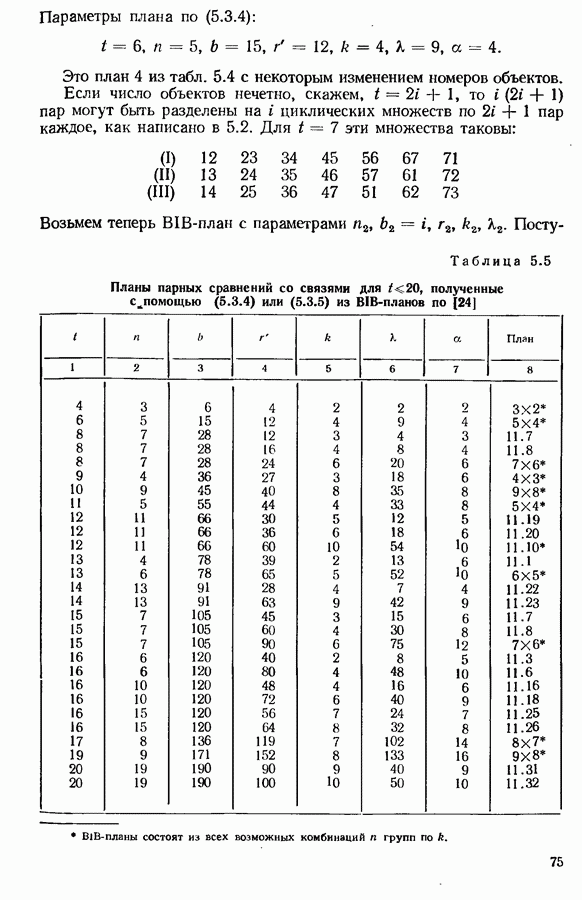
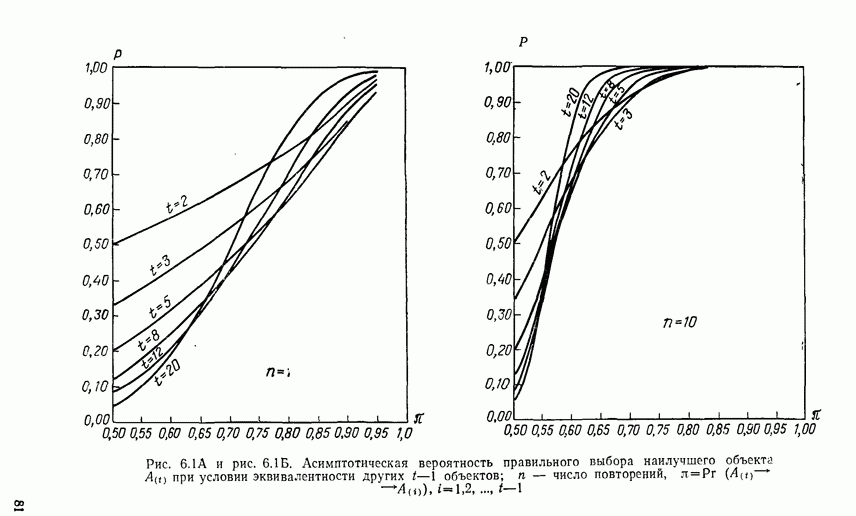
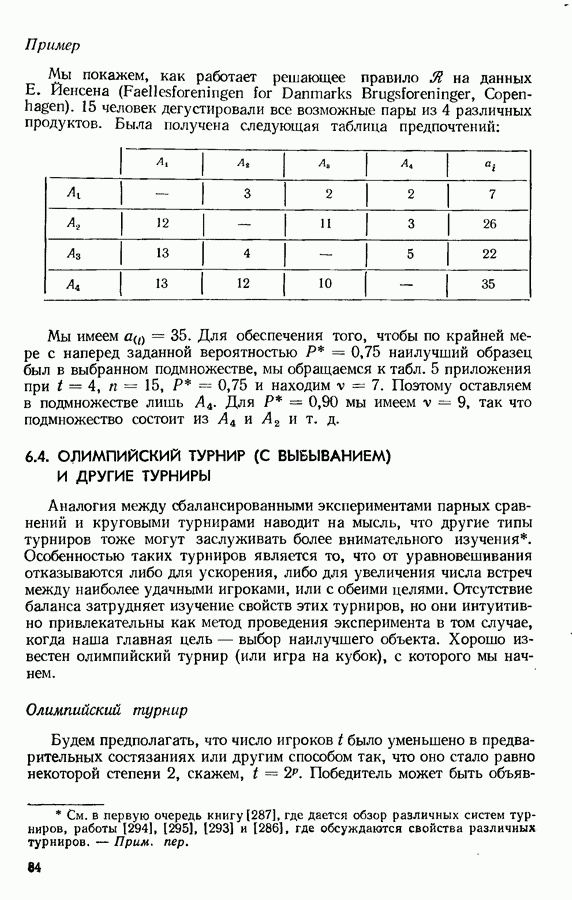
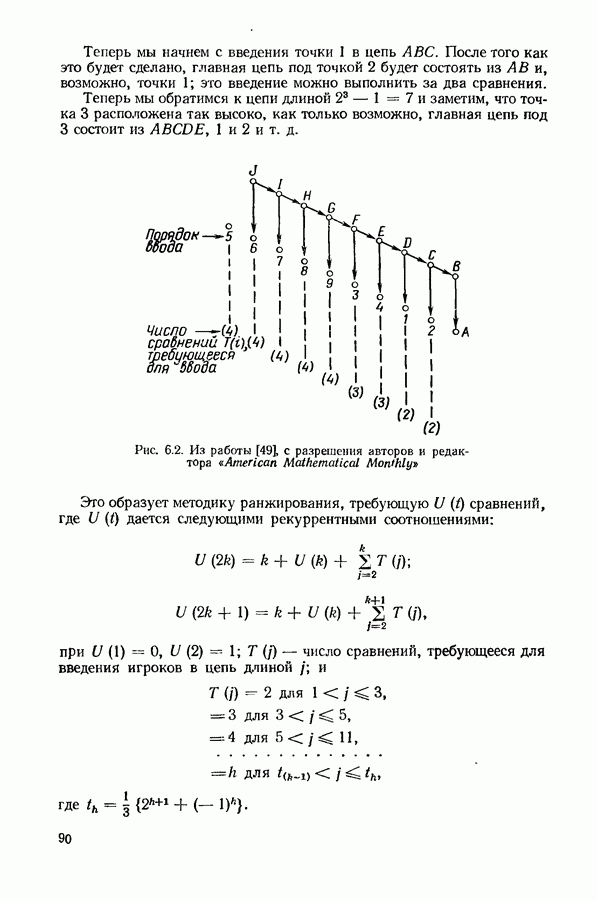
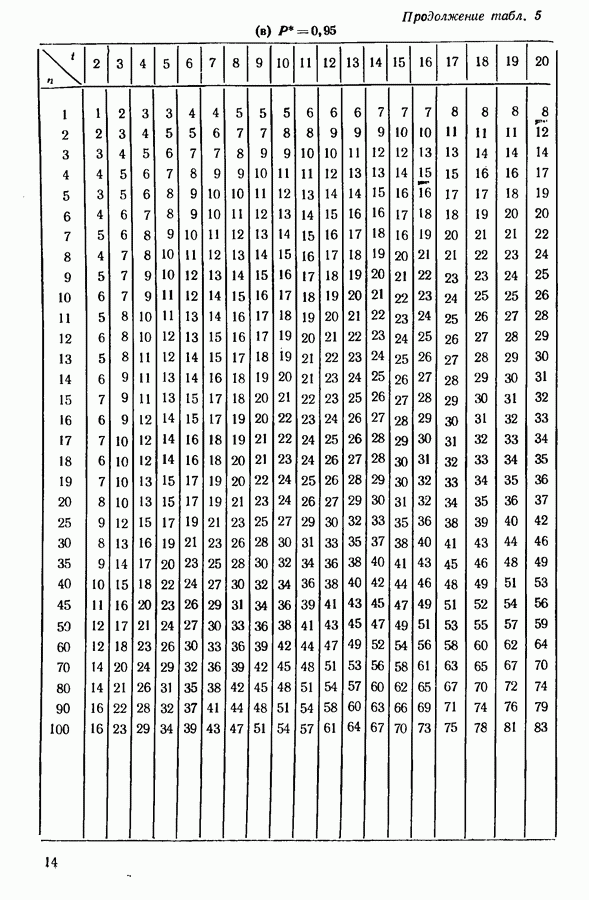
(см. скан)
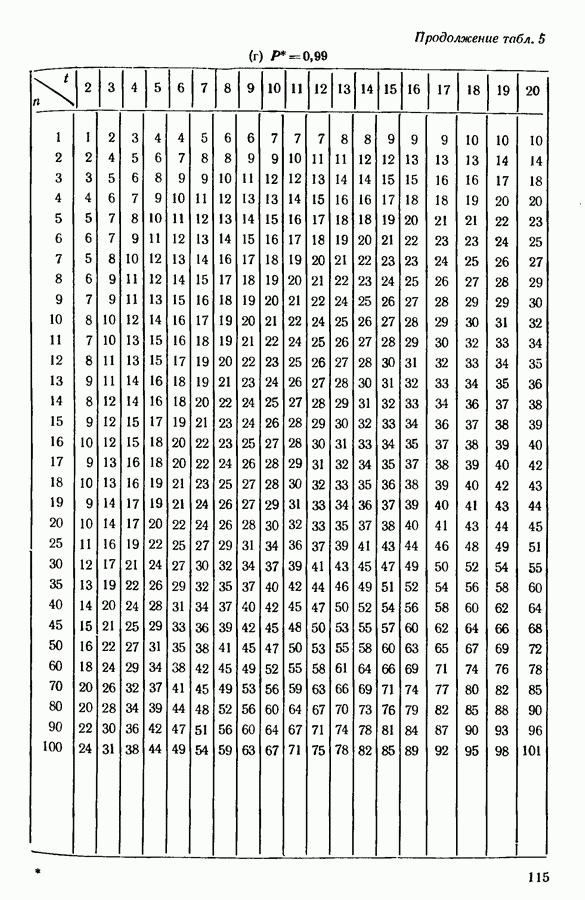
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
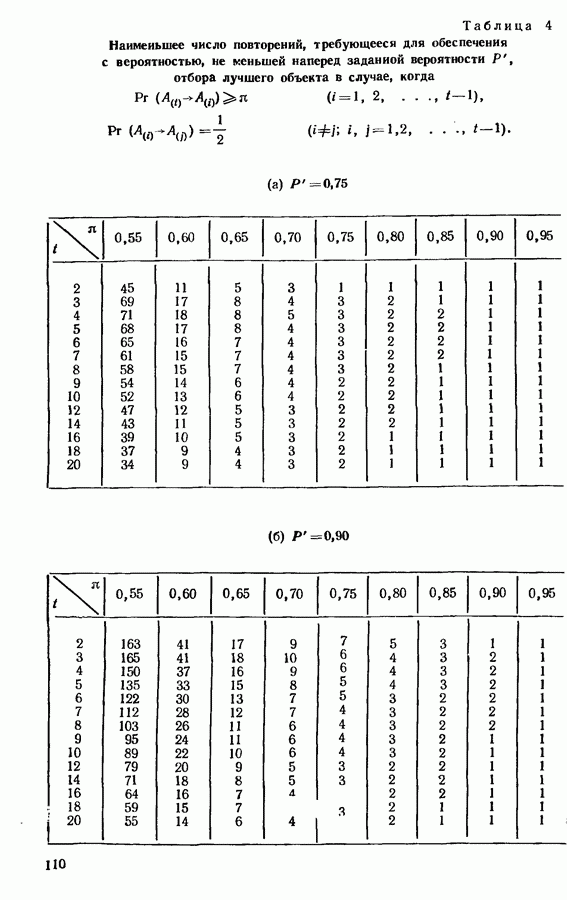
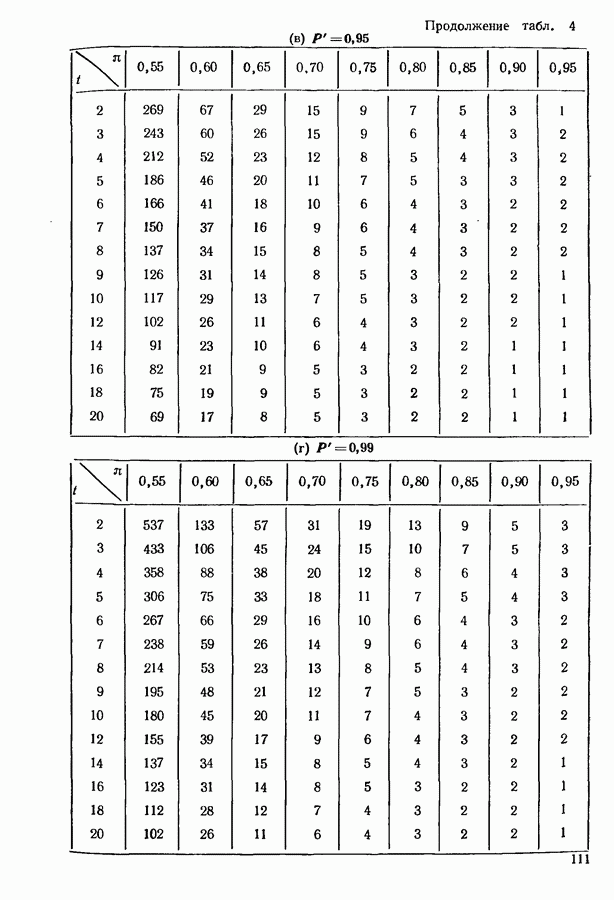
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
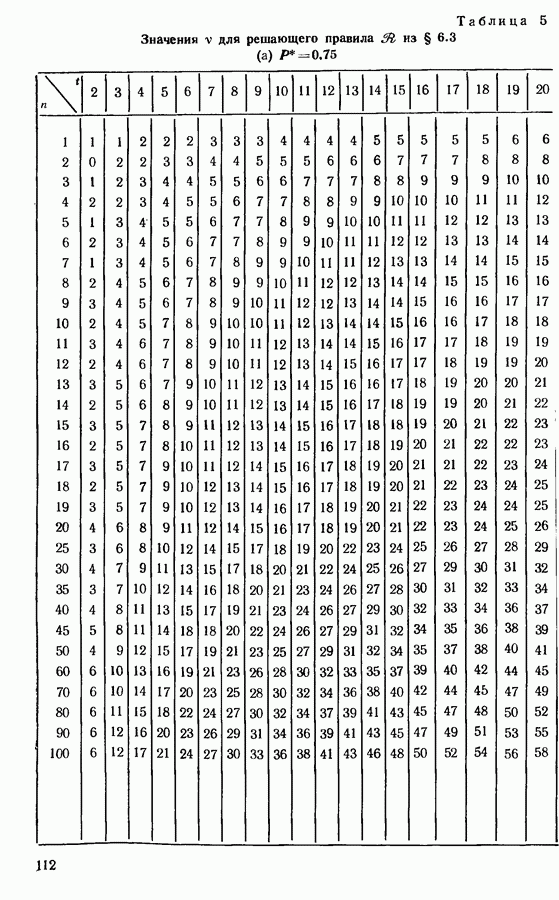
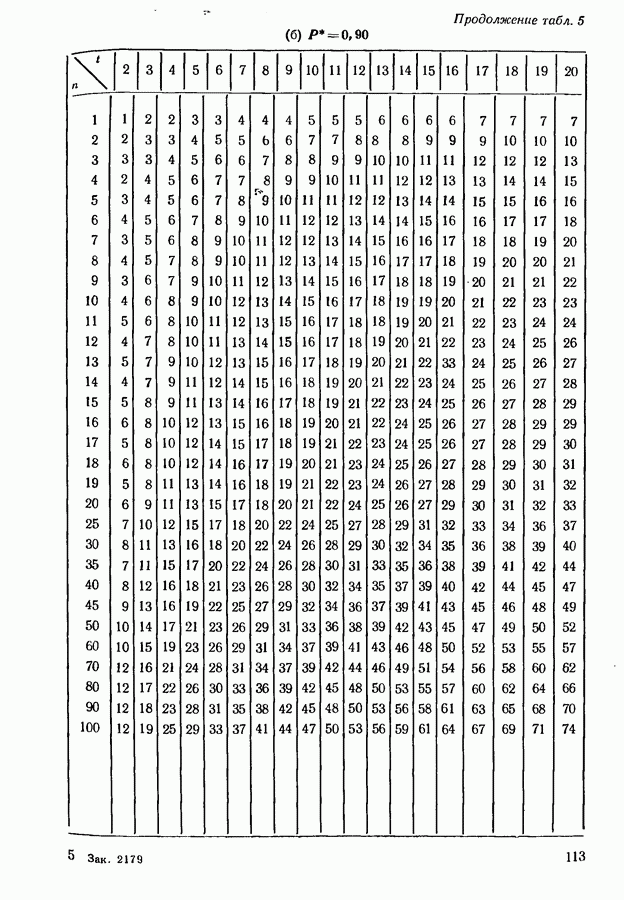
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ