| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
Рассмотрим множество объектов  и пусть
и пусть  будет подмножеством
будет подмножеством  состоящим из объектов с высокими местами. В этом разделе наша цель состоит в выделении множества
состоящим из объектов с высокими местами. В этом разделе наша цель состоит в выделении множества  настолько большого, чтобы обеспечить с вероятностью, не меньшей наперед заданной вероятности
настолько большого, чтобы обеспечить с вероятностью, не меньшей наперед заданной вероятности  что лучший объект
что лучший объект  включен в
включен в  Следуя Гупте и Собелю [68], мы используем решающее правило
Следуя Гупте и Собелю [68], мы используем решающее правило  оставлять в
оставлять в  только те объекты
только те объекты  для которых
для которых  где
где  есть высшая сумма и
есть высшая сумма и  неотрицательное целое число, функция от
неотрицательное целое число, функция от  и
и 
Для  и широкого диапазона значений
и широкого диапазона значений  значения
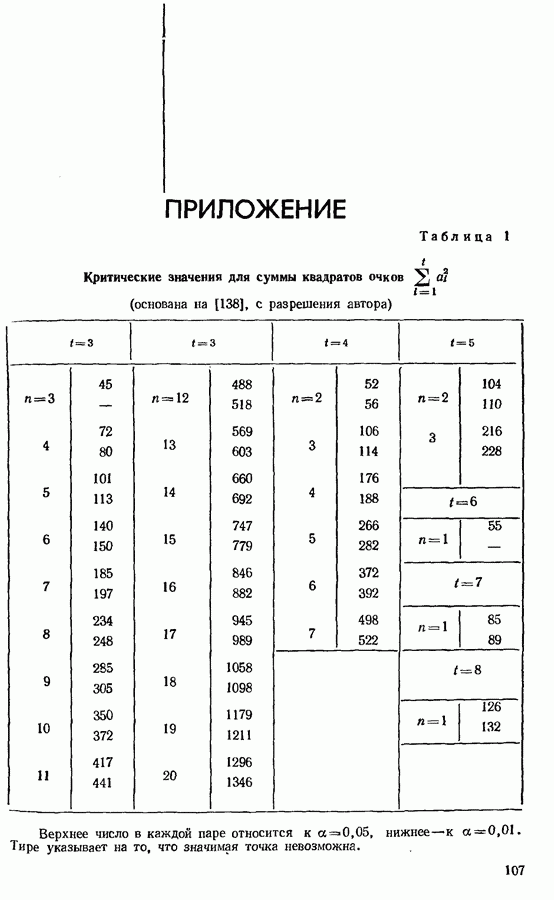
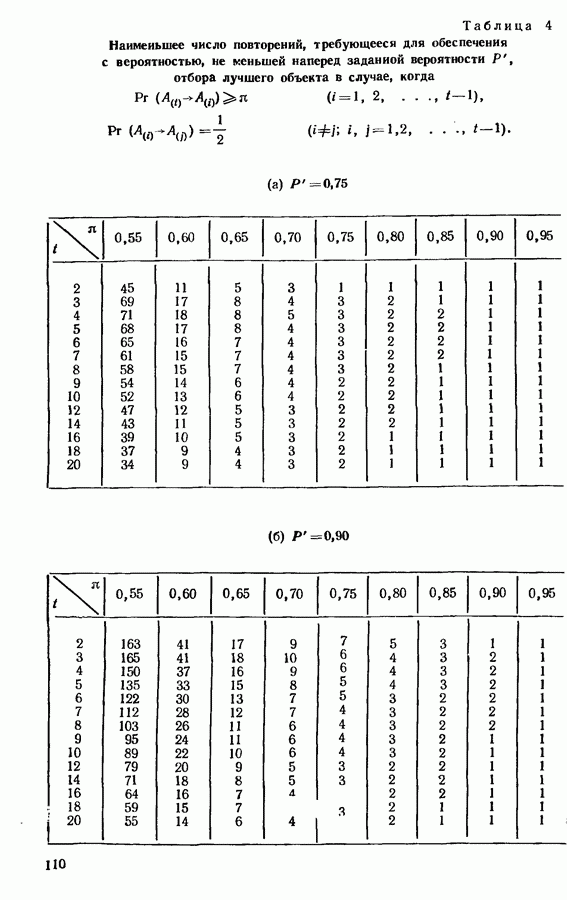
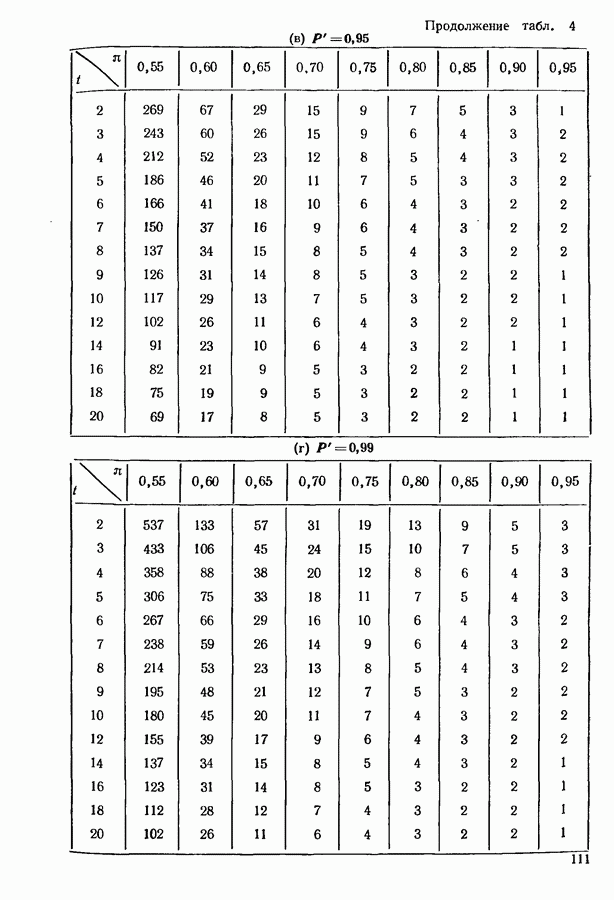
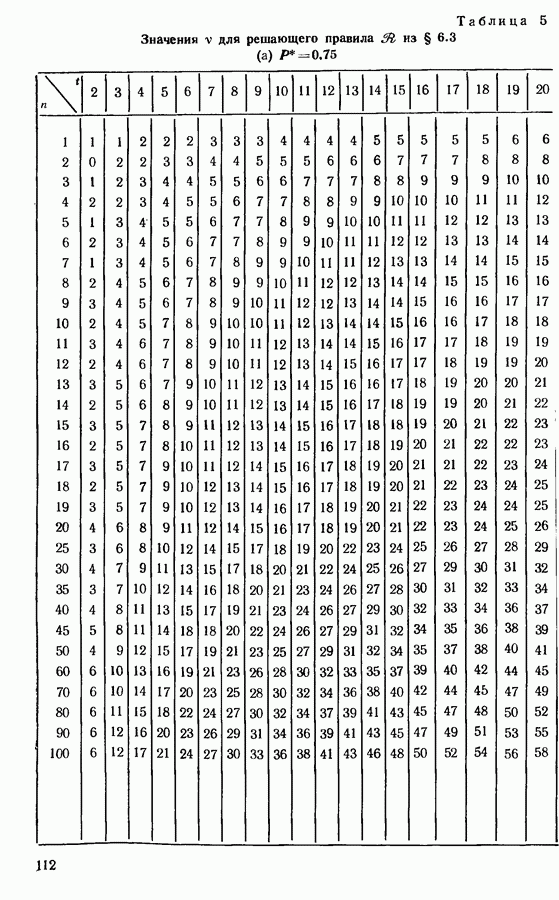
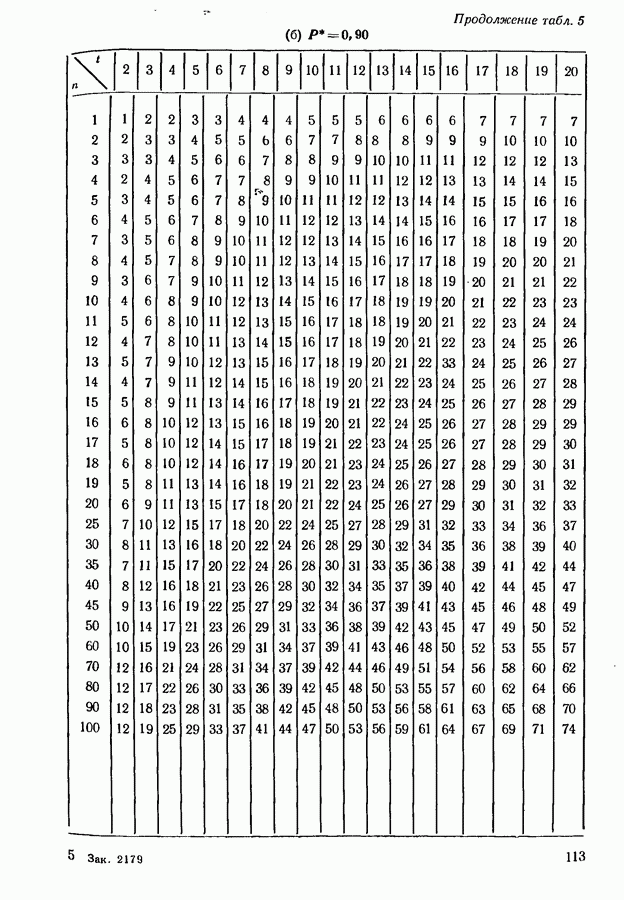
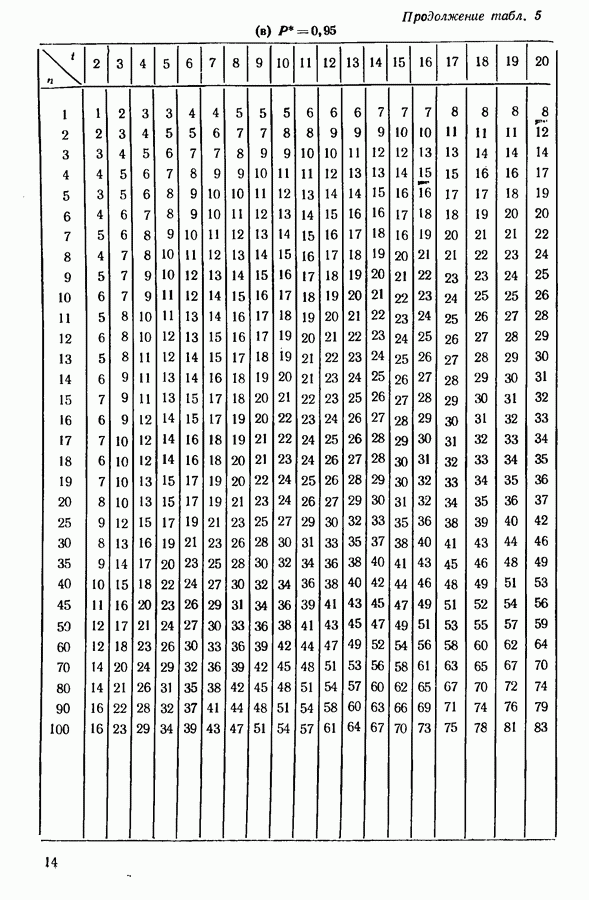
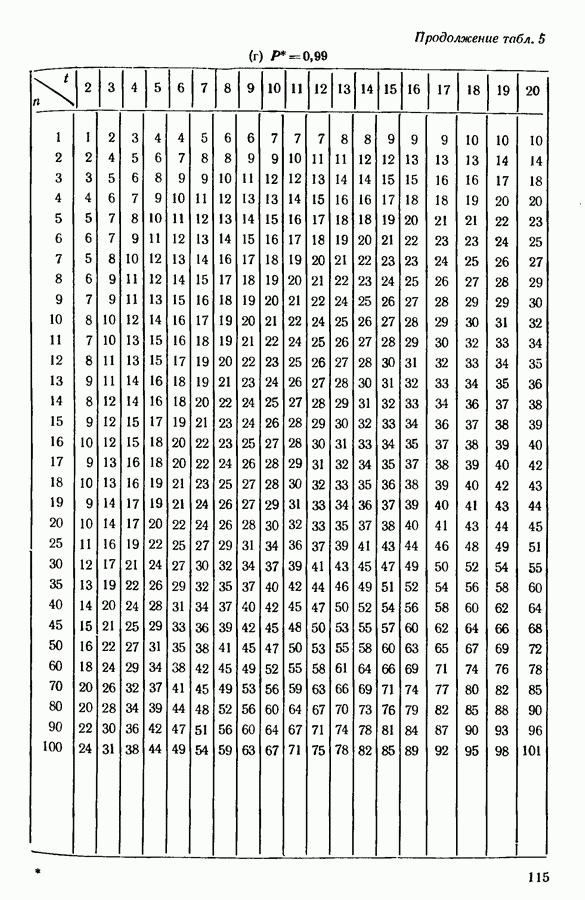
значения  определенные как из точной, так и из асимптотической теории, даны в табл. 5 приложения. Следует заметить, что размер
определенные как из точной, так и из асимптотической теории, даны в табл. 5 приложения. Следует заметить, что размер
 случайная величина, которая изменяется от 1 до
случайная величина, которая изменяется от 1 до  Правило, дающее верный отбор, таково:
Правило, дающее верный отбор, таково:

Для фиксированных  вероятность правильного выбора
вероятность правильного выбора  зависит от
зависит от  и конфигурации вероятностей предпочтений
и конфигурации вероятностей предпочтений  и мы имеем
и мы имеем

В таблице  выбирается как наименьшее целое число, такое, что
выбирается как наименьшее целое число, такое, что  когда
когда  т. е. когда все объекты эквивалентны (мы метим объект
т. е. когда все объекты эквивалентны (мы метим объект  так что
так что  вполне определенно). Можно показать [139], что для фиксированных
вполне определенно). Можно показать [139], что для фиксированных  конфигурация
конфигурация  приводит к нижней грани
приводит к нижней грани  Для любых
Для любых  удовлетворяющих линейной модели. В этом случае мы можем говорить
удовлетворяющих линейной модели. В этом случае мы можем говорить  как о конфигурации, которая обеспечивает надежность, и дает
как о конфигурации, которая обеспечивает надежность, и дает

Точное определение 
Для значений  охватываемых таблицей размещения, упомянутой в 2.2, можно определить
охватываемых таблицей размещения, упомянутой в 2.2, можно определить  точно. Мы покажем эту процедуру для
точно. Мы покажем эту процедуру для  . В этом случае есть 16 возможных размещений, для которых типичным является
. В этом случае есть 16 возможных размещений, для которых типичным является  с частотой
с частотой  При
При  частота, с которой
частота, с которой  равно или больше, чем
равно или больше, чем  должна быть кратна
должна быть кратна  Мы имеем для
Мы имеем для

Так, вклад  из этого размещения для данного
из этого размещения для данного  есть
есть  где делитель есть коэффициент, переводящий частоты в вероятности. Если соответствующие вклады от всех 16 размещений сложить, получатся такие
где делитель есть коэффициент, переводящий частоты в вероятности. Если соответствующие вклады от всех 16 размещений сложить, получатся такие 

отсюда сразу же получаются входы в табл. 5 приложения при 
Пример
Мы покажем, как работает решающее правило  на данных
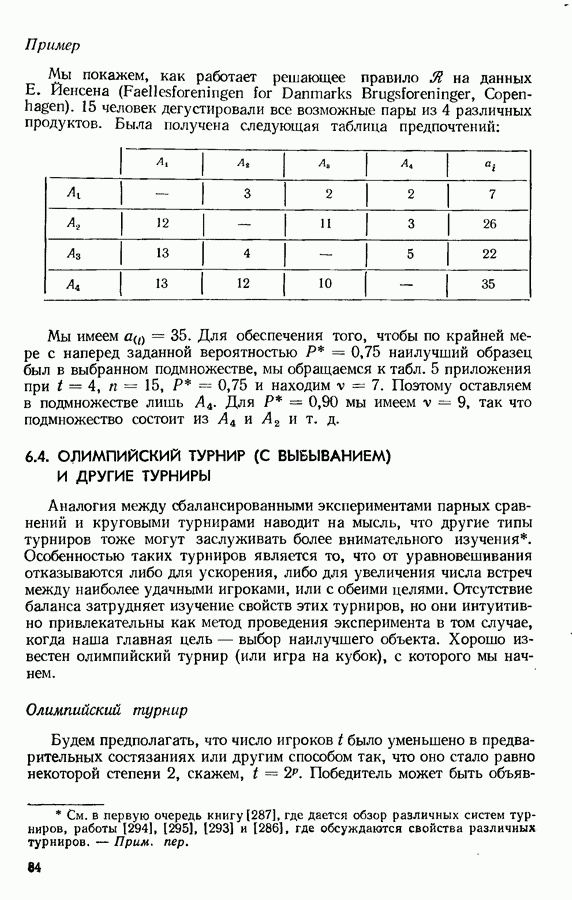
на данных  Иенсена (Faellesforeningen for Danmarks Brugsforeninger, Copenhagen). 15 человек дегустировали все возможные пары из 4 различных продуктов. Была получена следующая таблица предпочтений:
Иенсена (Faellesforeningen for Danmarks Brugsforeninger, Copenhagen). 15 человек дегустировали все возможные пары из 4 различных продуктов. Была получена следующая таблица предпочтений:
(см. скан)
Мы имеем  Для обеспечения того, чтобы по крайней мере с наперед заданной вероятностью
Для обеспечения того, чтобы по крайней мере с наперед заданной вероятностью  наилучший образец был в выбранном подмножестве, мы обращаемся к табл. 5 приложения при
наилучший образец был в выбранном подмножестве, мы обращаемся к табл. 5 приложения при  и находим
и находим  Поэтому оставляем в подмножестве лишь
Поэтому оставляем в подмножестве лишь  Для
Для  мы имеем
мы имеем  так что подмножество состоит из
так что подмножество состоит из 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
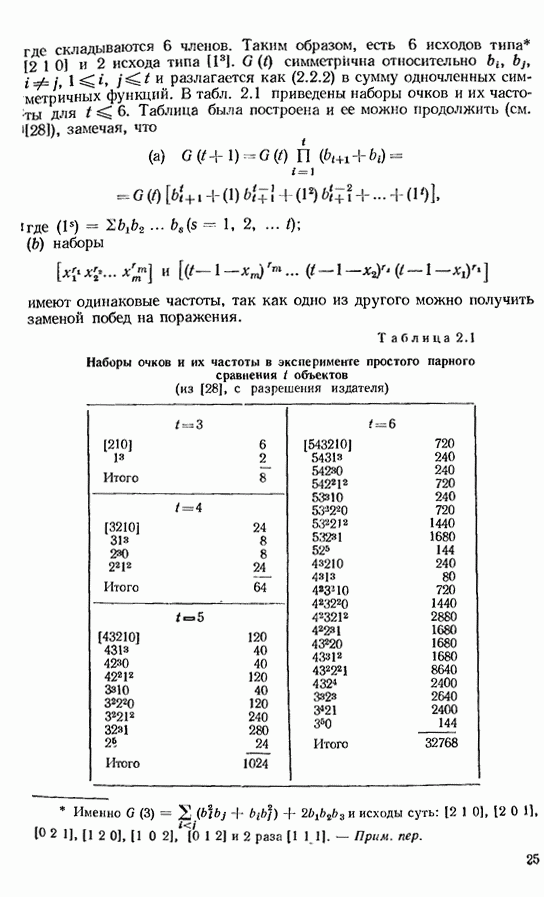
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
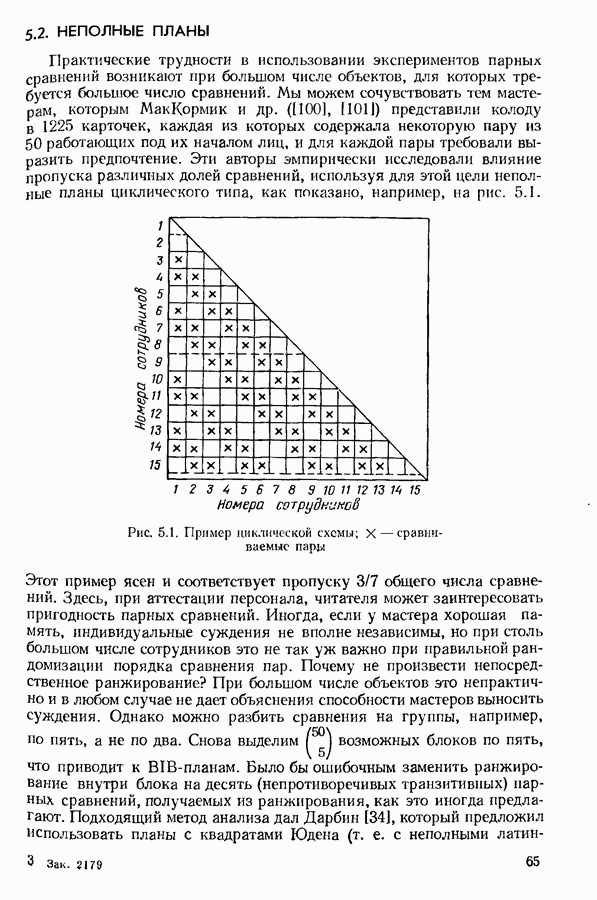
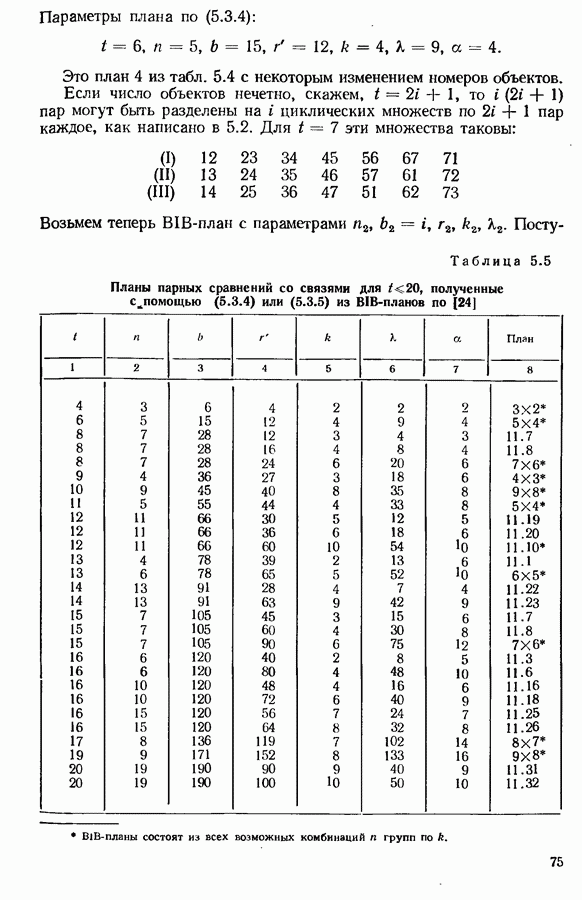
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
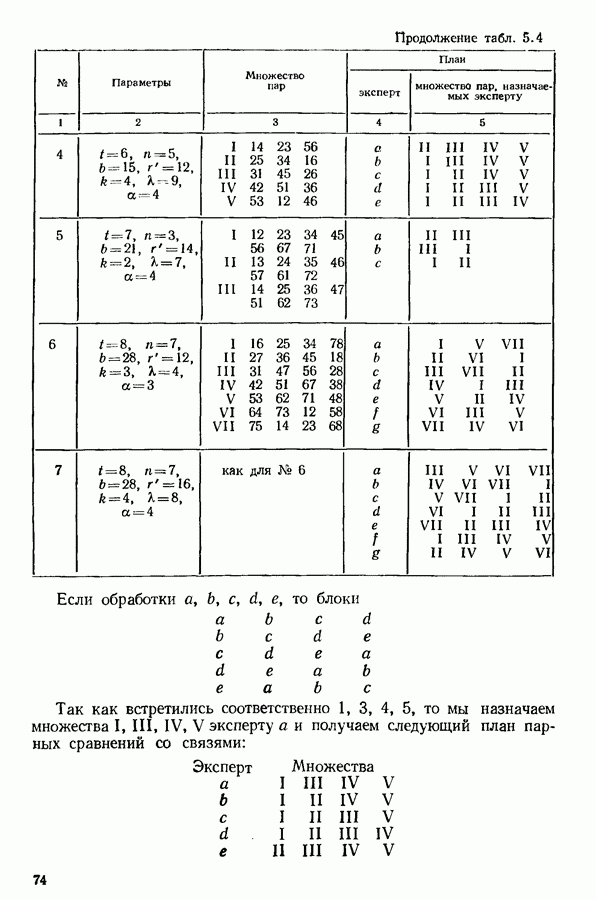
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ