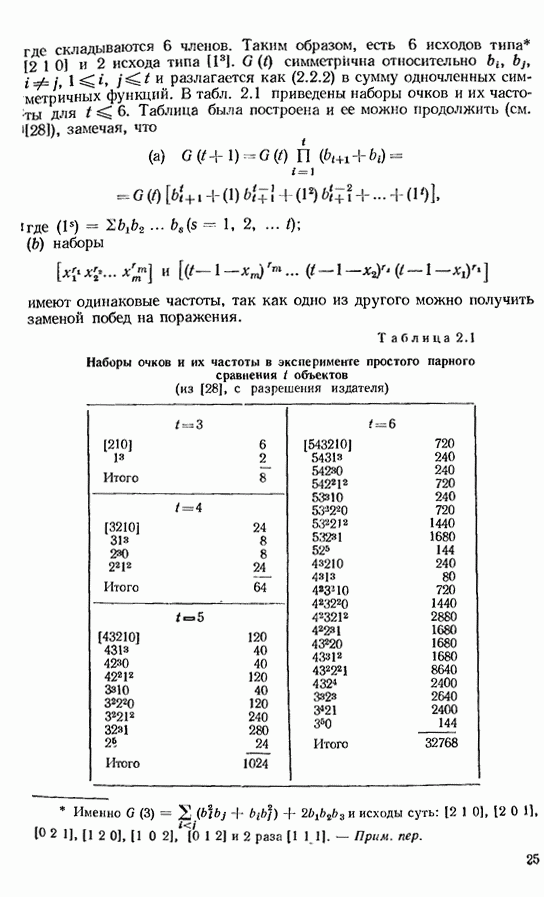
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 7. СМЕЖНЫЕ ВОПРОСЫ
7.1. ОТБОР ЭКСПЕРТОВ
До сих пор в наших исследованиях мы не обращали внимания на практически важную задачу выбора группы экспертов. На этот выбор, конечно, влияют такие факторы, как стоимость эксперимента и наличие подходящих экспертов. Еще более важный фактор — цель эксперимента парных сравнений, для которого отбираются эксперты.
Изучать предпочтения в «полевых условиях» надо в большой комиссии потребителей, представляющих популяцию, которая нас интересует, а для выявления тонких различий в лабораторных условиях и установлении стандартов качества привлекается небольшая группа экспертов.
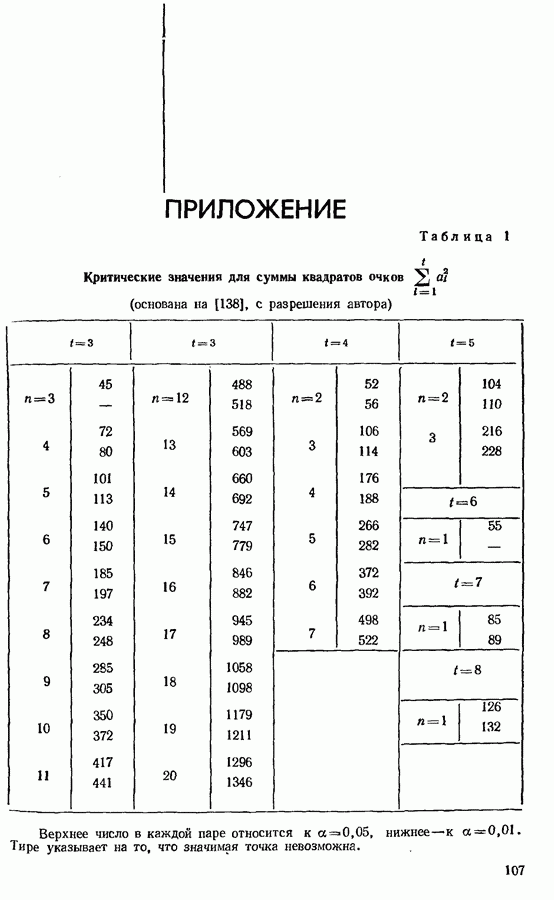
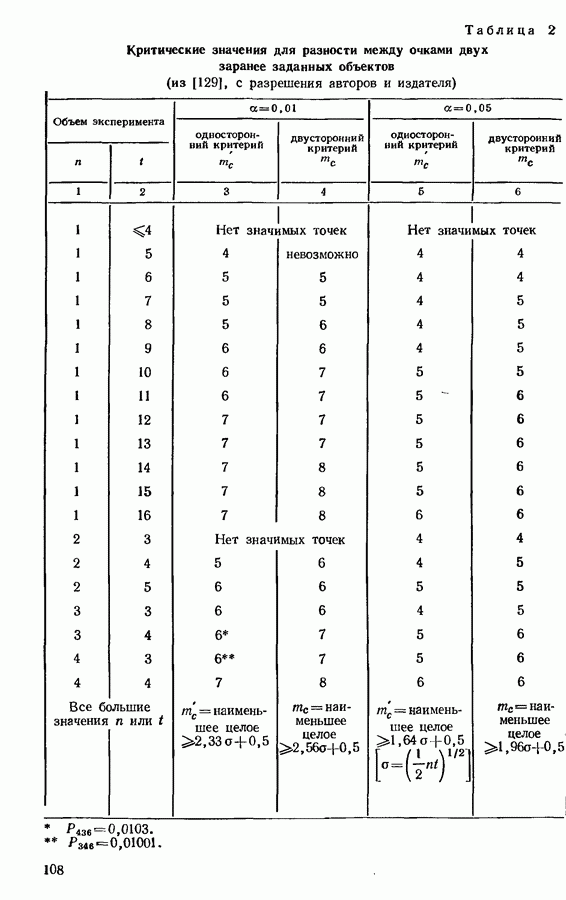
Более подробно о комиссиях потребителей мы поговорим в § 7.2. Что касается экспертных групп, то первоначальный интерес представляет выявление различий между объектами, одно или более из которых могут быть «стандартными». Должна рассматриваться каждая попытка определить тип различия. В пищевой промышленности отбор экспертов обыкновенно основывается на простых тестах, таких, как парный, тройной и двойной-тройной. До обсуждения мы отметим, что они включают лишь два различных типа объектоь Чтобы охватить широкий диапазон, экспериментатор может организовать сбалансированный эксперимент парных сравнений с несколькими объектами. Следует выбирать экспертов с наименьшим числом циклов, если нет априорного упорядочения, или с наименьшим числом разделений (§ 2.1) плюс циклы, если есть такое упорядочение.
Ранжироьание [143] и приписывание очков [44] также могут использоваться как методы отбора, но это представляется менее желательным, когда последующие эксперименты проводятся путем парных сравнений (см. также [10]).
Парный, тройной и двойной-тройной тесты
При парном тесте два различных объекта представляются эксперту. Один из них заведомо «лучший» по некоторому признаку, и верный ответ получается, если эксперт опознает этот объект. Другие
два теста включают три объекта, два из которых близки. Назовем их  и пусть
и пусть  означает непарный объект. В обоих случаях эксперт пытается указать
означает непарный объект. В обоих случаях эксперт пытается указать  в двойном-тройном тесте он дополнительно устанавливает идентичность
в двойном-тройном тесте он дополнительно устанавливает идентичность  Можно видеть, что вероятность верного ответа вполне случайна и равна для парного и двойного-тройного тестов и для тройного теста.
Можно видеть, что вероятность верного ответа вполне случайна и равна для парного и двойного-тройного тестов и для тройного теста.
Несколько свойств этих тестов были проверены в прекрасной работе [142], которая местами слишком сокращена со ссылкой на ограничение объема. Дальнейшие детали даны у Дэвида и Трайведи [30]. Пусть наблюдаемые ценности объектов  равны соответственно
равны соответственно  Юэре предполагает фактически, что верна линейная модель и что наблюдаемые ценности есть непрерывные независимые случайные величины. Без потери общности мы можем считать
Юэре предполагает фактически, что верна линейная модель и что наблюдаемые ценности есть непрерывные независимые случайные величины. Без потери общности мы можем считать  лучшим объектом. Правильные ответы получаются, если
лучшим объектом. Правильные ответы получаются, если

Обозначим соответствующие вероятности через  и
и  Для
Для  распределенных нормально
распределенных нормально  и
и  распределенной нормально
распределенной нормально  мы имеем
мы имеем

где  стандартная нормальная функция распределения и
стандартная нормальная функция распределения и  Можно показать, что
Можно показать, что

и (упражнение 7.1)

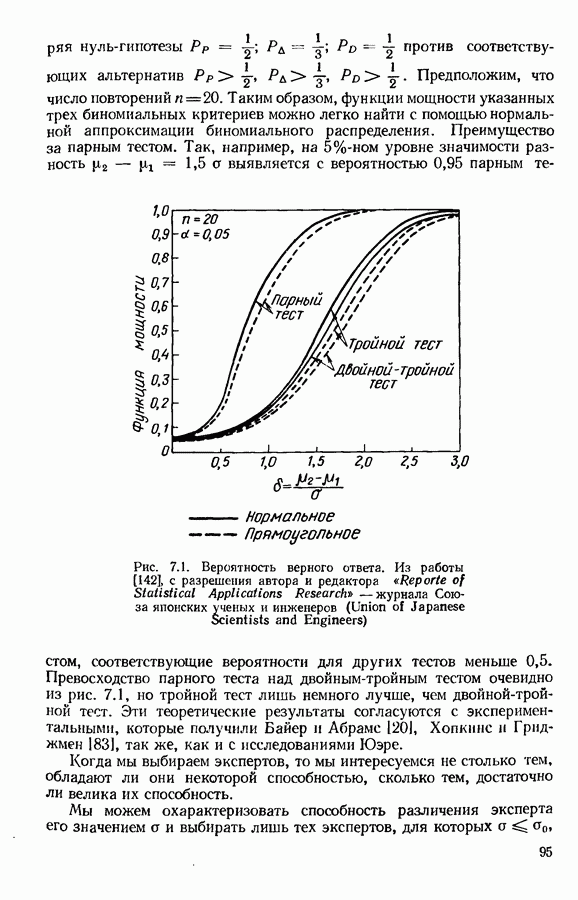
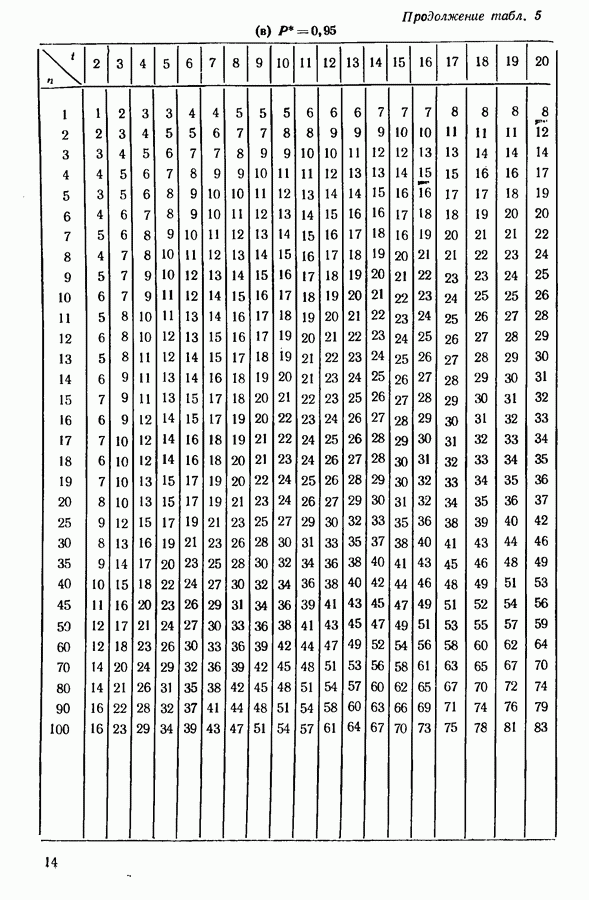
Юэре также получил соответствующие выражения для случая, когда у распределены равномерно с выписанными выше математическими ожиданиями и дисперсиями (упражнение 7.2). Результаты как функции от 6 показаны на рис. 7.1 и неожиданно близки для двух распределений. Если на мгновение мы сочтем три размещения средством выявления различий между двумя похожими объектами (а не средством выбора экспертов), то мы сможем сравнить их действие,
проверяя нуль-гипотезы  против соответствующих альтернатив
против соответствующих альтернатив  Предположим, что число повторений
Предположим, что число повторений  Таким образом, функции мощности указанных трех биномиальных критериев можно легко найти с помощью нормальной аппроксимации биномиального распределения. Преимущество за парным тестом. Так, например, на
Таким образом, функции мощности указанных трех биномиальных критериев можно легко найти с помощью нормальной аппроксимации биномиального распределения. Преимущество за парным тестом. Так, например, на  -ном уровне значимости разность
-ном уровне значимости разность  а выявляется с вероятностью 0,95 парным тестом, соответствующие вероятности для других тестов меньше 0,5.
а выявляется с вероятностью 0,95 парным тестом, соответствующие вероятности для других тестов меньше 0,5.

Рис. 7.1. Вероятность верного ответа. Из работы [142], с разрешения автора и редактора «Reporte of Statistical Applications Research» - журнала Союза японских ученых и инженеров (Union of Japanese Scientists and Engineers)
Превосходство парного теста над двойным-тройным тестом очевидно из рис. 7.1, но тройной тест лишь немного лучше, чем двойной-тройной тест. Эти теоретические результаты согласуются с экспериментальными, которые получили Байер и Абраме [20], Хопкинс и Грнджмен [83], так же, как и с исследованиями Юэре.
Когда мы выбираем экспертов, то мы интересуемся не столько тем, обладают ли они некоторой способностью, сколько тем, достаточно ли велика их способность.
Мы можем охарактеризовать способность различения эксперта его значением а и выбирать лишь тех экспертов, для которых 
где  соответствует предписанной степени способности. Для разницы
соответствует предписанной степени способности. Для разницы  между
между  вероятность правильного ответа может быть выражена как
вероятность правильного ответа может быть выражена как  Так как это возрастающая функция от а для фиксированного
Так как это возрастающая функция от а для фиксированного  гипотезы
гипотезы

эквивалентны

При известных очках х верных ответов экспертов в  испытаниях мы отвергаем
испытаниях мы отвергаем  применяя преобразование
применяя преобразование  если
если

где  — верхняя
— верхняя  -процентная точка нормированного нормального распределения. Функция мощности этого критерия, приближенно равная
-процентная точка нормированного нормального распределения. Функция мощности этого критерия, приближенно равная

функция  Так как величина
Так как величина  может варьировать, перед экспериментатором встает вопрос, каково ее оптимальное значение. Из изучения функций мощности Юэре заключает, что для
может варьировать, перед экспериментатором встает вопрос, каково ее оптимальное значение. Из изучения функций мощности Юэре заключает, что для  должно быть примерно таким, чтобы вероятность верного ответа была 0,95 для эксперта, который вполне приемлем
должно быть примерно таким, чтобы вероятность верного ответа была 0,95 для эксперта, который вполне приемлем  Более того, он находит, что тройной тест наиболее приемлем в этих обстоятельствах.
Более того, он находит, что тройной тест наиболее приемлем в этих обстоятельствах.
Так как (7.1.5) означает просто нулевую и альтернативную гипотезы для биномиального параметра, можно ожидать, что последовательные методы для проверки биномиальной доли дадут уменьшение в среднем числа повторений для каждого эксперта [13]. В дополнение к  мы требуем теперь
мы требуем теперь  чтобы эксперты с а а, оказались нежелательными. Затем мы проверяем последовательно
чтобы эксперты с а а, оказались нежелательными. Затем мы проверяем последовательно

С другой стороны, можно работать с вероятностью правильного ответа  фиксируя подходящие значения
фиксируя подходящие значения  и проверяя
и проверяя

Это в то же время критерий

Можно заметить, что если нет ясной методики определения приемлемых значений  то можно использовать методы принятия множественных решений для биномиальной совокупности [68] для отсеивания плохих экспертов.
то можно использовать методы принятия множественных решений для биномиальной совокупности [68] для отсеивания плохих экспертов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
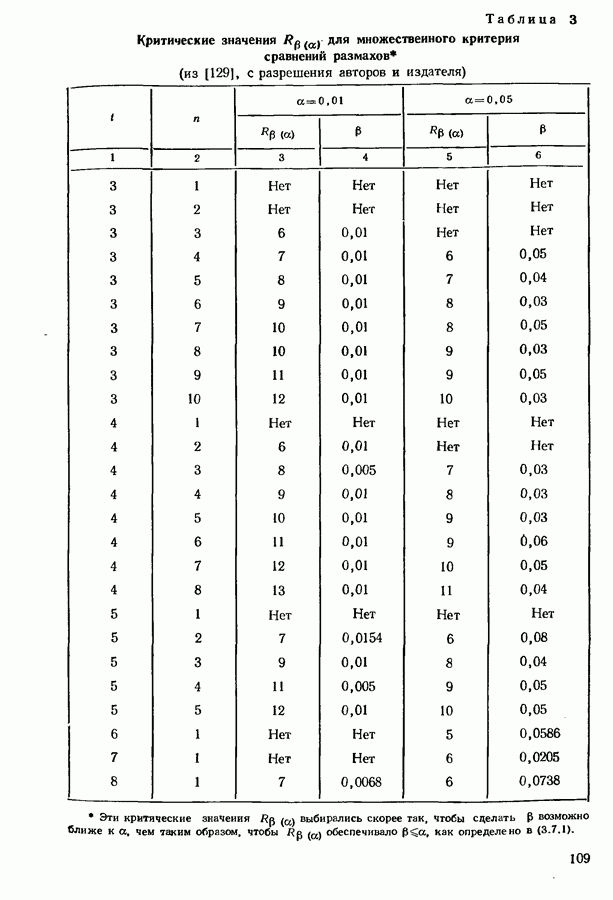
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
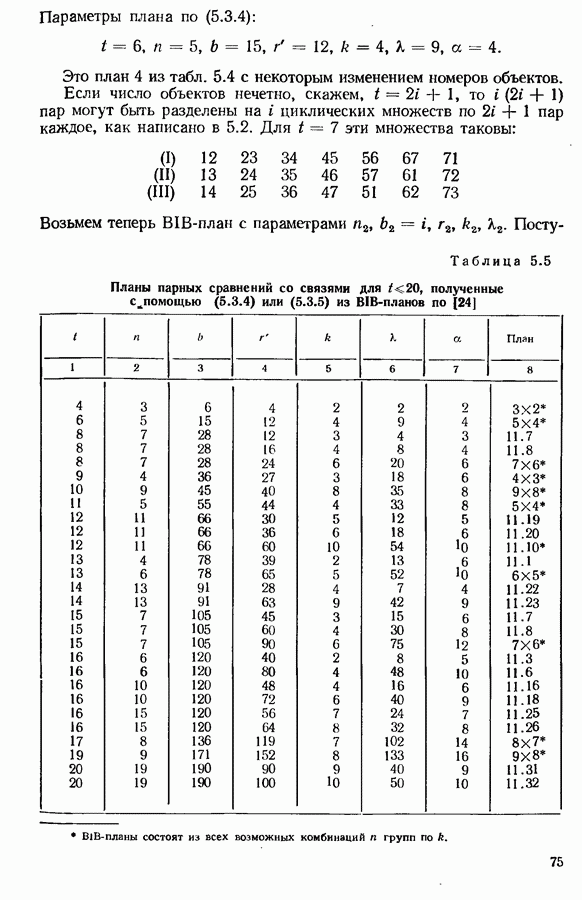
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
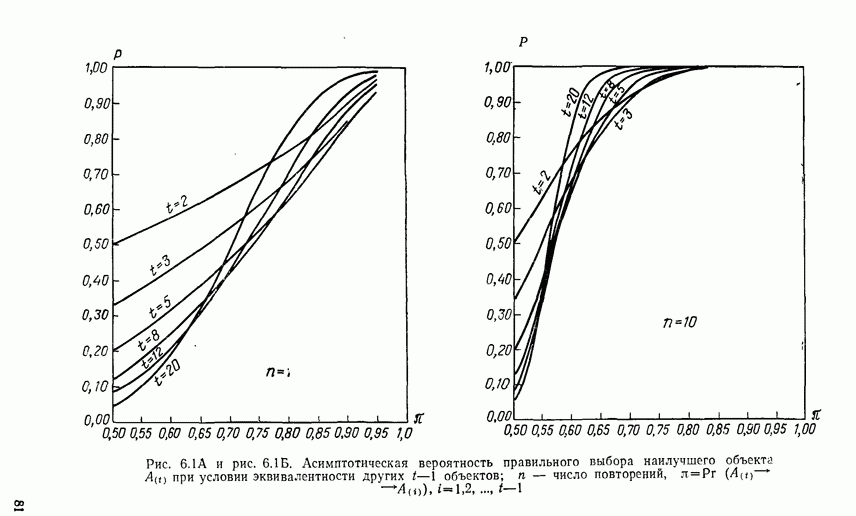
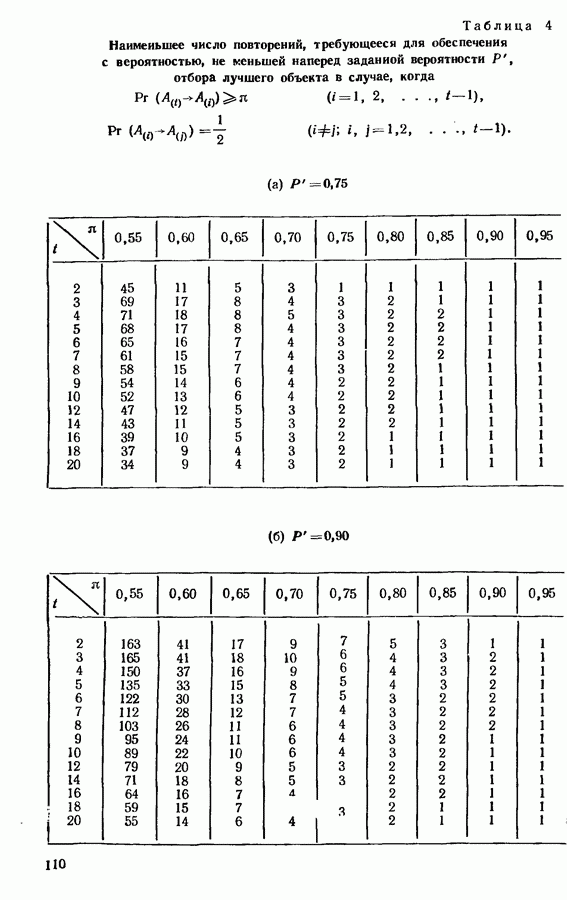
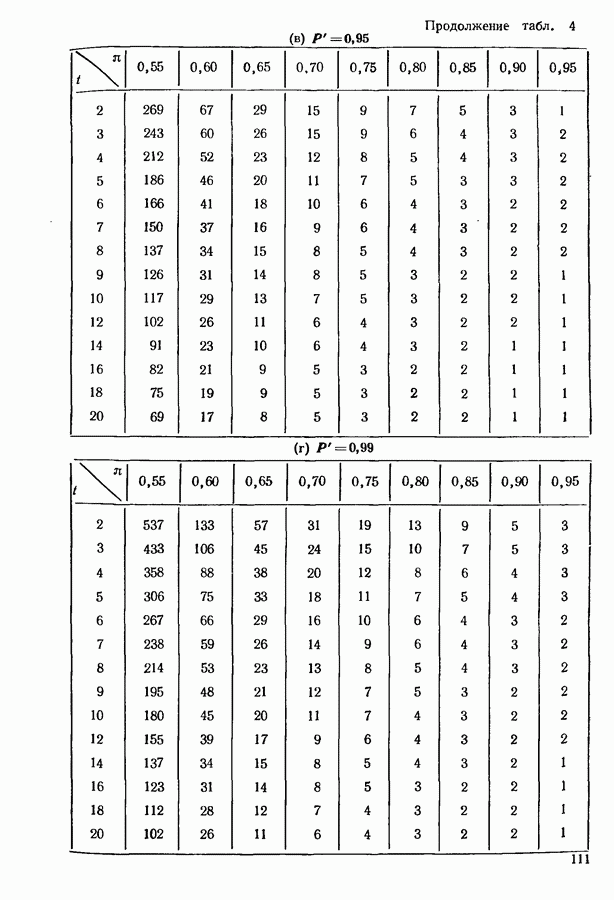
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
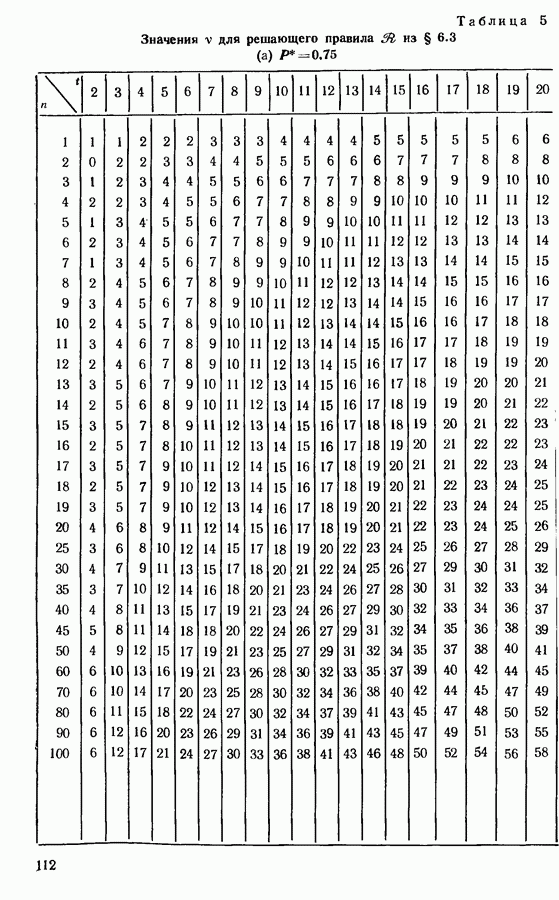
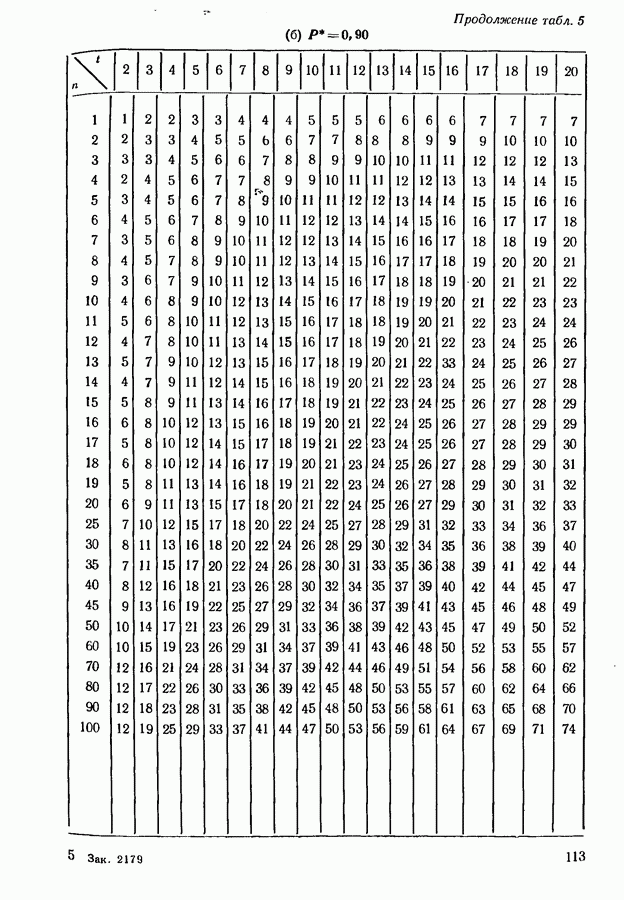
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ