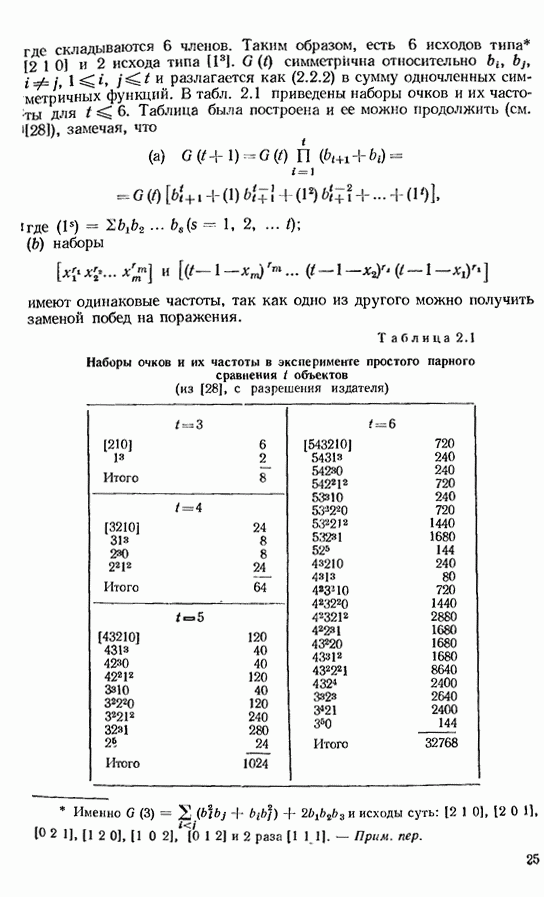
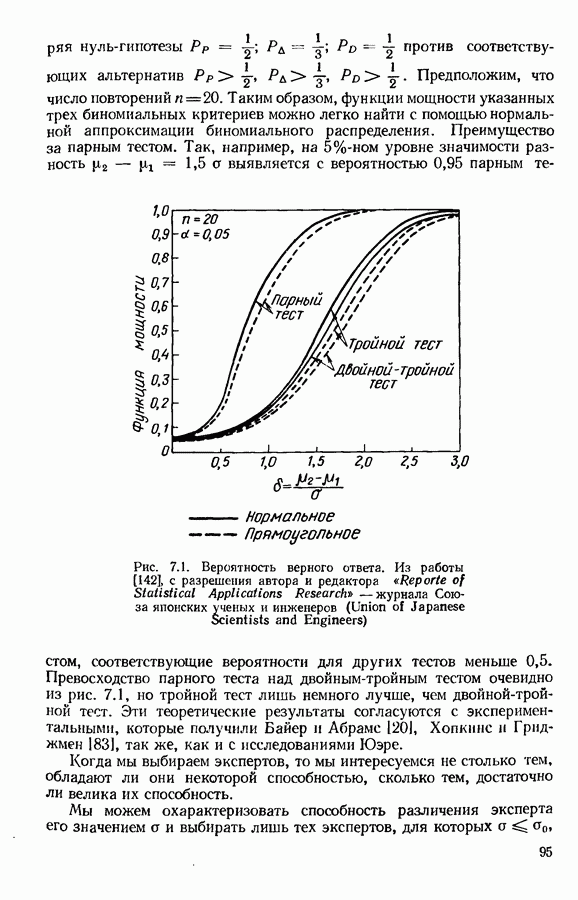
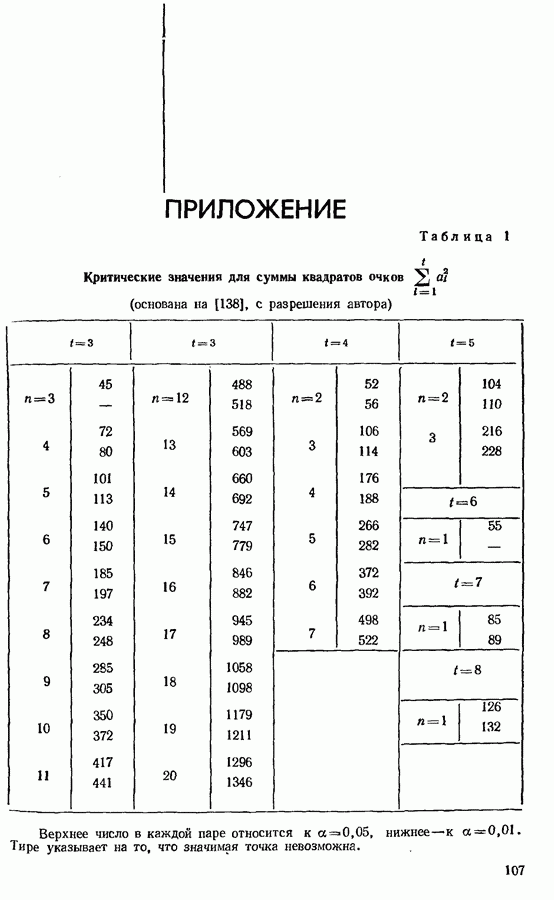
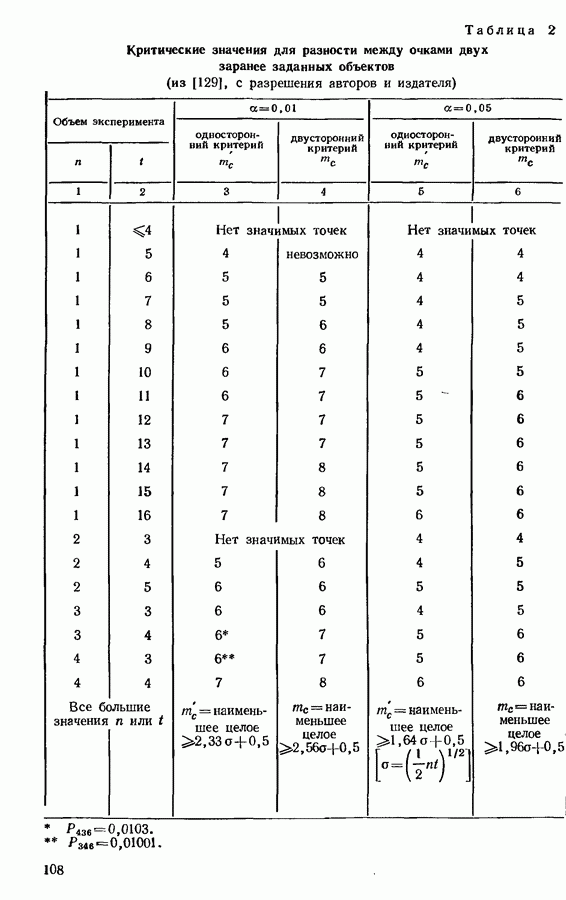
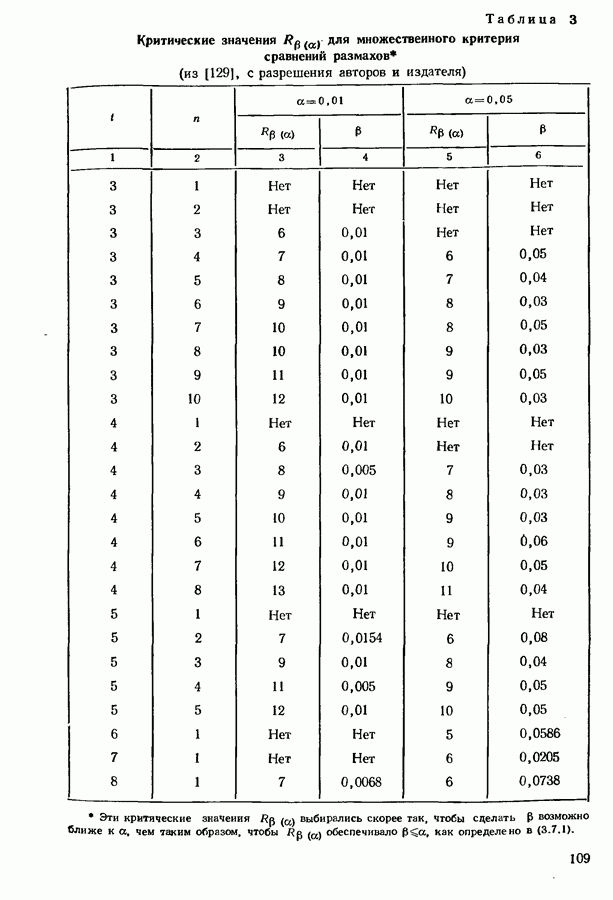
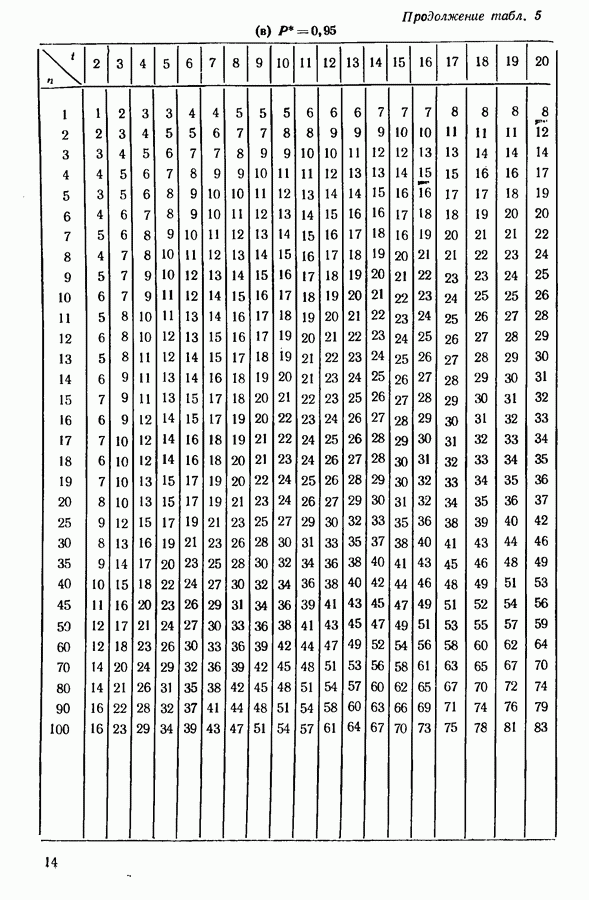
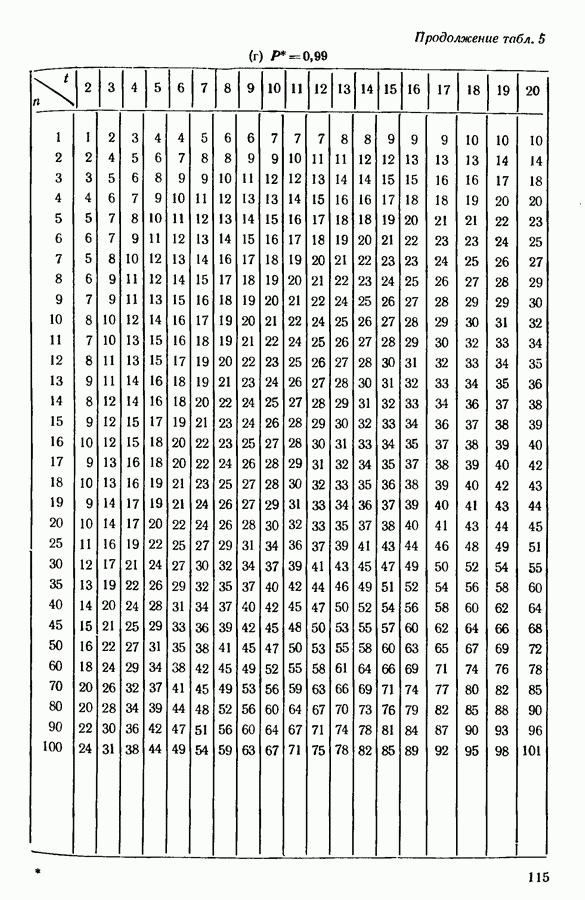
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.4. МЕТОДИКА ШЕФФЕ
Шеффе [122] предложил метод анализа экспериментов парных сравнений, включающих две особенности:
1) применение 7- или 9-точечной шкалы предпочтений;
2) введение специальных предположений о возможном эффекте порядка представления эксперту объектов в парах.
Вторая особенность требует пояснений. Хотя уже Фехнер всегда принимал во внимание, как важные, «пространственный» и «временной» эффекты, мы до сих пор не обращали на них внимания во всех способах анализа. Зная, что порядковые эффекты могут вызвать смещение результатов, мы имеем возможность сбалансировать их на стадии
планирования эксперимента  Если их влияние невелико или не представляет интереса, то этого довольно. Рассмотрим, например, случай четного числа сравнений
Если их влияние невелико или не представляет интереса, то этого довольно. Рассмотрим, например, случай четного числа сравнений  по
по  в каждом из порядков предъявления. Пусть
в каждом из порядков предъявления. Пусть  означают вероятности, с которыми
означают вероятности, с которыми  когда А предъявляется первым и вторым соответственно, и пусть
когда А предъявляется первым и вторым соответственно, и пусть  соответствующие числа предпочтений для А. Тогда
соответствующие числа предпочтений для А. Тогда  есть несмещенная оценка средней вероятности предпочтения. Дисперсия
есть несмещенная оценка средней вероятности предпочтения. Дисперсия  равна:
равна:

что демонстрирует обычно уменьшение, обусловленное неоднородностью. Видно, что  должно быть весьма большим, чтобы уменьшение стало заметным. Более того, неучет неоднородности приводит к затруднениям при установлении различия между
должно быть весьма большим, чтобы уменьшение стало заметным. Более того, неучет неоднородности приводит к затруднениям при установлении различия между  (сравните § 3.2).
(сравните § 3.2).
В методике Шеффе должны различаться упорядоченные пары  и
и  Пусть
Пусть  очки
очки  сравнении первой пары. Мы используем здесь термин «очки» в несколько измененном смысле:
сравнении первой пары. Мы используем здесь термин «очки» в несколько измененном смысле:  для
для  -точечной шкалы. Затем
-точечной шкалы. Затем  очки
очки  причем
причем  очки
очки  сравнении
сравнении  Общая сумма очков для
Общая сумма очков для  по всем сравнениям с
по всем сравнениям с  есть
есть

Предполагается, что все  независимы и что для фиксированной упорядоченной пары
независимы и что для фиксированной упорядоченной пары  все
все  случайных величин
случайных величин  имеют одно математическое ожидание и дисперсию
имеют одно математическое ожидание и дисперсию  которая не зависит от
которая не зависит от  Для критериев значимости и доверительных границ добавляется допущение о нормальности очков. Это последнее предположение может быть в лучшем случае приближенно верным; то, что дисперсия одинакова для всех пар, также сомнительно. Все же может случиться, что эти предположения не опровергаются полностью последующим дисперсионным анализом с точки зрения общей устойчивости (робастности) анализа для сбалансированных экспериментов. Также предполагается, что каждое сравнение выполняется различными экспертами, всего требуется
Для критериев значимости и доверительных границ добавляется допущение о нормальности очков. Это последнее предположение может быть в лучшем случае приближенно верным; то, что дисперсия одинакова для всех пар, также сомнительно. Все же может случиться, что эти предположения не опровергаются полностью последующим дисперсионным анализом с точки зрения общей устойчивости (робастности) анализа для сбалансированных экспериментов. Также предполагается, что каждое сравнение выполняется различными экспертами, всего требуется  экспертов, причем они выбираются случайным образом из интересующей нас генеральной совокупности. Как было сказано в § 7.1, такая организация эксперимента применима к тестированию потребителей, но ее можно приспособить и для других ситуаций.
экспертов, причем они выбираются случайным образом из интересующей нас генеральной совокупности. Как было сказано в § 7.1, такая организация эксперимента применима к тестированию потребителей, но ее можно приспособить и для других ситуаций.
Пусть математическое ожидание очков предпочтения для  в упорядоченных парах
в упорядоченных парах  есть — соответственно. Обозначим среднее из них как
есть — соответственно. Обозначим среднее из них как 

а их разность — через 

Так,  есть разность «от порядка представления» в математическом ожидании предпочтений для
есть разность «от порядка представления» в математическом ожидании предпочтений для  против
против  в то время как
в то время как  среднее предпочтение для
среднее предпочтение для  против
против  , усредненное по двум упорядоченным парам. Мы замечаем, что
, усредненное по двум упорядоченным парам. Мы замечаем, что

Мы можем также определить средний эффект порядка 

Шеффе вводит теперь гипотезу о «разностности», которая есть просто гипотеза линейности, а именно, что существуют параметры  для которых
для которых

Отклонение от разностности измеряется параметром  так что в общем случае мы можем написать:
так что в общем случае мы можем написать:

где  очевидно, удовлетворяет соотношениям
очевидно, удовлетворяет соотношениям 
С другой стороны,  можно выразить через
можно выразить через 

Оценки по методу наименьших квадратов получаются сразу. Начнем с

 можно оценить по очереди из (7.4.1), (7.4.2), (7.4.3) и (7.4.6).
можно оценить по очереди из (7.4.1), (7.4.2), (7.4.3) и (7.4.6).
Очки  можно выразить так:
можно выразить так:

где ошибки в правой части  есть случайные величины. Несмещенная оценка дисперсии
есть случайные величины. Несмещенная оценка дисперсии  равна:
равна:

Сумма квадратов ошибки  определяется в табл. 7.1, которая дает разложение общей суммы квадратов очков
определяется в табл. 7.1, которая дает разложение общей суммы квадратов очков  Можно построить приближенный критерий
Можно построить приближенный критерий  -отношения.
-отношения.
Таблица 7.1 (см. скан) Разбиение суммы квадратов очков
Параметры нецентральности в последнем столбце табл. 7.1. определяются [141] следующим образом:

Шеффе снабдил анализ примерами и обсудил построение доверительных интервалов для разностей 
Модель Тэрстоуна для дисперсионного анализа, предложенного Шеффе, была дана Юэре при следующих допущениях:
а) наблюдаемые ценности  объекта
объекта  нормальны
нормальны 
б) случайные величины  представляющие предпочтение
представляющие предпочтение  против
против  , когда они предъявляются в порядке
, когда они предъявляются в порядке  нормальны
нормальны  Величины
Величины  можно разложить:
можно разложить:

где  есть отклонения от разности и
есть отклонения от разности и  эффекты порядка, удовлетворяющие тем же условиям, которые были сформулированы выше для
эффекты порядка, удовлетворяющие тем же условиям, которые были сформулированы выше для 
в) для  -точечной системы шкала
-точечной системы шкала  делится на
делится на  части и очки располагают для
части и очки располагают для  следующим образом:
следующим образом:

Вероятность  того, что
того, что  наберет
наберет  очков против
очков против  поэтому равна:
поэтому равна:

где  функция нормированного нормального распределения. Если
функция нормированного нормального распределения. Если

то для малых различий между объектами можно найти приближенные соотношения между параметрами моделей Юэре и Шеффе. Юэре также рассмотрел мощность критерия Шеффе для главных эффектов и использовал ее для первого приближения к оптимальной системе очков.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
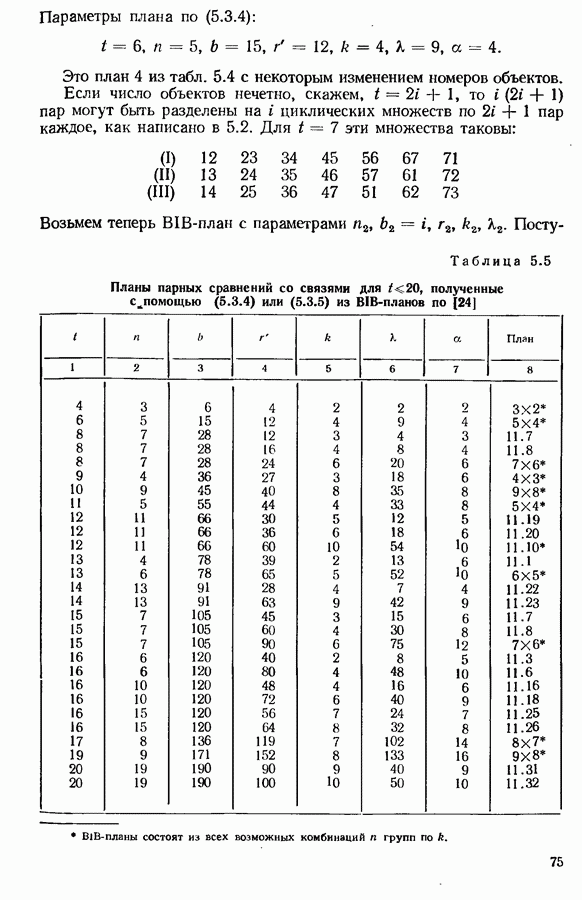
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
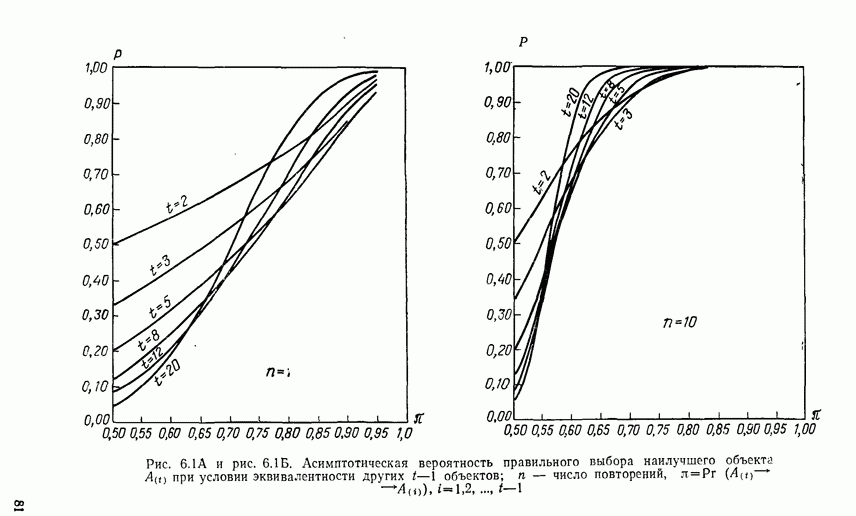
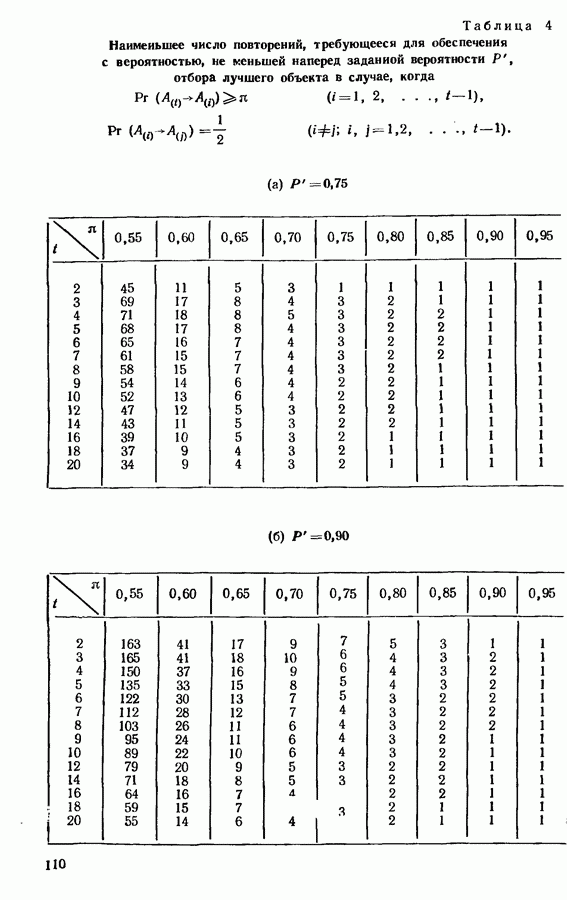
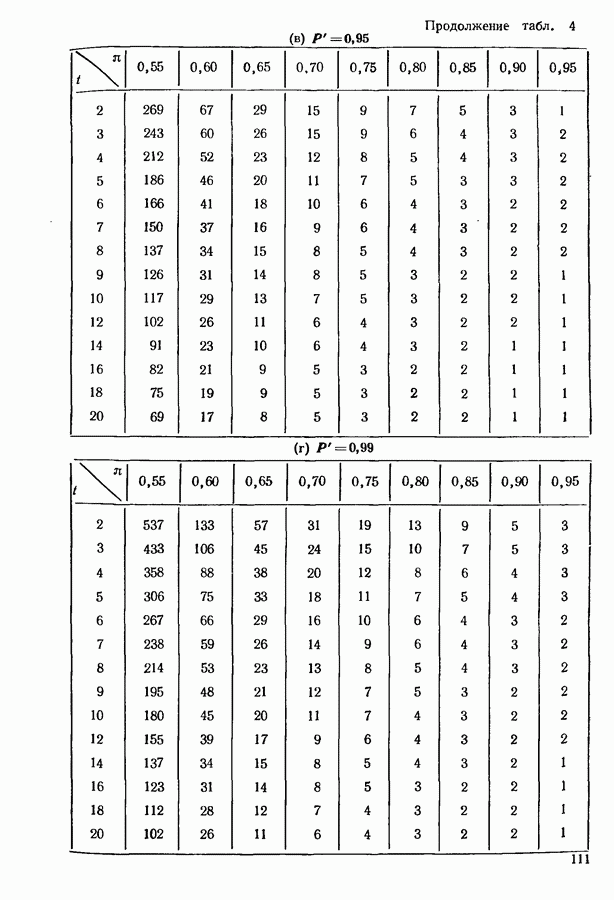
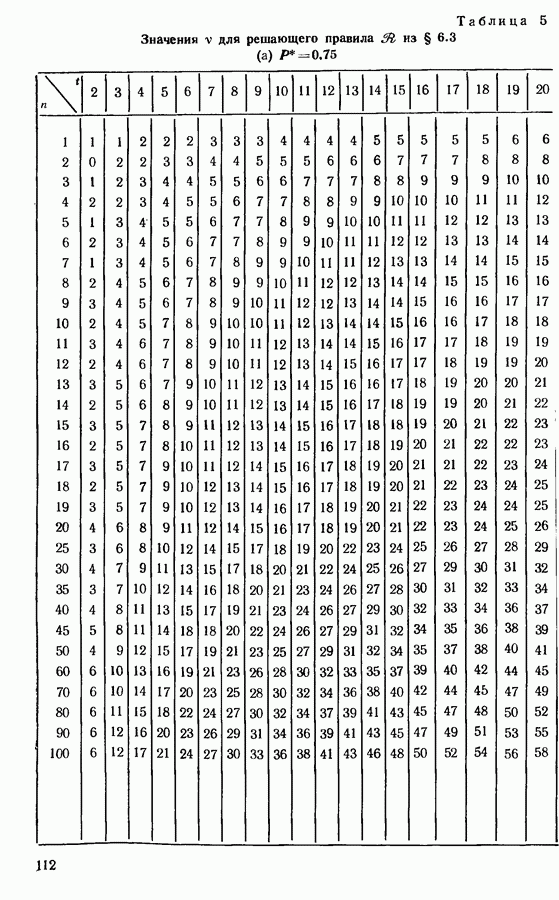
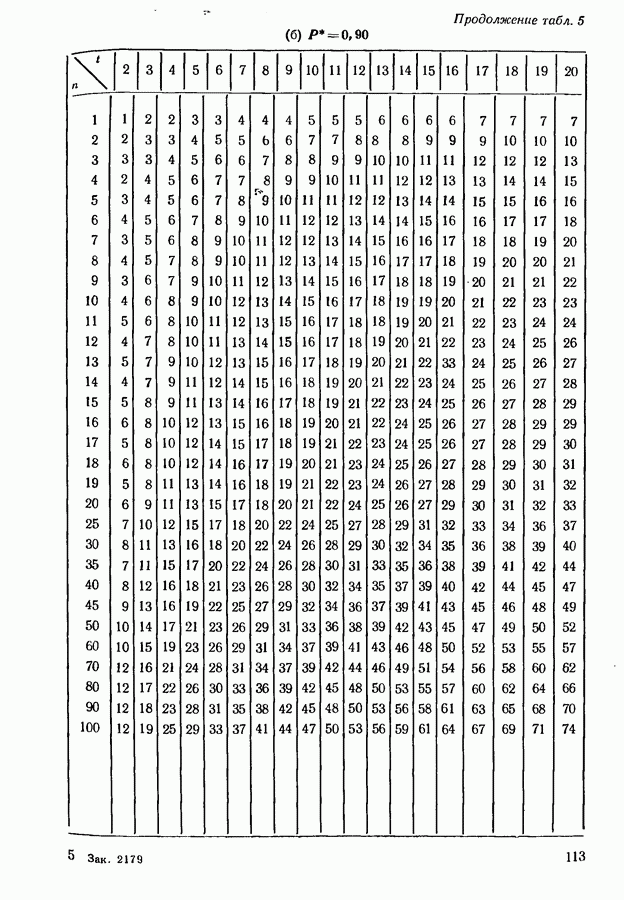
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
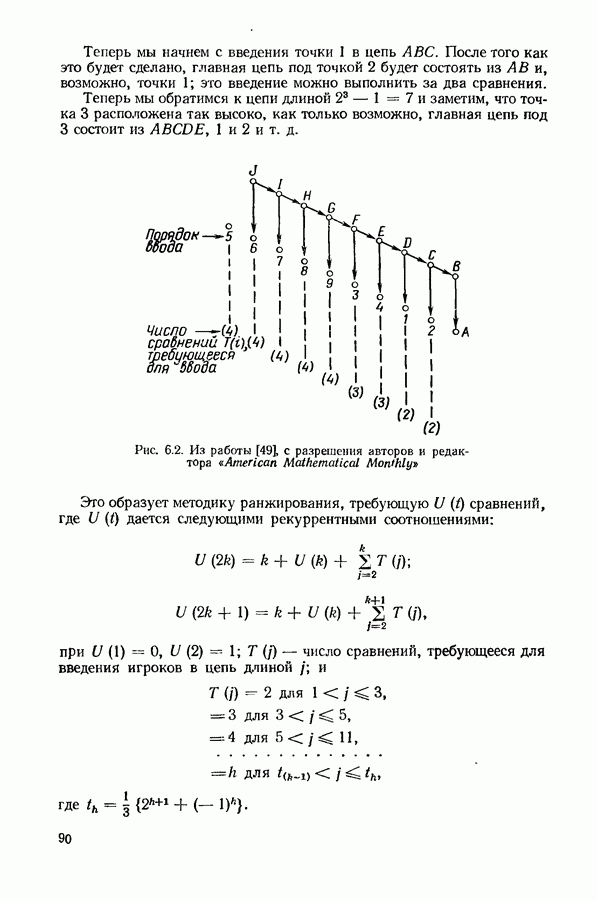
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ