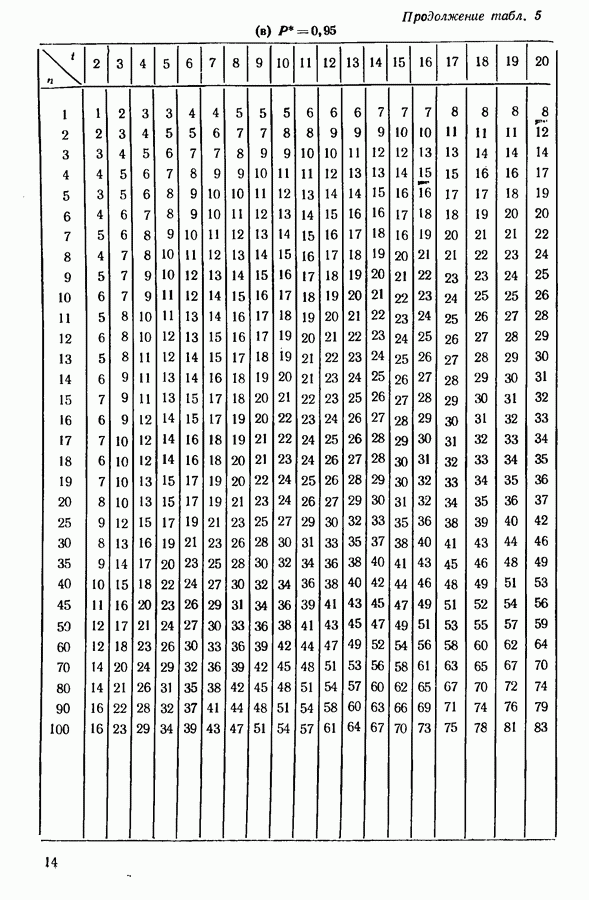
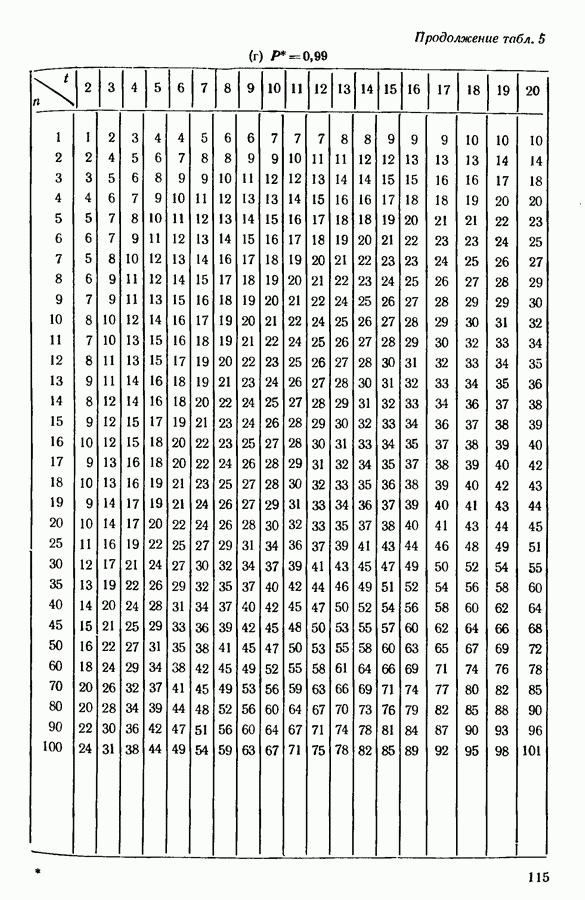
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
Розражение, которое может быть выдвинуто против предшествующего общего подхода, состоит в том, что сумма квадратов, минимизируемая в (4.1.8), есть невзвешенная сумма. Например, в случае модели Тэрстоуна-Аюстеллера  , хстя и получены из таблиц нормального распределения, не являются нормированными нормально распределенными случайными величинами, так как они могут принимать лишь
, хстя и получены из таблиц нормального распределения, не являются нормированными нормально распределенными случайными величинами, так как они могут принимать лишь  различных значений, соответствующих
различных значений, соответствующих  -му значению
-му значению  Более того, дисперсия каждой
Более того, дисперсия каждой  зависит от истинного значения
зависит от истинного значения  Если
Если  достаточно велико, мы имеем, например,
достаточно велико, мы имеем, например,

Таким образом, мы должны минимизировать

но веса  неизвестны, так что необходима трудоемкая итеративная процедура (см. 186, с. 66]. Чтобы обойти эти трудности, выполняется тригонометрическое преобразование. Полагая
неизвестны, так что необходима трудоемкая итеративная процедура (см. 186, с. 66]. Чтобы обойти эти трудности, выполняется тригонометрическое преобразование. Полагая

мы имеем приближенно для больших 

Преобразование (4.2.1) удобно выполнять с помощью табл. XII [70]. Если надо, то можно еще улучшить свойство преобразования — стабилизировать дисперсию для малых  заменой
заменой  на
на

Заметим, что (4.2.1) соответствует

Поэтому мы могли работать с тригонометрическим преобразованием в § 4.1. Новой чертой будет лишь то, что невзвешенная сумма квадратов  здесь приближенно равна взвешенной сумме. Более того, для всей области, кроме площадей нижнего и верхнего
здесь приближенно равна взвешенной сумме. Более того, для всей области, кроме площадей нижнего и верхнего  -ных «хвостов», распределение тригонометрического преобразования полностью аналогично нормальному с точностью до масштаба.
-ных «хвостов», распределение тригонометрического преобразования полностью аналогично нормальному с точностью до масштаба.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
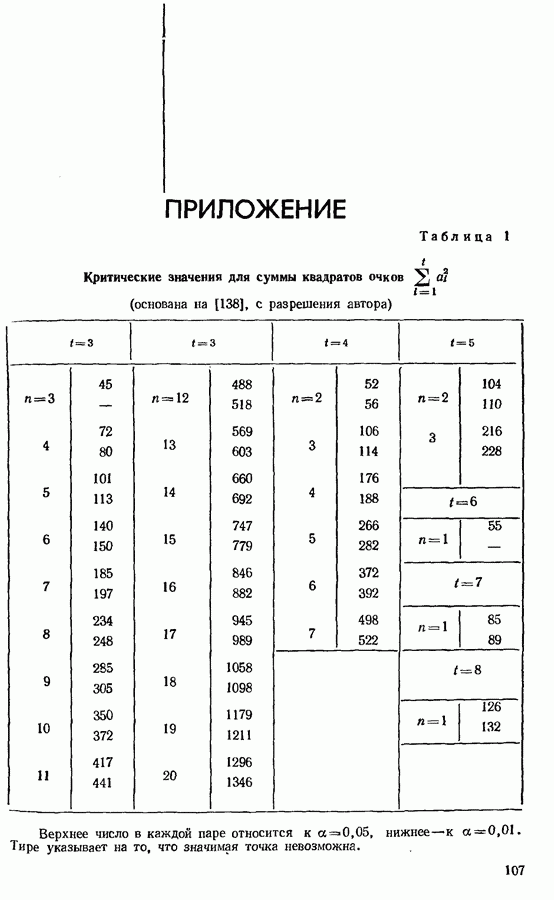
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
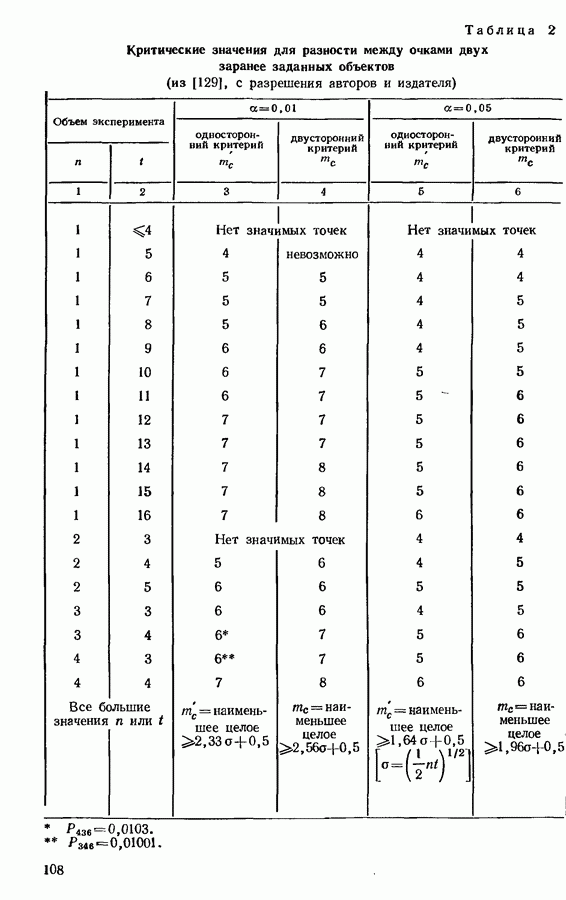
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
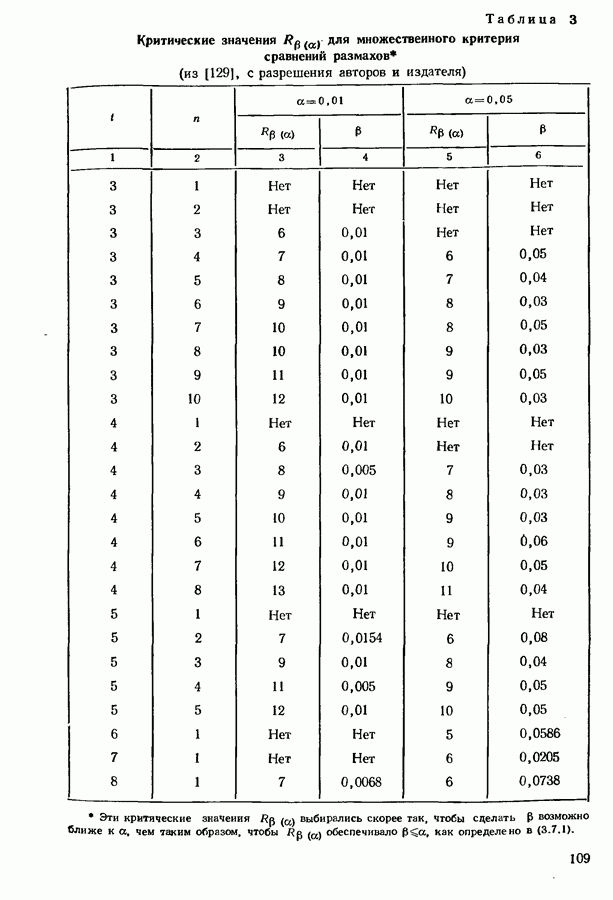
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
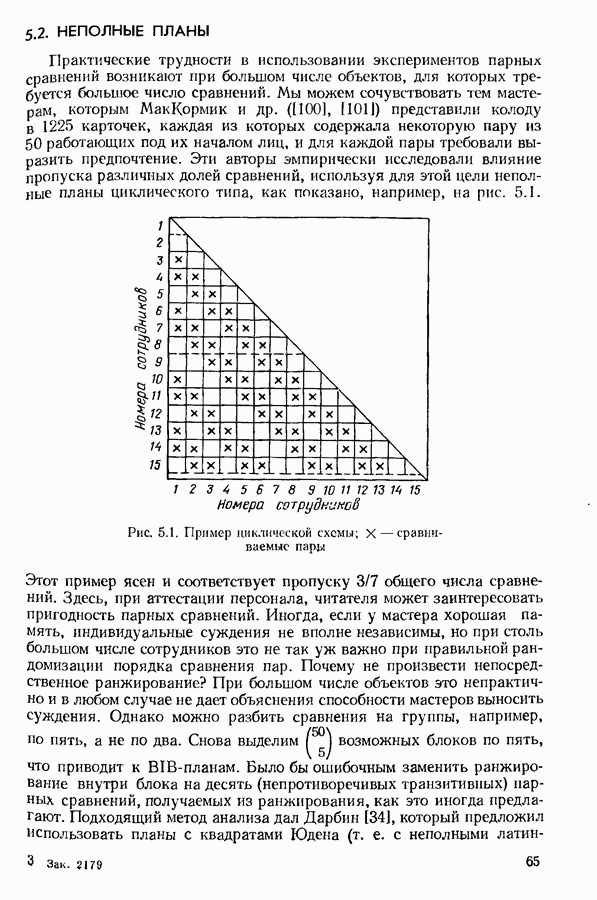
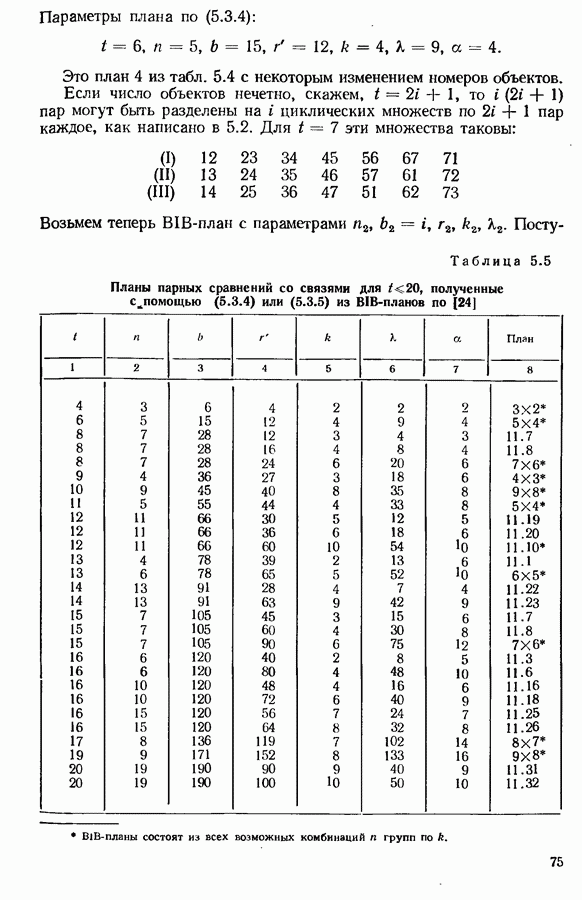
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
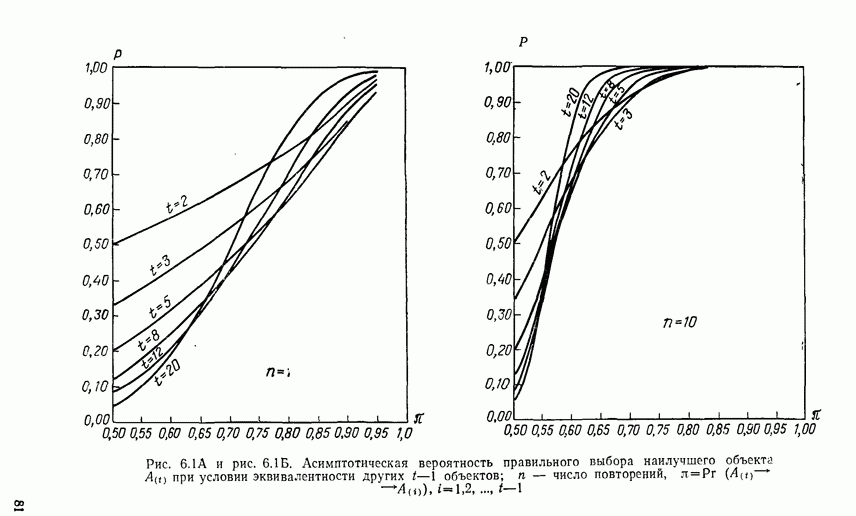
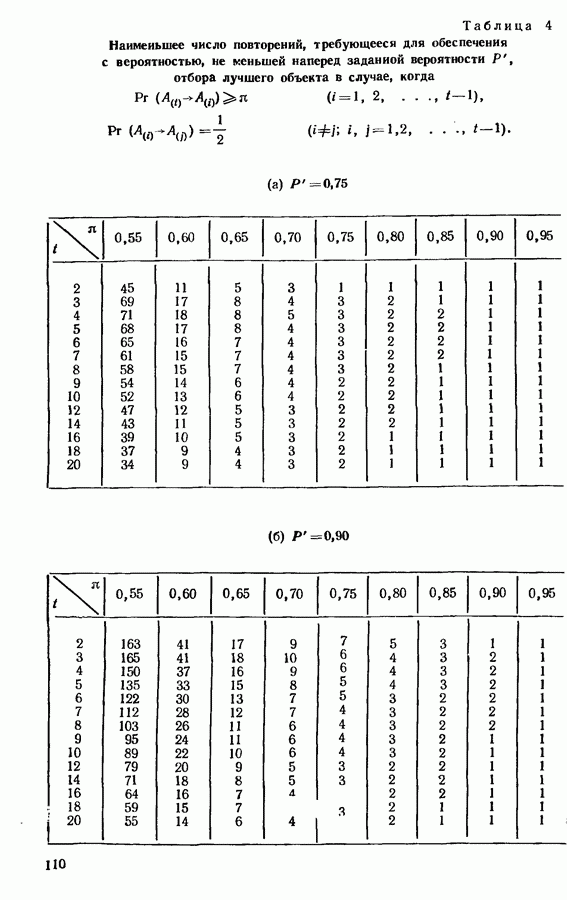
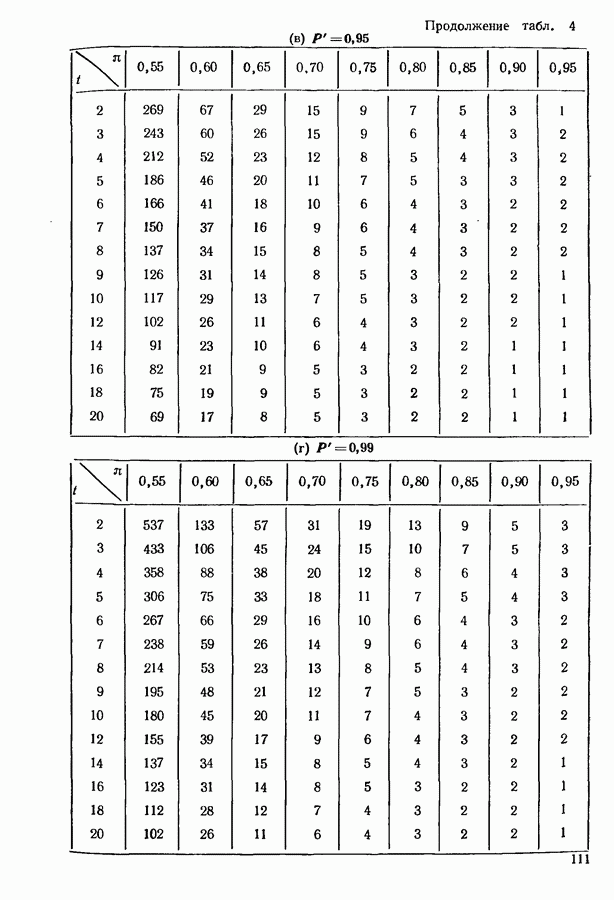
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
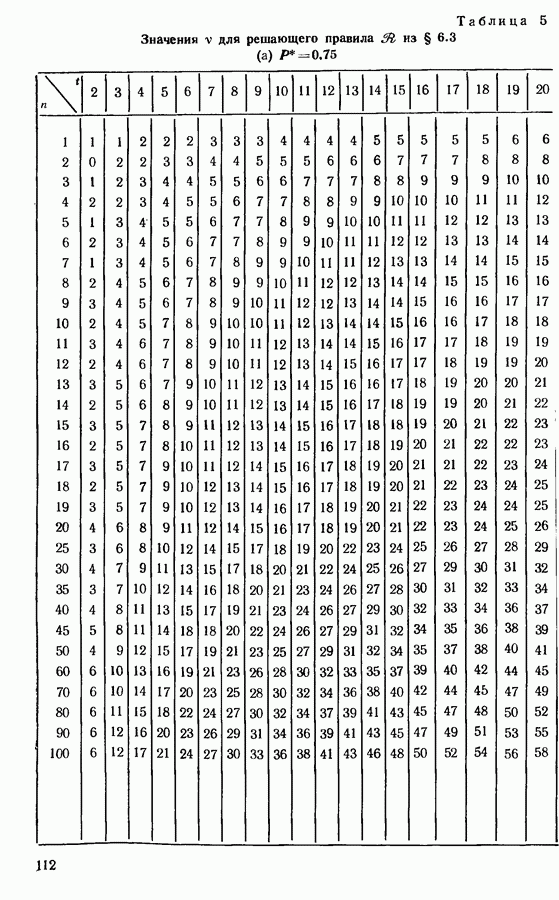
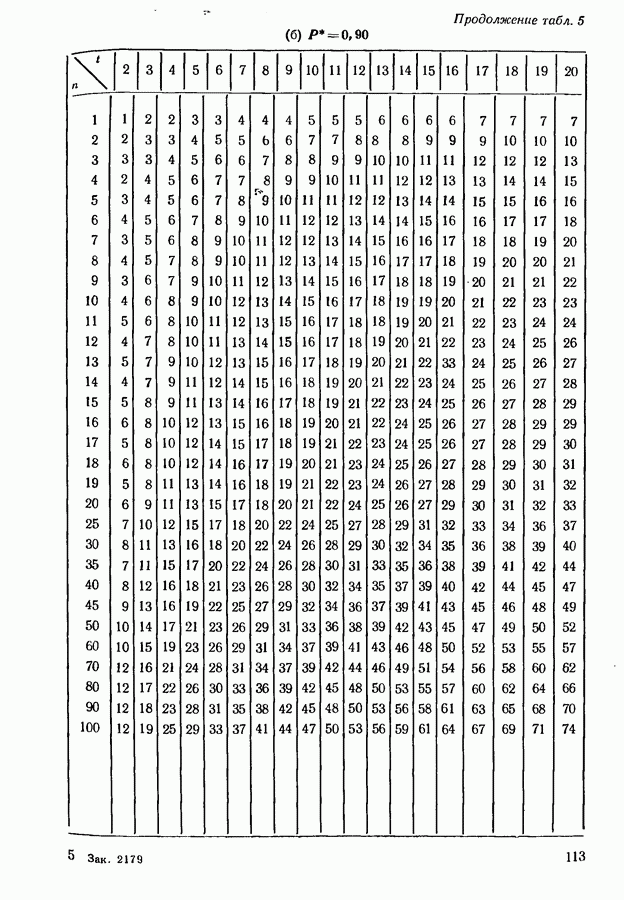
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
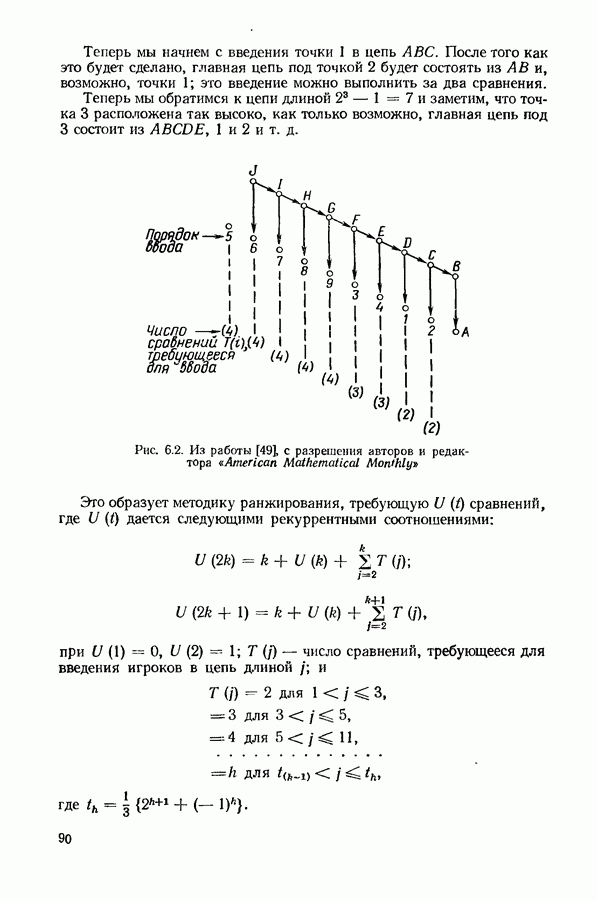
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
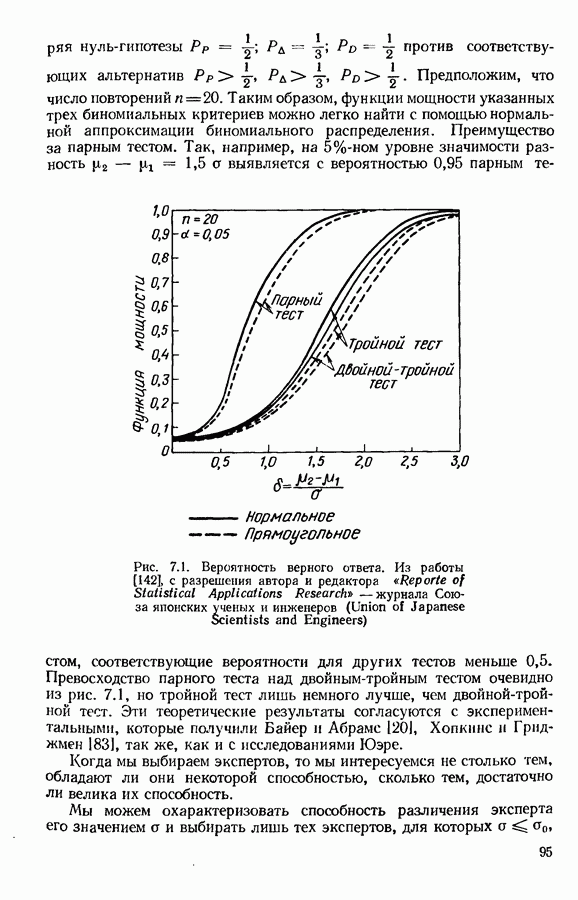
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ