| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
Мы начнем со случая, когда сравниваются попарно три объекта  . В этой простой ситуации проявляются многие существенные черты экспериментов парных сравнений. Если не утверждается обратное. будет предполагаться, что каждое суждение состоит из простого предпочтения того или иного объекта. В частности, «ничьи» не допускаются.
. В этой простой ситуации проявляются многие существенные черты экспериментов парных сравнений. Если не утверждается обратное. будет предполагаться, что каждое суждение состоит из простого предпочтения того или иного объекта. В частности, «ничьи» не допускаются.
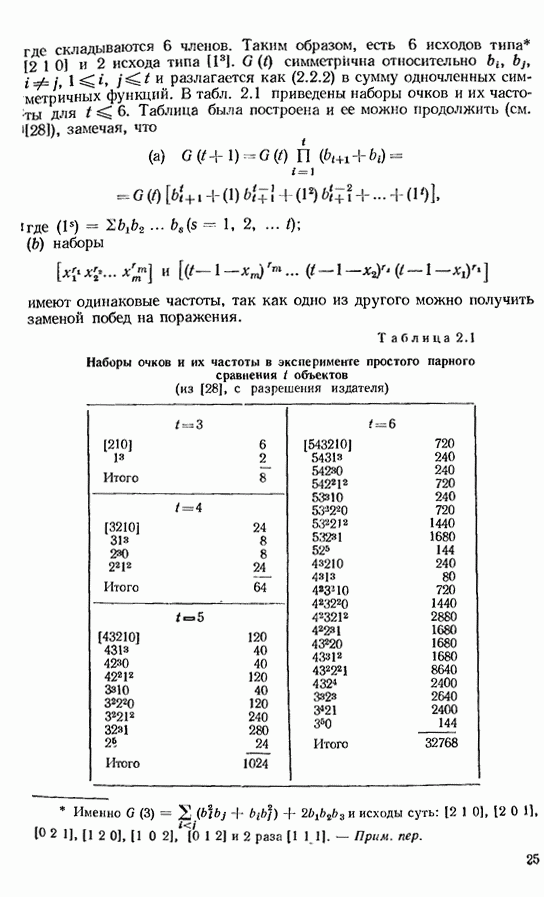
Для каждого из трех сравнений  возможны два исхода, так что есть 8 разных экспериментальных результатов. Из них 6 результатов типа
возможны два исхода, так что есть 8 разных экспериментальных результатов. Из них 6 результатов типа

где стрелка означает «предпочтительнее, чем», удобно представить как тройки чисел [2 1 0], которые указывают, что один объект (не обязательно А) «выигрывает» два раза, другой — один раз, а третий — ни разу. Два оставшихся результата

имеют представление [1 1 1] или  и названы (см. [93]) циклическими триадами.
и названы (см. [93]) циклическими триадами.
Ясно, что циклическая триада означает непоследовательность в суждениях части экспертов и ее простейшее объяснение состоит в том, что эксперт иногда гадает, объявляя свои предпочтения. Он может гадать из-за своей некомпетентности или потому, что на самом деле объекты весьма похожи; вероятность циклической триады равна 1/4, когда объекты идентичны. Но гадание — не единственное объяснение. Приемлемого упорядочения трех объектов может не быть, даже если они заметно различаются Их важность может зависеть более чем от одного показателя, а попытка упорядочить их на линейной шкале может оказаться несколько искусственной При этих с бстоятельствах эксперт должен сконструировать некоторую функцию от соответствующих показателей и пользоваться ею как основанием для сравнения. Неудивитзльно, что при изучении сложных предпочтений эта функция неизвестна, да еще может изменяться от одного парною сравнения к другому, особенно когда различные пары объектов побуждают эксперта концентрировать сьое внимание на различных признаках. Это последнее обстоятельство объясняет те ситуации, где некоторые циклические триады часто встречаются в повторных опытах Аналогичные случаи обычны в турнирах, где в повторных встречах игроков или команд  возможно, что, как правило.
возможно, что, как правило.  но С побеждает
но С побеждает  чаще, чем проигрывает. Фокус с камешком, ножницами и бумагой доставляет крайний пример.
чаще, чем проигрывает. Фокус с камешком, ножницами и бумагой доставляет крайний пример.
Важное свойство метода парных сравнений — возможность проявления таких противоречий, а это путь к некоторым критериям,
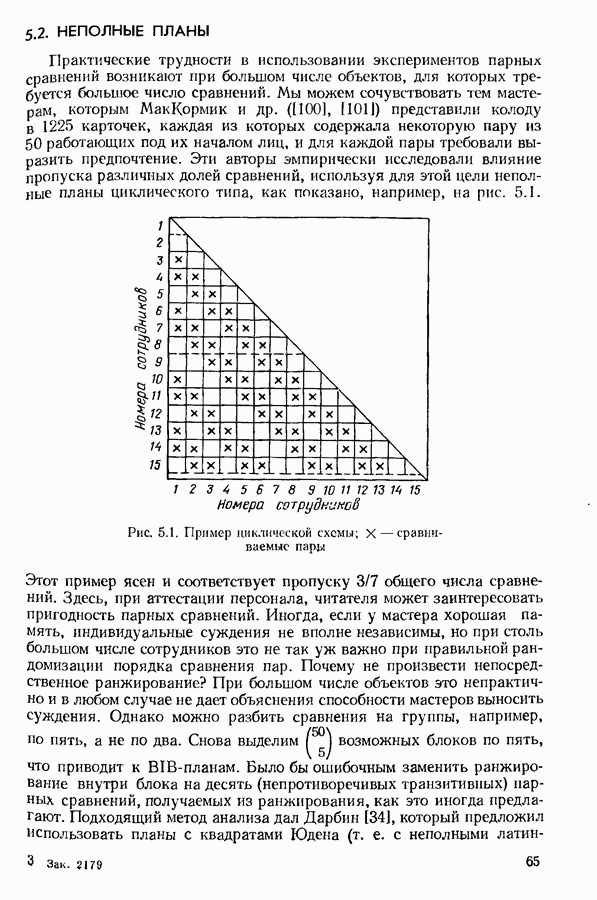
описываемым в следующих двух главах. Стоит принять тюбые доступные меры для обеспечения независимости отдельных парных сравнений или чего-то близкого к ней. Это не так трудно в дегустации,  идентичность изучаемых предметов может быть скрьпа, чему способствует и то, что в эксперименте обычно число сравнений больше трех. С другой стороны, в индивидуальном рейтинге есть реальная опасность, что из-за хорошей памяти эксперта его парные сравнения выродятся в ранжирование, если число сравниваемых людей не очень велико. Частичный выход из этого положения — выполнение одним экспертом только части из всех возможных парных сравнений. Это порождает интересные задачи планирования эксперимента (см. гл. 5). Если в некотором эксперименте не Оыла достигнута приближенная независимость, получается ситуация промежуточная между прямым ранжированием и независимыми парными сравнениями. Тогда приходится вести анализ обоими методами. И только если результаты согласуются, заключение можно сделать с некоторой уверенностью.
идентичность изучаемых предметов может быть скрьпа, чему способствует и то, что в эксперименте обычно число сравнений больше трех. С другой стороны, в индивидуальном рейтинге есть реальная опасность, что из-за хорошей памяти эксперта его парные сравнения выродятся в ранжирование, если число сравниваемых людей не очень велико. Частичный выход из этого положения — выполнение одним экспертом только части из всех возможных парных сравнений. Это порождает интересные задачи планирования эксперимента (см. гл. 5). Если в некотором эксперименте не Оыла достигнута приближенная независимость, получается ситуация промежуточная между прямым ранжированием и независимыми парными сравнениями. Тогда приходится вести анализ обоими методами. И только если результаты согласуются, заключение можно сделать с некоторой уверенностью.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
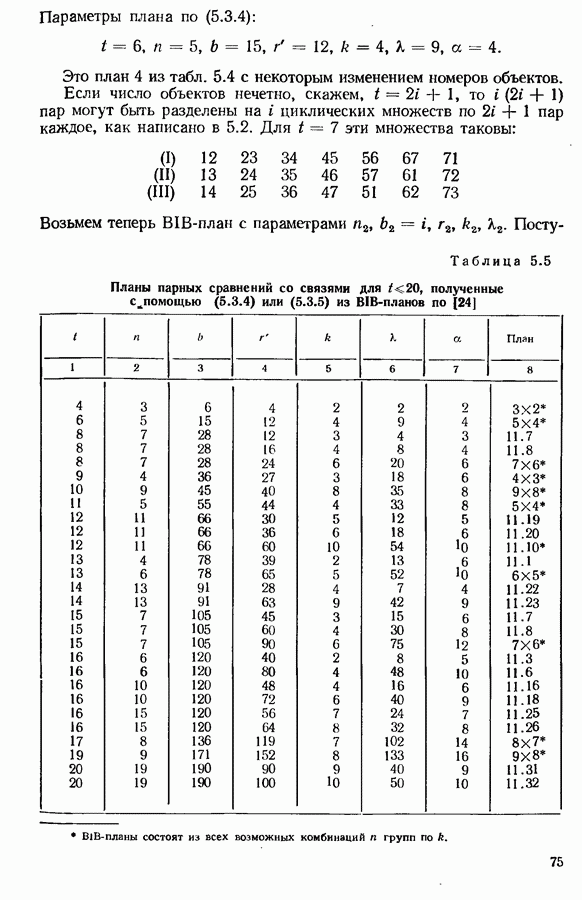
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
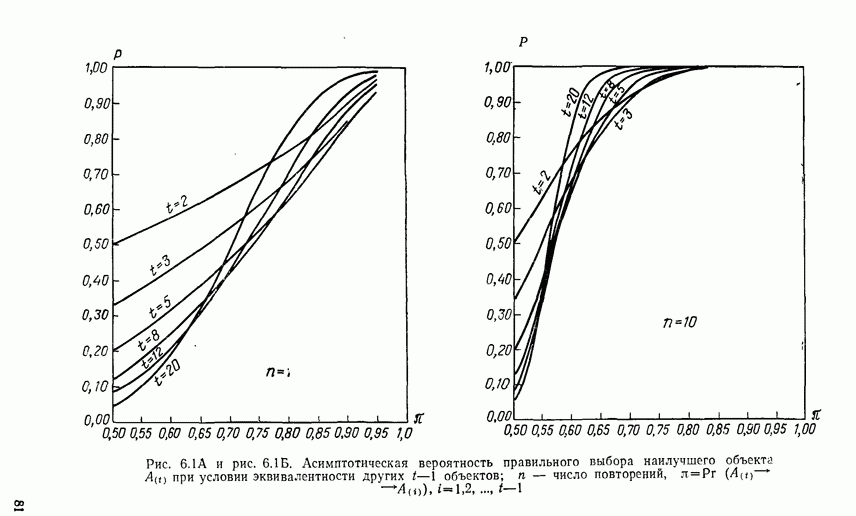
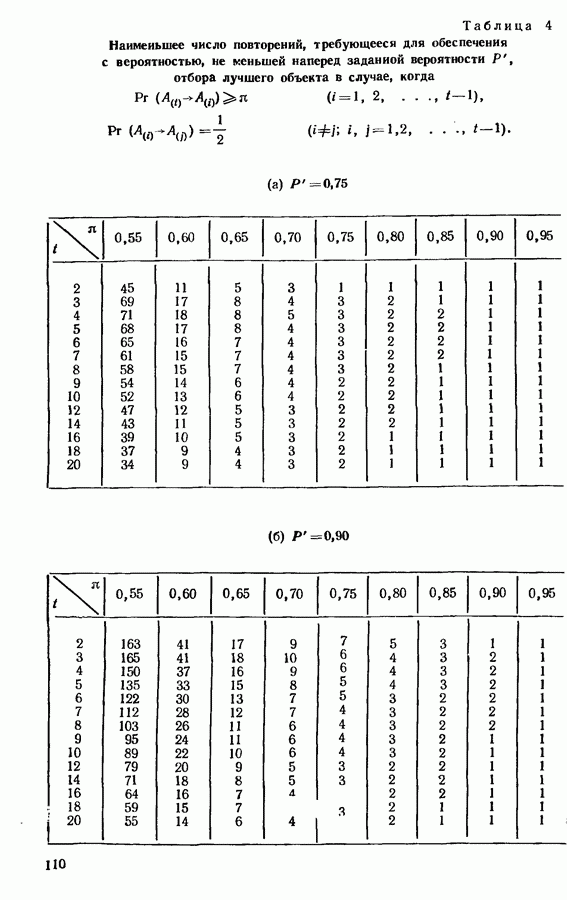
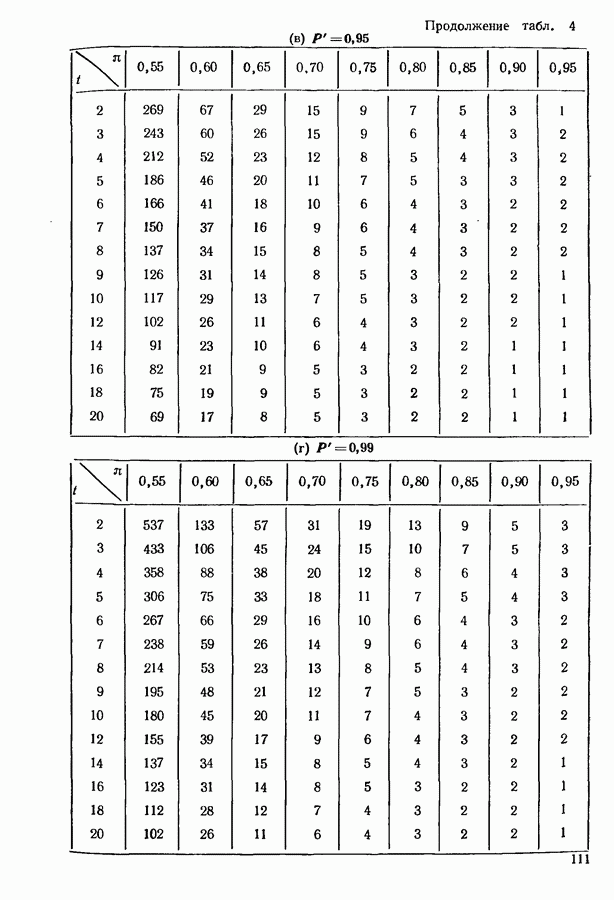
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
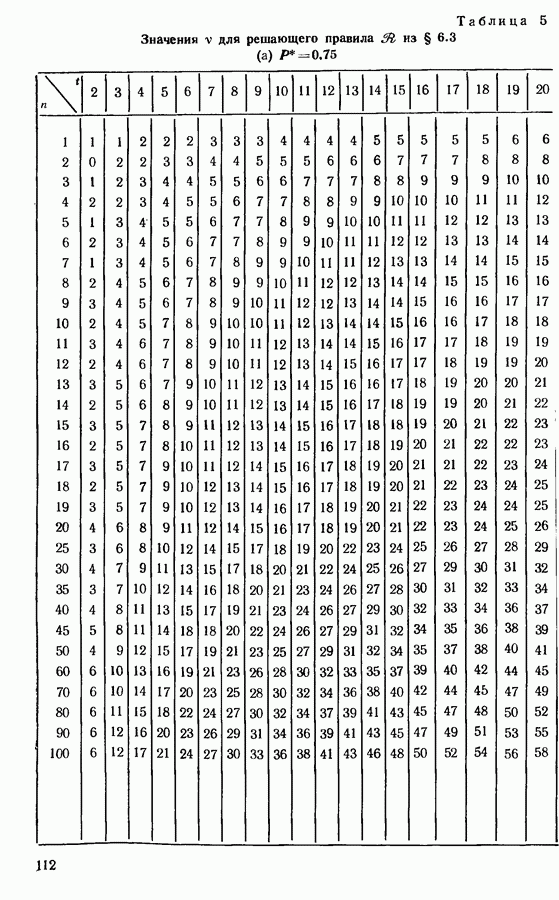
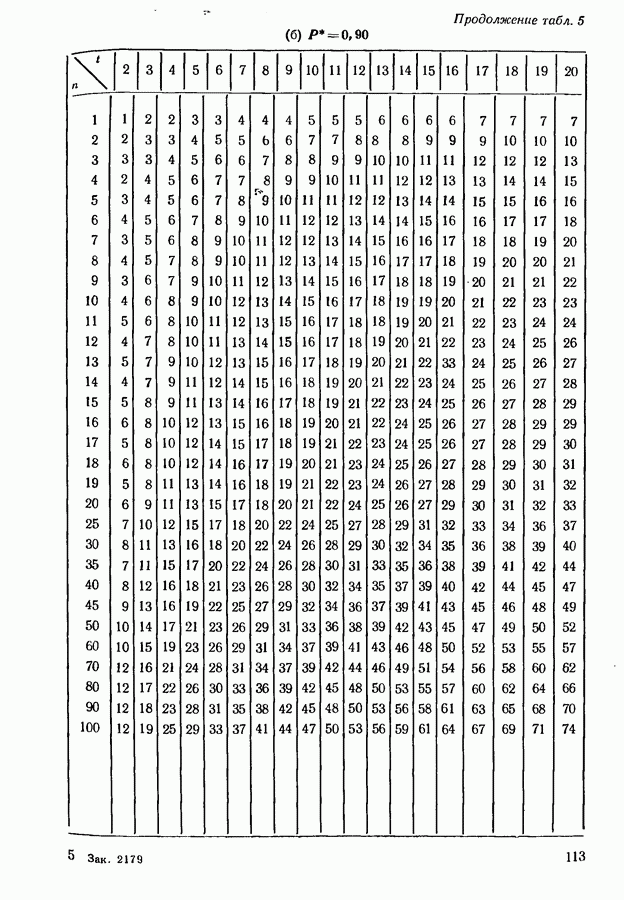
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
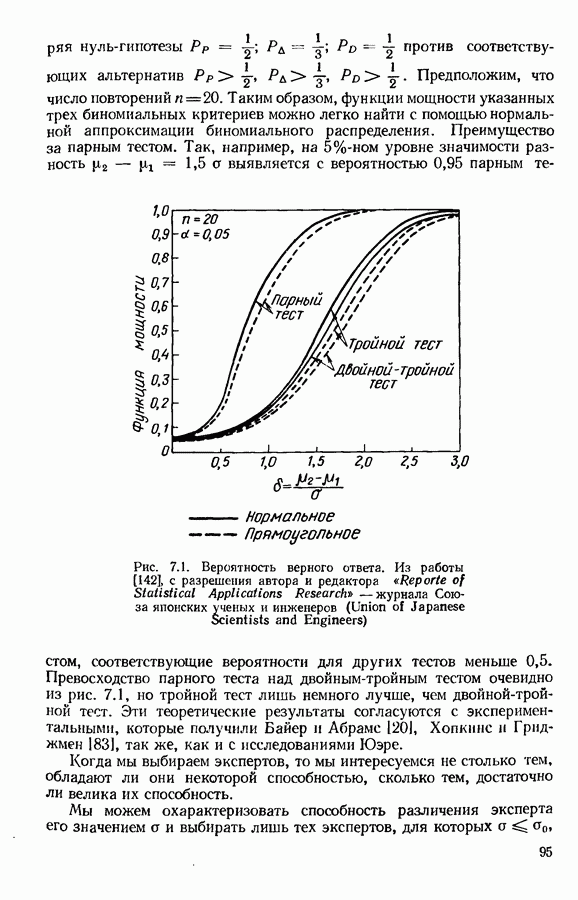
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
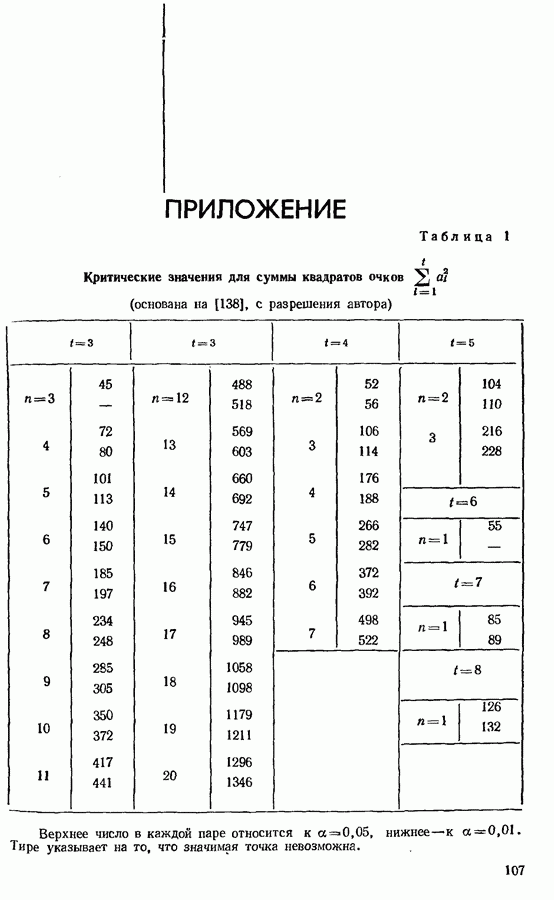
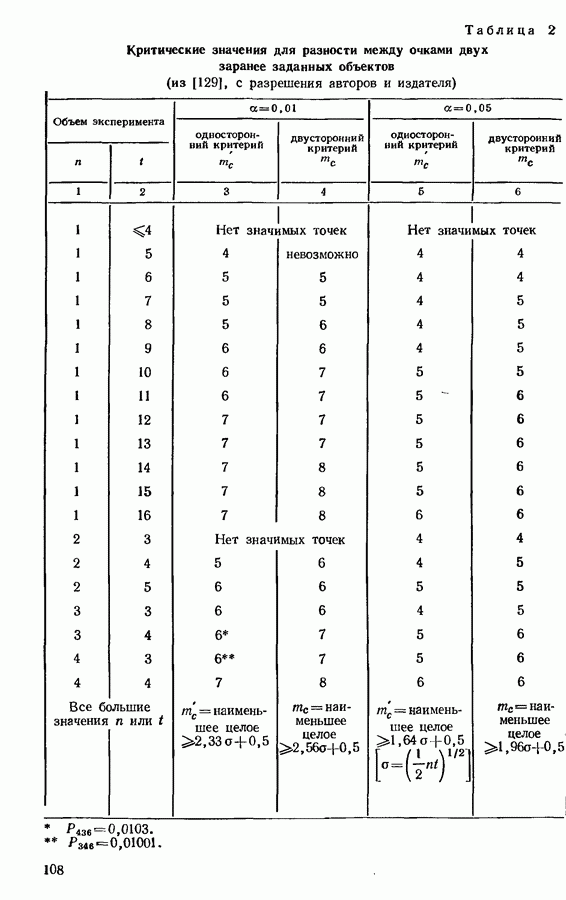
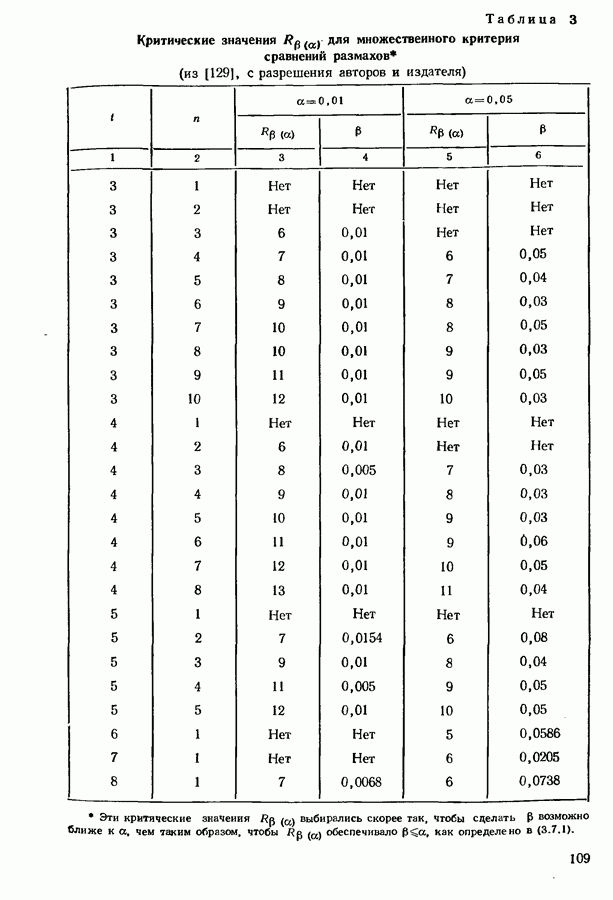
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ