| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
Обсуждавшиеся до сих пор линейные модели не позволяют учитывать возможные различия между экспертами. Бок [111 предложил, чтобы наблюдаемая ценность объекта  в его сравнении с
в его сравнении с  экспертом у была представлена в виде
экспертом у была представлена в виде

где скобки, в которые взято  указывают, что этот нижний индекс служит просто обозначением. Малые буквы обозначают случайные величины,
указывают, что этот нижний индекс служит просто обозначением. Малые буквы обозначают случайные величины,  взаимно независимые
взаимно независимые  величины. Особая черта этой модели заключается в
величины. Особая черта этой модели заключается в  компонентах, которые характеризуют определенные объекты и экспертов, независимо от выборки экспертов. Для одного и того же эксперта они коррелированы,
компонентах, которые характеризуют определенные объекты и экспертов, независимо от выборки экспертов. Для одного и того же эксперта они коррелированы,  имеют двумерное нормальное распределение
имеют двумерное нормальное распределение  Это допущение равносильно
Это допущение равносильно  представлению
представлению  в виде суммы нормально распределенного эффекта от экспертов и нормально распределенного эффекта взаимодействия. «Смешанная» природа модели отражает особый интерес к объектам, но эксперты рассматриваются лишь как выборка из бесконечной совокупности экспертов. Если мы положим
в виде суммы нормально распределенного эффекта от экспертов и нормально распределенного эффекта взаимодействия. «Смешанная» природа модели отражает особый интерес к объектам, но эксперты рассматриваются лишь как выборка из бесконечной совокупности экспертов. Если мы положим  то заметим, что оно нормально распределено с математическим ожиданием
то заметим, что оно нормально распределено с математическим ожиданием  и дисперсией
и дисперсией  откуда следует, что модель линейна. Полагая дисперсию равной единице, мы получаем
откуда следует, что модель линейна. Полагая дисперсию равной единице, мы получаем

где  функция распределения единичной нормальной переменной, как в модели Тэрстоуна-Мостеллера. Может показаться, что это одна и та же модель, если сделана стандартизация. Однако в данном случае сравнения различны для общего объекта и выполняются не независимо для одного и того же эксперта с ковариацией
функция распределения единичной нормальной переменной, как в модели Тэрстоуна-Мостеллера. Может показаться, что это одна и та же модель, если сделана стандартизация. Однако в данном случае сравнения различны для общего объекта и выполняются не независимо для одного и того же эксперта с ковариацией

В терминах характеристических случайных переменных  из § 1.3 мы имеем, например,
из § 1.3 мы имеем, например,

и

Поскольку  то
то

и

Исходя из соображений, рассмотренных в 4.2, Бок применил тригонометрическое преобразование (4.2.1) к  Хотя это преобразование приближенно стабилизирует дисперсию для больших
Хотя это преобразование приближенно стабилизирует дисперсию для больших  оно, как все такие преобразования, оставляет корреляцию неизменной. Она равна:
оно, как все такие преобразования, оставляет корреляцию неизменной. Она равна:

Для того чтобы получить решение, с которым можно работать в трехкомпонентной модели, Бок предположил, что эта корреляция  скажем) одна и та же для всех
скажем) одна и та же для всех  допущение, которое, как мы
допущение, которое, как мы
говорили, не будет хорошим в общем случае, но в случае, когда все близки к 1/2, приемлемо. Это так близко к нулевой гипотезе, что даже для больших  требуется чувствительный критерий.
требуется чувствительный критерий.
Подчиняясь различным введенным приближениям, мы выразим  в виде
в виде

где  ценность объекта
ценность объекта  на преобразованной шкале,
на преобразованной шкале,  Удобно положить
Удобно положить  Тогда случайная ошибка
Тогда случайная ошибка  имеет следующие свойства:
имеет следующие свойства:

и для  не равных между собой
не равных между собой

Если

то сумма квадратов между строками матрицы  есть
есть

и равна сумме квадратов между столбцами  Из (4.6.2) мы имеем
Из (4.6.2) мы имеем

так что с учетом (4.6.3) и (4.6.4)

Аналогично остаточная сумма квадратов

имеет математическое ожидание

Эти результаты могут быть сведены в таблицу дисперсионного анализа.
(см. скан)
За исключением приближения нормального распределения угловым, критерий согласия Мостеллера эквивалентен приближению  распределением
распределением  степенями свободы.
степенями свободы.
Но для  мы видим, что имеет малое математическое ожидание. Модель Бока, таким образом, может использоваться для учета отклонений критерия Мостеллера.
мы видим, что имеет малое математическое ожидание. Модель Бока, таким образом, может использоваться для учета отклонений критерия Мостеллера.
Также можно заметить из таблицы, что при проверке эквивалентности объектов, пользуясь  как
как  -распределенной случайной величиной с
-распределенной случайной величиной с  степенями свободы, мы можем отвергать гипотезу так же легко и при
степенями свободы, мы можем отвергать гипотезу так же легко и при 
Замечания
Наше рассмотрение важной модели Тэрстоуна-Мостеллера и других «случаев» (см. упражнение 1.5) отличается от того, которое было проведено Тэрстоуном [132] и вкратце обобщено Джонсом и Боком  и Торгерсоном [137]. Более специальные ссылки, видимо, можно извлечь из обсуждения случая неполных данных у Галликсена [63] и в работах Мостеллера [108b], Гибсона [52], Берроса и Гибсона [19].
и Торгерсоном [137]. Более специальные ссылки, видимо, можно извлечь из обсуждения случая неполных данных у Галликсена [63] и в работах Мостеллера [108b], Гибсона [52], Берроса и Гибсона [19].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
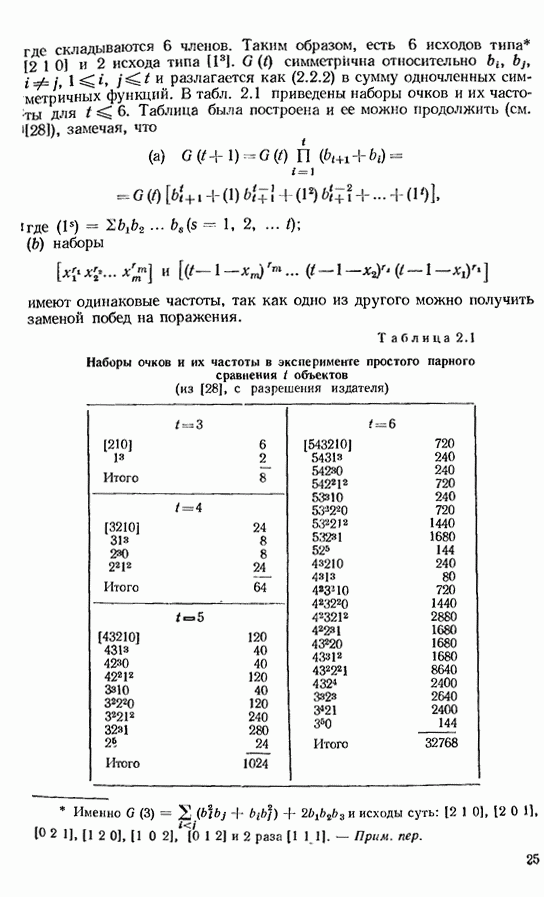
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
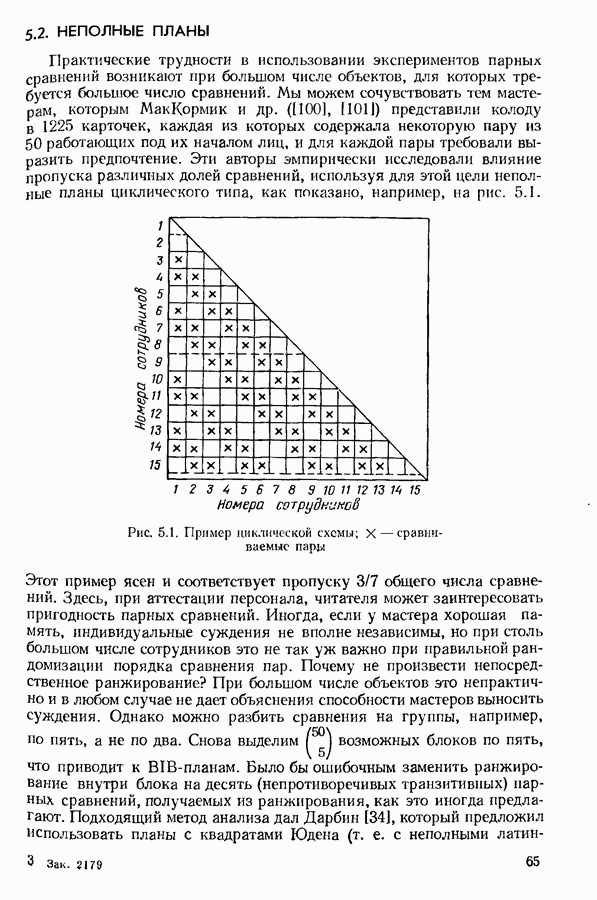
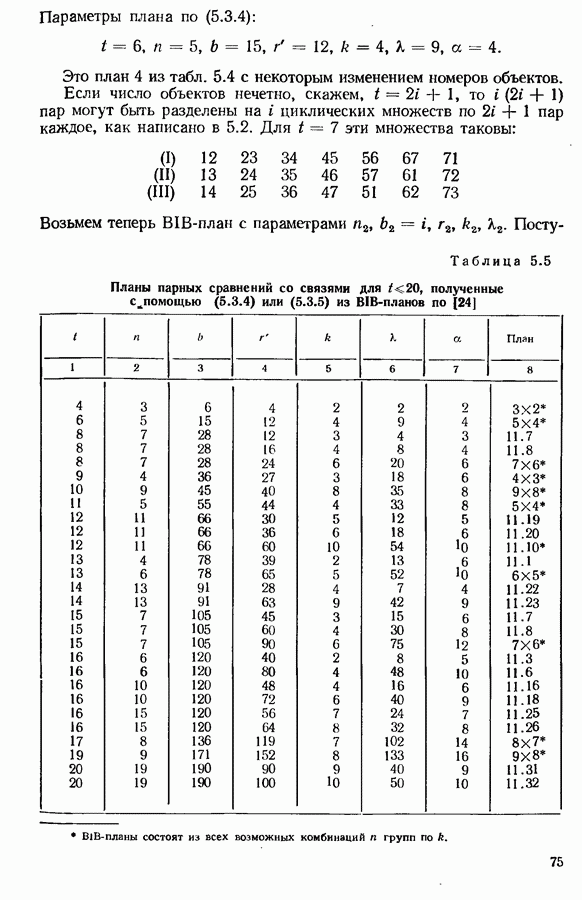
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
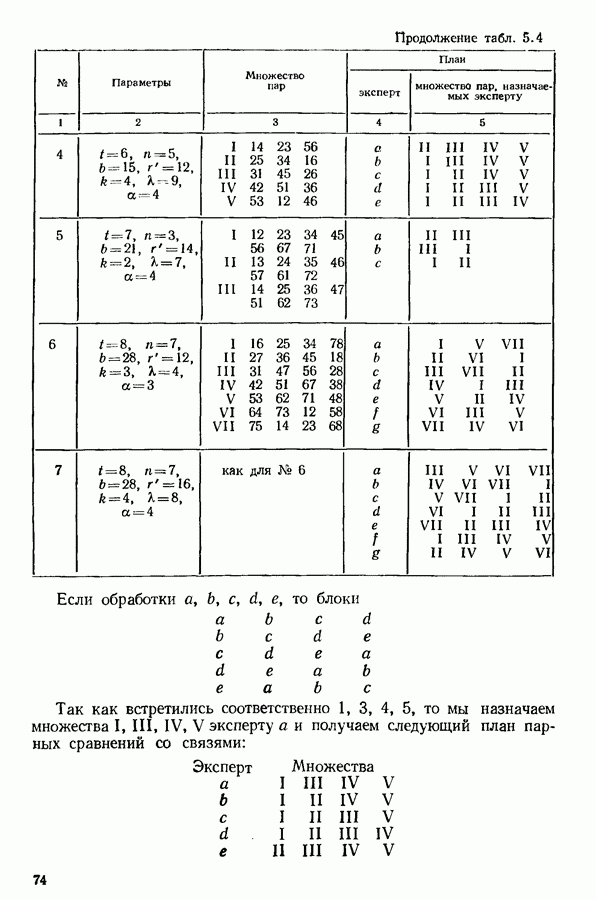
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
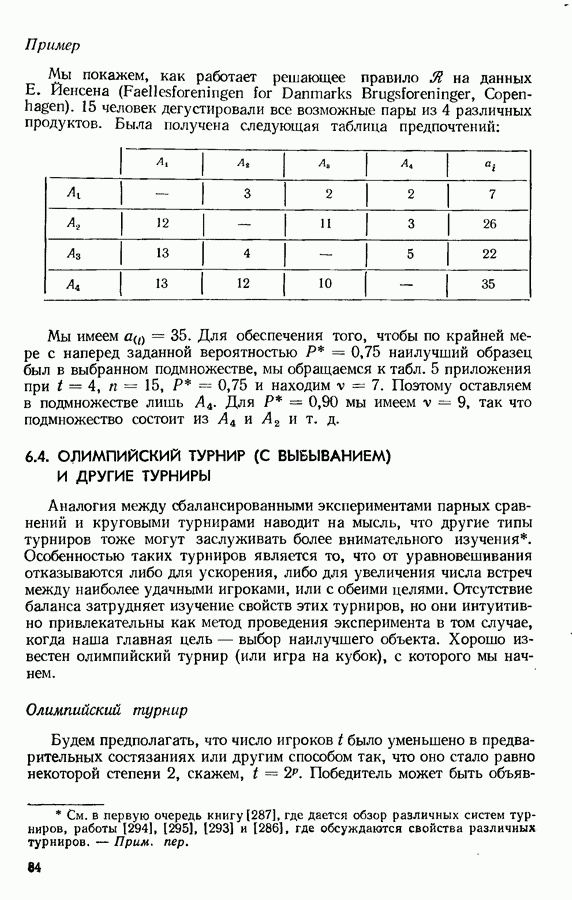
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
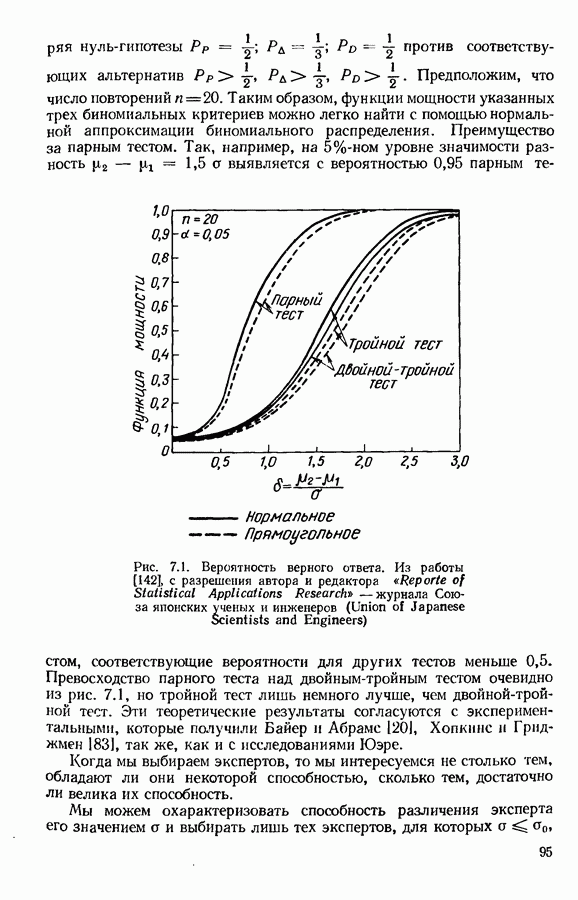
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ