| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
2.1. Введение
Предположим, что эксперт выполнил все  парных сравнений. Совпадения не допускаются, так что результаты можно представить в виде таблицы предпочтений с двумя входами, составленной из единиц и нулей и известной как турнирная таблица. Для
парных сравнений. Совпадения не допускаются, так что результаты можно представить в виде таблицы предпочтений с двумя входами, составленной из единиц и нулей и известной как турнирная таблица. Для  обычный исход эксперимента может быть следующим:
обычный исход эксперимента может быть следующим:
(см. скан)
Главная диагональ слева направо свободна и входы (места) ниже, строго говоря, избыточны. Видно, что  предпочтительнее, чем
предпочтительнее, чем  но не чем
но не чем  и набрал 3 очка. В общем, число предпочтений, отданных
и набрал 3 очка. В общем, число предпочтений, отданных  обозначим
обозначим  Понятно, что
Понятно, что

и возможно всего 2 различных таблиц предпочтении.
Альтернативное геометрическое представление, принадлежащее, как и большая часть этого параграфа, Кендэлу и Бэбингтону Смиту [93],
иногда более наглядно. Для приведенного выше примера, который иллюстрирует общий случай, картинка имеет форму правильного пятиугольника, со всеми его связями (рис. 2.1). Направление стрелок указывает 10 предпочтений, так что  число стрелок, выходящих из вершины
число стрелок, выходящих из вершины 
Быть может, первые вопросы, на которые дает ответ таблица предпочтений или многоугольник предпочтений, это  Последователен ли эксперт в своих суждениях? 2) Есть ли значимые различия между объектами?
Последователен ли эксперт в своих суждениях? 2) Есть ли значимые различия между объектами?

Рис. 2.1. Многоугольник предпочтений
Важно понимать, что эти вопросы тесно связаны; если нет различия между объектами, неразумно ожидать от эксперта состоятельности, и, наоборот, ему легко быть состоятельным, если различия велики. Мы будем обращаться к нулевой гипотезе, согласно 1 которой суждения выносятся случайно  Для всех
Для всех 
Ее разумно называть «гипотезой случайности».
Для группы из трех объектов результат непоследовательного (несостоятельного) эксперта есть циклическая триада; для большой группы множество суждений можно считать тем более последовательным, чем меньше циклических триад оно содержит. Видно, что из 10 триад нашего примера  циклические триады. Ясно, что прямое перечисление неудобно, если
циклические триады. Ясно, что прямое перечисление неудобно, если  не очень мало. Однако число циклов с связано с числом очков соотношением:
не очень мало. Однако число циклов с связано с числом очков соотношением:

Для доказательства этого мы покажем сначала, что если изменить направление некоторого предпочтения (на противоположное) и число циклов возрастет на  то
то  уменьшится на
уменьшится на  и наоборот. Рассмотрим множество предпочтений, включающих
и наоборот. Рассмотрим множество предпочтений, включающих  Если X — объект, отличный от
Если X — объект, отличный от  должно быть
должно быть  предпочтений типа
предпочтений типа  типа
типа  Только в триадах, содержащих
Только в триадах, содержащих 
произошла смена  на
на  Имеется четыре типа таких триад:
Имеется четыре типа таких триад:

Когда предпочтение  меняет направление, первые две триады остаются нециклическими. Триада третьего типа становится циклической, триада четвертого типа перестает быть таковой. Прирост числа циклических триад
меняет направление, первые две триады остаются нециклическими. Триада третьего типа становится циклической, триада четвертого типа перестает быть таковой. Прирост числа циклических триад

Так как

соответствующее уменьшение  есть
есть

Более общо: если в результате инверсии некоторого числа предпочтений с увеличивается на  то
то  должно уменьшиться на
должно уменьшиться на  при инверсии предпочтений влияние на
при инверсии предпочтений влияние на  накапливается одновременно. Поэтому ясно, что
накапливается одновременно. Поэтому ясно, что

 константа, зависящая только от
константа, зависящая только от 
Для определения  заметим, что при
заметим, что при  возникает полная согласованность. В этом случае
возникает полная согласованность. В этом случае  просто перестановка
просто перестановка  дает
дает

откуда 

Это доказывает 
Кендэл и Бэбингтон Смит определили коэффициент совместимости как

Если и только если  не существует несовместимостей в конфигурации предпочтений, которая, следовательно, немедленно порождает ранжировку. По мере того как
не существует несовместимостей в конфигурации предпочтений, которая, следовательно, немедленно порождает ранжировку. По мере того как  уменьшается до нуля, несовместимость, измеряемая числом циклических триад, возрастает (см. упр. 2.1).
уменьшается до нуля, несовместимость, измеряемая числом циклических триад, возрастает (см. упр. 2.1).
Поскольку  есть линейная функция от обе они, по существу, эквивалентны. Хотя
есть линейная функция от обе они, по существу, эквивалентны. Хотя  не дает непосредственной меры совместимости в суждениях экспертов, представляется, что можно легко обобщить результаты на ситуации, где каждое парное сравнение повторяется
не дает непосредственной меры совместимости в суждениях экспертов, представляется, что можно легко обобщить результаты на ситуации, где каждое парное сравнение повторяется  раз. Таким образом, если
раз. Таким образом, если  теперь обозначает число очков
теперь обозначает число очков  объекта для эксперимента с повторениями, мы можем просто определить
объекта для эксперимента с повторениями, мы можем просто определить  как общую сумму квадратов очков:
как общую сумму квадратов очков:

так что  В основном по этой причине мы будем использовать далее
В основном по этой причине мы будем использовать далее  -статистику. Большие значения приведут нас к отклонению нулевой гипотезы о случайности
-статистику. Большие значения приведут нас к отклонению нулевой гипотезы о случайности  Для проверки значимости мы покажем в § 2.3, что для удобства стандартизированное
Для проверки значимости мы покажем в § 2.3, что для удобства стандартизированное  распределено при
распределено при  приближенно как
приближенно как  степенями свободы.
степенями свободы.
Циклические триады представляют собой весьма фундаментальный тип непоследовательности во мнениях экспертов. Нет необходимости рассматривать отдельно циклы, включающие больше чем три объекта, поскольку их можно разбить на циклические триады. Однако если
существует предварительное (априорное) упорядочение объектов по отношению к заданному параметру (например, интенсивности серого цвета в примере Кумбса, § 1.3), может возникнуть другой тип несовместимости во мнениях экспертов. В ситуации, иллюстрируемой ниже, результаты  несовместимы (хотя они не допускают возникновения циклической триады); для
несовместимы (хотя они не допускают возникновения циклической триады); для  предполагается, что идеал
предполагается, что идеал  находится слева от
находится слева от  а для
а для  предполагается, что
предполагается, что  находится справа от
находится справа от  Джерард и Шапиро
Джерард и Шапиро

[51] назвали этот тип несовместимости в суждениях сепарацией. Они показали, что число сепарации  в попарном сравнении
в попарном сравнении  объектов может быть получено из таблицы предпочтений с помощью формулы
объектов может быть получено из таблицы предпочтений с помощью формулы

где  суммы по
суммы по  столбцу и
столбцу и  строке элементов выше главной диагонали.
строке элементов выше главной диагонали.
Таким образом, в примере, помещенном в начале этого раздела,  Доказательство (2.1.4) следует немедленно с учетом того, что
Доказательство (2.1.4) следует немедленно с учетом того, что  и
и  это числа случаев предпочтения объектов, лежащих соответственно слева и справа от
это числа случаев предпочтения объектов, лежащих соответственно слева и справа от  объекту
объекту 
Коэффициент согласия
До сих пор мы рассматривали случай, когда работал один эксперт. Если же работают  экспертов и каждый из них выполняет (2) сравнений, результаты также можно представить в виде таблицы (матрицы) предпочтений с элементами
экспертов и каждый из них выполняет (2) сравнений, результаты также можно представить в виде таблицы (матрицы) предпочтений с элементами  равными числу случаев, когда
равными числу случаев, когда  предпочтительнее, чем
предпочтительнее, чем  Тогда
Тогда  Если мнения экспертов полностью совпадают, одна половина
Если мнения экспертов полностью совпадают, одна половина  равна
равна  а другая — нулю. Заметим, что согласие экспертов может быть полным, даже если в их суждениях есть несовместимости; наоборот, отсутствие согласия не влечет за собой несовместимости. Пусть
а другая — нулю. Заметим, что согласие экспертов может быть полным, даже если в их суждениях есть несовместимости; наоборот, отсутствие согласия не влечет за собой несовместимости. Пусть

где суммирование ведется по  членам.
членам.  — это сумма числа случаев совпадения мнений между парами экспертов. Кендэл и Бэбингтон Смит определили коэффициент согласия и как
— это сумма числа случаев совпадения мнений между парами экспертов. Кендэл и Бэбингтон Смит определили коэффициент согласия и как

Если существует полная согласованность экспертов, и только в этом случае,  Чем дальше мы отклоняемся от этого случая, что измеряется числом совпадений между парами экспертов, тем меньше становится и. Минимальное число совпадений будет тогда, когда каждое
Чем дальше мы отклоняемся от этого случая, что измеряется числом совпадений между парами экспертов, тем меньше становится и. Минимальное число совпадений будет тогда, когда каждое  равно
равно  , при
, при  четном, или
четном, или  при
при  нечетном.
нечетном.
Соответственно  будет равно
будет равно  или
или  По-другому 2 можно выразить так:
По-другому 2 можно выразить так:

причем последняя форма записи удобней для вычислений, если объекты упорядочены по возрастанию числа очков, так что  будут в большинстве своем относительно невелики.
будут в большинстве своем относительно невелики.
Проверка значимости и возможна при нуль-гипотезе о том, что предпочтения всех экспертов случайны. Это можно сделать [90] с помощью таблиц распределения 2 для комбинаций  при малых
при малых  а когда они велики, можно полагать, что
а когда они велики, можно полагать, что

распределено приближенно как  с числом степеней свободы, равным
с числом степеней свободы, равным

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
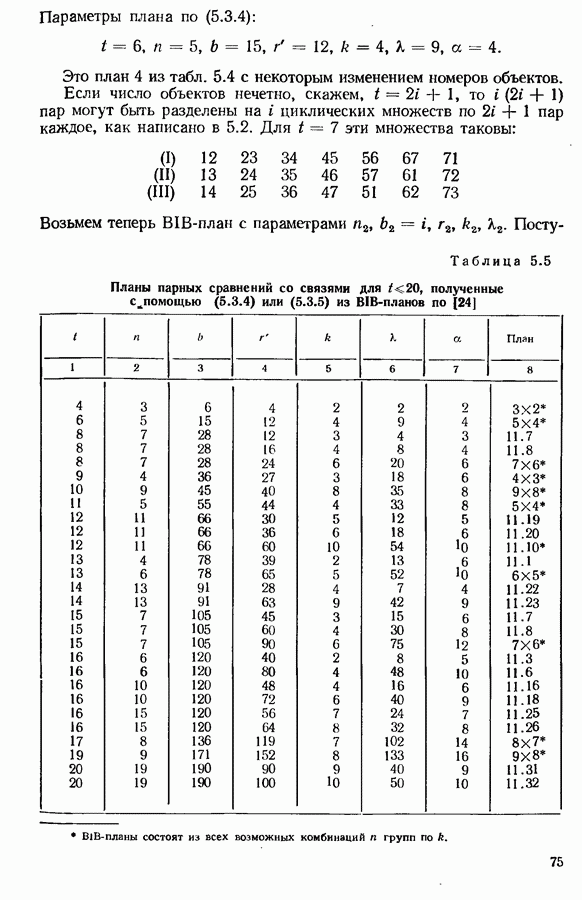
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
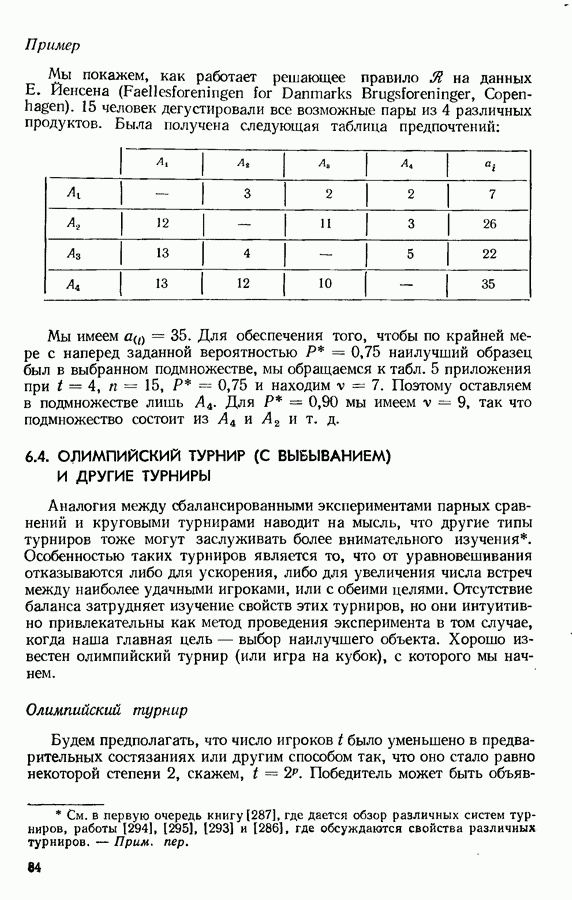
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ