3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)

После проведения эксперимента парных сравнений часто хочется знать, является ли объект с наибольшим значением существенно лучшим, чем средний. Назовем этот объект и соответствующую среднюю вероятность предпочтения — Тогда нужная нулевая гипотеза

должна проверяться против альтернативы

Рассмотрение распределения наибольшего значения в § 2.3 приводит к следующей процедуре проверки:

1) выбираем желаемый уровень значимости а;

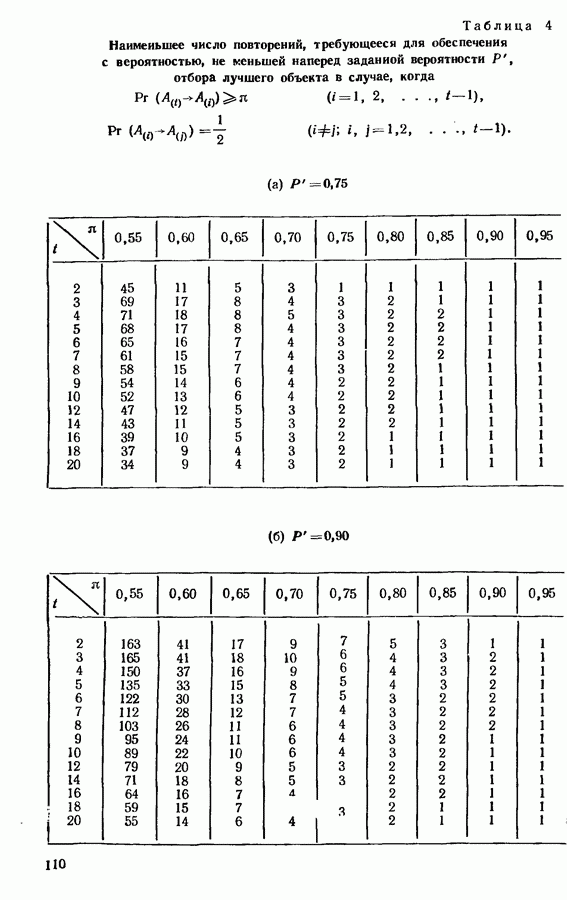
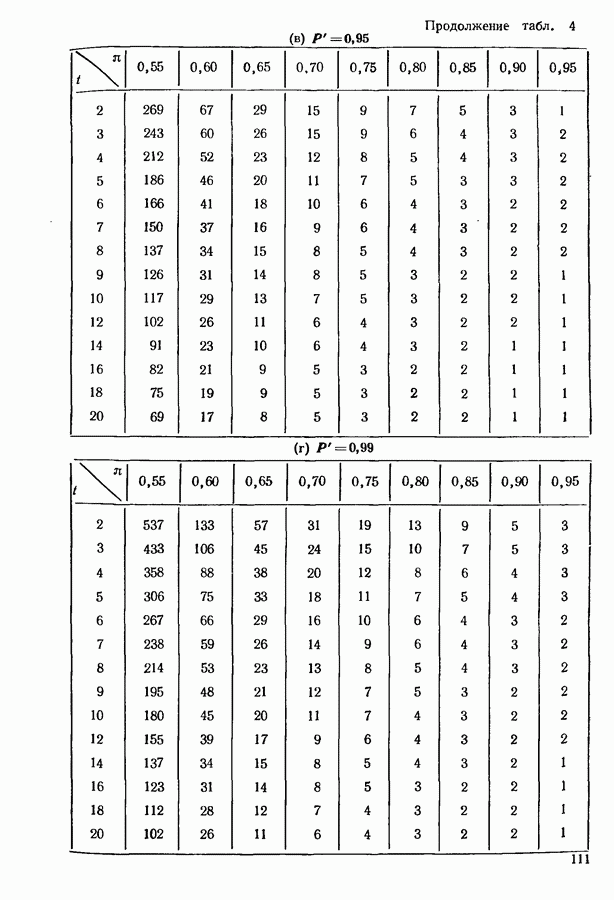
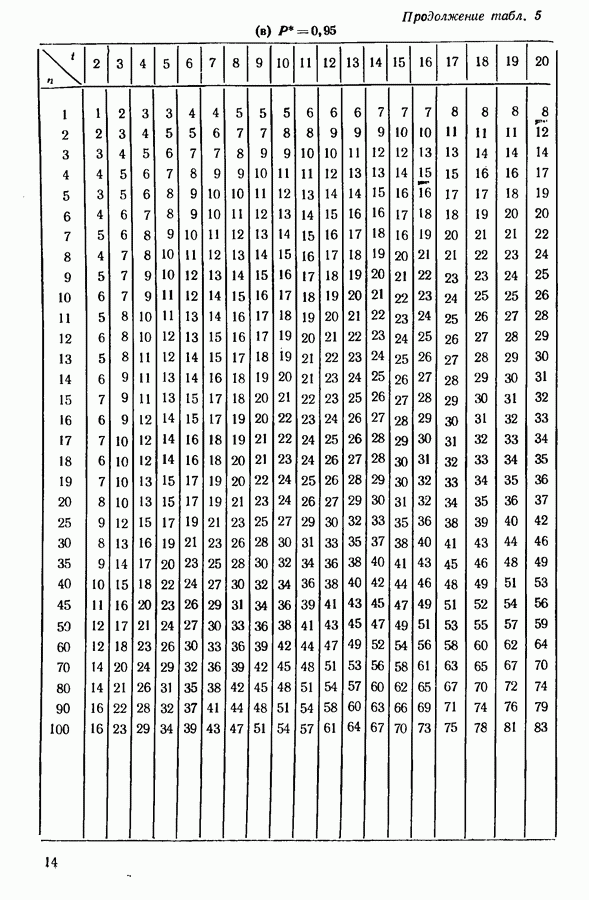
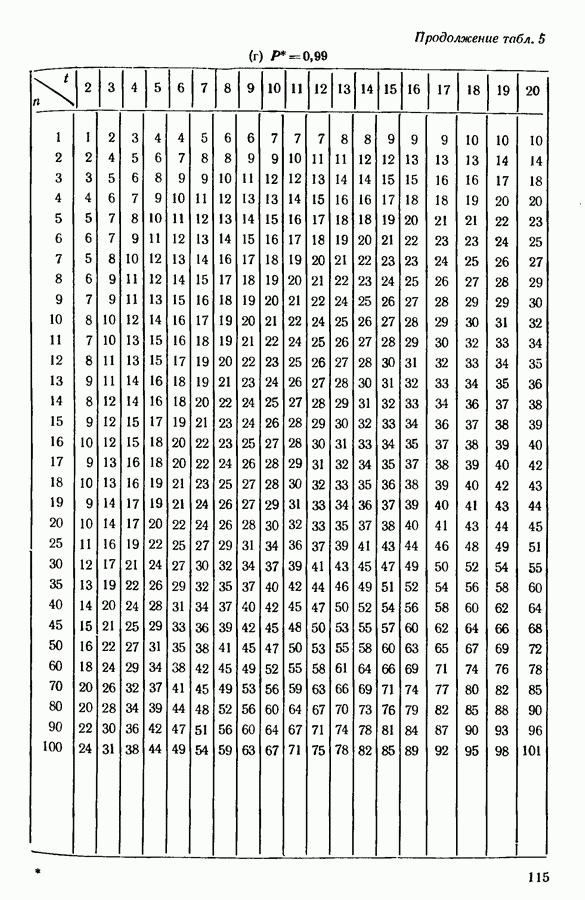
2) находим в таблице кумулятивной функции биномиального распределения целое число такое, что

3) если наибольшее значение в эксперименте равно или больше принимаем гипотезу о том, что соответствующий объект лучше, чем средний.

С очевидными модификациями процедуру можно использовать для проверки гипотезы о том, будет ли объект с наименьшим значением хуже среднего.

Ясно, что критерии, рассматриваемые в данном параграфе, по существу, отличаются от предшествующих критериев тем, что нет априорного выделения каких-либо особых объектов. Следует также отметить, что частная нуль-гипотеза Н в данном случае фактически эквивалентна гипотезе случайности если исходная вероятностная модель линейна. Однако без такой линейности может быть равно 1/2 и без равенства между собой.