| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
Может привести в замешательство число способов обработки равных рангов. Мы можем предупредить их грубым вмешательством, требуя, чтобы эксперт мысленно бросал монету, если он не может принять решение, или позволяя ему для удобства суждения в действительности бросать монету. Эти два приема имеют то преимущество, что полученные с их помощью данные можно изучать методами предыдущих глав. Это не совсем верно, если для каждой пары очки просто делятся поровну. Тем не менее этот метод имеет преимущество независимости от более или менее произвольных способов преодоления дележа мест; в частности, физическая рандомизация ведет к различным выводам при одних и тех же экспериментальных данных. Другой возможностью является теоретическая рандомизация. Рассмотрим, например, коэффициент согласия и формулу (2.1.5) ([90], 

Если в результате  сравнений
сравнений  появляется а «ничьих», деление поровну приводит к замене
появляется а «ничьих», деление поровну приводит к замене  на
на  на
на  а, где
а, где  число ясных предпочтений объекта. Теоретическая рандомизация достигается заменой членов
число ясных предпочтений объекта. Теоретическая рандомизация достигается заменой членов  в (7.3.1) на
в (7.3.1) на

это получается из-за случайного нарушения а ничьих, что может дать прирост, и взвешивания с учетом соответствующих вероятностей неходов. Выражение (7.3.2), как можно показать, больше

значения при равном делении ничьих по  Соответственно при теоретической рандомизации легко вычислить и.
Соответственно при теоретической рандомизации легко вычислить и.
При сравнении этих и других процедур обработки ничьих полезно делать различие между проверкой гипотез и оцениванием. Для  когда метод парных сравнений приводит к критерию знаков, показано, что игнорирование ничьих ведет в общем к более мощным критериям, чем их равное или случайное деление ([79], [118]). Этот интересный результат относится к анализу данных, содержащих ничьи; связанный с этим вопрос: можно ли разрешать ничьи? — должен быть решен в первую очередь. Кажется разумной стратегией инструктировать экспертов так, чтобы они выражали предпочтение лишь тогда, когда они вполне уверены. Экспериментальные результаты ухудшаются угадыванием. Однако на практике ситуация не вполне ясна, так как разрешение ничьих делает экспертов более небрежными [60].
когда метод парных сравнений приводит к критерию знаков, показано, что игнорирование ничьих ведет в общем к более мощным критериям, чем их равное или случайное деление ([79], [118]). Этот интересный результат относится к анализу данных, содержащих ничьи; связанный с этим вопрос: можно ли разрешать ничьи? — должен быть решен в первую очередь. Кажется разумной стратегией инструктировать экспертов так, чтобы они выражали предпочтение лишь тогда, когда они вполне уверены. Экспериментальные результаты ухудшаются угадыванием. Однако на практике ситуация не вполне ясна, так как разрешение ничьих делает экспертов более небрежными [60].
Возвращаясь к оцениванию, мы ясно видим, что ничьими в экспериментальных данных не следует пренебрегать: при одном и том же числе ясных предпочтений два объекта  ближе друг к другу по ценности при большем количестве ничьих между ними. Четкие предпочтения в пользу
ближе друг к другу по ценности при большем количестве ничьих между ними. Четкие предпочтения в пользу  можно аргументировать тем, что
можно аргументировать тем, что  вероятно, «выше ничьих». Это относится ко всем упомянутым выше «беспристрастным» методам, но может быть достигнуто и с помощью следующей модели [56]. Как обычно, пусть
вероятно, «выше ничьих». Это относится ко всем упомянутым выше «беспристрастным» методам, но может быть достигнуто и с помощью следующей модели [56]. Как обычно, пусть  наблюдаемые ценности объектов
наблюдаемые ценности объектов  Предположим, что эксперт объявляет объекты равными, если
Предположим, что эксперт объявляет объекты равными, если  ; предпочитает
; предпочитает  если
если  и предпочитает
и предпочитает  если
если  . В эту модель легко включить модель Тэрстоуна — Мостеллера и правило
. В эту модель легко включить модель Тэрстоуна — Мостеллера и правило  Метод наименьших квадратов можно использовать не только для оценивания ценностей
Метод наименьших квадратов можно использовать не только для оценивания ценностей  но и для оценивания параметра порога (и, возможно, различного
но и для оценивания параметра порога (и, возможно, различного  для различных экспертов; это утверждение можно проверить). Не разрушая равные ранги на самом деле, можно таким образом использовать исходные наблюдения.
для различных экспертов; это утверждение можно проверить). Не разрушая равные ранги на самом деле, можно таким образом использовать исходные наблюдения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
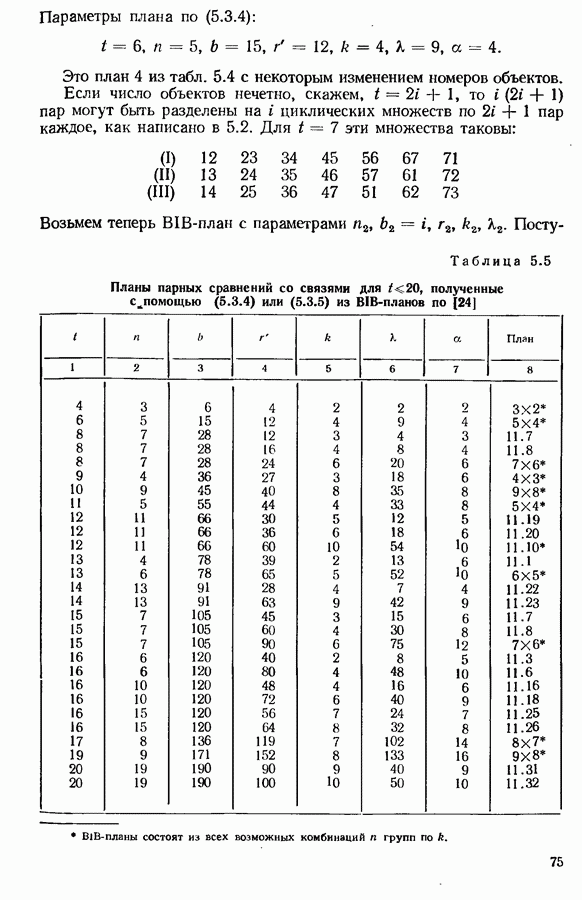
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
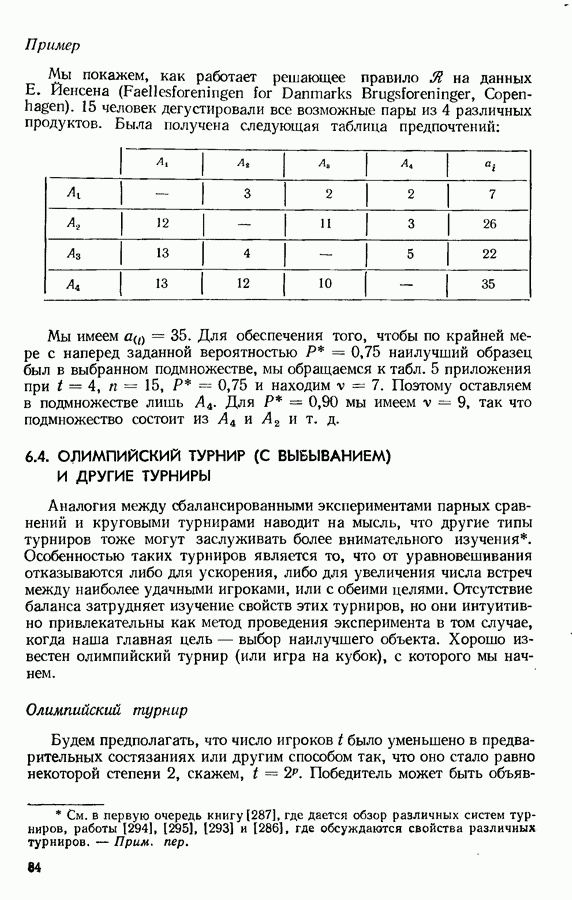
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ