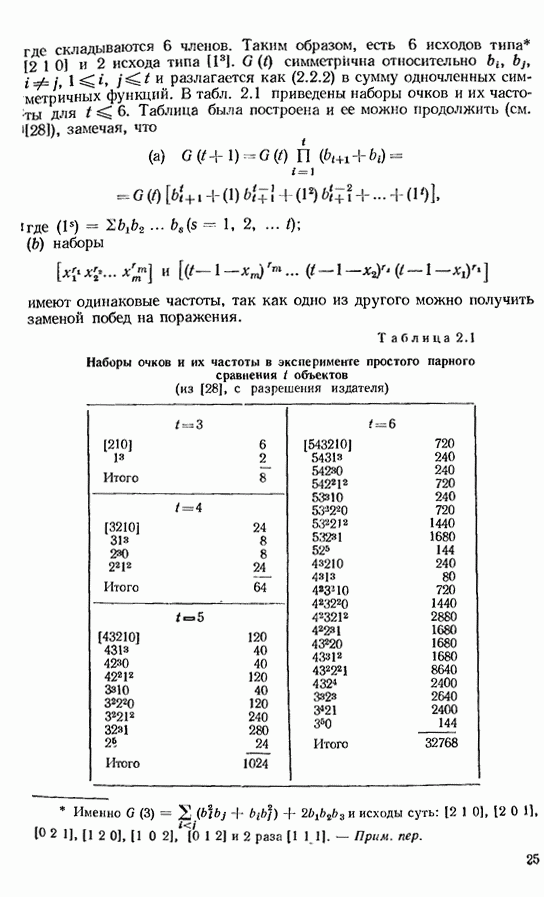
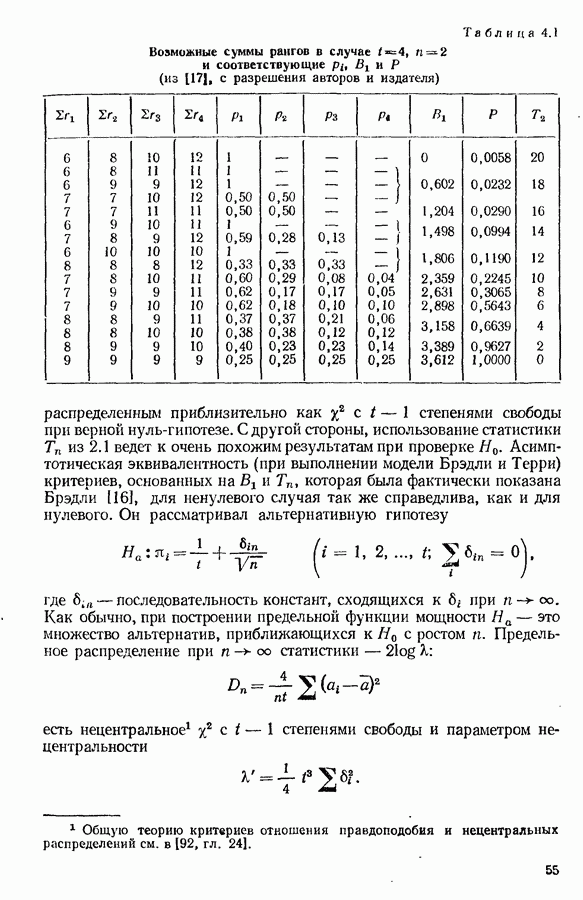
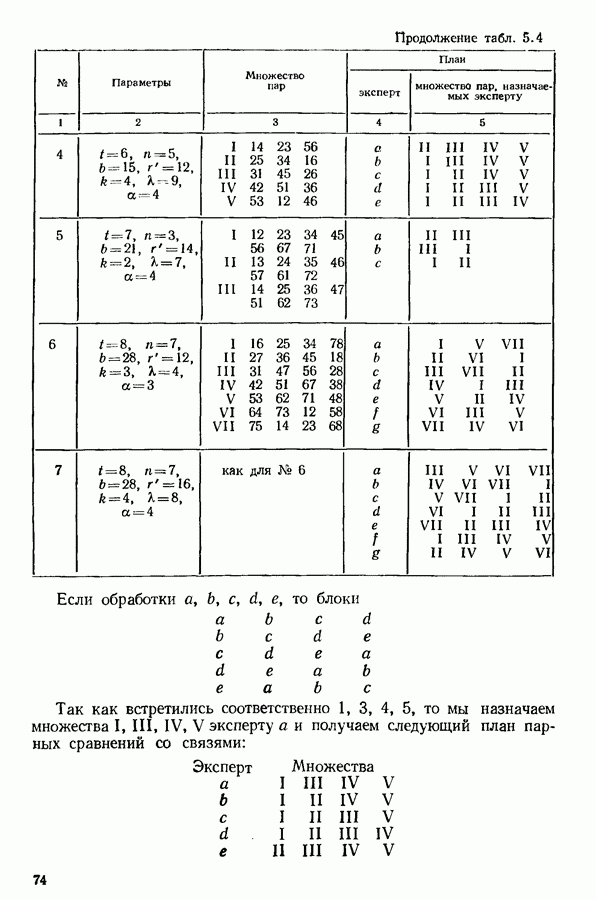
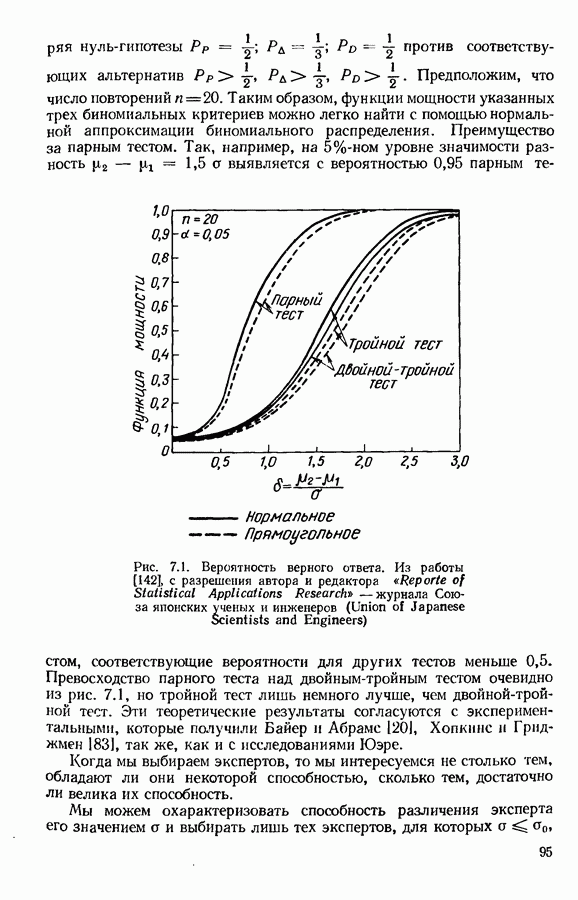
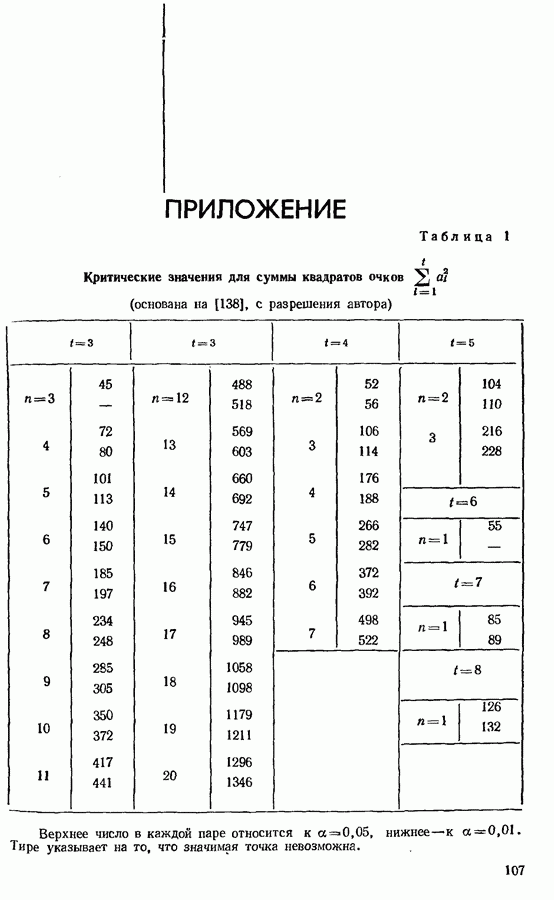
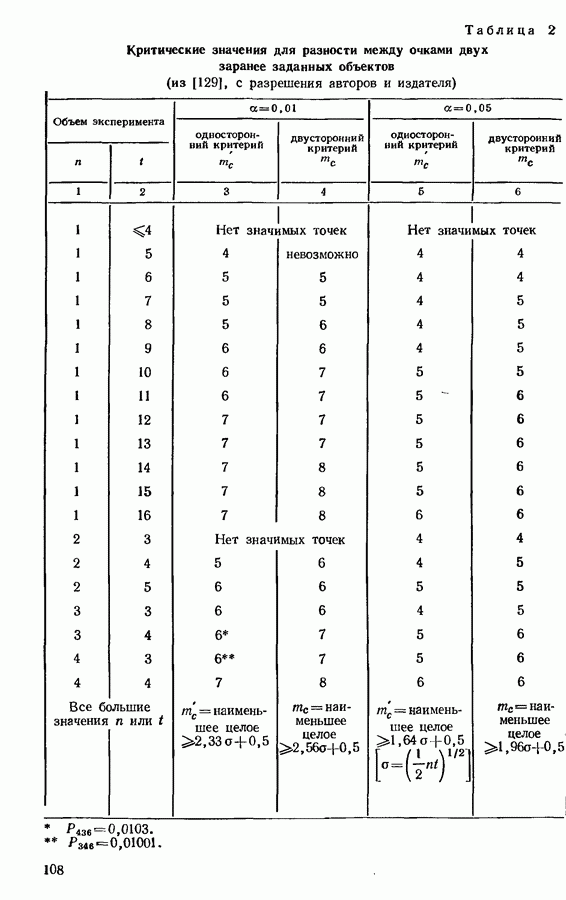
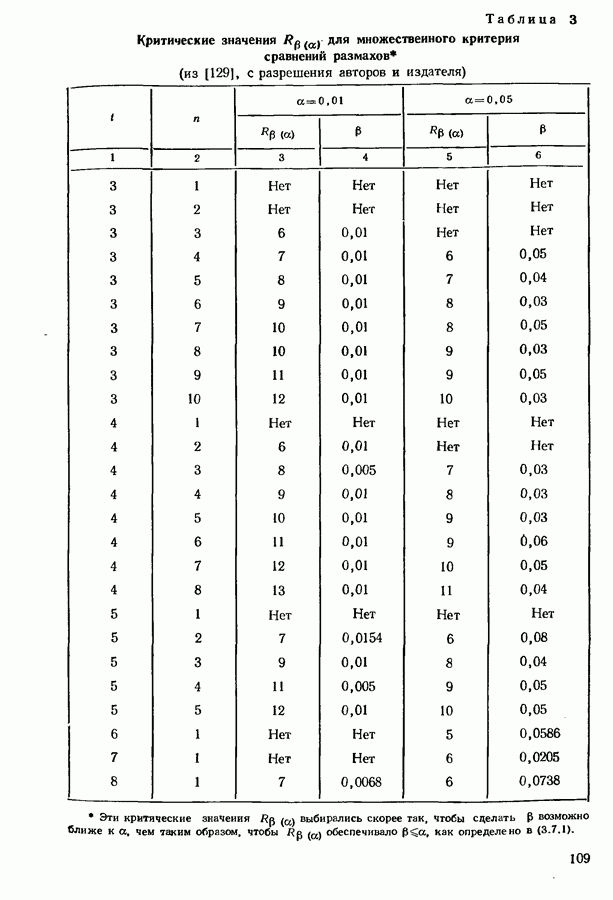
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
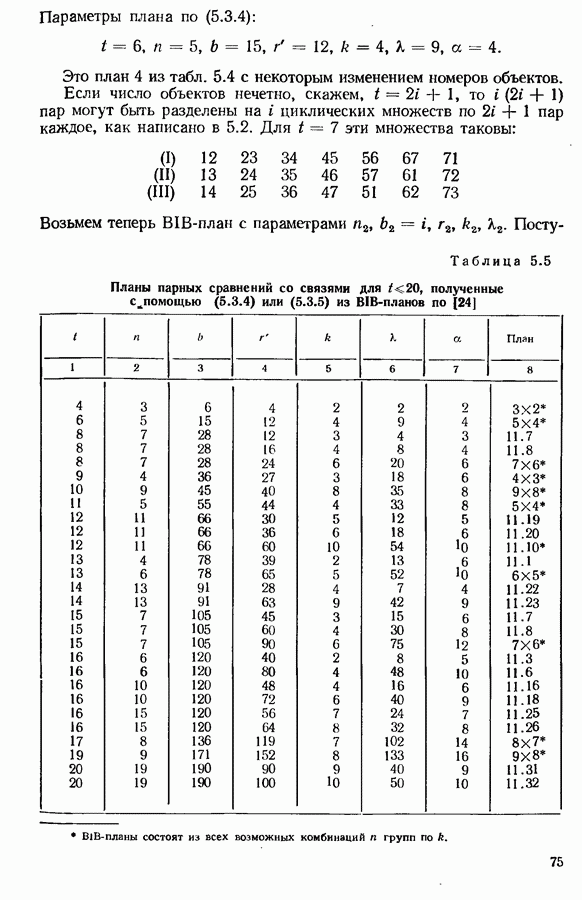
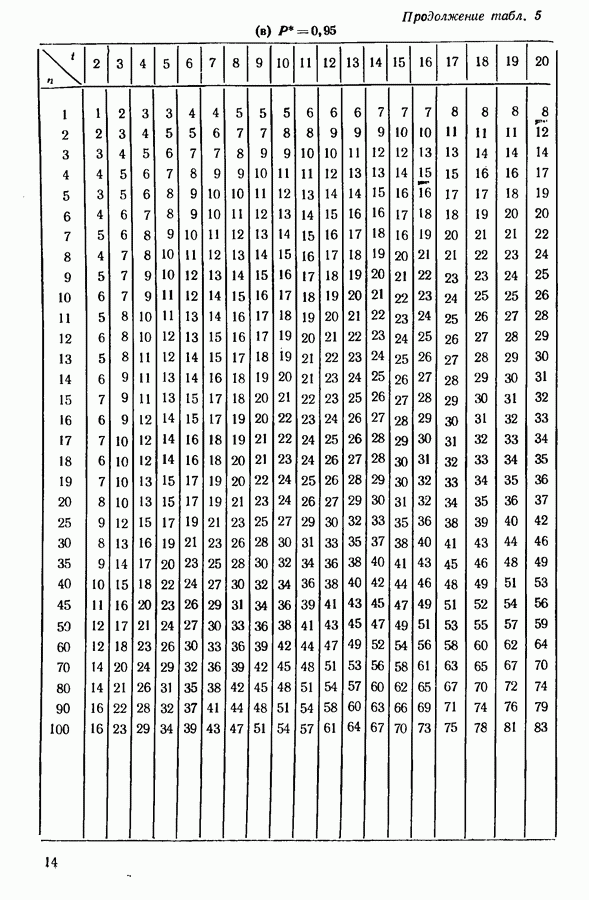
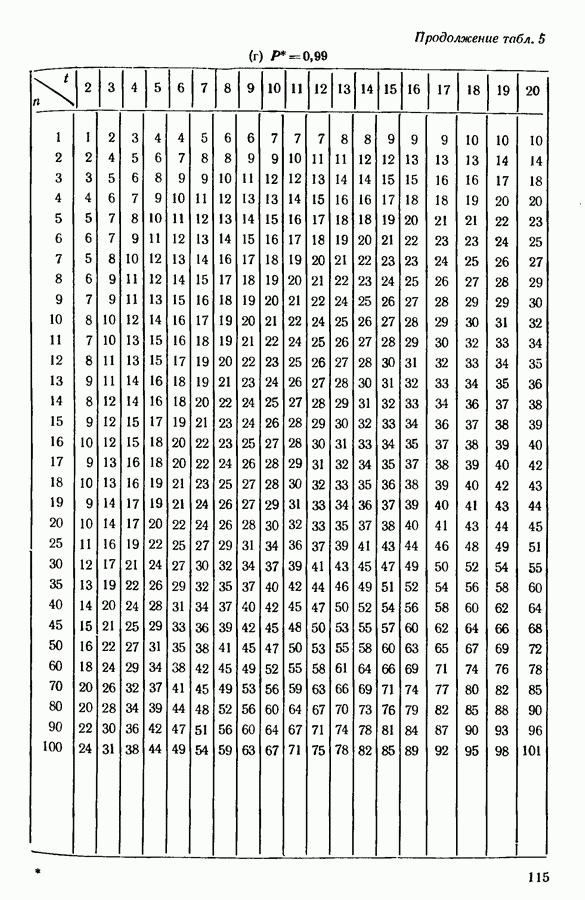
5.2. НЕПОЛНЫЕ ПЛАНЫ
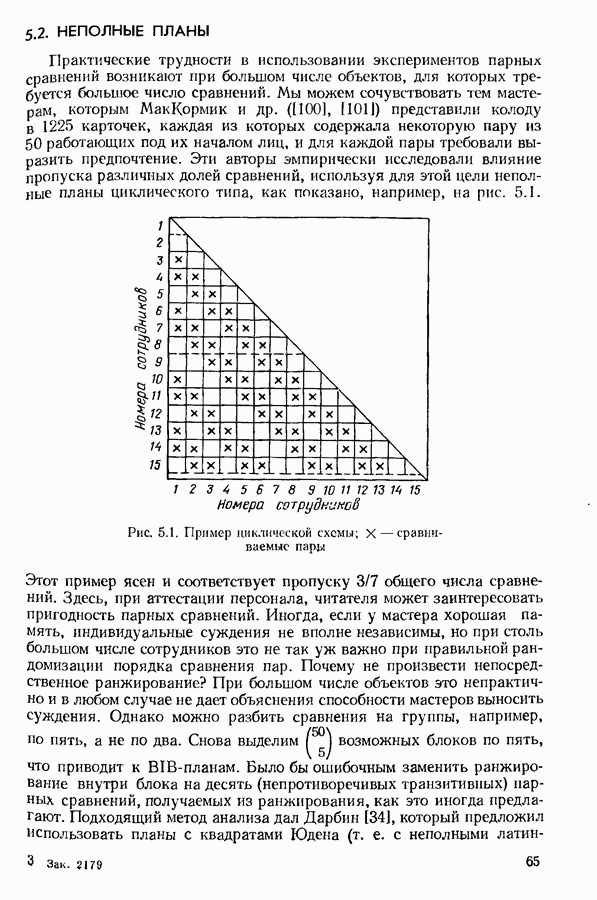
Практические трудности в использовании экспериментов парных сравнений возникают при большом числе объектов, для которых требуется большое число сравнений. Мы можем сочувствовать тем мастерам, которым МакКормик и др. ([100], [1011) представили колоду в 1225 карточек, каждая из которых содержала некоторую пару из 50 работающих под их началом лиц, и для каждой пары требовали выразить предпочтение. Эти авторы эмпирически исследовали влияние пропуска различных долей сравнений, используя для этой цели неполные планы циклического типа, как показано, например, на рис. 5.1.

Рис. 5.1. Пример циклической схемы;  -сравниваемые пары
-сравниваемые пары
Этот пример ясен и соответствует пропуску 3/7 общего числа сравнений. Здесь, при аттестации персонала, читателя может заинтересовать пригодность парных сравнений. Иногда, если у мастера хорошая память, индивидуальные суждения не вполне независимы, но при столь большом числе сотрудников это не так уж важно при правильной рандомизации порядка сравнения пар. Почему не произвести непосредственное ранжирование? При большом числе объектов это непрактично и в любом случае не дает объяснения способности мастеров выносить суждения. Однако можно разбить сравнения на группы, например, по пять, а не по два  возможных блоков по пять, что приводит к
возможных блоков по пять, что приводит к  -планам. Было бы ошибочным заменить ранжирование внутри блока на десять (непротиворечивых транзитивных) парных сравнений, получаемых из ранжирования, как это иногда предлагают. Подходящий метод анализа дал Дарбин [34], который предложил использовать планы с квадратами Юдена (т. е. с неполными
-планам. Было бы ошибочным заменить ранжирование внутри блока на десять (непротиворечивых транзитивных) парных сравнений, получаемых из ранжирования, как это иногда предлагают. Подходящий метод анализа дал Дарбин [34], который предложил использовать планы с квадратами Юдена (т. е. с неполными
латинскими квадратами), поскольку эти компактные  -планы элиминируют эффект порядка представления внутри блока (см. также 166]).
-планы элиминируют эффект порядка представления внутри блока (см. также 166]).
Когда размер блоков не обязательно ограничен двумя, возникает более определенная ситуация для неполных планов парных сравнений.
Задача о том, что составляет удовлетворительное подмножество сравнений, рассматривалась в [89], где выдвинуты два следующих минимальных требования: (а) каждый объект должен появляться одинаково часто; (б) предпочтения не должны делиться, в том смысле, что мы не можем расщепить объекты на два множества и не сравнивать между собой объекты из разных множеств.
Циклические планы
Рассмотрим сначала случай  показанный на рис. 2.1. Ясно, что наименьшее подмножество, удовлетворяющее (а) и (б), состоит из 5 сравнений, которые при удобных обозначениях номеров объектов мы всегда можем выбрать так:
показанный на рис. 2.1. Ясно, что наименьшее подмножество, удовлетворяющее (а) и (б), состоит из 5 сравнений, которые при удобных обозначениях номеров объектов мы всегда можем выбрать так:

Еще остается множество

и мы замечаем, что порядок представления сбалансирован в этих двух циклических планах. Мы можем поэтому рассматривать (I) по существу как эквивалент  полученного сменой порядка представления каждой пары в (I). Нет никакой разницы в выборе (I) или (II), так как перенумерация (12345) в (13524) превращает (I) в (II) и (II) в
полученного сменой порядка представления каждой пары в (I). Нет никакой разницы в выборе (I) или (II), так как перенумерация (12345) в (13524) превращает (I) в (II) и (II) в  Если, например, три эксперта не могут индивидуально выполнить все десять сравнений, то мы можем дать им любые три из планов (I), (II),
Если, например, три эксперта не могут индивидуально выполнить все десять сравнений, то мы можем дать им любые три из планов (I), (II),  или (II). При этом предполагается, что измерение согласия между экспертами не интересно. Если же это не так, то можно взять планы парных сравнений со связями из § 5.3.
или (II). При этом предполагается, что измерение согласия между экспертами не интересно. Если же это не так, то можно взять планы парных сравнений со связями из § 5.3.
Для  ситуация несколько другая. Мы можем все же написать 2 циклических упорядочения:
ситуация несколько другая. Мы можем все же написать 2 циклических упорядочения:

но тогда остается «полуупорядочение»

(I)-(III) удовлетворяют условию (а), но лишь (I) удовлетворяет (б). (II) не связано и распадается на два подмножества 13 35 51 и 24 46 62, причиной этому служит, конечно, то, что 6 делится на 2. Однако (I) можно объединять с (II) или даже (III), если пренебречь порядком объектов в парах.
Некоторые обобщения очевидны. Для нечетного  пары числом можно разделить на
пары числом можно разделить на  множеств из
множеств из  для четного
для четного  на
на 
— 1 множеств из  и одно из
и одно из  пар. Ведущее множество, которое можно обозначить
пар. Ведущее множество, которое можно обозначить  всегда будет удовлетворять (а) и (б) так же, как и
всегда будет удовлетворять (а) и (б) так же, как и  множество
множество  при условии, что
при условии, что  взаимно просты
взаимно просты  Если
Если  имеют наибольший общий множитель
имеют наибольший общий множитель  то
то  множество разбивается на
множество разбивается на  подмножеств. (I) или любое другое связанное множество можно объединять с другими множествами в план, удовлетворяющий (а) и
подмножеств. (I) или любое другое связанное множество можно объединять с другими множествами в план, удовлетворяющий (а) и  Для заданного числа пар, оцениваемых экспертами, мы будем интуитивно предпочитать «более связанный» план из тех, что можно построить с минимумом повторений.
Для заданного числа пар, оцениваемых экспертами, мы будем интуитивно предпочитать «более связанный» план из тех, что можно построить с минимумом повторений.

Рис. 5.2.
Вернемся к случаю  Множества (I)-(III) можно сделать сбалансированными и связанными. Ясно, что в отдельности они одинаково хороши, но если выбирать два из них, то будет ли какая-нибудь пара предпочтительнее других? Чтобы увидеть, что ответ отрицателен, расположим три множества, вместе с множествами
Множества (I)-(III) можно сделать сбалансированными и связанными. Ясно, что в отдельности они одинаково хороши, но если выбирать два из них, то будет ли какая-нибудь пара предпочтительнее других? Чтобы увидеть, что ответ отрицателен, расположим три множества, вместе с множествами  по кругу, как показано на рис. 5.2. Множество
по кругу, как показано на рис. 5.2. Множество  есть просто
есть просто

и его можно назвать зеркальным отображением (III), которое эквивалентно (III), за исключением смены порядка в каждой паре. Аналогично  и
и  есть зеркальные отображения (II) и (I) соответственно. Мы будем пренебрегать эффектом порядка, так что
есть зеркальные отображения (II) и (I) соответственно. Мы будем пренебрегать эффектом порядка, так что  эквивалентны
эквивалентны  нечетное). Рассмотрим теперь перенумерацию
нечетное). Рассмотрим теперь перенумерацию  объектов (1 234 567) в
объектов (1 234 567) в  Она превращает (I) в (II), (II) в
Она превращает (I) в (II), (II) в  и
и  в (I), как легко проверить. Так, пары
в (I), как легко проверить. Так, пары  заменяются на
заменяются на  и
и  заменяются на
заменяются на  чем демонстрируют, по сути дела, эквивалентность всех трех пар.
чем демонстрируют, по сути дела, эквивалентность всех трех пар.
Наши соображения в пользу введения множеств  состоят в обобщении на другие, нечетные значения
состоят в обобщении на другие, нечетные значения  Для
Для  преобразование
преобразование  дает эффект замены множества
дает эффект замены множества  на (21), где последнее множество должно быть делимо но модулю
на (21), где последнее множество должно быть делимо но модулю  и для эквивалентностей. Так, для
и для эквивалентностей. Так, для  заменяется на
заменяется на  что эквивалентно
что эквивалентно  Для
Для  связанные множества есть (I, II, IV);
связанные множества есть (I, II, IV);  преобразует их в
преобразует их в  , так что все пары связанных множеств эквивалентны. Действуя таким образом, можно выбрать
, так что все пары связанных множеств эквивалентны. Действуя таким образом, можно выбрать
приемлемые комбинации подмножеств для любого  подобные рассмотрения проводятся и для четного но мы не станем систематизировать их здесь. Смотрите также [88] и [102].
подобные рассмотрения проводятся и для четного но мы не станем систематизировать их здесь. Смотрите также [88] и [102].
Частично сбалансированные неполноблочные планы
Отношение циклических планов к частично сбалансированным не-полноблочным планам с двумя ассоциативными классами представляет некоторый интерес. В нашем случае, когда каждый блок состоит из двух объектов,  схемы определяются следующим образом:
схемы определяются следующим образом:
а) существует  объектов и
объектов и  блоков;
блоков;
б) каждый из  объектов встречается
объектов встречается  раз (так что
раз (так что  ;
;
в) каждая пара объектов встречается либо  либо
либо  раз (и объекты называют соответственно или первично связанными, или вторично связанными);
раз (и объекты называют соответственно или первично связанными, или вторично связанными);
г) существует соотношение ассоциативности между каждой парой объектов, удовлетворяющее следующим условиям:
1) каждый объект имеет  первичных и
первичных и  вторичных связей;
вторичных связей;
2) для любых двух объектов, которые  -связаны, число объектов,
-связаны, число объектов,  -связанных с первым и
-связанных с первым и  -связанных со вторым, обозначается
-связанных со вторым, обозначается  и это число не зависит от пары объектов, с которой мы начали. Более того,
и это число не зависит от пары объектов, с которой мы начали. Более того, 
Клэтуорси 123] дал перечисление всех таких планов, для которых каждый объект повторяется не более 10 раз. Эти планы имеют высокую степень симметрии и потому весьма удобны для неполноблочных экспериментов парных сравнений. Можно различать четыре основных типа планов, один из которых циклический тип. Для  легко проверить, что каждое из множеств (I) и (II), выписанных выше, и любые комбинации из них, которые не полностью сбалансированы, образуют
легко проверить, что каждое из множеств (I) и (II), выписанных выше, и любые комбинации из них, которые не полностью сбалансированы, образуют  -план с двумя ассоциативными классами. Так, для (I) и (II) мы имеем
-план с двумя ассоциативными классами. Так, для (I) и (II) мы имеем  объекта 1 соответственно 2 и 5 — первично связанные, 3 и 4 — вторично связанные объекты и т. д. Также
объекта 1 соответственно 2 и 5 — первично связанные, 3 и 4 — вторично связанные объекты и т. д. Также

Однако это лишь частный случай (отличный от  когда данное множество в такой высокой степени сбалансировано. Несколько другие циклические планы, полученные Клэтуорси, являются комбинациями множеств (II, V, VI) для
когда данное множество в такой высокой степени сбалансировано. Несколько другие циклические планы, полученные Клэтуорси, являются комбинациями множеств (II, V, VI) для  и множеств (III, V, VI, VII) для
и множеств (III, V, VI, VII) для  Конечно, эквивалентные комбинации можно получить, меняя номера объектов.
Конечно, эквивалентные комбинации можно получить, меняя номера объектов.
Мы рассмотрим сейчас другие  -планы с двумя ассоциативными классами:
-планы с двумя ассоциативными классами:
(1) Планы с делением на группы
Если  выразимо как произведение двух больших, чем 1, чисел
выразимо как произведение двух больших, чем 1, чисел  то объекты можно разделить на
то объекты можно разделить на  групп размера
групп размера  Пары встречаются или
Пары встречаются или  раз, в зависимости от того, принадлежат ли они одной и той же группе. Список всех таких планов для
раз, в зависимости от того, принадлежат ли они одной и той же группе. Список всех таких планов для  приведен в табл. 5.1 (сравните с [37]). При построении плана 2, например, мы можем взять объекты 1, 2, 3 в качестве одной группы,
приведен в табл. 5.1 (сравните с [37]). При построении плана 2, например, мы можем взять объекты 1, 2, 3 в качестве одной группы,  -как другую. Так как пары внутри групп не образуются, эксперимент состоит из блоков
-как другую. Так как пары внутри групп не образуются, эксперимент состоит из блоков

Планы с различными значениями 7 можно построить из базисных планов повторением приведенных случаев или комбинацией их с полными планами.
(2) Треугольные планы
Если  ассоциативная схема, то можно получить таблицу, размещая объекты по порядку и симметрично относительно вычеркнутой главной диагонали. Например, для
ассоциативная схема, то можно получить таблицу, размещая объекты по порядку и симметрично относительно вычеркнутой главной диагонали. Например, для  схема такова:
схема такова:

Таблица 5.1 (см. скан) Планы с делением на группы для  (из [23] с разрешения автора)
(из [23] с разрешения автора)
Два объекта, находящихся в одной строке (или столбце), первично связаны, тогда как объекты, не лежащие в одной строке, связаны вторично. Для  мы получаем план
мы получаем план

который, будучи «перевернут», эквивалентен плану 3 (упражнение 5.1). Другие базисные треугольные планы даны в табл. 5.2 и состоят из всех различных групп с делением.
Таблица 5.2 (см. скан) Треугольные планы для  (из [23], с разрешения автора)
(из [23], с разрешения автора)
(3) Квадратные планы
Если  есть квадрат целого числа
есть квадрат целого числа  ассоциативную схему можно получить, располагая объекты по порядку в квадрате
ассоциативную схему можно получить, располагая объекты по порядку в квадрате  Так, для
Так, для  мы имеем
мы имеем

Здесь объекты, находящиеся в одной строке или в одном столбце, связаны первично, остальные — вторично. При  мы получаем план 24 табл. 5.3, а именно
мы получаем план 24 табл. 5.3, а именно

Другие базисные квадратные планы даны в табл. 5.3.
Таблица 5.3 (см. скан) Квадратные планы для  (из [23], с разрешения автора)
(из [23], с разрешения автора)
Заканчивая наше описание базисных планов, мы можем добавить номера 29—31, соответствующие трем циклическим схемам для  которые упоминались выше. Клэтуорси дал некоторые другие планы (включающие 16 и 27 объектов), которые не относятся к четырем главным классам.
которые упоминались выше. Клэтуорси дал некоторые другие планы (включающие 16 и 27 объектов), которые не относятся к четырем главным классам.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
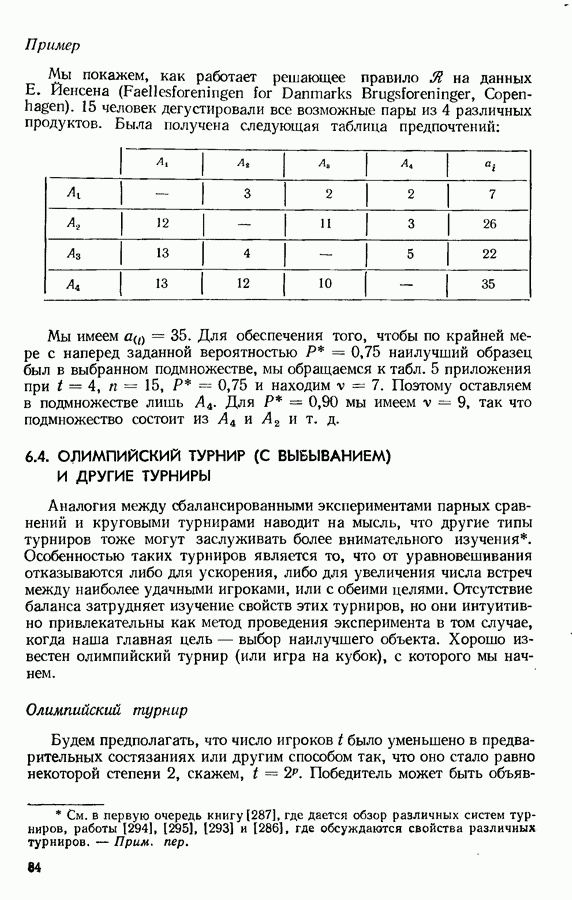
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
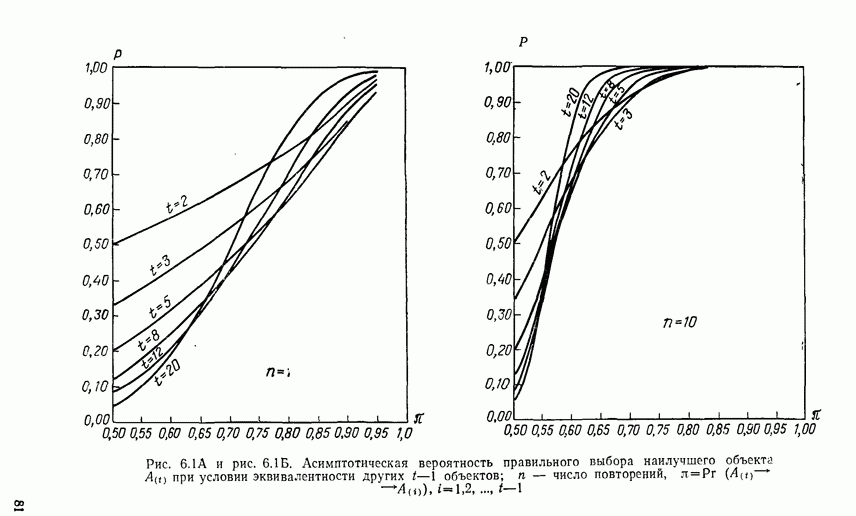
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
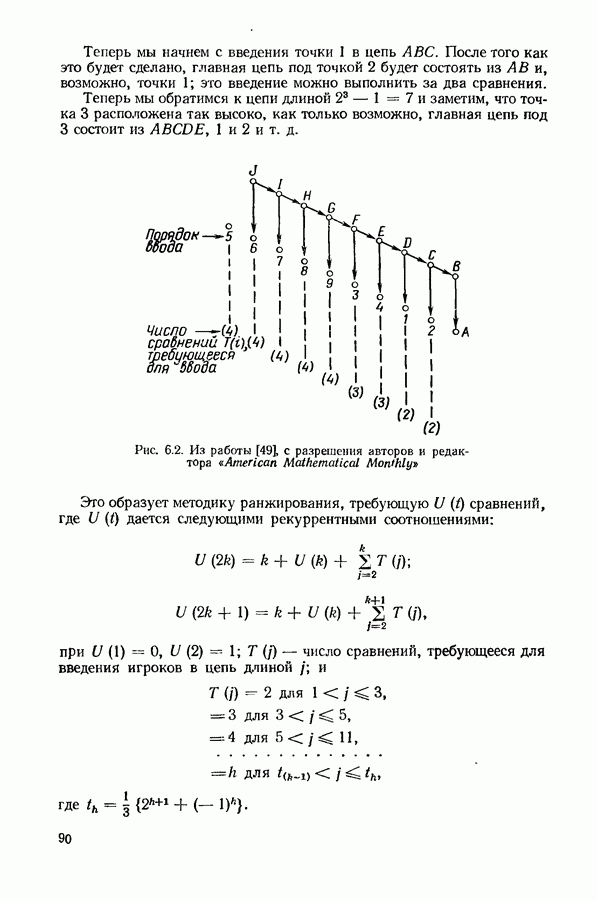
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ