| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.5. МЕТОДИКА ГУТМАНА
Интересный метод превращения данных парных сравнений в количественные, который не использует специальной модели, был предложен Гутманом [69]. Как и раньше, пусть  очки эксперта у для объекта
очки эксперта у для объекта  и пусть
и пусть  Далее, пусть
Далее, пусть  есть среднее очков
есть среднее очков  объектов, которые эксперт у ранжирует выше (ниже), чем другие объекты, взвешенное на соответствующие относительные частоты
объектов, которые эксперт у ранжирует выше (ниже), чем другие объекты, взвешенное на соответствующие относительные частоты

где  Также пусть
Также пусть

Сумму квадратов отклонений очков

можно разложить на 2 слагаемых:

и

суммы квадратов между экспертами и «внутри экспертов» соответственно.
Подход Гутмана сродни дискриминантному анализу и заключается в нахождении очков, минимизирующих вариацию «внутри экспертов», сравниваемых с вариацией группы экспертов в целом. Это значит, что мы делаем 5 как можно меньше или  как можно больше по сравнению с
как можно больше по сравнению с  Если мы определим корреляционное отношение
Если мы определим корреляционное отношение  через
через  то искомые очки и, - получают из уравнений, в которых
то искомые очки и, - получают из уравнений, в которых  приравнены к нулю, т. е. из уравнений стационарности
приравнены к нулю, т. е. из уравнений стационарности

Производные от  можно вычислить из (7.5.5) и (7.5.1):
можно вычислить из (7.5.5) и (7.5.1):

Из (7.5.4) — производные от 

Если мы положим

то (7.5.7) можно переписать в виде

Рассмотрим первое подтверждение того, что решение (7.5.9) удовлетворяет  Суммируя обе части (7.5.9) по
Суммируя обе части (7.5.9) по  и используя (7.5.8), мы получим
и используя (7.5.8), мы получим

так что  если только не
если только не  что практически можно исключить.
что практически можно исключить.
Всегда существует тривиальное решение (7.5.9), для которого  формально равно 1. Это
формально равно 1. Это  для всех
для всех  как легко проверить. Для получения нетривиального решения, обозначим
как легко проверить. Для получения нетривиального решения, обозначим  вектор-столбец
вектор-столбец  и пусть
и пусть  симметричная матрица
симметричная матрица  Тогда (7.5.9) становится матричным уравнением
Тогда (7.5.9) становится матричным уравнением

показывающим, что  есть собственное число
есть собственное число  с соответствующим собственным вектором
с соответствующим собственным вектором  Поскольку мы хотим найти наибольшее корреляционное отношение, мы ищем наибольшее из нетривиальных собственных чисел. Численное решение (7.5.10) можно получить простым итеративным методом для получения собственных чисел и векторов. Такие итерации сходятся, вообще говоря, к вектору, соответствующему наибольшему числу. Чтобы избежать сходимости к тривиальному решению (которое формально имеет наибольшее собственное число), исходные векторы должны удовлетворять условию
Поскольку мы хотим найти наибольшее корреляционное отношение, мы ищем наибольшее из нетривиальных собственных чисел. Численное решение (7.5.10) можно получить простым итеративным методом для получения собственных чисел и векторов. Такие итерации сходятся, вообще говоря, к вектору, соответствующему наибольшему числу. Чтобы избежать сходимости к тривиальному решению (которое формально имеет наибольшее собственное число), исходные векторы должны удовлетворять условию 
Гутман полагал, что его подход ведет к очкам, которые для модели Тэрстоуна-Мостеллера лишь линейным преобразованием отличаются от тех, что получаются в 4.1. Однако этот метод применим в том случае, когда предположения модели не выполняются. Что касается недостатков, то следует заметить, что методика Гутмана — это скорее процедура оценивания, чем теория распределения.
Читатель может обратиться к работе Гутмана, в которой приведены дальнейшие обсуждения и обобщение подхода на ситуации, в которых сравниваются наборы, а не отдельные объекты.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
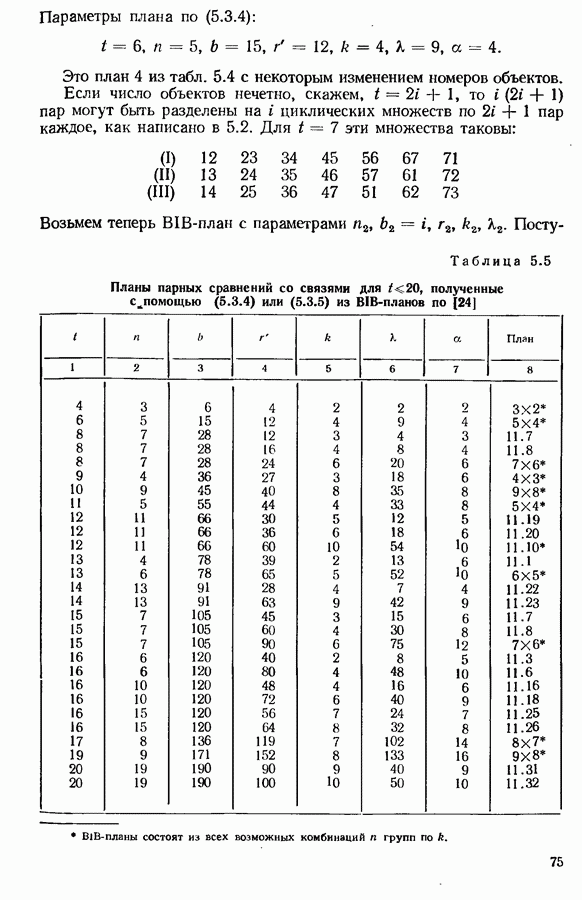
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
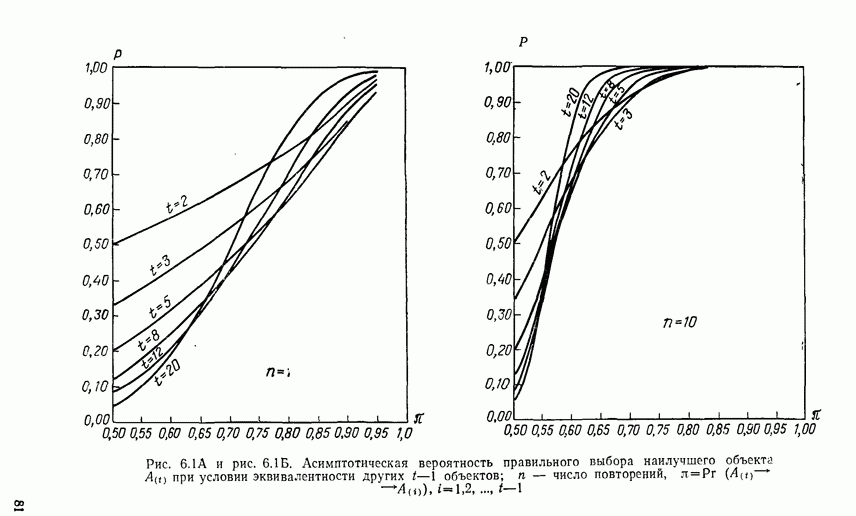
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
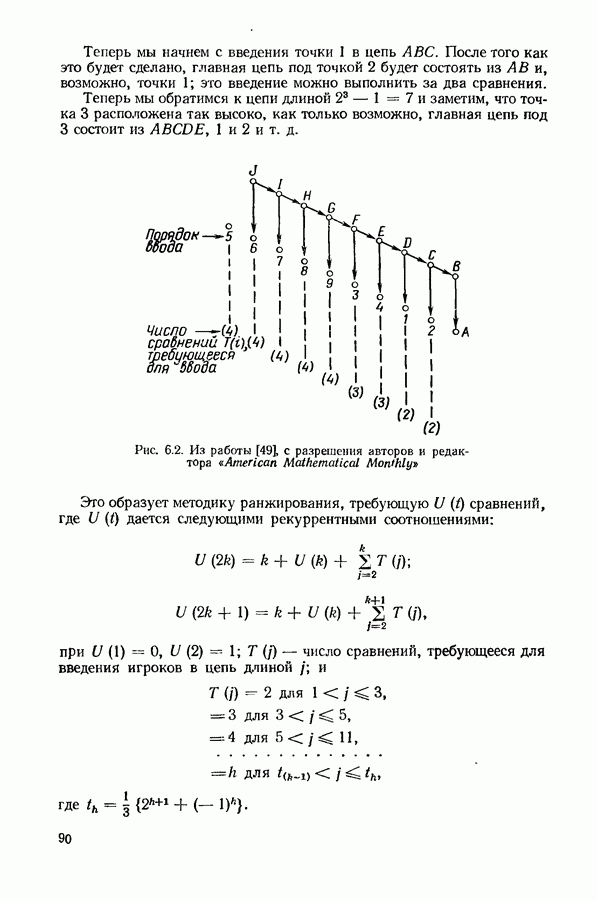
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ