| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
5.1. ПОЛНОСТЬЮ СБАЛАНСИРОВАННЫЕ ПЛАНЫ
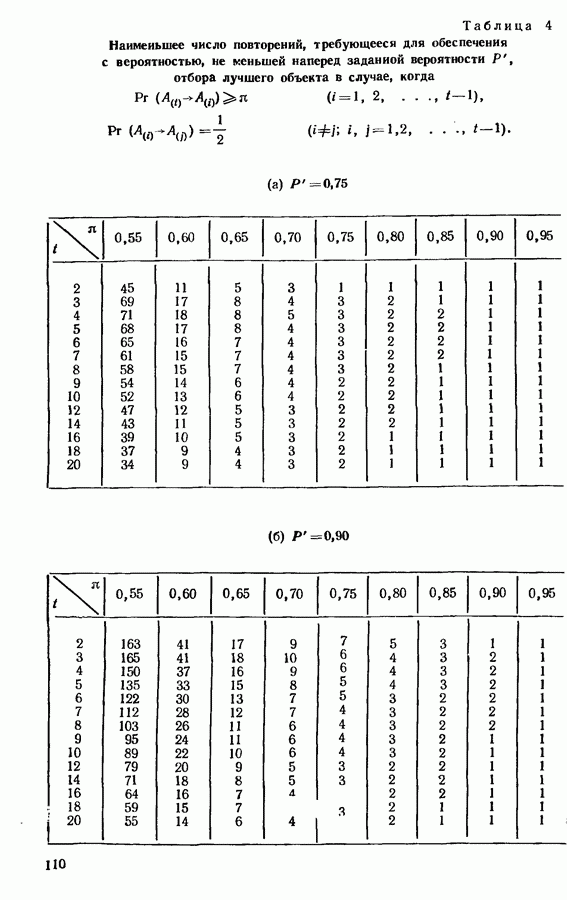
На языке планирования эксперимента  что мы называем сбалансированным экспериментом парных сравнений, известно как «сбалансированный неполноблочный план»
что мы называем сбалансированным экспериментом парных сравнений, известно как «сбалансированный неполноблочный план»  с блоком размером два. Задача планирования, конечно, остается одной и той же, имеем ли мы для каждого блока выражение предпочтения, как в парном сравнении, или два различных значения, как в обычной экспериментальной ситуации. Есть также тесная связь между сбалансированным экспериментом парных сравнений и круговым турниром, используемым во многих видах спорта, когда каждый из игроков (или команд) играет с каждым один или несколько раз. Планирование полностью сбалансированного эксперимента не представляет трудностей, однако может быть интересен, в частности, простой подход, данный Крейчиком [94]. Его процедуру можно рассмотреть на примере
с блоком размером два. Задача планирования, конечно, остается одной и той же, имеем ли мы для каждого блока выражение предпочтения, как в парном сравнении, или два различных значения, как в обычной экспериментальной ситуации. Есть также тесная связь между сбалансированным экспериментом парных сравнений и круговым турниром, используемым во многих видах спорта, когда каждый из игроков (или команд) играет с каждым один или несколько раз. Планирование полностью сбалансированного эксперимента не представляет трудностей, однако может быть интересен, в частности, простой подход, данный Крейчиком [94]. Его процедуру можно рассмотреть на примере  Напишем числа 1—7 последовательно в семь строк по четыре
Напишем числа 1—7 последовательно в семь строк по четыре  Получается четыре столбца цифр, напечатанных жирным шрифтом. Затем продолжим запись цифр в обратном порядке, начиная с правого нижнего угла и располагая при этом числа в три столбца, как показано цифрами, напечатанными обычным шрифтом.
Получается четыре столбца цифр, напечатанных жирным шрифтом. Затем продолжим запись цифр в обратном порядке, начиная с правого нижнего угла и располагая при этом числа в три столбца, как показано цифрами, напечатанными обычным шрифтом.

Результат — расположение семи игроков в круговом турнире, требующем 7 туров. Игроки из первого столбца свободны от игры. Заметим, что каждый игрок появляется первым в трех из его 6 игр, что соответствует проведению 3 игр дома или белыми фигурами и т. д. С точки зрения эксперимента парных сравнений мы имеем, исключая объекты первого столбца, план, в котором любой эффект порядка
представления (объектов) сбалансирован и учтены другие предосторожности. Этот процесс возможен для любых нечетных  Если
Если  четное, скажем,
четное, скажем,  мы просто ставим восьмого игрока в пару с игроком, свободным от игры, записывая 8 поочередно то слева, то справа от первого столбца, как показано. Влияние порядка представления в этом случае сбалансировано лишь приближенно; полный баланс будет достигнут повторением всего эксперимента с изменением порядка в каждой паре на противоположный и строками, которые перерандомизированы. Другой простой подход см. в [50].
мы просто ставим восьмого игрока в пару с игроком, свободным от игры, записывая 8 поочередно то слева, то справа от первого столбца, как показано. Влияние порядка представления в этом случае сбалансировано лишь приближенно; полный баланс будет достигнут повторением всего эксперимента с изменением порядка в каждой паре на противоположный и строками, которые перерандомизированы. Другой простой подход см. в [50].
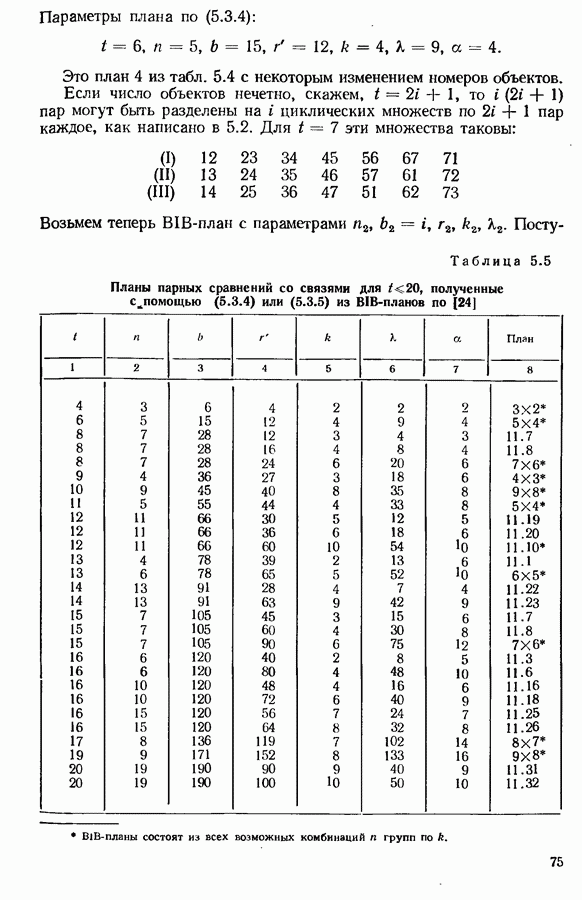
Метод, который дополнительно дает наибольшее возможное разделение между парами, имеющими общий объект, был дан Россом [121]. Для нечетных  выпишем пары следующим образом:
выпишем пары следующим образом:

Для  мы имеем после уравновешивания следующий порядок представления: 12, 73, 64, 51, 32, 47, 56, 13, 24, 75, 61, 43, 52, 67, 14, 35, 26, 71, 45, 36, 27. Случай
мы имеем после уравновешивания следующий порядок представления: 12, 73, 64, 51, 32, 47, 56, 13, 24, 75, 61, 43, 52, 67, 14, 35, 26, 71, 45, 36, 27. Случай  может быть получен из вышеприведенного (без полного баланса) путем пропуска всех пар, содержащих 7. Росс табулировал сбалансированные схемы для нечетных
может быть получен из вышеприведенного (без полного баланса) путем пропуска всех пар, содержащих 7. Росс табулировал сбалансированные схемы для нечетных 
Планы парных турниров также рассматривались — Крейчиком и позднее Шайдом [124]. Джилберт [53] изучал турниры смешанных пар. Парные турниры интересны для работы с парными сравнениями, когда мы хотим сравнить одну пару объектов с другой парой. Например, при создании цветовой шкалы наблюдателей просят сравнить различия (является ли различие между  большим, чем различие между
большим, чем различие между  и
и  Смешанно-парная ситуация возникает, когда два объекта составляют одну «команду» при сравнениях пар различных объектов (предпочитается ли блюдо
Смешанно-парная ситуация возникает, когда два объекта составляют одну «команду» при сравнениях пар различных объектов (предпочитается ли блюдо  с напитком А 2 блюду А 3 с напитком
с напитком А 2 блюду А 3 с напитком  Однако аналогия неполная, так как игрок может быть лишь в одной команде, тогда как с объектами можно проводить также сравнения типа
Однако аналогия неполная, так как игрок может быть лишь в одной команде, тогда как с объектами можно проводить также сравнения типа  против
против 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВЕРОЯТНОСТНЫЕ МОДЕЛИ
- 1.2. ПОПАРНЫЕ СРАВНЕНИЯ ТРЕХ ОБЪЕКТОВ
- 1.3. ОСНОВНЫЕ МОДЕЛИ
- 1.4. ОБОБЩЕНИЯ ДЛЯ ЗАДАЧИ МНОЖЕСТВЕННОГО ВЫБОРА
- 1.5. ОБ ИСТОРИИ МЕТОДА ПАРНЫХ СРАВНЕНИЙ
- Глава 2. КОМБИНАТОРНЫЕ МЕТОДЫ
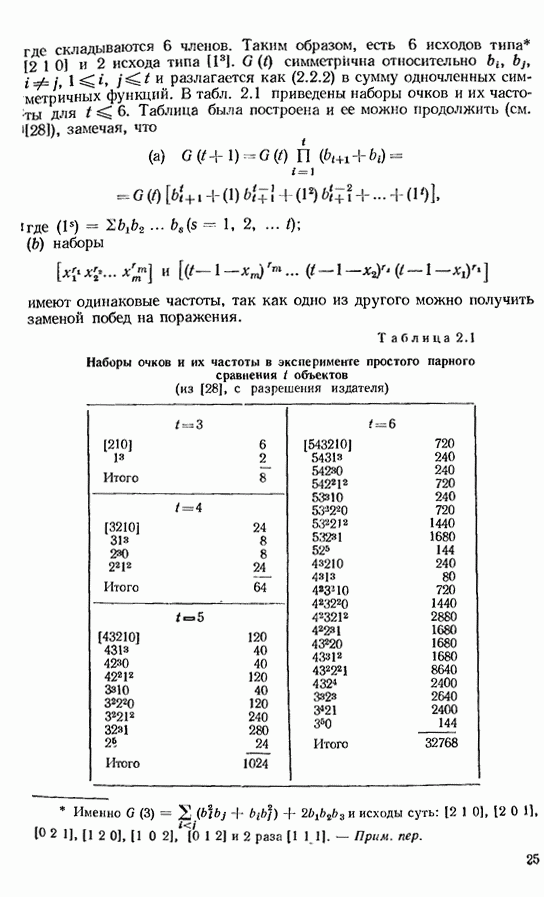
- 2.2. ОСНОВЫ ТЕОРИИ РАСПРЕДЕЛЕНИЙ
- 2.3. РАСПРЕДЕЛЕНИЕ ОЧКОВ И ФУНЧЦИЙ ОТ НИХ
- 2.4. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ НЕНУЛЕВОЙ ГИПОТЕЗЫ
- Глава 3. ПРОВЕРКА ЗНАЧИМОСТИ
- 3.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ ДВУХ ОСОБЫХ ОБЪЕКТОВ
- 3.4. КРИТЕРИЙ ДЛЯ НАИБОЛЬШЕГО ЗНАЧЕНИЯ («ПОБЕДИТЕЛЯ»)
- 3.5. ОБЩИЙ КРИТЕРИЙ ЭКВИВАЛЕНТНОСТИ
- 3.6. МЕТОД НАИМЕНЬШЕЙ ЗНАЧИМОЙ РАЗНОСТИ
- 3.7. КРИТЕРИЙ МНОЖЕСТВЕННОГО СРАВНЕНИЯ ДЛЯ РАЗМАХОВ
- 3.8. МЕТОД СУЖДЕНИЯ О КОНТРАСТАХ ЗНАЧЕНИЙ
- 3.9. ПРИМЕР
- Глава 4. ЛИНЕЙНЫЕ МОДЕЛИ
- 4.2. УГЛОВОЕ (ТРИГОНОМЕТРИЧЕСКОЕ) ПРЕОБРАЗОВАНИЕ
- 4.3. МОДЕЛЬ БРЭДЛИ-ТЕРРИ — ОЦЕНИВАНИЕ
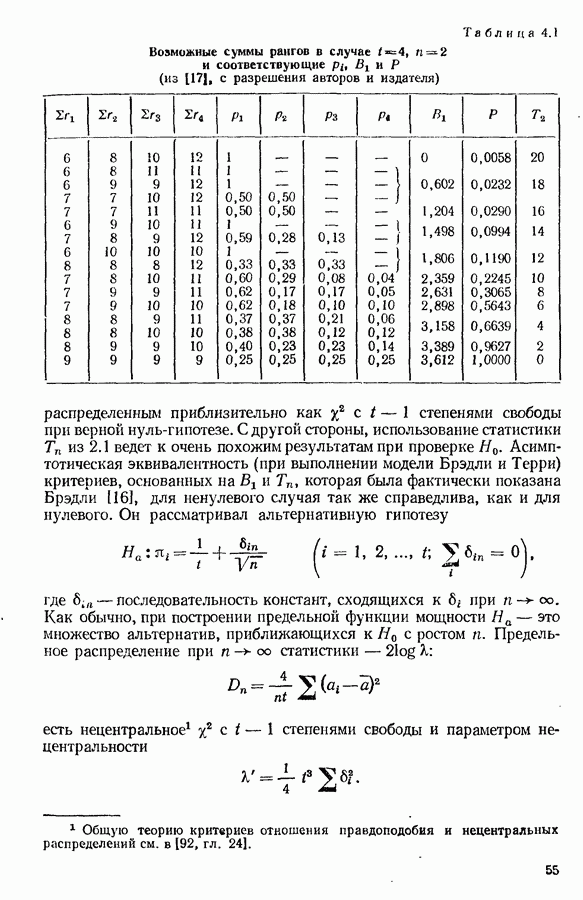
- 4.4. МОДЕЛЬ БРЭДЛИ—ТЕРРИ — ПРОВГРКИ ГИПОТЕЗ
- 4.5. КРИТЕРИИ СОГЛАСИЯ МОДЕЛЕЙ
- 4.6. ТРЕХКОМПОНЕНТКАЯ МОДЕЛЬ БОКА
- Глава 5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
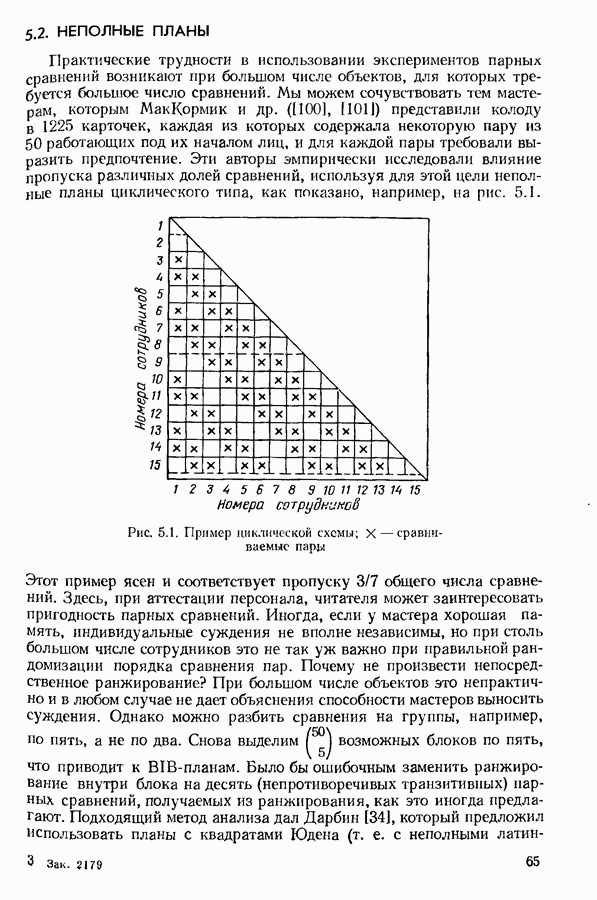
- 5.2. НЕПОЛНЫЕ ПЛАНЫ
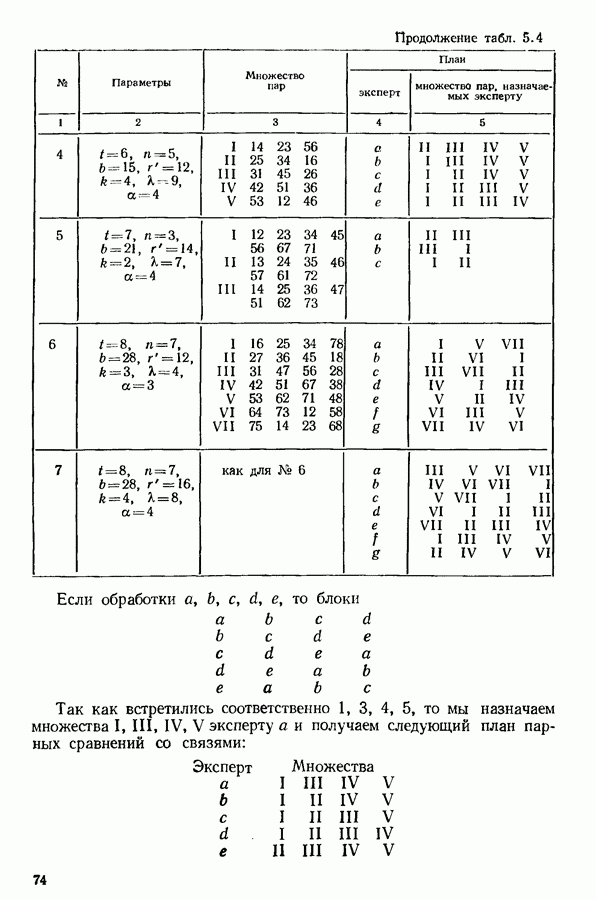
- 5.3. ПЛАНЫ ПАРНЫХ СРАВНЕНИЙ СО СВЯЗЯМИ (ЦЕПНЫЕ)
- Глава 6. ВЫБОР НАИЛУЧШЕГО ОБЪЕКТА
- 6.2. ПОДХОДЯЩИЙ РАЗМЕР ЭКСПЕРИМЕНТА
- 6.3. ВЫБОР ПОДМНОЖЕСТВА, СОДЕРЖАЩЕГО НАИЛУЧШИЙ ОБЪЕКТ
- 6.4. ОЛИМПИЙСКИЙ ТУРНИР (С ВЫБЫВАНИЕМ) И ДРУГИЕ ТУРНИРЫ
- Глава 7. СМЕЖНЫЕ ВОПРОСЫ
- 7.1. ОТБОР ЭКСПЕРТОВ
- 7.2. ТЕСТИРОВАНИЕ ПОТРЕБИТЕЛЕЙ
- 7.3. ОБРАБОТКА РАВНЫХ РАНГОВ
- 7.4. МЕТОДИКА ШЕФФЕ
- 7.5. МЕТОДИКА ГУТМАНА
- 7.6. ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К РУССКОМУ ПЕРЕВОДУ