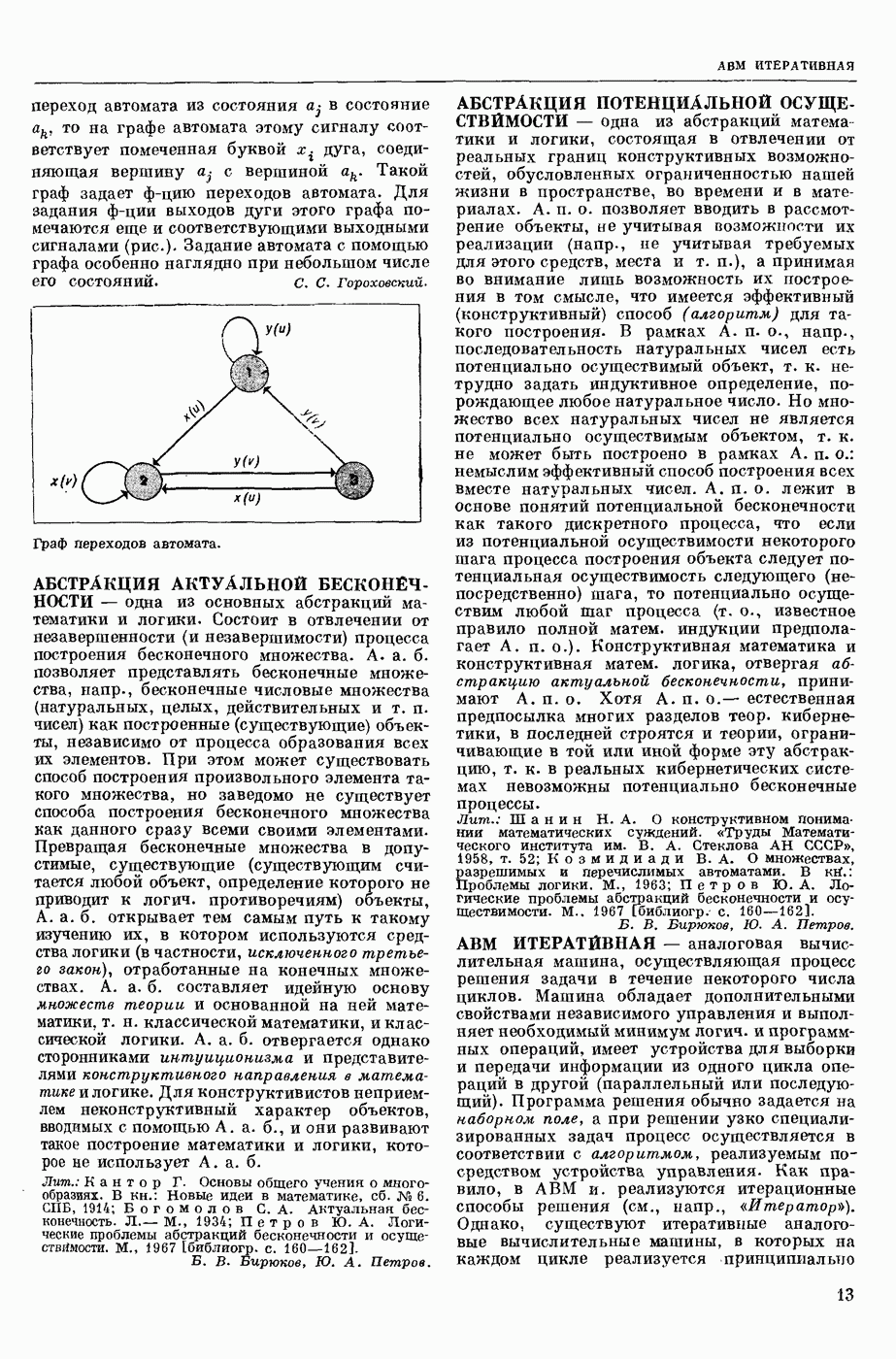
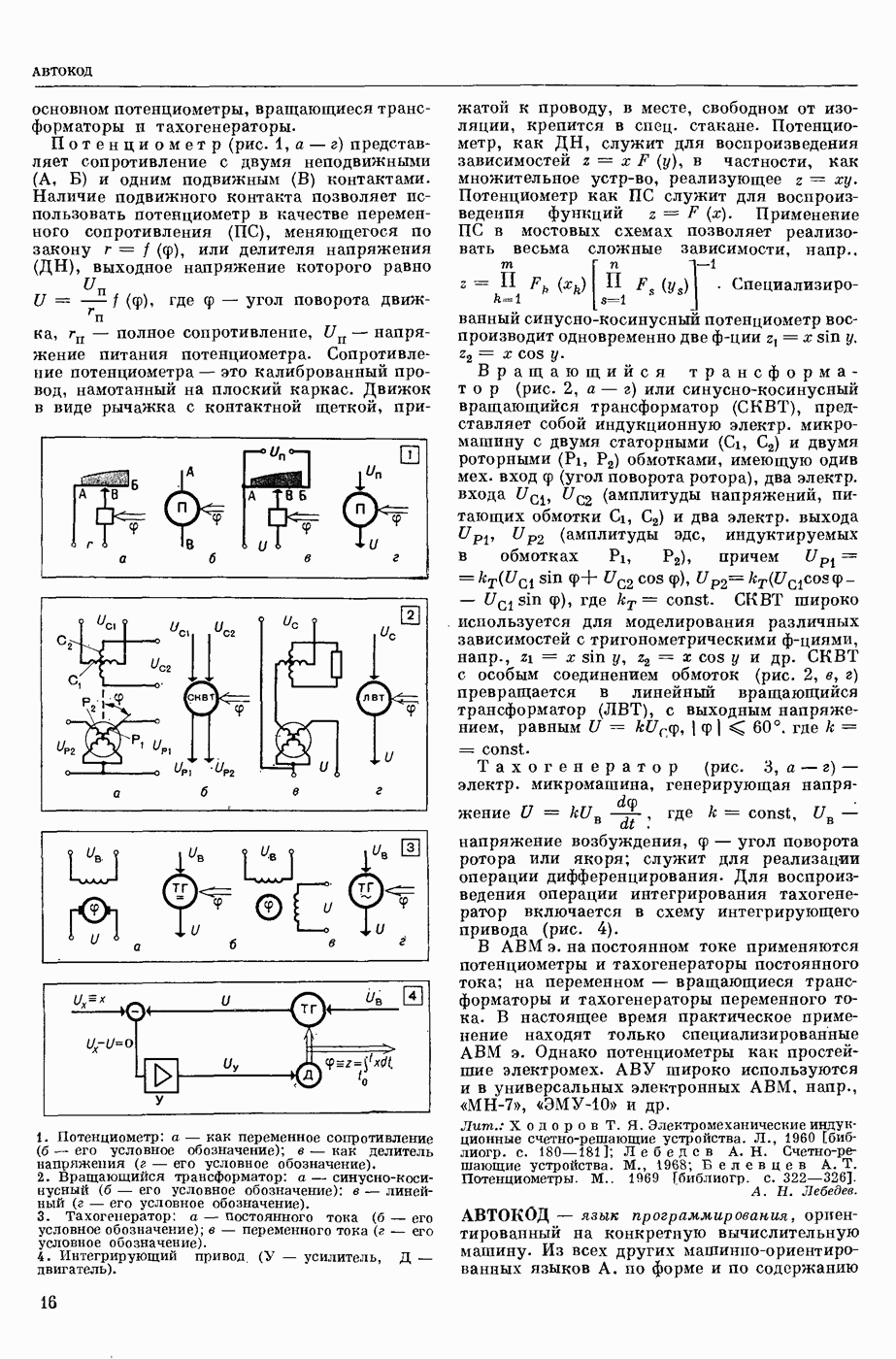
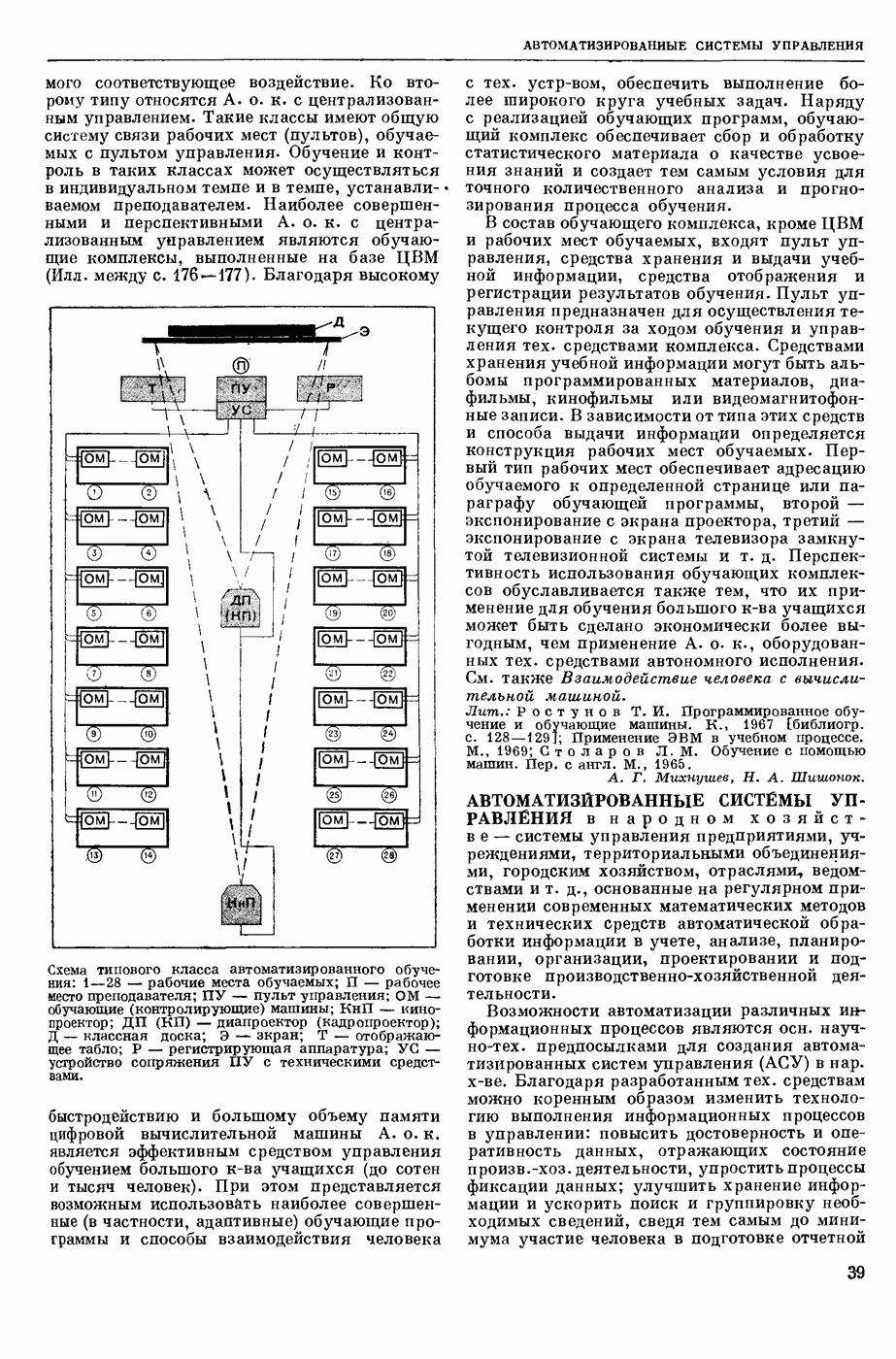
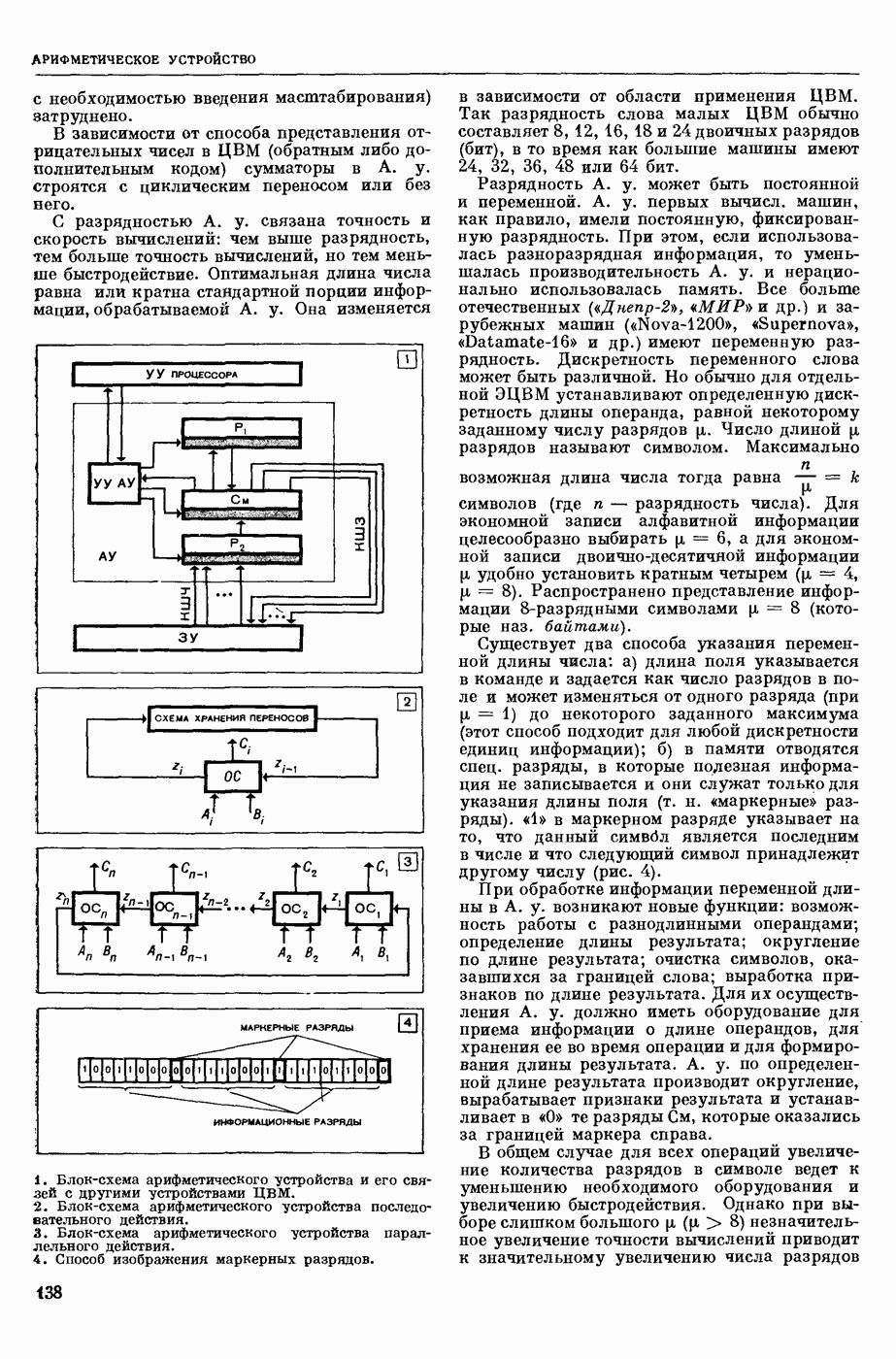
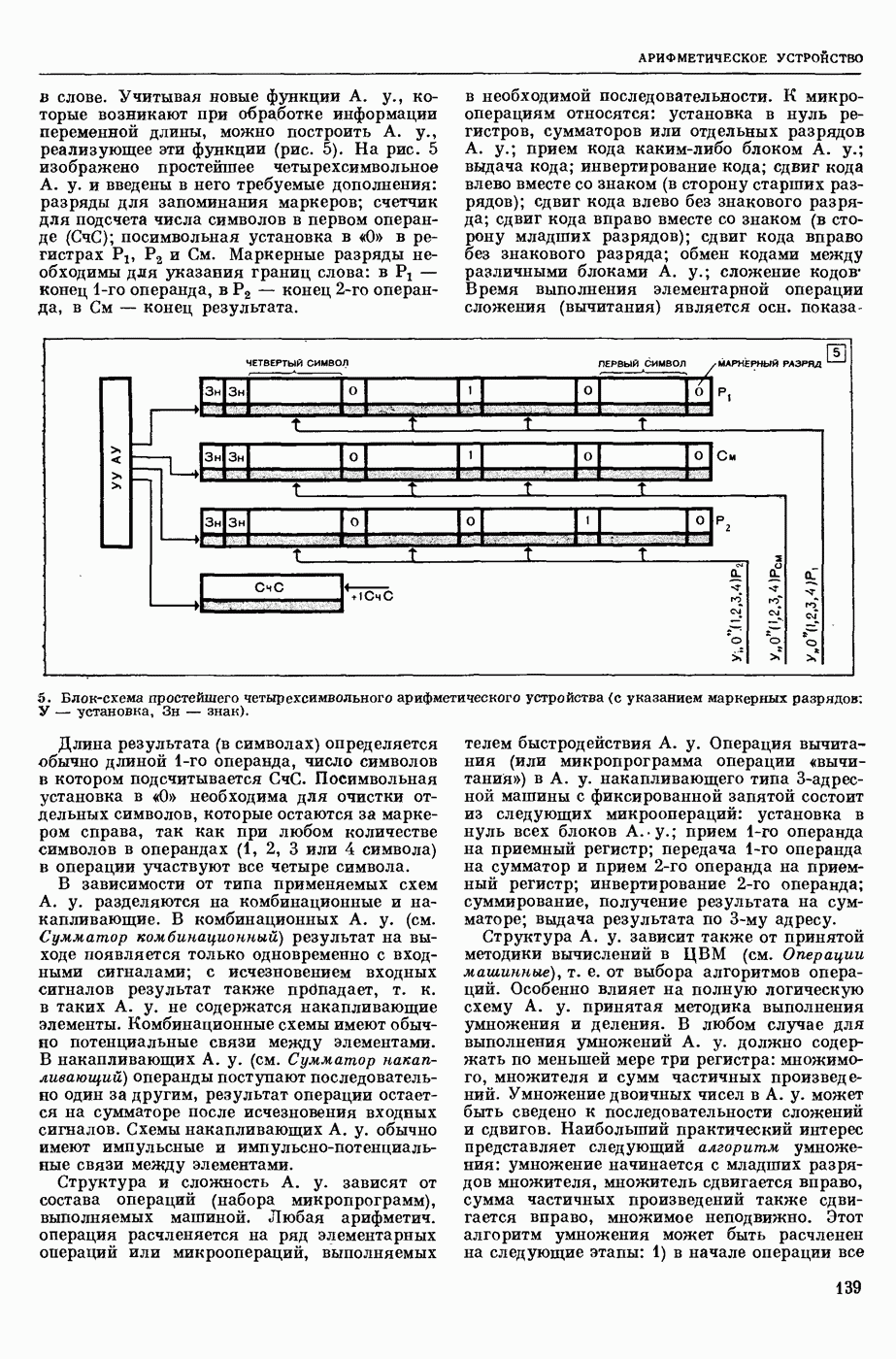
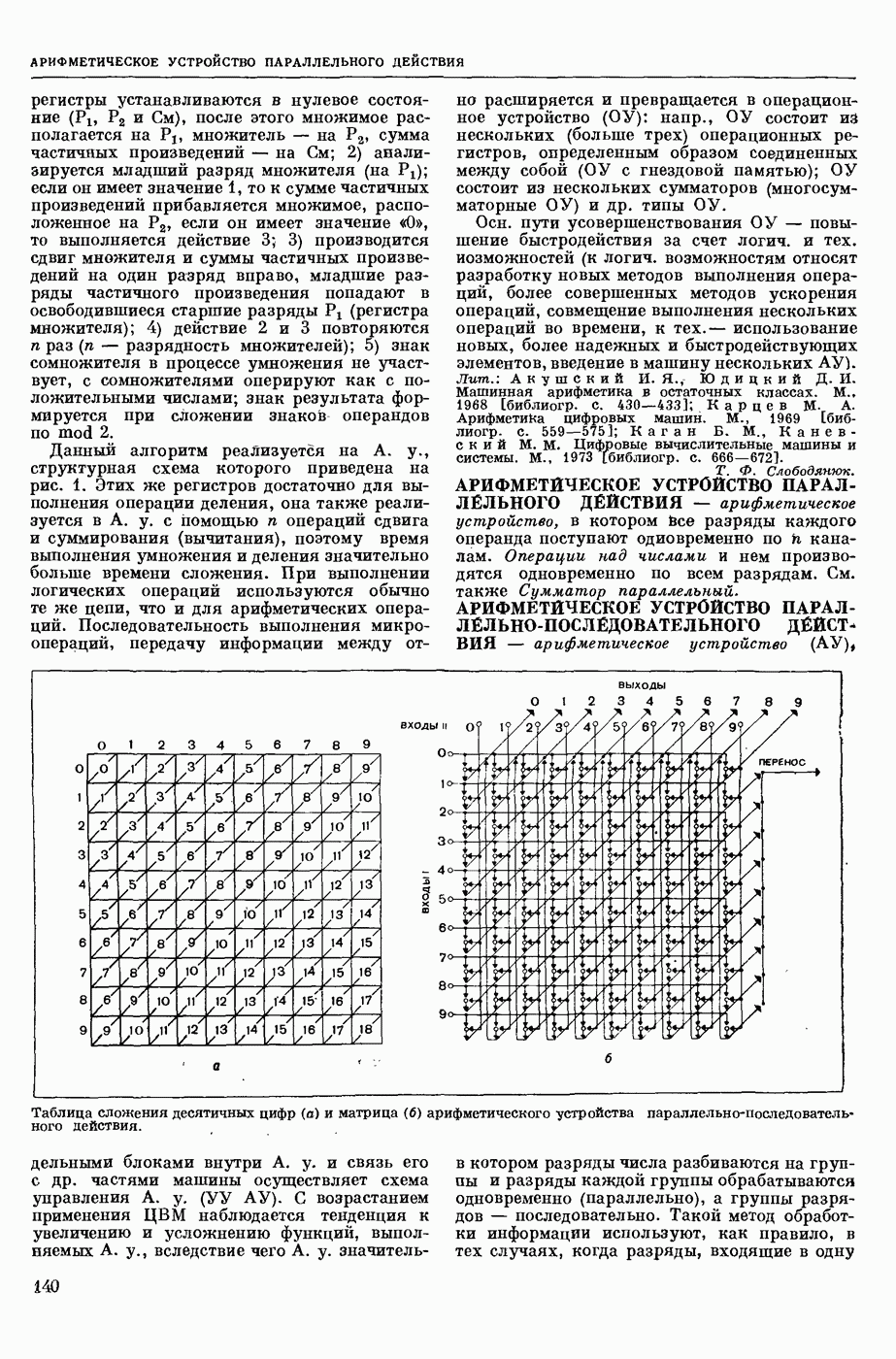
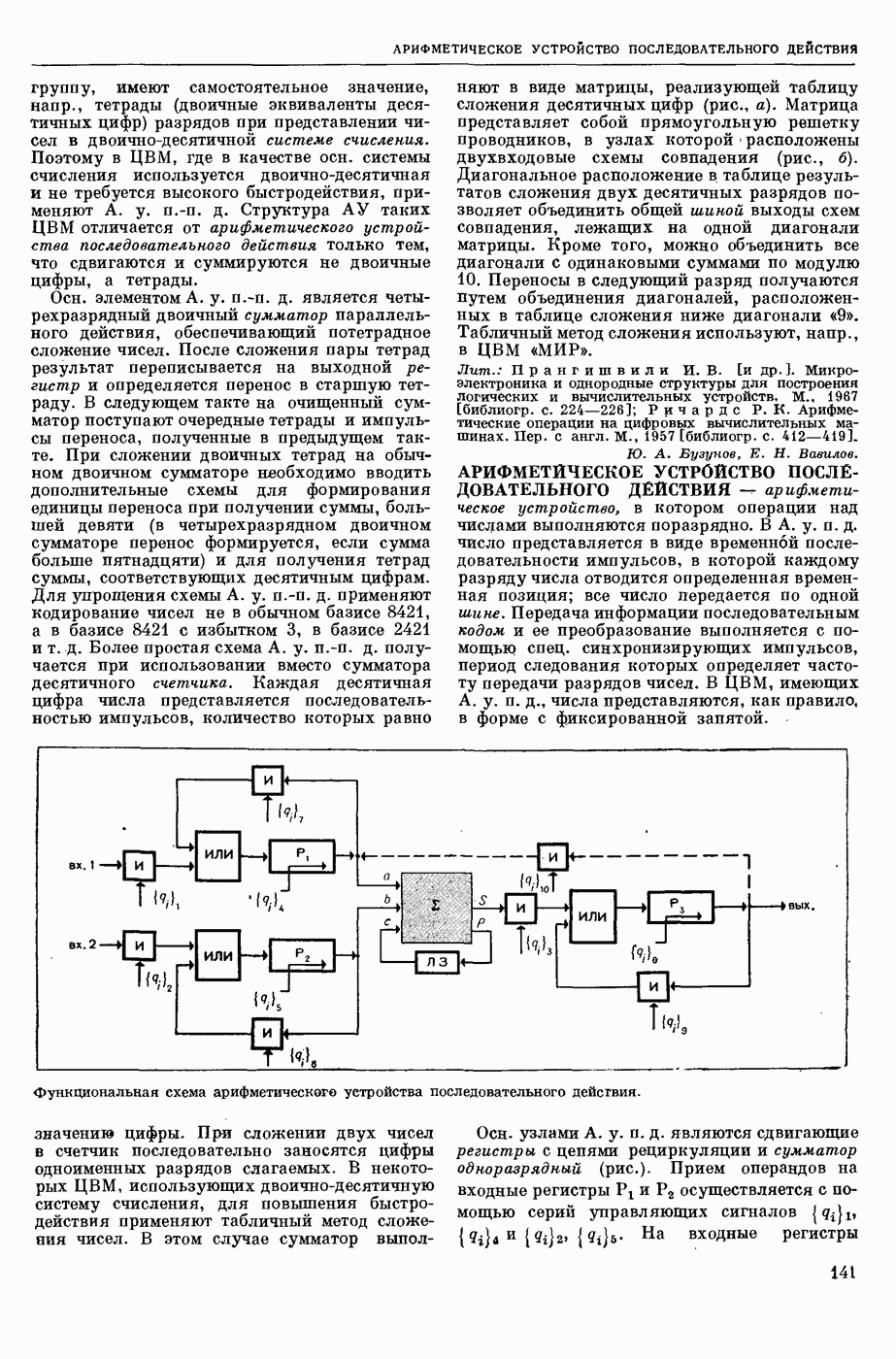
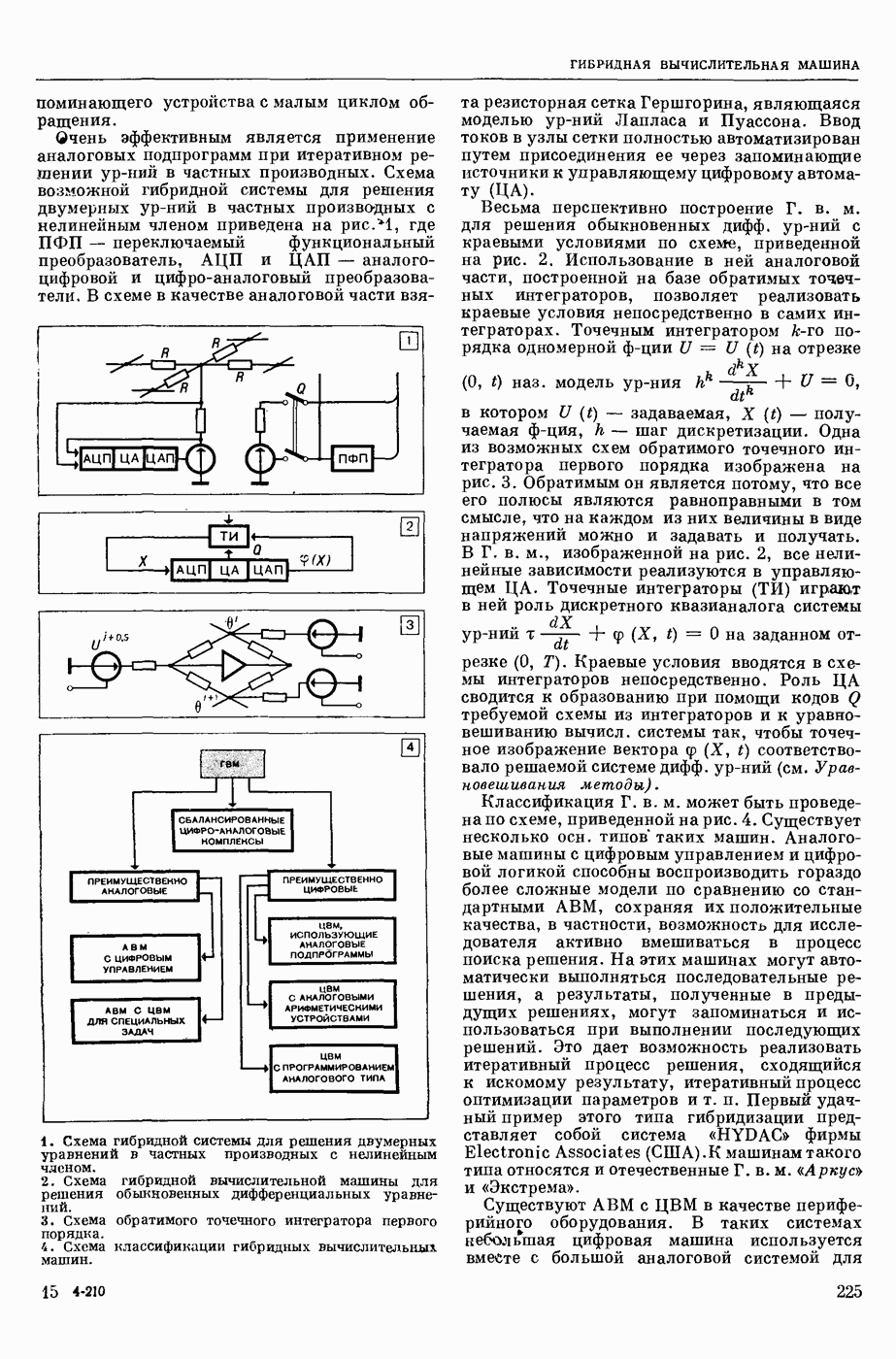
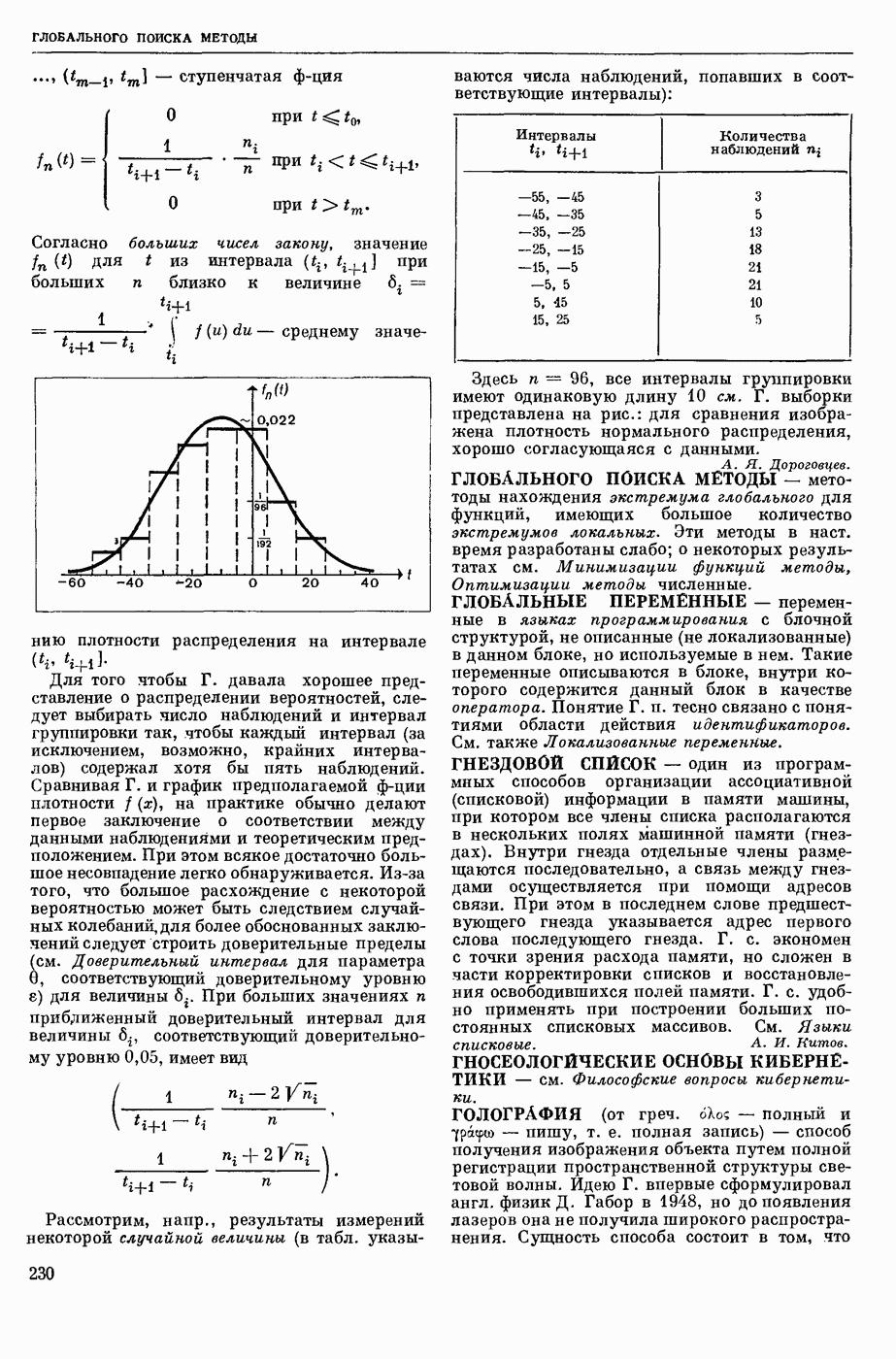
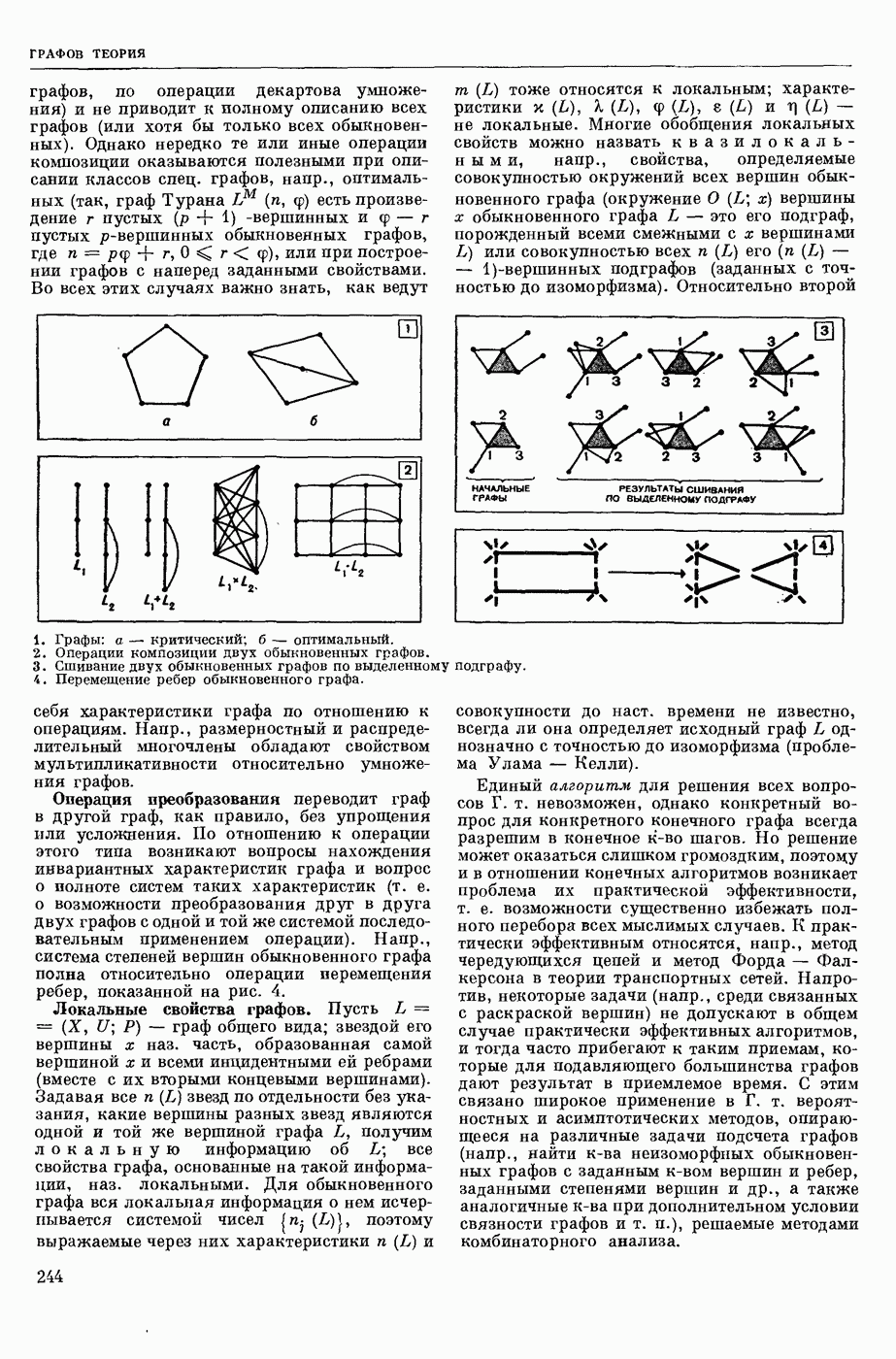
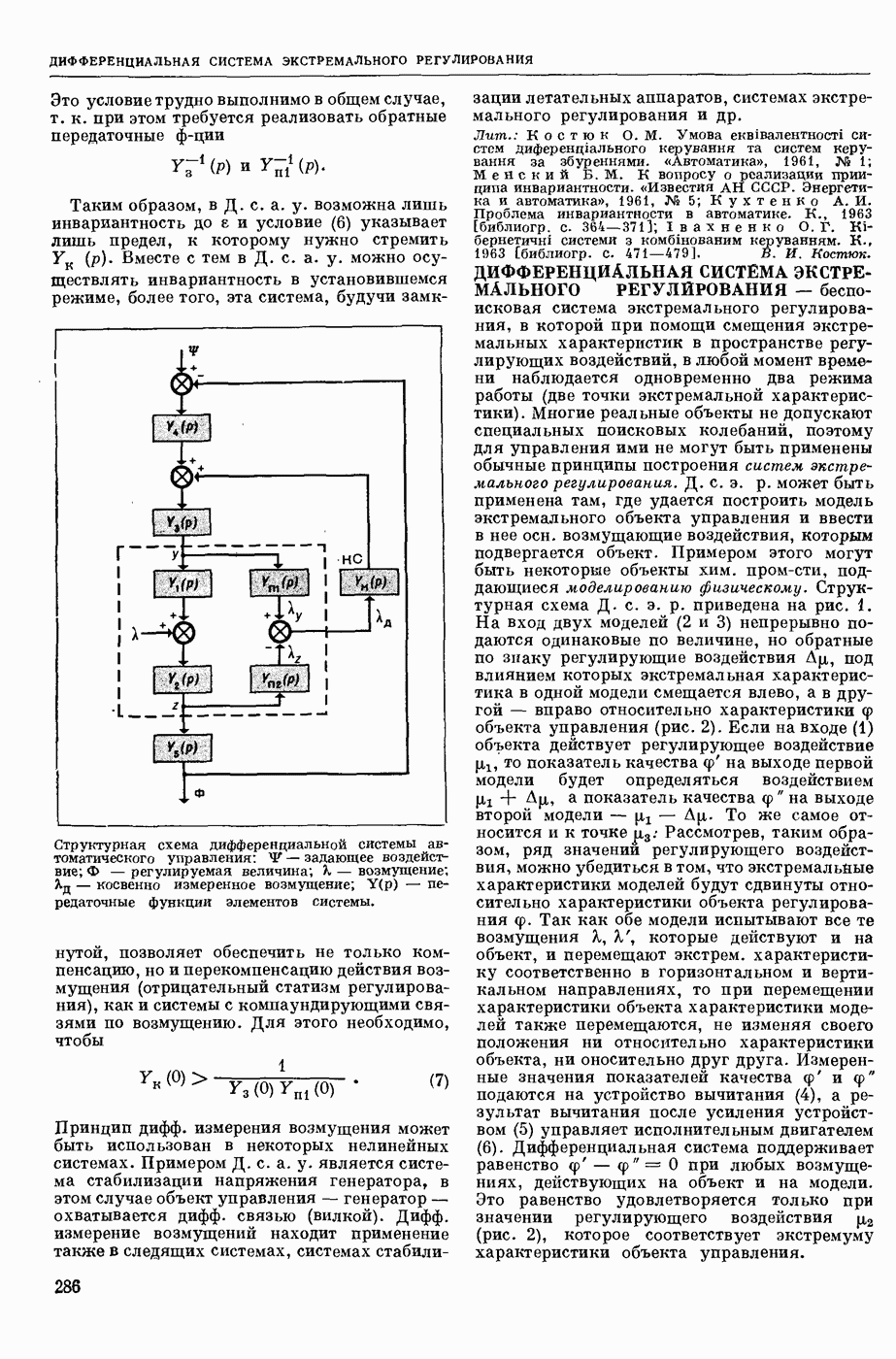
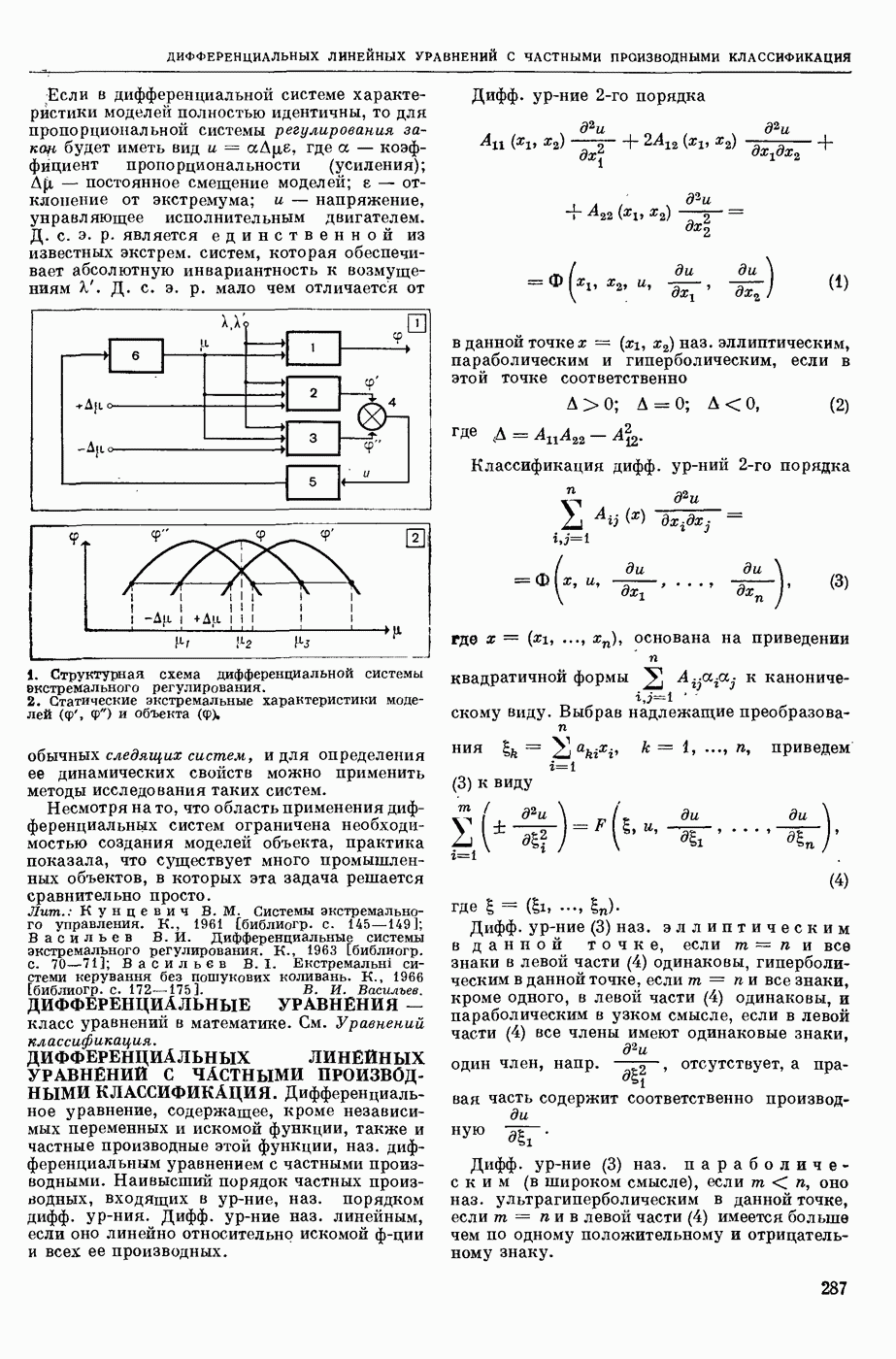
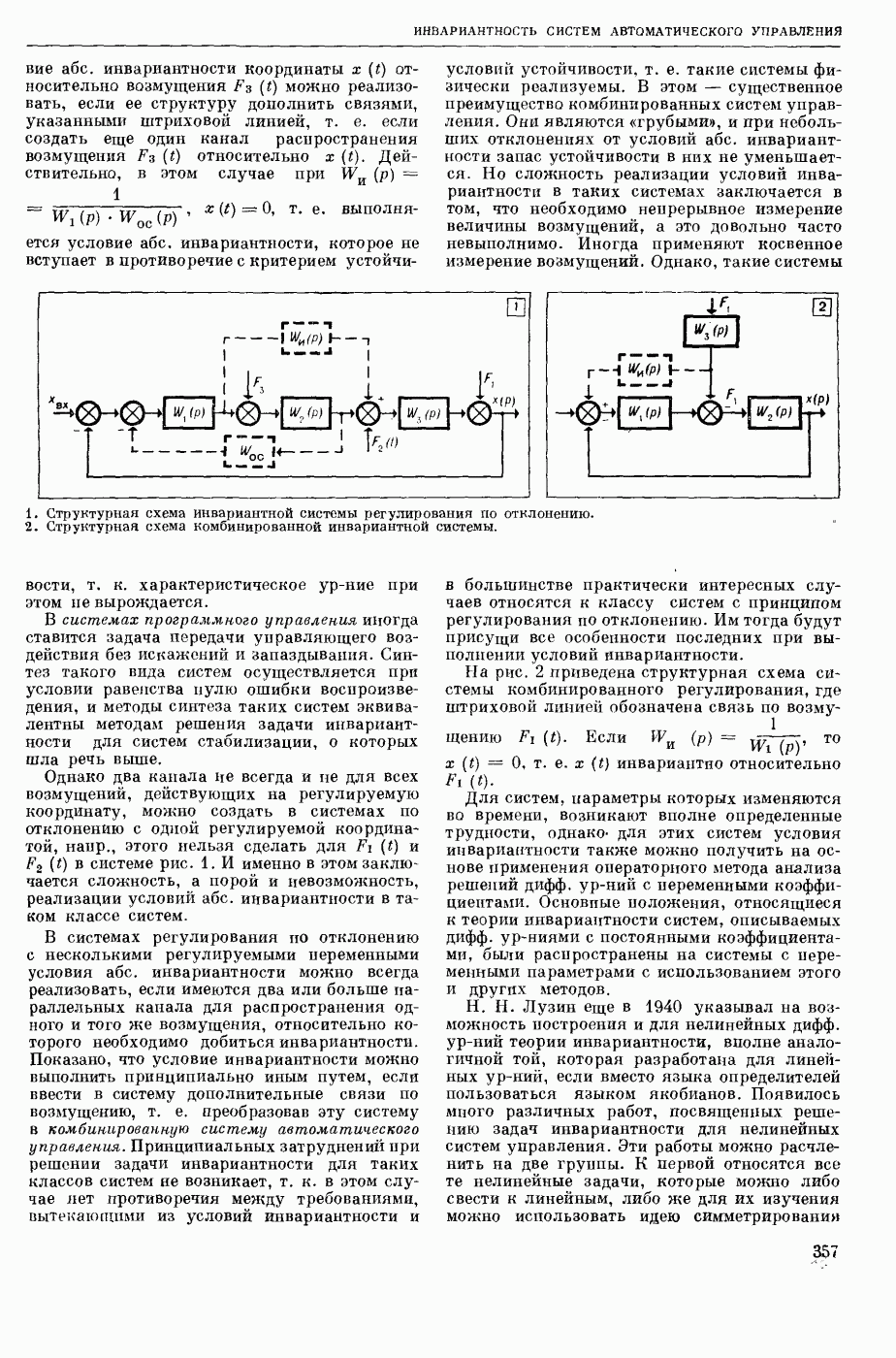
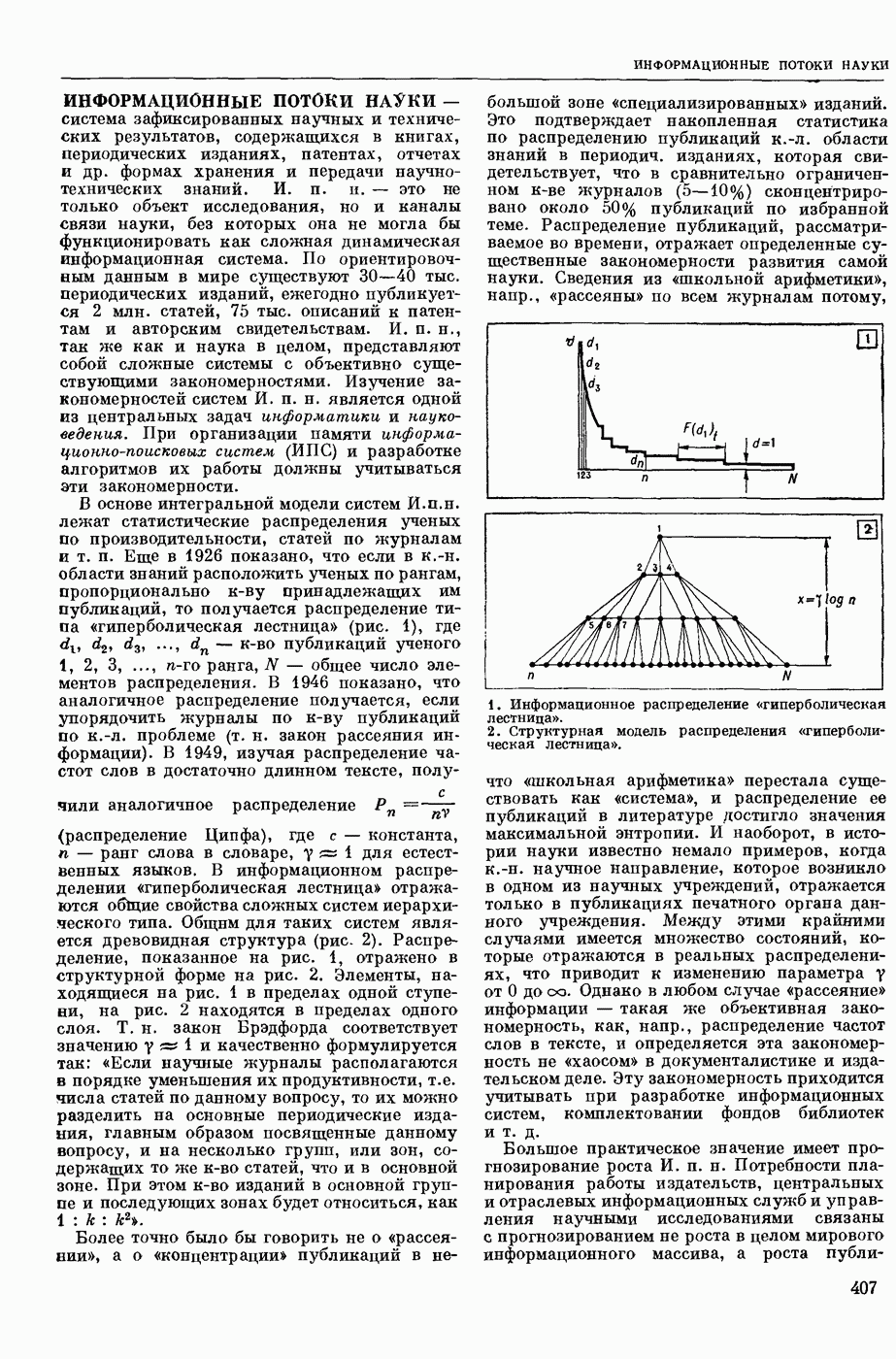
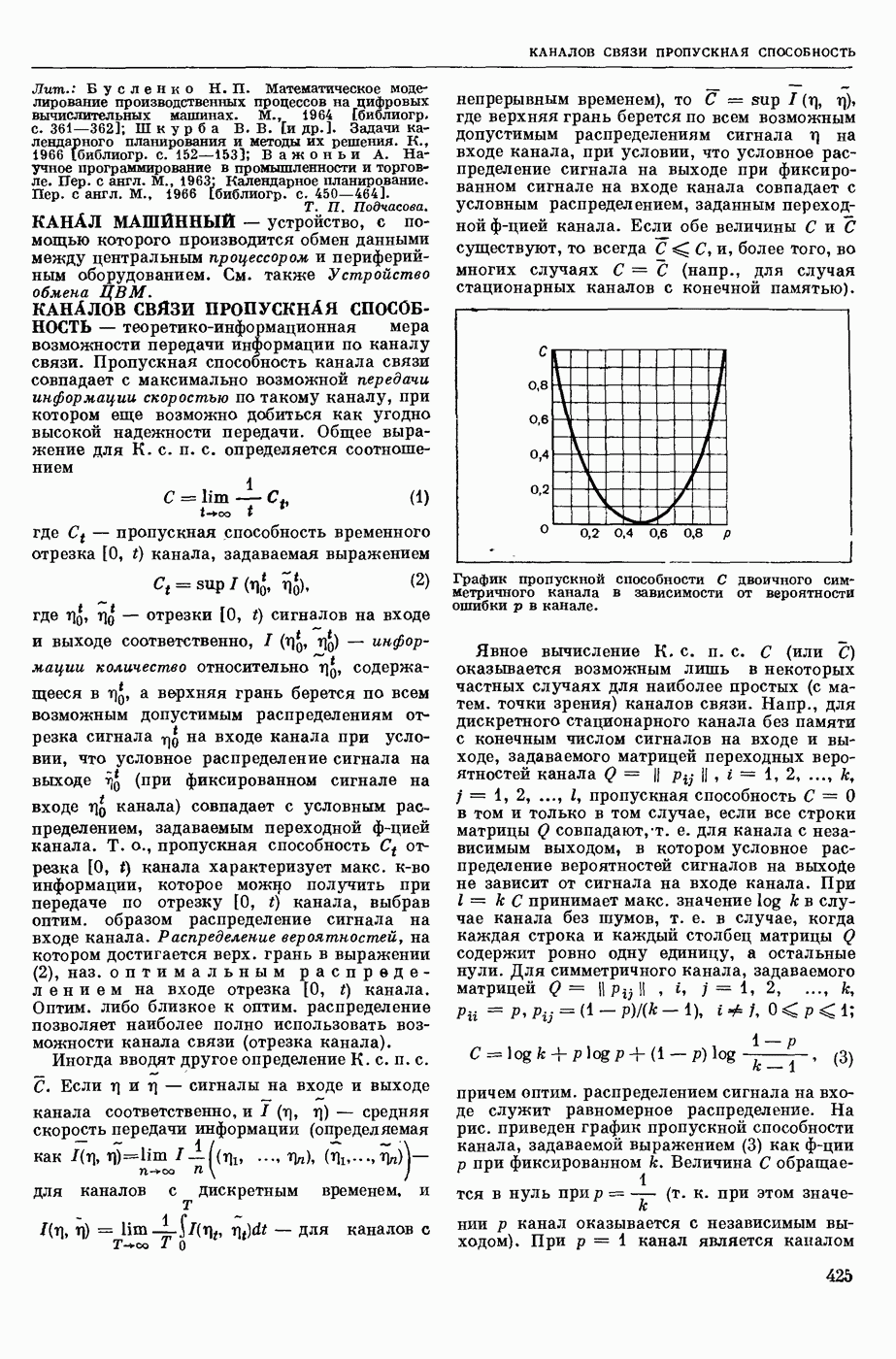
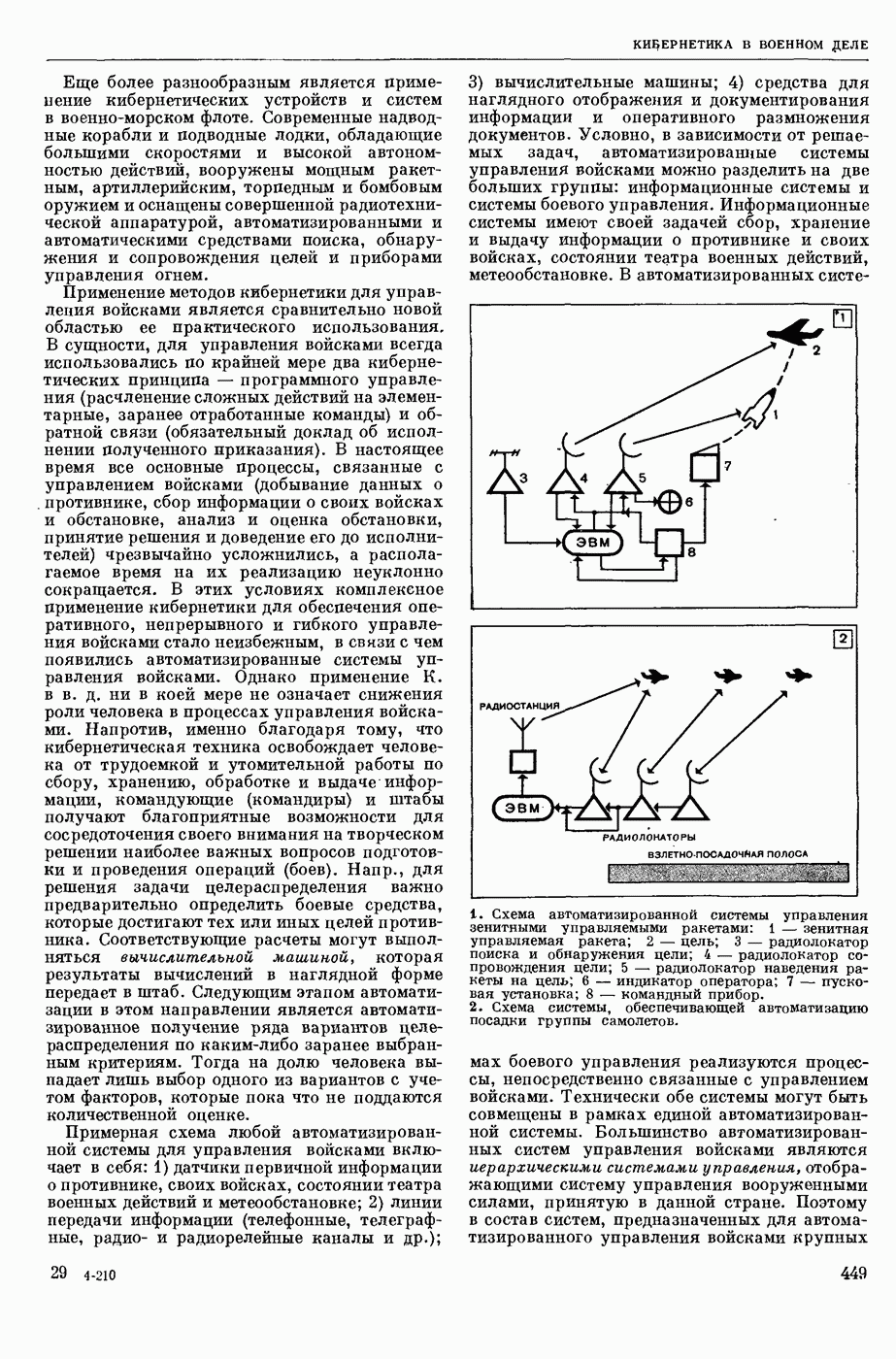
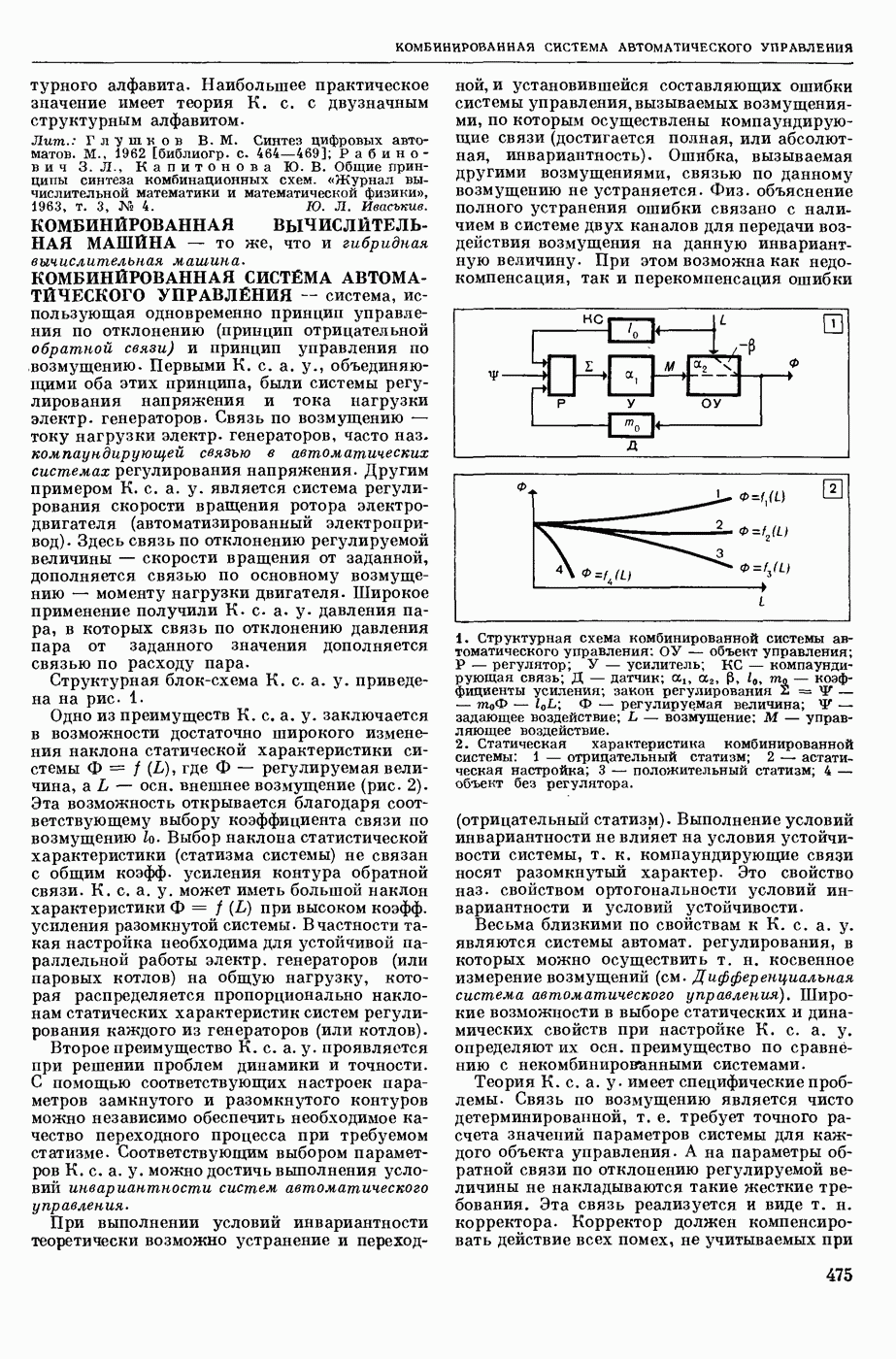
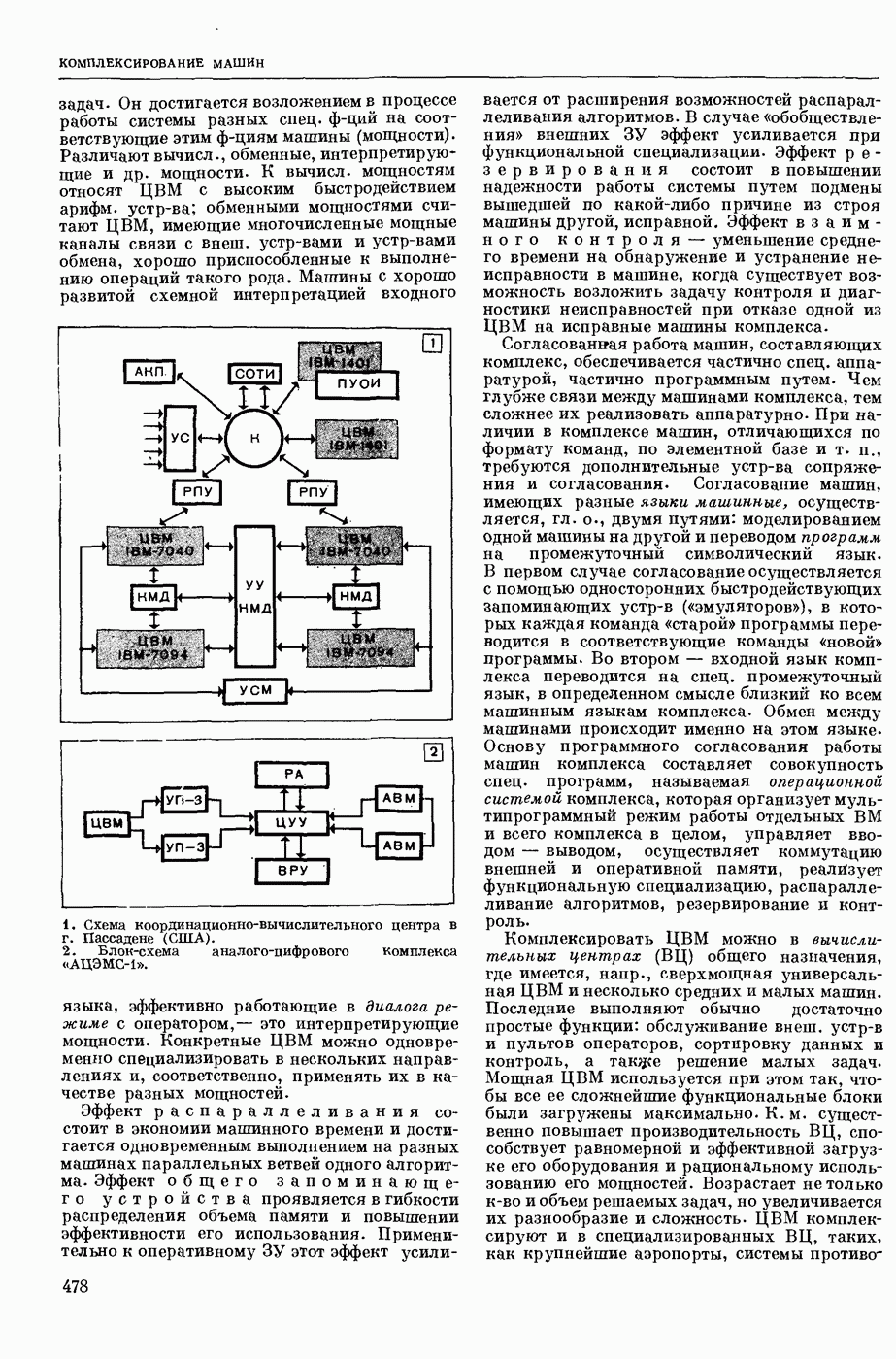
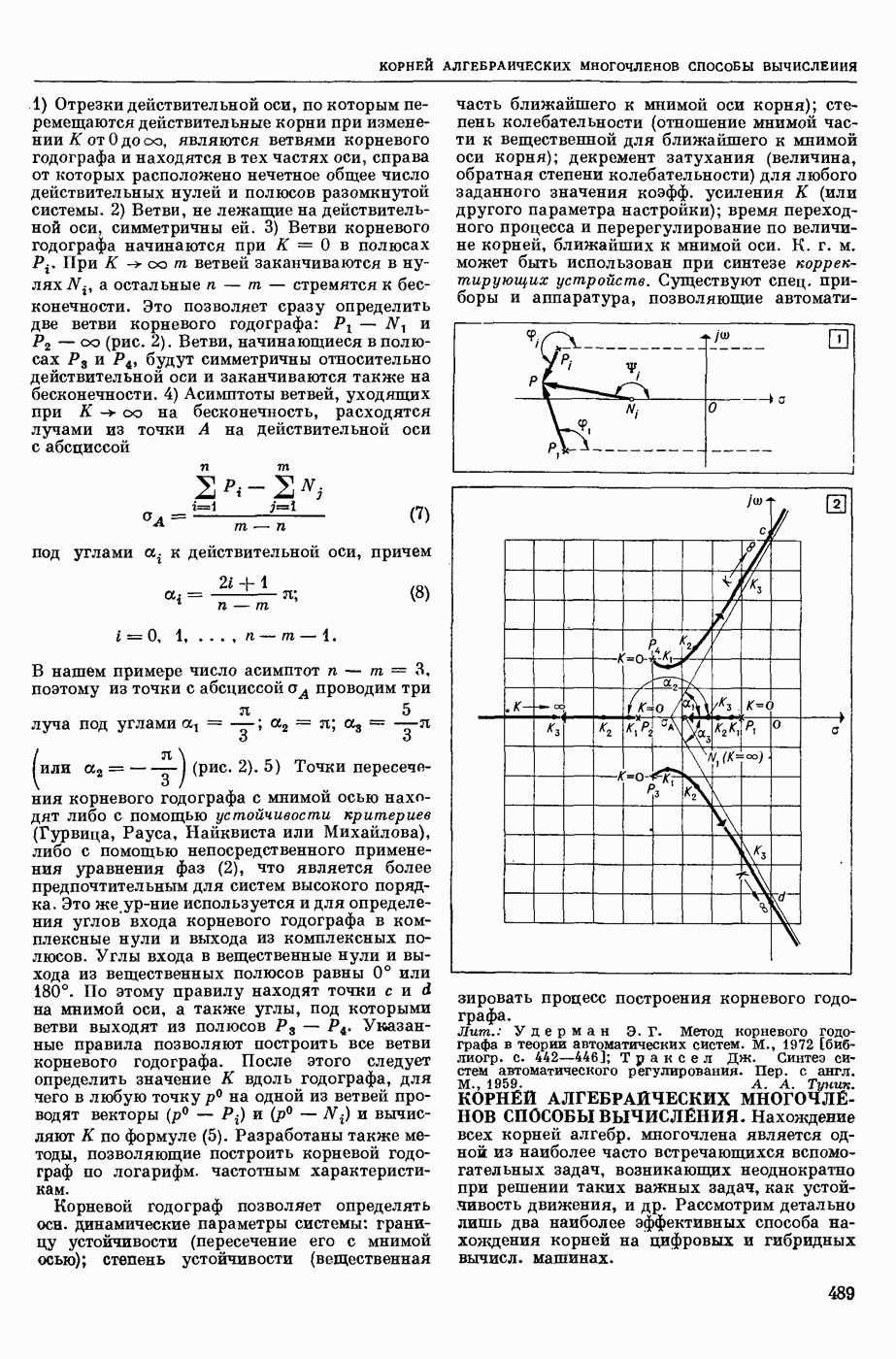
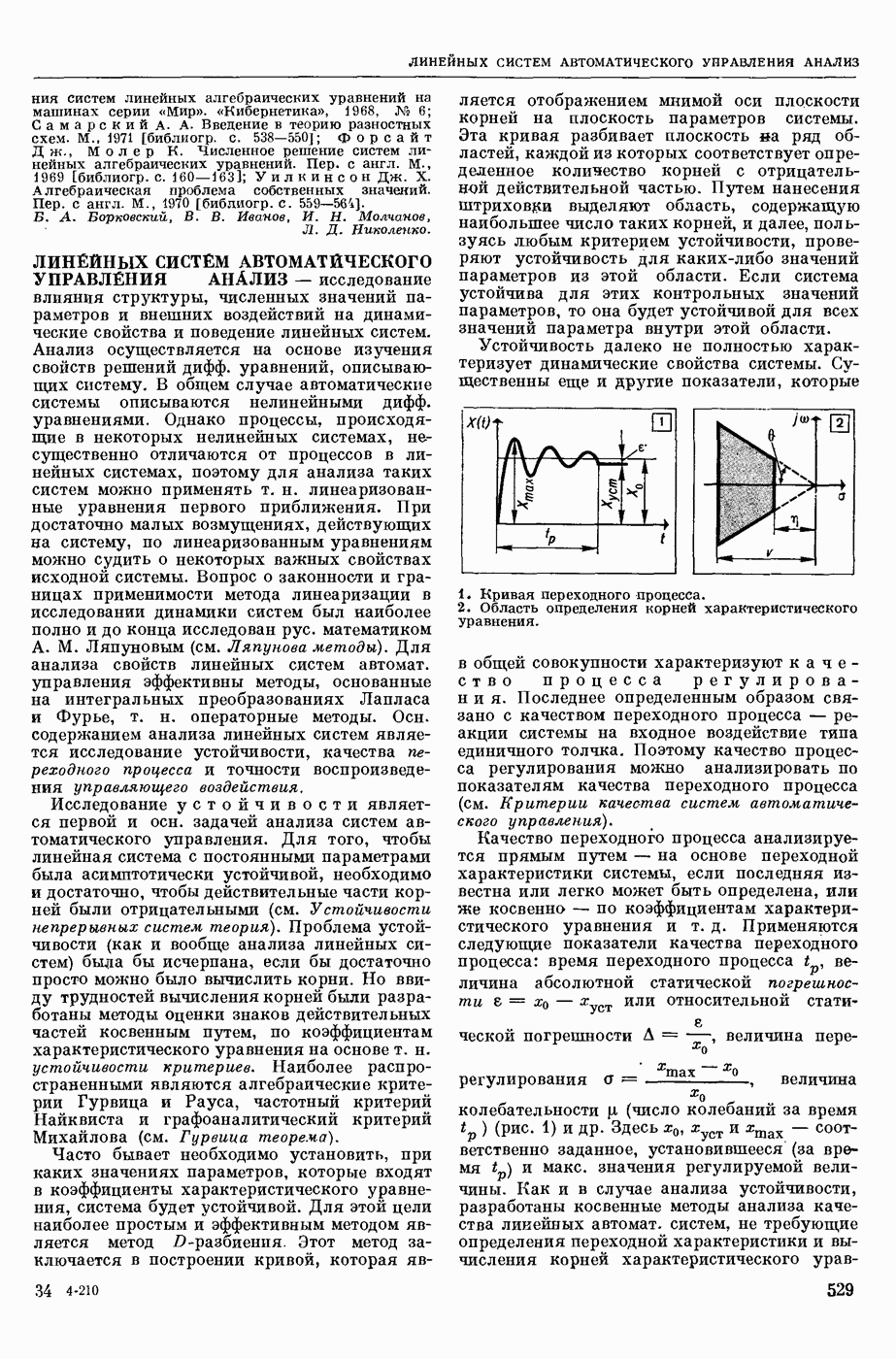
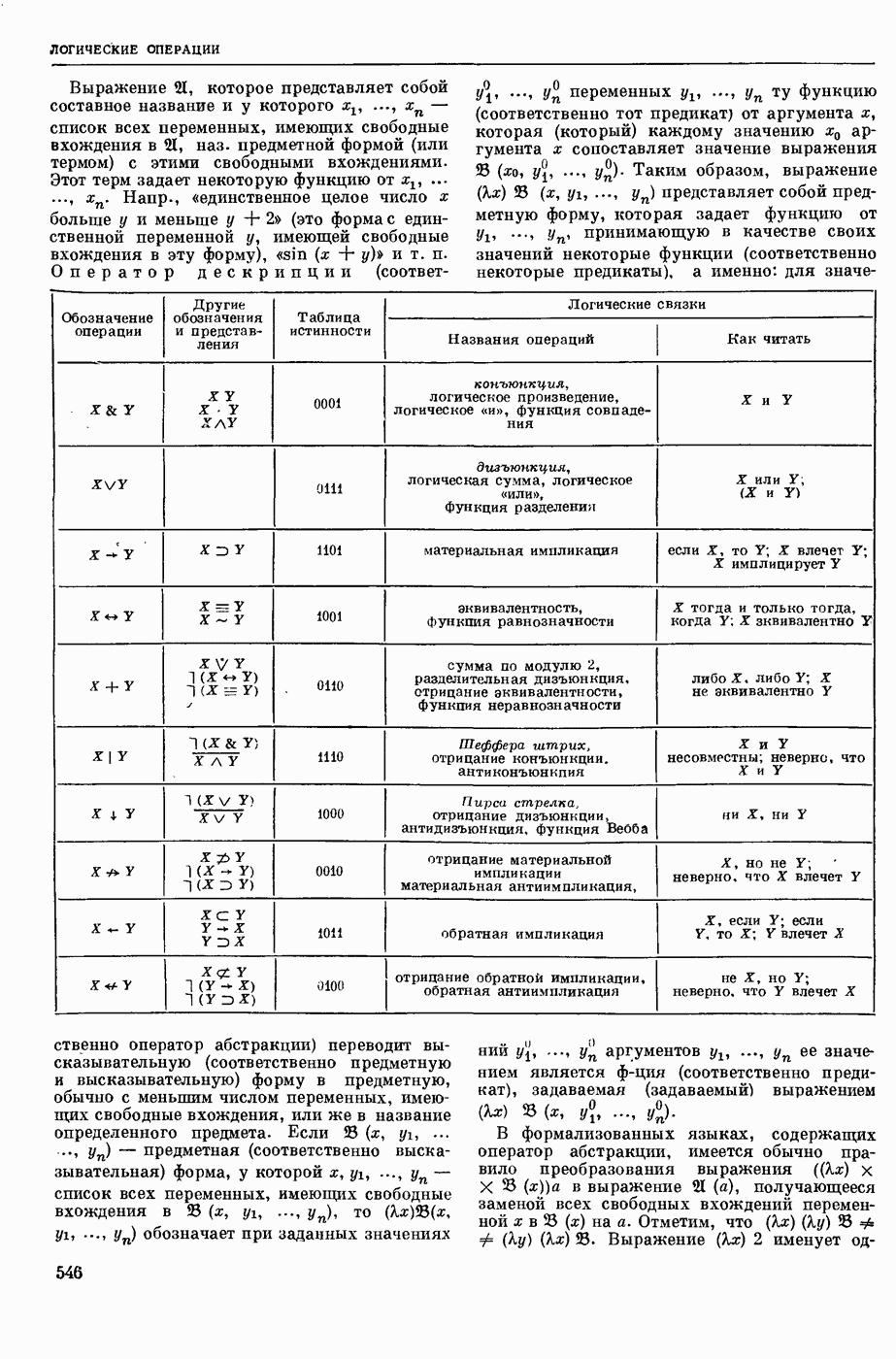
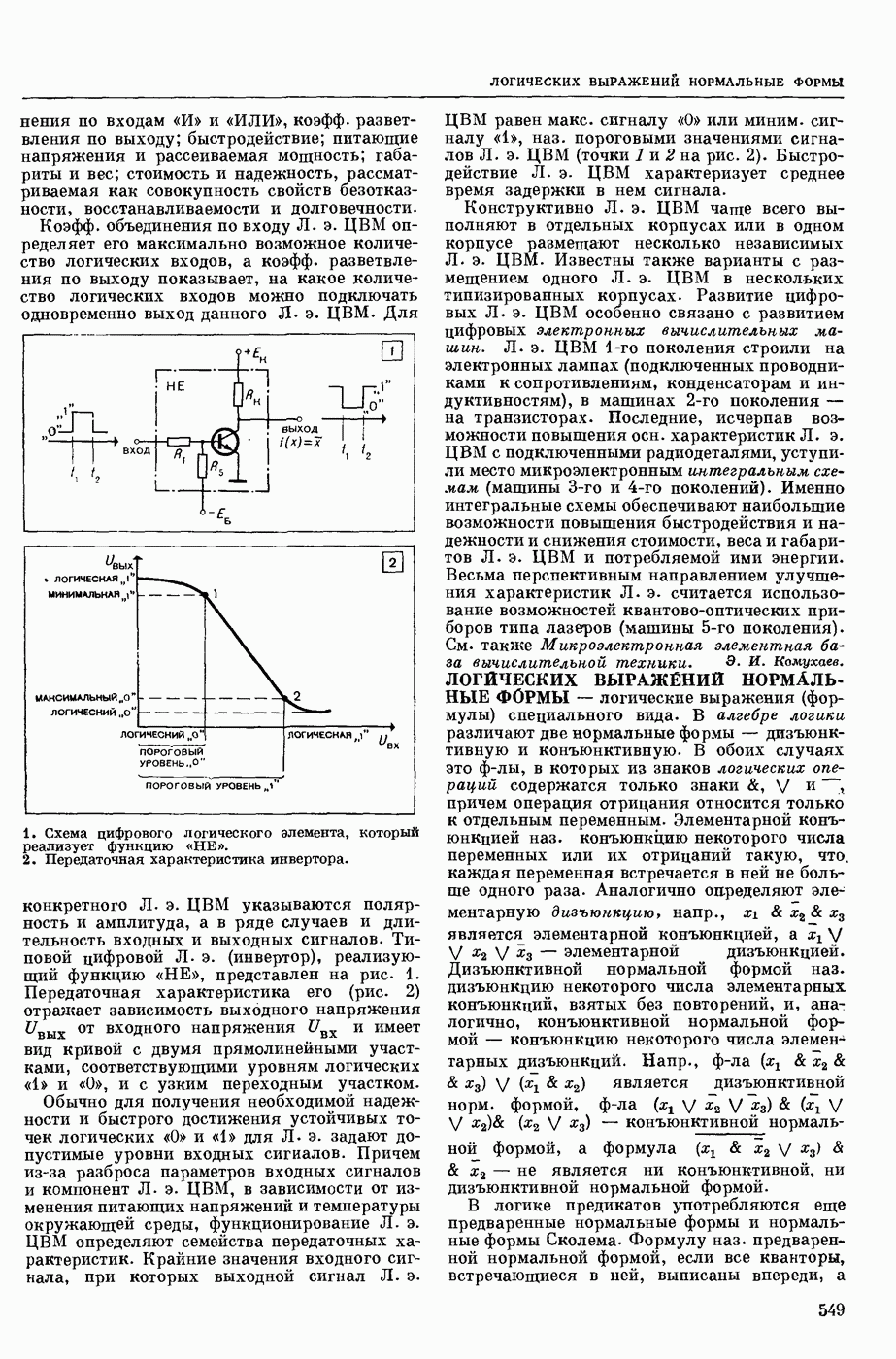
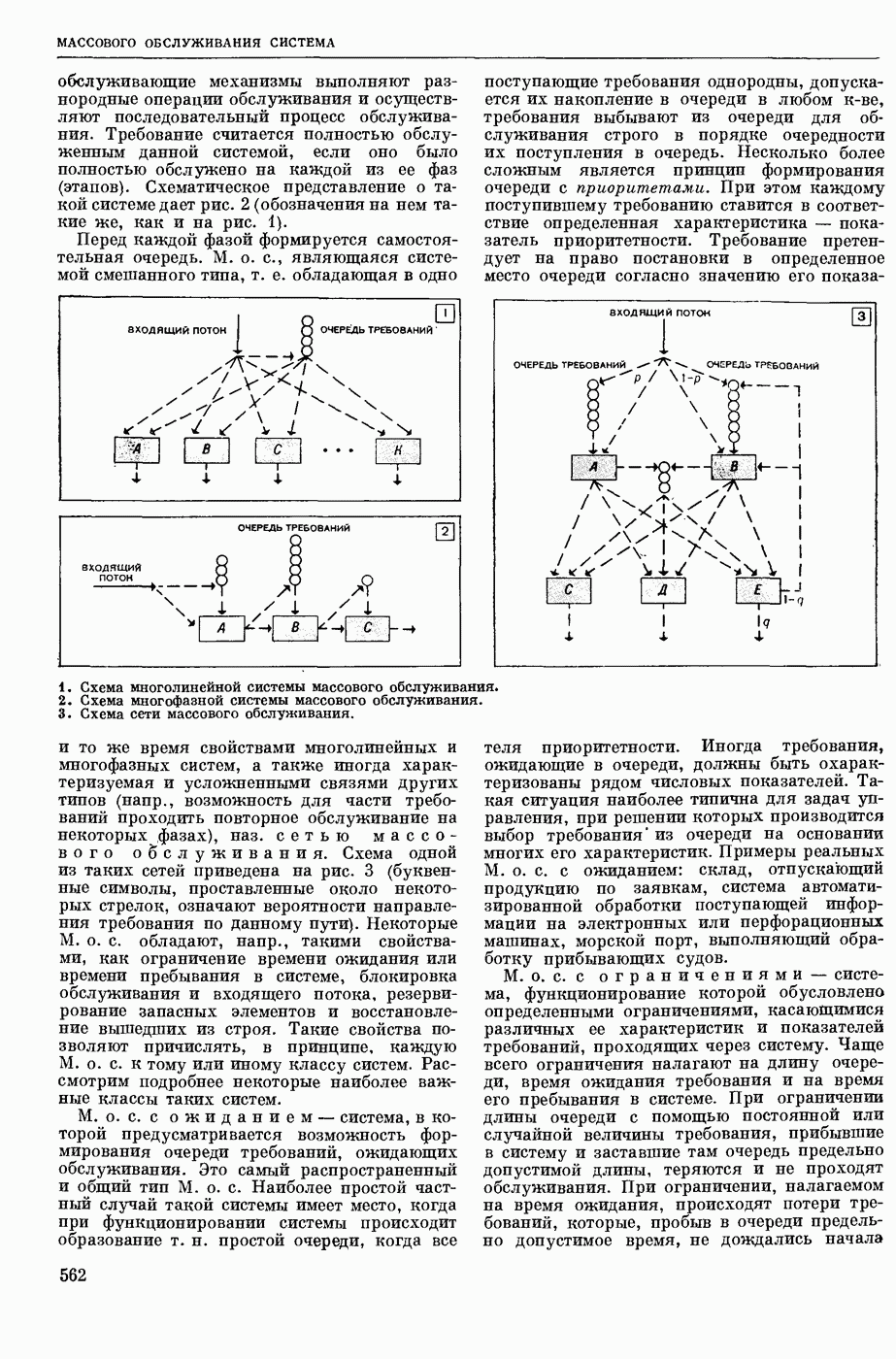
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
КОРРЕЛЯТОР, коррелометр, коррелограф
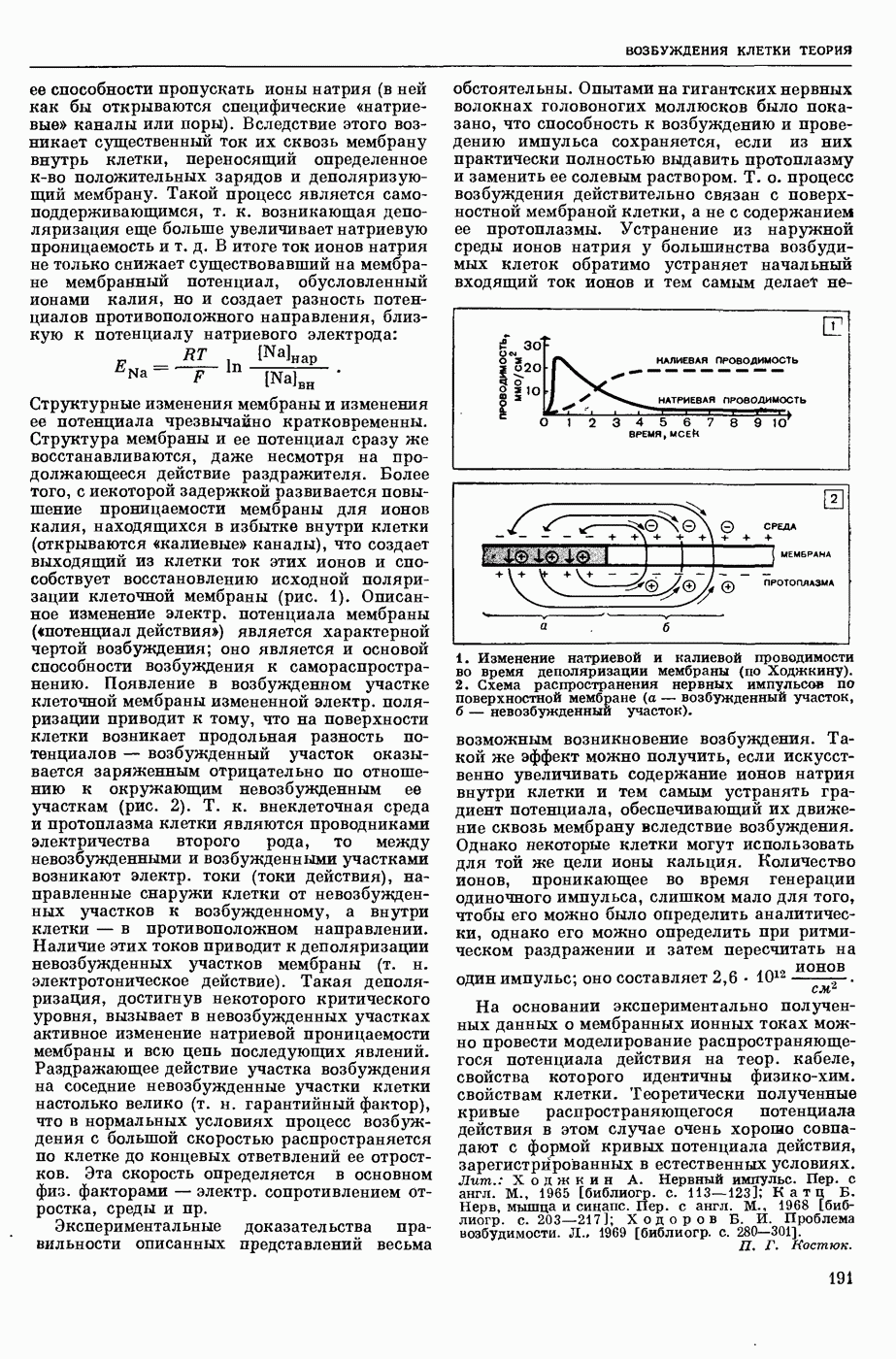
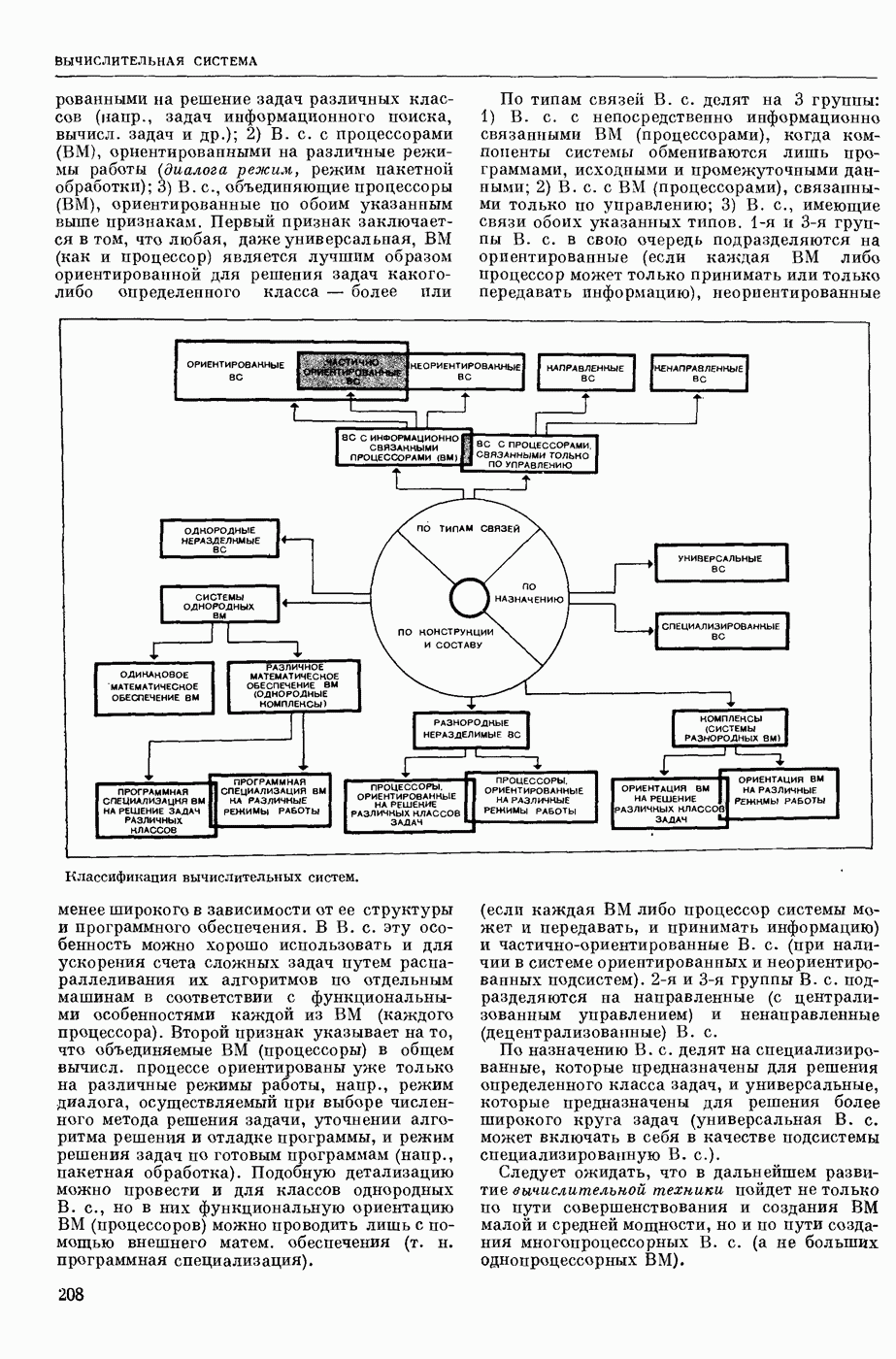
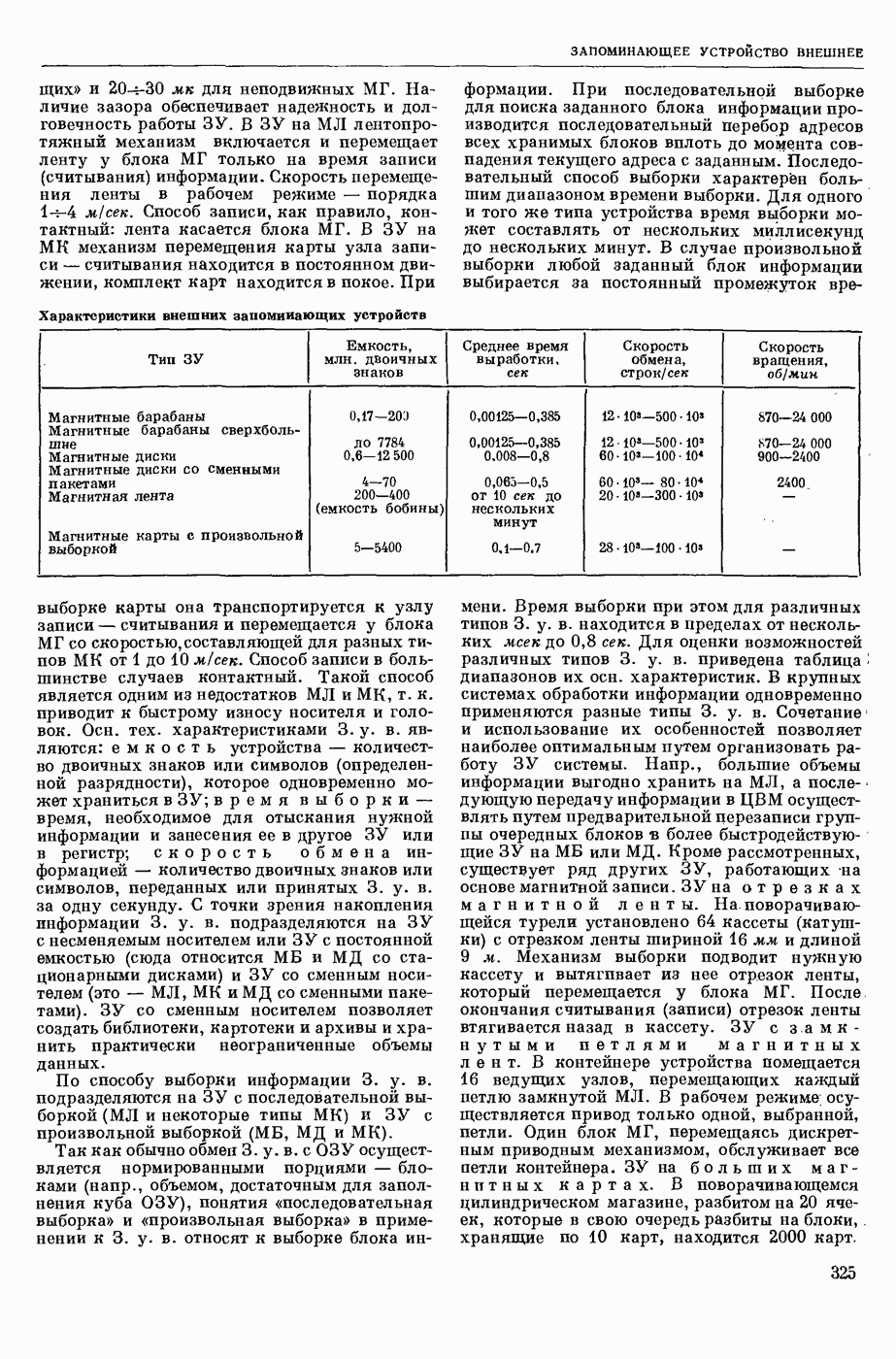
— специализированное устройство для автоматического вычисления автокорреляционных функций и взаимных корреляционных функций стационарных процессов (либо процессов, приводимых к стационарным). Обычно термин «К.» применяется для определения любого преобразователя, выходной сигнал которого можно рассматривать как корреляционную функцию входных сигналов. Такие К. широко применяются в радиотехнике, технике автоматического управления и т. д. К., вычисляющий некоторую совокупность значений корреляционной функции, соответствующую определенному интервалу изменения ее аргумента (временных задержек), и снабженный измерительный прибором для отсчетов этих значений, обычно наз. коррелометром. К., обеспечивающий автоматическую регистрацию графиков корреляционной функции (коррелограмм) на каких-либо носителях (бумажной ленте, киноленте), наз. коррелографом.При аппаратурном вычислении корреляционных функций стационарных случайных процессов предполагается, что эти процессы обладают свойством эргодичности (см. Эргодическая теория). Это позволяет использовать в К. усреднение по времени. Вычисление корреляционных функций требует бесконечно большого интервала усреднения, однако на практике всегда приходится ограничиваться интервалом конечной длительности, т. е. К. вычисляет не корреляционную функцию случайного процесса, а ее оценку:

где Т — интервал усреднения,  центрированное значение случайного процесса
центрированное значение случайного процесса  математическое ожидание случайного процесса
математическое ожидание случайного процесса  . Длительность интервала усреднения зависит от спектрального состава исследуемых случайных процессов и необходимой степени точности вычисления корреляционных функций.
. Длительность интервала усреднения зависит от спектрального состава исследуемых случайных процессов и необходимой степени точности вычисления корреляционных функций.
Аналогично вычисляется оценка взаимной корреляционной функции случайных процессов 

где х (t) и у (t) - центрированные значения случайных процессов  .
.
Ввиду того, что практически могут быть реализованы лишь положительные задержки  , при вычислении автокорреляционной функции ее значения определяют только для положительных
, при вычислении автокорреляционной функции ее значения определяют только для положительных  , что, однако, не имеет существенного значения, т. к.
, что, однако, не имеет существенного значения, т. к.  . При определении значений взаимной корреляционной функции
. При определении значений взаимной корреляционной функции  для отрицательных
для отрицательных  учитывают, что
учитывают, что  Это позволяет менять местами входные сигналы
Это позволяет менять местами входные сигналы  и определять значения взаимной корреляционной функции
и определять значения взаимной корреляционной функции  при положительных
при положительных  .
.
Наибольшее распространение нашли К., в которых вычисляют корреляционные ф-ции с использованием приведенных выше формул. В этих К. входные сигналы (задержанный и незадержанный) перемножают, в связи с чем они получили название мультипликационных К., или К. с умножением входных сигналов.

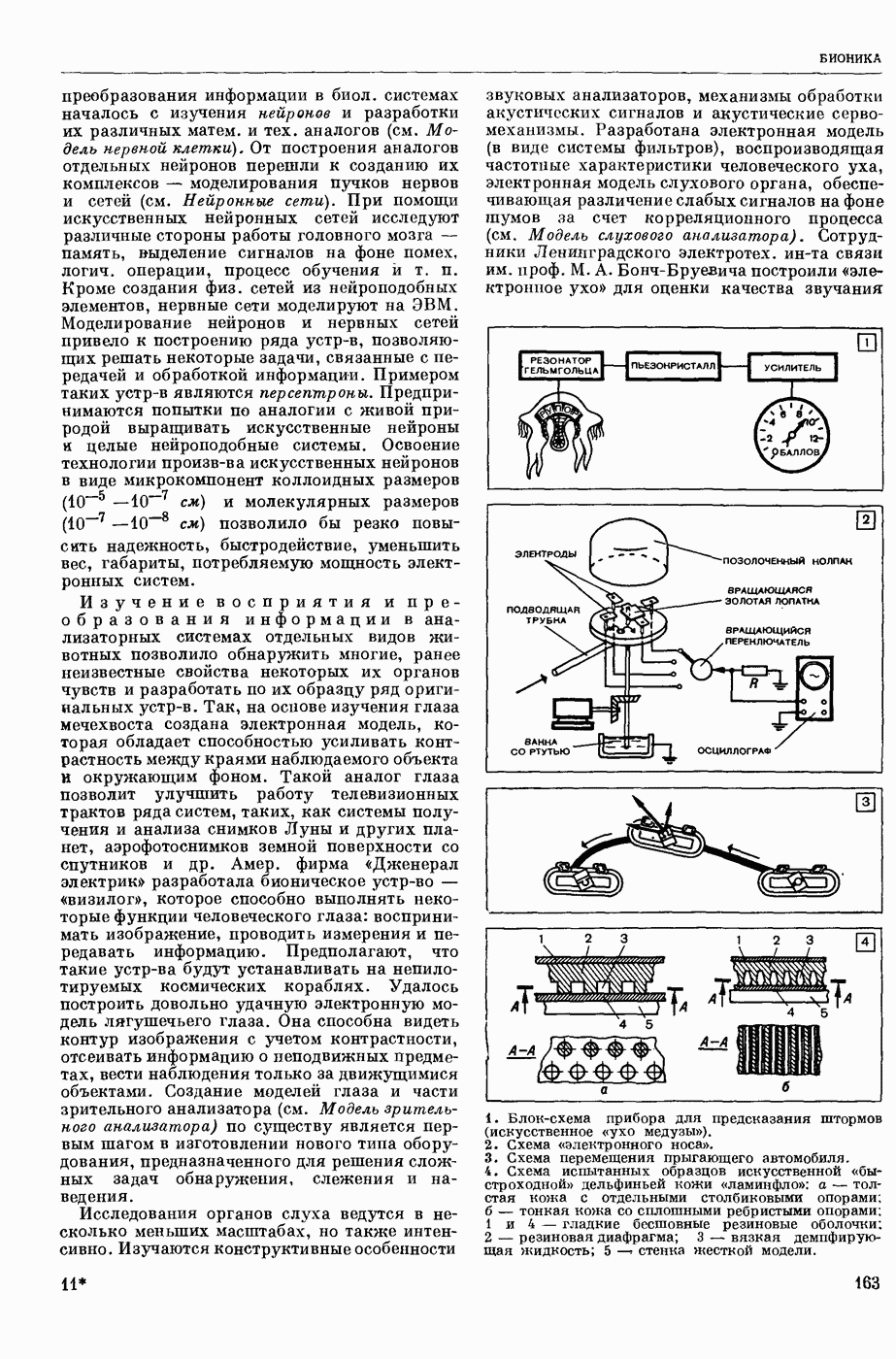
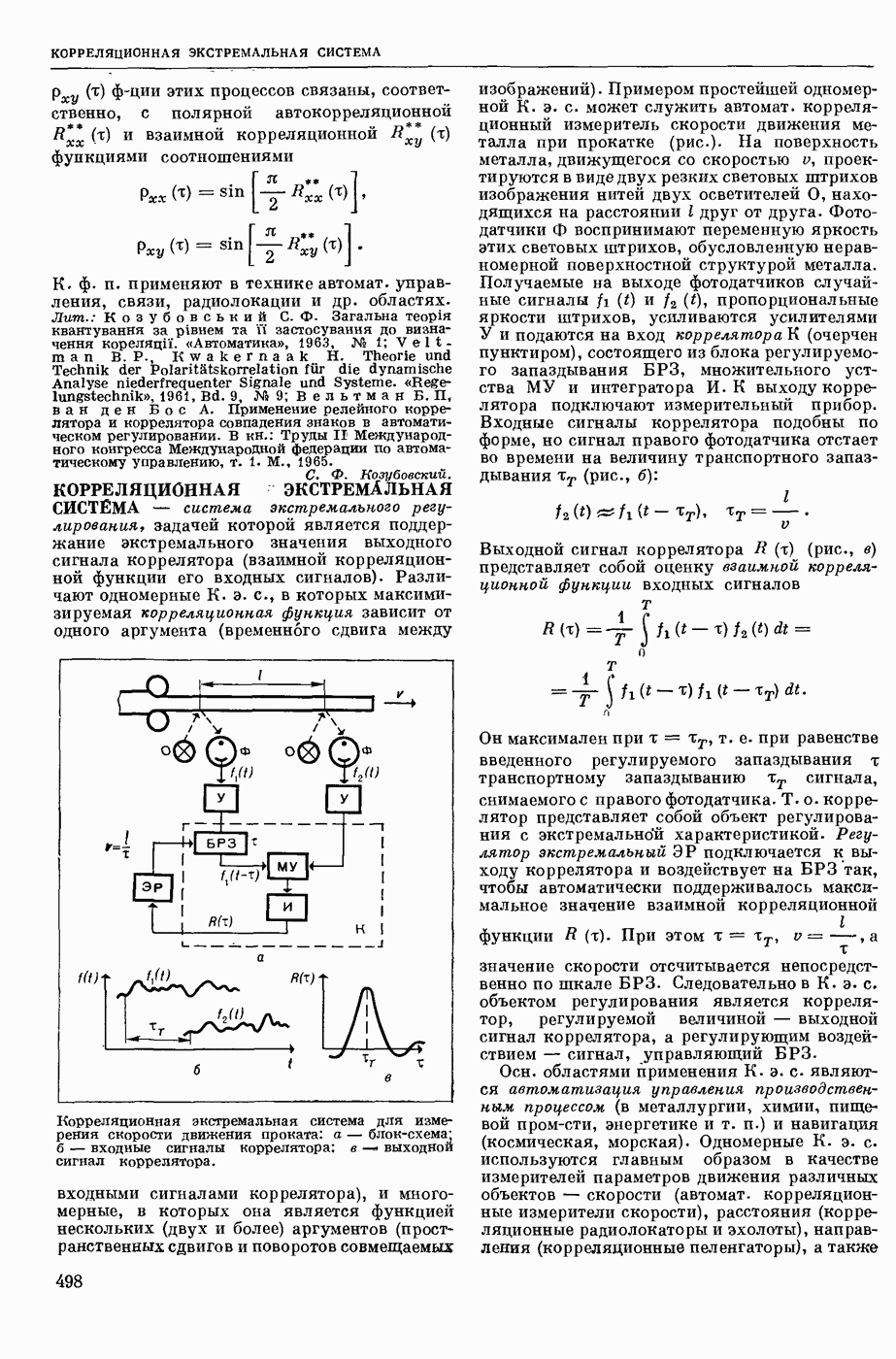
1. Блок-схема мультипликационного коррелятора (ВУ — входное устройство).
2. Блок-схема мультипликационного коррелятора параллельного действия, вычисляющего пять точек корреляционной функции:  блоки запаздывания; РУ — регистрирующее устройство.
блоки запаздывания; РУ — регистрирующее устройство.
Мультипликационный К. для вычисления взаимной корреляционной функции (рис. 1) осуществляет: преобразование входных сигналов  в соответствующие физ. величины (напряжение, ток, световой поток) с предварительной обработкой их (центрирование, квантование по уровню или по времени и т. д.); относительный сдвиг (задержку) одного из сигналов на время
в соответствующие физ. величины (напряжение, ток, световой поток) с предварительной обработкой их (центрирование, квантование по уровню или по времени и т. д.); относительный сдвиг (задержку) одного из сигналов на время  в блоке регулируемого запаздывания БРЗ (см. Запаздывания блок), перемножение двух сигналов
в блоке регулируемого запаздывания БРЗ (см. Запаздывания блок), перемножение двух сигналов  и
и  в множительном устройстве МУ; усреднение полученного произведения в течение интервала времени Т в усредняющем (или интегрирующем) звене И (см. Устройство интегрирующее), показ или регистрацию вычисленных значений корреляционной функции, соответствующих заданным значениям аргумента
в множительном устройстве МУ; усреднение полученного произведения в течение интервала времени Т в усредняющем (или интегрирующем) звене И (см. Устройство интегрирующее), показ или регистрацию вычисленных значений корреляционной функции, соответствующих заданным значениям аргумента  с помощью индикаторного, или регистрирующего, устройства ИУ.
с помощью индикаторного, или регистрирующего, устройства ИУ.
Процесс вычисления корреляционных функций может осуществляться как последовательным, так и параллельным способом. В первом случае вычисление производится последовательно, точка за точкой, для каждого заданного значения  . Для получения всей кривой корреляционной функции операции вычисления повторяются при различных значениях т. при этом
. Для получения всей кривой корреляционной функции операции вычисления повторяются при различных значениях т. при этом  может изменяться как непрерывно, так и дискретно. Полное время вычисления
может изменяться как непрерывно, так и дискретно. Полное время вычисления  где Т — время усреднения при вычислении одной точки корреляционной функции,
где Т — время усреднения при вычислении одной точки корреляционной функции,  вычисленных точек. Для параллельного способа вычисления К. выполняется в виде многоканального устройства с числом каналов, равным числу одновременно вычисляемых Точек корреляционных функций. Каждый канал содержит свое множительное устройство МУ и усредняющее (интегрирующее) звено И, а также устройство задержки, обеспечивающее запаздывание, соответствующее данной точке корреляционной функции. Упрощенная блок-схема мультипликационного К. параллельного действия изображена на рис. 2. Использование схем параллельного действия ускоряет время анализа, однако существенно усложняет схему К.
вычисленных точек. Для параллельного способа вычисления К. выполняется в виде многоканального устройства с числом каналов, равным числу одновременно вычисляемых Точек корреляционных функций. Каждый канал содержит свое множительное устройство МУ и усредняющее (интегрирующее) звено И, а также устройство задержки, обеспечивающее запаздывание, соответствующее данной точке корреляционной функции. Упрощенная блок-схема мультипликационного К. параллельного действия изображена на рис. 2. Использование схем параллельного действия ускоряет время анализа, однако существенно усложняет схему К.
Наряду с мультипликационным К. значительное распространение получили К., в которых операция умножения осуществляется при помощи двух устройств для возведения в квадрат (квадраторов) с использованием выражения

Иногда К. строятся с использованием одного квадратора. В атом случае вычисление корреляционных функций выполняется по формуле

К., использующие квадраторы, наз. интерференционными. Существуют и другие методы вычисления корреляционных функций: компенсационный метод, метод диаграмм рассеяния и пр. Значительное распространение начал получать метод аппроксимации корреляционных функций с помощью системы ортогональных функций, при котором определяются коэффициенты разложения корреляционной функции в некоторый ряд (напр., по полиномам Лагерра и др.).
В зависимости от формы представления сигналов при вычислении корреляционных функций различают К. аналоговые (непрерывного действия) и цифровые (дискретного действия). Известен также ряд гибридных К., в которых используется как аналоговая, так и цифровая формы представления сигналов. Наиболее распространены аналоговые К., обеспечивающие при сравнительной простоте устройства удовлетворительную точность вычисления функций (погрешность порядка нескольких процентов). Цифровые К. позволяют получать точность значительно выше по сравнению с аналоговыми, но они более сложны.
Рассмотренные методы и схемы вычисления корреляционных функций часто используются с квантованием исследуемых сигналов как по времени, так и по уровню. Значительное распространение начали получать К. с грубым квантованием сигналов по уровню — релейные, полярные (знаковые) К. и К. Стилтьеса, вычисляющие соответственно релейные корреляционные функции, корреляционные функции полярные и Стилтьеса корреляционные функции. В релейных и полярных К. соответственно, один или оба входных сигнала подвергаются квантованию по двум уровням с использованием информации лишь о знаке исходного сигнала. Благодаря использованию в них элементов дискретной техники, релейные и полярные К. отличаются схемной простотой. Так, вместо множительных устройств в них используются простые схемы совпадения, а вместо блока регулируемого запаздывания — регистры сдвига с регулируемой частотой тактовых (продвигающих) импульсов. Вычисляемые при этом релейные и полярные корреляционные функции отличаются от действительных оценок корреляционных функций на величину некоторой методической погрешности, которую можно учесть при градуировке К. В то же время значительная простота таких К. делает их весьма перспективными во многих областях техники (автоматическое управление, техника связи, техническая диагностика, корреляционные экстремальные системы и др.). В К. Стилтьеса один из двух исследуемых случайных сигналов грубо квантуется по нескольким уровням (обычно по 3—4), а другой остается неизменным. Квантованный сигнал подвергается временной задержке и перемножается с неквантованным при помощи обычных схем совпадения. К. Стилтьеса сочетает простоту устройства с достаточно высокой точностью вычисления корреляционной функции (при пяти уровнях квантования погрешность составляет лишь доли процента).
Схемные и конструктивные особенности различных К. весьма разнообразны. Так, существуют пневматические, электромех., фотоэлектронные, оптические и электронные К. (последние наиболее распространены).
Лит.: Синицын Б. С. Автоматические корреляторы и их применение. Новосибирск, 1964 [библиогр. с. 202—216]; Балл Г. А. Аппаратурный корреляционный анализ случайных процессов. М., 1968 [библиогр. с. 150—158]; Чеголин П. М. Автоматизация спектрального и корреляционного анализа. М., 1969 [библиогр. с. 375—381]; Грибанов Ю. И., Веселова Г. П., Андреев В. Н. Автоматические цифровые корреляторы. М., 1971 [библиогр. с. 234—238]; Мирский Г. Я. Аппаратурное определение характеристик случайных процессов. М., 1972 [библиогр. с. 437—452]; Ланге Ф. Корреляционная электроника. Пер. с нем. Л., 1963 [библиогр. с. 426—442]. С. Ф. Козубовский.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- КАК ПОЛЬЗОВАТЬСЯ ЭНЦИКЛОПЕДИЕЙ КИБЕРНЕТИКИ
- ОСНОВНЫЕ СОКРАЩЕНИЯ И УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- АБСТРАКТНАЯ ТЕОРИЯ АВТОМАТОВ
- АБСТРАКТНОГО АВТОМАТА ГРАФ
- АБСТРАКЦИЯ АКТУАЛЬНОЙ БЕСКОНЕЧНОСТИ
- АБСТРАКЦИЯ ПОТЕНЦИАЛЬНОЙ ОСУЩЕСТВИМОСТИ
- АВМ ИТЕРАТИВНАЯ
- АВМ МЕХАНИЧЕСКАЯ
- АВМ ПНЕВМАТИЧЕСКАЯ
- АВМ ЭЛЕКТРОМЕХАНИЧЕСКАЯ
- АВТОКОД
- АВТОКОЛЕБАНИЯ
- АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- АВТОМАТ
- АВТОМАТ АВТОНОМНЫЙ
- АВТОМАТ АСИНХРОННЫЙ
- АВТОМАТ БЕЗ ПАМЯТИ
- АВТОМАТ ВЕРОЯТНОСТНЫЙ
- АВТОМАТ ДЕТЕРМИНИРОВАННЫЙ
- АВТОМАТ ДЕФИНИТНЫЙ
- АВТОМАТ ИНИЦИАЛЬНЫЙ
- АВТОМАТ КОНЕЧНЫЙ
- АВТОМАТ ЛИНЕЙНЫЙ
- АВТОМАТ МАГАЗИННЫЙ
- АВТОМАТ МИКРОПРОГРАММНЫЙ
- АВТОМАТ МИНИМАЛЬНЫЙ
- АВТОМАТ НЕДЕТЕРМИНИРОВАННЫЙ
- АВТОМАТ ОПЕРАЦИОННЫЙ
- АВТОМАТ ПРИВЕДЁННЫЙ
- АВТОМАТ ПУШ-ДАУН
- АВТОМАТ РЕГИСТРОВЫЙ
- АВТОМАТ С МАГАЗИННОЙ ПАМЯТЬЮ
- АВТОМАТ САМОВОСПРОИЗВОДЯЩИЙСЯ
- АВТОМАТ СВОБОДНЫЙ.
- АВТОМАТ СВЯЗНЫЙ
- АВТОМАТ УПРАВЛЯЮЩИЙ
- АВТОМАТ ЧАСТИЧНЫЙ
- АВТОМАТА ДИАГРАММА
- АВТОМАТА МАТРИЦА ПЕРЕХОДОВ
- АВТОМАТА ПАМЯТЬ
- АВТОМАТА ТАБЛИЦА
- АВТОМАТА ФУНКЦИЯ
- АВТОМАТИЗАЦИЯ КОМПЛЕКСНАЯ
- АВТОМАТИЗАЦИЯ ЛИНГВИСТИЧЕСКИХ ИССЛЕДОВАНИЙ
- АВТОМАТИЗАЦИЯ МЕДИЦИНСКОЙ ДИАГНОСТИКИ
- АВТОМАТИЗАЦИЯ ПРОГРАММИРОВАНИЯ
- АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ
- АВТОМАТИЗАЦИЯ УПРАВЛЕНИЯ ПРОИЗВОДСТВЕННЫМ ПРОЦЕССОМ
- АВТОМАТИЗАЦИЯ УПРАВЛЕНЧЕСКОГО ТРУДА
- АВТОМАТИЗИРОВАННАЯ СИСТЕМА ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
- АВТОМАТИЗИРОВАННАЯ СИСТЕМА ПРОЕКТИРОВАНИЯ
- АВТОМАТИЗИРОВАННОГО ОБУЧЕНИЯ КЛАСС
- АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ПРЕДПРИЯТИЕМ (АСУП)
- АВТОМАТИЗИРОВАННЫЙ ПОИСК ДОКАЗАТЕЛЬСТВ ТЕОРЕМ
- «АВТОМАТИКА»
- «АВТОМАТИКА И ТЕЛЕМЕХАНИКА»
- АВТОМАТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- АВТОМАТИЧЕСКИЙ АНАЛИЗ МЕДИКО-БИОЛОГИЧЕСКИХ ПРОЦЕССОВ
- АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
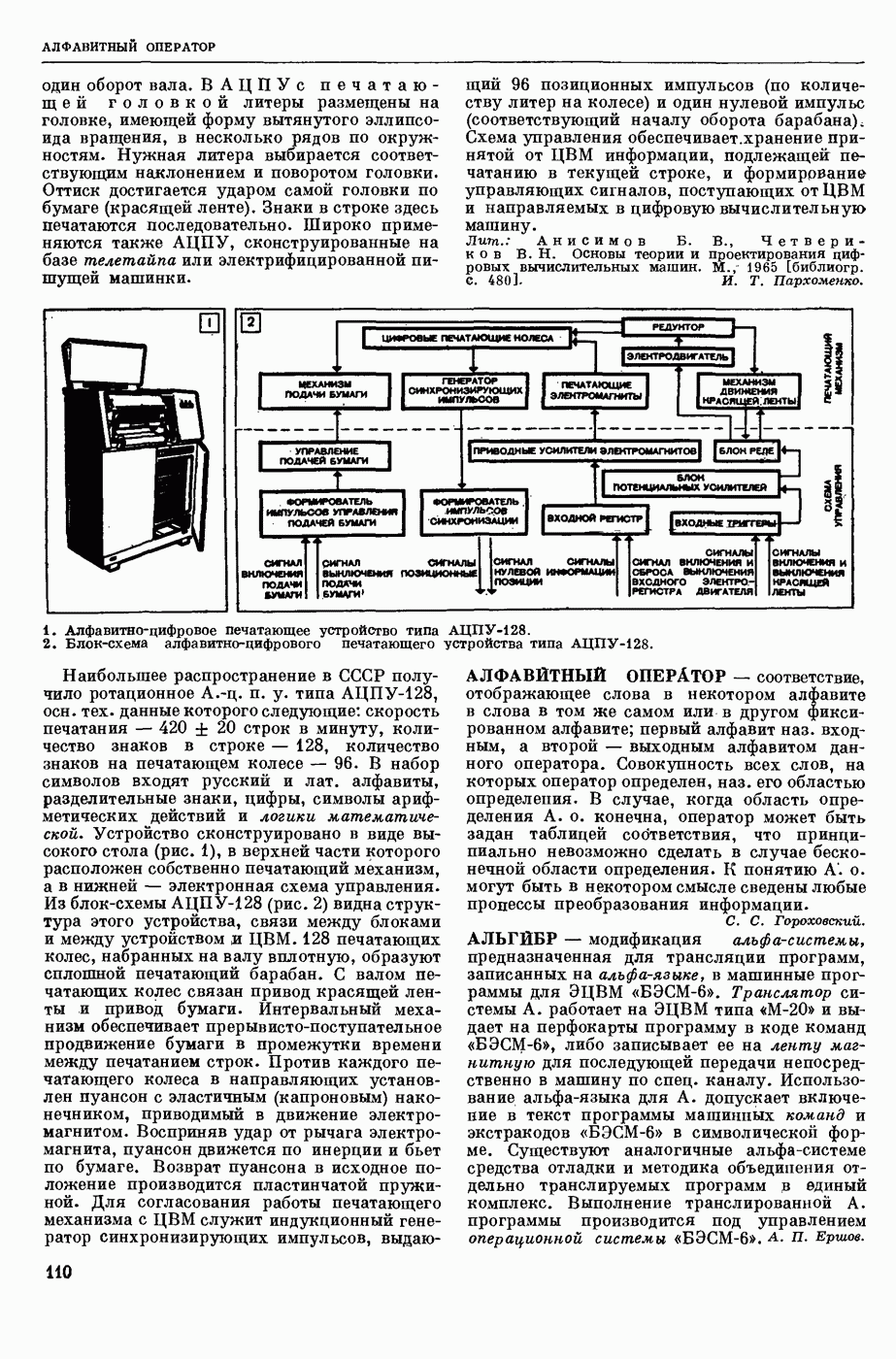
- АВТОМАТИЧЕСКОЕ ЦИФРО-ПЕЧАТАЮЩЕЕ УСТРОЙСТВО
- АВТОМАТНОЕ ОТОБРАЖЕНИЕ
- АВТОМАТОВ АБСТРАКТНАЯ ТЕОРИЯ
- АВТОМАТОВ АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ
- АВТОМАТОВ АНАЛИЗ
- АВТОМАТОВ ГОМОМОРФИЗМ.
- АВТОМАТОВ ДЕКОМПОЗИЦИЯ
- АВТОМАТОВ ИГРЫ
- АВТОМАТОВ ИЗОМОРФИЗМ
- АВТОМАТОВ КОМПОЗИЦИИ
- АВТОМАТОВ МИНИМИЗАЦИЯ
- АВТОМАТОВ ПОВЕДЕНИЕ
- АВТОМАТОВ ПРОИЗВЕДЕНИЕ
- АВТОМАТОВ ПРЯМАЯ СУММА
- АВТОМАТОВ СИНТЕЗ
- АВТОМАТОВ СПОСОБЫ ЗАДАНИЯ
- АВТОМАТОВ СТРУКТУРНАЯ ТЕОРИЯ
- АВТОМАТОВ СУПЕРПОЗИЦИЯ
- АВТОМАТОВ ТЕОРИЯ
- АВТОМАТОВ ЭКВИВАЛЕНТНОСТЬ
- АВТОМАТЫ БЕСКОНЕЧНЫЕ
- АВТОМАТЫ ИТЕРАТИВНЫЕ
- АВТОМАТЫ РАСТУЩИЕ
- АВТОНОМНОСТЬ
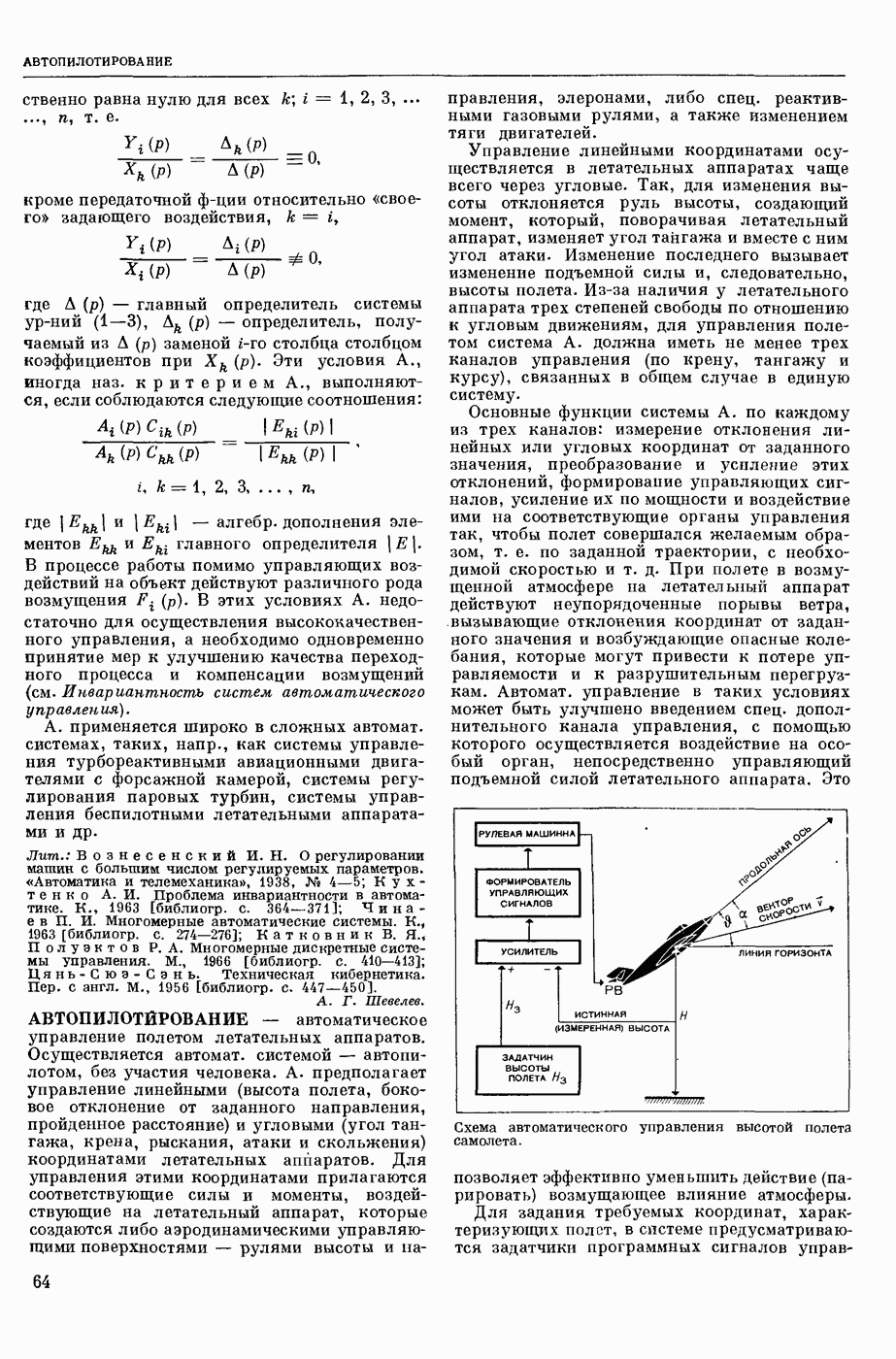
- АВТОПИЛОТИРОВАНИЕ
- АГРЕГАТНАЯ УНИФИЦИРОВАННАЯ СИСТЕМА (АУС)
- АГРЕГАТНО-БЛОЧНОЕ ПОСТРОЕНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- АДАМСА МЕТОД
- АДАПТАЦИЯ В КИБЕРНЕТИКЕ
- АДАПТИВНАЯ СИСТЕМА
- АДРЕС В ПРОГРАММИРОВАНИИ
- АДРЕС МАТЕМАТИЧЕСКИЙ
- АДРЕСНЫЙ ЯЗЫК
- АДРЕСОВ МОДИФИКАЦИЯ
- АИКА
- АЛГЕБРА АЛГОРИТМОВ
- АЛГЕБРА ЛИНЕЙНАЯ
- АЛГЕБРА ЛОГИКИ
- АЛГЕБРА МАТРИЦ
- АЛГЕБРА МНОЖЕСТВ
- АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ АВТОМАТОВ
- АЛГЕБРАИЧЕСКАЯ ТОПОЛОГИЯ
- АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
- АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
- АЛГЕБРЫ СОБЫТИЙ
- АЛГЕБРЫ УНИВЕРСАЛЬНЫЕ.
- АЛГОЛ-60
- АЛГОЛ-68
- АЛГОРИТМ, АЛГОРИФМ
- АЛГОРИТМ ЛОКАЛЬНЫЙ
- АЛГОРИТМ РАСПОЗНАВАНИЯ
- АЛГОРИТМИЗАЦИЯ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ
- АЛГОРИТМИЗАЦИЯ ТВОРЧЕСКИХ ПРОЦЕССОВ
- АЛГОРИТМИЧЕСКАЯ СТРУКТУРА ЦВМ
- АЛГОРИТМИЧЕСКИЙ СИНТЕЗ ЦВМ
- АЛГОРИТМИЧЕСКИЙ ЯЗЫК
- АЛГОРИТМИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- АЛГОРИТМОВ ГРАФ-СХЕМЫ, ГРАФ-СХЕМЫ АЛГОРИТМОВ
- АЛГОРИТМОВ РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- АЛГОРИТМОВ СЛОЖНОСТЬ
- АЛГОРИТМОВ СХЕМА
- АЛГОРИТМОВ ТЕОРИЯ
- АЛГОРИТМОВ ЭКВИВАЛЕНТНОСТЬ
- АЛГЭК
- АЛГЭМ
- АЛМО
- АЛФАВИТНО-ЦИФРОВОЕ ПЕЧАТАЮЩЕЕ УСТРОЙСТВО (АЦПУ)
- АЛФАВИТНЫЙ ОПЕРАТОР
- АЛЬГИБР
- АЛЬФА-СИСТЕМА
- АЛЬФА-ЯЗЫК
- АМПЛИТУДНО-ИМПУЛЬСНАЯ МОДЕЛЬ
- АНАЛИЗАТОРНЫЕ СИСТЕМЫ
- АНАЛИТИК
- АНАЛИТИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ НА ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ.
- АНАЛОГ ЦИФРОВОЙ, ЦИФРОВАЯ МОДЕЛЬ
- АНАЛОГИИ
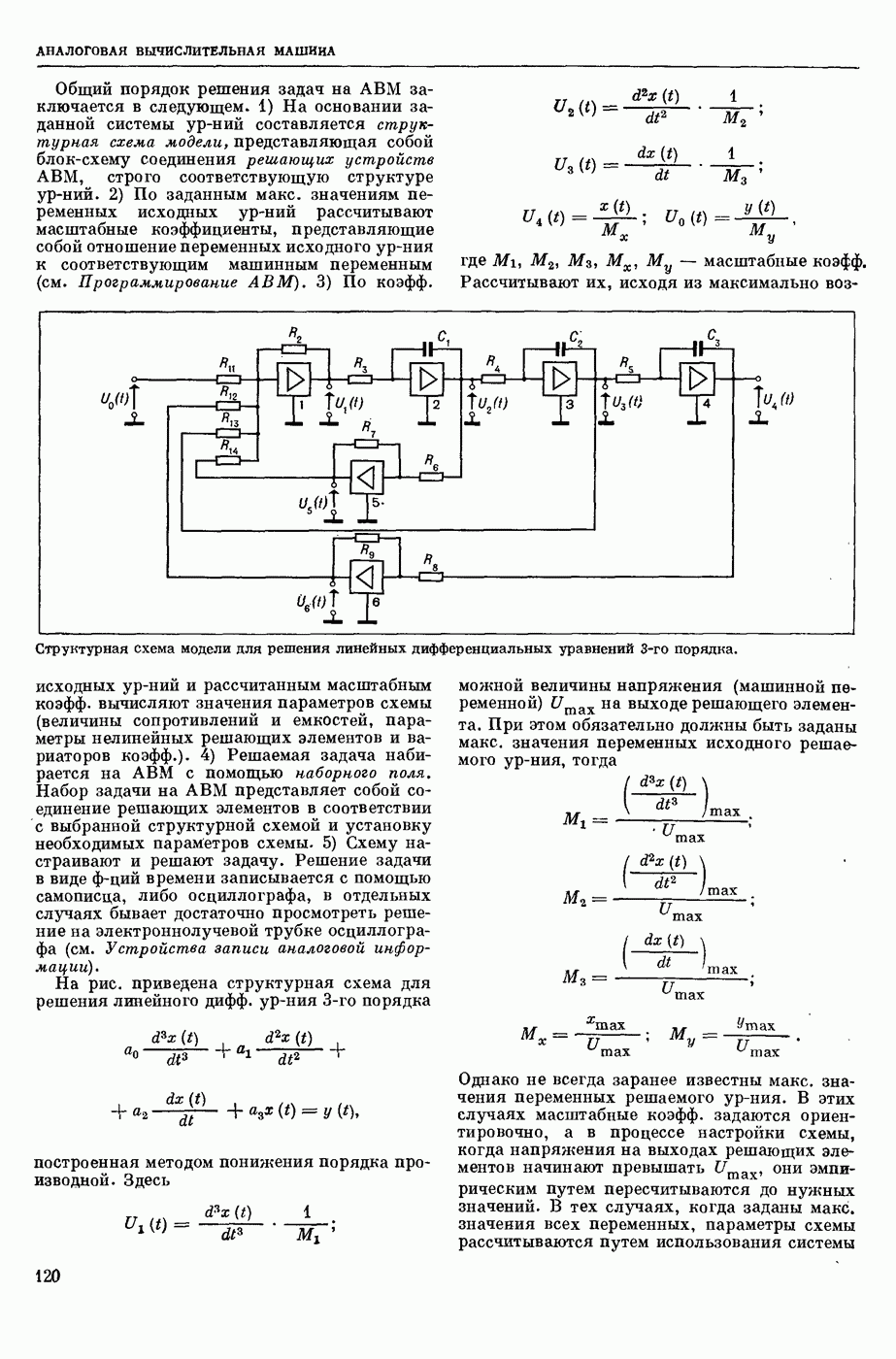
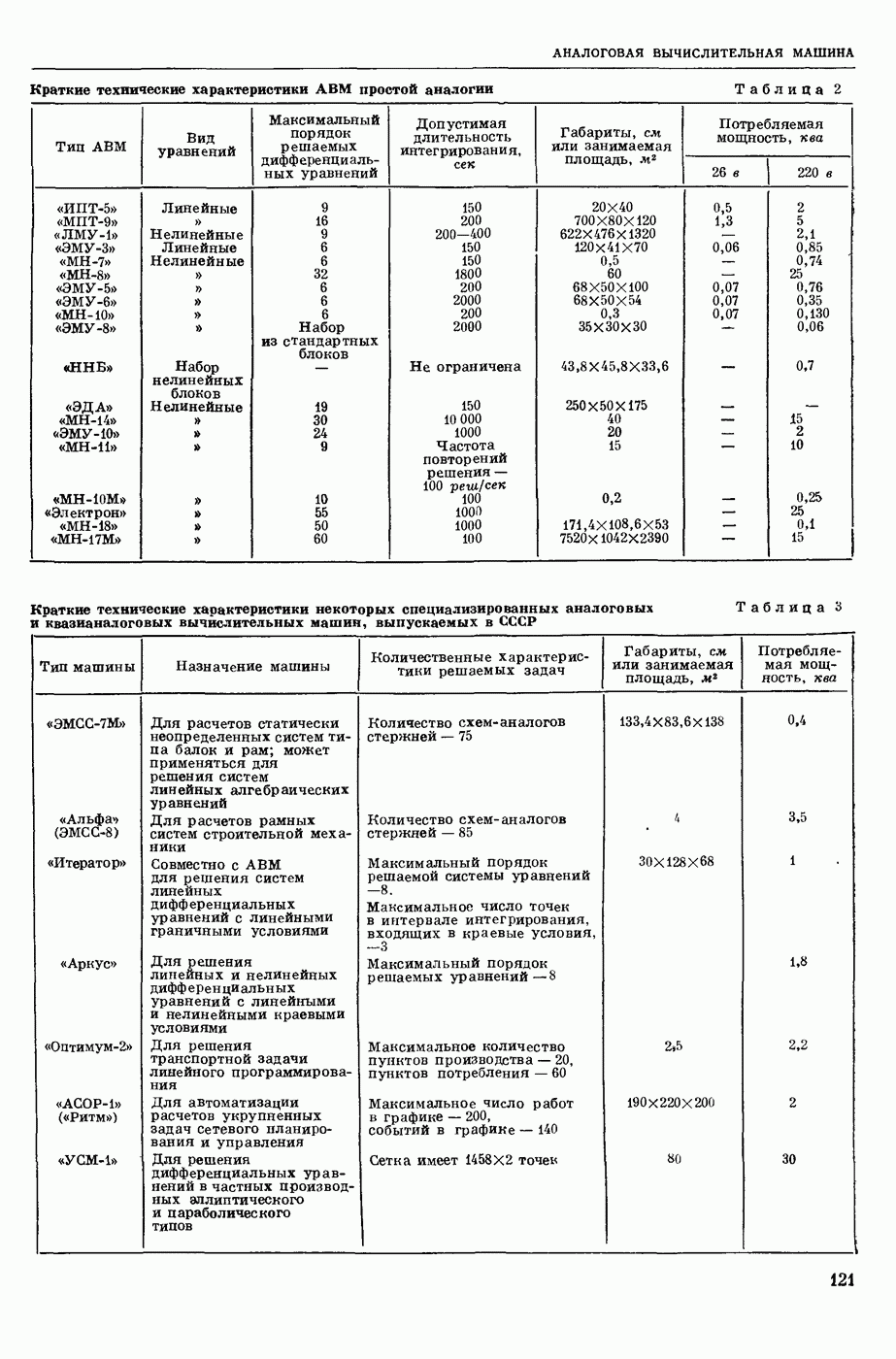
- АНАЛОГОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ABM)
- АНАЛОГО-ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- АНАЛОГО-ЦИФРОВАЯ СИСТЕМА
- АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ, ПРЕОБРАЗОВАТЕЛЬ АНАЛОГ-КОД
- АННОТИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- АНСАМБЛЬ СООБЩЕНИЙ
- АНТИГРАДИЕНТ ФУНКЦИИ
- АППРОКСИМАЦИЯ ФУНКЦИИ СРЕДНЕКВАДРАТИЧНАЯ
- АППРОКСИМАЦИЯ ФУНКЦИЙ
- АППРОКСИМАЦИЯ ФУНКЦИЙ РАВНОМЕРНАЯ (чебышевская)
- АРИФМЕТИЗАЦИЯ МАТЕМАТИКИ
- АРИФМЕТИКА С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
- АРИФМЕТИКА С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- АРИФМЕТИКА ФОРМАЛЬНАЯ
- АРИФМЕТИЧЕСКАЯ И АНАЛИТИЧЕСКАЯ ИЕРАРХИИ
- АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ ЦВМ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО (АУ)
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПАРАЛЛЕЛЬНОГО ДЕЙСТВИЯ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- АРХИВ в автоматизированных системах управления или системах обработки данных
- АСИНХРОННЫХ АВТОМАТОВ ТЕОРИЯ
- «АСОР», автоматизированная система организации работ
- АССЕМБЛЕР
- АССОЦИАТИВНЫЙ ЭЛЕМЕНТ
- АСТАТИЗМ n-ПОРЯДКА
- БАЗА ДАННЫХ
- БАЙЕСА ФОРМУЛА, формула вероятностей гипотез
- БАЙЕСОВСКИЙ МЕТОД
- БАЙЕСОВСКОЕ ОБУЧЕНИЕ
- БАЙЕСОВСКОЕ РЕШАЮЩЕЕ ПРАВИЛО
- БАЙТ (англ. byte)
- БАЛАНС МЕЖОТРАСЛЕВОЙ
- БАЛАНСОВЫЕ МОДЕЛИ
- БАНК ДАННЫХ
- БАРАБАН МАГНИТНЫЙ
- ВЕЛЛМАНА ПРИНЦИП ОПТИМАЛЬНОСТИ
- ВЕЛЛМАНА УРАВНЕНИЕ
- БЕЛЫЙ ШУМ
- БЕРЖА ГРАФ
- БЕРНУЛЛИ РАСПРЕДЕЛЕНИЕ
- «БЕРРАУЗ КОРПОРЕЙШЕН» (Burroughs Corporation)
- БИАКС
- БИБЛИОГРАФИЧЕСКИЙ ПОИСК
- БИБЛИОТЕКА СТАНДАРТНЫХ ПОДПРОГРАММ
- БИБЛИОТЕЧНЫХ ПОДПРОГРАММ МЕТОД
- БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ.
- БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- БИОЛОГИЧЕСКИЕ СИСТЕМЫ
- БИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ МАТЕМАТИЧЕСКИЕ МЕТОДЫ
- БИОЛОГИЧЕСКИХ СИСТЕМ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- БИОЛОГИЧЕСКИХ СИСТЕМ ОРГАНИЗАЦИЯ
- БИОМЕДИЦИНСКАЯ ЭЛЕКТРОНИКА
- БИОНИКА
- БИОЭЛЕКТРИЧЕСКОЕ УПРАВЛЕНИЕ
- БИТ
- БЛЕЙКА АЛГОРИТМ
- БЛОК в программировании
- БЛОК ПЕРЕМЕННЫХ КОЭФФИЦИЕНТОВ
- БЛОК ХРАНЕНИЯ ИНФОРМАЦИИ
- БЛОКИ ЦВМ ТИПОВЫЕ
- БЛОКИРОВКА ОБСЛУЖИВАНИЯ
- БЛОК-СХЕМА ПРОГРАММЫ
- БЛОЧНЫЙ СИНТЕЗ ЦВМ
- БОЛЬЦА ЗАДАЧА
- БОЛЬШАЯ ИНТЕГРАЛЬНАЯ СХЕМА (БИС)
- БОЛЬШИЕ СИСТЕМЫ УПРАВЛЕНИЯ
- БОЛЬШИХ ЧИСЕЛ ЗАКОН
- БУБНОВА — ГАЛЕРКИНА МЕТОД
- БУЛЕВА АЛГЕБРА
- БУЛЕВЫ ФУНКЦИИ
- БУХГАЛТЕРСКОГО УЧЁТА АВТОМАТИЗАЦИЯ
- БЫСТРОДЕЙСТВИЕ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- БЫСТРОДЕЙСТВИЕ ЦВМ
- БЭКУСА НОРМАЛЬНАЯ ФОРМА
- «БЭСМ»
- ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
- ВАРИАЦИОННЫЕ МЕТОДЫ
- ВАРИАЦИОННЫЙ РЯД
- ВВОДА ИНФОРМАЦИИ УСТРОЙСТВО
- ВЕЙЧА ДИАГРАММА
- ВЕКТОР ОБОБЩЕННОГО ГРАДИЕНТА
- ВЕНГЕРСКИЙ МЕТОД
- ВЕРОЯТНОСТЕЙ РАСПРЕДЕЛЕНИЕ
- ВЕРОЯТНОСТЕЙ ТЕОРИЯ
- ВЕРОЯТНОСТНАЯ МАШИНА
- ВЕРОЯТНОСТНЫЙ ПРОЦЕСС
- ВЕРОЯТНОСТЬ
- ВЕРОЯТНОСТЬ УСЛОВНАЯ
- «ВЕСНА»
- ВЕСОВАЯ ФУНКЦИЯ
- ВЕТВЕЙ И ГРАНИЦ МЕТОД
- ВЕТВЯЩИЙСЯ ПРОЦЕСС
- ВЗАИМНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- ВЗАИМОДЕЙСТВИЕ ЧЕЛОВЕКА С ВЫЧИСЛИТЕЛЬНОЙ МАШИНОЙ
- ВИНЕРА—ХОПФА УРАВНЕНИЕ первого рода
- ВНЕШНЕЕ ОБОРУДОВАНИЕ
- ВНЕШНИЕ УСТРОЙСТВА
- «ВНИИЭМ»
- ВОЗБУЖДЕНИЯ КЛЕТКИ ТЕОРИЯ
- ВОЗМОЖНЫХ НАПРАВЛЕНИЙ МЕТОД
- ВОЗМУЩАЮЩЕЕ ВОЗДЕЙСТВИЕ,
- ВОЛЬТЕРРЫ УРАВНЕНИЕ
- ВОССТАНОВЛЕНИЯ ТЕОРИЯ
- ВРЕМЕННОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ
- ВРЕМЕННЫЕ ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ВРЕМЯ ВОССТАНОВЛЕНИЯ после отказа
- ВРЕМЯ ВЫБОРКИ ИНФОРМАЦИИ
- ВРЕМЯ МОДЕЛИРОВАНИЯ ДЕЙСТВИТЕЛЬНОЕ
- ВРЕМЯ ОБРАЩЕНИЯ К ЗАПОМИНАЮЩЕМУ УСТРОЙСТВУ
- ВРЕМЯ ОЖИДАНИЯ
- ВРЕМЯ РАБОТЫ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ ПОЛЕЗНОЕ
- ВСЕСОЮЗНЫЙ ИНСТИТУТ НАУЧНОЙ И ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ (ВИНИТИ)
- ВСПОМОГАТЕЛЬНОГО ОПЕРАТОРА МЕТОД
- ВХОДНОЕ УСТРОЙСТВО
- ВЫБОРКА ТРЕНИРОВОЧНАЯ
- ВЫВОДА ИНФОРМАЦИИ УСТРОЙСТВО
- ВЫДЕЛЕНИЕ СИГНАЛОВ НА ФОНЕ ПОМЕХ
- ВЫИГРЫША ФУНКЦИЯ
- ВЫИГРЫШЕЙ МАТРИЦА
- ВЫПУКЛАЯ ОБОЛОЧКА
- ВЫПУКЛАЯ ФУНКЦИЯ
- ВЫПУКЛОЕ МНОГОГРАННОЕ МНОЖЕСТВО
- ВЫПУКЛОЕ МНОЖЕСТВО
- ВЫПУКЛЫЙ КОНУС
- ВЫПУКЛЫЙ МНОГОГРАННИК
- ВЫПУКЛЫЙ МНОГОГРАННЫЙ КОНУС
- ВЫСКАЗЫВАНИЙ ИСЧИСЛЕНИЕ
- ВЫСКАЗЫВАНИЯ ЛОГИЧЕСКИ ИСТИННЫЕ, высказывания тождественно истинные
- ВЫСКАЗЫВАНИЯ ЭКЗИСТЕНЦИАЛЬНЫЕ
- ВЫХОДНОЕ УСТРОЙСТВО
- ВЫЧИСЛЕНИЯ В РЕАЛЬНОЕ ВРЕМЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА КЛАВИШНАЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА ОБЩЕГО НАЗНАЧЕНИЯ
- ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА
- ВЫЧИСЛИТЕЛЬНАЯ СХЕМА
- ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
- ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА ПОГРЕШНОСТЬ
- ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА СХОДИМОСТЬ
- ВЫЧИСЛИТЕЛЬНЫЕ СРЕДЫ
- ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК АРМЯНСКОЙ ССР И ЕРЕВАНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК СССР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР СИБИРСКОГО ОТДЕЛЕНИЯ АКАДЕМИИ НАУК СССР
- ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ ХАРАКТЕРИСТИКИ
- ВЫЧИСЛИТЕЛЬНЫХ МАШИН И СИСТЁМ КОМПЛЕКСЫ
- ВЫЧИСЛИТЕЛЬНЫХ РАБОТ МЕТОДЫ ОРГАНИЗАЦИИ
- ВЫЧИСЛИТЕЛЬНЫХ ЦЕНТРОВ СЕТИ
- ГАМИЛЬТОНОВ ПУТЬ (контур)
- ГАМИЛЬТОНОВА ЦЕПЬ
- ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- ГАУССА МЕТОД
- ГАУССА РАСПРЕДЕЛЕНИЕ
- ГАУССОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- ГЕДЕЛЯ ТЕОРЕМЫ О НЕПОЛНОТЕ
- ГЕНЕРАТОР ПРОГРАММ
- ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ
- ГЕНЦЕНА ФОРМАЛЬНЫЕ СИСТЕМЫ
- ГИБРИДНАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- ГИДРОБИОНИКА
- ГИПЕРБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ГИПЕРГРАФ
- ГИПЕРПЛОСКОСТИ ОТСЕКАЮЩЕЙ МЕТОД
- ГИПОТЕЗА КОМПАКТНОСТИ
- ГИСТОГРАММА
- ГЛОБАЛЬНОГО ПОИСКА МЕТОДЫ
- ГЛОБАЛЬНЫЕ ПЕРЕМЕННЫЕ
- ГНЕЗДОВОЙ СПИСОК
- ГНОСЕОЛОГИЧЕСКИЕ ОСНОВЫ КИБЕРНЕТИКИ
- ГОЛОГРАФИЯ
- ГОМЕОСТАЗИС
- ГОМЕОСТАТИЧЕСКАЯ СИСТЕМА
- ГОМОРИ МЕТОД
- ГОНОК ПРОБЛЕМА
- ГОРНЕРА СХЕМА
- ГОСУДАРСТВЕННЫЙ ФОНД АЛГОРИТМОВ И ПРОГРАММ (ГФАП)
- ГРАДИЕНТ
- ГРАДИЕНТНЫЙ МЕТОД
- ГРАММАТИКА АВТОМАТНАЯ, грамматика с конечным числом состояний
- ГРАММАТИКА БЕСКОНТЕКСТНАЯ, грамматика контекстно-свободная
- ГРАММАТИКА ЗАВИСИМОСТЕЙ, грамматика управлений
- ГРАММАТИКА КАТЕГОРИАЛЬНАЯ
- ГРАММАТИКА ЛИНЕЙНАЯ
- ГРАММАТИКА ПОРОЖДАЮЩАЯ
- ГРАММАТИКА РАСПОЗНАЮЩАЯ
- ГРАММАТИКА СОСТАВЛЯЮЩИХ, грамматика непосредственно составляющих
- ГРАММАТИКА ТРАНСФОРМАЦИОННАЯ
- ГРАММАТИКА ФОРМАЛЬНАЯ
- ГРАНИЧНАЯ ЗАДАЧА
- ГРАФ
- ГРАФ ВЗВЕШЕННЫЙ
- ГРАФ РАСКРАШЕННЫЙ
- ГРАФИЧЕСКОЕ РЕГИСТРИРУЮЩЕЕ УСТРОЙСТВО
- ГРАФОВ СВЯЗНОСТЬ
- ГРАФОВ ТЕОРИЯ
- ГРАФОПОСТРОИТЕЛЬ
- ГРУПП ТЕОРИЯ
- ГРУППА в алгебре
- ГРУППОВОЙ ИСТОЧНИК НАПРЯЖЕНИЯ
- ГРУППЫ НЕПРЕРЫВНЫЕ.
- ГУРВИЦА КРИТЕРИЙ
- ГУРВИЦА ТЕОРЕМА
- ДАННЫЕ
- ДАТЧИК ВРЕМЕНИ,
- ДАТЧИК ОДИНОЧНЫХ ИМПУЛЬСОВ
- ДАТЧИК РАБОЧЕГО ЦИКЛА
- ДАТЧИК СЛУЧАЙНЫХ ЧИСЕЛ
- ДВИГАТЕЛЬ ПОЛИМЕРНЫЙ
- ДВОЙСТВЕННАЯ ЗАДАЧА ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ.
- ДВОЙСТВЕННАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- ДВОЙСТВЕННОСТИ ЗАКОН, принцип двойственности
- ДВОЙСТВЕННОСТИ ТЕОРИЯ в программировании линейном
- ДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- ДВОЙСТВЕННЫЙ ГРАДИЕНТНЫЙ МЕТОД
- ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД, метод последовательного уточнения оценок
- ДВОЙСТВЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ДВУПОЛЮСНИК КОНТАКТНЫЙ
- ДВУХТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ДЕЙСТВИТЕЛЬНОЕ ВРЕМЯ МОДЕЛИРОВАНИЯ
- ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО
- ДЕКОМПОЗИЦИИ МЕТОД, блочный метод
- ДЕЛЕЖ в теории игр
- ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ
- ДЕЛЬТА-ФУНКЦИЯ
- ДЕМОДУЛЯТОР, детектор
- ДЕМПФИРОВАНИЕ
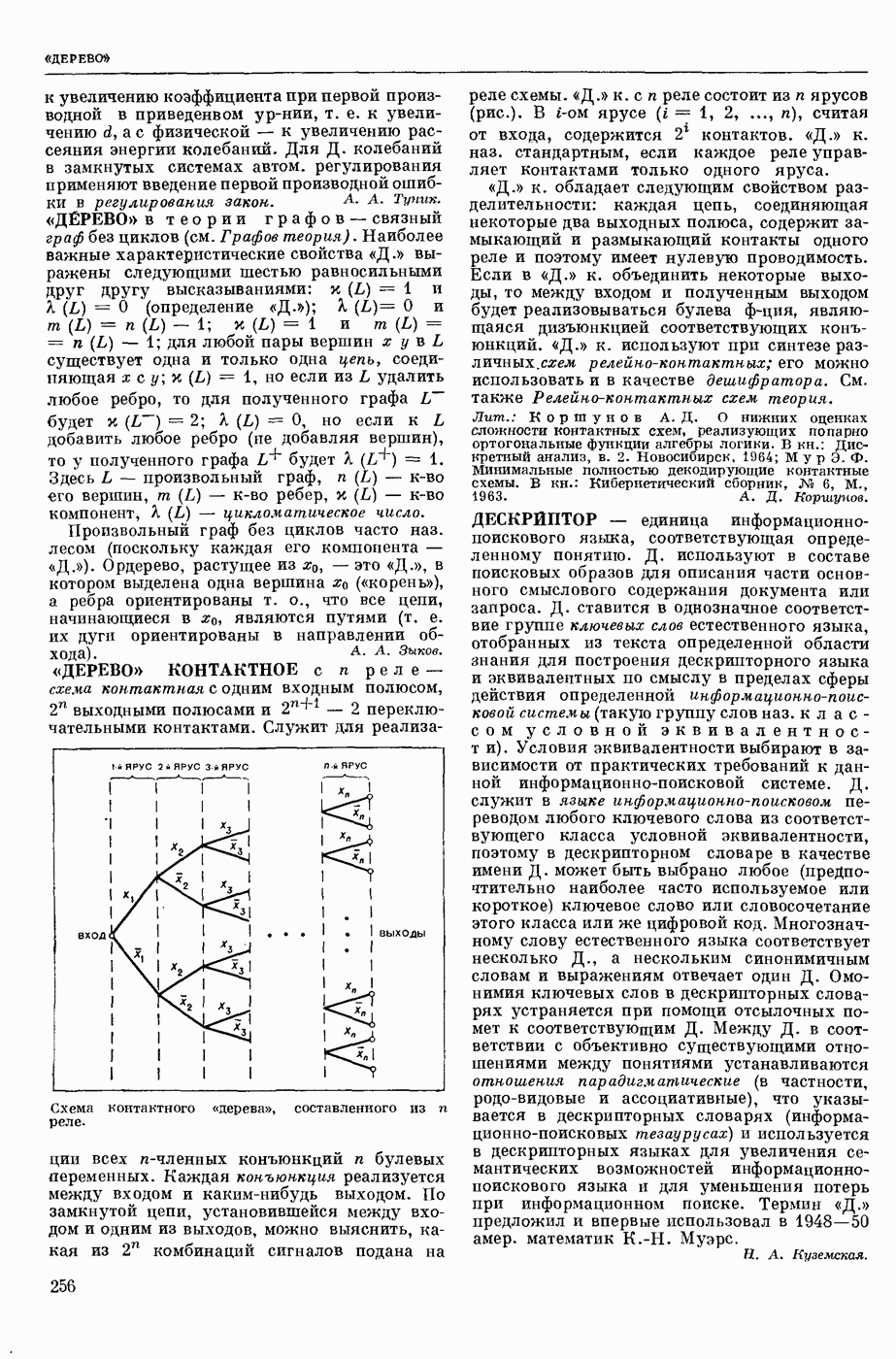
- «ДЕРЕВО» в теории графов
- «ДЕРЕВО» КОНТАКТНОЕ с n реле
- ДЕСКРИПТОР
- ДЕТЕРМИНИРОВАННЫЕ СИСТЕМЫ
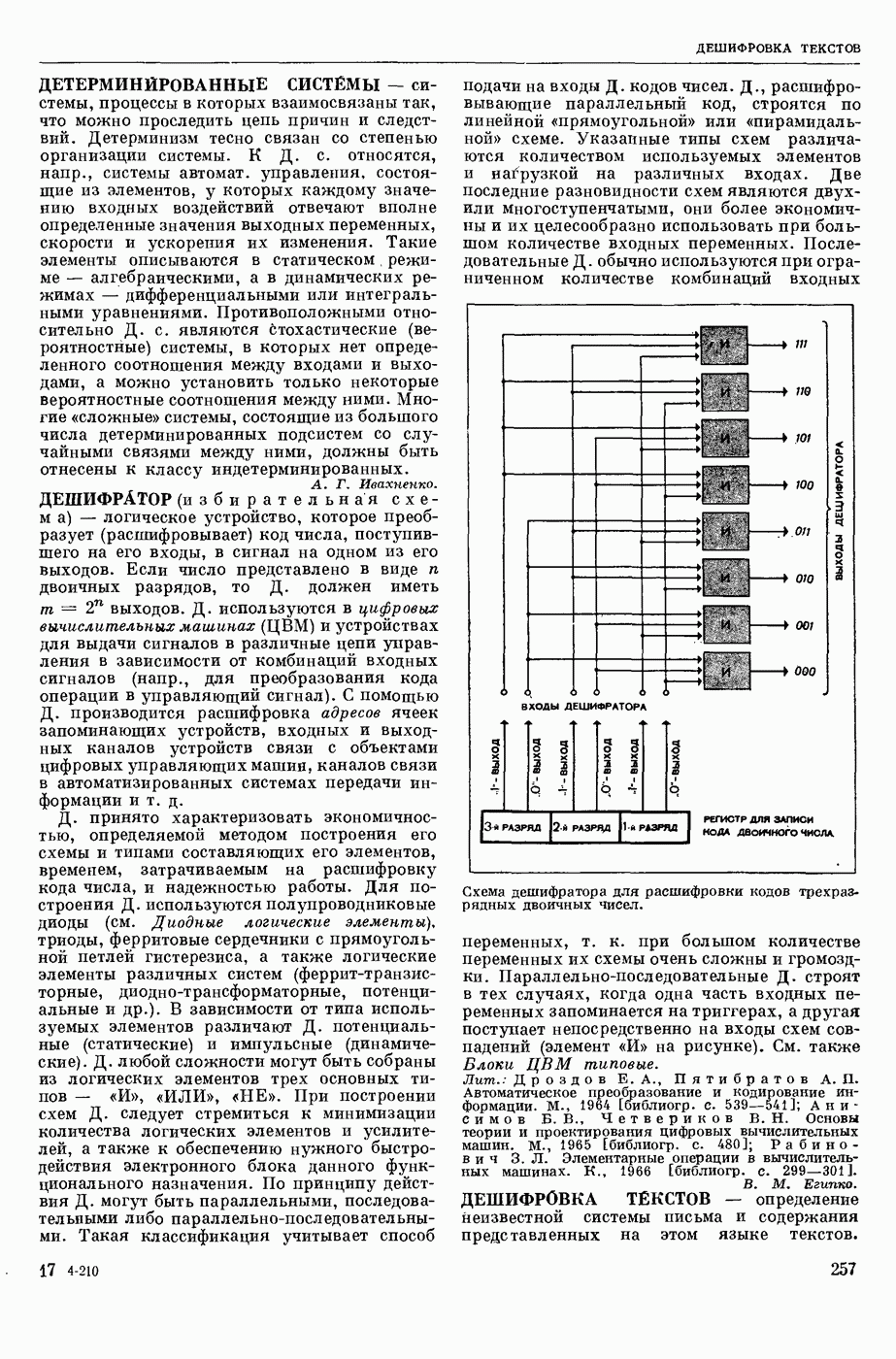
- ДЕШИФРАТОР
- ДЕШИФРОВКА ТЕКСТОВ
- ДИАГНОСТИКА АВТОМАТИЧЕСКАЯ
- ДИАГНОСТИКА НЕИСПРАВНОСТЕЙ ЦВМ
- ДИАГНОСТИРОВАНИЕ СЛОЖНЫХ ТЕХНИЧЕСКИХ КОМПЛЕКСОВ, техническая диагностика
- ДИАЛОГА РЕЖИМ
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (ДНФ)
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА ТУПИКОВАЯ.
- ДИЗЪЮНКЦИЯ
- ДИЗЪЮНКЦИЯ СЛАБАЯ
- ДИЗЪЮНКЦИЯ СТРОГАЯ, антиэквивалентность, сложение по модулю 2
- ДИНАМИЧЕСКИХ СИСТЕМ ТЕОРИЯ ЧУВСТВИТЕЛЬНОСТИ
- ДИНАМИЧЕСКИХ СИСТЕМ УСЛОВИЯ ГРУБОСТИ
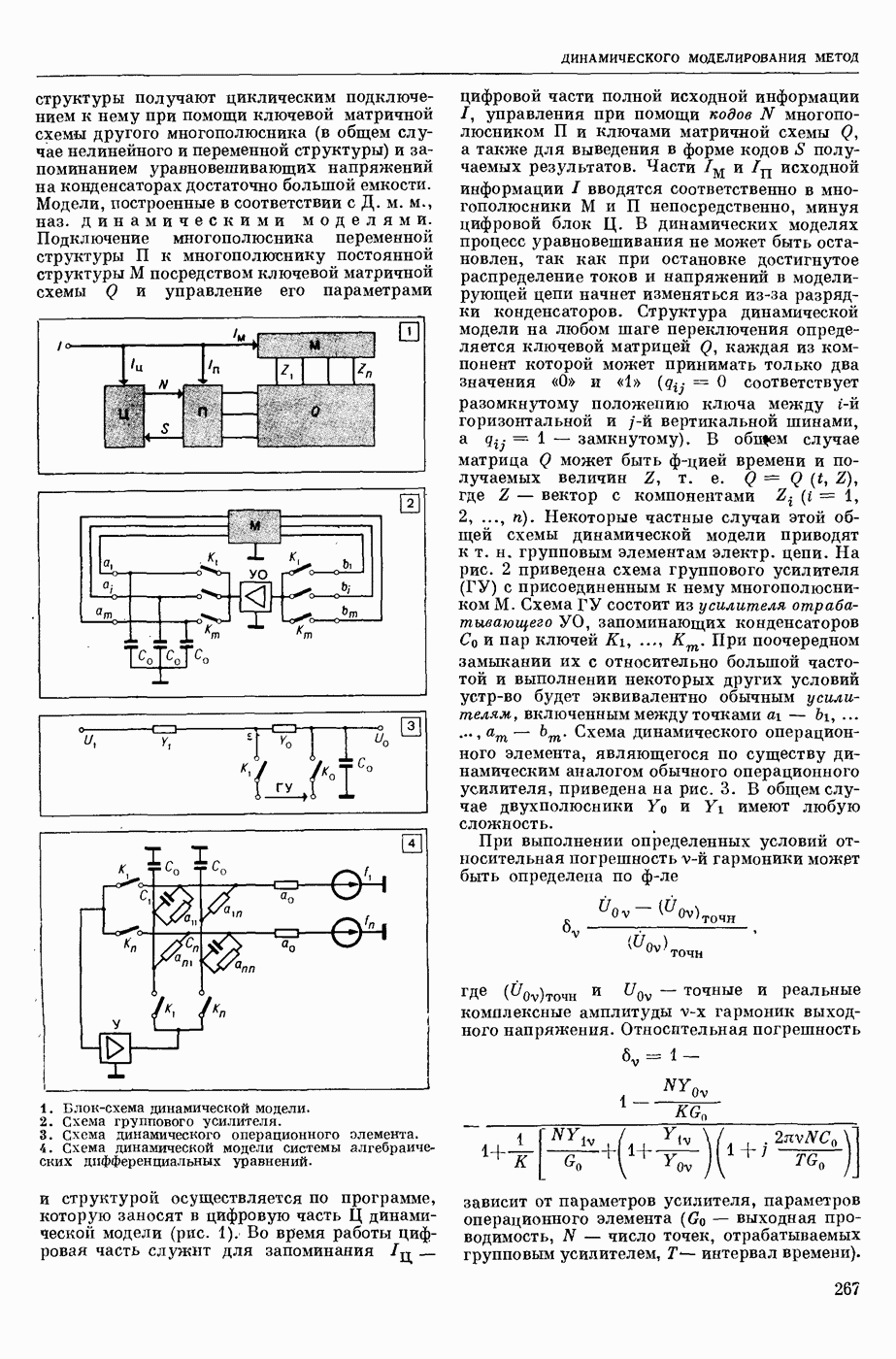
- ДИНАМИЧЕСКОГО МОДЕЛИРОВАНИЯ МЕТОД
- ДИНАМИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПАМЯТИ
- ДИОД ПОЛУПРОВОДНИКОВЫЙ
- ДИОДНАЯ ЛИНЕЙКА
- ДИОДНАЯ МАТРИЦА
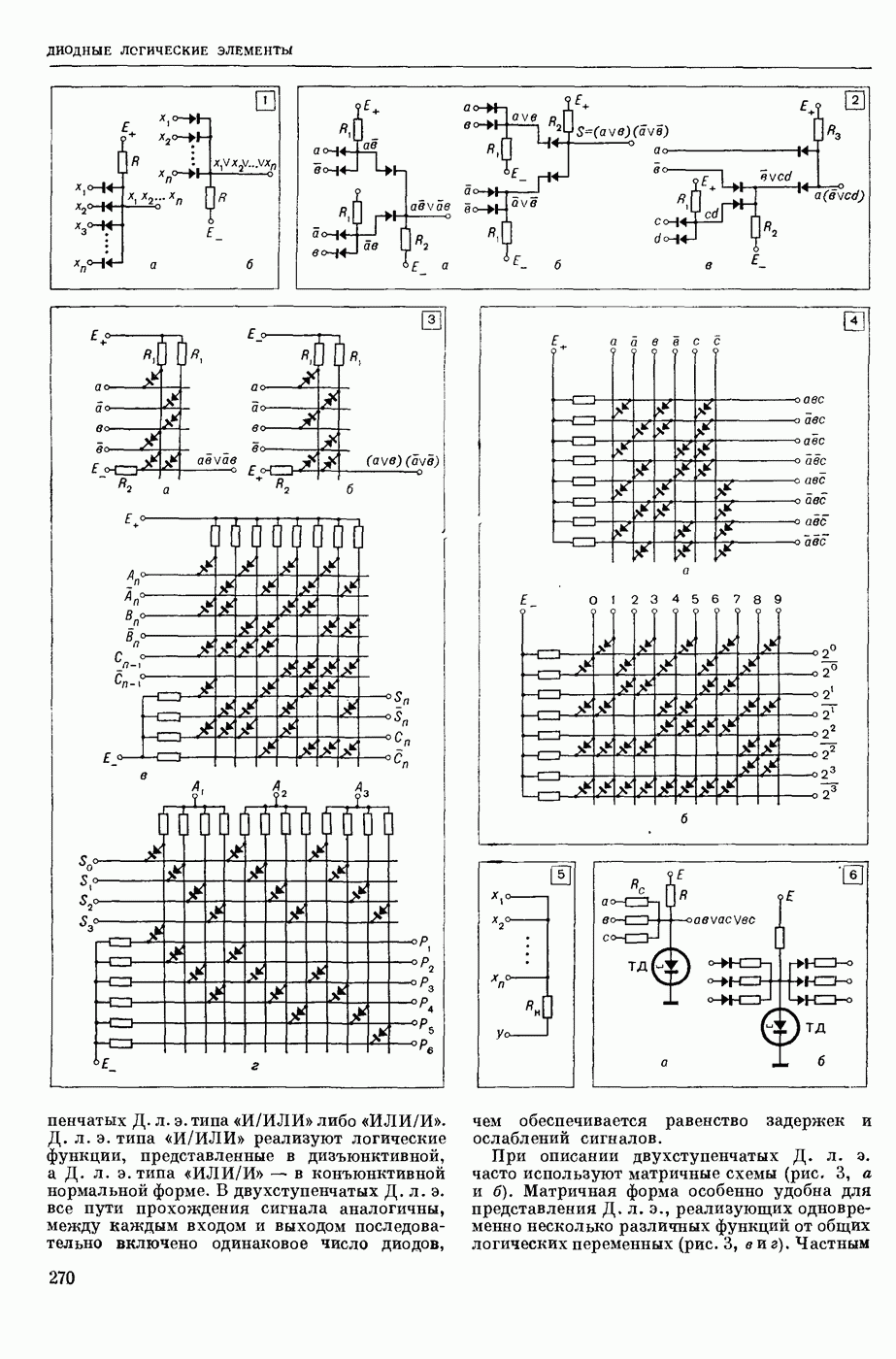
- ДИОДНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ДИРАКА ФУНКЦИЯ
- ДИСК МАГНИТНЫЙ
- ДИСКРЕТИЗАЦИЯ ИЗОБРАЖЕНИЙ
- ДИСКРЕТНАЯ МОДЕЛИРУЮЩАЯ СРЕДА
- ДИСКРЕТНАЯ СИСТЕМА
- ДИСКРЕТНАЯ СИСТЕМА УПРАВЛЕНИЯ, импульсная система управления
- ДИСКРЕТНЫЙ АНАЛИЗ
- ДИСКРЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ ТЕОРИЯ
- ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- ДИСКРЕТНЫХ ЭЛЕМЕНТОВ СИСТЕМА
- ДИСПЕРСИОННЫЙ АНАЛИЗ
- ДИСПЕРСИЯ
- ДИСПЕТЧЕР в программировании
- ДИСПЕТЧЕРСКОГО УПРАВЛЕНИЯ АВТОМАТИЗАЦИЯ
- ДИСТАНЦИОННОЕ УПРАВЛЕНИЕ
- ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- ДИФФЕРЕНЦИАЛЬНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ КЛАССИФИКАЦИЯ.
- ДИФФЕРЕНЦИАЛЬНЫХ РЕНТ МЕТОД
- ДИФФЕРЕНЦИАТОР
- ДИФФЕРЕНЦИРОВАНИЕ СИГНАЛОВ
- ДИФФЕРЕНЦИРОВАНИЕ СИМВОЛЬНОЕ, дифференцирование аналитическое
- ДИФФЕРЕНЦИРОВАНИЕ ЧИСЛЕННОЕ
- ДИФФУЗИОННЫЙ ПРОЦЕСС
- ДЛИНА ОЧЕРЕДИ
- ДЛИТЕЛЬНОСТЬ ОЖИДАНИЯ
- «ДНЕПР»
- ДОВЕРИТЕЛЬНАЯ ОБЛАСТЬ
- ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ
- ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ
- ДОВЕРИТЕЛЬНЫЙ УРОВЕНЬ
- ДОКАЗАТЕЛЬСТВ ТЕОРИЯ, метаматематика
- ДОКАЗАТЕЛЬСТВО ТЕОРЕМ НА ЭВМ, машинный поиск логического вывода
- ДОКУМЕНТ НАУЧНЫЙ
- ДОКУМЕНТАЛЬНАЯ ИНФОРМАЦИОННОПОИСКОВАЯ СИСТЕМА
- ДОКУМЕНТАЛЬНО-ФАКТОГРАФИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
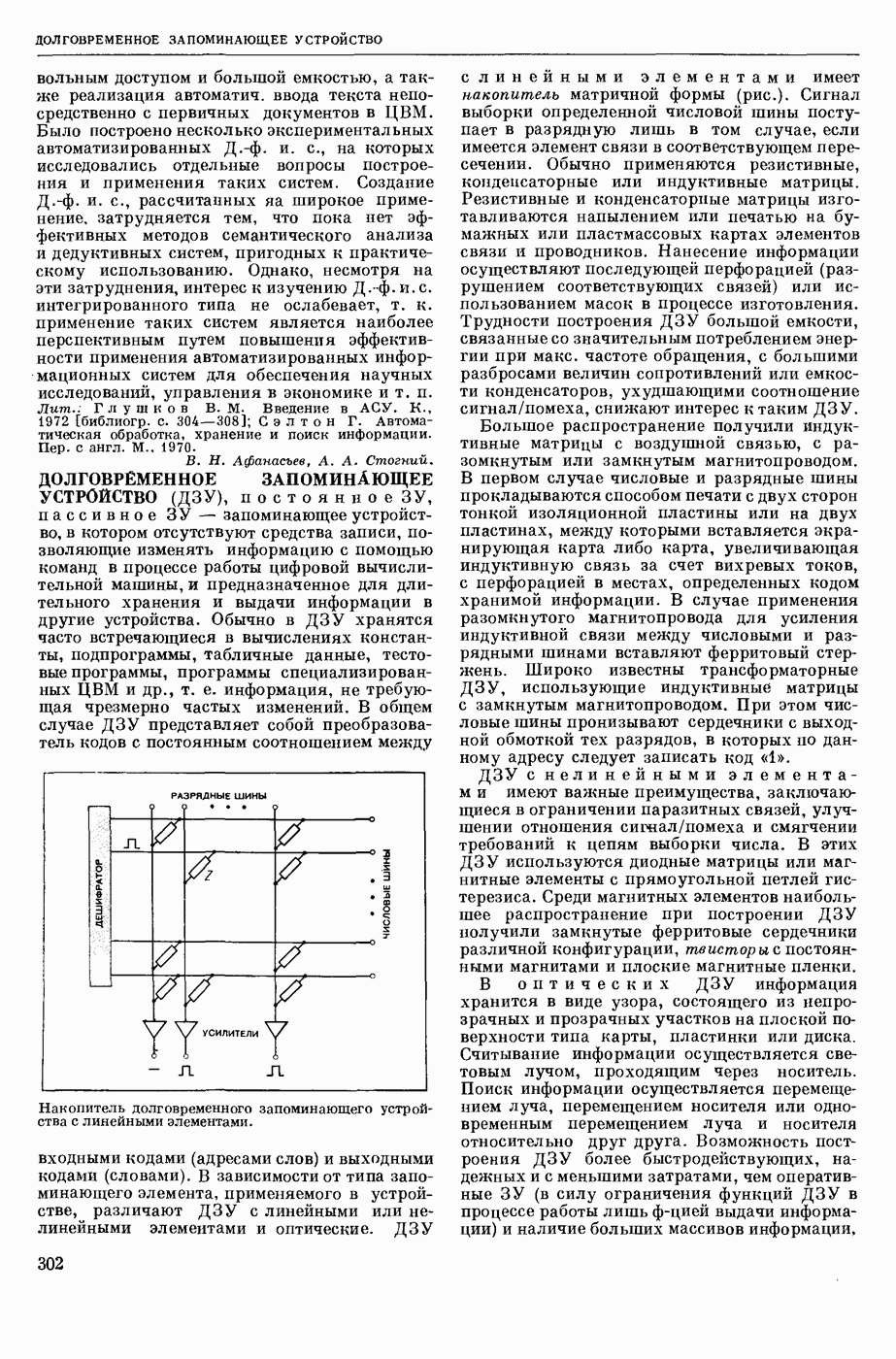
- ДОЛГОВРЕМЕННОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ДЗУ)
- ДОМИНИРОВАНИЕ в теории игр.
- ДОПУСТИМАЯ ОБЛАСТЬ
- ДОПУСТИМАЯ ТОЧКА
- ДОПУСТИМОЕ МНОЖЕСТВО
- ДОПУСТИМОЕ УПРАВЛЕНИЕ
- ДОПУСТИМЫЙ ВЕКТОР
- ДОПУСТИМЫЙ ПУТЬ в теории графов
- ДОПУСТИМЫХ НАПРАВЛЕНИЙ МЕТОД
- ДОСТАТОЧНОСТЬ ПРИЗНАКОВ.
- ДОСТАТОЧНЫЕ СТАТИСТИКИ
- ДОСТУП ПОСЛЕДОВАТЕЛЬНЫЙ
- ДОСТУП ПРОИЗВОЛЬНЫЙ
- ДРЕЙФ НУЛЕВОГО УРОВНЯ операционного усилителя
- ДРОБНО-ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ЗАДАЧА
- ДРОБНЫХ ШАГОВ МЕТОД
- ДУАЛЬНОЕ УПРАВЛЕНИЕ
- ДУГА графа
- ДУЭЛЬ в теории игр
- ЕДИНАЯ СИСТЕМА ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН (ЕС ЭВМ)
- ЕДИНИЦЫ КОЛИЧЕСТВА ИНФОРМАЦИИ
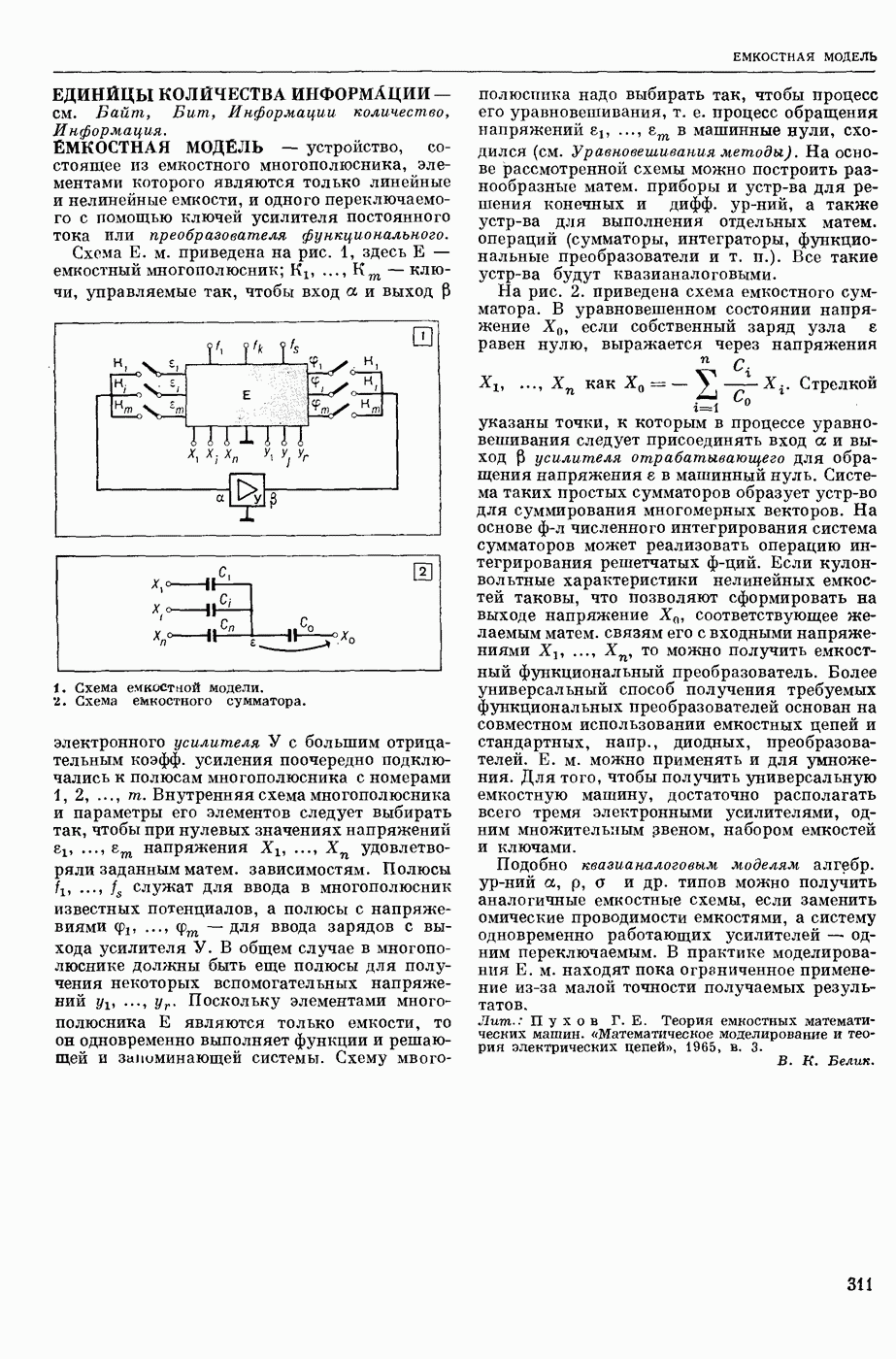
- ЕМКОСТНАЯ МОДЕЛЬ
- ЖЕГАЛКИНА АЛГЕБРА
- ЗАГРУЗЧИК в программировании
- ЗАДАЧА О КОММИВОЯЖЕРЕ
- ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ
- ЗАДАЧА О НАЗНАЧЕНИЯХ
- ЗАДАЧА О ПЕРЕВОЗКАХ С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
- ЗАДАЧА О РАСПРЕДЕЛЕНИИ ПОСТАВОК
- ЗАДАЧА О РЮКЗАКЕ
- ЗАДАЧА О СКЛАДЕ
- ЗАДАЧА ОБ ОПТИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
- ЗАДАЧА ОБ УЗКИХ МЕСТАХ
- ЗАДАЧА С ЗАКРЕПЛЕННЫМ ВРЕМЕНЕМ
- ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
- ЗАМЫКАНИЕ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА
- ЗАПАЗДЫВАНИЯ БЛОК
- ЗАПАСОВ ТЕОРИЯ, теория управления запасами
- ЗАПИСЬ
- ЗАПИСЬ БЕССКОБОЧНАЯ, польская запись
- ЗАПОМИНАЮЩЕГО УСТРОЙСТВА ЕМКОСТЬ
- ЗАПОМИНАЮЩЕГО УСТРОЙСТВА ЗОНА
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ЗУ)
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АВМ (ЗУ АВМ)
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АДРЕСНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АССОЦИАТИВНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО БУФЕРНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ВНЕШНЕЕ, внешний накопитель
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ДОЛГОВРЕМЕННОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО МАГАЗИННОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО НА ЛИНИЯХ ЗАДЕРЖКИ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ОПЕРАТИВНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПОСЛЕДОВАТЕЛЬНЫМ ОБРАЩЕНИЕМ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПРОИЗВОЛЬНЫМ ОБРАЩЕНИЕМ
- ЗАПОМИНАЮЩИЙ ЭЛЕМЕНТ
- ЗАЦИКЛИВАНИЕ
- ЗАЩИТА ПАМЯТИ
- ЗНАКОВЫЙ РАЗРЯД
- ЗНАЧАЩИЕ ЦИФРЫ приближенного числа
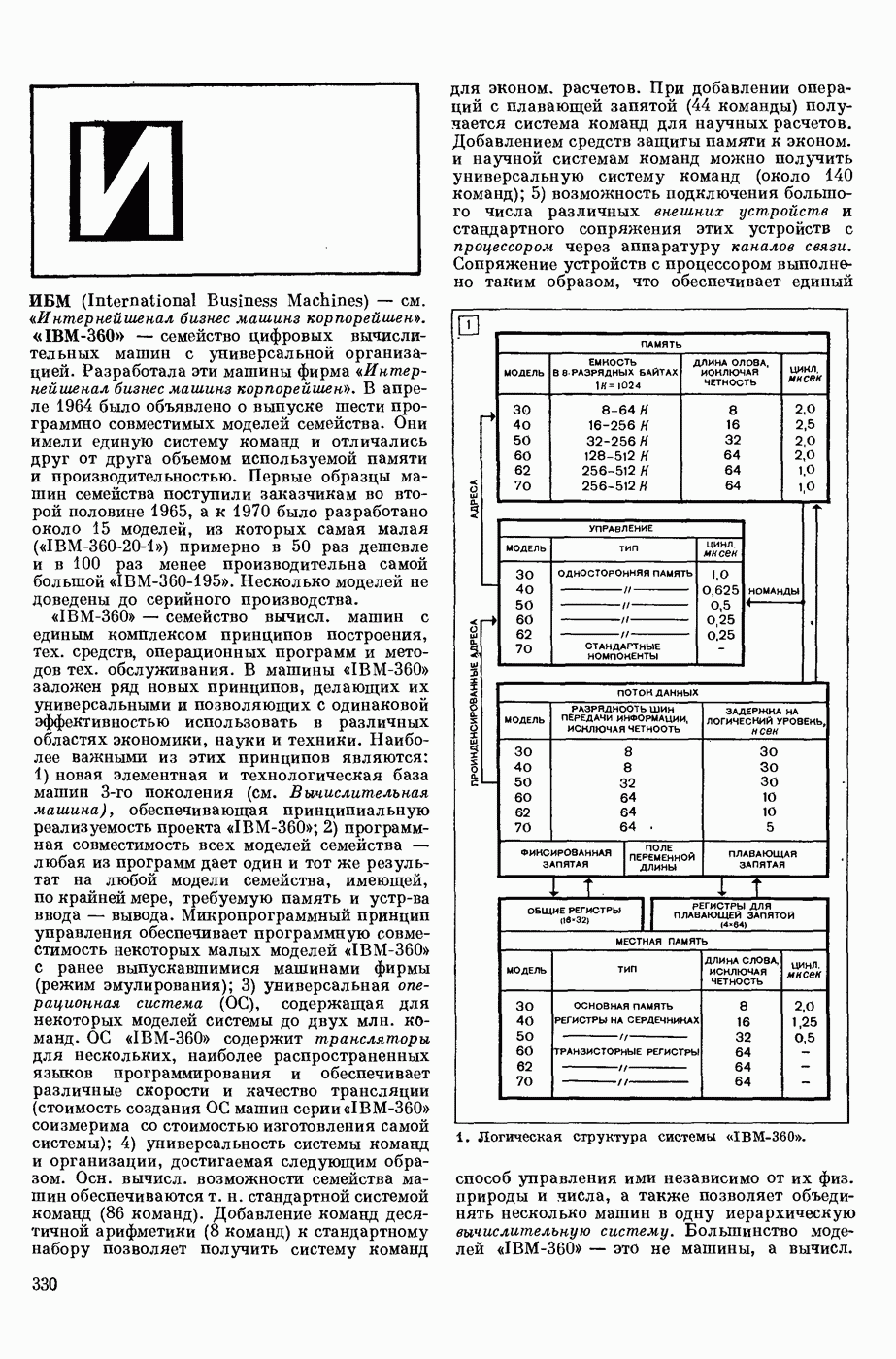
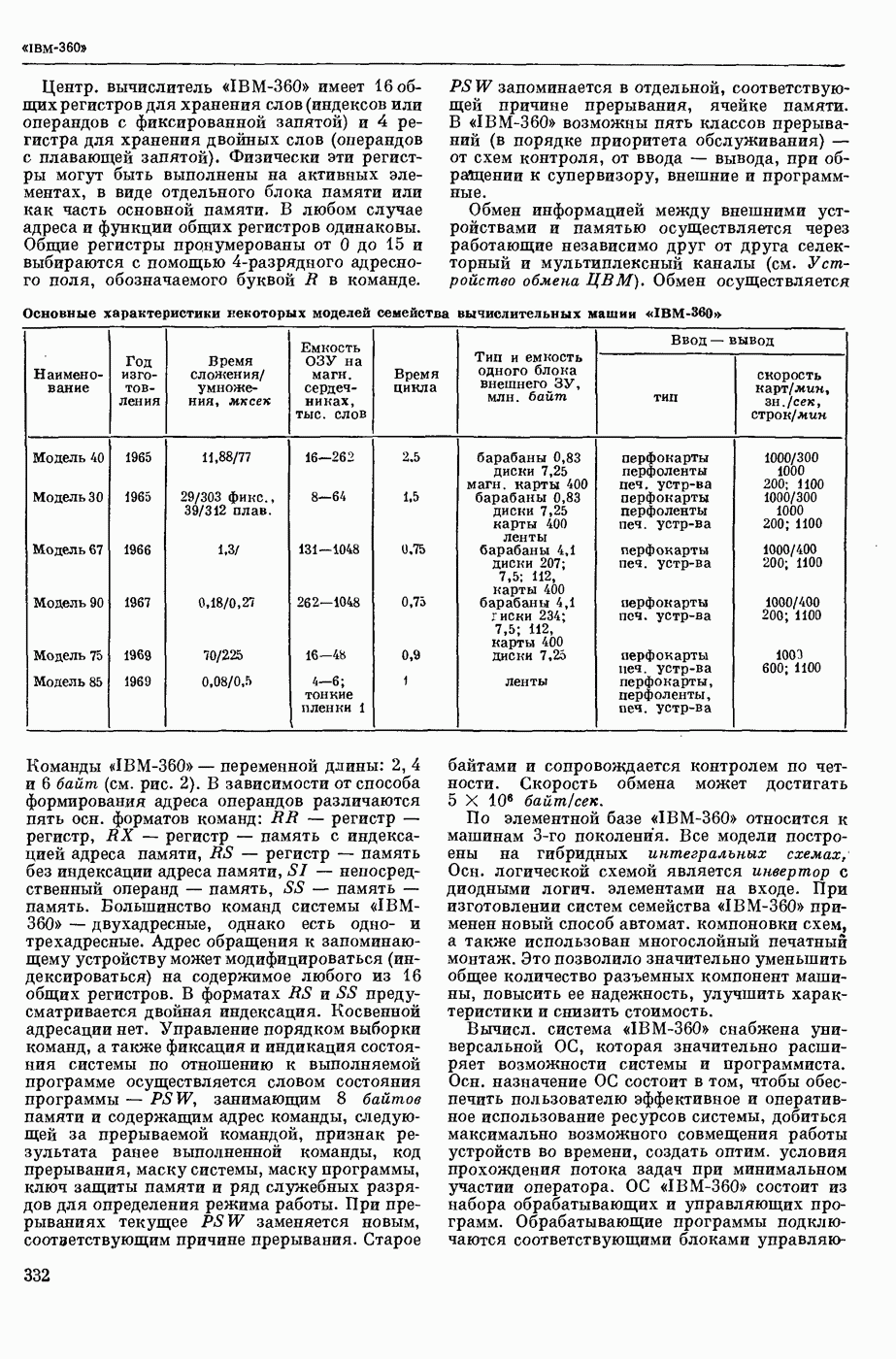
- ИБМ (International Business Machines)
- ИГР ТЕОРИЯ
- ИГРА АЗАРТНАЯ
- ИГРА БЕЗ ПОБОЧНЫХ ПЛАТЕЖЕЙ
- ИГРА БЕСКОАЛИЦИОННАЯ
- ИГРА ВЫПУКЛАЯ
- ИГРА ВЫРОЖДЕННАЯ
- ИГРА ДИНАМИЧЕСКАЯ
- ИГРА КООПЕРАТИВНАЯ
- ИГРА НА ГРАФЕ
- ИГРА НА ЕДИНИЧНОМ КВАДРАТЕ
- ИГРА ПОЗИЦИОННАЯ
- ИГРА ПРОСТАЯ
- ИГРА РЕКУРСИВНАЯ
- ИГРА С ВЫБОРОМ МОМЕНТА ВРЕМЕНИ
- ИГРА СТОХАСТИЧЕСКАЯ
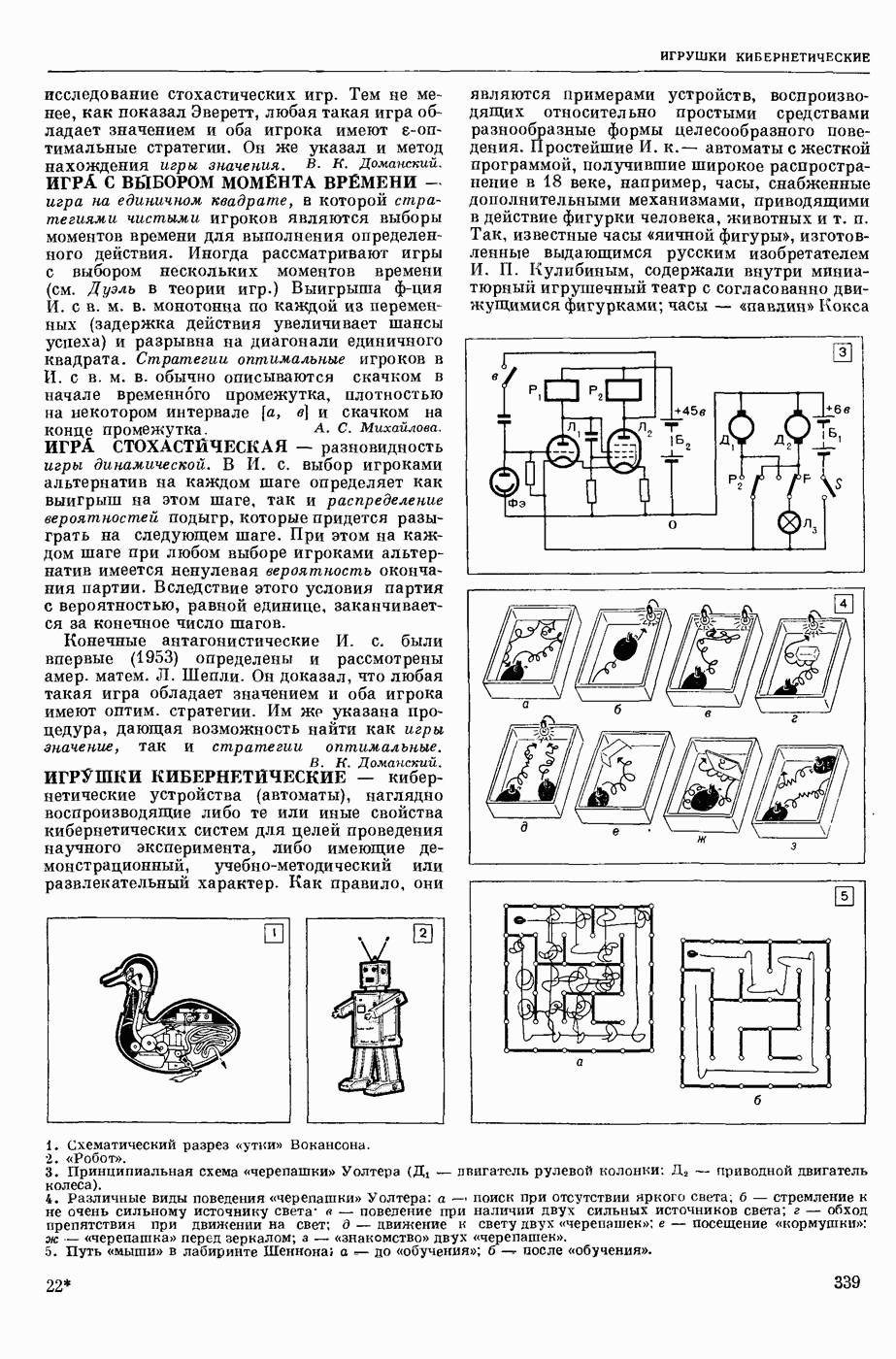
- ИГРУШКИ КИБЕРНЕТИЧЕСКИЕ
- ИГРЫ АНТАГОНИСТИЧЕСКИЕ
- ИГРЫ ДИФФЕРЕНЦИАЛЬНЫЕ
- ИГРЫ ЗНАЧЕНИЕ
- ИГРЫ МАТРИЧНЫЕ
- ИГРЫ НА ВЫЖИВАНИЕ
- ИГРЫ РЕФЛЕКСИВНЫЕ
- ИДЕНТИФИКАТОР
- ИДЕНТИФИКАЦИЯ ОБЪЕКТОВ УПРАВЛЕНИЯ
- ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ (ИСУ)
- ИЕРАРХИЧНОСТЬ УПРАВЛЕНИЯ
- ИЗБЫТОЧНОСТЬ СИСТЕМЫ
- ИЗБЫТОЧНОСТЬ СООБЩЕНИЙ
- ИМПЛИКАЦИЯ в алгебре логики
- ИМПЛИКАЦИЯ СТРОГАЯ
- ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ
- ИМПУЛЬСНАЯ СИСТЕМА УПРАВЛЕНИЯ
- ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ИНВАРИАНТНОСТЬ ПРИЗНАКОВ
- ИНВАРИАНТНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ИНВЕРТОР
- ИНГВЕ ГИПОТЕЗА, гипотеза глубины
- ИНДЕКСИРОВАНИЕ
- ИНДИКАТОРЫ ИНФОРМАЦИИ
- ИНЖЕНЕРНЫЕ МЕТОДЫ СИНТЕЗА ДИСКРЕТНЫХ АВТОМАТОВ
- ИНЖЕНЕРНЫХ РАСЧЕТОВ АВТОМАТИЗАЦИЯ
- ИНСТИТУТ АВТОМАТИКИ АКАДЕМИИ НАУК КИРГИЗСКОЙ ССР
- ИНСТИТУТ АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ (ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ) АКАДЕМИИ НАУК СССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК АЗЕРБАЙДЖАНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК ЭСТОНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ С ВЫЧИСЛИТЕЛЬНЫМ ЦЕНТРОМ АКАДЕМИИ НАУК УЗБЕКСКОЙ ССР
- ИНСТИТУТ ПРИКЛАДНОЙ МАТЕМАТИКИ И МЕХАНИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- ИНСТИТУТ СИСТЕМ УПРАВЛЕНИЯ АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ИНСТИТУТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ АКАДЕМИИ НАУК БЕЛОРУССКОЙ ССР
- ИНСТИТУТ ТОЧНОЙ МЕХАНИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ АКАДЕМИИ НАУК СССР
- ИНСТИТУТ ЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ АКАДЕМИИ НАУК ЛАТВИЙСКОЙ ССР
- ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ, приборная погрешность
- ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ИНТЕГРАЛЬНАЯ СХЁМА
- ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- ИНТЕГРАЛЬНЫХ ЛИНЕЙНЫХ СИНГУЛЯРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАЛЬНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАЛЬНЫХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАТОР
- ИНТЕГРИРОВАНИЕ СИМВОЛЬНОЕ, интегр ирование аналитическое
- ИНТЕГРИРОВАНИЕ ЧИСЛЕННОЕ
- ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- ИНТЕНСИВНОСТЬ ПОТОКА в теории массового обслуживания
- «ИНТЕРНЕЙШЕНАЛ БИЗНЕС МАШЙНЗ КОРПОРЕЙШЕН», ИБМ (International Business Machines Corporation, IBM)
- «ИНТЕРНЕЙШЕНАЛ КОМПЬЮТЕРЗ ЛЙМИТЕД» (International Computers Limited, I. С. L.)
- ИНТЕРПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
- ИНТЕРПОЛЯТОР
- ИНТЕРПРЕТАЦИЯ ЯЗЫКА СТРУКТУРНАЯ
- ИНТЕРПРЕТИРУЮЩАЯ СИСТЕМА
- ИНТУИЦИОНИЗМ
- ИНФОРМАТИВНОСТЬ ПРИЗНАКОВ
- ИНФОРМАТИКА
- ИНФОРМАЦИИ КОЛИЧЕСТВО
- ИНФОРМАЦИИ ПЕРЕДАЧА
- ИНФОРМАЦИИ ТЕОРИЯ
- ИНФОРМАЦИИ ХРАНЕНИЕ
- ИНФОРМАЦИОННО-ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР ПРЕДПРИЯТИЯ
- ИНФОРМАЦИОННО-ЛОГИЧЕСКАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ ЯЗЫК
- ИНФОРМАЦИОННО-ПЛАНИРУЮЩАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА ДОКУМЕНТАЛЬНАЯ
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА ФАКТОГРАФИЧЕСКАЯ
- ИНФОРМАЦИОННО-ПОИСКОВОЕ УСТРОЙСТВО
- ИНФОРМАЦИОННО-ПОИСКОВЫЙ ЯЗЫК
- ИНФОРМАЦИОННО-СПРАВОЧНАЯ СИСТЕМА
- ИНФОРМАЦИОННО-УПРАВЛЯЮЩАЯ СИСТЕМА
- ИНФОРМАЦИОННО-УПРАВЛЯЮЩИХ СИСТЕМ ТЕХНИЧЕСКОЕ ОСНАЩЕНИЕ
- ИНФОРМАЦИОННЫЕ ПОТОКИ НАУКИ
- ИНФОРМАЦИОННЫХ РАБОТ АВТОМАТИЗАЦИЯ
- ИНФОРМАЦИЯ (лат. informatio — разъяснение, изложение, осведомленность)
- ИНФОРМАЦИЯ ДОКУМЕНТАЛЬНАЯ
- ИНФОРМАЦИЯ НАУЧНАЯ
- ИНФОРМАЦИЯ СЕМАНТИЧЕСКАЯ
- ИСКЛЮЧЕННОГО ТРЕТЬЕГО ЗАКОН
- «ИСКРА»
- ИСКУССТВЕННАЯ МЫШЦА
- ИСКУССТВЕННЫЙ РАЗУМ
- ИСПОЛНИТЕЛЬНЫЙ МЕХАНИЗМ
- ИСТОЧНИК ОПОРНОГО НАПРЯЖЕНИЯ
- ИСТОЧНИК СООБЩЕНИЙ
- ИСЧИСЛЕНИЕ, дедуктивная система
- ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ, пропозициональное исчисление
- ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ МИНИМАЛЬНОЕ, логика минимальная
- ИСЧИСЛЕНИЕ ЗАДАЧ, теория задач
- ИСЧИСЛЕНИЕ ПРЕДИКАТОВ УЗКОЕ, исчисление предикатов первой ступени
- ИСЧИСЛЕНИЕ ПРОПОЗИЦИОНАЛЬНОЕ
- «ИТЕРАТОР»
- ИТЕРАЦИОННЫЕ МЕТОДЫ
- ИТЕРАЦИЯ СОБЫТИЯ
- ИФАК (International Federation of Automatic Control)
- ИФИП (International Federation for Information Processing)
- КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ
- КАНАЛ МАШИННЫЙ
- КАНАЛОВ СВЯЗИ ПРОПУСКНАЯ СПОСОБНОСТЬ
- КАНАЛЫ СВЯЗИ
- КАРДИНАЛЬНЫЕ ЧИСЛА
- КАРНАУ КАРТА, Вейча диаграмма
- КАРТА МАГНИТНАЯ
- КАСКАДОВ МЕТОД
- КАТАЛОГ
- КАТЕГОРИЙ ТЕОРИЯ
- КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ
- КВАДРАТУРНЫЕ ФОРМУЛЫ
- КВАЗИАНАЛОГОВАЯ МОДЕЛИРУЮЩАЯ СРЕДА
- КВАЗИАНАЛОГОВАЯ МОДЕЛЬ
- КВАЗИАНАЛОГОВОЕ МОДЕЛИРОВАНИЕ
- КВАЗИРЕЗИСТОР
- КВАЙНА МЕТОД МИНИМИЗАЦИИ
- КВАНТОВАНИЕ
- КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- КВАНТОРЫ
- КИБЕРНЕТИКА
- «КИБЕРНЕТИКА»
- «КИБЕРНЕТИКА» — реферативный журнал,
- КИБЕРНЕТИКА БИОЛОГИЧЕСКАЯ
- КИБЕРНЕТИКА В ВОЕННОМ ДЕЛЕ
- КИБЕРНЕТИКА МЕДИЦИНСКАЯ
- КИБЕРНЕТИКА ТЕХНИЧЕСКАЯ
- КИБЕРНЕТИКА ЭКОНОМИЧЕСКАЯ
- КЛАСС ЗАМКНУТЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАСС ИНВАРИАНТНЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАСС ПРЕДПОЛНЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАССИФИКАЦИИ ИЕРАРХИЧЕСКИЕ
- КЛАССИФИКАЦИЯ АВТОМАТИЧЕСКАЯ
- КЛЮЧЕВОЕ СЛОВО
- КОБОЛ
- КОД (от лат. codex)
- КОД СЕМАНТИЧЕСКИЙ
- КОДИРОВАНИЕ АВТОМАТНОЕ
- КОДИРОВАНИЕ СОСТОЯНИЙ АВТОМАТА
- КОДИРОВАНИЯ ТЕОРИЯ
- КОДЫ КОРРЕКТИРУЮЩИЕ
- КОЛЕБАНИЯ СКРЫТЫЕ
- КОЛМОГОРОВА УРАВНЕНИЯ
- КОМАНД МОДИФИКАЦИЯ
- КОМАНД СИСТЕМА
- КОМАНДА МАШИННАЯ
- КОМАНДЫ ФОРМАТ
- КОМБИНАТОРНЫЙ АНАЛИЗ
- КОМБИНАЦИОННАЯ СХЕМА
- КОМБИНИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- КОМБИНИРОВАННАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КОМБИНИРОВАННЫЕ МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- КОМИТ
- КОММУНИКАЦИОННЫЙ ПРОЦЕССОР
- «КОМПАНИ ИНТЕРНАСЬОНАЛЬ ПУР Л’ИНФОРМАТИК» (Compagnie internationale pour l’informatique)
- КОМПАУНДИРУЮЩИЕ СВЯЗИ В АВТОМАТИЧЕСКИХ СИСТЕМАХ
- КОМПЕНСАЦИОННЫЙ СПОСОБ НАСТРОЙКИ И ИЗМЕРЕНИЯ РЕЗУЛЬТАТОВ РЕШЕНИЯ
- КОМПЛЕКСИРОВАНИЕ МАШИН
- КОМПЛЕКТ ПЕРФОРАЦИОННЫЙ ВЫЧИСЛИТЕЛЬНЫЙ
- КОМПЬЮТЕР
- КОНЕЧНОРАЗНОСТНЫЕ МЕТОДЫ, методы сеток
- КОНКУРЕНЦИИ МОДЕЛИ
- КОНСТРУКТИВНОЕ НАПРАВЛЕНИЕ В МАТЕМАТИКЕ, конструктивная математика
- КОНСТРУКТИВНЫЙ АНАЛИЗ, рекурсивный анализ, вычислимый анализ
- «КОНТРОЛ ДЕЙТА КОРПОРЁЙШЕН» (Control Data Corporation)
- КОНТРОЛЬ ABM
- КОНТРОЛЬ НАБОРА ЗАДАЧ В АВМ
- КОНТРОЛЬ ПРОГРАММНЫЙ
- КОНТРОЛЬ ЦВМ
- КОНТРОЛЬНИК
- КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
- КОНЪЮНКЦИЯ
- КООРДИНАЦИОННО — УПРАВЛЯЮЩИЙ ЦЕНТР ПРЕДПРИЯТИЯ
- КОРНЕВОГО ГОДОГРАФА МЕТОД
- КОРНЕЙ АЛГЕБРАИЧЕСКИХ МНОГОЧЛЕНОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- КОРНЕЙ НЕПРЕРЫВНЫХ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- КОРРЕКЦИЯ ДРЕЙФА НУЛЯ
- КОРРЕКЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КОРРЕЛЯТОР, коррелометр, коррелограф
- КОРРЕЛЯЦИОННАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ ПОЛЯРНАЯ (знаковая)
- КОРРЕЛЯЦИОННАЯ ЭКСТРЕМАЛЬНАЯ СИСТЕМА
- КОРРЕЛЯЦИОННЫЙ АППАРАТУРНЫЙ АНАЛИЗ случайных процессов
- КОРРЕЛЯЦИОННЫЙ МЕТОД РАСПОЗНАВАНИЯ
- КОРРЕЛЯЦИОННЫЙ ЧИТАЮЩИЙ АВТОМАТ
- КОРРЕЛЯЦИЯ в теории вероятностей
- КОШИ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ СПОСОБЫ РЕШЕНИЯ.
- КОЭФФИЦИЕНТ ПЕРЕДАЧИ АВМ
- КОЭФФИЦИЕНТ ПОЛНОТЫ ПОИСКА
- КОЭФФИЦИЕНТ ТОЧНОСТИ ПОИСКА
- КРАЕВАЯ ЗАДАЧА
- КРАЕВЫЕ УСЛОВИЯ
- КРАЕВЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- КРАЙНЯЯ ТОЧКА
- КРАТНЫХ ИНТЕГРАЛОВ СПОСОБЫ ПРИБЛИЖЁННОГО ВЫЧИСЛЕНИЯ
- КРИОГЕННЫЕ ЭЛЕМЕНТЫ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КРИОТРОН
- КРИТЕРИИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КРИТЕРИЙ СЕМАНТИЧЕСКОГО СООТВЕТСТВИЯ
- КРИТИЧЕСКИЙ ПУТЬ
- КУБ ФЕРРИТОВЫЙ
- КУБАТУРНЫЕ ФОРМУЛЫ
- «КИIВ-67»
- ЛАГ И ТАГ СИСТЕМЫ
- ЛАГРАНЖА ЗАДАЧА
- ЛАГРАНЖА ПРАВИЛО МНОЖИТЕЛЕЙ
- ЛАПЛАСА ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЛАПЛАСА ПРЕОБРАЗОВАНИЯ
- ЛЕЖАНДРА—КЛЕБША УСЛОВИЕ
- ЛЕНТА МАГНИТНАЯ
- ЛИНГВИСТИКА МАТЕМАТИЧЕСКАЯ
- ЛИНГВИСТИКА ПРИКЛАДНАЯ
- ЛИНГВИСТИЧЕСКАЯ СТАТИСТИКА
- ЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- ЛИНЕЙНАЯ ФОРМА, линейный функционал, ковектор
- ЛИНЕЙНЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ СИСТЕМ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ
- ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- ЛИСП
- ЛОГИКА КОНСТРУКТИВНАЯ
- ЛОГИКА МАЖОРИТАРНАЯ
- ЛОГИКА МАТЕМАТИЧЕСКАЯ, формальная логика
- ЛОГИКА МИНИМАЛЬНАЯ
- ЛОГИКА МНОГОЗНАЧНАЯ
- ЛОГИКА ПОРОГОВАЯ
- ЛОГИКА ПРЕДИКАТОВ ВЫСШИХ СТУПЕНЕЙ
- ЛОГИКИ НЕКЛАССИЧЕСКИЕ
- ЛОГИКО-МАТЕМАТИЧЕСКОЕ ИСЧИСЛЕНИЕ
- ЛОГИЧЕСКАЯ РАСПОЗНАЮЩАЯ СИСТЕМА
- ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- ЛОГИЧЕСКИЙ ЗАДЕРЖИВАЮЩИЙ ЭЛЕМЕНТ
- ЛОГИЧЕСКИЙ ЭЛЕМЕНТ АВМ
- ЛОГИЧЕСКИЙ ЭЛЕМЕНТ ЦВМ
- ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ НОРМАЛЬНЫЕ ФОРМЫ
- ЛОКАЛИЗОВАННЫЕ ПЕРЕМЕННЫЕ
- ЛОКАЛЬНОГО КОДИРОВАНИЯ ПРИНЦИП
- ЛЯПАС
- ЛЯПУНОВА МЕТОДЫ
- «М-20»
- МАЖОРИТАРНЫЙ ЭЛЕМЕНТ
- МАЙЕРА ЗАДАЧА
- МАК-КЛАСКИ АЛГОРИТМ
- МАКРОКОМАНДА
- МАКРОМОДЕЛИ ЭКОНОМИЧЕСКИЕ
- МАКСИМИНА ПРИНЦИП
- МАКСИМУМА ПРАВДОПОДОБИЯ МЕТОД
- МАНИПУЛЯТОР
- «MARK-1»
- МАРКЕР
- МАРКОВА ЦЕПЬ
- МАРКОВСКИЙ ПРОЦЕСС
- МАССИВ
- МАССИВ ИНФОРМАЦИОННЫЙ
- МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА
- МАССОВОГО ОБСЛУЖИВАНИЯ ТЕОРИЯ, теория очередей
- МАТЕМАТИКА ВЫЧИСЛИТЕЛЬНАЯ
- МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА
- МАТЕМАТИЧЕСКИЕ МЁТОДЫ В ПОЭТИКЕ
- МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЦВМ
- МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЦВМ ВНУТРЕННЕЕ
- МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, среднее значение
- МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- МАТРИЦА
- МАТРИЦА ВТОРЫХ МОМЕНТОВ
- МАТРИЦА ЗАПОМИНАЮЩАЯ
- МАТРИЦА ОБУЧАЕМАЯ
- МАТРИЦА ФЕРРИТОВАЯ МНОГООТВЕРСТНАЯ
- МАТРИЦА ФЕРРИТОВАЯ СЛОИСТАЯ
- МАТРИЧНЫЕ ИГРЫ
- МАШИНА
- МАШИНА ЦЕНТРАЛИЗОВАННОГО КОНТРОЛЯ
- МАШИННАЯ ПЕРЕМЕННАЯ
- МАШИННОЕ ПРОЕКТИРОВАНИЕ ИНТЕГРАЛЬНЫХ СХЕМ
- МАШИННОЕ СЛОВО
- МАШИННЫЙ «ИНТЕЛЛЕКТ»
- МАШИННЫЙ ПЕРЕВОД, автоматический перевод
- МЕДИЦИНСКАЯ ИНФОРМАЦИОННАЯ СИСТЕМА
- МЕДИЦИНСКАЯ ЭЛЕКТРОНИКА
- МЕЖДУНАРОДНАЯ АССОЦИАЦИЯ ПО АНАЛОГОВЫМ ВЫЧИСЛЕНИЯМ
- МЕЖДУНАРОДНАЯ ОРГАНИЗАЦИЯ ПО СТАНДАРТИЗАЦИИ
- МЕЖДУНАРОДНАЯ ФЕДЕРАЦИЯ ПО АВТОМАТИЧЕСКОМУ УПРАВЛЕНИЮ
- МЕЖДУНАРОДНАЯ ФЕДЕРАЦИЯ ПО ОБРАБОТКЕ ИНФОРМАЦИИ
- МЕМИСТОР
- МЕРЫ СЛОЖНОСТИ в теории автоматов.
- МЕТАЛОГИКА
- МЕТАМАТЕМАТИКА
- МЕТАСИМВОЛЫ
- МЕТАТЕОРИЯ
- МЕТАТРАНСЛЯТОР
- МЕТАЯЗЫК
- МЕТКА
- МЕТОД ЗАМЕНЫ ЯДРА ВЫРОЖДЕННЫМ
- МЕТРИЧЕСКИЕ СВОЙСТВА ДИЗЪЮНКТИВНЫХ НОРМАЛЬНЫХ ФОРМ
- МИКРОКОМАНДА
- МИКРОМОДЕЛЬ ЭКОНОМИЧЕСКАЯ
- МИКРООПЕРАЦИЯ
- МИКРОПРОГРАММ ПРЕОБРАЗОВАНИЯ.
- МИКРОПРОГРАММА
- МИКРОПРОГРАММНАЯ АЛГЕБРА
- МИКРОПРОГРАММНОЕ УПРАВЛЕНИЕ
- МИКРОСХЕМА
- МИКРОЭЛЕКТРОННАЯ ЭЛЕМЕНТНАЯ БАЗА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- МИЛИ АВТОМАТ
- МИНИМАКС
- МИНИМАКСНОЕ РЕШАЮЩЕЕ ПРАВИЛО
- МИНИМАЛЬНО-ФАЗОВАЯ СИСТЕМА
- МИНИМИЗАЦИИ ФУНКЦИЙ МЕТОДЫ
- МИНИМИЗАЦИЯ НАБОРА ПРИЗНАКОВ
- МИНИМИЗАЦИЯ СХЕМ ЦВМ
- МИНИМИЗАЦИЯ ЧИСЛА СОСТОЯНИЙ АВТОМАТА
- «МИНСК»
- «МИР», машина для инженерных расчетов
- «МИР-2» (разработана в 1969)