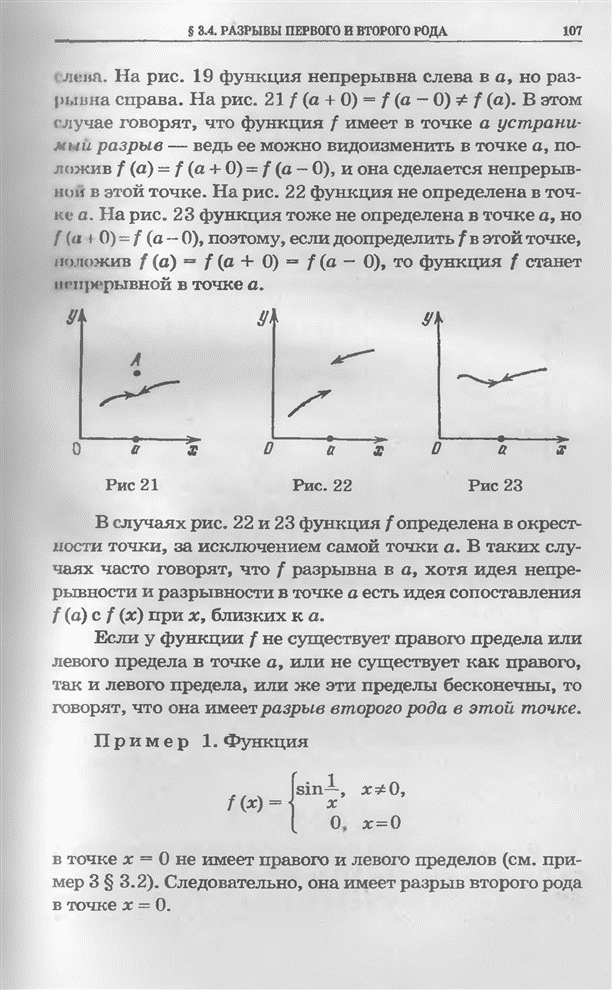
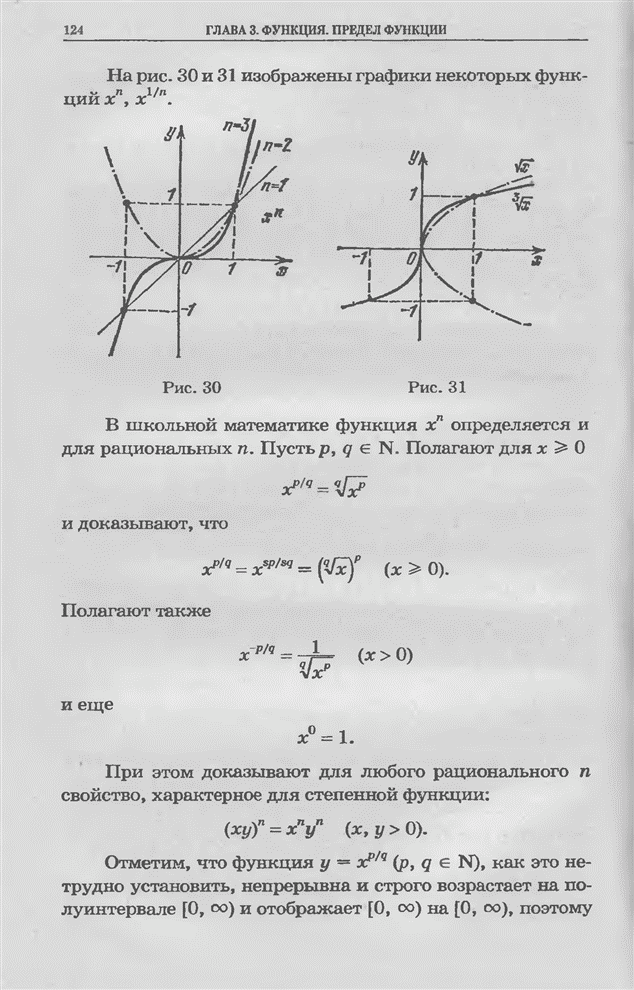
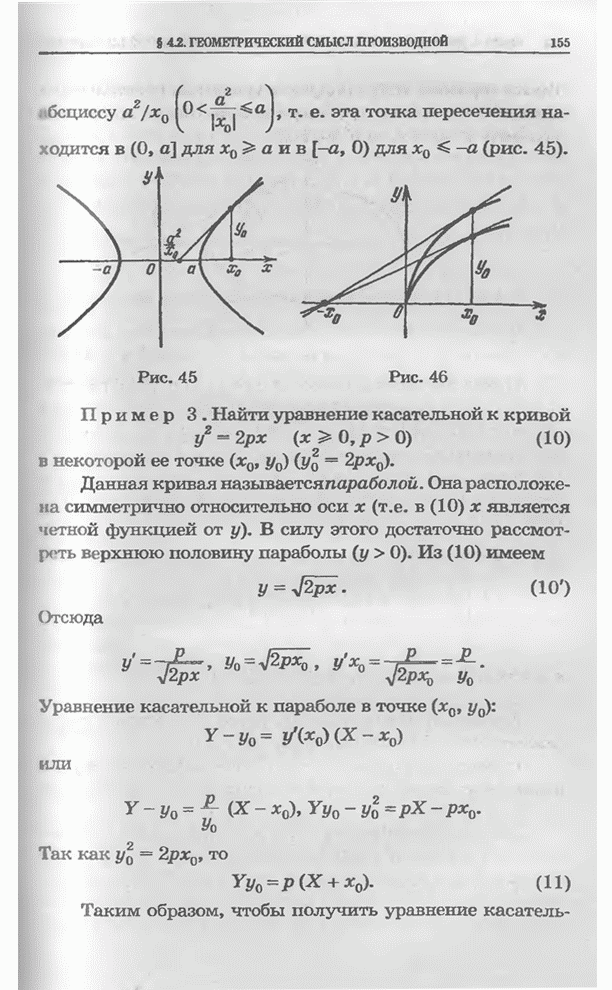
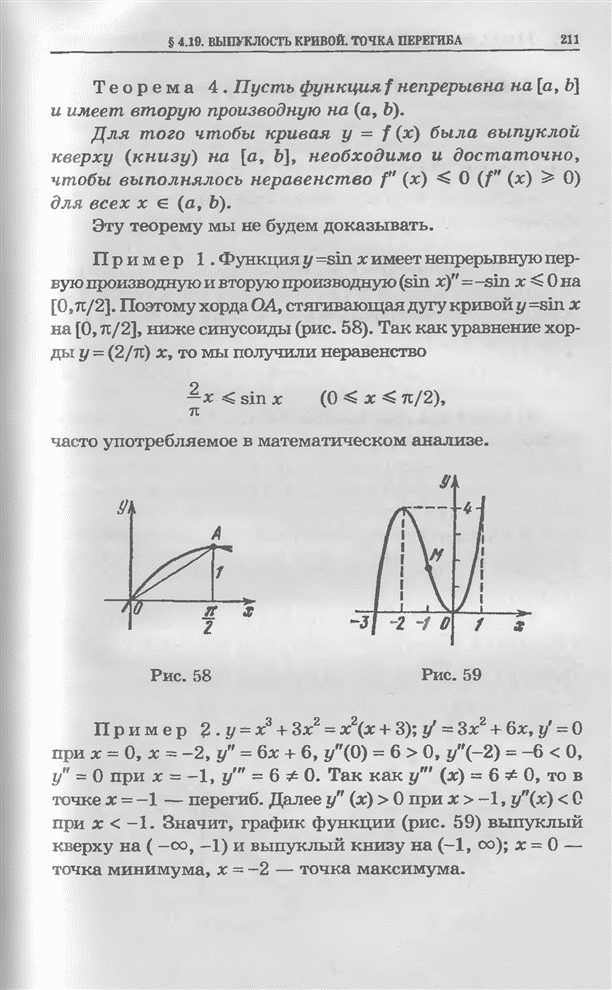
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. Предел последовательности
§ 2.1. Понятие предела последовательности
Пусть каждому
натуральному числу ![]() по некоторому закону поставлено в
соответствие действительное или комплексное число
по некоторому закону поставлено в
соответствие действительное или комплексное число ![]() .
.
Тогда говорят,
что этим определена последовательность чисел ![]() или, короче,
последовательность
или, короче,
последовательность
![]() .
.
Говорят еще,
что переменная ![]() пробегает
значения последовательности
пробегает
значения последовательности ![]() .
.
Отдельные числа
![]() последовательности
последовательности
![]() называются
ее элементами. Надо иметь в ввиду, что
называются
ее элементами. Надо иметь в ввиду, что ![]() и
и ![]() при
при ![]() считаются отличными как элементы
последовательности, хотя не исключено, что как числа они равны между собой, т.
е. может быть
считаются отличными как элементы
последовательности, хотя не исключено, что как числа они равны между собой, т.
е. может быть ![]() .
.
Если положить ![]() , то последовательность
, то последовательность
![]()
превратится во множество
![]() ,
,
которое в § 1.6 тоже было названо последовательностью.
В этой главе мы будем рассматривать последовательности действительных чисел, и это обстоятельство не будем оговаривать особо.
Примеры последовательностей:
П р и м е р 1.
![]() .
.
П р и м е р 2.
![]() .
.
П р и м е р 3. ![]() .
.
П р и м е р 4. ![]() .
.
П р и м е р 5. ![]() .
.
П р и м е р 6. ![]() .
.
В примере 2 переменная ![]() для четных
для четных ![]() принимает одно и то
же значение:
принимает одно и то
же значение:
![]() .
.
Тем не менее,
мы считаем, что элементы ![]() различны.
различны.
Если все
элементы последовательности ![]() равны одному и тому же числу
равны одному и тому же числу ![]() , то ее называют постоянной.
, то ее называют постоянной.
Легко видеть, что последовательности в примерах 1, 2 и 4 ограничены (см. § 1.6). В этом случае говорят также, что соответствующие переменные, пробегающие эти последовательности, ограничены. Что касается последовательностей в примерах 3, 5 и 6, то они неограниченны. Однако последовательность в примере 3, очевидно, ограничена снизу числом 2. Что касается последовательности в примере 6, то она не ограничена как снизу, так и сверху.
Введем понятие предела последовательности.
О п р е д е л е
н и е 1. Число ![]() называется
пределом последовательности
называется
пределом последовательности ![]() , если для всякого
, если для всякого ![]() найдется (зависящее от
найдется (зависящее от ![]() ) число
) число ![]() такое, что
выполняется неравенство
такое, что
выполняется неравенство
![]() (1)
(1)
для всех (натуральных) ![]() .
.
В этом случае пишут
![]() или
или ![]()
и говорят, что переменная ![]() или последовательность
или последовательность
![]() имеет
предел, равный числу
имеет
предел, равный числу ![]() , или стремится к
, или стремится к ![]() . Говорят также, что
переменная
. Говорят также, что
переменная ![]() или
последовательность
или
последовательность ![]() сходится к числу
сходится к числу ![]() .
.
Если ![]() , то, очевидно,
, то, очевидно, ![]() .
.
З а м е ч а н и
е. Если ![]() ,
то
,
то ![]() ; и
обратно. Это следует из того факта, что если
; и
обратно. Это следует из того факта, что если
![]() ,
,
то
![]() ,
,
и обратно.
Переменная примера 1 имеет предел, равный 0:
![]() .
(2)
.
(2)
В самом деле, зададим произвольное ![]() и решим неравенство:
и решим неравенство:
![]() или
или ![]() .
.
Этим для всякого ![]() найдено число
найдено число ![]() такое, что
неравенство
такое, что
неравенство
![]()
выполняется для всех ![]() , и мы доказали
равенство (2).
, и мы доказали
равенство (2).
П р и м е р 7. Переменная примера 4 стремится к 1:
![]() . (3)
. (3)
В самом деле, составим неравенство
![]() .
.
Оно, как мы видели, выполняется
для любого ![]() ,
если
,
если ![]() . Это
доказывает равенство (3).
. Это
доказывает равенство (3).
П р и м е р 8.
Если ![]() , то
, то
![]() .
(4)
.
(4)
В самом деле, пусть пока ![]() . Неравенство
. Неравенство
![]()
верно, если
![]() ,
,
т. е. если
![]() .
.
Мы доказали (4)
при ![]() . Если
. Если
![]() , то
равенство (4) тривиально. Ведь в этом случае переменная
, то
равенство (4) тривиально. Ведь в этом случае переменная ![]() есть постоянная, равная
нулю:
есть постоянная, равная
нулю:
![]() .
.
П р и м е р 9.
Разложим положительное число ![]() в бесконечную десятичную дробь:
в бесконечную десятичную дробь:
![]() .
.
Для его ![]() - й срезки
- й срезки
![]()
имеет место равенство
![]() . (5)
. (5)
В самом деле,
 .
.
Но если задать ![]() , то всегда найдется такое
, то всегда найдется такое ![]() , что
, что
![]() ,
,
(см. предыдущий пример, где надо
считать ![]() ).
Поэтому
).
Поэтому
![]() ,
,
и мы доказали (5).
З а м е ч а н и
е. Срезки ![]() -
рациональные числа. Из (5) следует, что всякое действительное число является
пределом последовательности рациональных чисел.
-
рациональные числа. Из (5) следует, что всякое действительное число является
пределом последовательности рациональных чисел.
Таким образом, всякое иррациональное число можно приблизить рациональным числом с любой наперед заданной степенью точности.
В силу этого
свойства про множество ![]() рациональных чисел говорят, что оно всюду
плотно в множестве
рациональных чисел говорят, что оно всюду
плотно в множестве ![]() всех действительных чисел.
всех действительных чисел.
Неравенство
![]()
эквивалентно двум неравенствам
![]() или
или ![]() ,
,
что эквивалентно тому факту, что
точка ![]() принадлежит
к
принадлежит
к ![]() -
окрестности точки
-
окрестности точки ![]() :
:
![]() (см. § 1.10).
(см. § 1.10).
Тогда
определение предела можно выразить следующими словами: Число (точка) ![]() есть предел
переменной
есть предел
переменной ![]() ,
если, каково бы ни было
,
если, каково бы ни было ![]() , найдется такое число
, найдется такое число ![]() , что все точки
, что все точки ![]() с индексами
с индексами ![]() попадут в
попадут в ![]() - окрестность точки
- окрестность точки ![]() :
:
![]() .
.
Очевидно,
какова бы ни была окрестность ![]() точки
точки ![]() , найдется такое
, найдется такое ![]() , что интервал
, что интервал ![]() содержится в
содержится в ![]() , т. е.
, т. е. ![]() (рис. 7).
(рис. 7).
Поэтому тот
факт, что ![]() можно
выразить еще и так: какова бы ни была окрестность
можно
выразить еще и так: какова бы ни была окрестность ![]() точки
точки ![]() , все точки
, все точки ![]() , начиная с
некоторого номера
, начиная с
некоторого номера ![]() ,
должны попасть в эту окрестность, т. е. должно существовать такое число
,
должны попасть в эту окрестность, т. е. должно существовать такое число ![]() , что
, что ![]() . Что же касается точек
. Что же касается точек
![]() с
индексами
с
индексами ![]() ,
то они могут принадлежать и могут не принадлежать к
,
то они могут принадлежать и могут не принадлежать к ![]() . Таким образом, если вне
. Таким образом, если вне ![]() имеются точки
имеются точки ![]() , то их конечное
число.
, то их конечное
число.

Рис. 7 Рис. 8
С другой стороны, если известно,
что вне ![]() имеется
только конечное число точек
имеется
только конечное число точек ![]() , то, обозначив
, то, обозначив
![]() ,
,
т. е. максимум среди индексов ![]() , мы можем сказать,
что точки
, мы можем сказать,
что точки ![]() с
индексом
с
индексом ![]() попадут
в интервал
попадут
в интервал ![]() .
Поэтому понятие предела можно сформулировать и так: переменная
.
Поэтому понятие предела можно сформулировать и так: переменная ![]() имеет своим
пределом точку
имеет своим
пределом точку ![]() ,
если вне любой окрестности этой точки имеется конечное или пустое множество
точек
,
если вне любой окрестности этой точки имеется конечное или пустое множество
точек ![]() .
.
П р и м е р 10. Переменная
![]() (6)
(6)
ни к какому пределу не стремится.
В самом деле,
допустим, что эта переменная имеет предел, равный числу ![]() . Рассмотрим окрестность этой
точки
. Рассмотрим окрестность этой
точки
![]() .
.
Длина ее равна ![]() . Очевидно, что эта
окрестность не может содержать в себе одновременно и точку 1 и точку -1 ,
потому что расстояние между этими точками равно
. Очевидно, что эта
окрестность не может содержать в себе одновременно и точку 1 и точку -1 ,
потому что расстояние между этими точками равно ![]() . Для определенности будем считать, что
точка 1 не принадлежит к нашей окрестности. Но
. Для определенности будем считать, что
точка 1 не принадлежит к нашей окрестности. Но ![]() для
для ![]() , т. е. вне нашей окрестности имеется
бесконечное число элементов последовательности.
, т. е. вне нашей окрестности имеется
бесконечное число элементов последовательности.
Таким образом,
точка ![]() не
может быть пределом нашей последовательности, и так как эта точка произвольна,
то последовательность (6) не имеет предела.
не
может быть пределом нашей последовательности, и так как эта точка произвольна,
то последовательность (6) не имеет предела.
Т е о р е м а 1. Если
переменная ![]() имеет
предел, то он единственный.
имеет
предел, то он единственный.
В самом деле,
допустим, вопреки теореме, что ![]() имеет два различных предела
имеет два различных предела ![]() и
и ![]() . Покроем точки
. Покроем точки ![]() соответственно
интервалами
соответственно
интервалами ![]() ,
,
![]() настолько
малой длины, чтобы эти интервалы не пересекались (рис. 8). Так как
настолько
малой длины, чтобы эти интервалы не пересекались (рис. 8). Так как ![]() , то в интервале
, то в интервале ![]() находятся все
элементы
находятся все
элементы ![]() ,
за исключением конечного их числа, но тогда интервал
,
за исключением конечного их числа, но тогда интервал ![]() не может содержать в себе
бесконечное число элементов
не может содержать в себе
бесконечное число элементов ![]() и
и ![]() не может стремиться к
не может стремиться к ![]() . Мы пришли к
противоречию. Теорема доказана.
. Мы пришли к
противоречию. Теорема доказана.
Т е о р е м а
2. Если последовательность ![]() сходится (имеет предел), то она
ограничена.
сходится (имеет предел), то она
ограничена.
Д о к а з а т е
л ь с т в о. Пусть ![]() . Зададим
. Зададим ![]() и подберем натуральное
и подберем натуральное ![]() так, чтобы
так, чтобы
![]() ,
,
но тогда ![]() и выполняется неравенство
и выполняется неравенство
![]()
для всех ![]() . Пусть
. Пусть ![]() - наибольшее среди чисел
- наибольшее среди чисел
![]() .
.
Тогда, очевидно,
![]() .
.
Теорема доказана.
З а м е ч а н и е. Ограниченность последовательности является необходимым условием сходимости последовательности, но не достаточным, как показывает пример 10.
Т е о р е м а
3. Если переменная ![]() имеет не равный нулю предел
имеет не равный нулю предел ![]() , то найдется такое
, то найдется такое ![]() , что
, что
![]() для
для ![]() .
.
Больше того,
для указанных ![]() ,
если
,
если ![]() , то
, то ![]() , если же
, если же ![]() , то
, то ![]() . Таким образом,
начиная с некоторого номера,
. Таким образом,
начиная с некоторого номера, ![]() сохраняет знак
сохраняет знак ![]() .
.
Д о к а з а т е
л ь с т в о. Пусть ![]() . Тогда для
. Тогда для ![]() должно найтись число
должно найтись число ![]() такое, что
такое, что
![]() ,
,
откуда ![]() , и первое утверждение
теоремы доказано. С другой стороны, неравенство
, и первое утверждение
теоремы доказано. С другой стороны, неравенство ![]() эквивалентно следующим двум:
эквивалентно следующим двум:
![]() .
.
Тогда, если ![]() , то
, то
![]() ,
,
а если ![]() , то
, то
![]() ,
,
и этим второе утверждение теоремы доказано.
Т е о р е м а 4. Если ![]() ,
, ![]() и
и ![]() для всех
для всех ![]() , то
, то ![]() .
.
Д о к а з а т е
л ь с т в о. Допустим, что ![]() . Зададим
. Зададим ![]() и подберем числа
и подберем числа ![]() и
и ![]() так, чтобы
так, чтобы ![]()
![]() : это возможно,
потому что
: это возможно,
потому что ![]() ,
а
,
а ![]() .
.
Если ![]() , то, очевидно,
, то, очевидно, ![]() , и мы пришли к
противоречию, так как по условию
, и мы пришли к
противоречию, так как по условию ![]() для всех
для всех ![]() .
.
С л е д с т в и
е. Если элементы сходящейся последовательности ![]() принадлежат
принадлежат ![]() , то ее предел также
принадлежит
, то ее предел также
принадлежит ![]() .
.
Д о к а з а т е
л ь с т в о. В самом деле, ![]() . Если
. Если ![]() , то по теореме 4
, то по теореме 4 ![]() , что и требовалось доказать.
, что и требовалось доказать.
З а м е ч а н и
е. Для интервала ![]() для
конечных
для
конечных ![]() и
и
![]() можно
утверждать только, что если
можно
утверждать только, что если ![]() , то
, то ![]() . Таким образом, неравенства в пределе
сохраняются или обращаются в равенство. Например,
. Таким образом, неравенства в пределе
сохраняются или обращаются в равенство. Например, ![]() , но
, но ![]() .
.
Т е о р е м а
5. Если переменные![]() и
и ![]() стремятся к одному и тому же пределу
стремятся к одному и тому же пределу ![]() и
и ![]() , то переменная
, то переменная ![]() также стремится к
также стремится к ![]() .
.
Д о к а з а т е
л ь с т в о. Задав ![]() можно найти
можно найти ![]() и
и ![]() , такие, что
, такие, что
![]() ,
,
откуда для ![]()
![]()
и
![]() ,
,
что и требовалось доказать.
Т е о р е м а
6. Если ![]() ,
то
,
то ![]() .
.
Доказательство
следует из неравенства ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
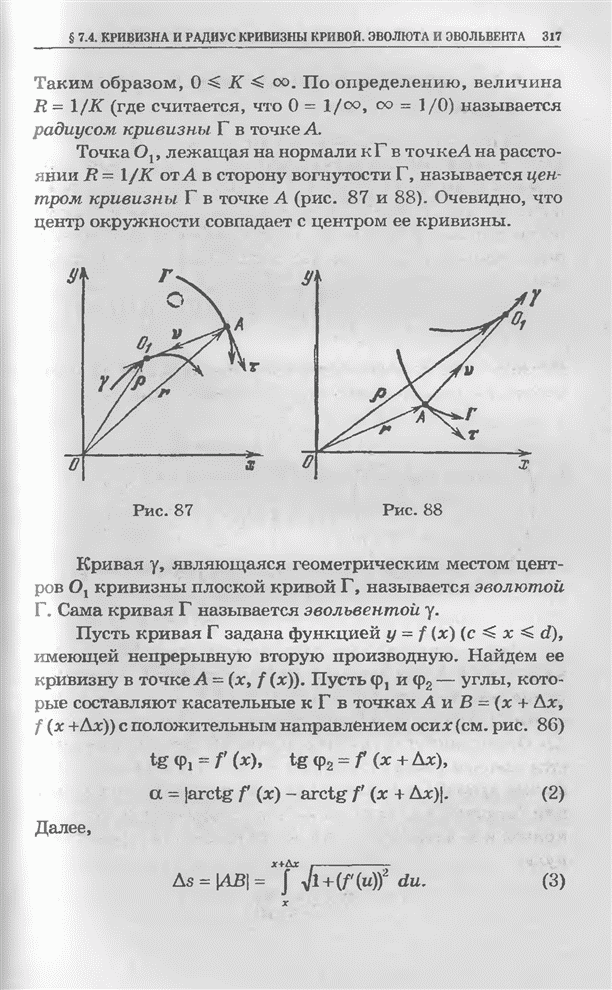
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
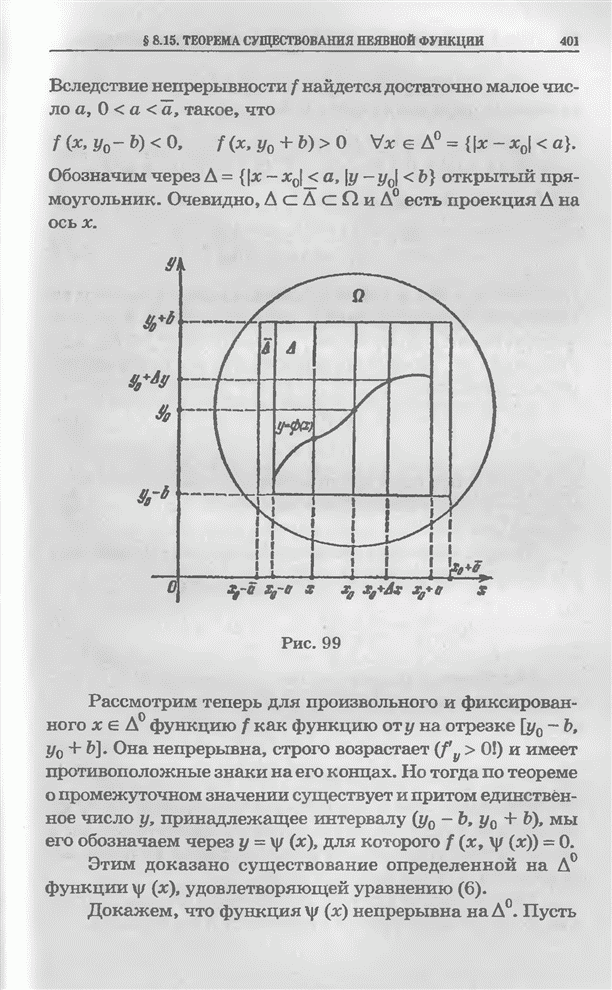
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
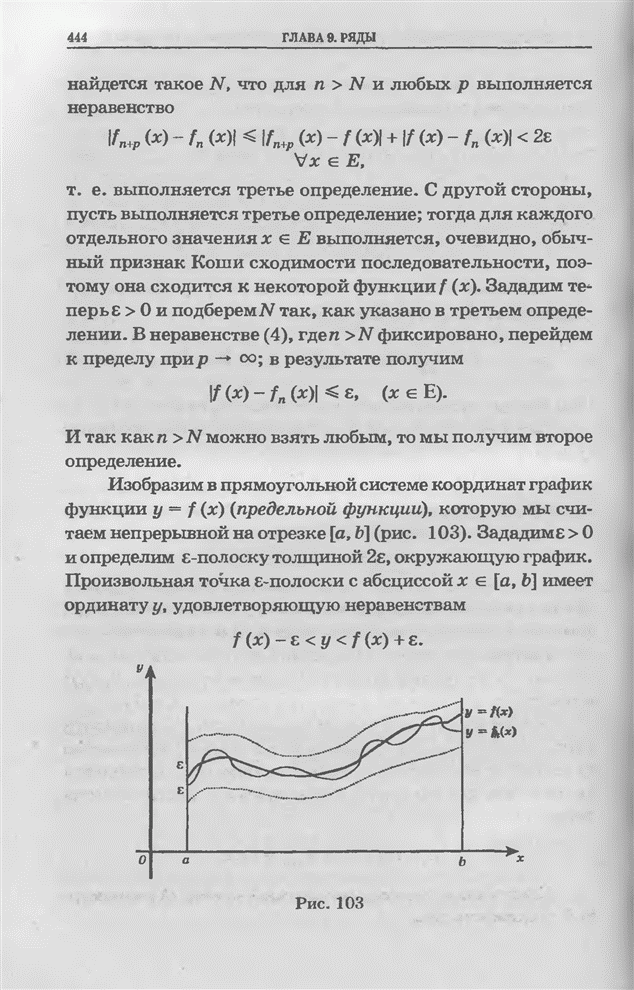
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей