9. АБСОЛЮТНАЯ ТЕРМОДИНАМИЧЕСКАЯ ТЕМПЕРАТУРА

В предыдущем разделе мы по сути дела описали некую машину, которая совершает круговой цикл Карно: производит работу поглощая теплоту от источника с температурой и передавая теплоту источнику с более низкой температурой Как видим, такая машина работает между температурами

Рассмотрим теперь произвольную машину, работающую между температурами (меньшей) и (большей). Пусть работа, совершаемая машиной во время каждого цикла, и пусть количества теплоты, поглощенной за цикл при температуре и отданной при температуре Машина не обязательно должна действовать по циклу Карно; ставится единственное условие: машина должна быть цикличной, т. е. по скончании процесса возвращаться в первоначальное состояние.

Можно легко показать, что если т. е. если машина совершает положительную работу, то

Допустим сначала, что Это означало бы, что машина поглощает во время цикла от источника с температурой теплоту Тогда можно было бы привести два источника в тепловой контакт и позволить теплоте самопроизвольно переходить от более горячего источника с температурой к более холодному с температурой до тех пор, пока последний не получит такое же количество теплоты, какое он передал машине во время цикла. Так как источник с температурой остался бы неизменным и машина снова была бы в своем начальном состоянии, то единственным конечным результатом процесса было бы превращение в работу теплоты, поглощенной из одного источника, который повсюду имел одинаковую температуру Поскольку это противоречит постулату Кельвина, то должно быть

Доказать, что теперь очень просто. Так как наша машипа возвращается после цикла к начальному состоянию, то из первого закона (см. уравнение имеем

Но по предположению, и уже доказано, что следовательно, мы должны иметь

Рассмотрим теперь вторую машину, работающую между теми же температурами Для нее являются величинами, соответствующими первой машины. Мы докажем следующую основную теорему:

а) если первая машина является обратимой, то

б) если вторая машина также обратима, то

В первой части теоремы мы ничего не предполагаем о второй машине; таким образом, она может быть обратимой, либо нет.

Если применим уравнение (16) (особый вид первого закона для циклов) к двум нашим машинам, то увидим, что работа, выполненная каждой машиной в течение цикла, должна быть равна разности между теплотой, полученной от источника с температурой и теплотой, отданной источнику с температурой Таким образом, имеем

Отношение конечно, может быть выражено рациональной

дробью с любой наперед заданной точностью. В результате можно написать

где положительные целые числа.

Рассмотрим теперь процесс, состоящий из циклов второй машины и обратных циклов первой машины. Этот процесс является допустимым, так как мы предположили, что первая машина обратима.

Когда первая машина действует в обратном направлении, она поглощает количество работы во время каждого обратного цикла, отдавая теплоту источнику с температурой и поглощая теплоту из источника с температурой

Общее количество работы, выполненной двумя машинами во время описанного выше сложного процесса, составляет

Общее количество теплоты, поглощенной из источника с температурой таково:

и общее количество теплоты, отданное источнику равно

Из (47) и (48) непосредственно получаем

но из (49) следует, что

откуда

Уравнение (50) устанавливает, что при завершении процесса не происходит изменения количества теплоты у источника с высокой температурой а из уравнения (51) видно, что теплота, поглощенная из источника с температурой (равная превращается в работу

Так как весь процесс составлен из циклов каждой из машин, то по окончании его обе машины вернутся к своим начальным состояниям. Из этого вытекает, что Ьобщ не может быть положительной, так как если бы опа была положительной, то единственным конечным результатом всего процесса должно было быть превращение в работу теплоты поглощенной из источника, который повсюду имеет температуру Но это противоречит постулату Кельвина. Следовательно, мы должны получить

Благодаря уравнению (51), это неравенство эквивалентно:

и, вспоминая выражение для общ» мы получаем

Если из этого выражения исключим при помощи уравнения то, поскольку все величины в (49) положительны, можно записать

или

что совпадает с (45).

Для полного доказательства нашей основной теоремы мы должны показать, что если вторая машина также обратима, то надо поставить знак равенства (см. уравнения (46)).

Если вторая машина обратима, то, изменяя направление действия обеих машин и применяя неравенство первой части теоремы, имеем

Полученное неравенство и неравенство (45) должны удовлетворяться в настоящем случае, потому что обе машины обратимы. Но эти неравенства справедливы только в случае равенства.

Мы можем заново сформулировать только что доказанную теорему следующим образом: если имеются различные циклические тепловые машины, действующие между температурами и если некоторые из этих машин обратимые, то коэффициент полезного действия всех обратимых машин одинаков, тогда как необратимые имеют коэффициенты полезного действия, которые не превышают коэффициент полезного действия обратимых машин.

Рассмотрим сначала две обратимые машины. Тот факт, что их коэффициенты полезного действия равны, следует непосредственно из (46) и определения коэффициента полезного действия (44).

Если мы имеем обратимую и необратимую машины, то получаем из неравенства (45)

Отсюда

Сравнивая это с уравнением (44), видим, что коэффициент полезного действия необратимой машины никогда не может превзойти таковой для обратимой машины.

Наша основная теорема показывает, что отношение имеет одинаковую величину для всех обратимых машин, которые работают в интервале одинаковых температур т. е., если машины обратимы, это отношение не зависит от их особенностей, а определяется только температурами Поэтому можно написать

где универсальная функция температур Теперь докажем, что функция имеет следующее свойство:

где три произвольные температуры.

Пусть две обратимые циклические машины, которые работают соответственно между температурами Если поглощает во время цикла количество теплоты при температуре и отдает количество теплоты при то имеем

Подобно этому, если во время каждого процесса поглощает количество теплоты при температуре и отдает количество теплоты (мы полагаем для простоты, что обе машины выбраны так, что они отдают равные количества теплоты при температуре то

Разделив это уравнение на предыдущее, запишем

Рассмотрим теперь сложный процесс, состоящий из прямого цикла машины и обратного цикла машины Этот процесс, очевидно, представляет собой обратимый цикл, так как он состоит из двух обратимых циклов. Во время сложного процесса при температуре теплота не изменяется, потому что количество теплоты которое передано машиной при температуре снова поглощается при этой температуре машиной работающей в обратном направлении. Однако во время цикла при температуре количество теплоты поглощается машиной и при температуре машине передается количество теплоты

Поэтому можно машины когда они работают совместно по описанному выше способу, рассматривать как единую обратимую циклическую машину, которая действует между температурами

Для этой машины, по определению функции мы имеем

Сравнивая это уравнение с (54), получаем равенство (53), что и требовалось доказать.

Поскольку температура в приведенном рассуждении является произвольной, то можно зафиксировать ее во всех уравнениях. Из этого следует, что можно рассматривать как функцию одной лишь температуры поэтому принимаем

где К — произвольная константа.

Используя (55), выразим (53) в форме

Это уравнение показывает, что равна отношению функции с аргументом к такой же функции с аргументом

Вследствие того, что мы использовали эмпирическую температуру очевидно, невозможно определить аналитическую форму функции Однако так как наша шкала температур произвольна, то удобно ввести новую температурную шкалу, используя вместо саму функцию вместо температуры.

Следует отметить, что определена не единственно возможным способом. Из (56) или (55) видно, что определена с точностью до произвольного постоянного множителя. Это позволяет нам надлежащим образом выбрать единицу новой температурной шкалы. Обычно, выбирая эту единицу, полагают разность между температурой кипения и температурой замерзания воды, равной 100 градусам.

Температурная шкала, которую мы только что определили, называется абсолютной термодинамической шкалой температуры. Ее преимущество в том, что она не зависит от особых свойств термометрического вещества. В дальнейшем все термодинамические законы при использовании термодинамической шкалы принимают простую форму.

Покажем теперь, что абсолютная термодинамическая температура совпадает с абсолютной температурой введенной во втором разделе при помощи газового термометра.

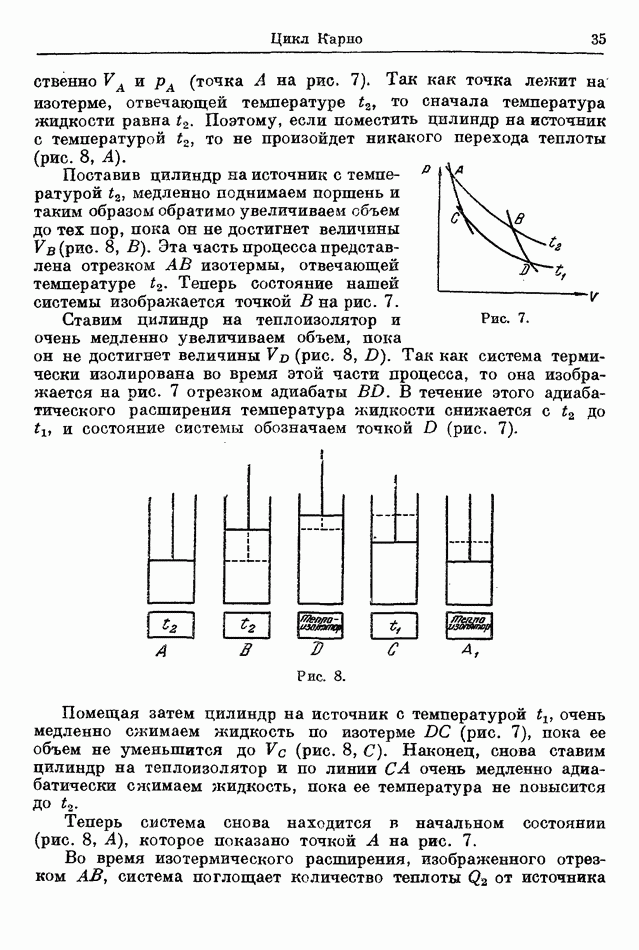
Рассмотрим совершаемый идеальным газом цикл Карно (для большей простоты возьмем один моль газа). Пусть температуры, соответствующие двум изотермам цикла Карно, измеренные газовым термометром (см. рис. 7). Подсчитаем сначала количество теплоты поглощенное при температуре во время изотермического расширения Применяя первый закон [уравнение (15)] к процессу и обозначая индексами величины, относящиеся к состояниям имеем

где работа, совершенная во время изотермического расширения, которая может быть подсчитана с помощью уравнения (10):

Используем тот факт, что энергия идеального газа является функцией только температуры (см. раздел 5); так как А и В

лежат на одной и той же изотерме, то должно быть так что

Подобным же образом можно доказать, что количество теплоты, отданной источнику с температурой во время изотермического сжатия, которое изображено отрезком составляет

Так как точки лежат на двух адиабатах, то из (38) имеем

и аналогичное уравнение

разделив которое на предыдущее и извлекая корень степени, получаем

Из этого уравнения и выражения для находим

Последнее равенство показывает, что отношение равно отношению температур источников, когда температуры выражены шкалой газового термометра. Но из (56) следует, что также равно отношению температур источников, когда температуры выражены в единицах абсолютной термодинамической шкалы. Отсюда: отношение двух температур абсолютной термодинамической шкалы равно отношению двух температур по шкале газового термометра, т. е. эти две температурные шкалы пропорциональны. Поскольку единицы температуры в обеих шкалах выбраны равными, можно заключить, что эти две шкалы совпадают, т. е.

Так как и равны, то нет больше необходимости употреблять для их обозначения две различные буквы. В дальнейшем

всегда будем обозначать абсолютную термодинамическую температуру буквой

Применяя вместо 9, мы имеем из (56) для обратимого цикла между температурами

И коэффициент полезного действия (44) обратимой машины принимает вид