| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23. ДРУГОЕ ДОКАЗАТЕЛЬСТВО УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ
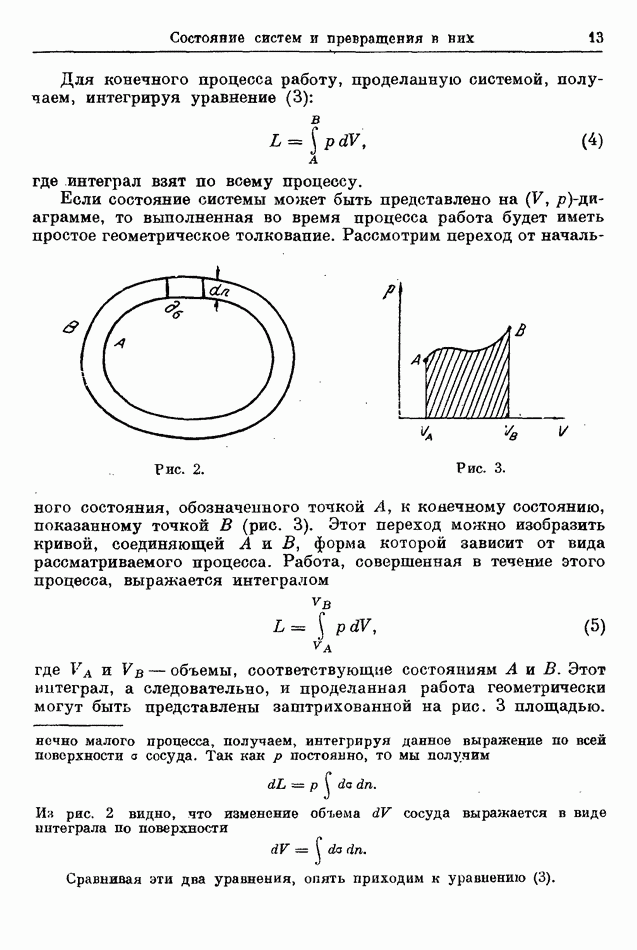
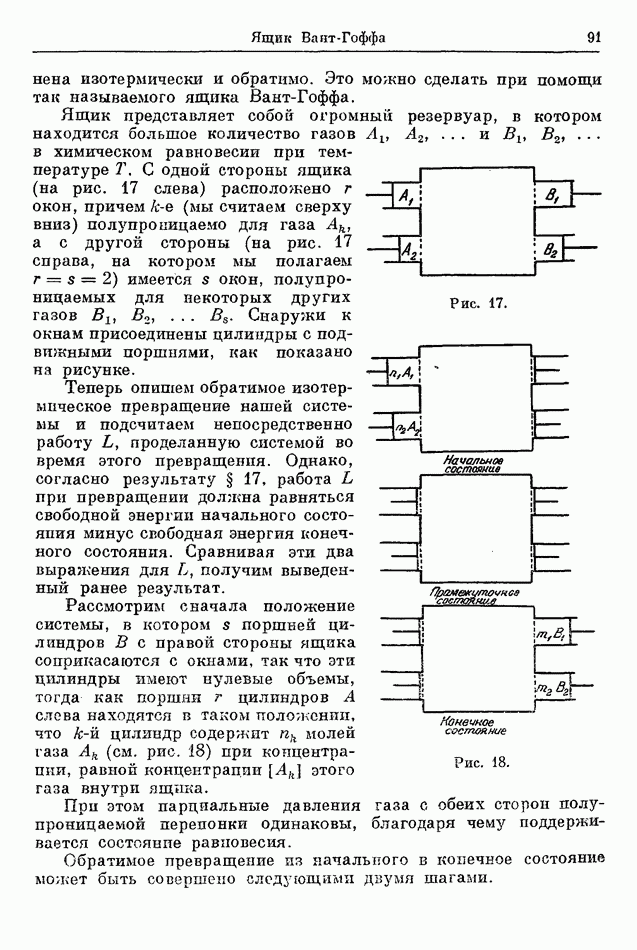
В этом параграфе мы выведем зфавнение (139), используя результаты, полученные в § 17, в котором было показано, что состояние равновесия системы при заданной температуре и заданном объеме соответствует минимуму свободной энергии.
Рассмотрим смесь газов  при температуре
при температуре  заключенных в сосуд определенного объема V и химически взаимодействующих согласно уравнению (135). Когда смесь внутри сосуда принимает участие в химических реакциях, то концентрация различных газов изменяется, в результате чего изменяется также свободная, энергия смеси. Выведем условие равновесия химических реакций из требования минимальности свободной энергии. Для этого следует сначала найти выражение для свободной энергии смеси газов с заданными концентрациями.
заключенных в сосуд определенного объема V и химически взаимодействующих согласно уравнению (135). Когда смесь внутри сосуда принимает участие в химических реакциях, то концентрация различных газов изменяется, в результате чего изменяется также свободная, энергия смеси. Выведем условие равновесия химических реакций из требования минимальности свободной энергии. Для этого следует сначала найти выражение для свободной энергии смеси газов с заданными концентрациями.
Закон Дальтона (см. § 2) устанавливает, что давление смеси (идеальных) газов составляет сумму парциальных давлений компонент смеси (парциальное давление компоненты — это давление, которое компонента оказала бы, если бы она одна занимала все пространство, занятое смесью). Этот закон указывает, что на каждую компоненту не воздействует присутствие других компонент и свойства компоненты в смеси не меняются. Теперь обобщим закон Дальтона, полагая, что для смеси идеальных газов энергия и энтропия также равны сумме энергий и энтропий (парциальных энергий и парциальных энтропий), которые каждая компонента имела бы, если бы она одна занимала весь объем, занятый смесью, при той же температуре, что и смесь.
Из определений (111) и (121) свободной энергии и термодинамического потенциала при постоянном давлении непосредственно следует, что для смеси идеальных газов эти величины соответственно равны сумме парциальных свободных энергий и сумме парциальных термодинамических потенциалов при постоянном давлении компонент смеси. Исходя из этих предположений, мы можем написать выражение для свободной энергии рассматриваемой смеси газов. Свободная энергия одного моля газа  представлена, как в предыдущем разделе, выражением
представлена, как в предыдущем разделе, выражением

Концентрация газа  в объеме V составляет
в объеме V составляет  Это значит, что всего имеется
Это значит, что всего имеется  молей газа
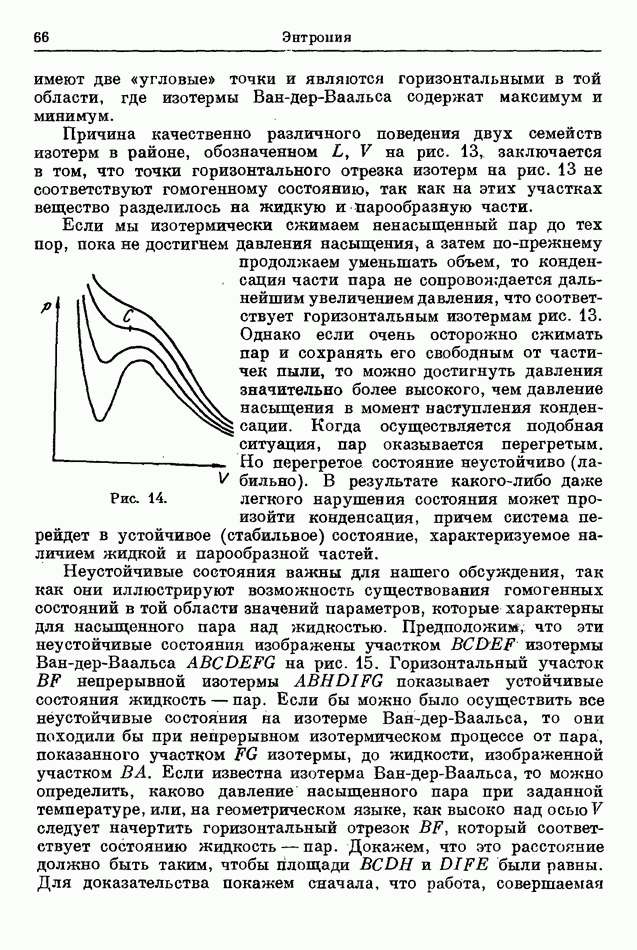
молей газа  Поэтому парциальная свободная энергия этой компоненты смеси составляет
Поэтому парциальная свободная энергия этой компоненты смеси составляет

Свободную энергию всей системы получаем, суммируя парциальные свободные энергии всех ее компонент. В результате суммирования для всей свободиой энергии имеем

Теперь рассмотрим бесконечно малую реакцию типа (135), т. е. реакцию, в которой в превращении принимают участие бесконечно малые количества вещества. Если реакция происходит слева направо в (135), то бесконечно малые количества газов  исчезают и образуются бесконечно малые количества газов
исчезают и образуются бесконечно малые количества газов 
Части молей газов  которые исчезают, пропорциональны соответственно коэффициентам
которые исчезают, пропорциональны соответственно коэффициентам 
а части молей, образующихся в результате реакции газов  , пропорциональны соответственно числам
, пропорциональны соответственно числам 
Следовательно, концентрации  подвергаются изменениям:
подвергаются изменениям:

где  является бесконечно малой константой пропорциональности.
является бесконечно малой константой пропорциональности.
Если  должна быть минимальна в данном состоянии, то изменение
должна быть минимальна в данном состоянии, то изменение  в результате бесконечно малой реакции должно быть равпо нулю. Так как это изменение можно подсчитать, как если бы оно было дифференциалом, то имеем
в результате бесконечно малой реакции должно быть равпо нулю. Так как это изменение можно подсчитать, как если бы оно было дифференциалом, то имеем

Разделив это уравнение на  и заменив производные их величинами, вычисленными из (140), получаем следующее уравнение:
и заменив производные их величинами, вычисленными из (140), получаем следующее уравнение:

Сразу видно, что это уравнение и уравнение (138) идентичны. Следовательно, уравнение равновесия может быть получено так же, как и в предыдущем разделе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ГЛАВА I. ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ
- 2. ИДЕАЛЬНЫЕ ГАЗЫ
- ГЛАВА II. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 3. ФОРМУЛИРОВКА ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 4. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К СИСТЕМАМ, СОСТОЯНИЕ КОТОРЫХ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 5. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К ГАЗАМ
- 6. АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В ГАЗАХ
- ГЛАВА III. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 7. ФОРМУЛИРОВКА ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 8. ЦИКЛ КАРНО
- 9. АБСОЛЮТНАЯ ТЕРМОДИНАМИЧЕСКАЯ ТЕМПЕРАТУРА
- 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА IV. ЭНТРОПИЯ
- 11. НЕКОТОРЫЕ СВОЙСТВА ЦИКЛОВ
- 12. ЭНТРОПИЯ
- 18. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ЭНТРОПИИ
- 14. ЭНТРОПИЯ СИСТЕМЫ, СОСТОЯНИЕ КОТОРОЙ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 15. УРАВНЕНИЕ КЛАПЕЙРОНА
- 16. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- ГЛАВА V. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
- 18. ТЕРМОДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 19. ПРАВИЛО ФАЗ
- 20. ТЕРМОДИНАМИКА ОБРАТИМОГО ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА
- ГЛАВА VI. РЕАКЦИИ В ГАЗОВОЙ ФАЗЕ
- 21. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗАХ
- 22. ЯЩИК ВАНТ-ГОФФА
- 23. ДРУГОЕ ДОКАЗАТЕЛЬСТВО УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ
- 24. ОБСУЖДЕНИЕ УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ. ПРИНЦИП ЛЕ ШАТЕЛЬЕ
- ГЛАВА VII. ТЕРМОДИНАМИКА СЛАБЫХ РАСТВОРОВ
- 28. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 27. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- 28. РАСПРЕДЕЛЕНИЕ РАСТВОРЕННОГО ВЕЩЕСТВА МЕЖДУ ДВУМЯ ФАЗАМИ
- 29. ДАВЛЕНИЕ ПАРА, ТОЧКА КИПЕНИЯ И ТОЧКА ЗАМЕРЗАНИЯ РАСТВОРА
- ГЛАВА VIII. ПОСТОЯННАЯ В ЗАВИСИМОСТИ ЭНТРОПИИ ОТ ТЕМПЕРАТУРЫ
- 30. ТЕОРЕМА НЕРНСТА
- 31. ПРИМЕНЕНИЕ ТЕОРЕМЫ НЕРНСТА К ТВЕРДЫМ ТЕЛАМ
- 32. ЭНТРОПИЙНАЯ КОНСТАНТА ГАЗОВ
- 33. ТЕРМИЧЕСКАЯ ИОНИЗАЦИЯ ГАЗА. ТЕРМОИОННЫЙ ЭФФЕКТ