| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
16. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
Уравнение состояния идеального газа достаточно хорошо изображает поведение реальных газов при высоких температурах и низких давлениях. Однако когда температура и давление таковы, что газ близок к конденсации, то наблюдаются значительные отклонения от законов идеального газа.
Среди ряда уравнений состояния, предложенных для изображения поведения реальных газов, особенно интересно уравнение Ван-дер-Ваальса вследствие его простоты и вследствие того, что оно удовлетворительно описывает поведение многих веществ в широком интервале температур и давлений.
Ван-дер-Ваальс вывел свое уравнение из соображений, основанных на кинетической теории, учитывая, в качестве первого приближения величину молекул и силы взаимодействия между ними. Его уравнение состояния (написанное для одного моля вещества) таково:

где  константы, зависящие от особенностей данного вещества. При
константы, зависящие от особенностей данного вещества. При  уравнение (99) превращается в уравнение идеального газа. Член
уравнение (99) превращается в уравнение идеального газа. Член  описывает эффект, связанный с конечной величиной молекул, а член
описывает эффект, связанный с конечной величиной молекул, а член  изображает эффект молекулярных сил взаимодействия.
изображает эффект молекулярных сил взаимодействия.
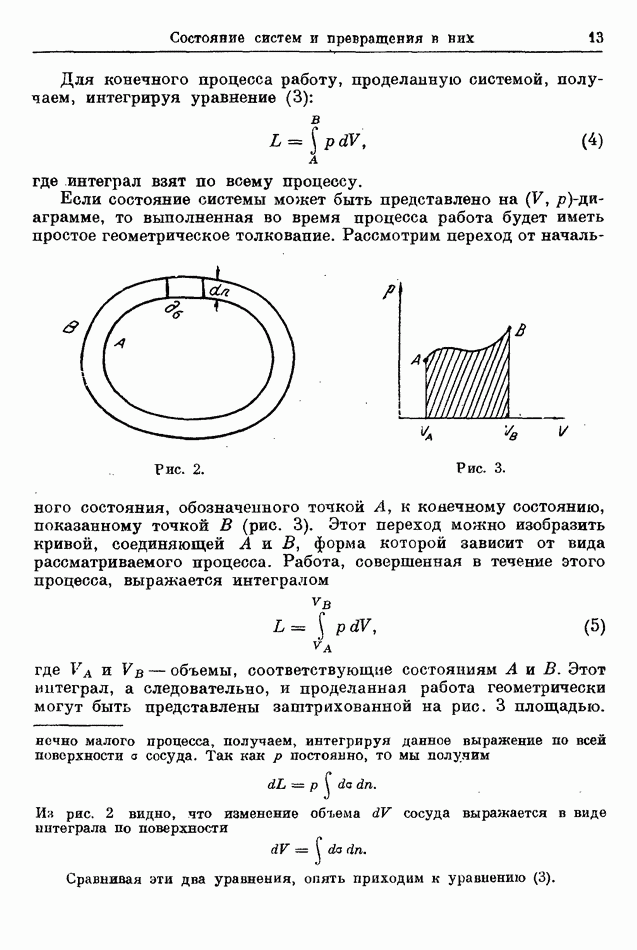
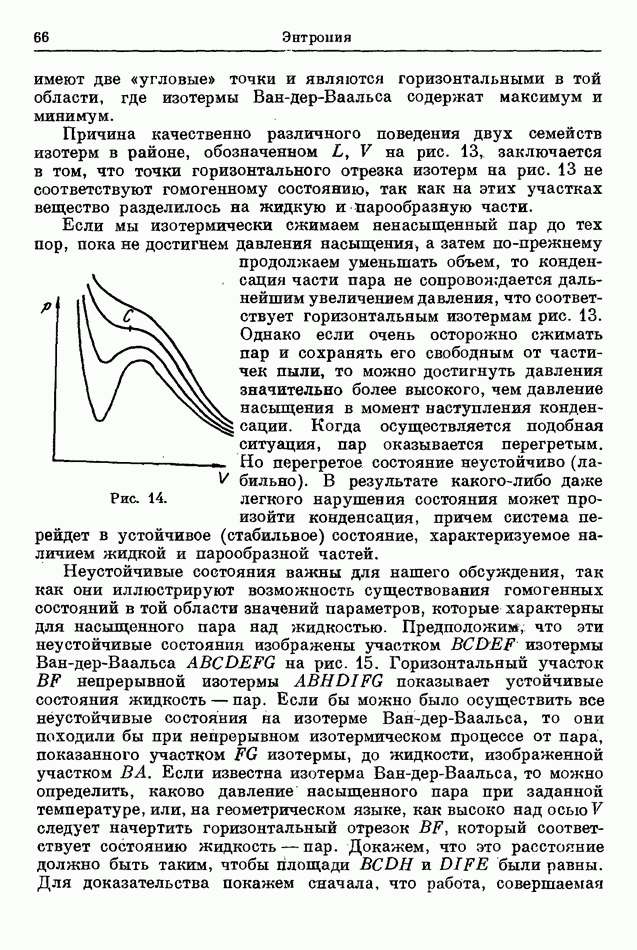
На рис. 14 показаны некоторые изотермы, вычисленные согласно уравнению Ван-дер-Ваальса. Сравнивая эти изотермы с изотермами рис. 13, мы видим, что их очертания имеют много сходства. В обоих случаях на одной изотерме есть точка перегиба  Изотерма, содержащая точку перегиба — критическая изотерма, а сама точка перегиба — критическая точка. Изотермы при температуре выше критической в обоих случаях ведут себя похоже. Однако изотермы ниже критической температуры существенно различаются. Изотермы Ван-дер-Ваальса являются непрерывными кривыми с минимумом и максимумом, тогда как изотермы на рис. 13
Изотерма, содержащая точку перегиба — критическая изотерма, а сама точка перегиба — критическая точка. Изотермы при температуре выше критической в обоих случаях ведут себя похоже. Однако изотермы ниже критической температуры существенно различаются. Изотермы Ван-дер-Ваальса являются непрерывными кривыми с минимумом и максимумом, тогда как изотермы на рис. 13
имеют две «угловые» точки и являются горизонтальными в той области, где изотермы Ван-дер-Ваальса содержат максимум и минимум.
Причина качественно различного поведения двух семейств изотерм в районе, обозначенном  на рис. 13, заключается в том, что точки горизонтального отрезка изотерм на рис. 13 не соответствуют гомогенному состоянию, так как на этих участках вещество разделилось на жидкую и парообразную части.
на рис. 13, заключается в том, что точки горизонтального отрезка изотерм на рис. 13 не соответствуют гомогенному состоянию, так как на этих участках вещество разделилось на жидкую и парообразную части.
Если мы изотермически сжимаем ненасыщенный пар до тех пор, пока не достигнем давления насыщения, а затем по-прежнему продолжаем уменьшать объем, то конденсация части пара не сопровождается дальнейшим увеличением давления, что соответствует горизонтальным изотермам рис. 13. Однако если очень осторожно сжимать пар и сохранять его свободным от частичек пыли, то можно достигнуть давления значительно более высокого, чем давление насыщения в момент наступления конденсации. Когда осуществляется подобная ситуация, пар оказывается перегретым. Но перегретое состояние неустойчиво (лабильно). В результате какого-либо даже легкого нарушения состояния может произойти конденсация, причем система перейдет в устойчивое (стабильное) состояние, характеризуемое наличием жидкой и парообразной частей.

Рис. 14.
Неустойчивые состояния важны для нашего обсуждения, так как они иллюстрируют возможность существования гомогенных состояний в той области значений параметров, которые характерны для насыщенного пара над жидкостью. Предположим, что эти неустойчивые состояния изображены участком  изотермы Ван-дер-Ваальса
изотермы Ван-дер-Ваальса  на рис. 15. Горизонтальный участок
на рис. 15. Горизонтальный участок  непрерывной изотермы
непрерывной изотермы  показывает устойчивые состояния жидкость — пар. Если бы можно было осуществить все нёустойчивые состояния на изотерме Ван-дер-Ваальса, то они походили бы при непрерывном изотермическом процессе от пара, показанного участком
показывает устойчивые состояния жидкость — пар. Если бы можно было осуществить все нёустойчивые состояния на изотерме Ван-дер-Ваальса, то они походили бы при непрерывном изотермическом процессе от пара, показанного участком  изотермы, до жидкости, изображенной участком
изотермы, до жидкости, изображенной участком  Если известна изотерма Ван-дер-Ваальса, то можно определить, каково давление насыщенного пара при заданной температуре, или, на геометрическом языке, как высоко над осью
Если известна изотерма Ван-дер-Ваальса, то можно определить, каково давление насыщенного пара при заданной температуре, или, на геометрическом языке, как высоко над осью  следует начертить горизонтальный отрезок
следует начертить горизонтальный отрезок  который соответствует состоянию жидкость — пар. Докажем, что это расстояние должно быть таким, чтобы площади
который соответствует состоянию жидкость — пар. Докажем, что это расстояние должно быть таким, чтобы площади  и
и  были равны. Для доказательства покажем сначала, что работа, совершаемая
были равны. Для доказательства покажем сначала, что работа, совершаемая
системой во время обратимого изотермического цикла, всегда равна нулю. Из уравнения (16) следует, что работа, совершаемая во время цикла, равна теплоте, поглощаемой системой. Но для обратимого цикла остается в силе равенство (66), а так как наш цикл изотермич ескии, то можно вынести  из-под знака интеграла в (66). Уравнение (66) показывает, что вся поглощаемая теплота и, следовательно, вся выполняемая во время цикла работа равпы нулю.
из-под знака интеграла в (66). Уравнение (66) показывает, что вся поглощаемая теплота и, следовательно, вся выполняемая во время цикла работа равпы нулю.
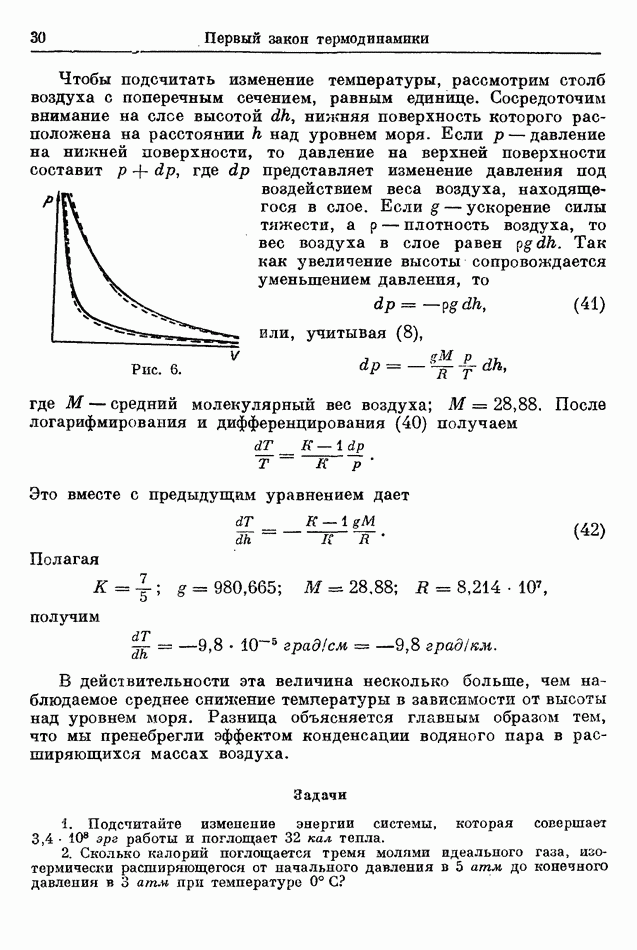
Теперь рассмотрим обратимый изотермический цикл  (рис. 15).
(рис. 15).

Рис. 15.
Работа, совершаемая во время цикла, должна обратиться в нуль.
Участок  проходится по ходу часовой стрелки, поэтому соответствующая площадь положительна, а участок
проходится по ходу часовой стрелки, поэтому соответствующая площадь положительна, а участок  против часовой стрелки, и соответствующая площадь отрицательна. Поскольку вся площадь цикла
против часовой стрелки, и соответствующая площадь отрицательна. Поскольку вся площадь цикла  равна нулю, то абсолютные величины площадей двух циклов
равна нулю, то абсолютные величины площадей двух циклов  и
и  должны быть равны, что и требовалось доказать.
должны быть равны, что и требовалось доказать.
Могло бы возникнуть следующее возражение против приведенного выше доказательства: так как площадь изотермического цикла  очевидно, не равна нулю, то не верно, что работа, совершаемая во время обратимого изотермического цикла, всегда равна нулю. Ответ на это возражение таков: цикл
очевидно, не равна нулю, то не верно, что работа, совершаемая во время обратимого изотермического цикла, всегда равна нулю. Ответ на это возражение таков: цикл  не является обратимым.
не является обратимым.
Чтобы убедиться в этом, заметим, что точка  на диаграмме изображает два различных состояния, в зависимости от того, рассматривается ли она как точка изотермы Ван-дер-Ваальса
на диаграмме изображает два различных состояния, в зависимости от того, рассматривается ли она как точка изотермы Ван-дер-Ваальса  или как точка на изотерме
или как точка на изотерме  жидкость — пар. Объем и давление, изображенные точкой
жидкость — пар. Объем и давление, изображенные точкой  одинаковы в обоих случаях, но на изотерме Ван-дер-Ваальса D изображает неустойчивое гомогенное (однородное) состояние, а на изотерме жидкость — пар
одинаковы в обоих случаях, но на изотерме Ван-дер-Ваальса D изображает неустойчивое гомогенное (однородное) состояние, а на изотерме жидкость — пар  устойчивое негомогенное (неоднородное) состояние, образованное из жидкой и газообразной частей. Когда мы совершаем цикл
устойчивое негомогенное (неоднородное) состояние, образованное из жидкой и газообразной частей. Когда мы совершаем цикл  то проходим от состояния
то проходим от состояния  на изотерме Ван-дер-Ваальса к состоянию
на изотерме Ван-дер-Ваальса к состоянию  на изотерме жидкость—пар. Так как состояние
на изотерме жидкость—пар. Так как состояние  на изотерме жидкость — пар более устойчиво, чем на изотерме Ван-дер-Ваальса, то этот путь необратим — его нельзя было бы самопроизвольно осуществить в обратном направлении. Таким образом, весь цикл
на изотерме жидкость — пар более устойчиво, чем на изотерме Ван-дер-Ваальса, то этот путь необратим — его нельзя было бы самопроизвольно осуществить в обратном направлении. Таким образом, весь цикл  является необратимым, и поэтому площадь цикла не должна равняться нулю.
является необратимым, и поэтому площадь цикла не должна равняться нулю.
Критические значения  вещества могут быть выражены через константы
вещества могут быть выражены через константы  которые входят в уравнение Ван-дер-Ваальса.
которые входят в уравнение Ван-дер-Ваальса.
Уравнение Ван-дер-Ваальса (99), когда  и
и  заданы, является уравнением третьей степени относительно
заданы, является уравнением третьей степени относительно  Поэтому, вообще говоря, существует три различных корня V (при фиксированных значениях
Поэтому, вообще говоря, существует три различных корня V (при фиксированных значениях  Однако критическая изотерма
Однако критическая изотерма  имеет горизонтальную точку перегиба при
имеет горизонтальную точку перегиба при  т. е. при
т. е. при  кривая третьего порядка — критическая изотерма — касается горизонтальной линии
кривая третьего порядка — критическая изотерма — касается горизонтальной линии  Отсюда следует, что кубическое уравнение для V, которое получится, если положить в
Отсюда следует, что кубическое уравнение для V, которое получится, если положить в  имеет тройной корень
имеет тройной корень  Это уравнение можно записать в виде
Это уравнение можно записать в виде

Так как  тройной корень приведенного уравнения, то левая часть должна иметь форму
тройной корень приведенного уравнения, то левая часть должна иметь форму  Сравнивая, находим
Сравнивая, находим

Решив эти три уравнения для  получим
получим

Эти уравнения выражают критические значения через 
Целесообразно отметить, что если  использовать как единицы объема, давления и температуры, то уравнение Ван-дер-Ваальса имеет одинаковую форму для всех веществ.
использовать как единицы объема, давления и температуры, то уравнение Ван-дер-Ваальса имеет одинаковую форму для всех веществ.
Полагая

и используя равенства (100), из (99) получим:

Так как это уравнение содеридат только численные константы, то оно одинаково для всех веществ. Состояния различных веществ, которые определяются теми же величинами  называются соответственными состояниями, и (101) часто называется «уравнением Ван-дер-Ваальса для соответственных состояний».
называются соответственными состояниями, и (101) часто называется «уравнением Ван-дер-Ваальса для соответственных состояний».
В разделе 14 было показано, что если вещество подчиняется уравнению состояния идеального газа  то можно вывести термодинамически, что его энергия определяется лишь температурой и не зависит от объема. Этот результат верен только для
то можно вывести термодинамически, что его энергия определяется лишь температурой и не зависит от объема. Этот результат верен только для
идеальных газов. Для реальных газов энергия  зависит также и от объема.
зависит также и от объема.
Из (99) выводим

Используя (88), получаем

Проинтегрировав это выражение по объему V при постоянной  найдем
найдем

Константа интегрирования  константа только относительно V и, конечно, — функция температуры
константа только относительно V и, конечно, — функция температуры  Член — в (103) представляет потенциальную энергию сил взаимодействия между молекулами;
Член — в (103) представляет потенциальную энергию сил взаимодействия между молекулами;  нельзя уточнить, используя лишь термодинамические соображения; для ее определения необходимо знать удельную теплоемкость.
нельзя уточнить, используя лишь термодинамические соображения; для ее определения необходимо знать удельную теплоемкость.
Пусть, например, молярная теплоемкость при постоянном объеме  постоянна. Тогда из (25) и (103) получаем
постоянна. Тогда из (25) и (103) получаем

Интегрируя, находим

где  константа. Тогда уравнение (103) примет вид
константа. Тогда уравнение (103) примет вид

При помощи этого выражения для энергии легко можно вычислить энтропию одного моля Ван-дер-Ваальсова газа. Иэ (72), (21), (102) и (104) получаем

или после интегрирования

Отметим сходство этой формулы с формулой (86), выражающей энтропию идеального газа через объем и температуру.
В разделе 6 мы определили адиабатический процесс, как обратимый процесс, во время которого система термически изолировала. Таким образом, при адиабатическом процессе  Но из
Но из  Следовательно,
Следовательно,  или
или  если в системе совершается адиабатический процесс, то ее энтропия остается постоянной. По этой причине адиабатические процессы иногда называют изоэнтропическими.
если в системе совершается адиабатический процесс, то ее энтропия остается постоянной. По этой причине адиабатические процессы иногда называют изоэнтропическими.
Уравнение адиабатического процесса газа Ван-дер-Ваальса сразу же получается из (105), если приравнять энтропию постоянной:

или

Это уравнение для адиабаты Ван-дер-Ваальсова газа очень сходно с уравнением (38) для адиабаты идеального газа.
Задачи
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ГЛАВА I. ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ
- 2. ИДЕАЛЬНЫЕ ГАЗЫ
- ГЛАВА II. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 3. ФОРМУЛИРОВКА ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 4. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К СИСТЕМАМ, СОСТОЯНИЕ КОТОРЫХ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 5. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К ГАЗАМ
- 6. АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В ГАЗАХ
- ГЛАВА III. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 7. ФОРМУЛИРОВКА ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 8. ЦИКЛ КАРНО
- 9. АБСОЛЮТНАЯ ТЕРМОДИНАМИЧЕСКАЯ ТЕМПЕРАТУРА
- 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА IV. ЭНТРОПИЯ
- 11. НЕКОТОРЫЕ СВОЙСТВА ЦИКЛОВ
- 12. ЭНТРОПИЯ
- 18. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ЭНТРОПИИ
- 14. ЭНТРОПИЯ СИСТЕМЫ, СОСТОЯНИЕ КОТОРОЙ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 15. УРАВНЕНИЕ КЛАПЕЙРОНА
- 16. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- ГЛАВА V. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
- 18. ТЕРМОДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 19. ПРАВИЛО ФАЗ
- 20. ТЕРМОДИНАМИКА ОБРАТИМОГО ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА
- ГЛАВА VI. РЕАКЦИИ В ГАЗОВОЙ ФАЗЕ
- 21. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗАХ
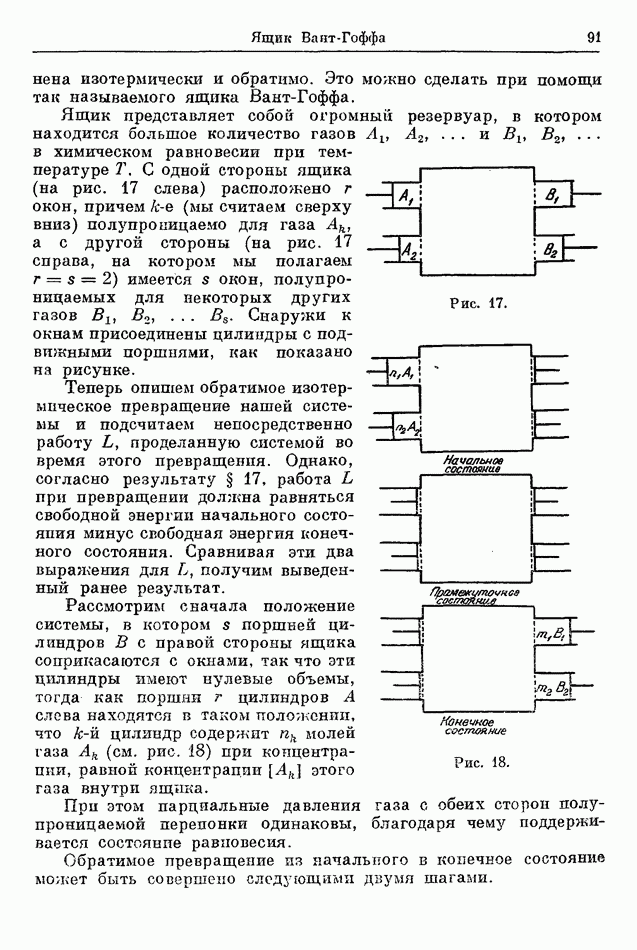
- 22. ЯЩИК ВАНТ-ГОФФА
- 23. ДРУГОЕ ДОКАЗАТЕЛЬСТВО УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ
- 24. ОБСУЖДЕНИЕ УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ. ПРИНЦИП ЛЕ ШАТЕЛЬЕ
- ГЛАВА VII. ТЕРМОДИНАМИКА СЛАБЫХ РАСТВОРОВ
- 28. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 27. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- 28. РАСПРЕДЕЛЕНИЕ РАСТВОРЕННОГО ВЕЩЕСТВА МЕЖДУ ДВУМЯ ФАЗАМИ
- 29. ДАВЛЕНИЕ ПАРА, ТОЧКА КИПЕНИЯ И ТОЧКА ЗАМЕРЗАНИЯ РАСТВОРА
- ГЛАВА VIII. ПОСТОЯННАЯ В ЗАВИСИМОСТИ ЭНТРОПИИ ОТ ТЕМПЕРАТУРЫ
- 30. ТЕОРЕМА НЕРНСТА
- 31. ПРИМЕНЕНИЕ ТЕОРЕМЫ НЕРНСТА К ТВЕРДЫМ ТЕЛАМ
- 32. ЭНТРОПИЙНАЯ КОНСТАНТА ГАЗОВ
- 33. ТЕРМИЧЕСКАЯ ИОНИЗАЦИЯ ГАЗА. ТЕРМОИОННЫЙ ЭФФЕКТ