ГЛАВА II. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

3. ФОРМУЛИРОВКА ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ

Первый закон термодинамики представляет собой формулировку принципа сохранения энергии для термодинамических систем. Таким образом, можно сказать, что изменение энергии системы во время процесса равно количеству энергии, которое система получает от среды.

Чтобы уточнить это определение, необходимо выяснить значение выражений «энергия системы» и «энергия, которую система получает от окружающей ее среды во время процесса».

В чисто механических изолированных системах энергия равна сумме потенциальной и кинетической энергий и, следовательно, является функцией динамического состояния системы, потому что знание динамического состояния системы эквивалентно знанию положения и скоростей всех точечных масс, содержащихся в системе. Если никакие внешние силы не действуют на систему, энергия остается постоянной. Таким образом, если два последовательные состояния изолированной системы, соответствующие им энергии, то

Когда на систему действуют внешние силы, то не обязательно сохраняется равенство и Если представляет работу, совершаемую внешними силами в процессе перехода от начального состояния А к конечному работа, выполняемая системой), то динамический принцип сохранения энергии приобретает такой вид:

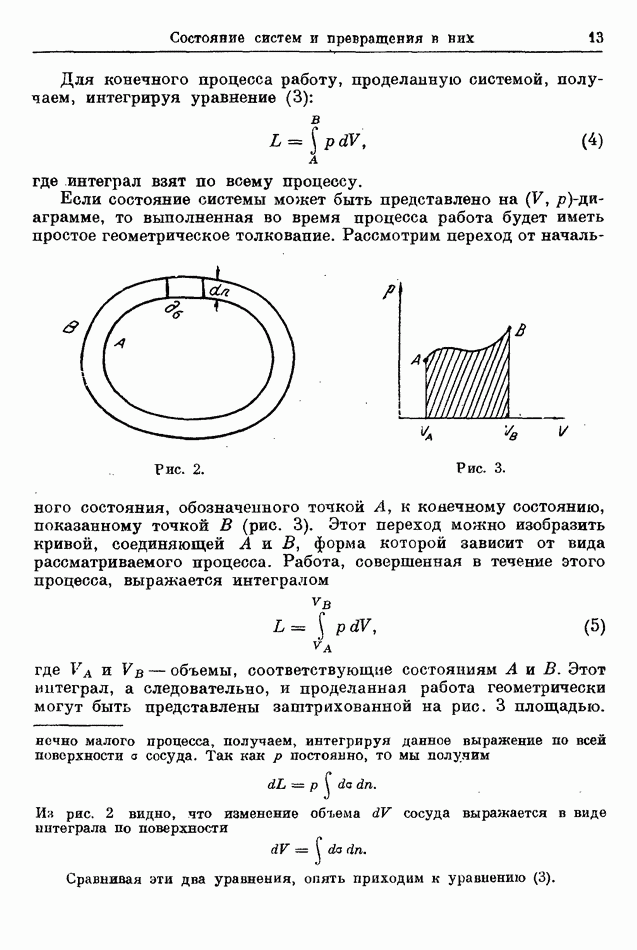
Из этого уравнения следует, что работа выполняемая во яремя процесса, зависит только от крайних состояний процесса и не зависит от пути, по которому происходил процеео между

Предположим теперь, что мы не знаем законов взаимодействия различных точечных масс в нашей динамической системе. Тогда мы не сможем подсчитать знергию системы, находящейся в данном динамическом состоянии. Однако, используя уравнение (11), мы тем не менее можем опытным путем определить энергию нашей системы. Энергию произвольно выбранного состояния О нашей системы примем равной нулю:

Впредь будем ссылаться на это состояние как на стандартное состояние системы. Рассмотрим теперь некоторое другое состояние А. Воздействуя на систему внешними силами, мы можем перевести ее из стандартного состояния, в котором, как мы предполагали, она находилась первоначально, в состояние А. Пусть означает работу, совершаемую системой во время зтого процесса как и раньше, является работой, выполняемой внешними силами над системой).

Применяя уравнение (11) к нашему процессу и вспоминая определение (12), находим, что

Это уравнение может быть использовано для опытного определения энергии нашей системы в состоянии А.

Очевидно, при определении (13) необходимо иметь в виду, что работа зависит только от состояний и не зависит от пути, по которому прошел процесс от О до А. Мы уже отметили, что это свойство следует из (11). Если бы оно не было обнаружено на опыте, то это означало бы, что энергия не сохраняется в нашей системе, или что, кроме механической работы, должны быть приняты в расчет другие виды превращения энергии.

Теперь предположим, что работа, выполняемая механической системой во время какого-либо процесса, зависит лишь от его начального и конечного состояний, и мы можем использовать (13) как определение энергии.

Можно вывести равенство (11) непосредственно из (13) следующим образом: процесс между любыми двумя состояниями всегда может быть выполнен как последовательность двух процессов: от А до стандартного состояния О и затем от О до В.

Так как система совершает при этих двух процессах работу то окончательная величина работы, выполненной во время процесса от А до В (она не зависит от пути, по которому совершается процесс), составляет:

Теперь из (13) и аналогичного уравнения

получаем

что идентично (11).

Наконец, заметим, что определение (13) не является единственно возможным, так как оно зависит от выбора стандартного состояния О. Если бы вместо О мы выбрали другое стандартное состояние О, то получили бы другую величину Для энергии состояния А. Однако можно легко показать, что отличаются лишь на аддитивную константу. Действительно, процесс от О до А можно считать суммой двух процессов: одного, идущего от О до О, и другого — от до А. Работа совершаемая системой при прихождении от О до А, равна

где работа, выполняемая при переходе от О до О. Тогда

так что

Это показывает, что значения энергии, основанные на двух определениях, различаются только аддитивной константой. Эта неопределенность, возникающая при определении энергии, представляет собой, как известно, существенную особенность понятия энергии. Но так как на практике всегда рассматривается только разность энергий, то дополнительная константа не влияет на окончательные результаты. Единственным предположением, положенным в приведенное выше эмпирическое определение энергии, является то, что общее количество работы, совершаемое системой, зависит лишь от начального и конечного состояний процесса. Мы уже отметили, что если это предположение противоречит опыту и еслп мы, тем не менее, не желаем отменять принцип сохранения энергии, то следует допустить существование, кроме механической работы, другого способа обмена энергией между системой и окружающей ее средой.

Возьмем, например, систему, состоящую из некоторого количества воды. Рассмотрим два состояния этой системы при атмосферном давлении. Пусть температуры системы в этих двух состояниях будут соответственно и причем Можно перевести нашу систему от А к В двумя различными путями.

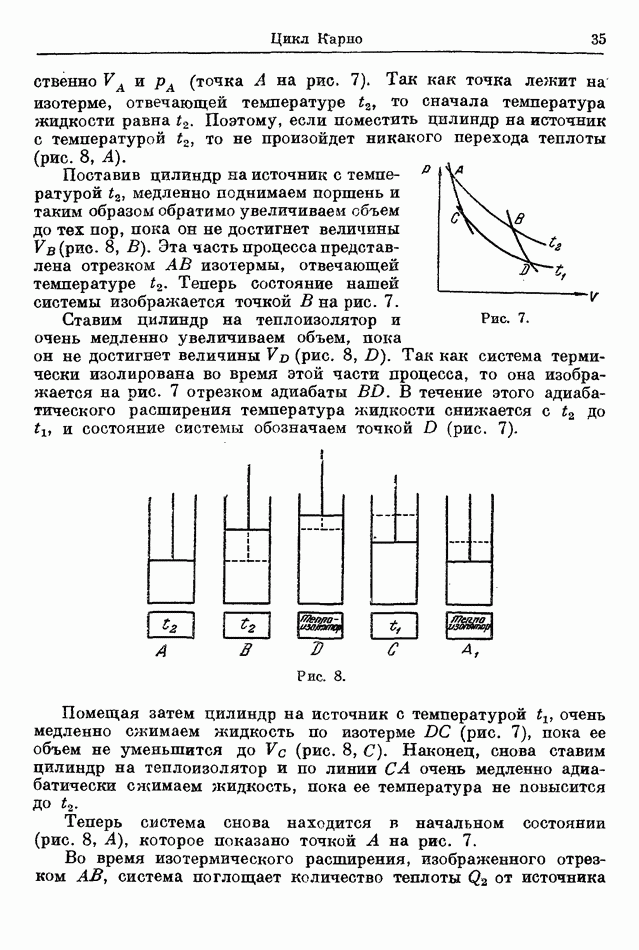
Первый путь. Нагреваем воду, помещая ее над пламенем, и повышаем температуру от начальной величины до конечной Внешняя работа, совершаемая системой во время процесса

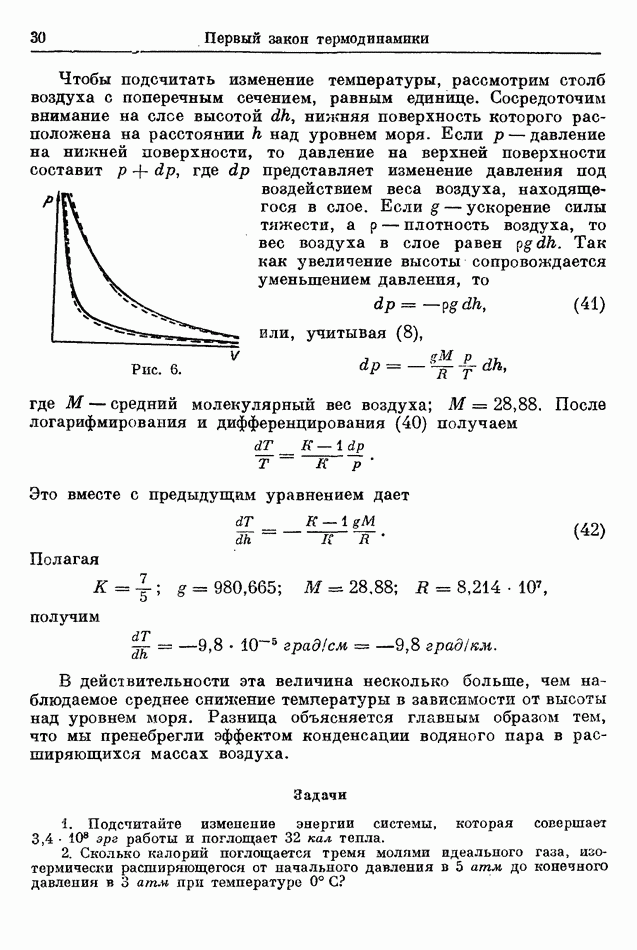
практически равна нулю. Она была бы в точности равна нулю, если бы изменение температуры не сопровождалось изменением объема воды. В действительности, однако, объем воды во время процесса изменяется незначительно, так что совершается небольшая работа (см. уравнение (3)). В наших рассуждениях будем пренебрегать этой малой величиной работы.

Второй путь. Повышаем температуру воды от до нагревая ее посредством трения. С одного конца сосуда погружаем в воду маленькую установку из прикрепленных к оси лопастей, которые, вращаясь, размешивают воду. Температура воды возрастает непрерывно до тех пор, пока лопасти продолжают вращаться. Но так как вода оказывает сопротивление движению лопастей, то мы должны совершить механическую работу, чтобы лопасти находились в движении до тех пор, пока будет достигнута конечная температура В соответствии с этим лопасти выполняют в воде значительную положительную работу; причем такое же количество отрицательной работы совершается водой, создающей сопротивление движению лопастей.

Следовательно, работа, совершаемая системой при переходе из состояния А в состояние В, зависит от того, переводится ли система от А к В по первому или же по второму пути.

Если мы предполагаем, что принцип сохранения энергии остается верным для нашей системы, то нужно допустить, что энергия, которая во втором случае передается воде в форме механической работы вращения лопастей, в первом случае передается воде в немеханической форме. Эта форма энергии называется теплотой. Такам образом, мы приходим к выводу, что теплота и механическая работа эквивалентны, т. е. являются двумя различными видами одного и того же, а именно, — энергии. Отсюда следует, что мы должны объединить названием «работа» также действие электрических и магнитных сил, наравне с механической работой. Однако первые два вида работы редко рассматриваются в термодинамике.

Чтобы выразить в более точной форме тот факт, что теплота и работа эквивалентны, продолжим рассмотрение.

Сначала поместим нашу систему в сосуд с нетеплопроводящими стенками, чтобы предотвратить обмен тепла с окружающей средой. Мы, однако, полагаем, что система и окружающая среда могут воздействовать друг на друга (например, система, заключена в цилиндр с нетеплопроводящими стенками, но с подвижным поршнем). Обмен энергией между внутренней и наружной

частями сосуда может теперь происходить только в форме работы, а из принципа сохранения энергии следует, что величина работы, совершаемой системой во время процесса, зависит лишь от начального и конечного состояний процесса.

Мы можем теперь использовать эмпирическое определение энергии (13) и рассматривать энергию как функцию одного лишь состояния системы.

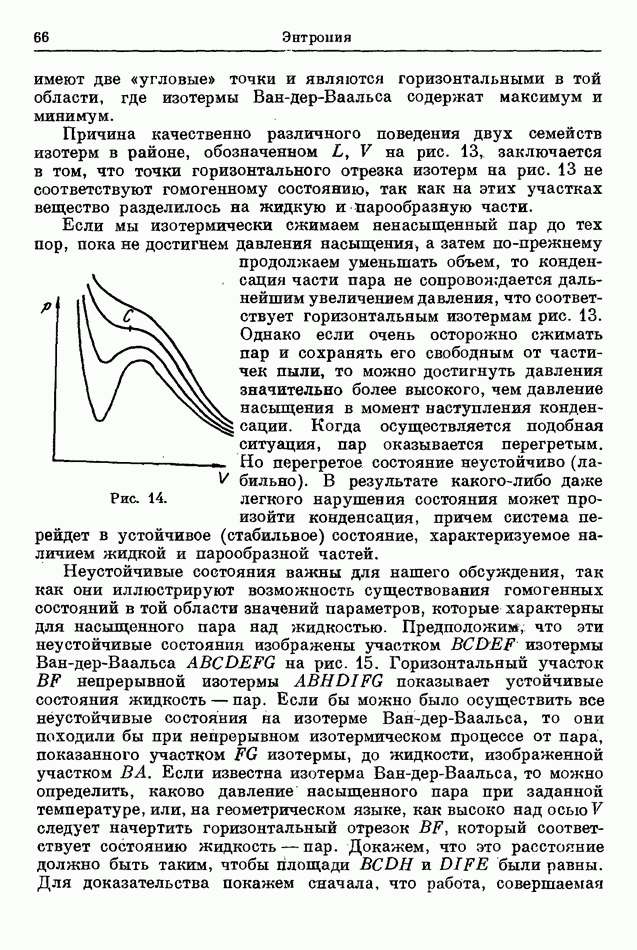
Обозначая через изменение энергии системы, происходящее во время перехода от состояния А к состоянию В, мы можем написать уравнение (11), которое применимо к этой термически изолированной системе, в следующей форме:

Если наша система термически не изолирована, то левая часть уравнения (14), вообще говоря, будет отличаться от нуля, потому что тогда обмен энергией может происходить в форме тепла. Поэтому заменим уравнение (14) более общим:

где равно нулю при процессах, происходящих в термически изолированных системах, и в общем случае отличается от нуля. Величину можно физически интерпретировать как количество энергии, получаемой системой в форме, отличающейся от работы.

Это непосредственно следует из того факта, что изменение энергии системы должно быть равно общему количеству энергии, получаемому системой от окружающей ее среды. Но из (15)

а энергия в форме работы. Отсюда должно представлять энергию в других формах.

Вводя определение мы назовем количеством тепла, полученного системой во время процесса.

Для циклического процесса уравнение (15) принимает очень простую форму. Так как начальные и конечные состояния цикла одинаковы, то изменение энергии равно нулю:

Таким образом, уравнение (15) принимает вид

т. е. работа, совершаемая системой в течение циклического процесса, равна теплоте, поглощенной системой.

Важно установить связь между абстрактным и элементарным калориметрическим определением теплоты. Калориметрическая единица теплоты, калория, определяется как количество теплоты, необходимое для повышения температуры воды от 14 до 15° С при атмосферном давлении. Таким образом, для того, чтобы повысить температуру граммов воды от 14 до 15° С при атмосферном давлении, требуется калорий теплоты. Пусть означает изменение энергии воды, а работу, проделанную в результате ее расширения, когда температура повышается от 14 до 15° С при атмосферном давлении. Для граммов воды изменение знергии и проделанная работа составляют:

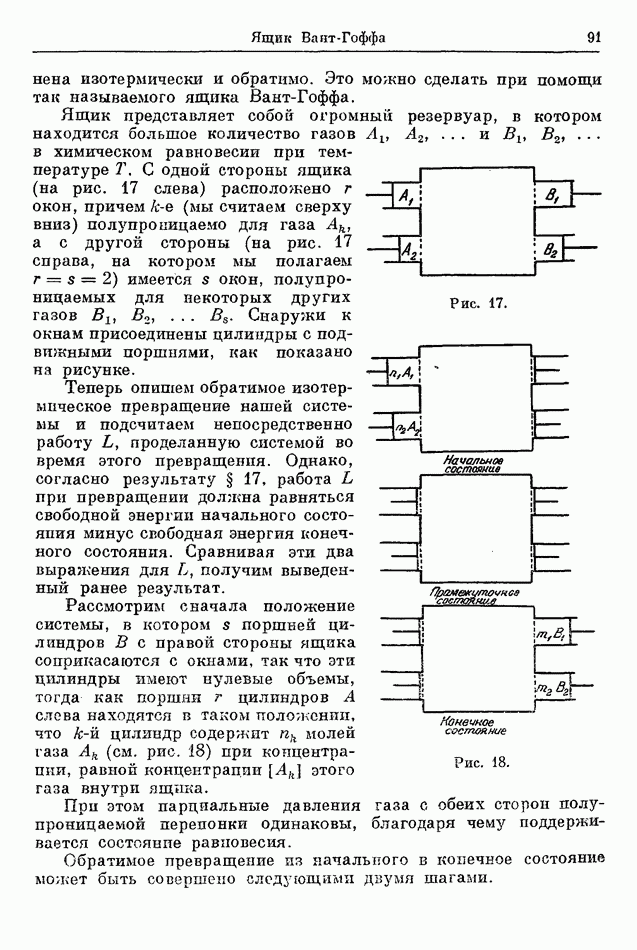
Рассмотрим теперь систему которая подвергается изменению. Чтобы измерить теплообмен между системой и окружающими телами, поместим систему в калориметр, содержащий граммов воды при 14° С. Выбираем массу воды таким образом, чтобы после завершения процесса температура ее достигла 15° С.

Так как идеальный калориметр термически совершенно изолирован, то сложная система, состоящая из системы и воды в калориметре, в течение процесса термически изолирована. Поэтому мы можем применить уравнение (14) к этому процессу.

Общее изменение энергии

где - изменение энергии системы и изменение энергии воды калориметра. Подобно этому для всей проделанной работы имеем

Затем запишем

или по (17):

Но, согласно определению количество теплоты полученной системой Таким образом, имеем

Отсюда видим, что количество теплоты пропорционально

С другой стороны, тот факт, что граммов воды калориметра нагрелось от 14 до 15° С в калориметре, означает, что калорий теплоты были переданы системой калориметру, т. е. система получила калорий, или, другими словами, выраженное в калориях, равно . Мы видим также, используя (18), что количество теплоты, выраженное уравнением (15), пропорционально количеству теплоты, выраженному в калориях, причем коэффициентом пропорциональности является

Согласно уравнению (15), теплота измеряется в единицах энергии (эргах). Постоянное соотношение между эргами и калориями было измерено многими исследователями, которые установили, что

В дальнейшем мы обычно будем выражать теплоту в энергетических единицах.

Уравнение (15), которое является точной формулировкой эквивалентности теплоты и работы, описывает первый закон термодинамики.