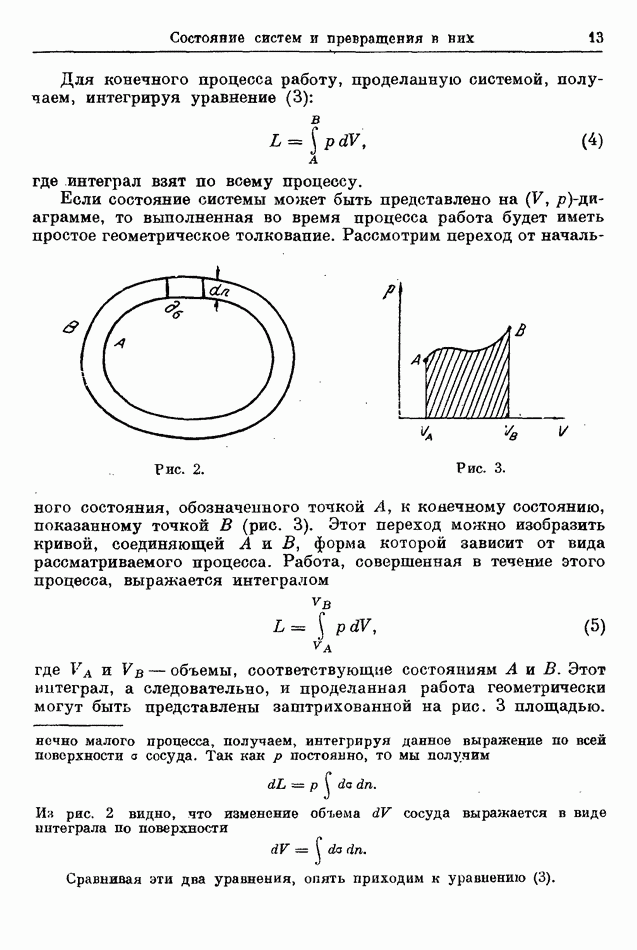
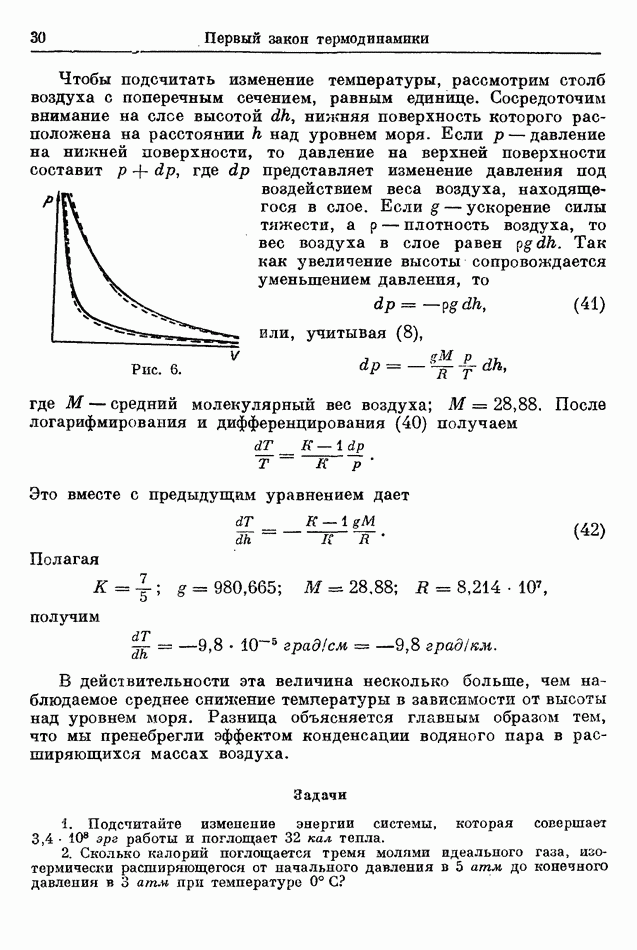
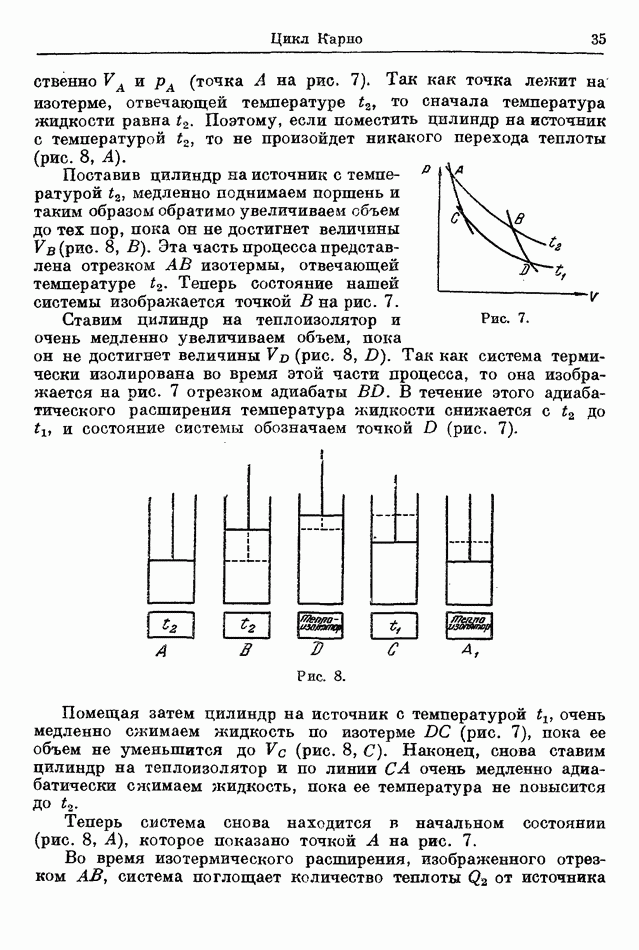
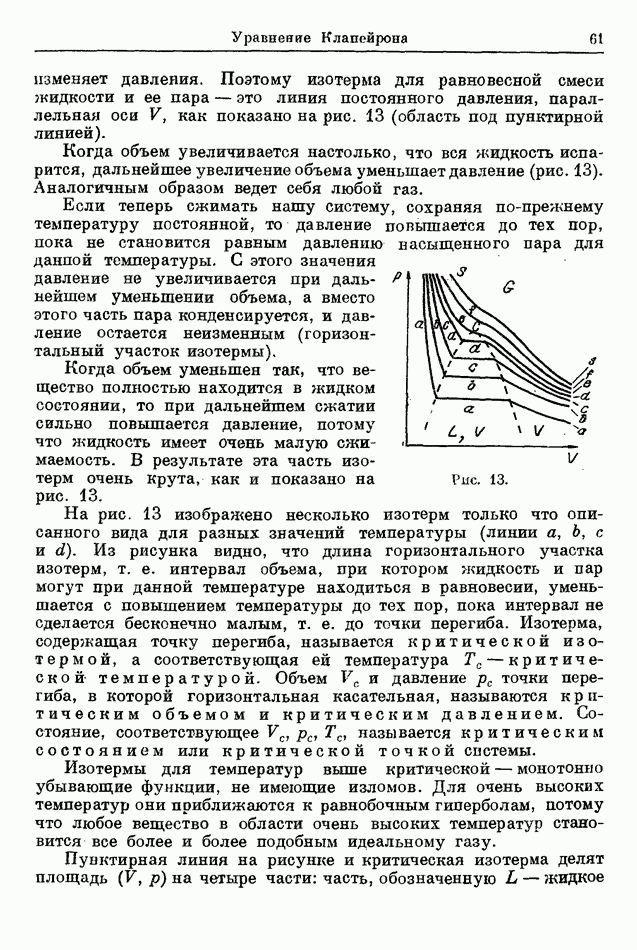
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
18. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ЭНТРОПИИ
Рассмотрим два состояния  системы. Из определения (69) имеем
системы. Из определения (69) имеем

если только интеграл берется вдоль обратимого процесса от А до В. Если интеграл берется вдоль необратимого процесса, то приведенное уравнение не выполняется. Покажем, что в таком случае справедливо неравенство

Чтобы доказать это неравенство, рассмотрим необратимый цикл, состоящий из необратимого процесса I от А до В и обратимого процесса  от В до А (см. рис. И). Применив (65) к этому необратимому циклу, получим
от В до А (см. рис. И). Применив (65) к этому необратимому циклу, получим

К обратимому процессу  от В к А можно применить равенство (69):
от В к А можно применить равенство (69):

Подставляя это выражение в предыдущее неравенство, получаем

Отсюда для произвольного процесса от А до В имеем

Этим доказано неравенство (73).
Для совершенно изолированных систем (73) принимает очень простую форму. Поскольку для таких систем  то находим, что
то находим, что

т. е. для любого процесса, происходящего в изолированной системе, энтропия конечного состояния никогда не может быть меньше энтропии начального состояния. Если процесс обратим, то в (74) стоит знак равенства — энтропия системы не изменяется.

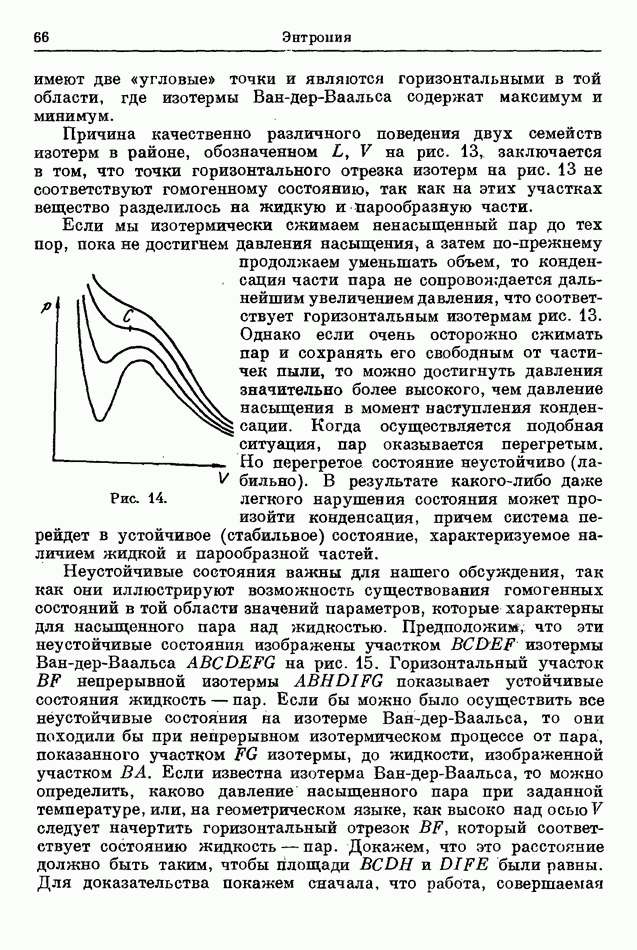
Рис. 11.
Следует подчеркнуть, что равенство (74) применимо только к изолированным системам. С помощью внешней системы можно уменьшить энтропию тела. Однако энтропия обеих систем (внешняя система  тело), взятых совместно, уменьшаться не может. Когда изолированная система находится в состоянии с максимальной энтропией, соответствующей ее энергии, то в ней не могут происходить никакие дальнейшие процессы, потому что любой процесс привел бы к уменьшению энтропии. Таким образом, состояние с максимальной энтропией является наиболее устойчивым состоянием изолированной системы. Тот факт, что все самопроизвольные процессы в изолированной системе происходят в направлении увеличения энтропии, может быть хорошо продемонстрирован двумя простыми примерами.
тело), взятых совместно, уменьшаться не может. Когда изолированная система находится в состоянии с максимальной энтропией, соответствующей ее энергии, то в ней не могут происходить никакие дальнейшие процессы, потому что любой процесс привел бы к уменьшению энтропии. Таким образом, состояние с максимальной энтропией является наиболее устойчивым состоянием изолированной системы. Тот факт, что все самопроизвольные процессы в изолированной системе происходят в направлении увеличения энтропии, может быть хорошо продемонстрирован двумя простыми примерами.
В качестве первого примера рассмотрим теплообмен путем теплопроводности между двумя частями системы — между  Пусть
Пусть  соответственно температуры этих двух частей, и пусть
соответственно температуры этих двух частей, и пусть  . Так как теплота распространяется от более горячего тела к более холодному, то тело
. Так как теплота распространяется от более горячего тела к более холодному, то тело  отдает некоторое количество теплоты
отдает некоторое количество теплоты  которое поглощается телом
которое поглощается телом  Таким образом, энтропия тела
Таким образом, энтропия тела  изменяется на величину
изменяется на величину  а энтропия тела
а энтропия тела  на величину —
на величину —  Общее изменение энтропии всей системы составляет
Общее изменение энтропии всей системы составляет

Поскольку  то это изменение, очевидно, положительно, и энтропия всей системы увеличивается.
то это изменение, очевидно, положительно, и энтропия всей системы увеличивается.
В качестве второго примера рассмотрим выделение теплоты при трепии. Этот необратимый процесс также приводит к увеличению энтропии. Часть системы, которая нагревается при трении, получает положительное количество теплоты, и ее энтропия увеличивается. Так как теплота получается из работы, а не от других частей системы, то это увеличение энтропии не компенсируется уменьшением энтропии в других частях системы.
Тот факт, что энтропия изолированной системы никогда не может уменьшиться во время процесса, имеет очень ясную интерпретацию со статистической точки зрения. Больцман доказал, что энтропия данного состояния термодинамической системы связана простым соотношением с вероятностью состояния.
Мы уже подчеркивали разницу между динамическим и термодинамическим понятиями состояния систем. Для того, чтобы определить динамическое состояние, необходимо детально знать положение и движение всех молекул, которые образуют систему. С другой стороны, термодинамическое состояние определяется заданием лишь небольшого числа параметров, таких как температура, давление и т. д. Отсюда следует, что одному термодинамическому состоянию соответствует большое число динамических состояний. В статистической механике принято характеризовать каждое термодинамическое состояние величиной  числом соответствующих динамических состояний, осуществляющих данное термодинамическое состояние (см. также раздел 30). Величина
числом соответствующих динамических состояний, осуществляющих данное термодинамическое состояние (см. также раздел 30). Величина  обычно называется вероятностью данного термодинамического состояния, хотя, строго говоря, она лишь пропорциональна вероятности в обычном смысле. Последняя может быть получена делением
обычно называется вероятностью данного термодинамического состояния, хотя, строго говоря, она лишь пропорциональна вероятности в обычном смысле. Последняя может быть получена делением  на число всех возможных динамических состояний.
на число всех возможных динамических состояний.
Используя статистические соображения, предположим, что в изолированной системе самопроизвольно могут происходить только такие процессы, которые приводят систему в наиболее вероятное состояние. Это означает, что наиболее устойчивое состояние системы будет состоянием с наибольшей вероятностью, совместимой с полной энергией системы.
Мы видим, что это предположение устанавливает параллелизм между вероятностью  и энтропией
и энтропией  нашей системы; иными словами, предполагается существование функциональной зависимости между ними. Такая зависимость действительно была установлена Больцманом, который доказал, что
нашей системы; иными словами, предполагается существование функциональной зависимости между ними. Такая зависимость действительно была установлена Больцманом, который доказал, что

где k — постоянная, называемая постоянной Больцмана и равная отношению газовой постоянной  к числу Авогадро А:
к числу Авогадро А:

Не приводя строгого доказательства соотношения (75), мы докажем, предполагая существование функциональной зависимости между 

что энтропия пропорциональна логарифму вероятности.
Рассмотрим систему, состоящую из двух частей, причем пусть  энтропии,
энтропии,  и — вероятности состояний этих частей. Из (77) имеем
и — вероятности состояний этих частей. Из (77) имеем

Но энтропия всей системы равна сумме энтропий ее частей:

а вероятность всей системы равна произведению вероятностей:

Из этих уравнений и из (77) получаем следующее: 

Функция  должна, таким образом, подчиняться функциональному уравнению
должна, таким образом, подчиняться функциональному уравнению

Эти свойства функции  дают нам возможность определить ее вид. Так как (78) верна для всех значений
дают нам возможность определить ее вид. Так как (78) верна для всех значений  то можно взять
то можно взять  где
где  бесконечно малая величина первого порядка. Тогда
бесконечно малая величина первого порядка. Тогда

Разлагая обе части в ряд Тейлора по  и пренебрегая всеми членами выше первого порядка, имеем
и пренебрегая всеми членами выше первого порядка, имеем

Для  находим
находим  Отсюда
Отсюда

где к представляет константу, или

Интегрируя, получаем

Вспоминая (77), окончательно имеем

Мы можем принять константу интегрирования равной нулю. Это допустимо, потому что энтропия определена с точностью да аддитивной постоянной. Таким образом, окончательно получаем выражение (75).
Конечно, следует подчеркнуть, что эти рассуждения не доказывают уравнения Больцмана (75), так как мы не показали, что существует функциональная зависимость между  Однако можно думать, что этот вывод делает существование функциональной зависимости правдоподобным.
Однако можно думать, что этот вывод делает существование функциональной зависимости правдоподобным.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ГЛАВА I. ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ
- 2. ИДЕАЛЬНЫЕ ГАЗЫ
- ГЛАВА II. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 3. ФОРМУЛИРОВКА ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 4. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К СИСТЕМАМ, СОСТОЯНИЕ КОТОРЫХ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 5. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К ГАЗАМ
- 6. АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В ГАЗАХ
- ГЛАВА III. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 7. ФОРМУЛИРОВКА ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 8. ЦИКЛ КАРНО
- 9. АБСОЛЮТНАЯ ТЕРМОДИНАМИЧЕСКАЯ ТЕМПЕРАТУРА
- 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА IV. ЭНТРОПИЯ
- 11. НЕКОТОРЫЕ СВОЙСТВА ЦИКЛОВ
- 12. ЭНТРОПИЯ
- 18. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ЭНТРОПИИ
- 14. ЭНТРОПИЯ СИСТЕМЫ, СОСТОЯНИЕ КОТОРОЙ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 15. УРАВНЕНИЕ КЛАПЕЙРОНА
- 16. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- ГЛАВА V. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
- 18. ТЕРМОДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 19. ПРАВИЛО ФАЗ
- 20. ТЕРМОДИНАМИКА ОБРАТИМОГО ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА
- ГЛАВА VI. РЕАКЦИИ В ГАЗОВОЙ ФАЗЕ
- 21. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗАХ
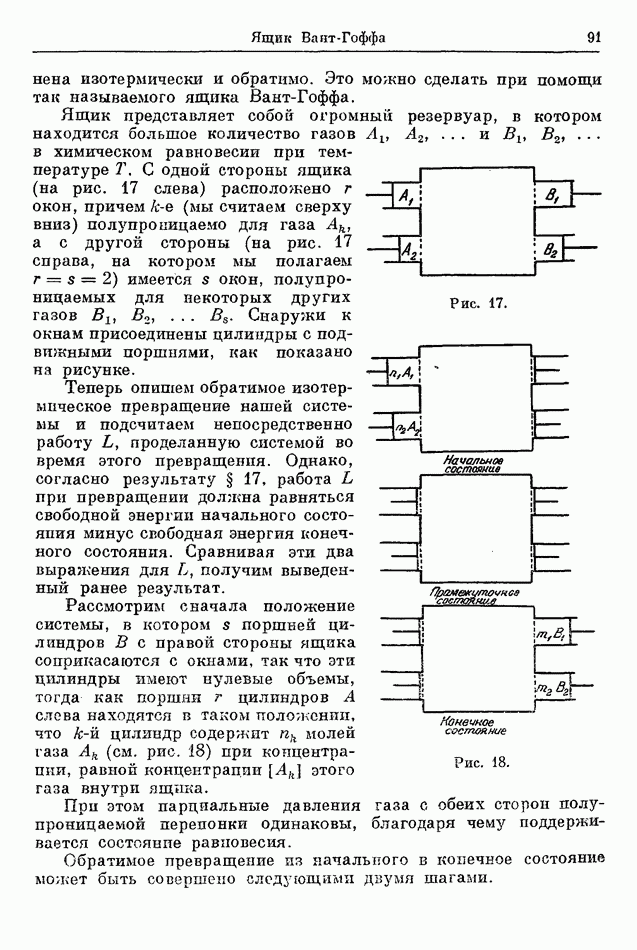
- 22. ЯЩИК ВАНТ-ГОФФА
- 23. ДРУГОЕ ДОКАЗАТЕЛЬСТВО УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ
- 24. ОБСУЖДЕНИЕ УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ. ПРИНЦИП ЛЕ ШАТЕЛЬЕ
- ГЛАВА VII. ТЕРМОДИНАМИКА СЛАБЫХ РАСТВОРОВ
- 28. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 27. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- 28. РАСПРЕДЕЛЕНИЕ РАСТВОРЕННОГО ВЕЩЕСТВА МЕЖДУ ДВУМЯ ФАЗАМИ
- 29. ДАВЛЕНИЕ ПАРА, ТОЧКА КИПЕНИЯ И ТОЧКА ЗАМЕРЗАНИЯ РАСТВОРА
- ГЛАВА VIII. ПОСТОЯННАЯ В ЗАВИСИМОСТИ ЭНТРОПИИ ОТ ТЕМПЕРАТУРЫ
- 30. ТЕОРЕМА НЕРНСТА
- 31. ПРИМЕНЕНИЕ ТЕОРЕМЫ НЕРНСТА К ТВЕРДЫМ ТЕЛАМ
- 32. ЭНТРОПИЙНАЯ КОНСТАНТА ГАЗОВ
- 33. ТЕРМИЧЕСКАЯ ИОНИЗАЦИЯ ГАЗА. ТЕРМОИОННЫЙ ЭФФЕКТ