2. ИДЕАЛЬНЫЕ ГАЗЫ

Уравнение состояния системы, которая содержит определенное количество газа, занимающего объем V при температуре и давлении может быть выражено простым аналитическим законом. Мы получим уравнение состояния газа в простейшей форме, заменив эмпирическую шкалу температур новой температурной шкалой

Временно определим как температуру, показываемую газовым термометром, в котором газ содержится при очень низком постоянном давлении.

Тогда температура пропорциональна объему, занимаемому газом. Хорошо известно, что показания различных газовых термометров в этих условиях в значительной степени не зависят от природы содержащегося в них газа при условии, что он достаточно далек от конденсации. Однако увидим далее (раздел 9), что можно определить ту же шкалу температур из общих термодинамических соображений совершенно независимо от каких бы то ни было специальных свойств газов.

Температура называется абсолютной температурой. Ее единицы выбраны таким образом, чтобы разность температур между точками кипения и замерзания воды при давлении, равном одной атмосфере, была равна 100°. Тогда, как известно, точка замерзания воды соответствует абсолютной температуре 273,1°.

Уравнение состояния системы, содержащей граммов газа с молекулярным весом записывается следующим образом:

В является универсальной постоянной, т. е. имеет одну и ту нее величину для всех газов: или (см. раздел 3) кал/град. Уравнение (6) называется уравнением состояния идеального газа; оно включает в себя законы Бойля, Гей-Люссака и Авогадро.

Ни один из реальных газов не подчиняется уравнению (6) точно. Вещество, которое точно подчиняется уравнению (6), называется идеальным газом.

Для грамм-молекулы или моля газа, т. е. для числа граммов газа, равного его молекулярному весу, имеем поэтому уравнение (6) сводится к

Используя (6) или (7), можно выразить плотность газа через давление и температуру:

Для изотермического превращения идеального газа (превращения при постоянной температуре) имеем

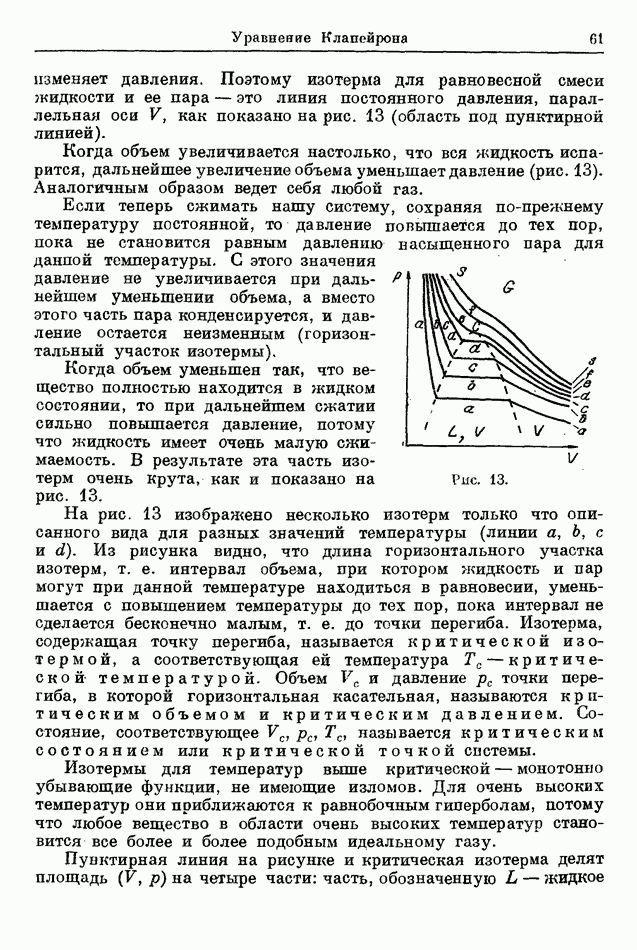
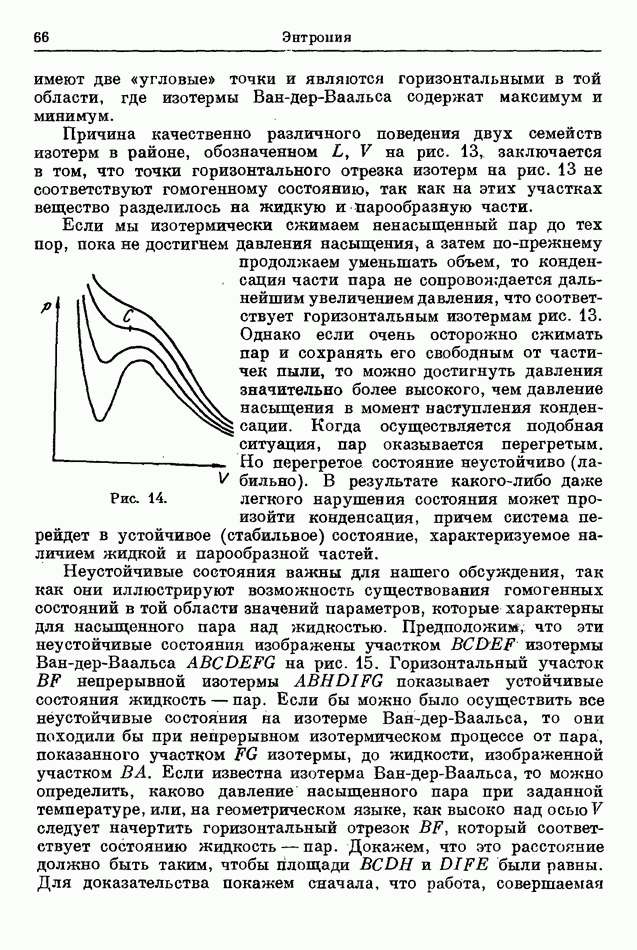
На диаграмме изотермическое превращение идеального газа представится, таким образом, равнобочной гиперболой, асимптотами которой являются оси V и.

Легко можно вычислить работу, совершаемую газом во время изотермического расширения от начального объема до конечного Сделаем это, воспользовавшись уравнениями (5) и (6),

где соответственно начальное и конечное давления. Для одного моля газа имеем

Смесь различных газов подчиняется законам, тождественным тем, которым подчиняются химически однородные газы. Мы назовем парциальным давлением компоненты смеси то давле-ияе, которое оказывала бы эта компонента, если бы она одна была помещена в объем, занимаемый смесью при температуре смеси. Теперь можно сформулировать закон Дальтона: давление, производимое смесью газов, равно сумме парциальных давлений всех компонент, содержащихся в смеси.

Этому закону реальные газы подчиняются лишь приближенно, но предполагается, что он совершенно точен для идеальных газов.

Задачи

(см. скан)