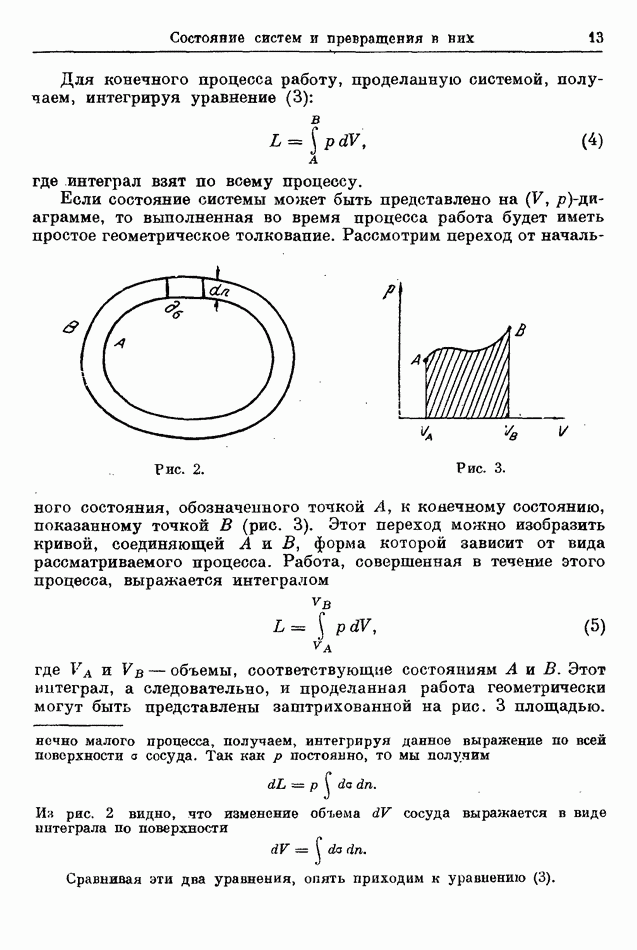
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14. ЭНТРОПИЯ СИСТЕМЫ, СОСТОЯНИЕ КОТОРОЙ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
Для этих систем состояние определяется какими-либо двумя из трех переменных  Если
Если  выбраны независимыми переменными, то теплота
выбраны независимыми переменными, то теплота  полученная системой во время бесконечно малого процесса, в результате которого
полученная системой во время бесконечно малого процесса, в результате которого  изменяются на величины
изменяются на величины  дается дифференциальным выражением (22) и
дается дифференциальным выражением (22) и

Из приведенного выражения, используя (72), получаем

Эти два дифференциальных выражения для  отличаются в одном очень важном отношении. Мы знаем из общей теории, что имеется функция
отличаются в одном очень важном отношении. Мы знаем из общей теории, что имеется функция  состояния системы. В нашем случае
состояния системы. В нашем случае  функция переменных
функция переменных  которые определяют состояние системы:
которые определяют состояние системы:

Дифференциальное выражение в правой части (80) является поэтому дифференциалом функции двух независимых переменных 
Вообще такое дифференциальное выражение в случае двух независимых переменных х и у, как

будет полным дифференциалом, если оно — дифференциал функции от  Следовательно, можно сказать, что
Следовательно, можно сказать, что  полный дифференциал при независимых переменных
полный дифференциал при независимых переменных 
Хорошо известно, что если  полный дифференциал, то
полный дифференциал, то  должны удовлетворять следующему соотношению:
должны удовлетворять следующему соотношению:

Если условие (83) выполняется, то можно проинтегрировать уравнение (82) и определить функцию, удовлетворяющую уравнению (82). С другой стороны, когда такой функции нет и  нельзя рассматривать как дифференциал некоторой функции
нельзя рассматривать как дифференциал некоторой функции  то интеграл (82) по пути, соединяющему две точки на плоскости
то интеграл (82) по пути, соединяющему две точки на плоскости  зависит не только от этих двух точек (пределов интегрирования), но также и от пути, соединяющего их.
зависит не только от этих двух точек (пределов интегрирования), но также и от пути, соединяющего их.

Рис. 12.
Что касается двух дифференциальных выражений (79) и (80), то мы уже отмечали, что  является полным дифференциалом. Если мы рассмотрим два состояния
является полным дифференциалом. Если мы рассмотрим два состояния  на диаграмме
на диаграмме  соединенные двумя различными обратимыми процессами I и II (см. рис. 12), и проинтегрируем
соединенные двумя различными обратимыми процессами I и II (см. рис. 12), и проинтегрируем  по путям I и II, то получим одинаковый результат в обоих случаях, а именно:
по путям I и II, то получим одинаковый результат в обоих случаях, а именно:  Если же проинтегрировать
Если же проинтегрировать  по этим двум различным путям, то получим два различных результата
по этим двум различным путям, то получим два различных результата  которые, вообще говоря, не равны друг другу. Это утверждение легко можно проверить, применяя первый закон термодинамики (15) к процессам X и II. Действительно, используя (15), находим
которые, вообще говоря, не равны друг другу. Это утверждение легко можно проверить, применяя первый закон термодинамики (15) к процессам X и II. Действительно, используя (15), находим

Взяв разность этих выражений, получим

причем величины  и определяются соответственно площадями
и определяются соответственно площадями 
Разность двух площадей равна площади  Отсюда следует, что
Отсюда следует, что  а следовательно, и
а следовательно, и  не равны нулю. Таким образом, уравнение (79) не является полным дифференциалом и не может быть найдено никакой функции
не равны нулю. Таким образом, уравнение (79) не является полным дифференциалом и не может быть найдено никакой функции  состояния системы. Следует отметить,
состояния системы. Следует отметить,  если бы тепловая жидкость (флогистон) действительно существовала, как предполагали до развития современной термодинамики, то можно было бы найти функцию состояния
если бы тепловая жидкость (флогистон) действительно существовала, как предполагали до развития современной термодинамики, то можно было бы найти функцию состояния 
Рассмотрим в качестве примера к предыдущему рассуждению выражение для  одного моля идеального газа. Из (30) имеем
одного моля идеального газа. Из (30) имеем

или, после исключения  с помощью уравнения состояния
с помощью уравнения состояния 

Это выражение не является полным дифференциалом, и можно проверить непосредственно, что условие (83) не выполняется.
Из (84) и (72) получаем

Так как теперь условие (83) выполняется, то это выражение представляет полный дифференциал.
После интегрирования (85) имеем

где а — константа интегрирования. Эта аддитивная константа остается неопределенной в соответствии с введением энтропии (68) (см., однако, раздел 32).
Можно изменить выражение (86) энтропии одного моля идеального газа, введя вместо V его значение  найденное из уравнения состояния. Вспоминая (33), получаем
найденное из уравнения состояния. Вспоминая (33), получаем

Возвращаясь к общему случаю какого-либо вещества, состояние которого определяется переменными  воспользуемся выражением (80) для дифференциала энтропии. Применяя к этому выражению условие (83), запишем
воспользуемся выражением (80) для дифференциала энтропии. Применяя к этому выражению условие (83), запишем

где индексы  опущены, потому что здесь везде
опущены, потому что здесь везде  приняты независимыми переменными. Если мы выполним дифференцирование, указанное в предыдущем уравнении, и соберем однородные члены, то получим важный результат:
приняты независимыми переменными. Если мы выполним дифференцирование, указанное в предыдущем уравнении, и соберем однородные члены, то получим важный результат:

Используя (88). яскажем, что энергия  вещества, которое подчиняется уравнению состояния
вещества, которое подчиняется уравнению состояния  является функцией
является функцией
одной лишь температуры и не зависит от объема. Как уже отмечалось, это было экспериментально подтверждено Джоулем. Однако данный результат интересно получить как прямое следствие из уравнения состояния.
Подставляя выражение  в (88), находим
в (88), находим

чем доказывается  что
что  не зависит от
не зависит от 
Если в качестве независимых переменных (вместо  ) выберем
) выберем  или
или  то получим два других уравнения, которые по существу эквивалентны (88). Таким образом, если мы берем
то получим два других уравнения, которые по существу эквивалентны (88). Таким образом, если мы берем  как величины, определяющие состояние системы, то
как величины, определяющие состояние системы, то  определяется соотношением (23). Так как
определяется соотношением (23). Так как  является полным дифференциалом, то с помощью (83) легко получаем
является полным дифференциалом, то с помощью (83) легко получаем

Подобно этому, принимая за независимые переменные  и V, находим из (24) и (83)
и V, находим из (24) и (83)

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ГЛАВА I. ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ
- 2. ИДЕАЛЬНЫЕ ГАЗЫ
- ГЛАВА II. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 3. ФОРМУЛИРОВКА ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 4. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К СИСТЕМАМ, СОСТОЯНИЕ КОТОРЫХ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 5. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К ГАЗАМ
- 6. АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В ГАЗАХ
- ГЛАВА III. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 7. ФОРМУЛИРОВКА ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 8. ЦИКЛ КАРНО
- 9. АБСОЛЮТНАЯ ТЕРМОДИНАМИЧЕСКАЯ ТЕМПЕРАТУРА
- 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА IV. ЭНТРОПИЯ
- 11. НЕКОТОРЫЕ СВОЙСТВА ЦИКЛОВ
- 12. ЭНТРОПИЯ
- 18. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ЭНТРОПИИ
- 14. ЭНТРОПИЯ СИСТЕМЫ, СОСТОЯНИЕ КОТОРОЙ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 15. УРАВНЕНИЕ КЛАПЕЙРОНА
- 16. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- ГЛАВА V. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
- 18. ТЕРМОДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 19. ПРАВИЛО ФАЗ
- 20. ТЕРМОДИНАМИКА ОБРАТИМОГО ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА
- ГЛАВА VI. РЕАКЦИИ В ГАЗОВОЙ ФАЗЕ
- 21. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗАХ
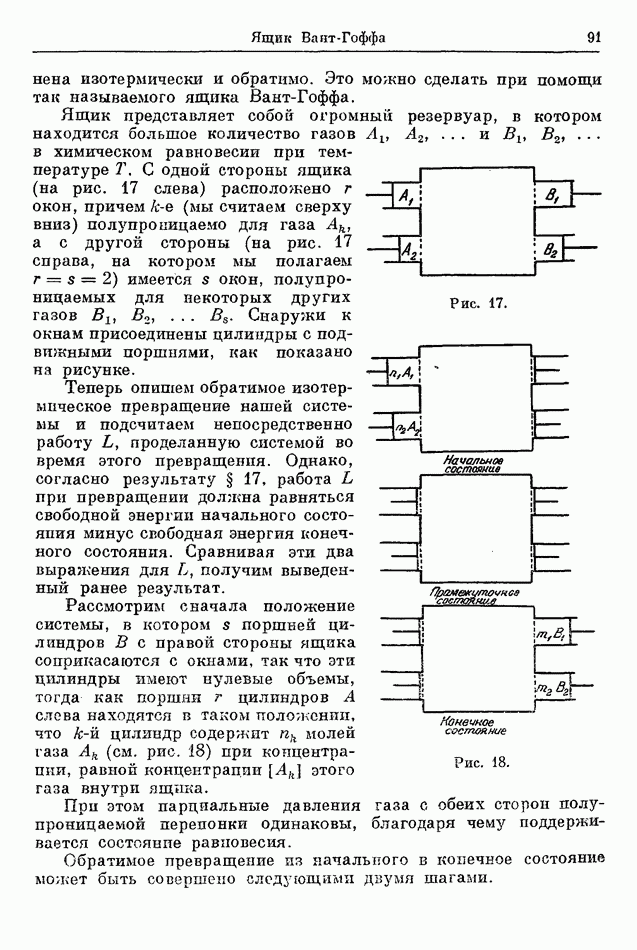
- 22. ЯЩИК ВАНТ-ГОФФА
- 23. ДРУГОЕ ДОКАЗАТЕЛЬСТВО УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ
- 24. ОБСУЖДЕНИЕ УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ. ПРИНЦИП ЛЕ ШАТЕЛЬЕ
- ГЛАВА VII. ТЕРМОДИНАМИКА СЛАБЫХ РАСТВОРОВ
- 28. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 27. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- 28. РАСПРЕДЕЛЕНИЕ РАСТВОРЕННОГО ВЕЩЕСТВА МЕЖДУ ДВУМЯ ФАЗАМИ
- 29. ДАВЛЕНИЕ ПАРА, ТОЧКА КИПЕНИЯ И ТОЧКА ЗАМЕРЗАНИЯ РАСТВОРА
- ГЛАВА VIII. ПОСТОЯННАЯ В ЗАВИСИМОСТИ ЭНТРОПИИ ОТ ТЕМПЕРАТУРЫ
- 30. ТЕОРЕМА НЕРНСТА
- 31. ПРИМЕНЕНИЕ ТЕОРЕМЫ НЕРНСТА К ТВЕРДЫМ ТЕЛАМ
- 32. ЭНТРОПИЙНАЯ КОНСТАНТА ГАЗОВ
- 33. ТЕРМИЧЕСКАЯ ИОНИЗАЦИЯ ГАЗА. ТЕРМОИОННЫЙ ЭФФЕКТ