6. АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В ГАЗАХ

Говорят, что термодинамическая система совершает адиабатический процесс, если он обратим и если система термически изолирована, так что во время процесса не может происходить теплообмена между системой и окружающей ее средой.

Можно адиабатически расширять или сжимать газ, помещая его в цилиндр с нетеплопроводящими стенками и поршнем, медленно перемещая поршень наружу или внутрь. Если дать возможность газу адиабатически расширяться, то он произведет внешнюю работу, и величина в уравнении (15) будет положительной.

Так как газ термически изолирован то значение должно быть отрицательным, т. е. во время адиабатического расширения энергия газа уменьшается. Зависимость энергии от температуры определяется уравнением (29), из которого следует, что уменьшение энергии означает также и уменьшение температуры газа.

Чтобы получить количественное соотношение между изменением температуры и объема в результате адиабатического расширения газа, заметим, что, поскольку то уравнение (30) можно представить в виде

Используя уравпение состояния можно исключить из приведенного выше уравнения и получить

или

Интегрирование дает

Потенцируя, получаем

Используя определение (36), можно написать предыдущее уравнение в форме

Это уравнение показывает нам количественно, как адиабатическое изменение объема идеального газа влияет на изменение его температуры. Если, например, объем двухатомного газа адиабаютески расширить вдвое по сравнению с начальным, то, полагая, согласно (37), из уравнения (38) находим, что температура понизится в отношении

Используя уравнение состояния можем выразить уравнение (38), соответствующее адиабатическому процессу, в следующей форме:

Уравнение (39) следует сравнить с уравнением

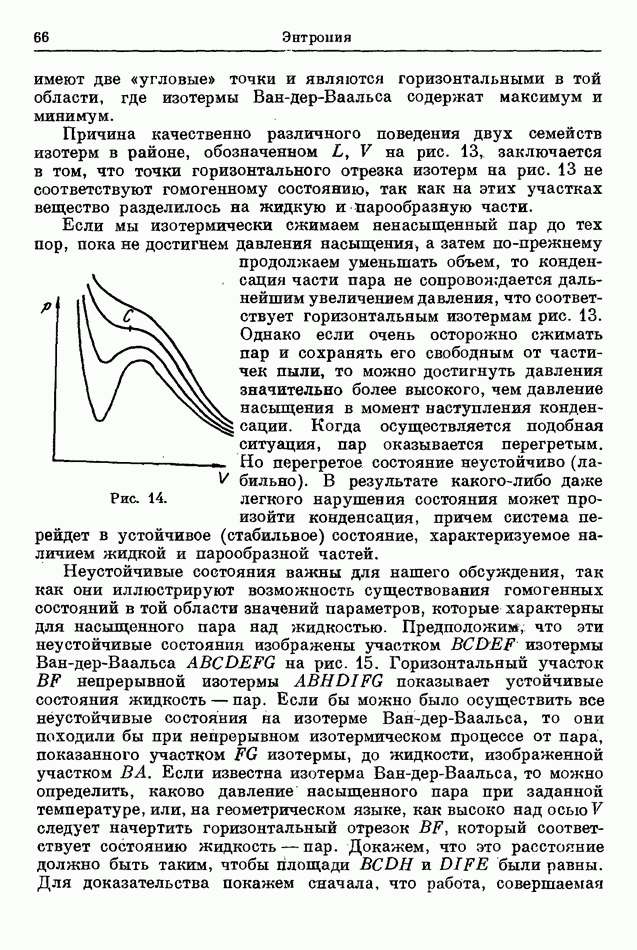
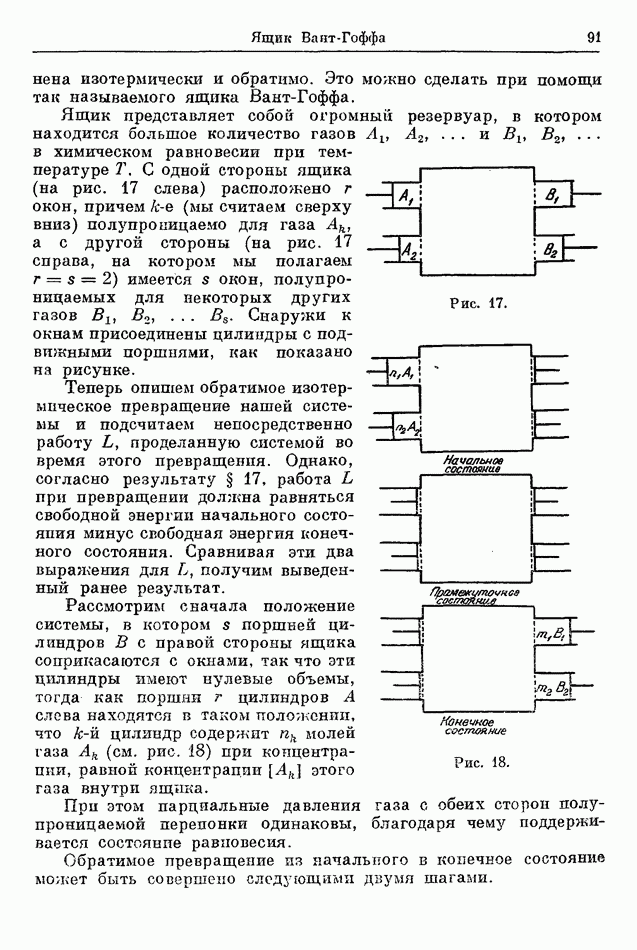
выражающим изотермический процесс. На диаграмме изотермы являются семейством равнобочных гипербол, адиабаты же, представленные уравнением (39), качественно похожи на гиперболы, но они идут круче, потому что Изотермы и адиабаты изображены на рис. 6, первые — сплошными линиями, вторые — пунктиром.

Интересным и простым приложением теории адиабатического расширения газов является вычисление изменения температуры атмосферы высоко над уровнем моря. Основной причиной изменения температуры являются конвекционные токи в тропосфере, которые непрерывно перемещают воздух из низших слоев в высшие и из высших в низшие. Когда воздух с уровня моря поднимается в верхние слои с низким давлением, он расширяется. Так как воздух — плохой проводник тепла, то тепло от окружающего воздуха очень плохо передается поднявшемуся воздуху, поэтому можно считать, что происходит адиабатическое расширение. Соответственно понижается температура поднявшегося воздуха. С другой стороны, воздух верхних слоев атмосферы, погружаясь в нижние слои, испытывает адиабатическое сжатие, вследствие чего повышается температура.

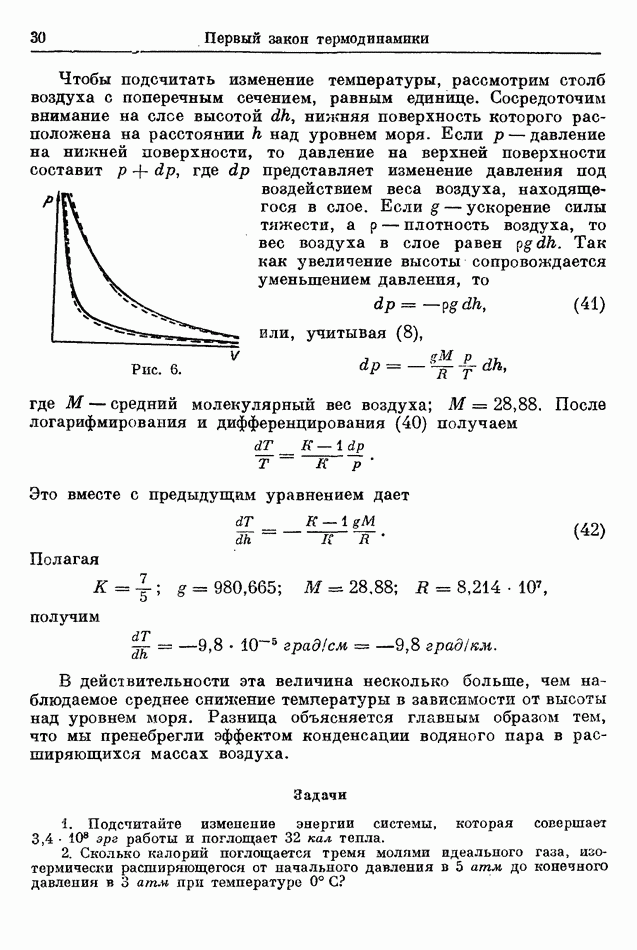
Чтобы подсчитать изменение температуры, рассмотрим столб воздуха с поперечным сечением, равным единице. Сосредоточим внимание на слое высотой нижняя поверхность которого расположена на расстоянии над уровнем моря. Если давление на нижней поверхности, то давление на верхней поверхности составит где представляет изменение давления под воздействием веса воздуха, находящегося в слое. Если ускорение силы тяжести, плотность воздуха, то вес воздуха в слое равен Так как увеличение высоты сопровождается уменьшением давления, то

или, учитывая (8),

где средний молекулярный вес воздуха; После логарифмирования и дифференцирования (40) получаем

Это вместе с предыдущим уравнением дает

Полагая

получим

В действительности эта величина несколько больше, чем наблюдаемое среднее снижение температуры в зависимости от высоты над уровнем моря. Разница объясняется главным образом тем, что мы пренебрегли эффектом конденсации водяного пара в расширяющихся массах воздуха.

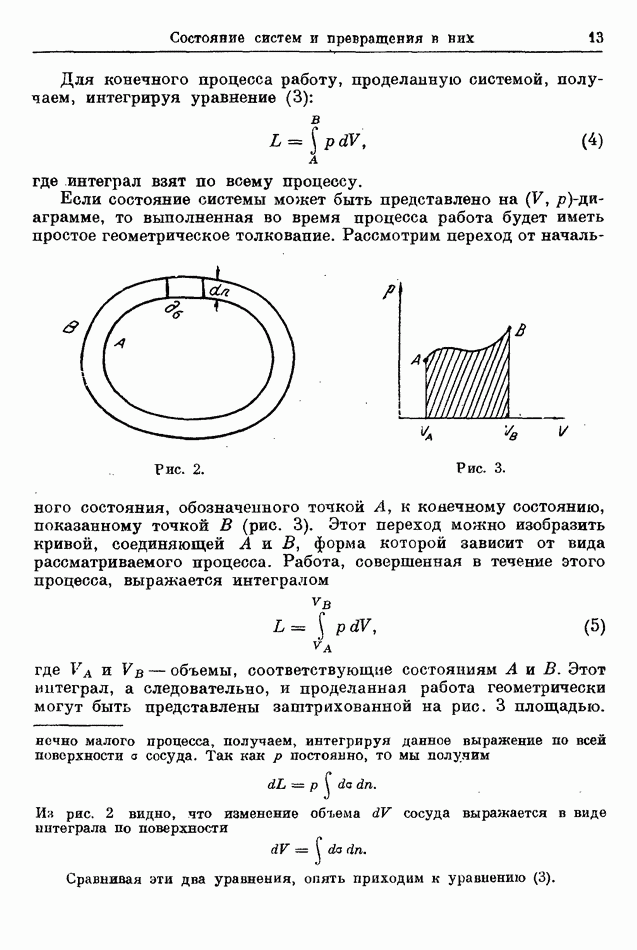
Рис. 6.

Задачи

(см. скан)

(см. скан)