5. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К ГАЗАМ

В случае газа мы можем конкретизировать зависимость энергии состояния от определяющих это состояние переменных величин. Принимаем за независимые переменные и сначала докажем, что энергия является функцией температуры и не зависит от объема. Подобно многим другим свойствам газов это свойство лишь приближенно верно для реальных газов. Предполагается, что точно оно выполняется для идеальных газов. В разделе 14, исходя из второго закона термодинамики, мы сделаем вывод, что энергия любого тела, подчиняющаяся уравнению состояния идеального газа (7), не должна зависеть от объема Сейчас, однако, мы приведем экспериментальное доказательство этой теоремы для газа; эксперименты были выполнены Джоулем.

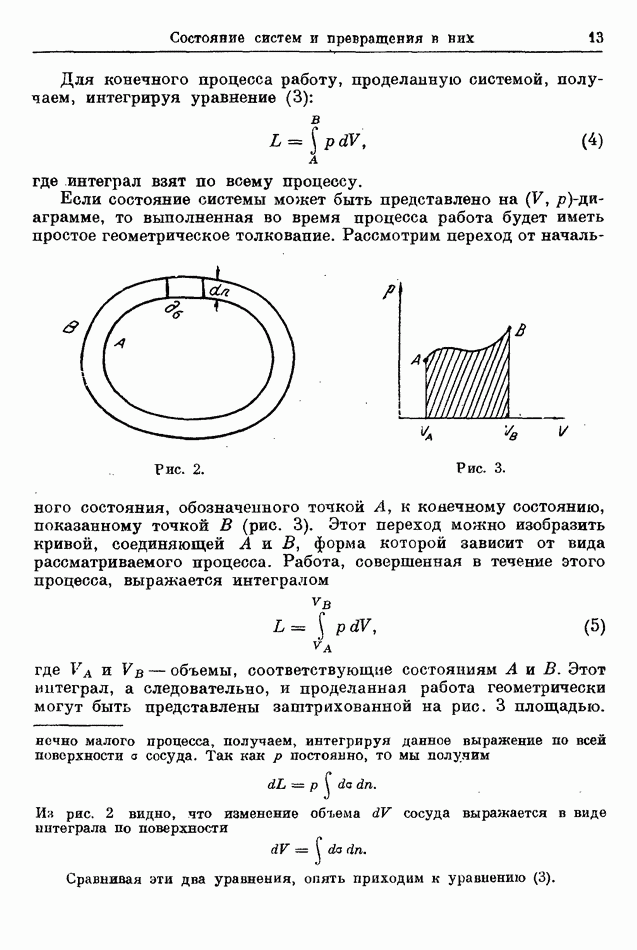
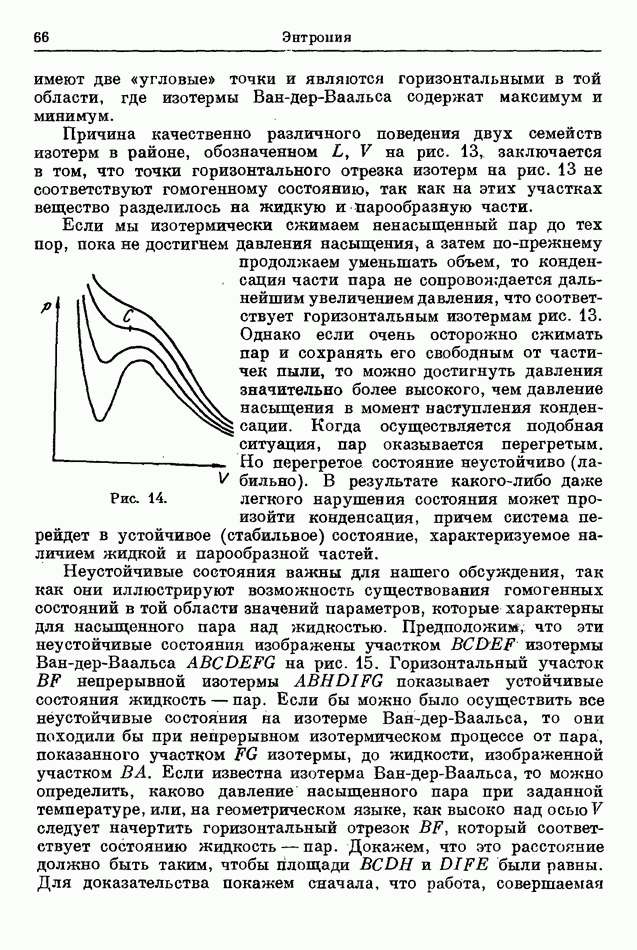
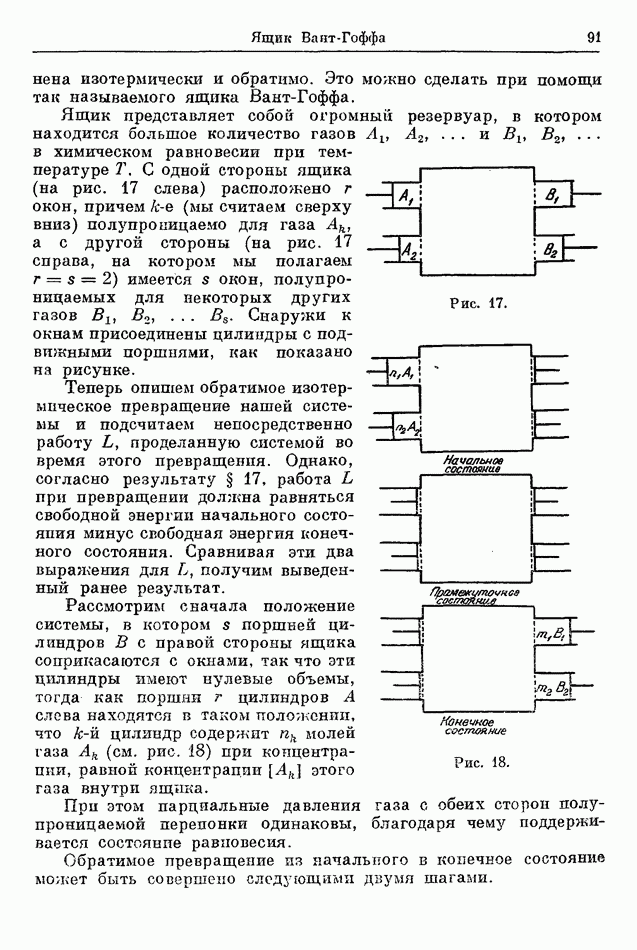
Внутрь калориметра Джоуль помещал сосуд, имеющий две камеры соединенные трубкой (рис. 5). Он наполнил камеру А газом и откачал камеру В, причем сначала обе камеры были перекрыты краном в соединяющей их трубке. После того, как термометр, помещенный в калориметр, показал, что наступало термическое равновесие, Джоуль открыл кран, вследствие чего газ поступал из до тех пор, пока давление не стало всюду одинаковым. При этом он обнаруживал лишь очень небольшое изменение в показаниях термометра. Это означало, что практически не происходил переход тепла от калориметра к камере и наоборот. Предполагается, что если бы этот опыт был выполнен с идеальным газом, то изменения температуры не было бы вовсе.

Применим теперь первый закон к описанному выше процессу. Так как то из уравнения (15) для системы из двух камер и заключенного в них газа имеем

где работа совершаемая системой и изменение энергии системы.

Поскольку объемы камер составляющих систему, не изменились во время опыта, то система не могла выполнить внешней работы, т. е. Поэтому

т. е. энергия системы и, следовательно, энергия газа не изменяется.

Рис. 5.

Рассмотрим теперь процесс в целом. Сначала газ занимал объем 4, а в конце процесса заполнял обе камеры т. е. объем его изменялся. Однако опыт показывает, что в результате процесса не изменилась температура газа. Так как не произошло изменения энергии во время процесса, то следует заключить, что изменение объема при постоянной температуре не приводит к изменению энергии. Другими словами, энергия идеального газа является функцией только температуры и не зависит от объема. Поэтому для энергии идеального газа можно записать

Чтобы определить вид этой зависимости, можно использовать результаты опыта, показывающего, что теплоемкость газа при постоянном объеме лишь слабо зависит от температуры. Предположим, что для идеального газа теплоемкость строго постоянна. данном разделе мы уже ссылались на понятие моль газа; пусть обозначают молярную теплоемкость соответственно при постоянном объеме и постоянном давлении.

Поскольку зависит только от то нет особой необходимости указывать, что объем постоянный в уравнении (25); так что для идеального газа можно записать

Так как величина предполагается постоянной, то после интегрирования получаем

где константа интегрирования, которая представляет энергию газа при температуре абсолютного нуля.

В применении к идеальному газу уравнение (21), выражающее первый закон термодинамики для бесконечно малых процессов, принимает форму

Дифференцируя уравнение (7) для одного моля идеального газа, получим

Подставляя его в (30), находим

Так как для процесса при постоянном давлении то это уравнение дает

т. е. разность между молярной теплоемкостью газа при постоянном давлении и при постоянном объеме равна газовой постоянной

Такой же результат можно получить из (26), (29) и (7). Действительно, для идеального газа из (29) и (7) имеем

Подставляя эти выражения в (26), снова получаем (33).

При помощи кинетической теории газов можно показать, что

Принимая эти величины, которые хорошо согласуются с опытом, из (33) делаем вывод, что

Если обозначим

то также получим