| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
12. ЭНТРОПИЯ
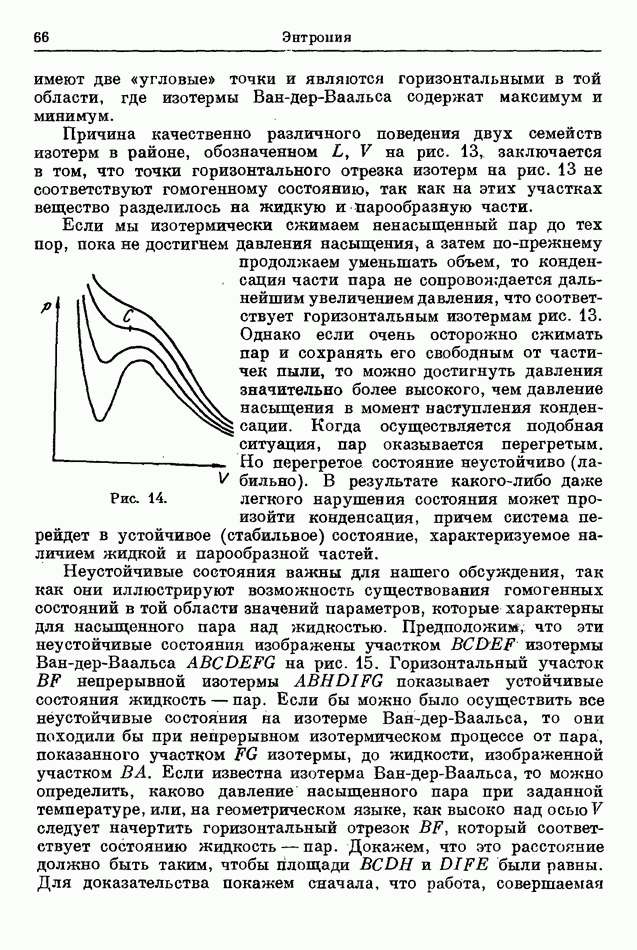
Свойства обратимых циклов, которые выражены уравнением (66), могут быть установлены также и в следующей форме. Пусть  два равновесных состояния системы
два равновесных состояния системы  Рассмотрим обратимый процесс, который проходит система от начального состояния А к конечному состоянию В. В большинстве случаев возможно большое количество обратимых процессов, переводящих систему из
Рассмотрим обратимый процесс, который проходит система от начального состояния А к конечному состоянию В. В большинстве случаев возможно большое количество обратимых процессов, переводящих систему из  Например, если состояние системы изобразить на диаграмме
Например, если состояние системы изобразить на диаграмме  то некоторая непрерывная кривая, которая соединяет две точки
то некоторая непрерывная кривая, которая соединяет две точки  (представляющие начальное и конечное состояния системы), будет соответствовать возможному обратимому процессу от А до В. На рис. 9 показаны три таких процесса.
(представляющие начальное и конечное состояния системы), будет соответствовать возможному обратимому процессу от А до В. На рис. 9 показаны три таких процесса.
Рассмотрим интеграл  распространенный на обратимый процесс от А до В
распространенный на обратимый процесс от А до В  количество теплоты, обратимо поглощенное системой при температуре
количество теплоты, обратимо поглощенное системой при температуре  Докажем, что приведенный выше интеграл является одним и тем же для всех обратимых процессов от А до В, т. е. величина интеграла при обратимом процессе зависит лишь от начала А и конца В процесса и не зависит от самого процесса.
Докажем, что приведенный выше интеграл является одним и тем же для всех обратимых процессов от А до В, т. е. величина интеграла при обратимом процессе зависит лишь от начала А и конца В процесса и не зависит от самого процесса.

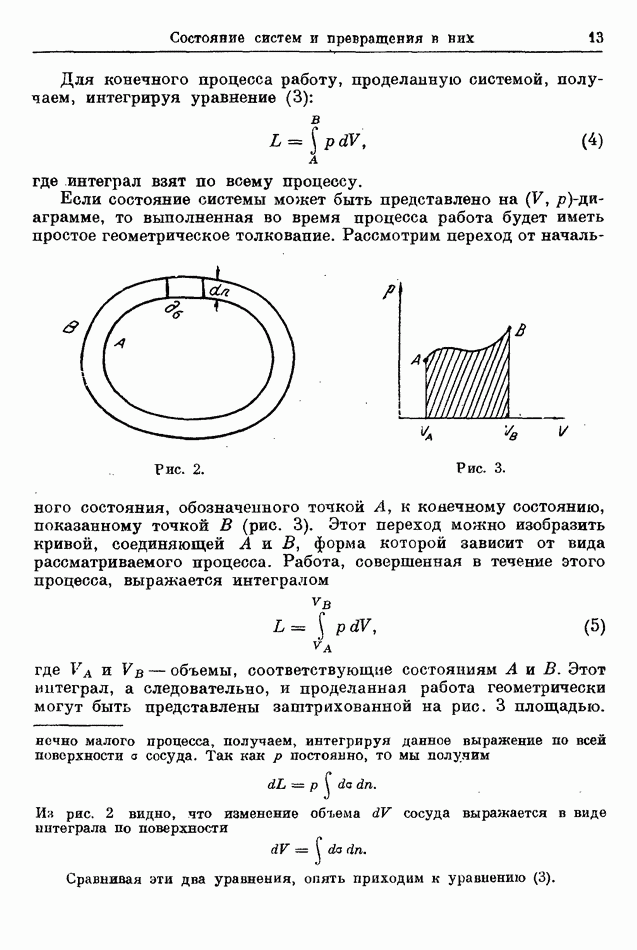
Рис. 9.
Для доказательства этой теоремы необходимо показать, что если  обратимые процессы от А до В (на рис. 10 состояния изображены точками и процессы линиями — только как нагляднее дополнение к доказательству), то
обратимые процессы от А до В (на рис. 10 состояния изображены точками и процессы линиями — только как нагляднее дополнение к доказательству), то

где два интеграла взяты соответственно по путям I и II.
Рассмотрим циклический процесс  Это обратимый цикл, так как он составлен из двух обратимых процессов, вследствие чего к нему можно применить (66), так что
Это обратимый цикл, так как он составлен из двух обратимых процессов, вследствие чего к нему можно применить (66), так что


Рис. 10.
Этот интеграл может быть представлен суммой двух интегралов

Второй интеграл приведенного выражения равен —  потому что в превращении от В к А по пути
потому что в превращении от В к А по пути  принимает те же значения (за исключением знака), как и в процессе от А к В по пути II. Отсюда получаем равенство (67) и таким образом доказываем теорему.
принимает те же значения (за исключением знака), как и в процессе от А к В по пути II. Отсюда получаем равенство (67) и таким образом доказываем теорему.
Свойство, выраженное равенством (67), дает возможность определить новую функцию состояния системы. Эта функция, которая называется энтропией и является крайне важной в термодинамике, определяется следующим путем. Выбираем произвольно
некоторое равновесное состояние О нашей системы и называем его стандартным состоянием, йусть А — некоторое другое равновесное состояние; рассмотрим интеграл

взятый по обратимому процессу. Мы уже знаем, что такой интеграл зависит от состояний  и не зависит от того, с помощью какого обратимого процесса перешли от О к А. Однако поскольку стандартное состояние О зафиксировано, можно сказать, что равенство
и не зависит от того, с помощью какого обратимого процесса перешли от О к А. Однако поскольку стандартное состояние О зафиксировано, можно сказать, что равенство  -функция одного лишь состояния А. Назовем эту функцию энтропией состояния А.
-функция одного лишь состояния А. Назовем эту функцию энтропией состояния А.
Рассмотрим теперь два равновесных состояния  Пусть
Пусть  соответственно энтропии этих состояний. Покажем, что
соответственно энтропии этих состояний. Покажем, что

где интеграл взят по обратимому процессу от состояния А до состояния В.
Чтобы это доказать, заметим, что величина интеграла в правой части (69) одинакова для всех обратимых процессов от А до В. Поэтому можно выбрать процесс, состоящий из двух последовательных обратимых процессов; первый обратимый процесс от А до стандартного состояния О, а затем обратимый процесс от О до В. Таким образом, интеграл в (69) можно представить в виде суммы двух интегралов:

По определению имеем (68):

так как процесс от О до В обратим. Далее запишем

Подставляя эти два значения интегралов в правую часть (70), получаем (69), что и требовалось доказать.
Определение (68) энтропии допускает произвол в выборе стандартного состояния О. Можно легко доказать, что если вместо О выбрать другое стандартное состояние О, то новая величина  которую мы получим для энтропии состояния А, отличается от прежнего значения
которую мы получим для энтропии состояния А, отличается от прежнего значения  только аддитивной константой.
только аддитивной константой.
Если мы рассматриваем О как новое стандартное состояние, то по определению имеем

где интеграл берется по обратимому процессу от О до А. Используя равенство (69), находим, что

или

Однако, так как новое стандартное состояние О зафиксировано, то  постоянная величина, т. е. не зависит от переменного состояния А. Таким образом, соотношение (71) показывает, что разность энтропий состояния А, полученная при двух различных стандартных состояниях
постоянная величина, т. е. не зависит от переменного состояния А. Таким образом, соотношение (71) показывает, что разность энтропий состояния А, полученная при двух различных стандартных состояниях  является константой.
является константой.
Итак, энтропия определена с точностью до аддитивной константы. Эта неопределенность не должна нас беспокоить, когда речь идет о разности энтропий; все же в отдельных задачах дополнительная константа в энтропии играет важную роль. Дальше мы покажем, как третий закон термодинамики завершает введение энтропии и дает возможность установить константу в определении энтропии (см. главу VIII).
Из (68) и (69) следует, что если мы определяем бесконечно малый обратимый процесс, во время которого энтропия изменяется
па величину  и система получает количество теплоты
и система получает количество теплоты  при температуре
при температуре  то
то

т. е. изменение энтропии во время бесконечно малого обратимого процесса есть результат деления количества теплоты, поглощенной системой, на температуру системы.
Энтропия системы, состоящей из различных частей, равна сумме энтропий всех частей. Это верно, если энергия системы является суммой энергий всех частей и если работа, совершаемая системой во время превращения, равна суммарному количеству работы, совершенной всеми частями. Отметим, что эти условия не вполне очевидны и в отдельных случаях могут быть не выполнены. Так, например, в случае системы, состоящей из двух гомогенных веществ, можно выразить энергию как сумму энергий этих двух веществ только тогда, когда можно пренебречь поверхностной энергией двух веществ, находящихся в контакте. Вообще говоря, поверхностной энергией можно пренебречь, только если эти два вещества не очень сильно измельчены; в противном случае поверхностная энергия может играть значительную роль.
Допустим для простоты, что наша система  состоит только из двух отдельных систем
состоит только из двух отдельных систем  Предположим, что энергия
Предположим, что энергия  системы
системы  равна сумме энергии
равна сумме энергии  систем
систем 

и что работа  совершенная системой
совершенная системой  во время процесса, равна сумме
во время процесса, равна сумме  т. е. сумме работ, совершенных соответственно системами
т. е. сумме работ, совершенных соответственно системами 

Согласно этому предложению, из (15) следует, что теплота  полученная системой во время процесса, может быть записана как сумма количеств теплоты, полученных двумя частями:
полученная системой во время процесса, может быть записана как сумма количеств теплоты, полученных двумя частями:

Это дает возможность написать интеграл (68), который определяет энтропию в виде суммы двух интегралов, определяющих энтропию двух отдельных систем 

Когда условия разбиения системы на аддитивные подсистемы выполнены, то это определение энтропии позволяет определить энтропию системы, даже если система не находится в состоянии равновесия. Это возможно сделать, если суметь разделить систему на ряд частей, каждая из которых находится в состоянии равновесия. Тогда можно ввести энтропию каждой из этих частей и по определению считать энтропию всей системы равной сумме энтропий всех частей.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ГЛАВА I. ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ
- 2. ИДЕАЛЬНЫЕ ГАЗЫ
- ГЛАВА II. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 3. ФОРМУЛИРОВКА ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 4. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К СИСТЕМАМ, СОСТОЯНИЕ КОТОРЫХ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 5. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА К ГАЗАМ
- 6. АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В ГАЗАХ
- ГЛАВА III. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 7. ФОРМУЛИРОВКА ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ
- 8. ЦИКЛ КАРНО
- 9. АБСОЛЮТНАЯ ТЕРМОДИНАМИЧЕСКАЯ ТЕМПЕРАТУРА
- 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА IV. ЭНТРОПИЯ
- 11. НЕКОТОРЫЕ СВОЙСТВА ЦИКЛОВ
- 12. ЭНТРОПИЯ
- 18. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ЭНТРОПИИ
- 14. ЭНТРОПИЯ СИСТЕМЫ, СОСТОЯНИЕ КОТОРОЙ МОЖЕТ БЫТЬ ИЗОБРАЖЕНО НА ДИАГРАММЕ (V, p)
- 15. УРАВНЕНИЕ КЛАПЕЙРОНА
- 16. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- ГЛАВА V. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
- 18. ТЕРМОДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 19. ПРАВИЛО ФАЗ
- 20. ТЕРМОДИНАМИКА ОБРАТИМОГО ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА
- ГЛАВА VI. РЕАКЦИИ В ГАЗОВОЙ ФАЗЕ
- 21. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗАХ
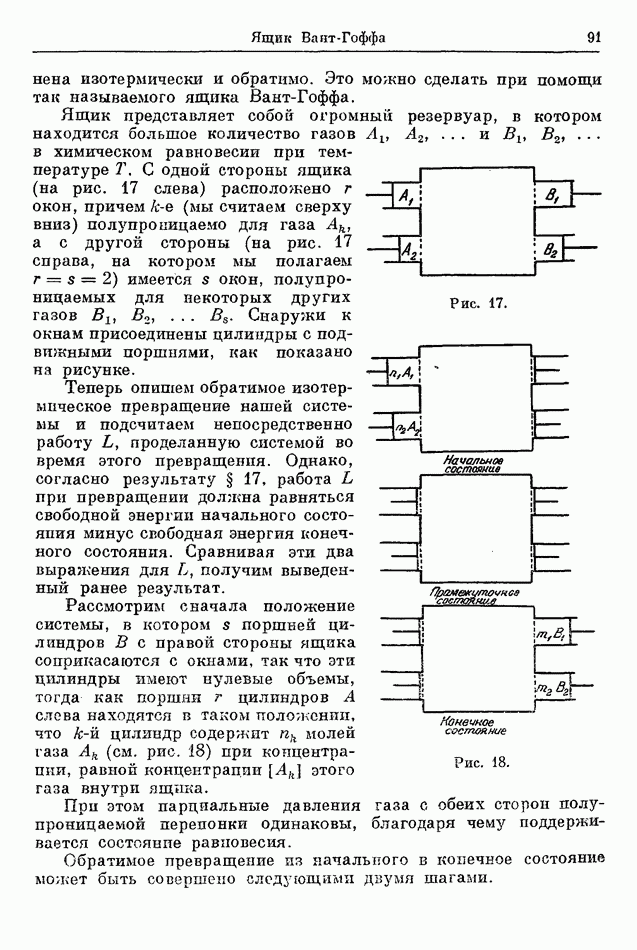
- 22. ЯЩИК ВАНТ-ГОФФА
- 23. ДРУГОЕ ДОКАЗАТЕЛЬСТВО УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ
- 24. ОБСУЖДЕНИЕ УРАВНЕНИЯ ГАЗОВОГО РАВНОВЕСИЯ. ПРИНЦИП ЛЕ ШАТЕЛЬЕ
- ГЛАВА VII. ТЕРМОДИНАМИКА СЛАБЫХ РАСТВОРОВ
- 28. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 27. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- 28. РАСПРЕДЕЛЕНИЕ РАСТВОРЕННОГО ВЕЩЕСТВА МЕЖДУ ДВУМЯ ФАЗАМИ
- 29. ДАВЛЕНИЕ ПАРА, ТОЧКА КИПЕНИЯ И ТОЧКА ЗАМЕРЗАНИЯ РАСТВОРА
- ГЛАВА VIII. ПОСТОЯННАЯ В ЗАВИСИМОСТИ ЭНТРОПИИ ОТ ТЕМПЕРАТУРЫ
- 30. ТЕОРЕМА НЕРНСТА
- 31. ПРИМЕНЕНИЕ ТЕОРЕМЫ НЕРНСТА К ТВЕРДЫМ ТЕЛАМ
- 32. ЭНТРОПИЙНАЯ КОНСТАНТА ГАЗОВ
- 33. ТЕРМИЧЕСКАЯ ИОНИЗАЦИЯ ГАЗА. ТЕРМОИОННЫЙ ЭФФЕКТ