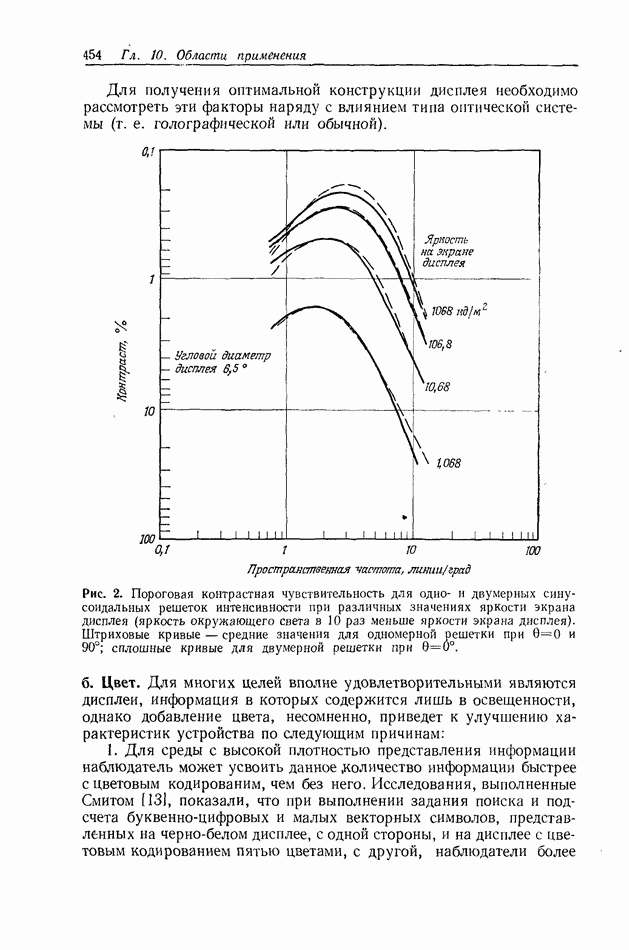
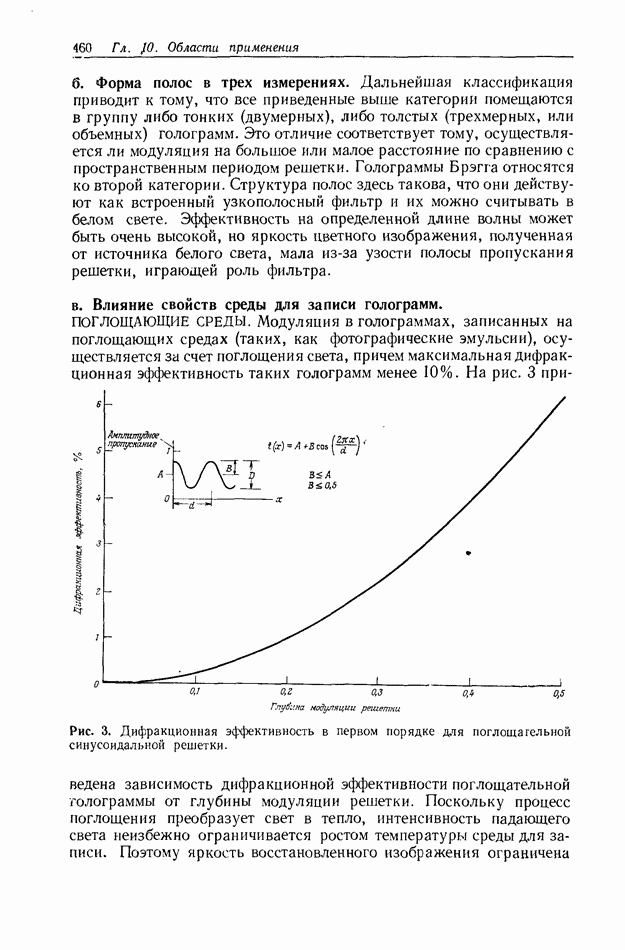
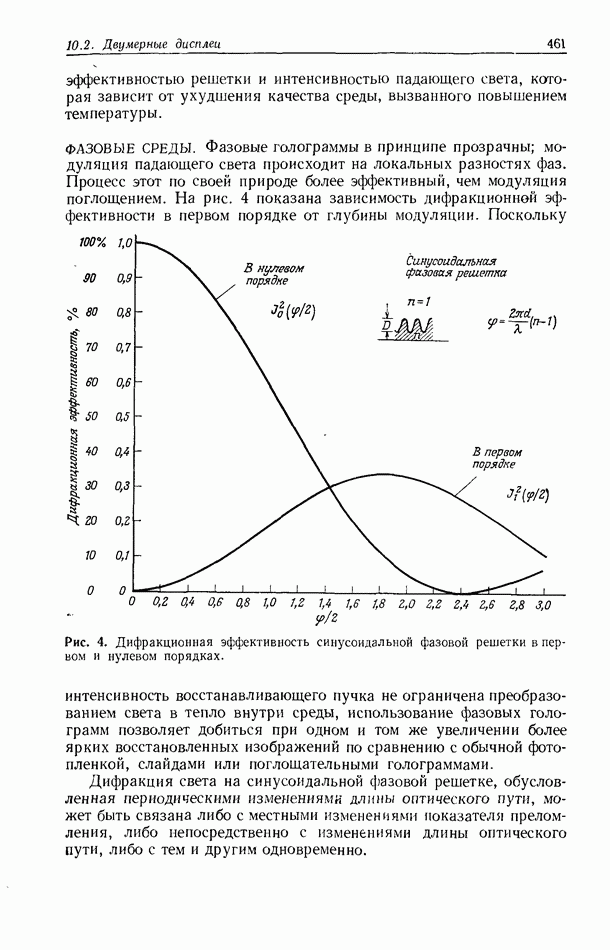
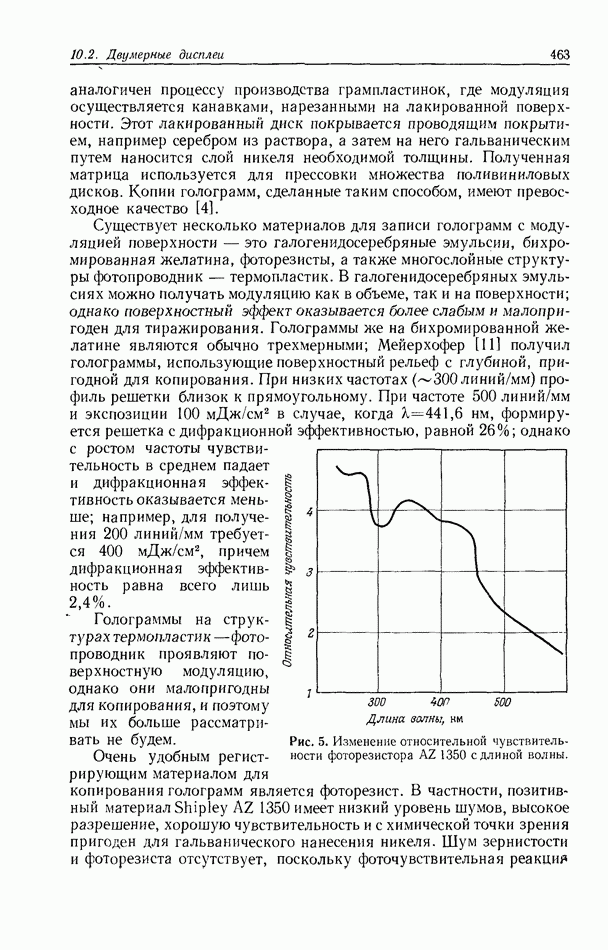
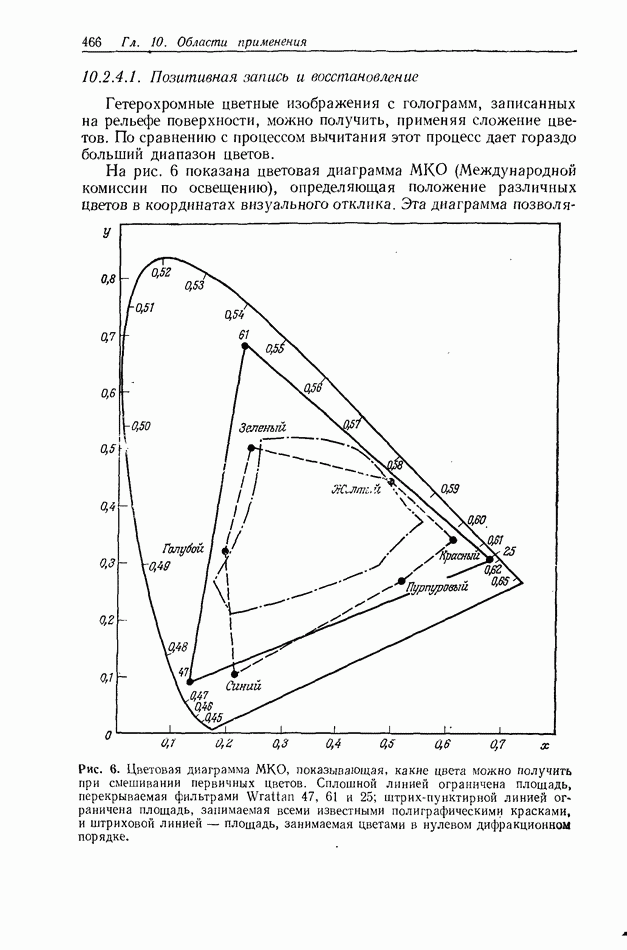
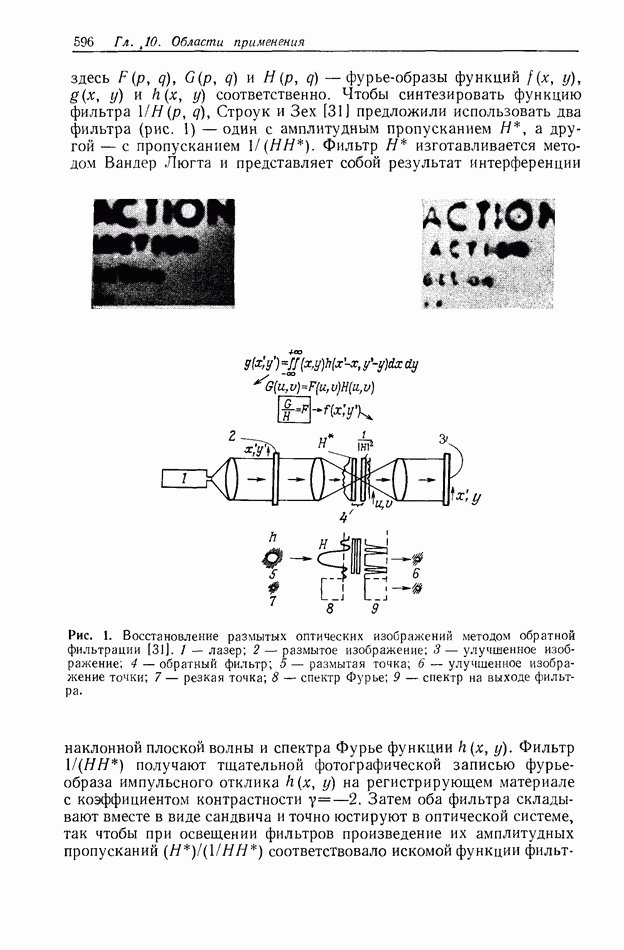
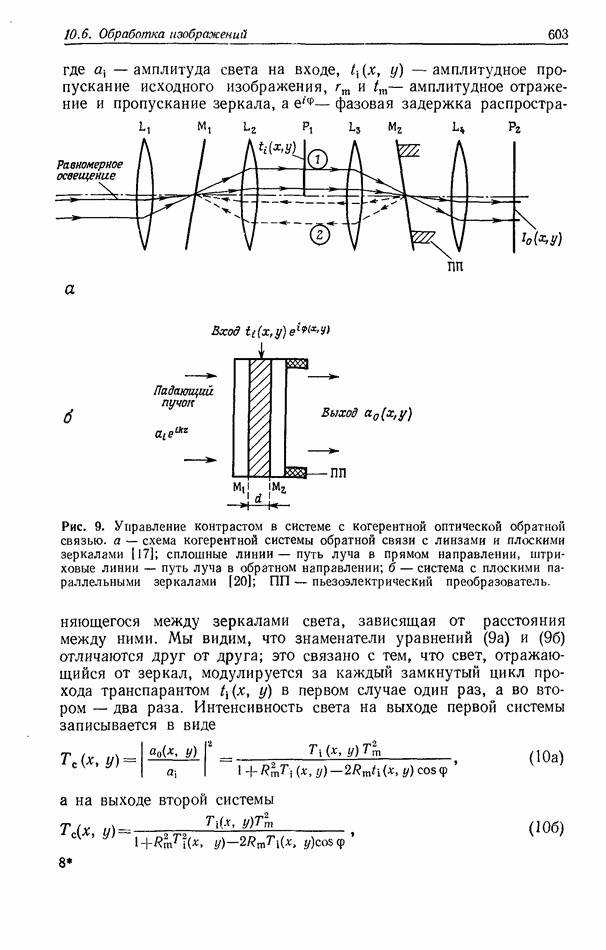
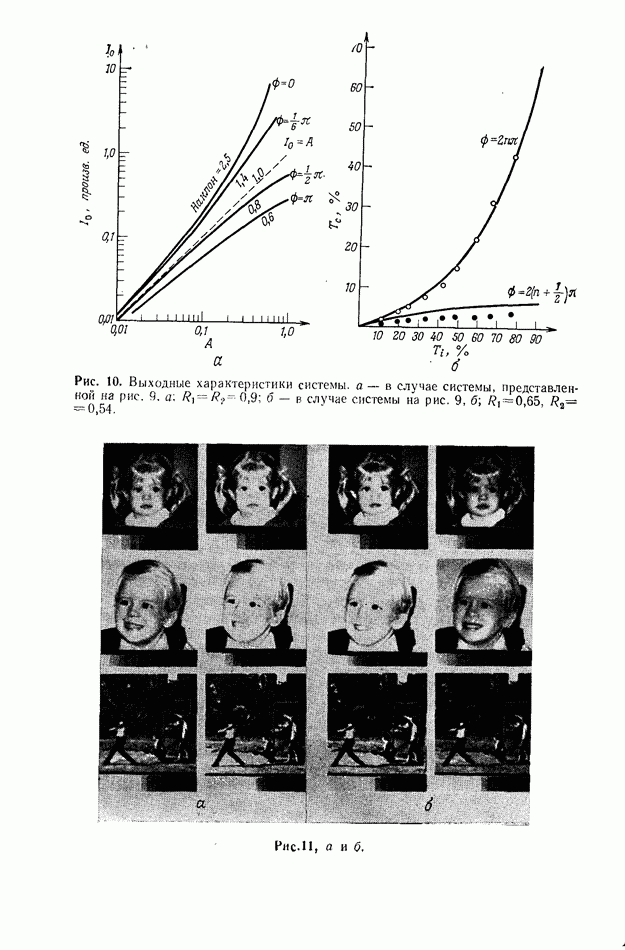
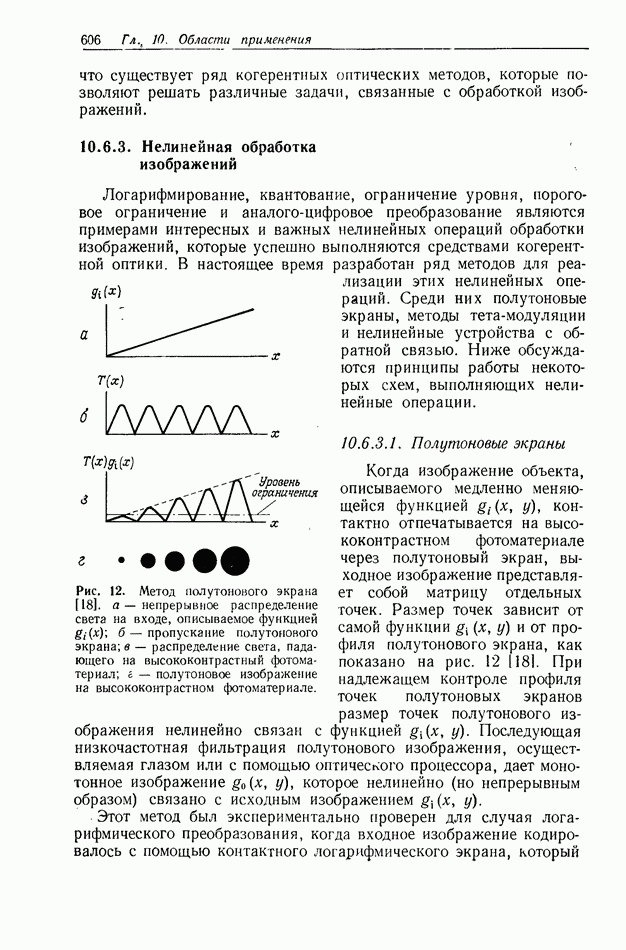
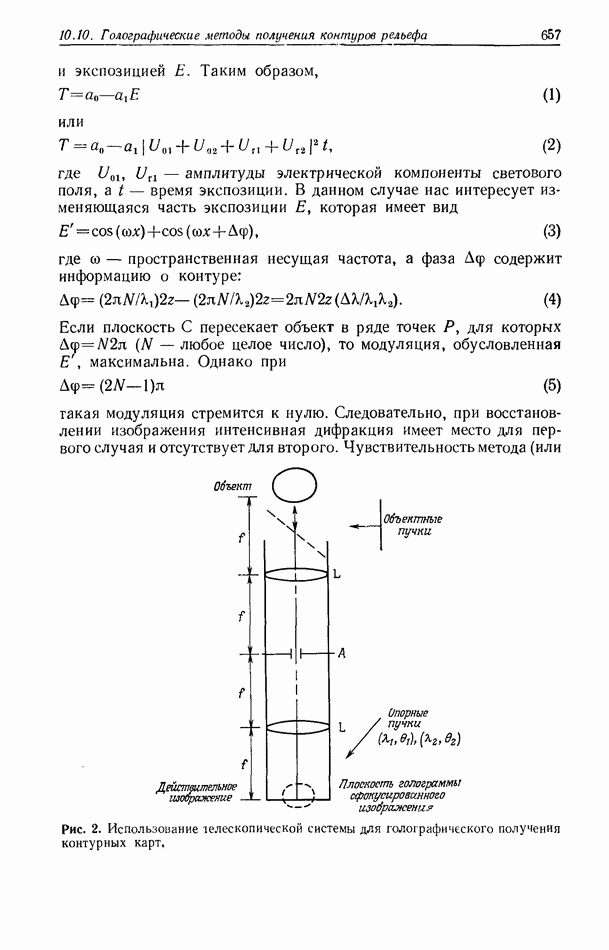
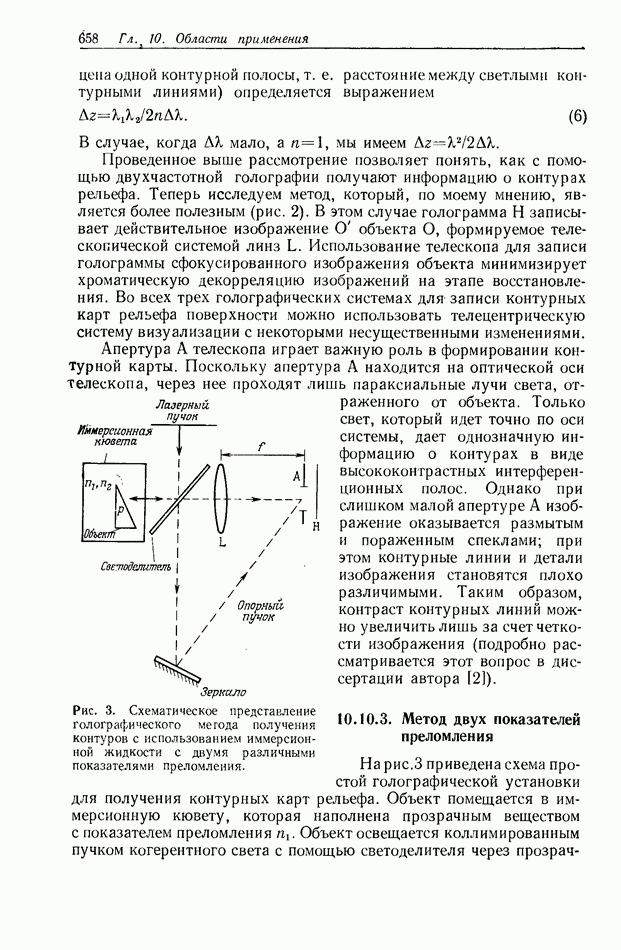
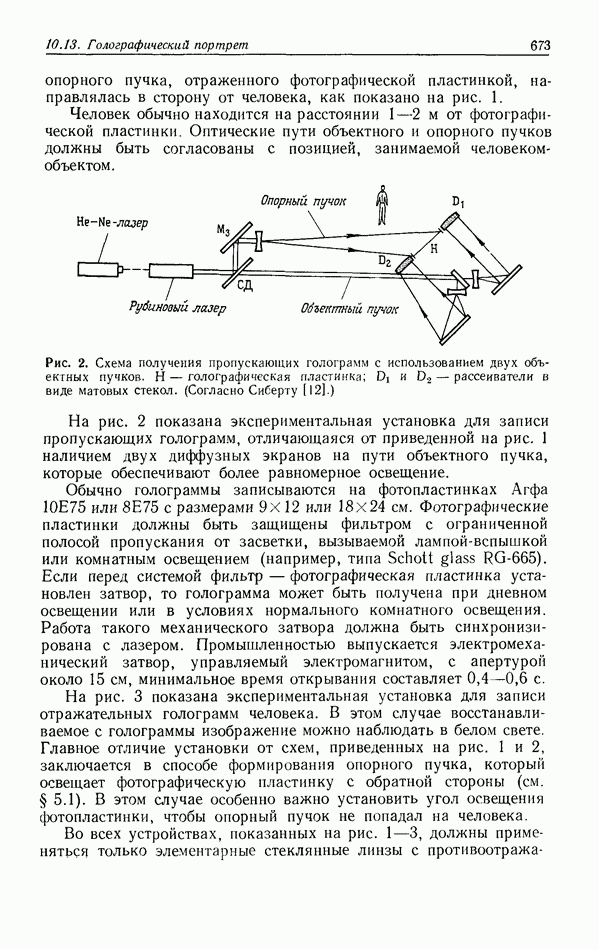
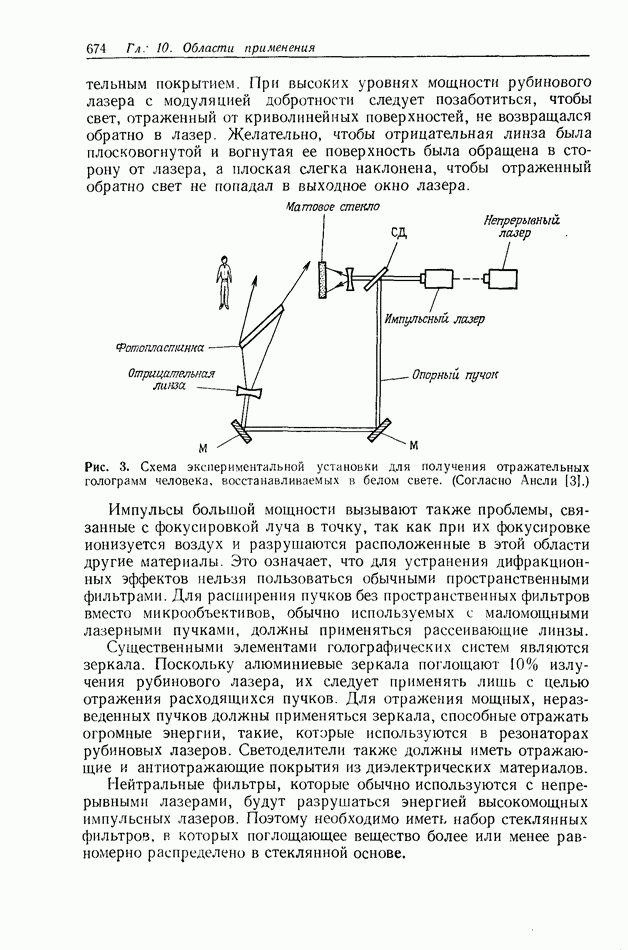
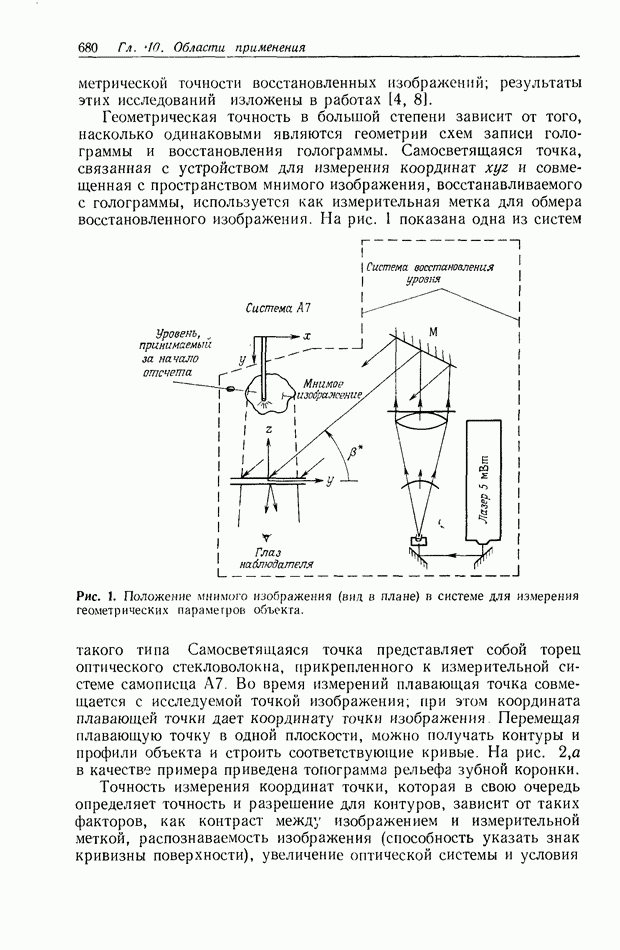
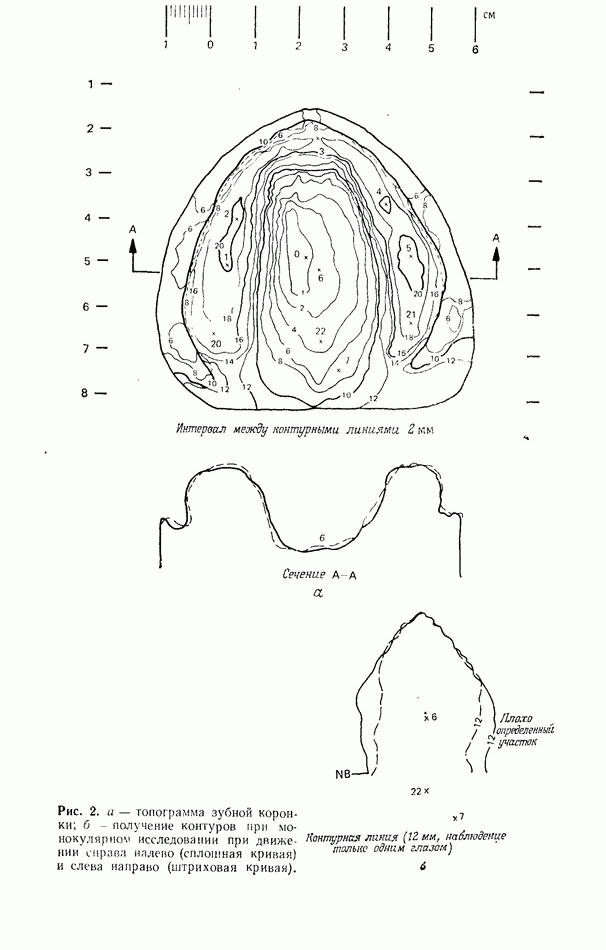
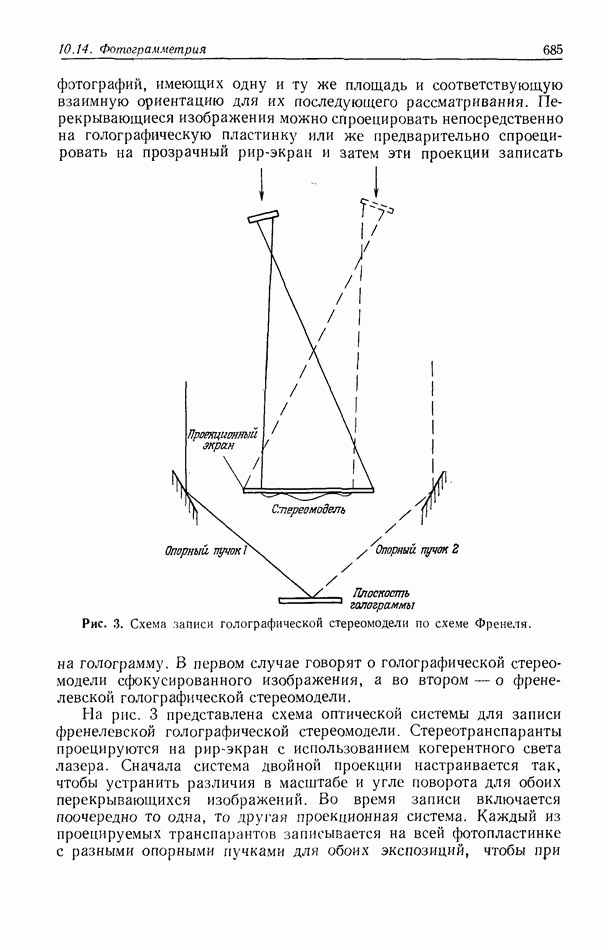
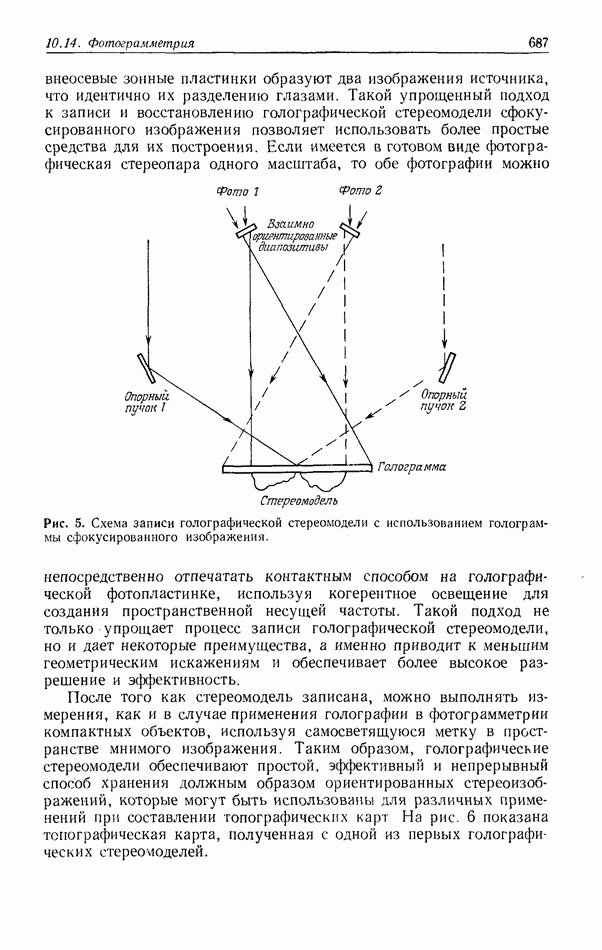
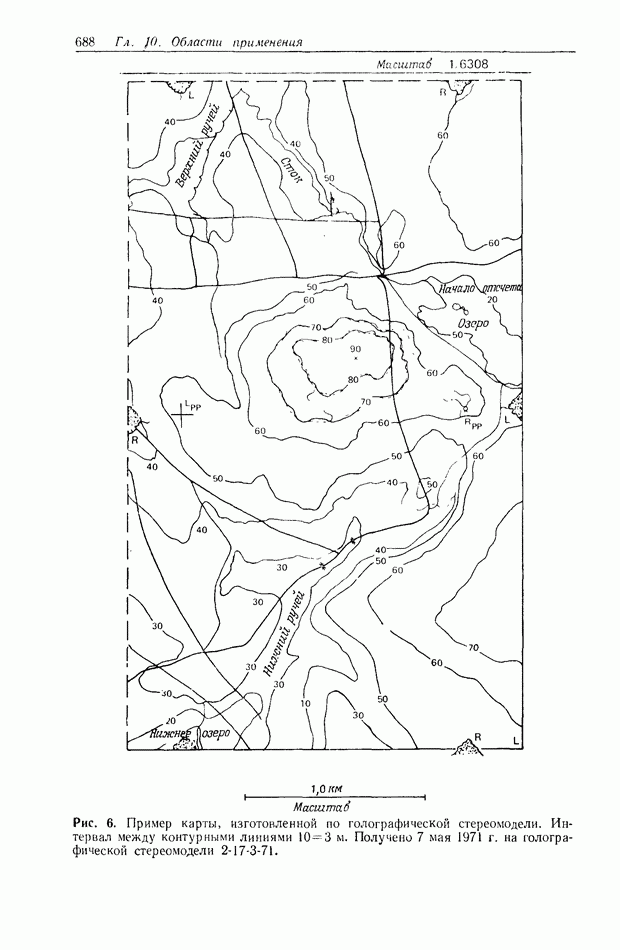
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.5.10. Коррелятор с преобразованием Меллина
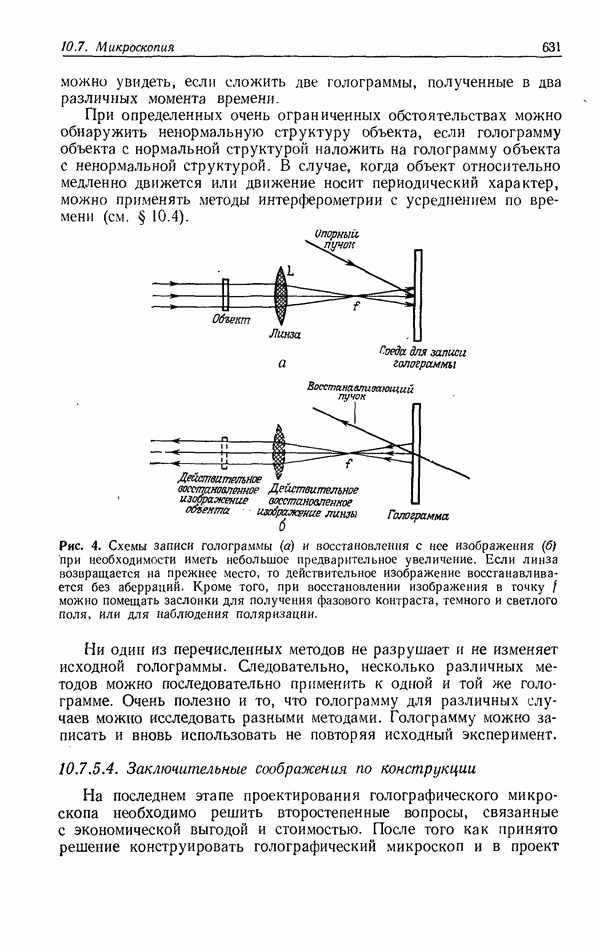
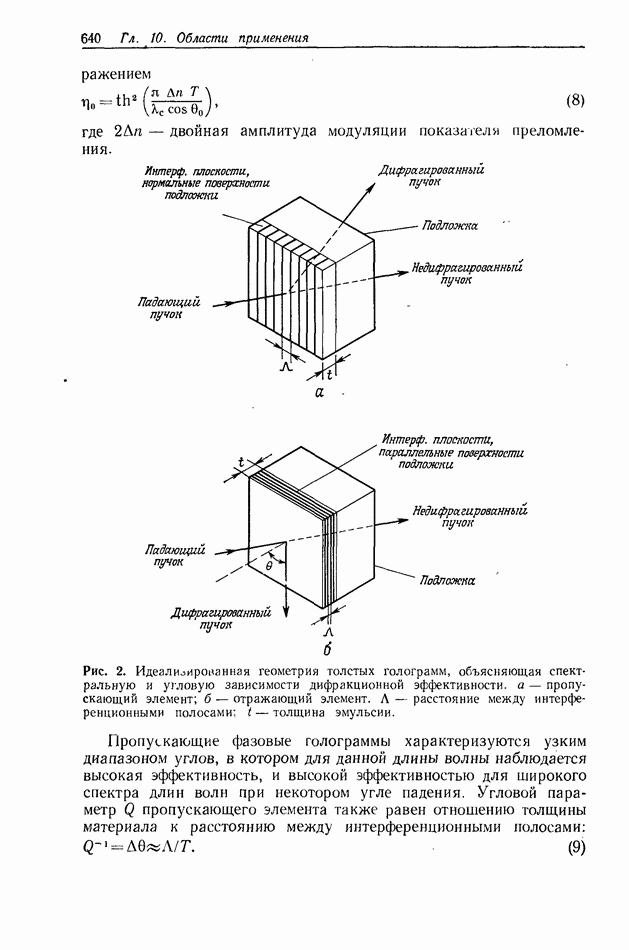
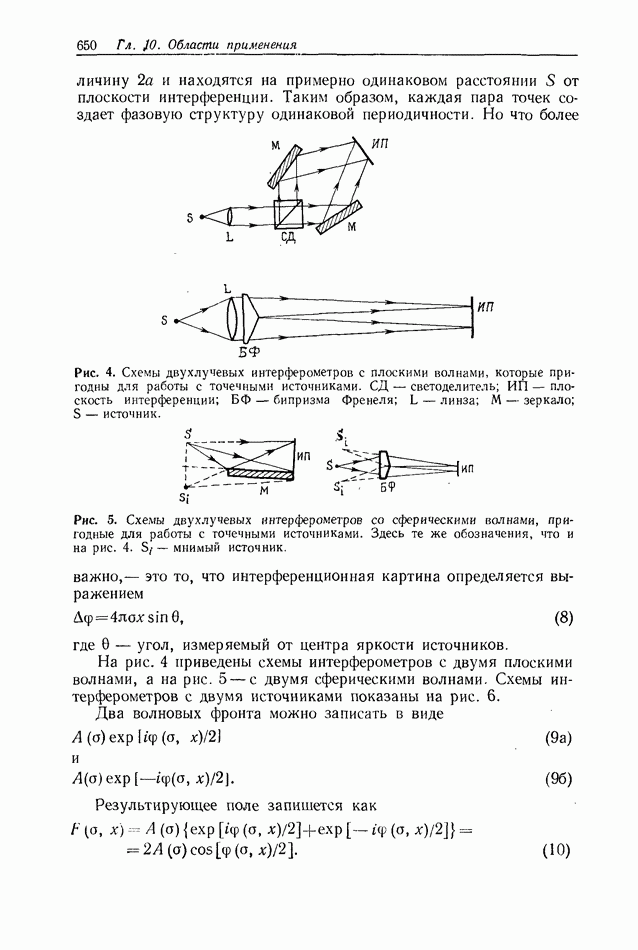
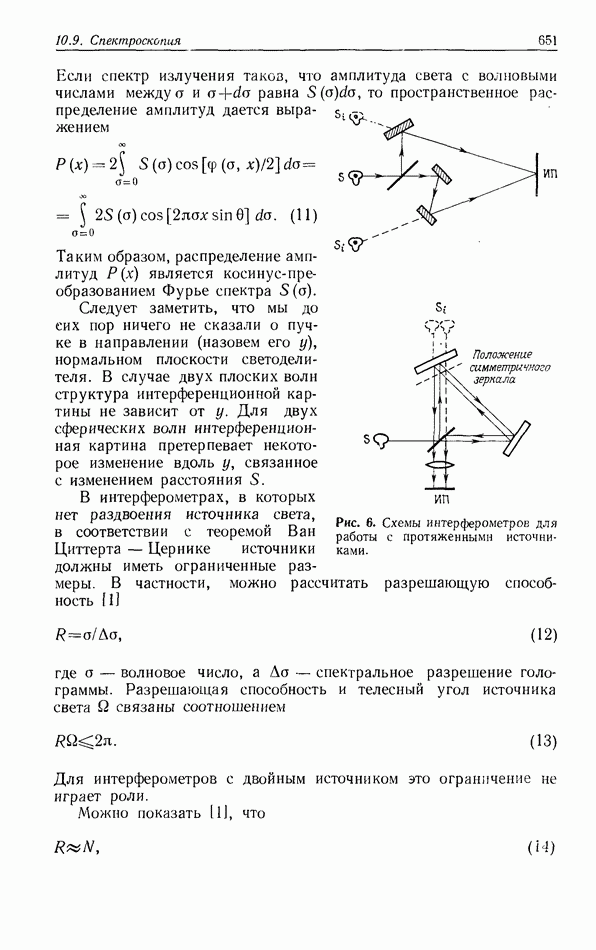
Обычный оптический процессор является пространственно-инвариантной системой, и, следовательно, характеристики всех оптических систем распознавания образов, основанных на использовании преобразования Фурье, станут ухудшаться, если масштаб входной и эталонной функций будет различным. В цифровых процессорах эта проблема, имеющая практическое значение, решается применением изощренных алгоритмов средств программирования; поэтому такие процессоры оказались значительно более пригодными, чем конкурирующие с ними оптические корреляторы, которые требуют точного согласования масштабов входной и эталонной функций во избежание уменьшения интенсивности корреляционного пика  или отношения сигнал/шум на выходе. Новый подход к решению этой проблемы оптическими средствами состоит в использовании пространственно-неинвариантного коррелятора, в котором осуществляется преобразование координат входных данных. Полученные в результате координатного преобразования данные затем подаются на вход в обычный пространственно-инвариантный коррелятор.
или отношения сигнал/шум на выходе. Новый подход к решению этой проблемы оптическими средствами состоит в использовании пространственно-неинвариантного коррелятора, в котором осуществляется преобразование координат входных данных. Полученные в результате координатного преобразования данные затем подаются на вход в обычный пространственно-инвариантный коррелятор.
В конкретной системе, используемой для получения инвариантного к изменению масштаба коррелятора, координаты входной функции  сначала изменяются по логарифмическому закону, а полученная функция
сначала изменяются по логарифмическому закону, а полученная функция  затем подается на вход обычного коррелятора. Фурье-образ функции
затем подается на вход обычного коррелятора. Фурье-образ функции  представляет собой преобразование Меллина функции
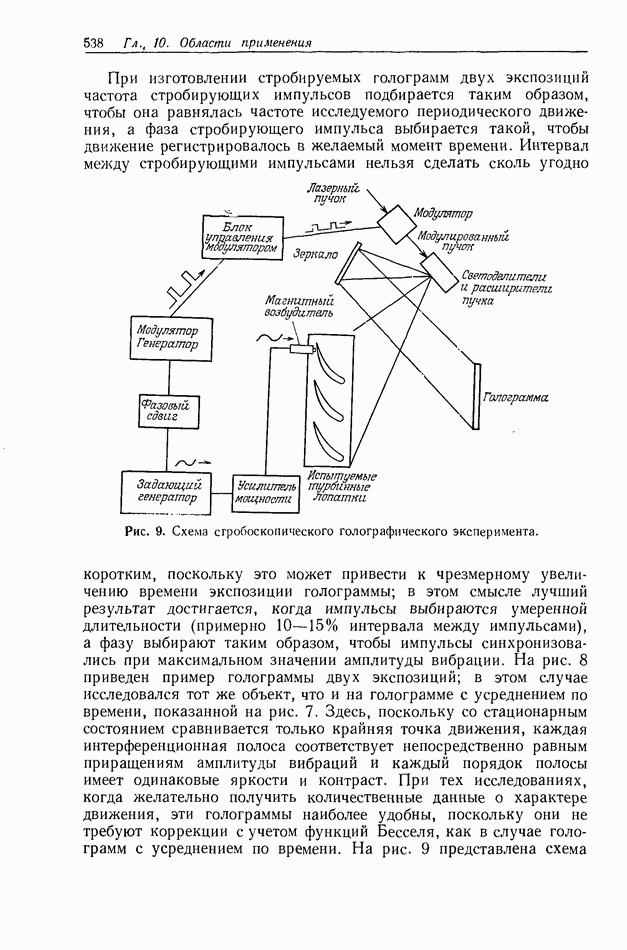
представляет собой преобразование Меллина функции  Требуемое для этого логарифмическое преобразование координат можно осуществить с помощью аналоговых логарифмических модулей, применяемых
Требуемое для этого логарифмическое преобразование координат можно осуществить с помощью аналоговых логарифмических модулей, применяемых
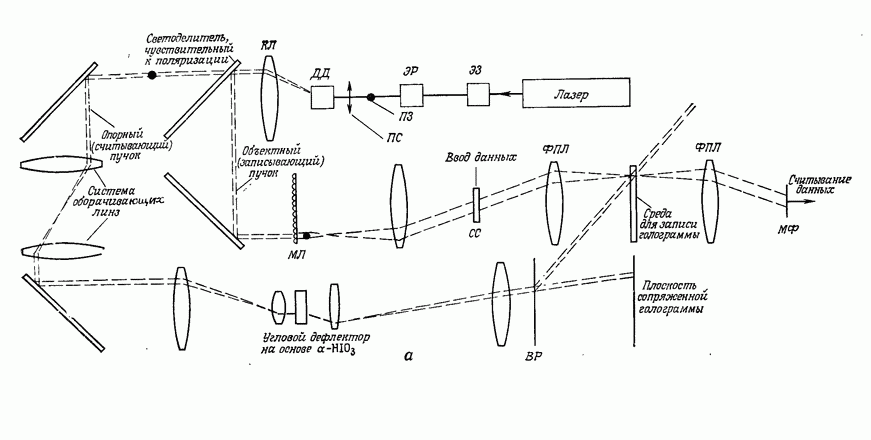
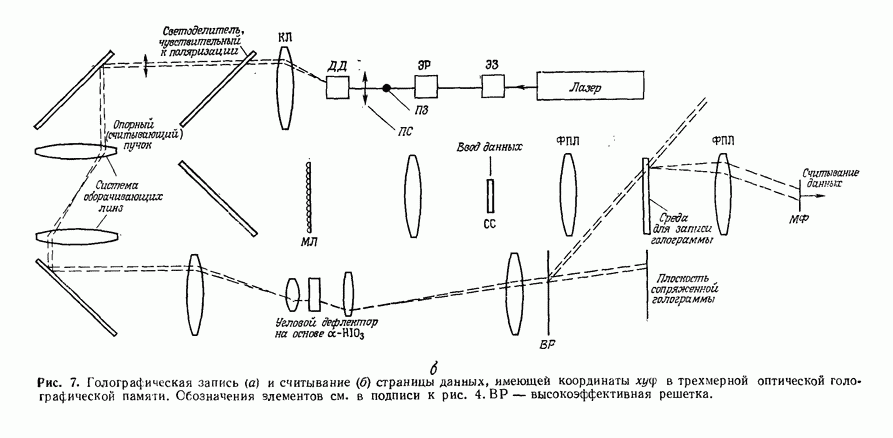
в системе отклонения входного устройства (пространственно-временного модулятора света или замкнутой телевизионной системы), или с помощью голограмм, синтезированных на ЭВМ. На рис. 8 приведена функциональная схема системы, используемой в рассматриваемом или подобном ему (см. разд. 10.5.11) простран-ственно-неинвариантном корреляторе.

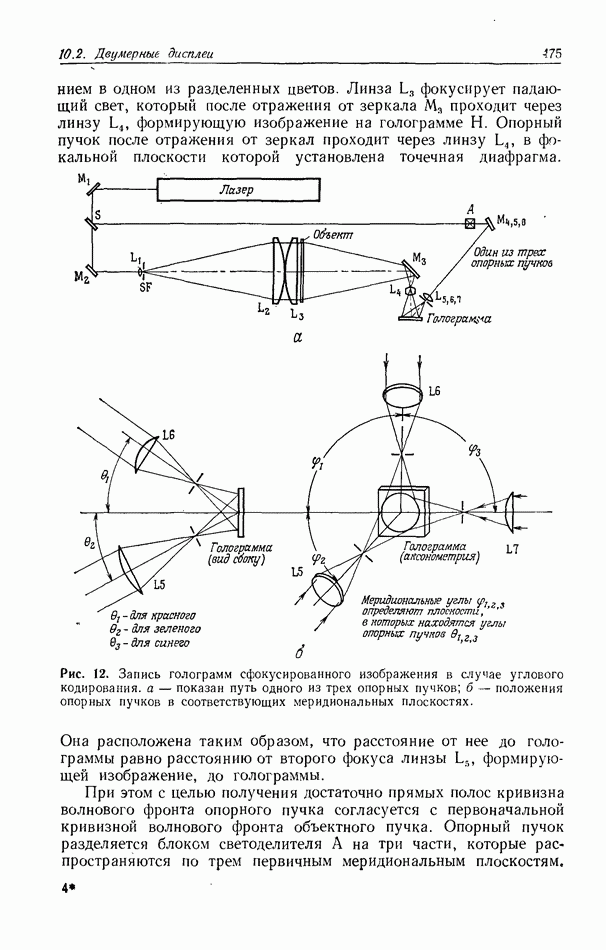
Рис. 8. Схема просгранственно-неинвариантного коррелятора.
Система состоит из обычного коррелятора, такого, как на рис. 1, но на входе этого коррелятора помещается устройство предварительного преобразования входных координат. Для получения инвариантного к изменению масштаба преобразования Меллина необходимо реализовать преобразование координат вида  Чтобы математически описать работу данного коррелятора, применим подход, изложенный в разд. 10.5.2, причем для простоты будем рассматривать одномерные функции. Будем учитывать лишь корреляционный член, который представляет интерес. Запишем во входной плоскости
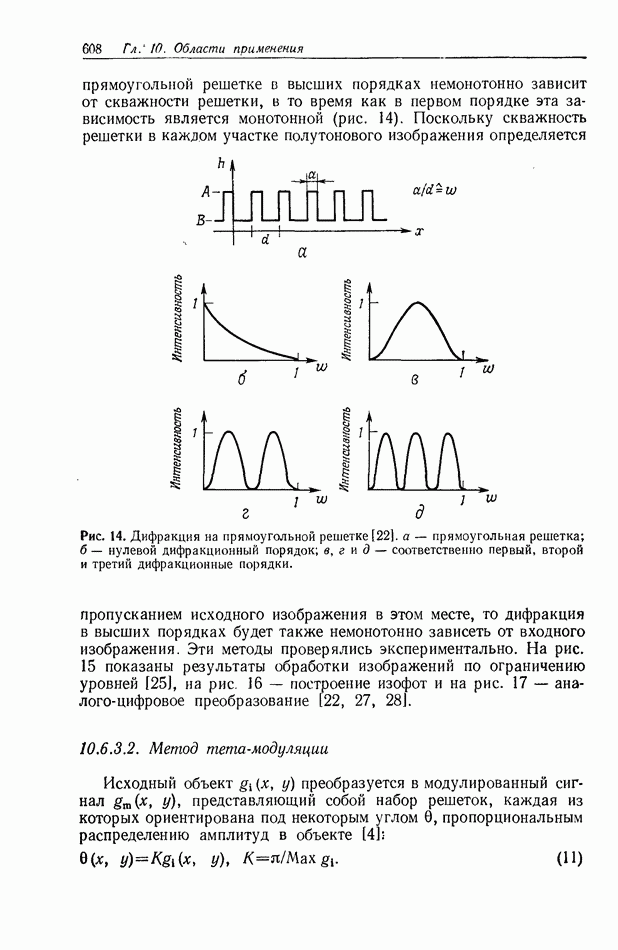
Чтобы математически описать работу данного коррелятора, применим подход, изложенный в разд. 10.5.2, причем для простоты будем рассматривать одномерные функции. Будем учитывать лишь корреляционный член, который представляет интерес. Запишем во входной плоскости  эталонную функцию
эталонную функцию  Распределение комплексных амплитуд в плоскости
Распределение комплексных амплитуд в плоскости  представляет собой фурье-образ функции
представляет собой фурье-образ функции  или преобразование Меллина Мн
или преобразование Меллина Мн  этой функции. После регистрации в плоскости
этой функции. После регистрации в плоскости  картины интерференции полученного распределения и наклонной опорной волны интересующий нас член результирующего амплитудного пропускания запишется в виде
картины интерференции полученного распределения и наклонной опорной волны интересующий нас член результирующего амплитудного пропускания запишется в виде

Установим теперь полученный фильтр в плоскости  и подадим на вход функцию
и подадим на вход функцию  именно измененную по масштабу копию функции
именно измененную по масштабу копию функции  с масштабным коэффициентом
с масштабным коэффициентом  Тогда в плоскости
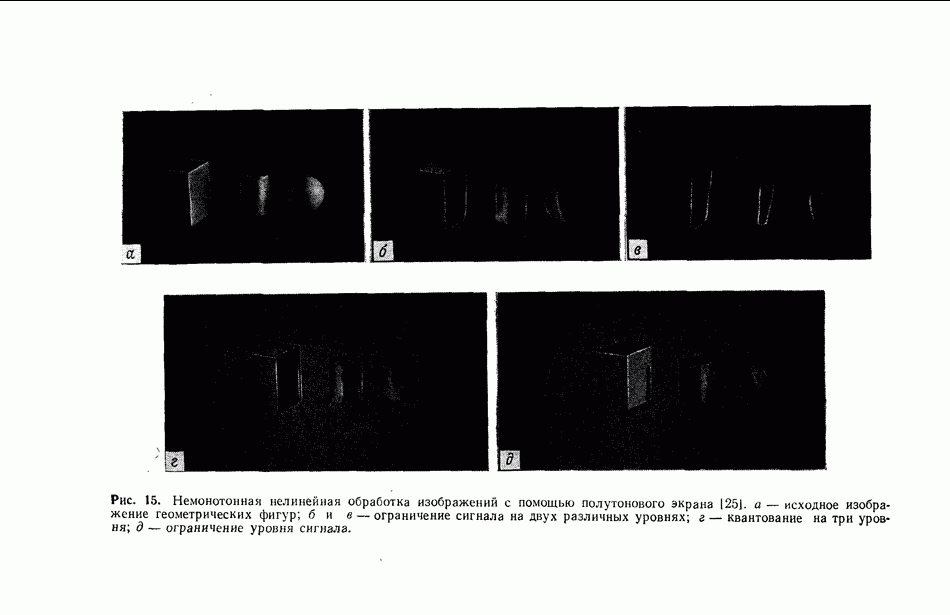
Тогда в плоскости  мы запишем логарифмически преобразованную копию этой функции в виде
мы запишем логарифмически преобразованную копию этой функции в виде  При этом распределение комплексных амплитуд света в плоскости
При этом распределение комплексных амплитуд света в плоскости  будет равно
будет равно  Преобразования Меллина
Преобразования Меллина  связаны между собой соотношением
связаны между собой соотношением

из которого следует, что  или, что то же самое, преобразование Меллина инвариантно к изменению масштаба
или, что то же самое, преобразование Меллина инвариантно к изменению масштаба
преобразуемой функции. Таким образом, непосредственно за плоскостью  распределение комплексных амплитуд запишется теперь в виде
распределение комплексных амплитуд запишется теперь в виде

Линза  формирует в плоскости
формирует в плоскости  фурье-образ этого распределения, и на выходе мы имеем следующее распределение комплексных амплитуд:
фурье-образ этого распределения, и на выходе мы имеем следующее распределение комплексных амплитуд:

Из этого выражения следует, что распределение комплексных амплитуд в функции взаимной корреляции двух функций, отличающихся друг от друга масштабом, представляет собой их автокорреляционную функцию; таким образом, не должно быть потерь интенсивности  пика корреляции и отношение сигнал/шум не должно уменьшаться, т. е. коррелятор с преобразованием Меллина действительно оказывается инвариантным к изменению масштаба. Из выражения (37) также следует, что положение пика корреляции смещено относительно обычного положения
пика корреляции и отношение сигнал/шум не должно уменьшаться, т. е. коррелятор с преобразованием Меллина действительно оказывается инвариантным к изменению масштаба. Из выражения (37) также следует, что положение пика корреляции смещено относительно обычного положения  на величину
на величину  и, следовательно, по положению корреляционного пика можно найти разницу в масштабах входной и эталонной функций. Этот анализ непосредственно обобщается на двумерный случай, в котором горизонтальное и вертикальное смещения корреляционного пика относительно его нормального положения оказывается пропорциональным разнице в масштабах входной и эталонной функций соответственно в горизонтальном и вертикальном направлениях.
и, следовательно, по положению корреляционного пика можно найти разницу в масштабах входной и эталонной функций. Этот анализ непосредственно обобщается на двумерный случай, в котором горизонтальное и вертикальное смещения корреляционного пика относительно его нормального положения оказывается пропорциональным разнице в масштабах входной и эталонной функций соответственно в горизонтальном и вертикальном направлениях.
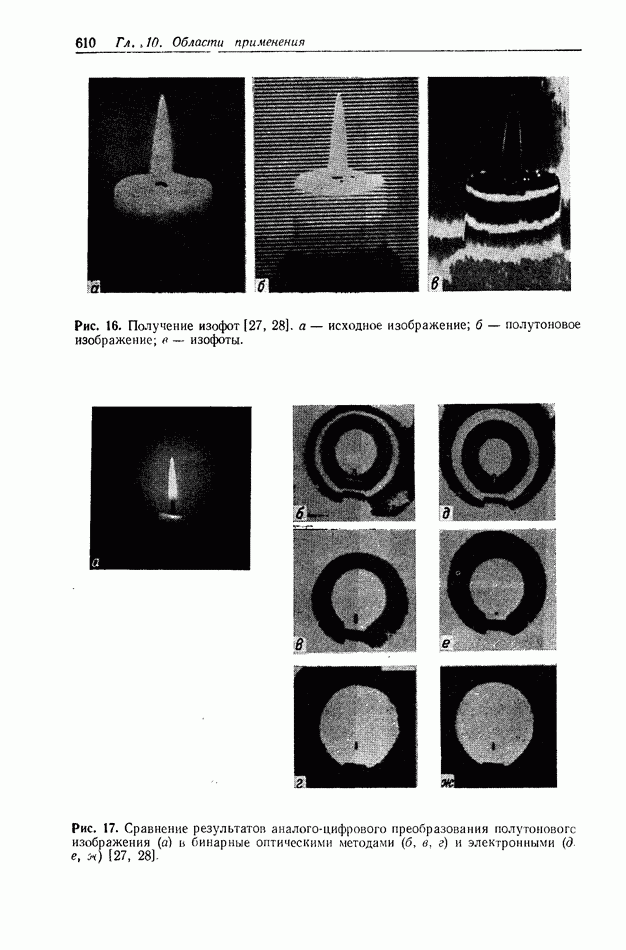
Особенно интересно применение рассматриваемого инвариантного к изменению масштаба коррелятора при обработке сигналов в доплеровских радиолокаторах. Поскольку доплеровский сдвиг по частоте эквивалентен изменению масштаба входного сигнала, а положение корреляционного пика на выходе пропорционально величине этого изменения масштаба и, следовательно, величине доплеровского сдвига между входным и эталонным сигналами, то становится очевидным новый подход к обработке доплеровских сигналов, основанный на использовании системы, реализующей преобразование Меллина. Чтобы проиллюстрировать реализацию этого подхода, а также возможности управления форматом входных данных, которое жизненно необходимо при решении задачи оптического распознавания образов, мы рассмотрим схему еще одного нового коррелятора, а именно многоканального одномерного коррелятора с одновременным преобразованием (рис. 9, а). В левой части входной плоскости  на
на  строках записан один и тот же эталонный сигнал
строках записан один и тот же эталонный сигнал  с масштабом по оси
с масштабом по оси  измененным по логарифмическому закону, а в правой части — преобразованные таким же способом
измененным по логарифмическому закону, а в правой части — преобразованные таким же способом  реализаций принятого доплеровского сигнала
реализаций принятого доплеровского сигнала  которые после координатного преобразования имеют вид
которые после координатного преобразования имеют вид  Предположим, что физическая длина каждого
Предположим, что физическая длина каждого
сигнала на входе равна  а расстояние между центрами двух записанных растров равно
а расстояние между центрами двух записанных растров равно 
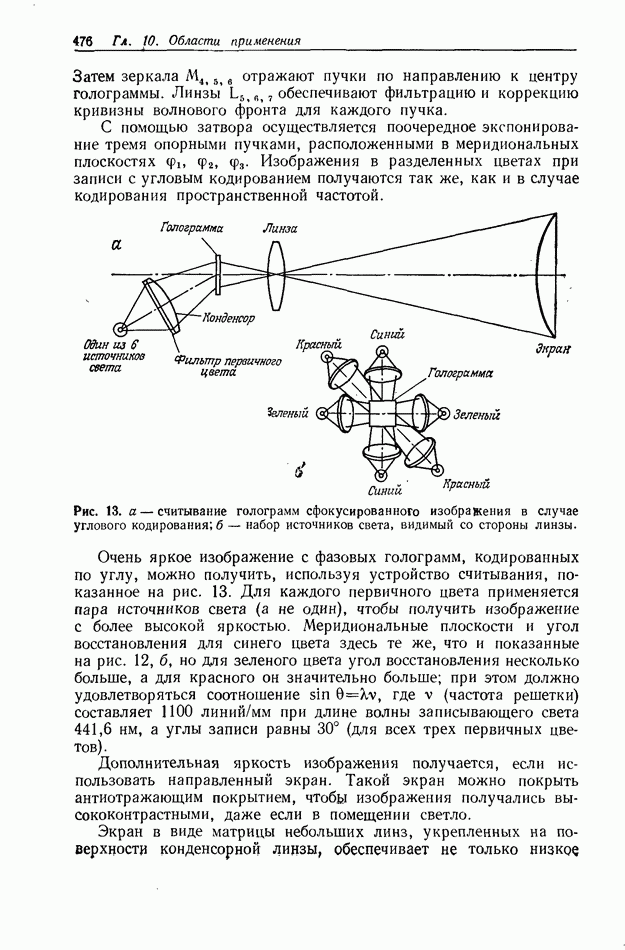
Рис. 9. (см. скан) Оптический процессор доплеровских сигналов, использую  преобразование Мелдина. а — схема одномерного коррелятора с одновременным преобразованием;
преобразование Мелдина. а — схема одномерного коррелятора с одновременным преобразованием;  -картина корреляции доплеровских сигналов на выходе [10].
-картина корреляции доплеровских сигналов на выходе [10].
Тогда мы можем написать следующее выражение для амплитудного пропускания в плоскости 

Регистрируемое в плоскости  распределение амплитуд формируется системой из цилиндрической
распределение амплитуд формируется системой из цилиндрической  и сферической
и сферической  линз
линз
и представляет собой одномерное преобразование Фурье пропускания  отображаемое в горизонтальном направлении. Таким образом, амплитудное пропускание записанного в плоскости
отображаемое в горизонтальном направлении. Таким образом, амплитудное пропускание записанного в плоскости  фильтра запишется в виде
фильтра запишется в виде

Распределение комплексных амплитуд в плоскости  представляет собой одномерный фурье-образ выражения (39) и имеет вид
представляет собой одномерный фурье-образ выражения (39) и имеет вид

откуда следует, что распределение интенсивности света в выходной плоскости состоит из  ярких пятен, расположенных на
ярких пятен, расположенных на  строках. Интенсивность в максимуме каждого пятна пропорциональна пику автокорреляционной функции эталонного сигнала (таким образом, отсутствуют какие-либо потери отношения сигнал/шум или интенсивности
строках. Интенсивность в максимуме каждого пятна пропорциональна пику автокорреляционной функции эталонного сигнала (таким образом, отсутствуют какие-либо потери отношения сигнал/шум или интенсивности  а смещение каждого пятна по строке пропорционально масштабному коэффициенту а (и, следовательно, величине доплеровского сдвига по частоте) между входным и эталонным сигналом на рассматриваемой строке. На рис. 9, б приведена фотография выходной плоскости корреляции для случая
а смещение каждого пятна по строке пропорционально масштабному коэффициенту а (и, следовательно, величине доплеровского сдвига по частоте) между входным и эталонным сигналом на рассматриваемой строке. На рис. 9, б приведена фотография выходной плоскости корреляции для случая  сигналов. В данном случае частота сигнала на верхней строке отличалась от частоты сигнала, записанного на нижней строке, на 100% и, следовательно, горизонтальные смещения корреляционных пиков на рис. 9, б вычерчивают часть логарифмической кривой вида
сигналов. В данном случае частота сигнала на верхней строке отличалась от частоты сигнала, записанного на нижней строке, на 100% и, следовательно, горизонтальные смещения корреляционных пиков на рис. 9, б вычерчивают часть логарифмической кривой вида  а при изменении величины а от
а при изменении величины а от  до 1.
до 1.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
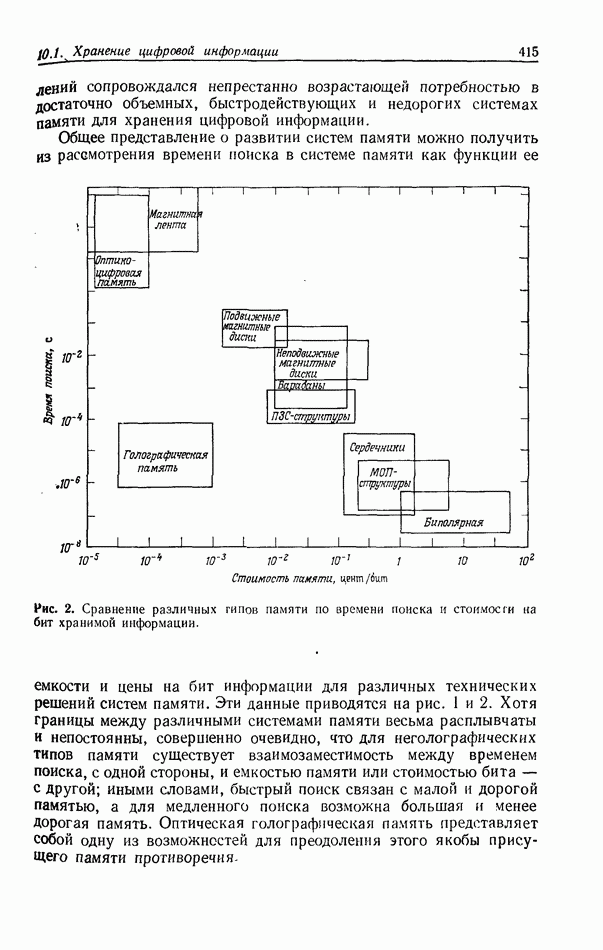
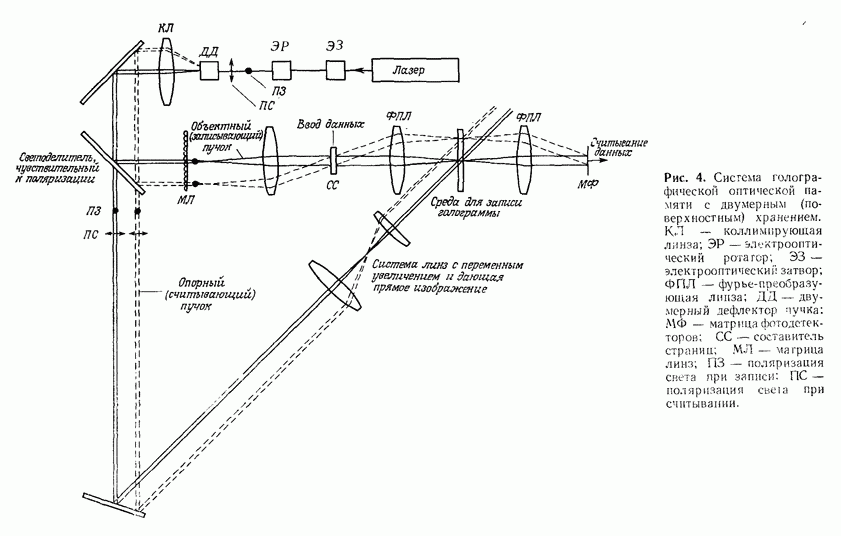
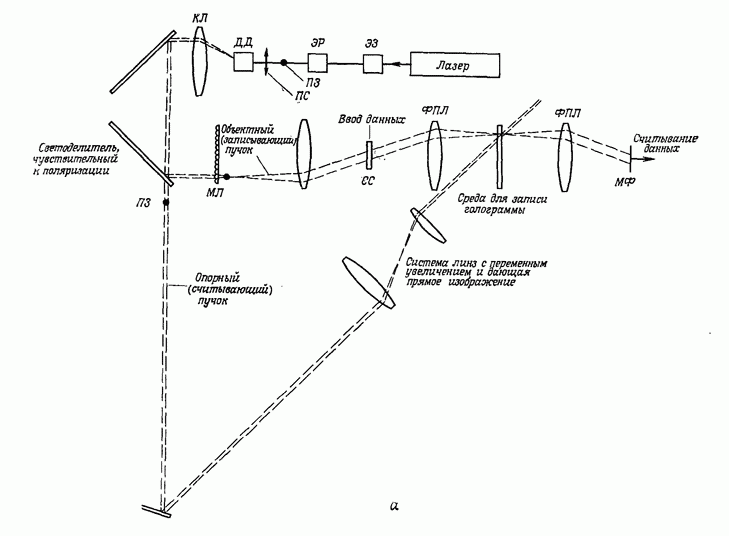
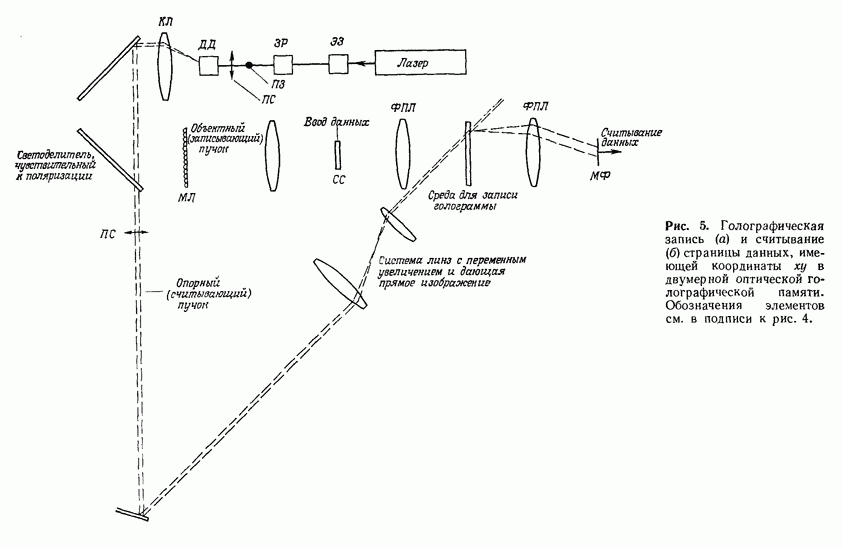
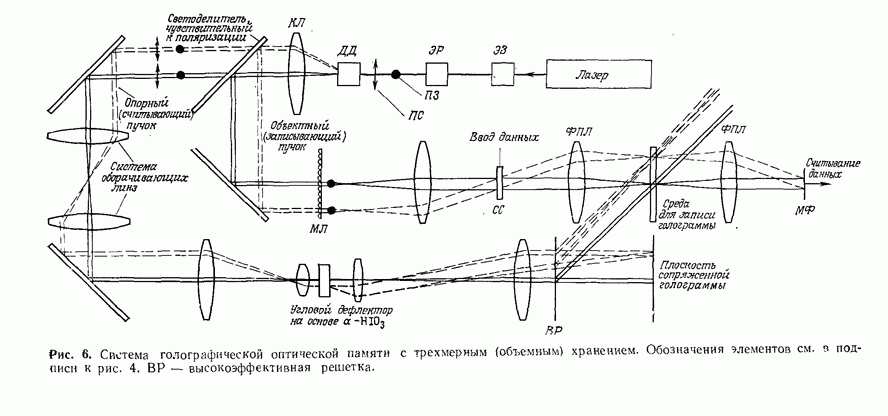
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
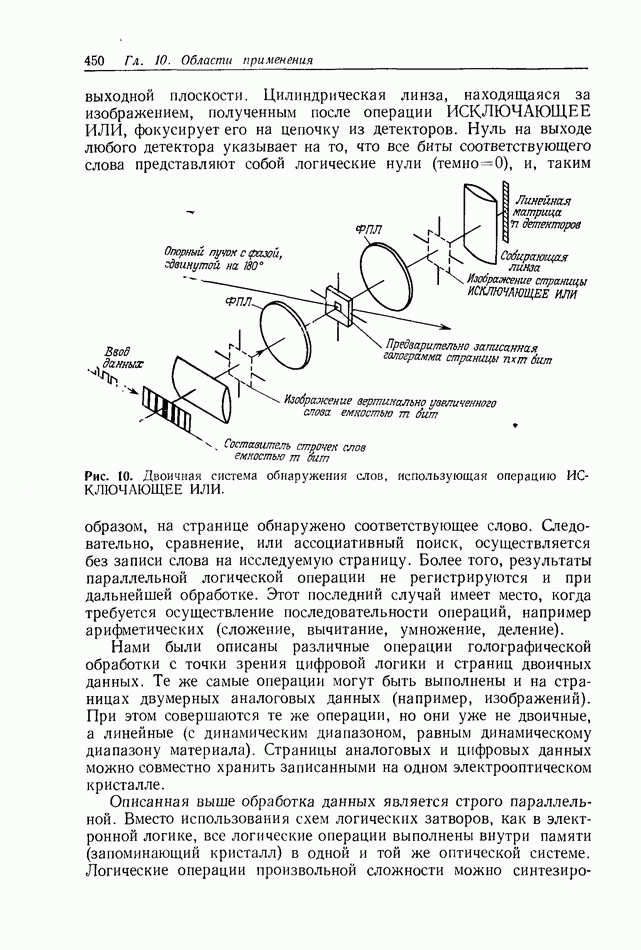
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
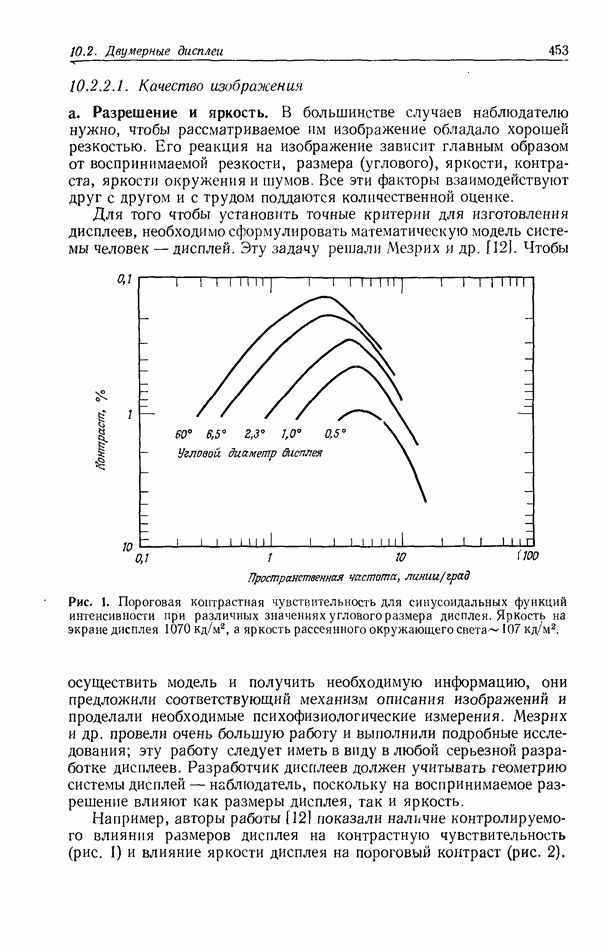
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
- 10.9. СПЕКТРОСКОПИЯ
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
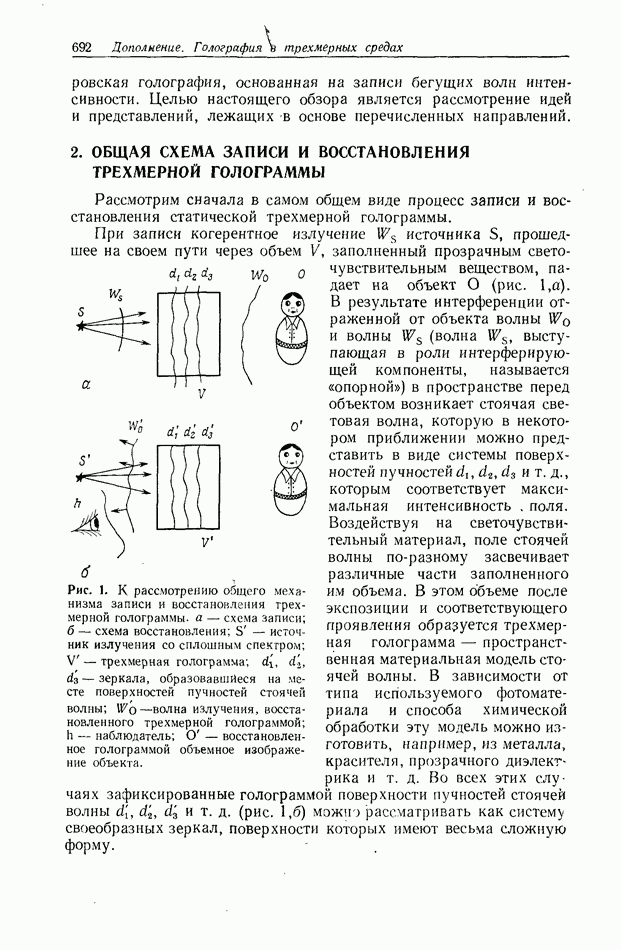
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
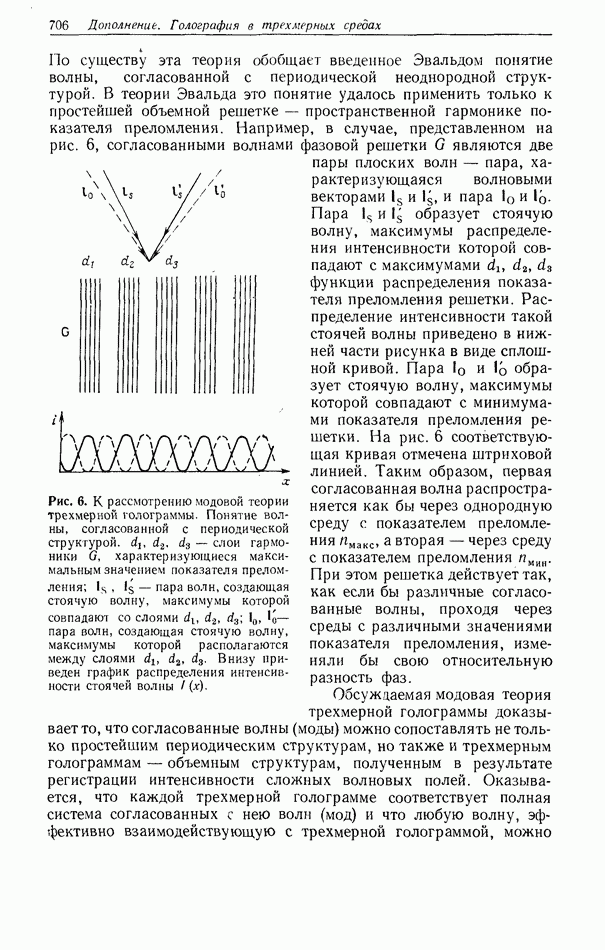
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
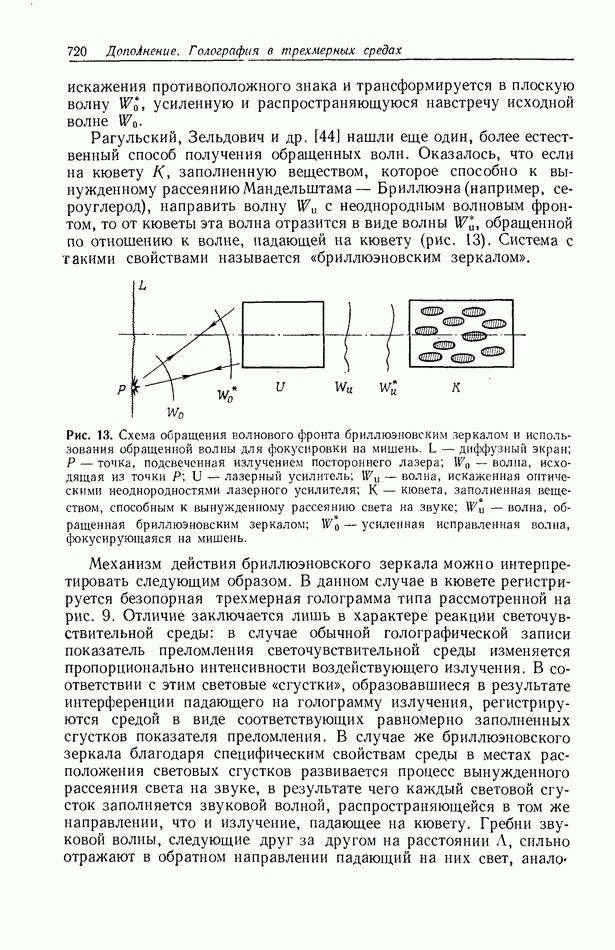
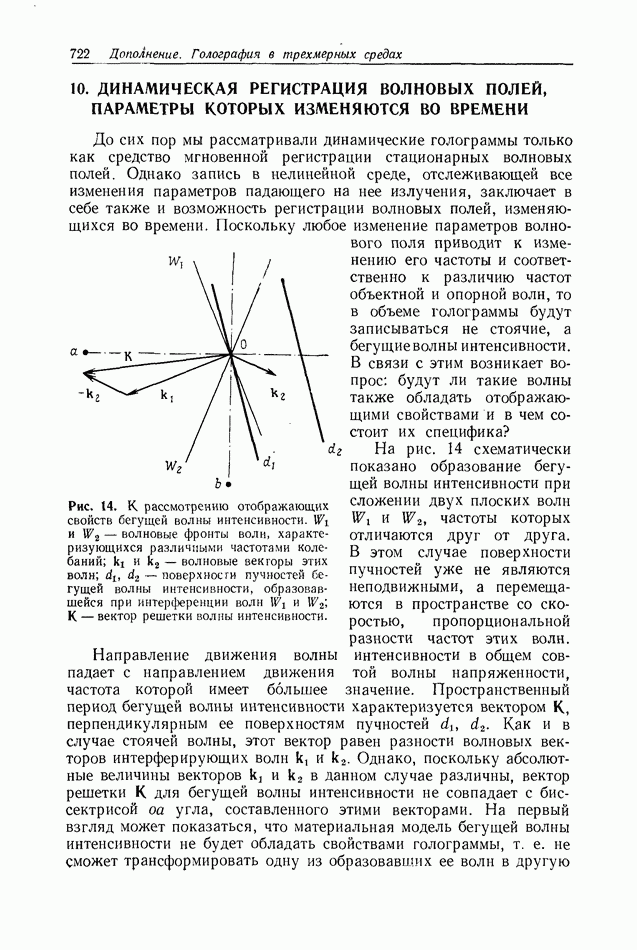
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ