| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
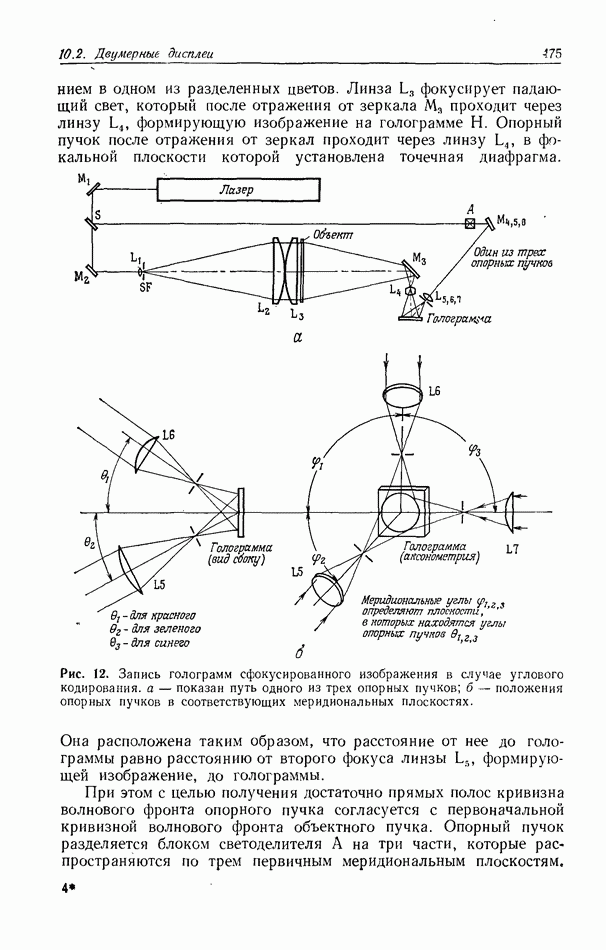
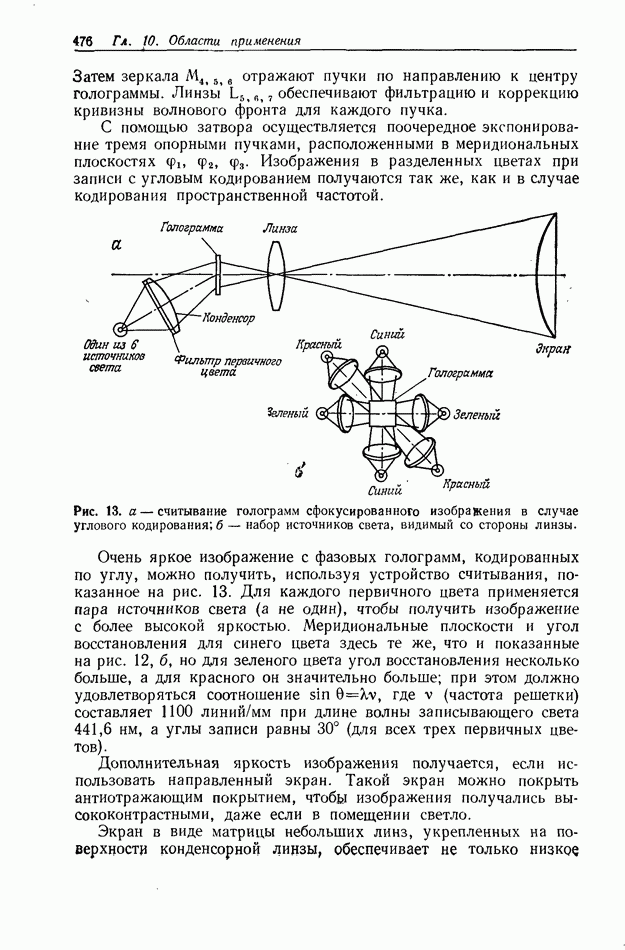
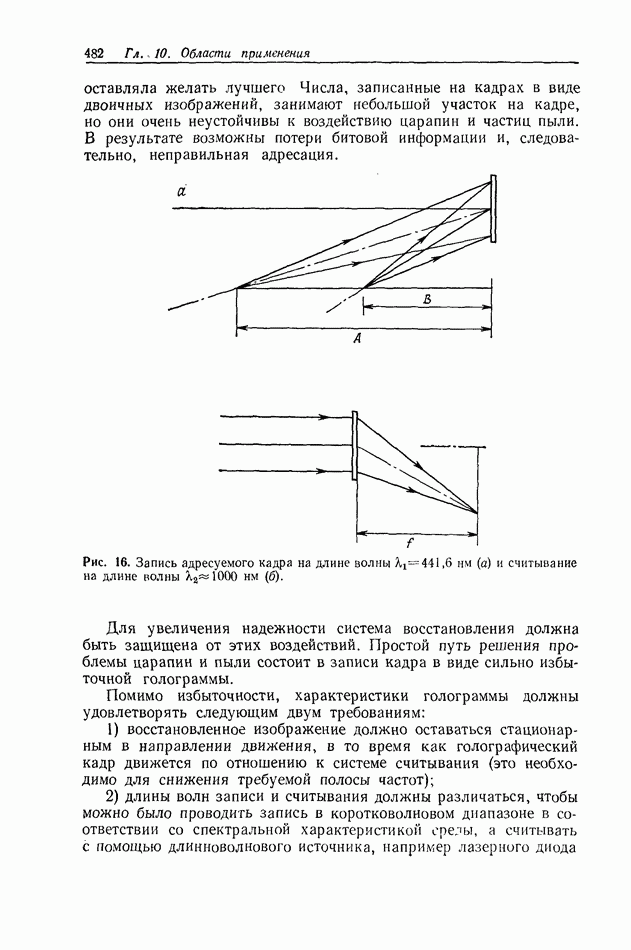
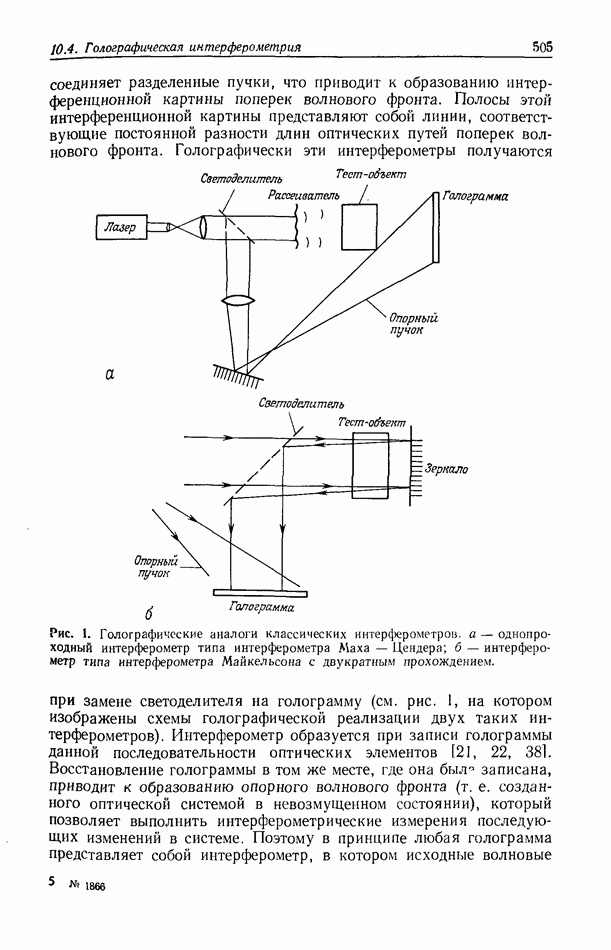
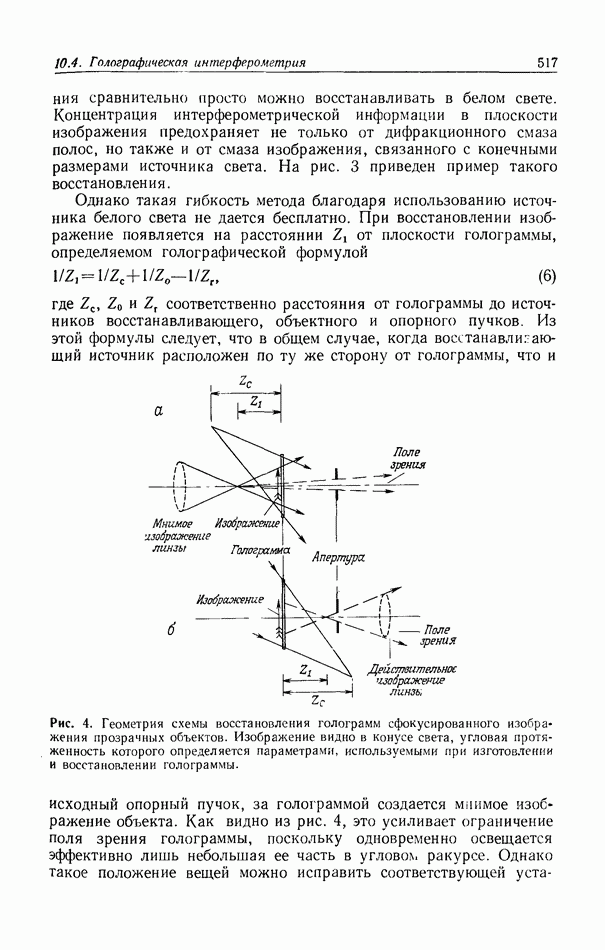
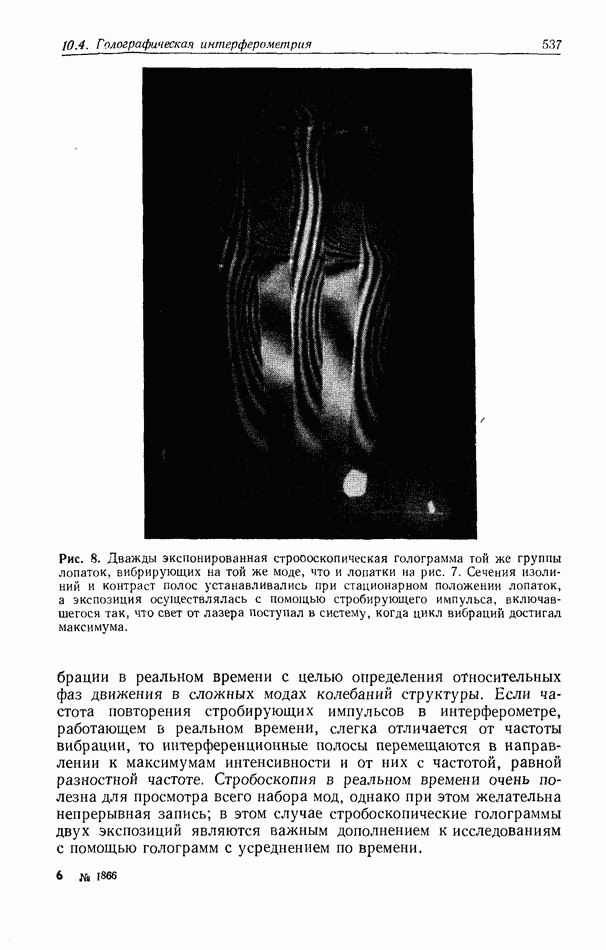
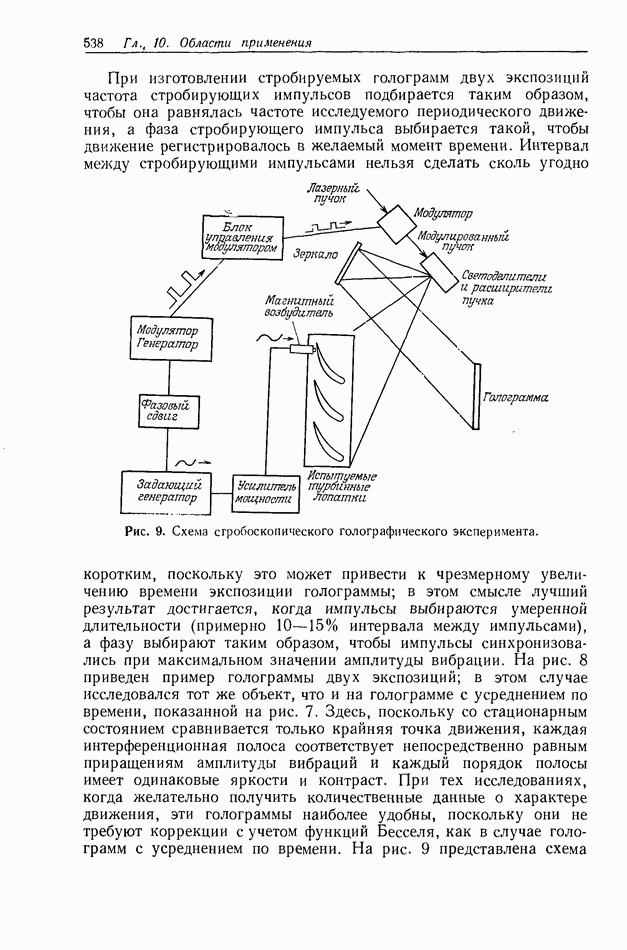
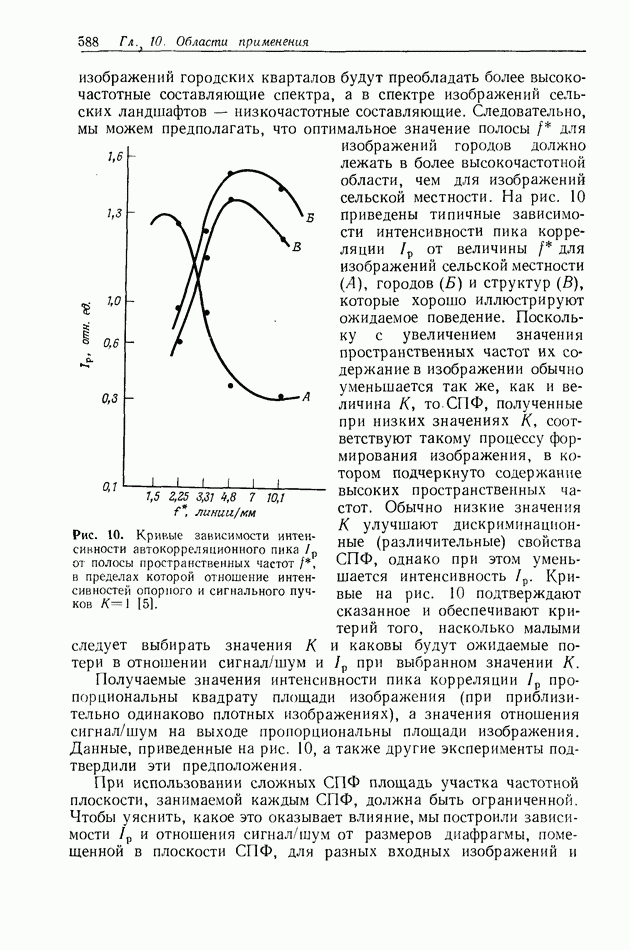
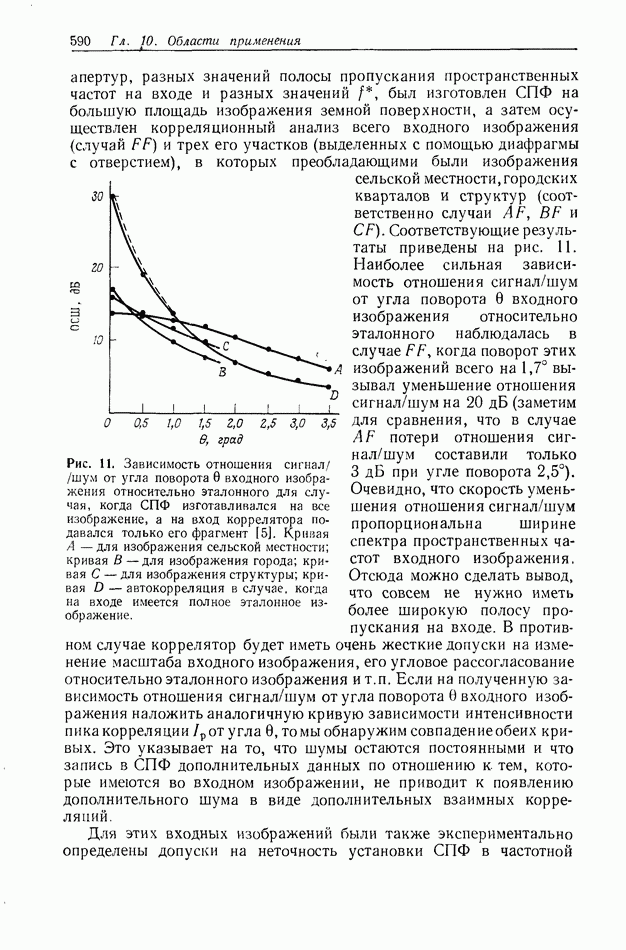
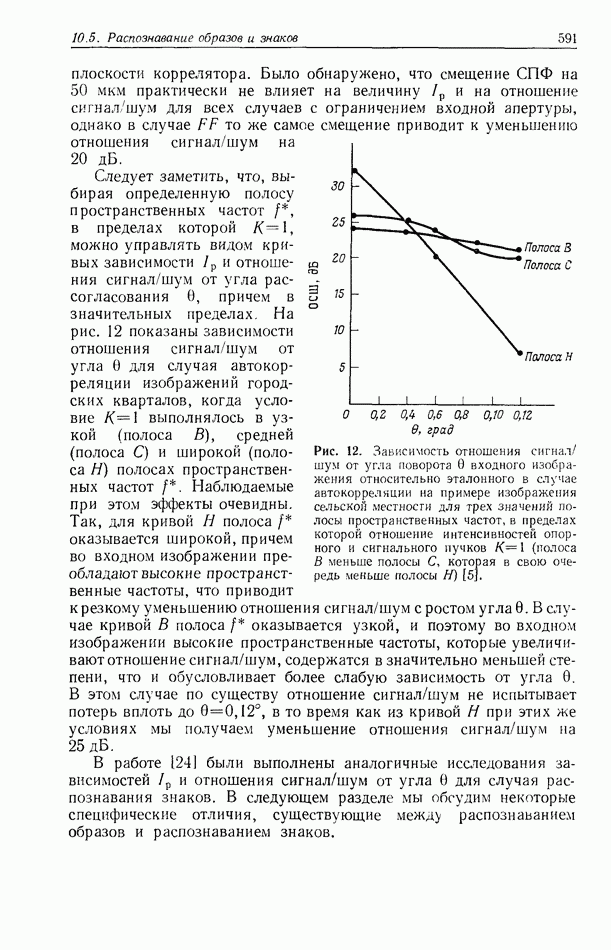
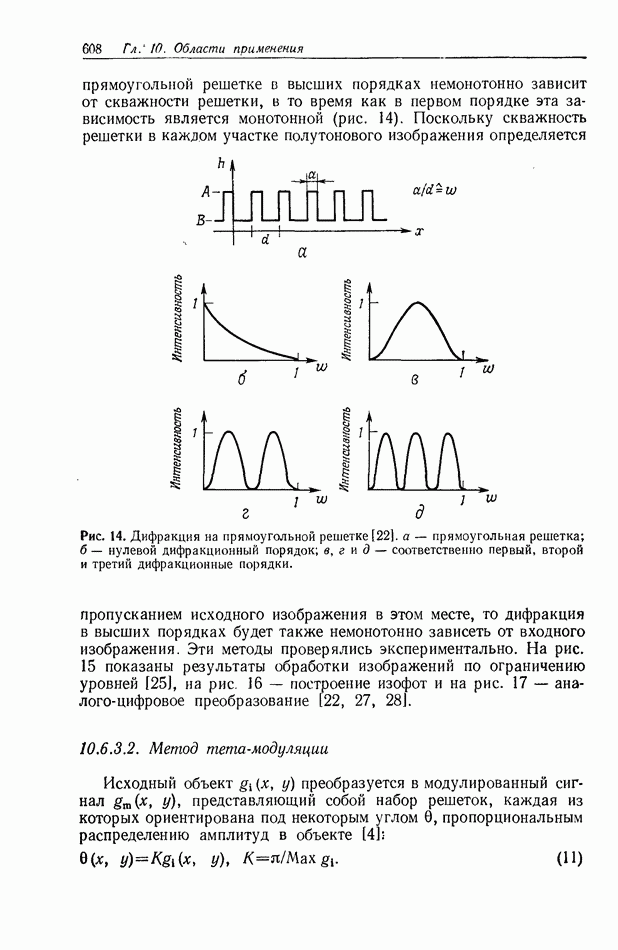
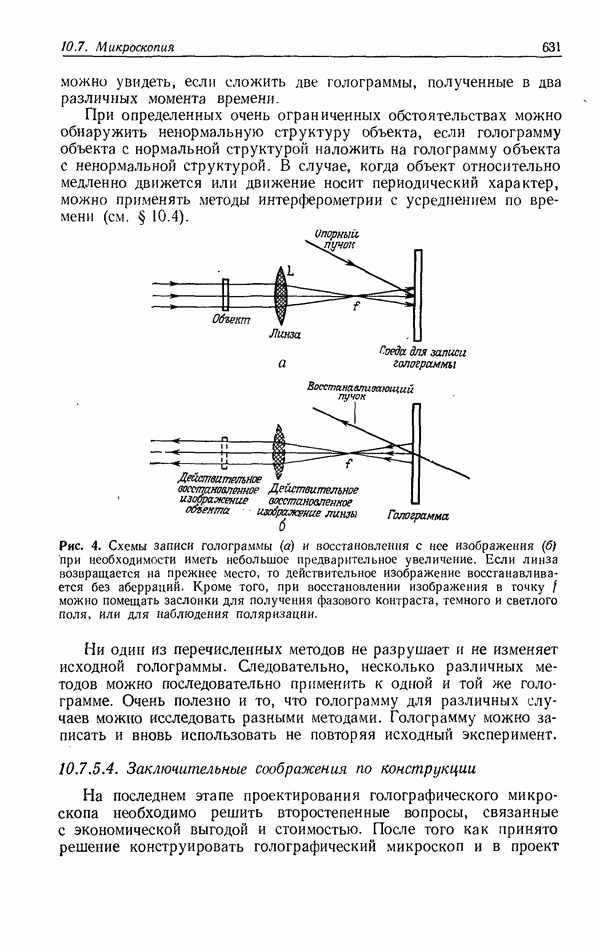
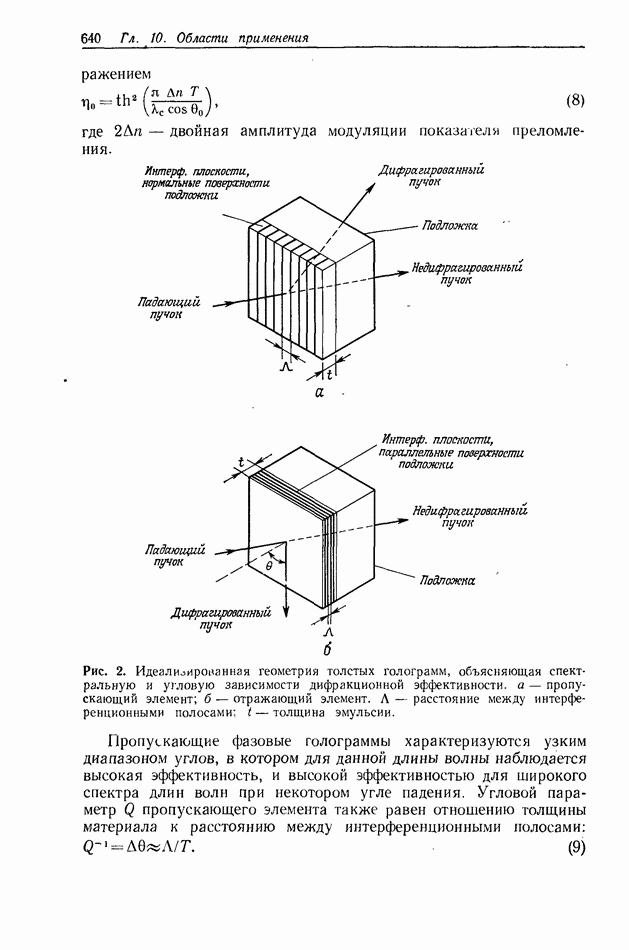
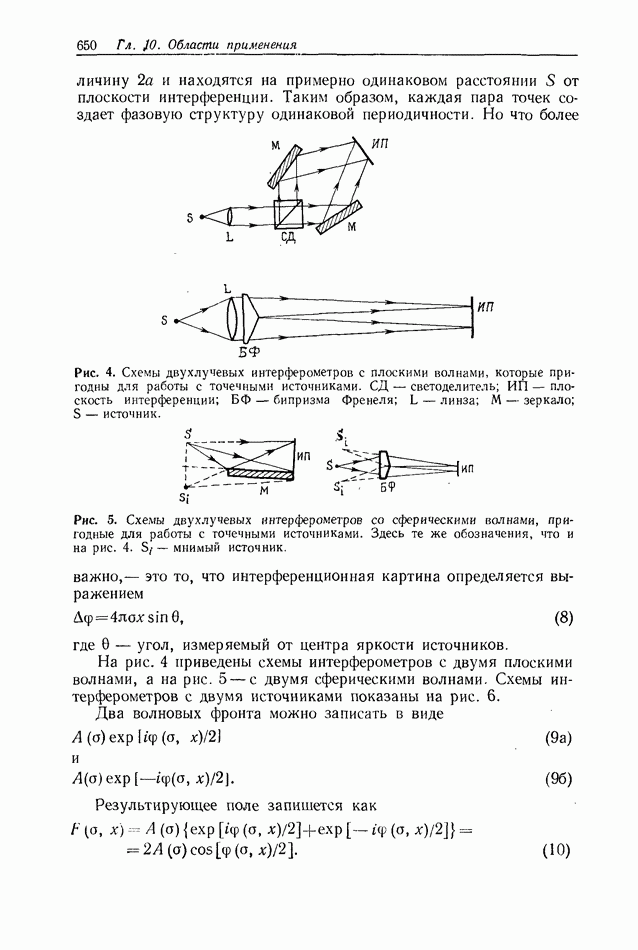
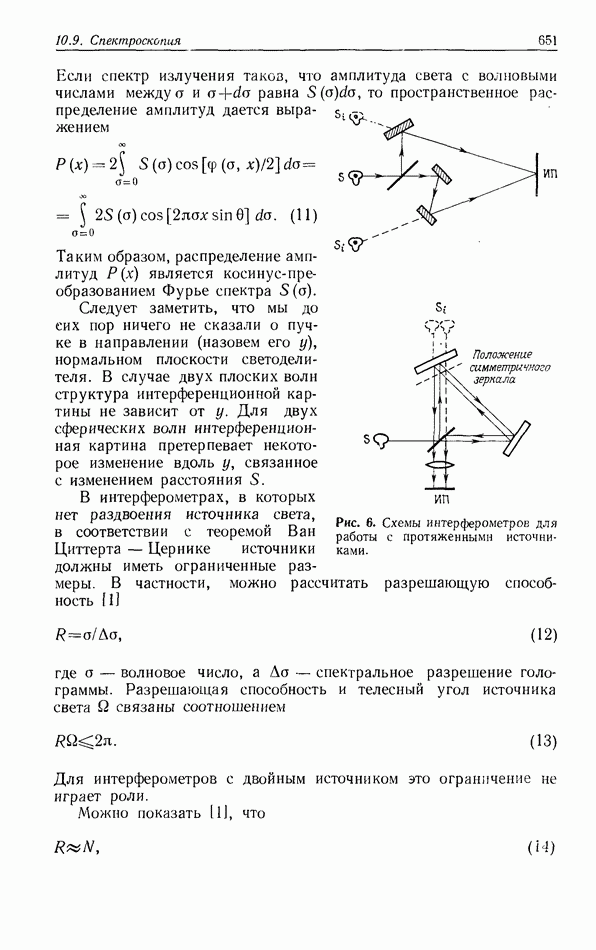
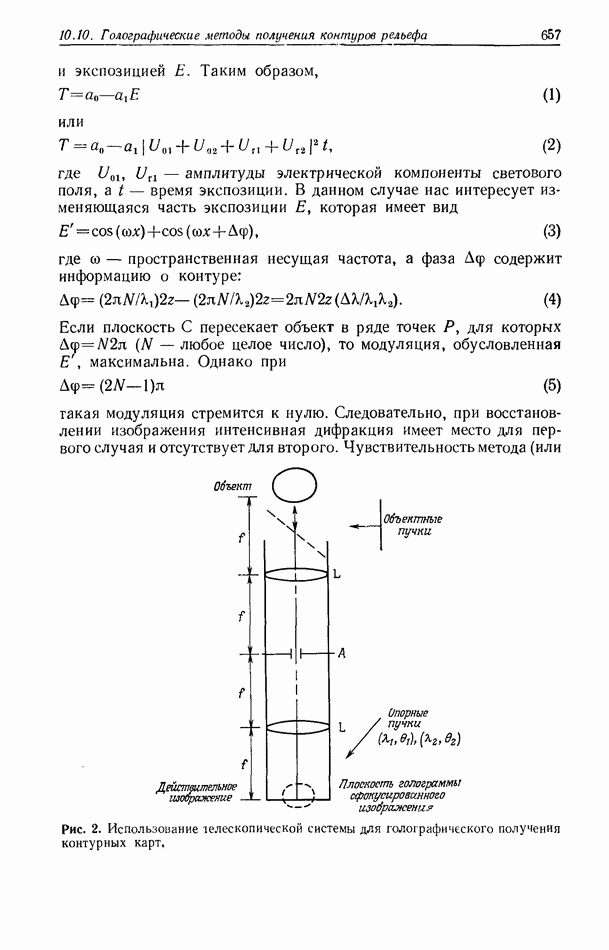
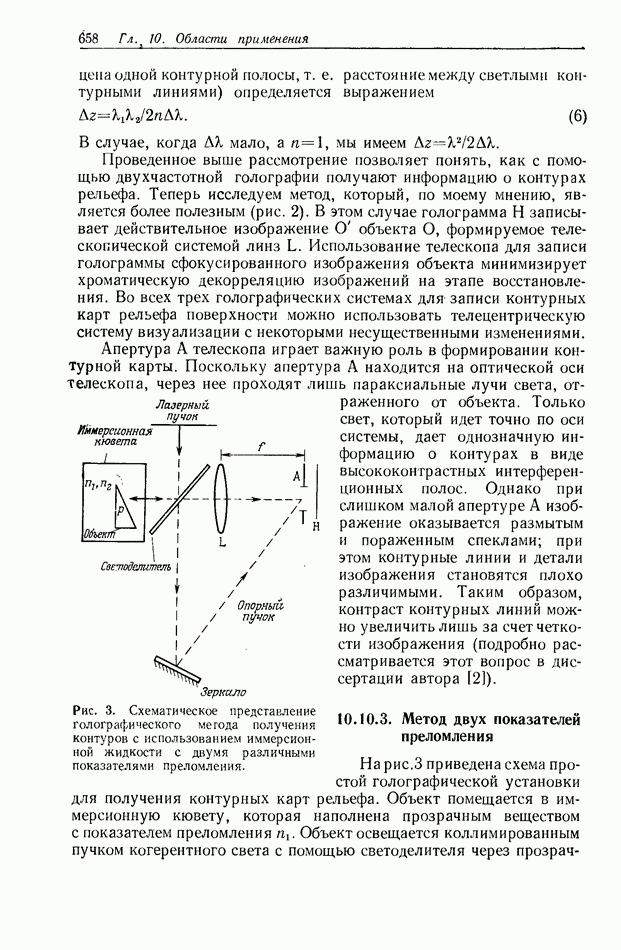
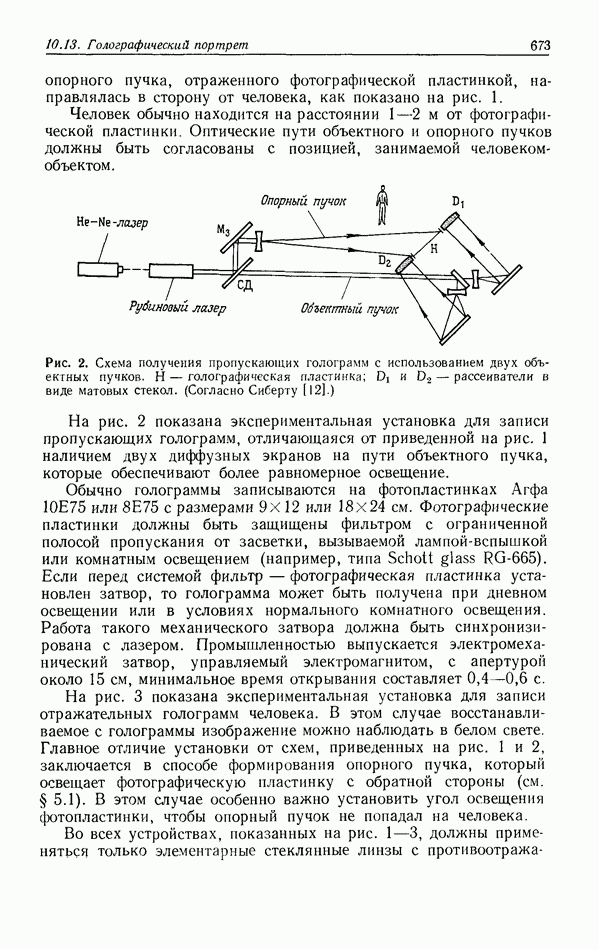
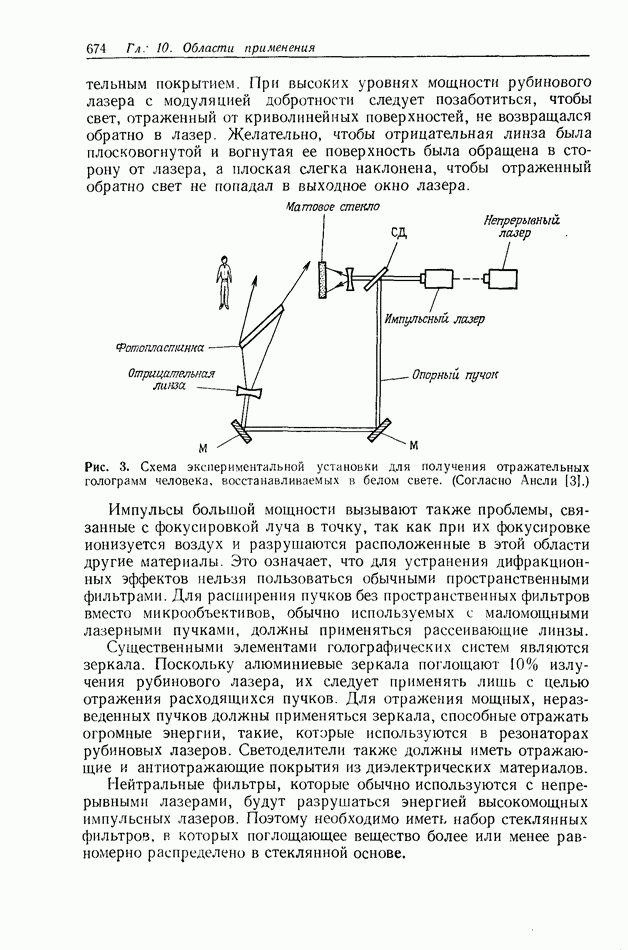
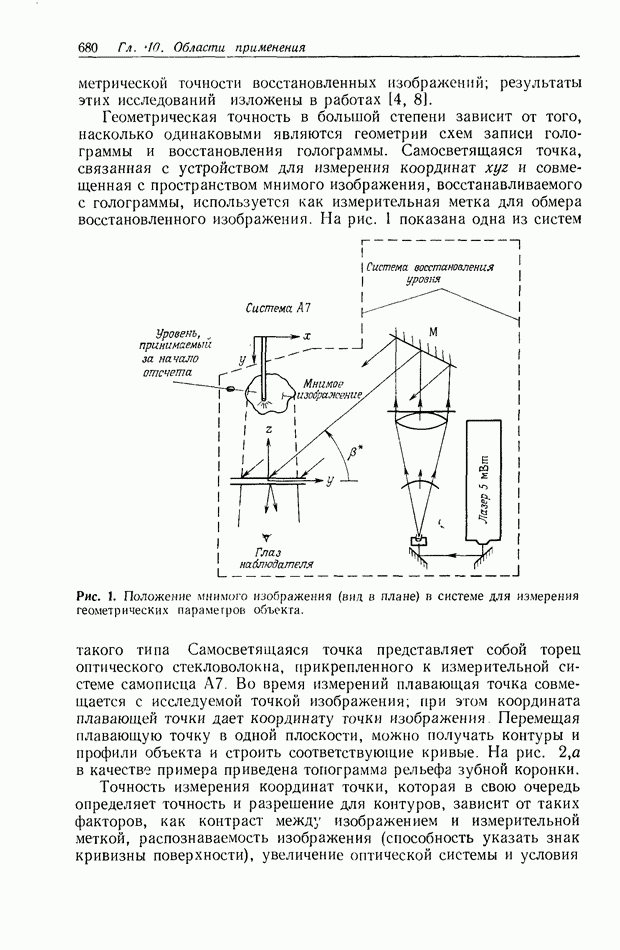
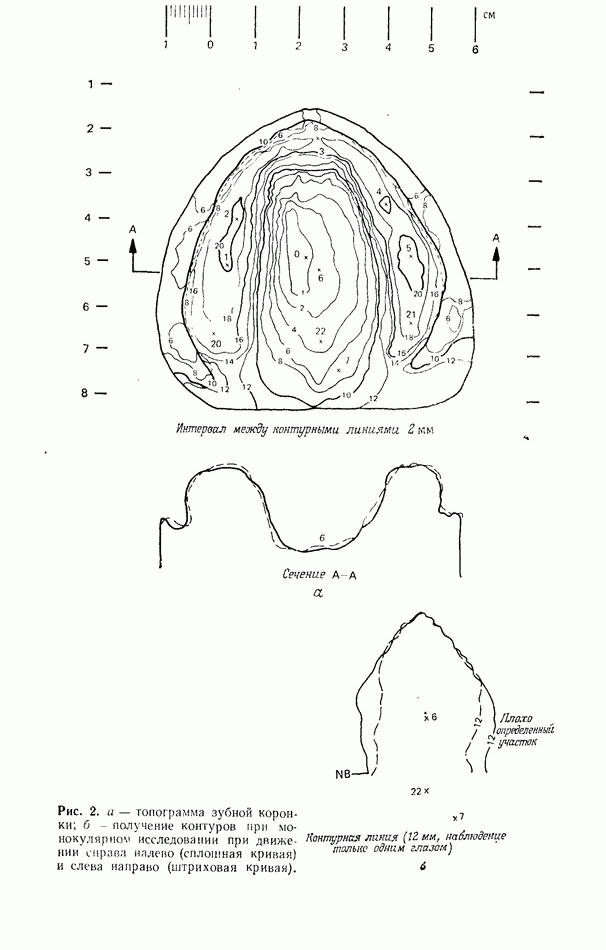
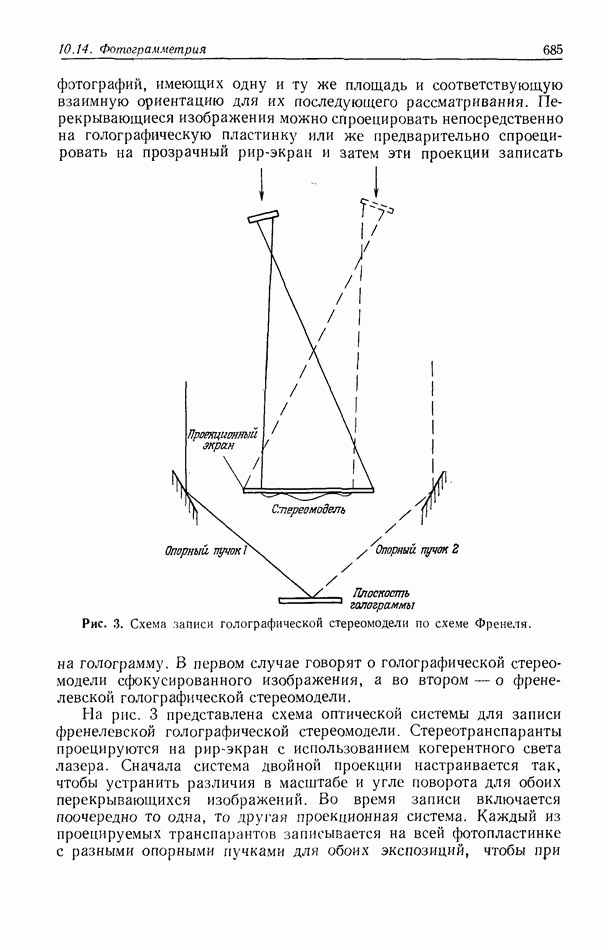
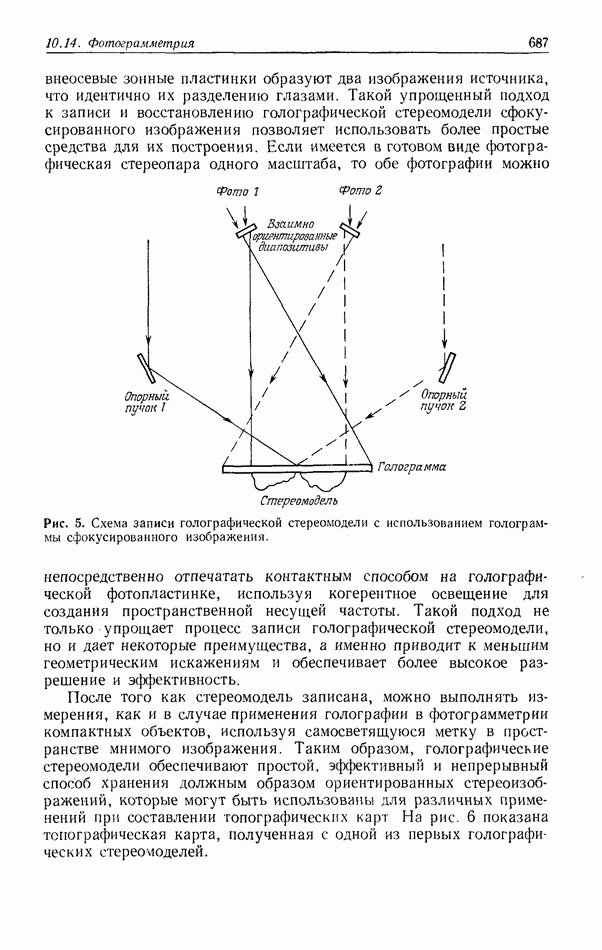
10.6.4. Пространственно-неинвариантная обработка изображений
В разд. 10.6.2 и 10.6.3 рассматривались линейные и нелинейные операции обработки изображений. Большинство этих операций являются пространственно-инвариантными в том смысле, что все точки входного изображения подвергаются одной и той же обработке. В этом разделе мы рассмотрим пространственно-неинвариантные методы обработки, когда разные точки входного изображения подвергаются различным операциям.
Примером пространственно-неинвариантной обработки служит геометрическое преобразование изображения 
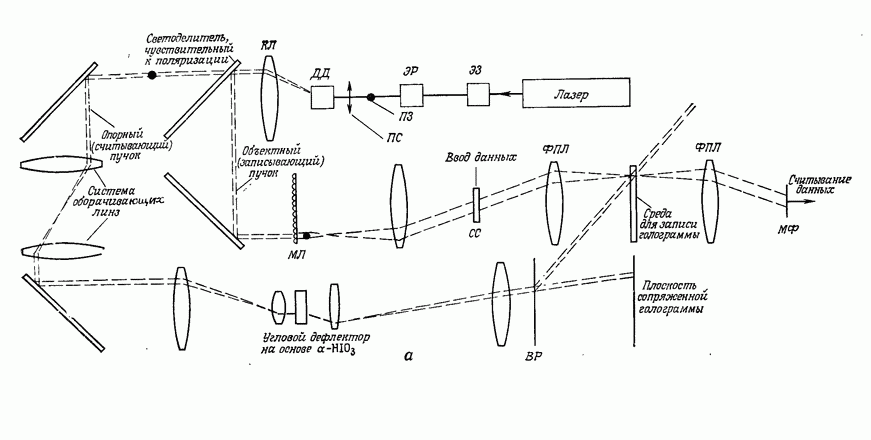
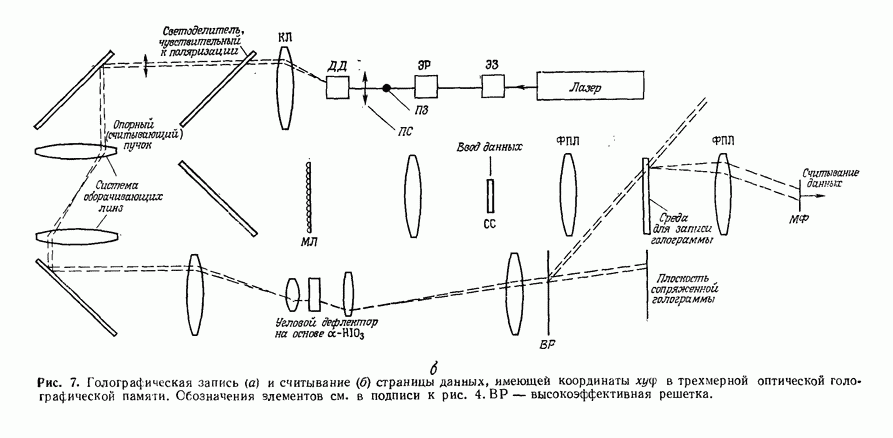
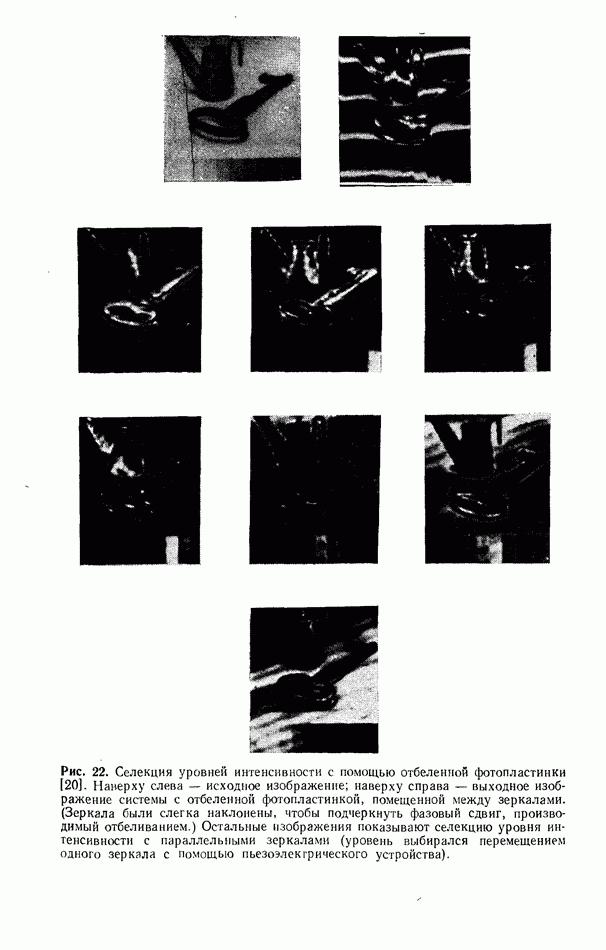
С помощью синтезированной на ЭВМ голограммы и оптической системы, схематически показанной на рис. 23, а, Брингдал [8, 91 получил экспериментальные результаты, приведенные на рис. 23, б. Принцип использования синтезированной на ЭВМ голограммы для геометрических преобразований изображений можно понять, рассматривая ее как обобщенный случай пространственной решетки с частотой, изменяющейся в зависимости от координат х, у. Пространственная частота решетки  на участке с координатами х, у дифрагирует свет в точку фокальной плоскости линзы с координатами
на участке с координатами х, у дифрагирует свет в точку фокальной плоскости линзы с координатами 

здесь К — длина волны света, а  фокусное расстояние линзы. Разумеется, геометрические преобразования можно также выполнить с помощью нелинейного сканирующего устройства, которое записывает изображение на когерентный пространственно-временной модулятор света с памятью
фокусное расстояние линзы. Разумеется, геометрические преобразования можно также выполнить с помощью нелинейного сканирующего устройства, которое записывает изображение на когерентный пространственно-временной модулятор света с памятью  Но этот метод сводит на нет преимущества параллельной обработки, обычно характерные для
Но этот метод сводит на нет преимущества параллельной обработки, обычно характерные для
оптической обработки, хотя в некоторых случаях его можно вполне применять.
Имеются и другие оптические методы, позволяющие выполнять различные пространственно-неинвари-антные операции,например методы голографического мультиплицирования изображений [12] и перемножения матриц [14]. Представление о том, в каком состоянии находится сейчас исследование этих методов, можно получить из замечательной обзорной работы Гудмена [13]. В этой работе приводится также и подробное описание методов. Несмотря на то что интерес к пространственно-неинвариантным методам обработки возник сравнительно недавно, в будущем можно ожидать дальнейшего прогресса ввиду возрастающего внимания к этой проблеме.

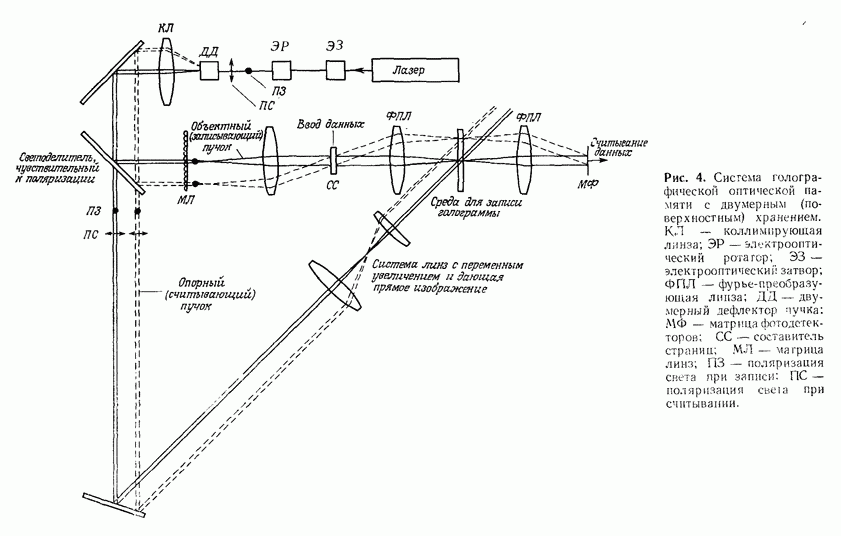
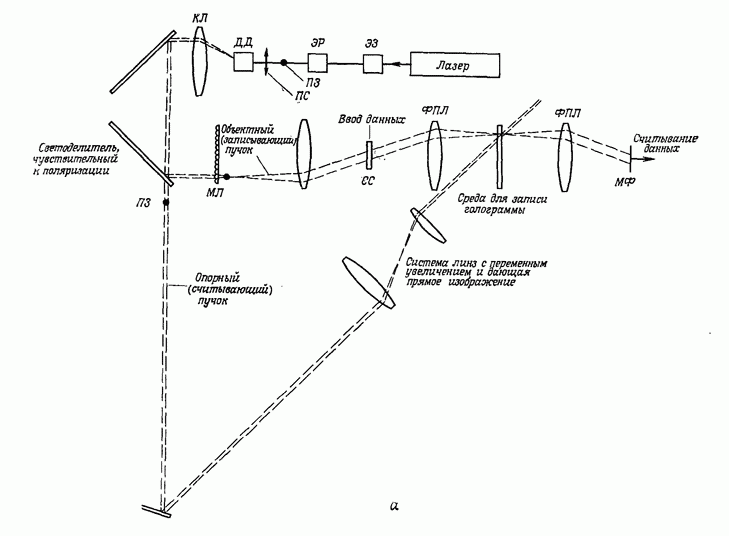
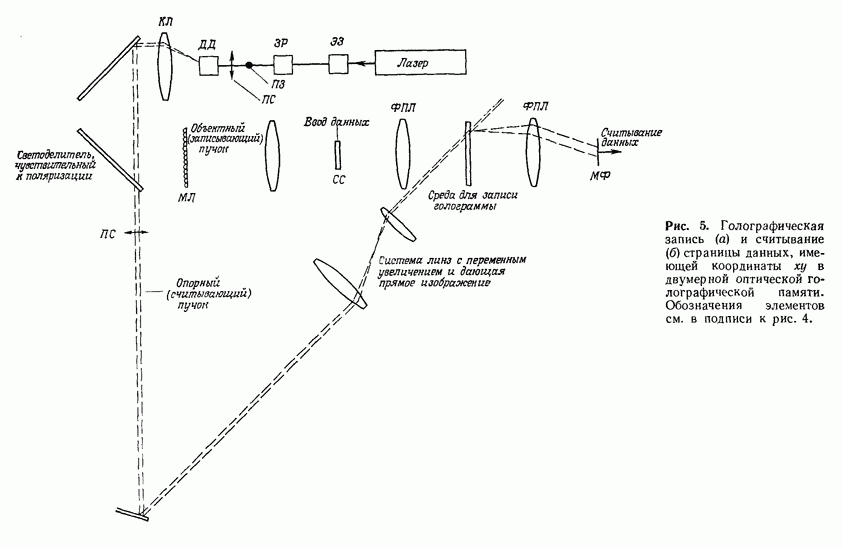
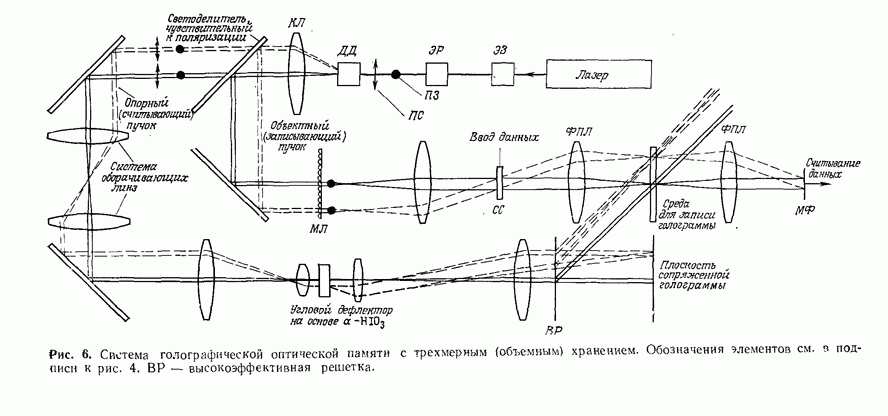
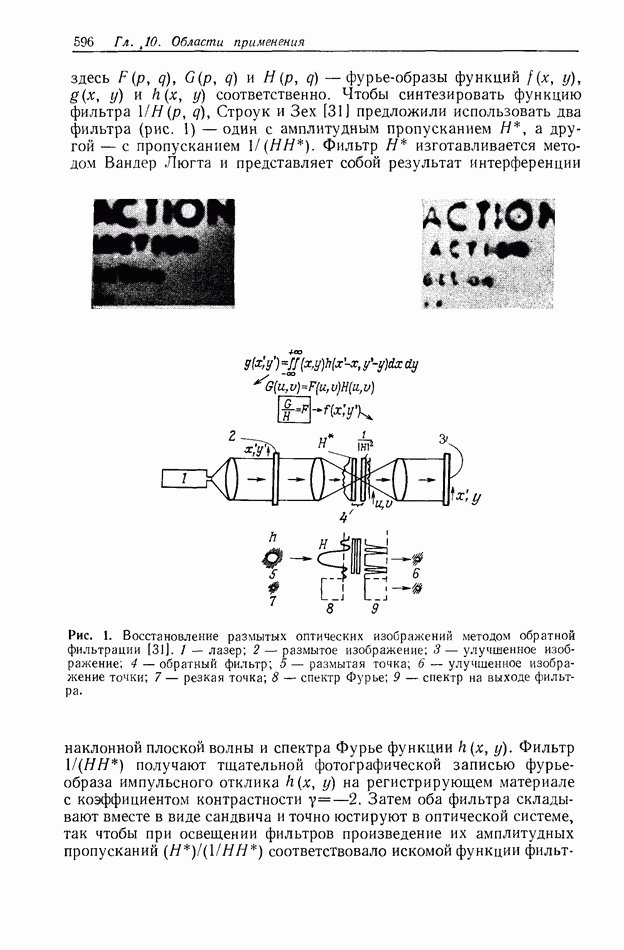
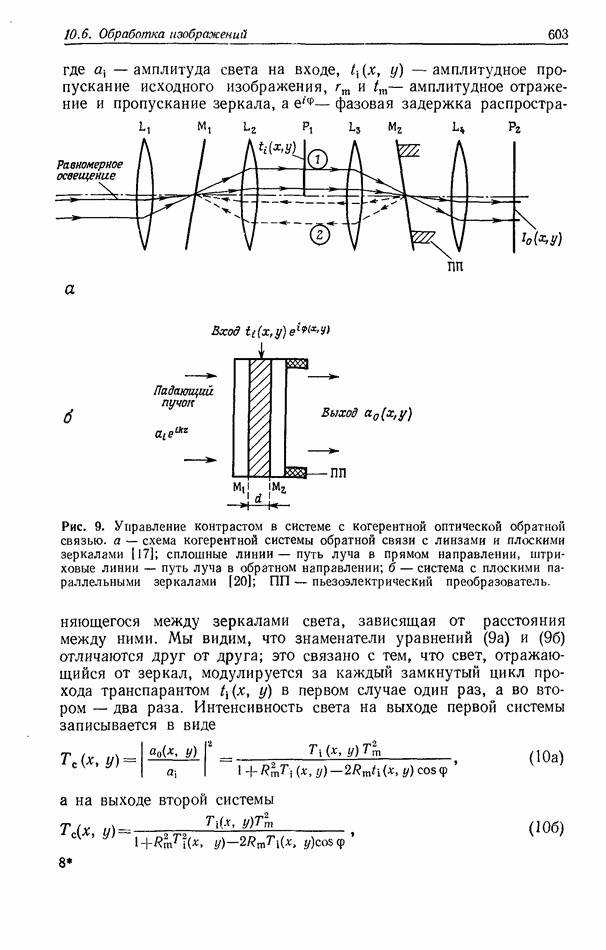
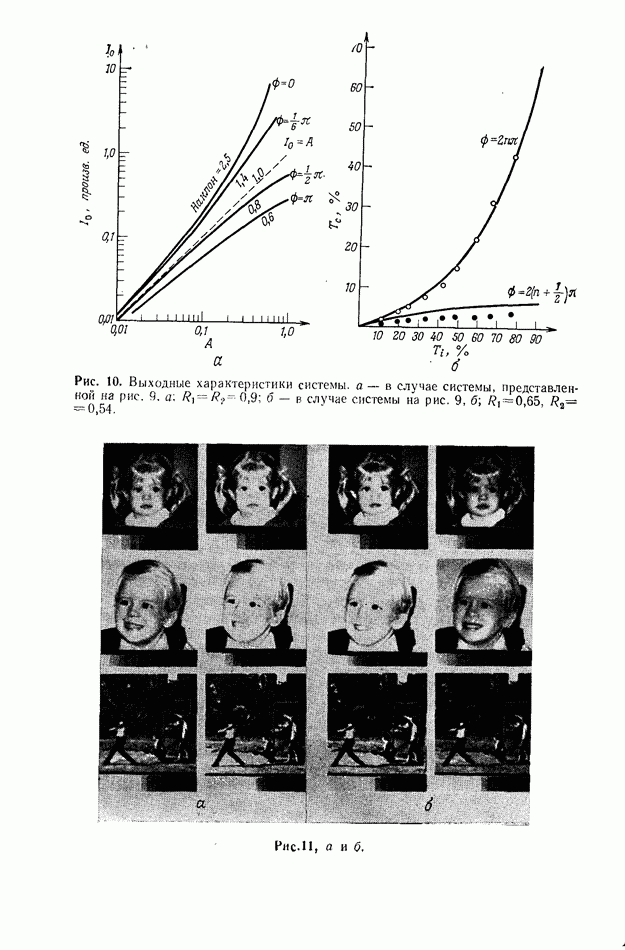
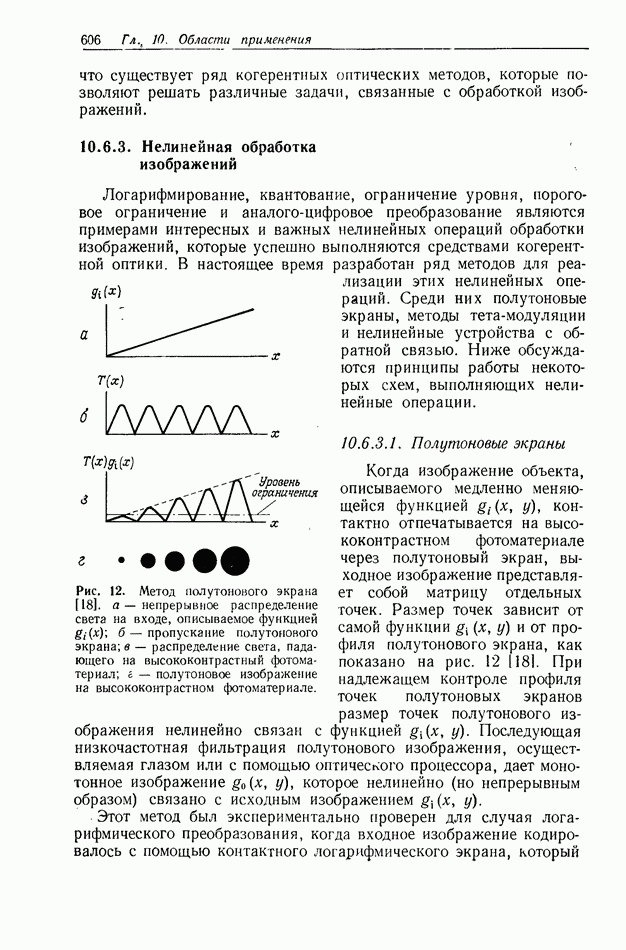
Рис. 23. а — оптический метод координатного преобразования с помощью синтезированной на ЭВМ голограммы;  экспериментальные результаты, полученные этим методом. (Согласно работе [81.)
экспериментальные результаты, полученные этим методом. (Согласно работе [81.)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
- 10.9. СПЕКТРОСКОПИЯ
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
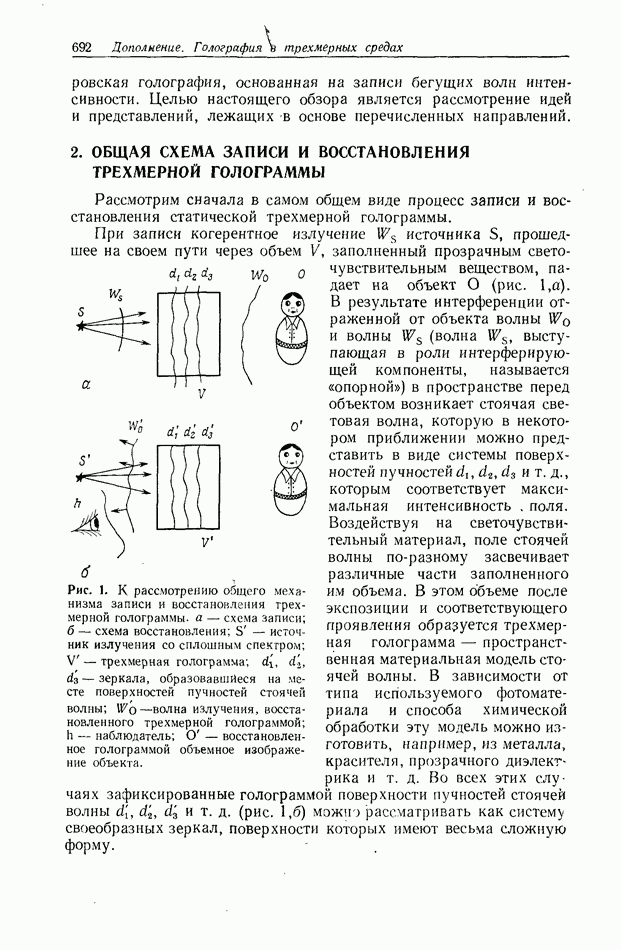
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
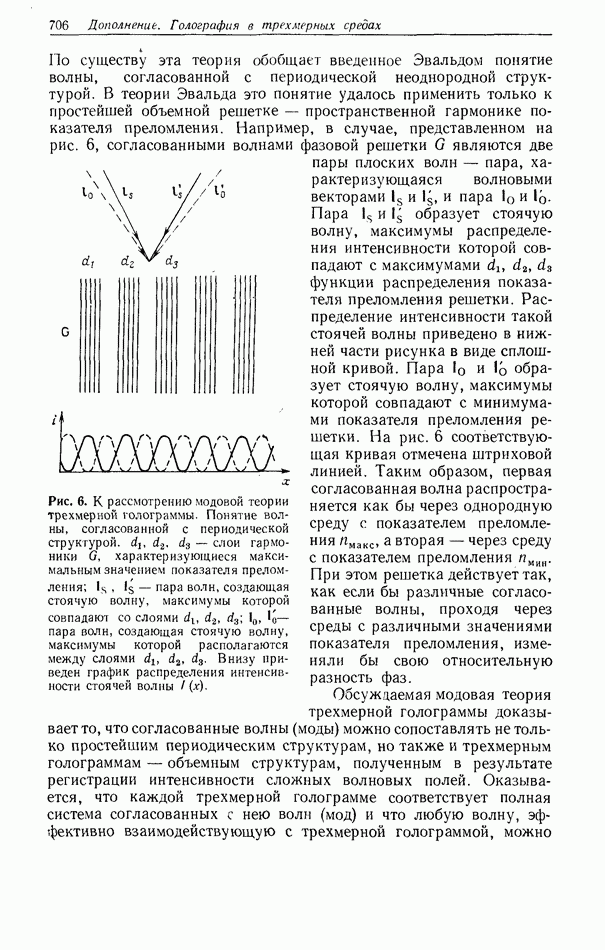
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
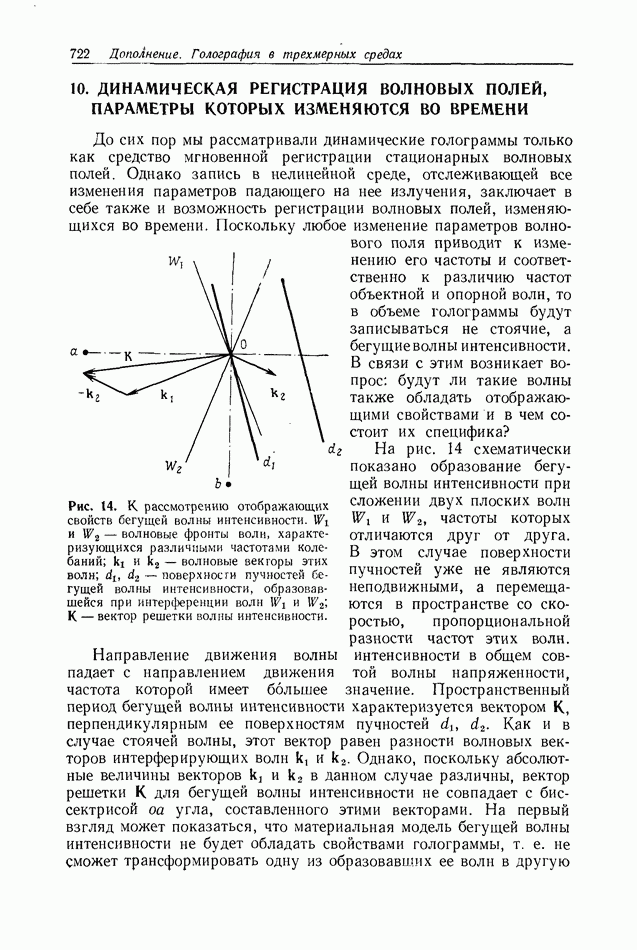
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ