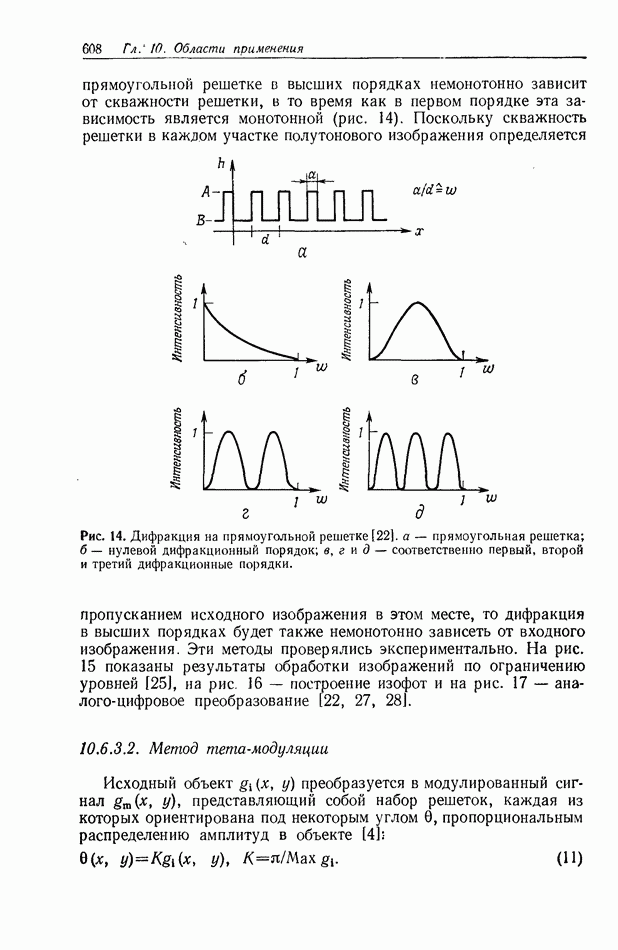
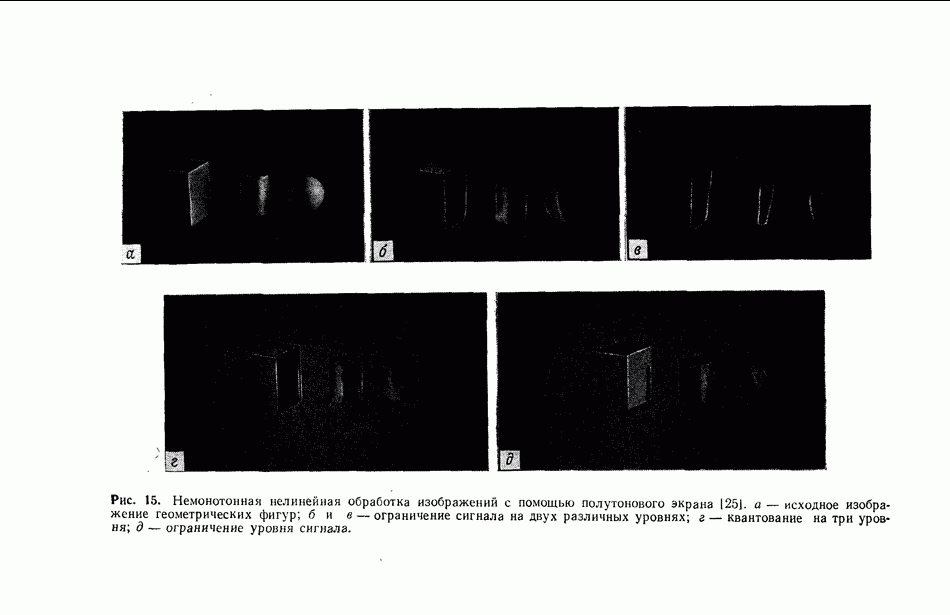
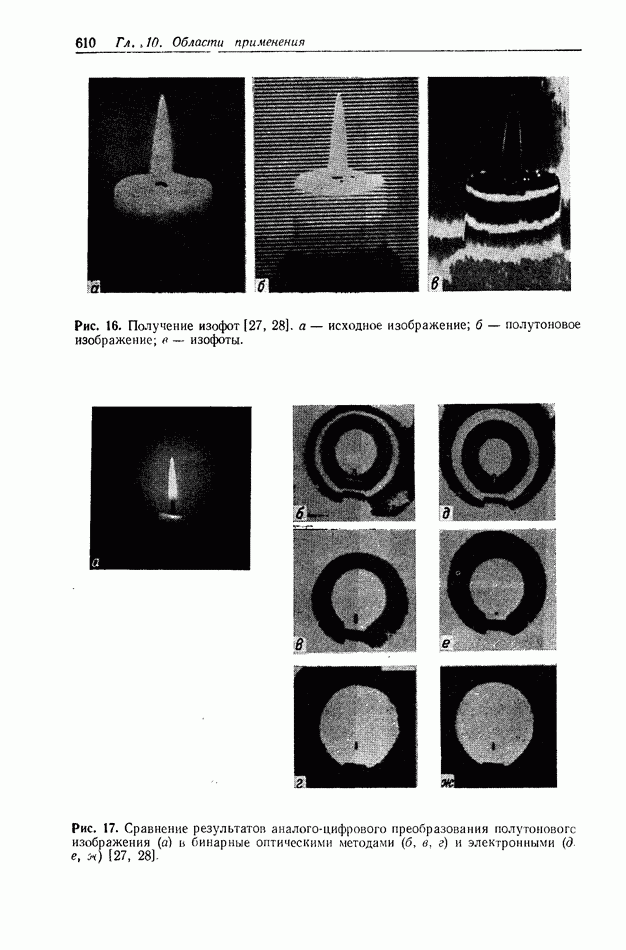
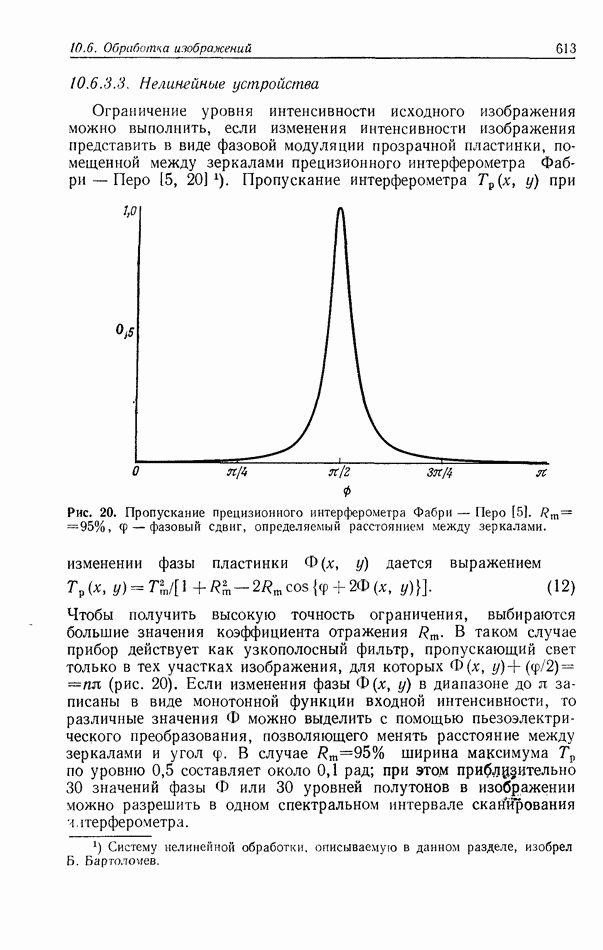
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.5.2. Коррелятор с частотной плоскостью
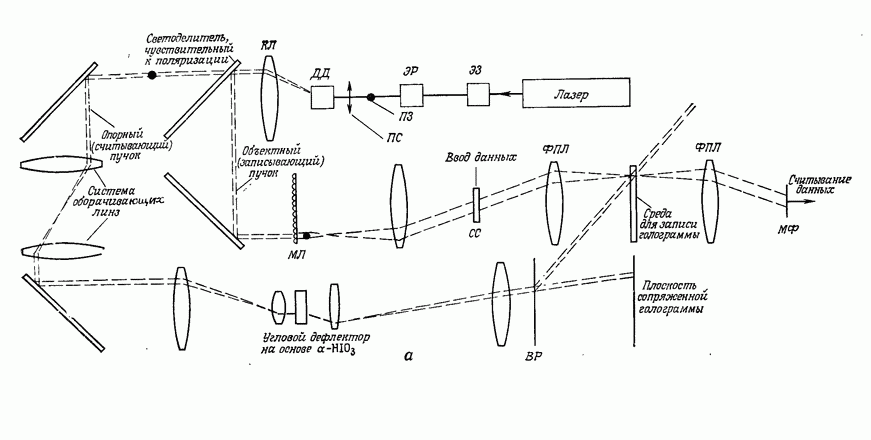
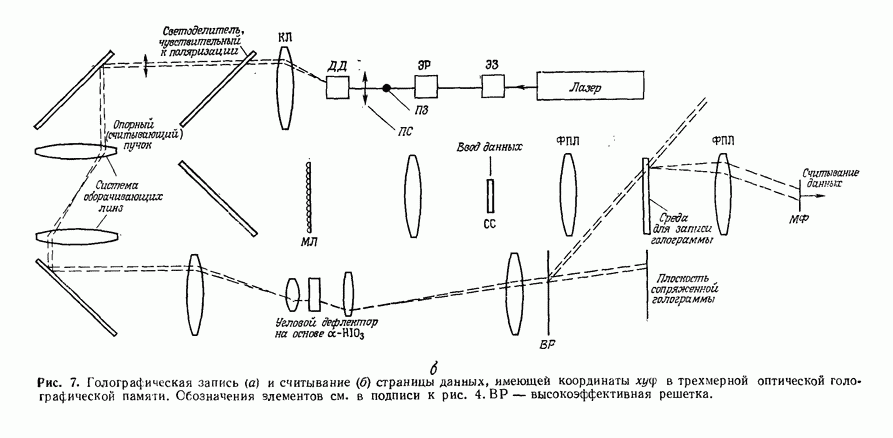
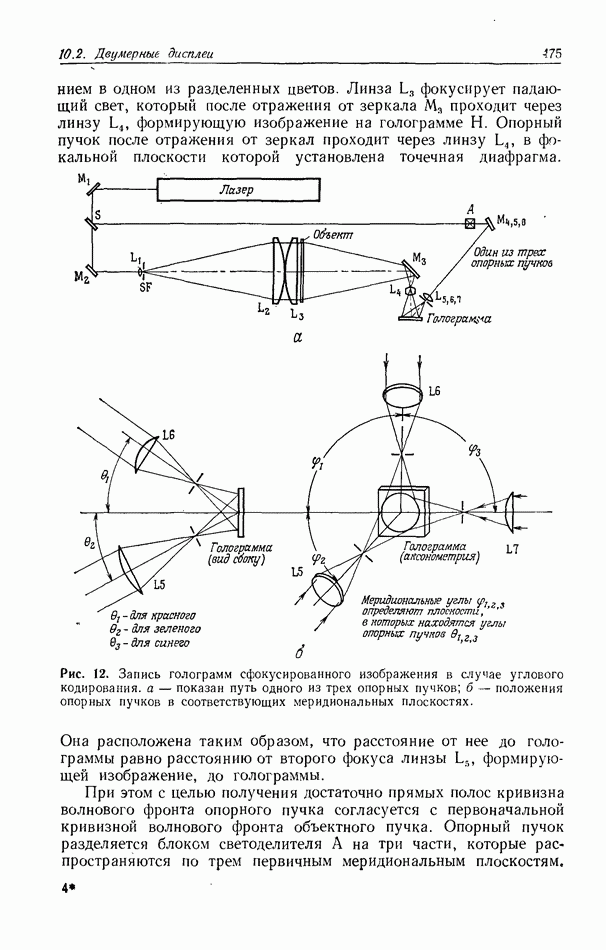
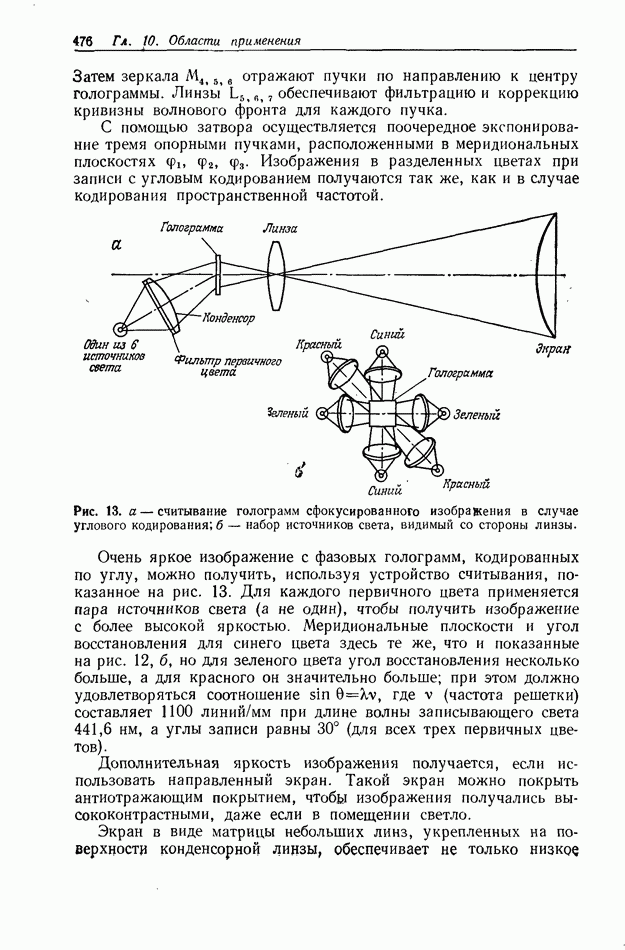
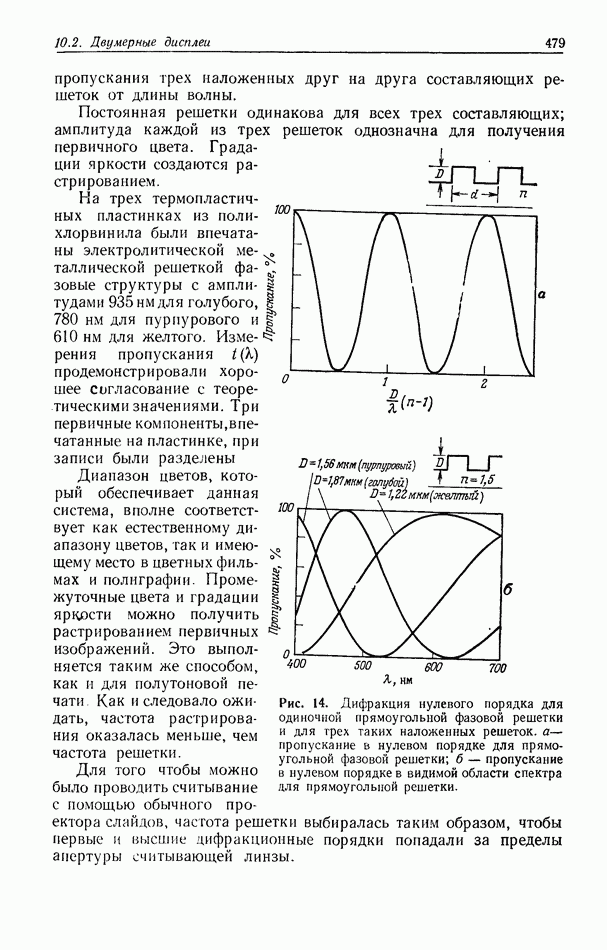
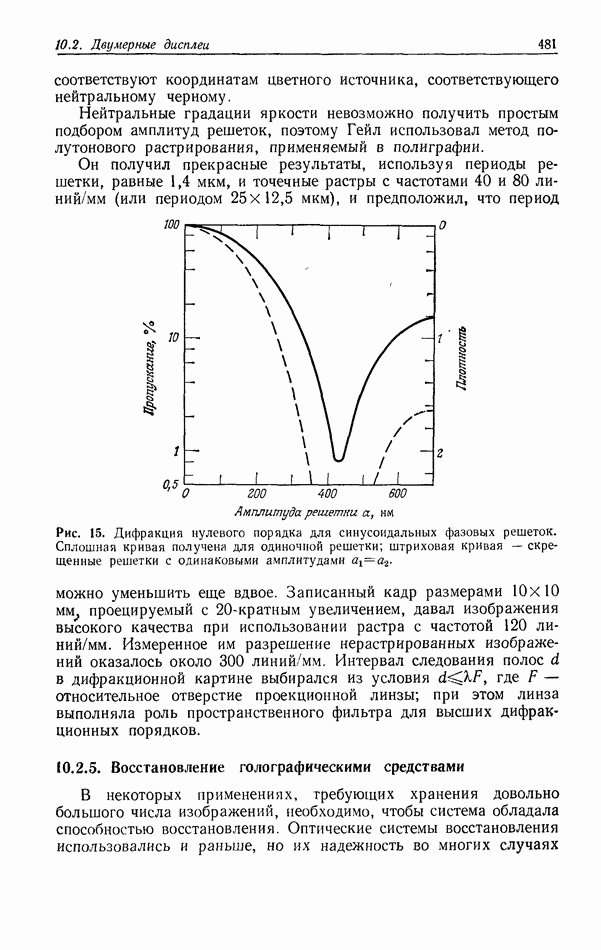
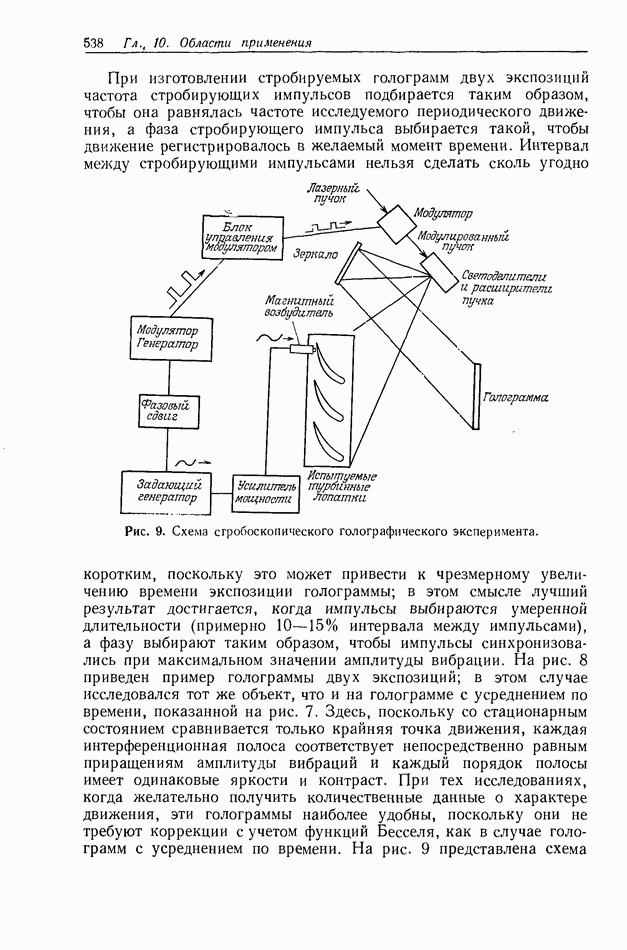
Первым и самым распространенным оптическим коррелятором является коррелятор с частотной плоскостью 1) [22] или система согласованной пространственной фильтрации. На рис. 1 приведена схема такого коррелятора, используемого в лабораторных исследованиях. Чтобы получить взаимную корреляцию функций  необходимо сначала синтезировать в плоскости
необходимо сначала синтезировать в плоскости  пространственный фильтр Я (
пространственный фильтр Я ( согласованный с
согласованный с 

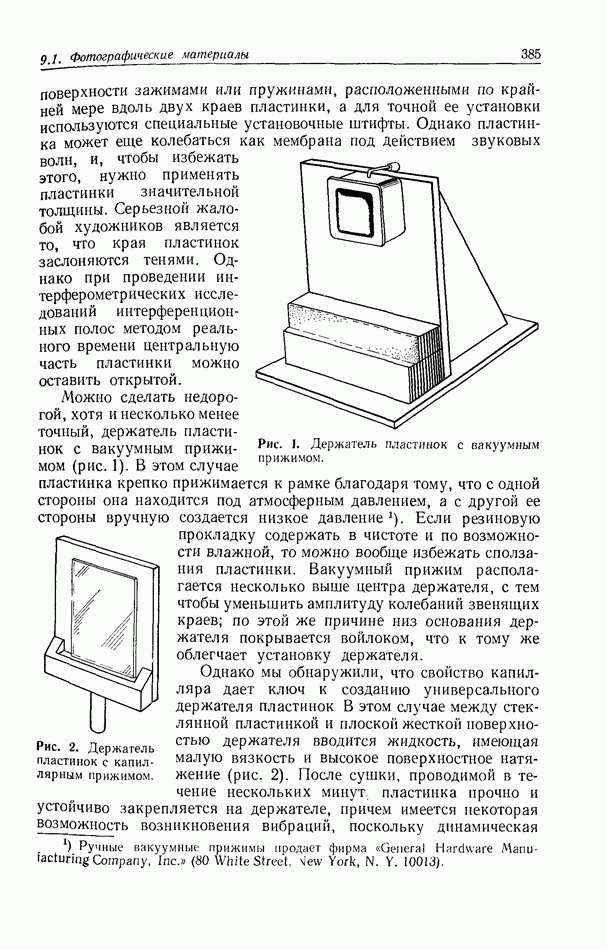
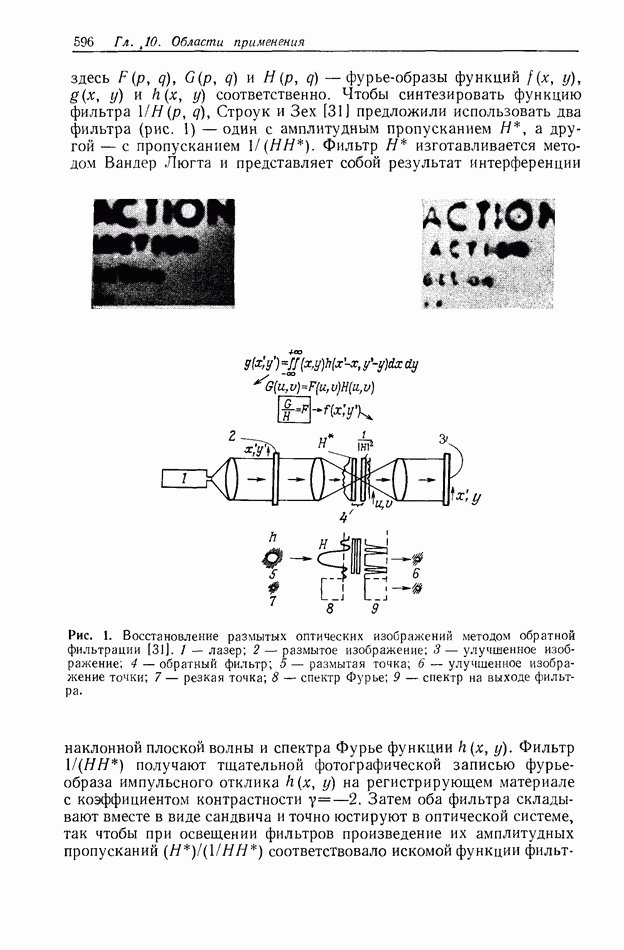
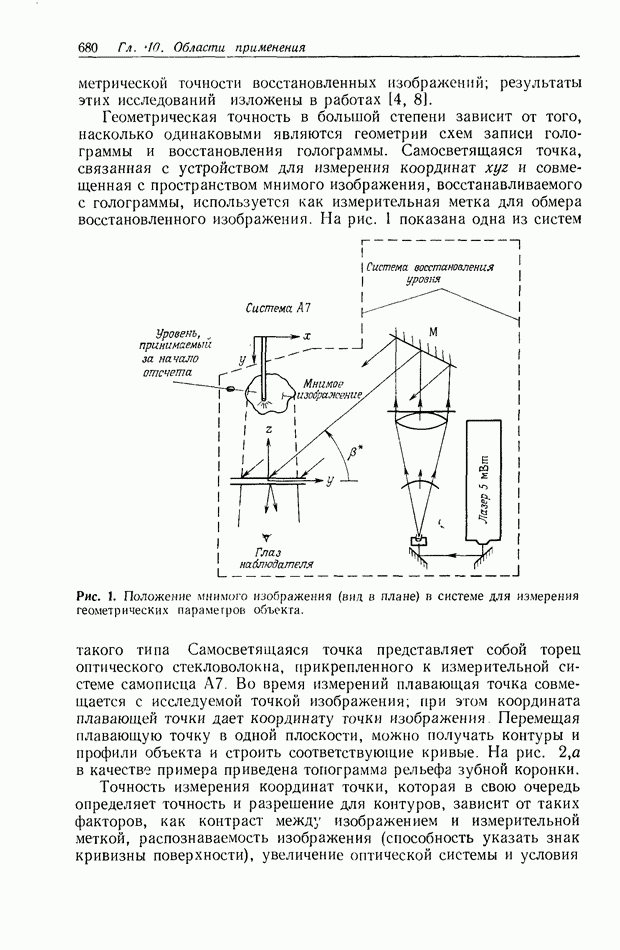
Рис. 1. Схема коррелятора с частотной плоскостью.  переменный аттенюатор;
переменный аттенюатор;  фотозатвор;
фотозатвор;  зеркало;
зеркало;  регулируемый светоделитель;
регулируемый светоделитель;  линза микрообъектива;
линза микрообъектива;  точечный пространственный фильтр низких частот;
точечный пространственный фильтр низких частот;  коллнмирующие линзы;
коллнмирующие линзы;  фурье-преобразующие линзы.
фурье-преобразующие линзы.
Для синтеза этого фильтра во входную плоскость  помещают транспарант с записью функции
помещают транспарант с записью функции  а в плоскости
а в плоскости  записывают интерференционную картину, создаваемую фурье-образом
записывают интерференционную картину, создаваемую фурье-образом  функции
функции  (формируемым линзой
(формируемым линзой  в плоскости
в плоскости  плоской опорной волной. Переменный аттенюатор
плоской опорной волной. Переменный аттенюатор  облегчает настройку элементов схемы и обеспечивает визуальный контроль картин распределений света в различных плоскостях схемы. Переменный светоделитель
облегчает настройку элементов схемы и обеспечивает визуальный контроль картин распределений света в различных плоскостях схемы. Переменный светоделитель  позволяет управлять отношением интенсивностей опорного и объектного пучков.
позволяет управлять отношением интенсивностей опорного и объектного пучков.
Для выравнивания длин оптических путей, проходимых опорным и объектным пучками, применяется зеркало  Такая геометрия облегчает также установку угла между опорным и объектным пучками, который в наших экспериментах составлял обычно 15°, а также упрощает компоновку элементов коррелятора на столе. При этом значении угла пространственные частоты интерференционной картины оказываются достаточно высокими 2). Чтобы зарегистрировать эту интерференционную картину, фотопленка должна обладать соответствующей разрешающей способностью.
Такая геометрия облегчает также установку угла между опорным и объектным пучками, который в наших экспериментах составлял обычно 15°, а также упрощает компоновку элементов коррелятора на столе. При этом значении угла пространственные частоты интерференционной картины оказываются достаточно высокими 2). Чтобы зарегистрировать эту интерференционную картину, фотопленка должна обладать соответствующей разрешающей способностью.
Если же разрешающая способность используемого материала недостаточна для записи столь высоких пространственных частот, между опорным и объектным пучками следует установить меньший угол При этом для сведения пучков под малым углом потребуются светоделитель и дополнительные оптические элементы (или линзы с большим фокусным расстоянием). Использование в каждом из пучков системы пространственной фильтрации, состоящей из микрообъектива  и точечной диафрагмы
и точечной диафрагмы  помогает устранить шумы лазерного пучка. Эти системы устанавливаются после зеркал, чтобы уменьшить влияние их дефектов. В наших экспериментах мы использовали коллимирующую оптику, обеспечивающую формирование очень однородных плоских волн, причем изменение интенсивности по сечению пучка составляет не более 5%. Однако во многих случаях не обязательны такие жесткие требования.
помогает устранить шумы лазерного пучка. Эти системы устанавливаются после зеркал, чтобы уменьшить влияние их дефектов. В наших экспериментах мы использовали коллимирующую оптику, обеспечивающую формирование очень однородных плоских волн, причем изменение интенсивности по сечению пучка составляет не более 5%. Однако во многих случаях не обязательны такие жесткие требования.
После того как согласованный пространственный фильтр изготовлен и вновь установлен в плоскости  мы поворачиваем его на 180° вокруг оптической оси. Благодаря этому корреляция будет наблюдаться под углом
мы поворачиваем его на 180° вокруг оптической оси. Благодаря этому корреляция будет наблюдаться под углом  по отношению к оси объектного пучка, т. е. в пределах поверхности стола, а не под углом —15° в направлении продолжения опорного пучка. Этот простой прием позволяет использовать стол с меньшей площадью. При выполнении операции корреляционного анализа опорный пучок блокируется, а во входную плоскость помещают транспарант с амплитудным пропусканием
по отношению к оси объектного пучка, т. е. в пределах поверхности стола, а не под углом —15° в направлении продолжения опорного пучка. Этот простой прием позволяет использовать стол с меньшей площадью. При выполнении операции корреляционного анализа опорный пучок блокируется, а во входную плоскость помещают транспарант с амплитудным пропусканием  Волна, несущая информацию о корреляции входного и эталонного изображений, будет исходить из плоскости
Волна, несущая информацию о корреляции входного и эталонного изображений, будет исходить из плоскости  под углом 15° к оптической оси коррелятора. Вторая фурье-преобразующая линза
под углом 15° к оптической оси коррелятора. Вторая фурье-преобразующая линза  устанавливается вдоль этого направления на фокусном расстоянии от плоскости
устанавливается вдоль этого направления на фокусном расстоянии от плоскости  а не вдоль оси сигнального пучка, как это обычно делают. Такая схема коррелятора существенно уменьшает требования к размерам апертур и углам поля зрения используемых линз.
а не вдоль оси сигнального пучка, как это обычно делают. Такая схема коррелятора существенно уменьшает требования к размерам апертур и углам поля зрения используемых линз.
Рассмотрим основные математические соотношения, описывающие работу этого коррелятора. Сначала проанализируем стадию, на которой осуществляется синтез согласованного пространственного фильтра. Если во входной плоскости  поместить транспарант с амплитудным пропусканием
поместить транспарант с амплитудным пропусканием  то распределение комплексных амплитуд в плоскости
то распределение комплексных амплитуд в плоскости  будет равно
будет равно  (
( где
где  комплексный фурье-образ функции
комплексный фурье-образ функции  таким образом,
таким образом,

Предположим для простоты, что любые преобразования Фурье, реализуемые с помощью линз, выполняются точно и, следовательно,
мы пренебрегаем постоянными коэффициентами амплитудного пропускания, а также множителем  перед интегралом. Координаты пространственных частот
перед интегралом. Координаты пространственных частот  в плоскости
в плоскости  связаны с пространственными координатами
связаны с пространственными координатами  этой плоскости соотношениями
этой плоскости соотношениями  где
где  длина волны света, а
длина волны света, а  фокусное расстояние фурье-преобразующей линзы
фокусное расстояние фурье-преобразующей линзы 
Распределение комплексных амплитуд, создаваемое в плоскости  опорным пучком с постоянной амплитудой
опорным пучком с постоянной амплитудой  который падает на эту плоскость под углом
который падает на эту плоскость под углом  к объектному пучку, лмеет вид
к объектному пучку, лмеет вид  где
где  пространственная частота, связанная с наклонным падением опорной волны в предположении, что опорная волна образует угол
пространственная частота, связанная с наклонным падением опорной волны в предположении, что опорная волна образует угол  с осью в плоскости
с осью в плоскости 
При записи согласованного фильтра полагают, что амплитудное пропускание помещаемого в плоскости  светочувствительного материала (обычно это фотопленка) пропорционально распределению интенсивности падающего на неге света. (Это соответствует выполнению условия
светочувствительного материала (обычно это фотопленка) пропорционально распределению интенсивности падающего на неге света. (Это соответствует выполнению условия  рассмотренного в § 2.4 и 2.6.) При интерференции в плоскости
рассмотренного в § 2.4 и 2.6.) При интерференции в плоскости  распределений
распределений  создаваемых соответственно объектным и опорным пучками, амплитудное пропускание полученного согласованного фильтра запишется в виде
создаваемых соответственно объектным и опорным пучками, амплитудное пропускание полученного согласованного фильтра запишется в виде

Для получения корреляции опорный пучок перекрывается, в плоскости  помещается согласованный фильтр
помещается согласованный фильтр  а во входной плоскости
а во входной плоскости  устанавливается транспарант с амплитудным пропусканием
устанавливается транспарант с амплитудным пропусканием  При этом распределение комплексных амплитуд света, падающего на плоскость
При этом распределение комплексных амплитуд света, падающего на плоскость  описывается функцией
описывается функцией  и после прохождения этого распределения через согласованный фильтр мы имеем
и после прохождения этого распределения через согласованный фильтр мы имеем  Поскольку плоскость
Поскольку плоскость  совмещена с передней фокальной плоскостью второй фурье-преобразующей линзы
совмещена с передней фокальной плоскостью второй фурье-преобразующей линзы  с фокусным расстоянием
с фокусным расстоянием  распределение комплексных амплитуд в задней фокальной плоскости этой линзы представляет собой фурье-образ произведения
распределение комплексных амплитуд в задней фокальной плоскости этой линзы представляет собой фурье-образ произведения  таким образом,
таким образом,

здесь обозначает свертку, а — корреляцию.
В выражении (2) два первых слагаемых соответствуют распределениям, локализованным на оптической оси в выходной плоскости. Третье слагаемое представляет собой свертку  которая формируется пучком, исходящим из плоскости
которая формируется пучком, исходящим из плоскости  под углом
под углом  и это распределение локализуется в выходной плоскости в окрестности точки с координатами
и это распределение локализуется в выходной плоскости в окрестности точки с координатами  Распределение,
Распределение,
описываемое последним слагаемым с интересующем нас корреляцией  создается пучком, исходящим из плоскости
создается пучком, исходящим из плоскости  под углом
под углом  и локализуется в выходной плоскости вокруг точки с координатами
и локализуется в выходной плоскости вокруг точки с координатами  В действительности при установке фотопластинки с записанным на ней согласованным фильтром в плоскость
В действительности при установке фотопластинки с записанным на ней согласованным фильтром в плоскость  ее поворачивают на 180° вокруг оптической оси, а линзу
ее поворачивают на 180° вокруг оптической оси, а линзу  помещают в пучок, выходящий из плоскости
помещают в пучок, выходящий из плоскости  под углом
под углом  чтобы сформировать на выходе распределение, описываемое последним слагаемым. Тогда распределение, формируемое в задней фокальной плоскости линзы
чтобы сформировать на выходе распределение, описываемое последним слагаемым. Тогда распределение, формируемое в задней фокальной плоскости линзы  на ее оптической оси, представляет собой интересующую функцию взаимной корреляции
на ее оптической оси, представляет собой интересующую функцию взаимной корреляции  Различные другие участки входной плоскости отображаются в окрестности начала координат сформированной таким образом выходной корреляционной плоскости. Следует заметить, что положение яркого пятна света в этой плоскости однозначно связано с положением эталонной функции
Различные другие участки входной плоскости отображаются в окрестности начала координат сформированной таким образом выходной корреляционной плоскости. Следует заметить, что положение яркого пятна света в этой плоскости однозначно связано с положением эталонной функции  во входном изображении
во входном изображении  интенсивность этого пятна указывает на степень соответствия между
интенсивность этого пятна указывает на степень соответствия между  С целью упрощения обозначений при определении координат
С целью упрощения обозначений при определении координат  в плоскости
в плоскости  направления координатных осей, как правило, меняют на обратные по отношению к координатным осям в плоскостях
направления координатных осей, как правило, меняют на обратные по отношению к координатным осям в плоскостях  и
и 
В силу линейности рассматриваемого коррелятора наличие многих эталонных функций  во входном изображении
во входном изображении  приводит к появлению большого числа корреляционных пиков в плоскости
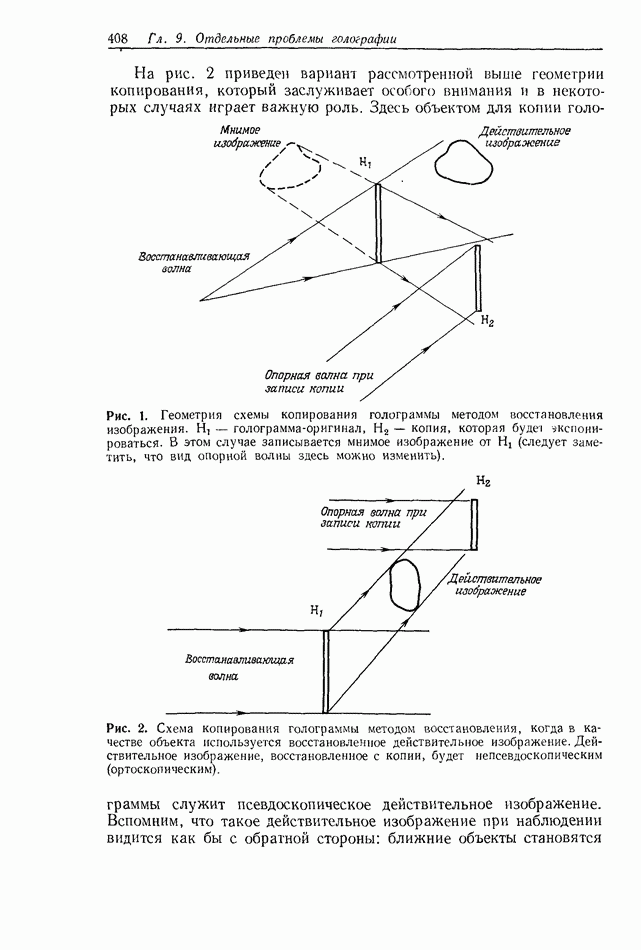
приводит к появлению большого числа корреляционных пиков в плоскости  Это хорошо иллюстрируется примером, приведенным на рис. 2. Здесь роль входной функции
Это хорошо иллюстрируется примером, приведенным на рис. 2. Здесь роль входной функции  выполняет часть текста, в которой шесть раз встречается слово RADAR (см. рис. 2, а), а в качестве эталонной функции
выполняет часть текста, в которой шесть раз встречается слово RADAR (см. рис. 2, а), а в качестве эталонной функции  используется согласованный фильтр для слова RADAR. На рис. 2, б показано распределение интенсивности в плоскости
используется согласованный фильтр для слова RADAR. На рис. 2, б показано распределение интенсивности в плоскости  полученное в результате корреляционного анализа по схеме на рис. 1. На рис. 2, в показано то же распределение в выходной плоскости, но после введения порогового ограничения. Из сравнения рис. 2, а и 2, в нетрудно заметить, что имеется шесть ярких точек, расположенных в соответствии с положениями шести слов RADAR во входной плоскости. Масштабный коэффициент между входной и корреляционной плоскостями равен отношению фокусных расстояний
полученное в результате корреляционного анализа по схеме на рис. 1. На рис. 2, в показано то же распределение в выходной плоскости, но после введения порогового ограничения. Из сравнения рис. 2, а и 2, в нетрудно заметить, что имеется шесть ярких точек, расположенных в соответствии с положениями шести слов RADAR во входной плоскости. Масштабный коэффициент между входной и корреляционной плоскостями равен отношению фокусных расстояний  двух фурье-преобразующих линз. Наличие на рис. 2, б многих хорошо заметных пиков взаимной корреляции, представляет собой одну из проблем, характерную для оптического распознавания слов и знаков. Эту проблему мы обсудим в разд. 10.5.17.
двух фурье-преобразующих линз. Наличие на рис. 2, б многих хорошо заметных пиков взаимной корреляции, представляет собой одну из проблем, характерную для оптического распознавания слов и знаков. Эту проблему мы обсудим в разд. 10.5.17.
Если эталонная функция  соответствует значительно большим размерам интересующей нас сцены или участка, описываемых функцией
соответствует значительно большим размерам интересующей нас сцены или участка, описываемых функцией  то корреляционный пик располагается на оси в плоскости
то корреляционный пик располагается на оси в плоскости  при условии, что
при условии, что  занимает то же самое положение во входной плоскости, которое занимала эталонная функция
занимает то же самое положение во входной плоскости, которое занимала эталонная функция  при
при

(кликните для просмотра скана)
записи фильтра. Любое смещение  из этого положения приведет к смещению корреляционного пика в плоскости
из этого положения приведет к смещению корреляционного пика в плоскости  Если функция
Если функция  расположена на оси во входной плоскости, то положение корреляционного пика в плоскости
расположена на оси во входной плоскости, то положение корреляционного пика в плоскости  будет характеризовать (с точностью до множителя
будет характеризовать (с точностью до множителя  взаимное положение
взаимное положение 
Перейдем теперь к рассмотрению весьма важной характеристики данного и других оптических корреляторов, а именно проанализируем требования к разрешающей способности материалов, используемых для записи согласованных фильтров в частотной плоскости [41. В целях упрощения анализа мы будем рассматривать одномерные функции. Обозначим ширины входной и эталонной функций соответственно через  и рассмотрим три случая:
и рассмотрим три случая:

Сначала установим требования к разрешающей способности в частотной плоскости  необходимые для осуществления записи СПФ. Для этого определим импульсный отклик согласованного пространственного фильтра, подставив в выражение (2) вместо входной функции
необходимые для осуществления записи СПФ. Для этого определим импульсный отклик согласованного пространственного фильтра, подставив в выражение (2) вместо входной функции  дельта-функцию
дельта-функцию  Таким образом,
Таким образом,

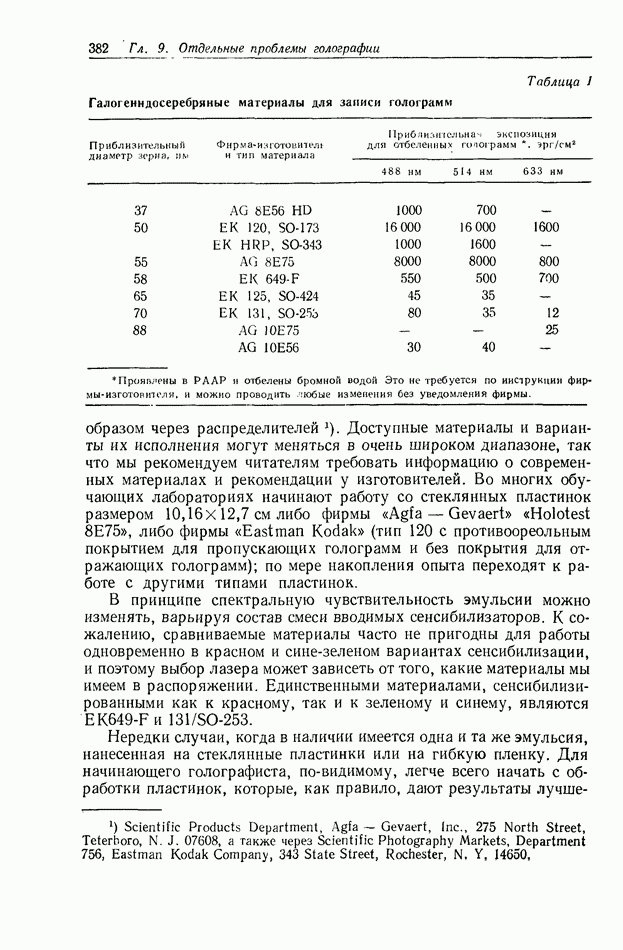
Положения каждого из этих членов импульсного отклика в корреляционной плоскости, а также их размеры для каждого из трех указанных выше случаев приведены в табл. 1, а в табл. 2 представлены аналогичные параметры для случая взаимной корреляции.
Таблица 1 (см. скан) Положение и ширина отдельных слагаемых импульсного отклика СПФ на выходе коррелятора с частотной плоскостью
В общем случае ширина распределения, соответствующего импульсному отклику согласованного фильтра, равна  (при обязательном выполнении условия
(при обязательном выполнении условия  чтобы обеспечить полное разделение всех членов импульсного отклика). Таким образом, требуемое разрешение (число линий на миллиметр) в плоскости
чтобы обеспечить полное разделение всех членов импульсного отклика). Таким образом, требуемое разрешение (число линий на миллиметр) в плоскости  оказывается равным
оказывается равным  а используемый для записи СПФ
а используемый для записи СПФ
Таблица 2 (см. скан) Положение и ширина отдельных слагаемых распределения на выходе коррелятора  частотной плоскостью
частотной плоскостью
материал должен обеспечить ширину полосы пропускания пространственных частот, равную  Однако, если нам необходимо обеспечить пространственное разделение члена взаимной корреляции от всех других, присутствующих в выходной плоскости, то из табл. 2 следует, что для этого должно выполняться условие
Однако, если нам необходимо обеспечить пространственное разделение члена взаимной корреляции от всех других, присутствующих в выходной плоскости, то из табл. 2 следует, что для этого должно выполняться условие  Используя при вычислении импульсного отклика удовлетворяющее этому условию значение величины
Используя при вычислении импульсного отклика удовлетворяющее этому условию значение величины  (например, в случае
(например, в случае  можно принять
можно принять  находим ширину импульсного отклика равной
находим ширину импульсного отклика равной 
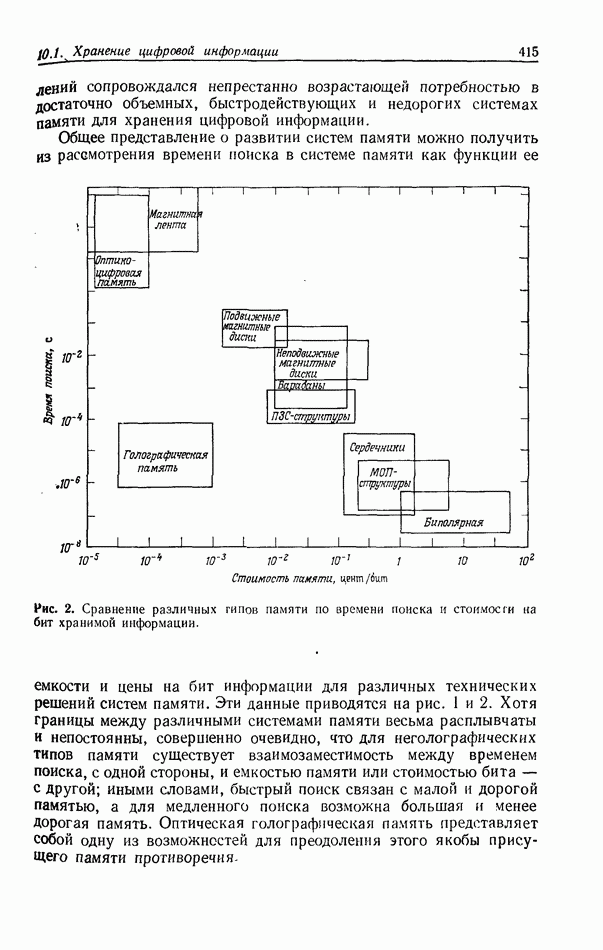
Таблица 3 (см. скан) Требования к разрешающей способности и полосе пропускания материала, используемого для записи СПФ в корреляторе с частотной плоскостью
В табл. 3 обобщены требования к разрешающей способности (в линиях на  и ширине полосы пропускания пространственных частот (определяемой по числу линий или разрешимых точек) коррелятора для трех указанных выше случаев.
и ширине полосы пропускания пространственных частот (определяемой по числу линий или разрешимых точек) коррелятора для трех указанных выше случаев.
Рассмотрим теперь контрастность интерференционной картины в плоскости  Это принесет пользу при обсуждении вопроса об оптимизации параметров СПФ (см. разд. 10.5.15), а также облегчит анализ других схем корреляторов. Если в выражении (1) записать амплитуду и фазу комплексной переменной
Это принесет пользу при обсуждении вопроса об оптимизации параметров СПФ (см. разд. 10.5.15), а также облегчит анализ других схем корреляторов. Если в выражении (1) записать амплитуду и фазу комплексной переменной  в виде
в виде  то можно получить следующее выражение для экспозиции в плоскости
то можно получить следующее выражение для экспозиции в плоскости 

где  время экспозиции. Если записать экспозицию смещения рабочей точки в виде
время экспозиции. Если записать экспозицию смещения рабочей точки в виде  среднюю экспозицию как
среднюю экспозицию как  а отношение интенсивностей опорного и объектного пучков примем равным
а отношение интенсивностей опорного и объектного пучков примем равным  то выражение (4) и принимает вид
то выражение (4) и принимает вид

где  Единственное замечание, которое мы хотим сделать, — это то, что К изменяется в пространстве, поскольку изменяется
Единственное замечание, которое мы хотим сделать, — это то, что К изменяется в пространстве, поскольку изменяется  и тем самым создается модуляция интерференционных полос, которая зависит от
и тем самым создается модуляция интерференционных полос, которая зависит от  и от характера кривой
и от характера кривой  (зависимость амплитудного пропускания от экспозиции) для материала, используемого при записи СПФ в плоскости
(зависимость амплитудного пропускания от экспозиции) для материала, используемого при записи СПФ в плоскости  Выбор оптимальных параметров СПФ и использование их для ослабления деградации корреляции мы подробно обсудим в разд. 10.5.15 и 10.5.16.
Выбор оптимальных параметров СПФ и использование их для ослабления деградации корреляции мы подробно обсудим в разд. 10.5.15 и 10.5.16.
В заключение рассмотрим вопрос о том, какие можно допустить с практической точки зрения относительные смещения элементов коррелятора с частотной плоскостью и их вибрацию. Для простоты проанализируем одномерный случай. Напишем выражение для автокорреляции входной функции 

где  одномерный фурье-образ функции
одномерный фурье-образ функции  определяемый следующим образом:
определяемый следующим образом:

Если СПФ вида  сместить в частотной плоскости на величину А и, то для автокорреляционной функции имеем
сместить в частотной плоскости на величину А и, то для автокорреляционной функции имеем

Отсюда следует, что фазовые искажения, обусловленные смещением фильтра на величину А и, должны удовлетворять соотношению где  ширина входного сигнала, причем предполагается. что ширина автокорреляционной функции равна
ширина входного сигнала, причем предполагается. что ширина автокорреляционной функции равна  Чтобы обеспечить хорошую интерференционную картину, мы
Чтобы обеспечить хорошую интерференционную картину, мы
должны потребовать выполнения условия  Сделав подстановку
Сделав подстановку  находим выражение для допуска на смещение фильтра:
находим выражение для допуска на смещение фильтра:

В случае  допустимое отклонение в положении фильтра не должно превышать
допустимое отклонение в положении фильтра не должно превышать 
Разумеется, в объеме данного параграфа нельзя подробно рассмотреть допуски на точность установки фильтра для каждой из рассматриваемых здесь 13 схем оптических корреляторов. Мы рассмотрели многие практически важные вопросы оптической корреляции на примере только одной схемы коррелятора, поскольку эта схема получила наиболее широкое применение. С другой стороны, приведенное здесь рассмотрение хорошо иллюстрирует методы анализа и операции, которые можно также с успехом использовать для определения аналогичных характеристик в случае других схем корреляторов.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
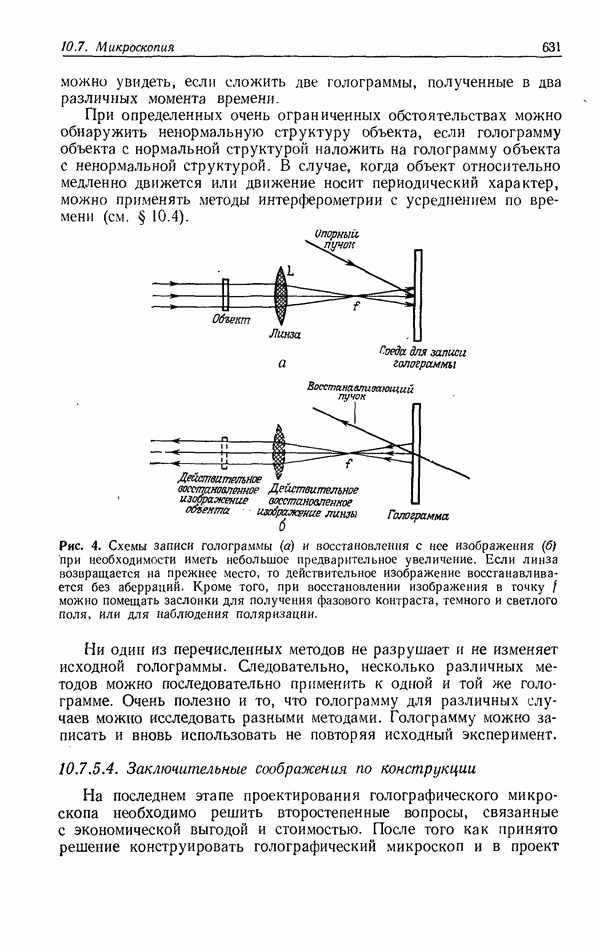
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
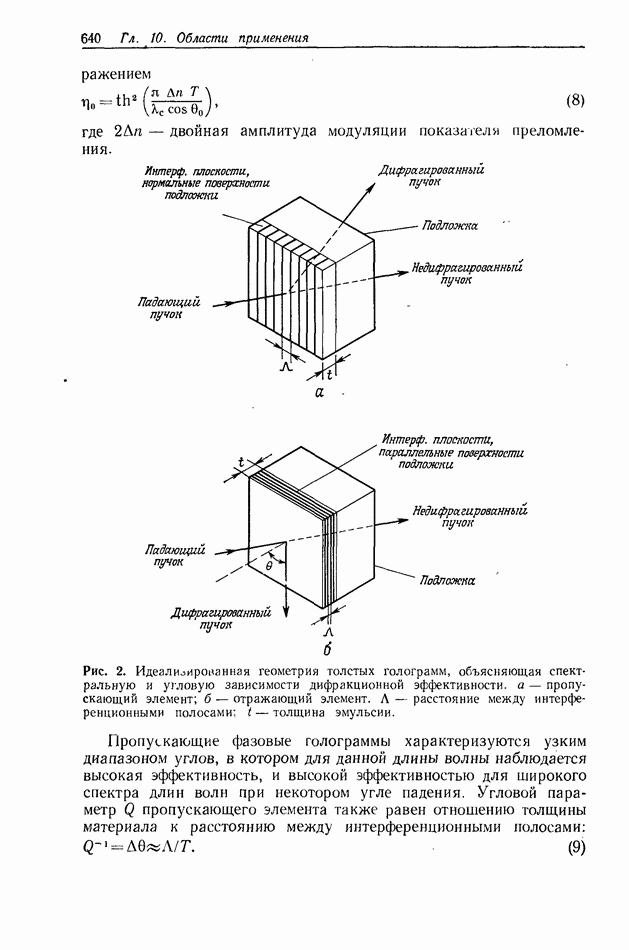
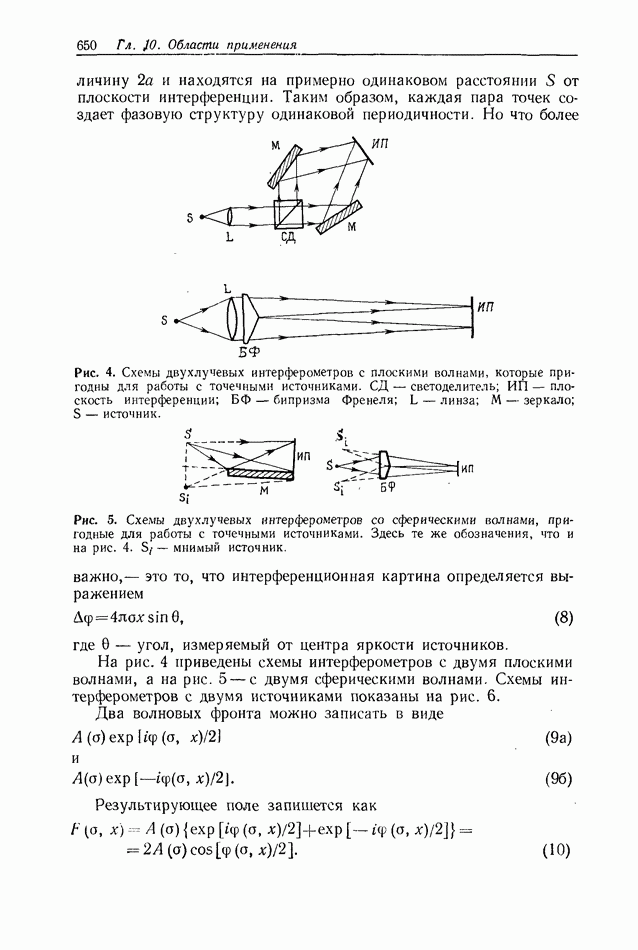
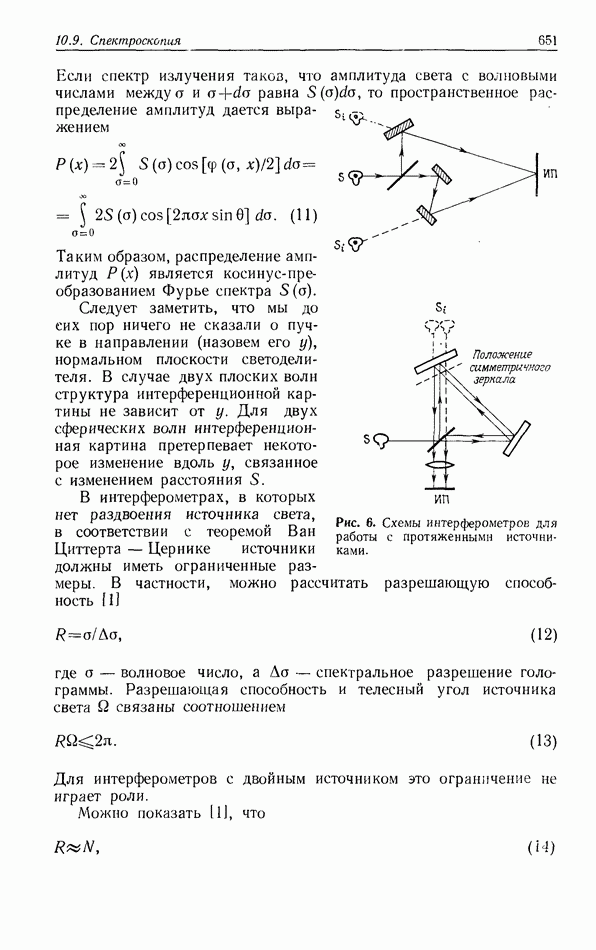
- 10.9. СПЕКТРОСКОПИЯ
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ