| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
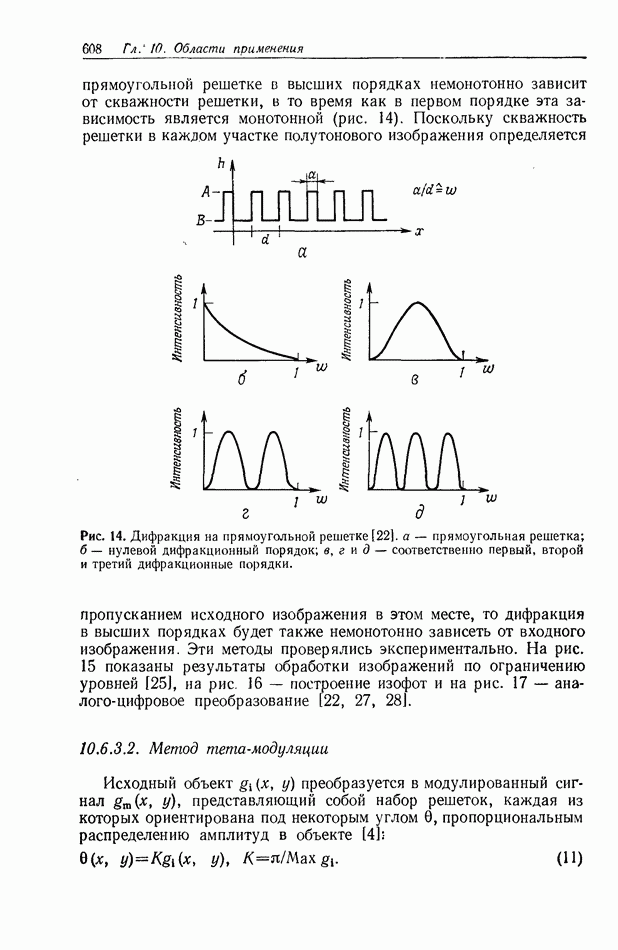
Рассмотренные ранее волновой и лучевой варианты теории трехмерной голограммы весьма наглядны, однако имеют тот недостаток, что в дополнение к ограничениям, накладываемым на величину дифракционной эффективности самим характером первого приближения, требуют также еще введения ограничений, свойственных приближению геометрической оптики. Вместе с тем такого рода ограничения совершенно не характерны для механизма записи голограммы, который, как известно, обеспечивает регистрацию не только малых объектов, но и объектов большой протяженности. В связи с этим рассмотрим два варианта теории, базирующейся на решении волнового уравнения, ограничиваясь при этом только рамками кинематического приближения и не накладывая каких-либо ограничений на размеры регистрируемого на голограмме объекта. В соответствии со смыслом характерных для этих представлений преобразований их можно назвать пространственным и частотным операторными вариантами теории трехмерной голограммы [2, 5].
Остановимся сначала на координатных представлениях. Пусть  волновые функции излучения, создаваемого источником
волновые функции излучения, создаваемого источником  и рассеянного объектом соответственно. Складывая эти функции
и рассеянного объектом соответственно. Складывая эти функции  и умножая результат на сопряженную величину, находим распределение интенсивности стоячей волны, записываемой в объеме голограммы:
и умножая результат на сопряженную величину, находим распределение интенсивности стоячей волны, записываемой в объеме голограммы:

здесь  амплитуды соответствующих волновых функций. Нетрудно заметить, что модуляционные члены, являющиеся третьим и четвертым слагаемыми, обладают интересным свойством. Третий член представляет собой оператор поточечного преобразования волновой функции в волновую функцию
амплитуды соответствующих волновых функций. Нетрудно заметить, что модуляционные члены, являющиеся третьим и четвертым слагаемыми, обладают интересным свойством. Третий член представляет собой оператор поточечного преобразования волновой функции в волновую функцию  о и соответствует случаю восстановления волны объекта. Четвертый член является оператором преобразования в
о и соответствует случаю восстановления волны объекта. Четвертый член является оператором преобразования в  и отвечает восстановлению обращенной волны. Введем для этих операторов специальные обозначения и запишем осуществляемые ими операции
и отвечает восстановлению обращенной волны. Введем для этих операторов специальные обозначения и запишем осуществляемые ими операции

Рассмотрим, каким образом это свойство распределения интенсивности стоячей волны определяет отображающие свойства голограммы. Предположим, что после экспозиции и проявления в объеме голограммы образовался фотографический осадок, характеризующийся распределением диэлектрической проницаемости  пропорциональным интенсивности стоячей волны. Это распределение можно записать в виде
пропорциональным интенсивности стоячей волны. Это распределение можно записать в виде

где  некоторое первоначальное значение диэлектрической проницаемости, а
некоторое первоначальное значение диэлектрической проницаемости, а  приращение, обусловленное экспозицией, причем
приращение, обусловленное экспозицией, причем

здесь  некоторый коэффициент пропорциональности, а
некоторый коэффициент пропорциональности, а  функция распределения интенсивности стоячей волны, определяемая выражением (6). Волновая функция излучения, восстановленного голограммой, должна удовлетворять уравнению Гельмгольца
функция распределения интенсивности стоячей волны, определяемая выражением (6). Волновая функция излучения, восстановленного голограммой, должна удовлетворять уравнению Гельмгольца

Запишем решение этого уравнения в виде суммы двух волновых функций: волновой функции удовлетворяющей уравнению
невозмущенной задачи, и малого возмущения обусловленного появлением небольшого приращения диэлектрической проницаемости. Таким образом,

Подставляя это равенство и выражение (11) в (13), получаем

В этом уравнении первые два члена обращаются в нуль, в силу того что они удовлетворяют уравнению невозмущенной задачи. Третьим членом можно пренебречь, поскольку он содержит произведение двух малых величин  и Оставшиеся три члена образуют неоднородное уравнение Гельмгольца
и Оставшиеся три члена образуют неоднородное уравнение Гельмгольца

Решение этого уравнения записывается в виде


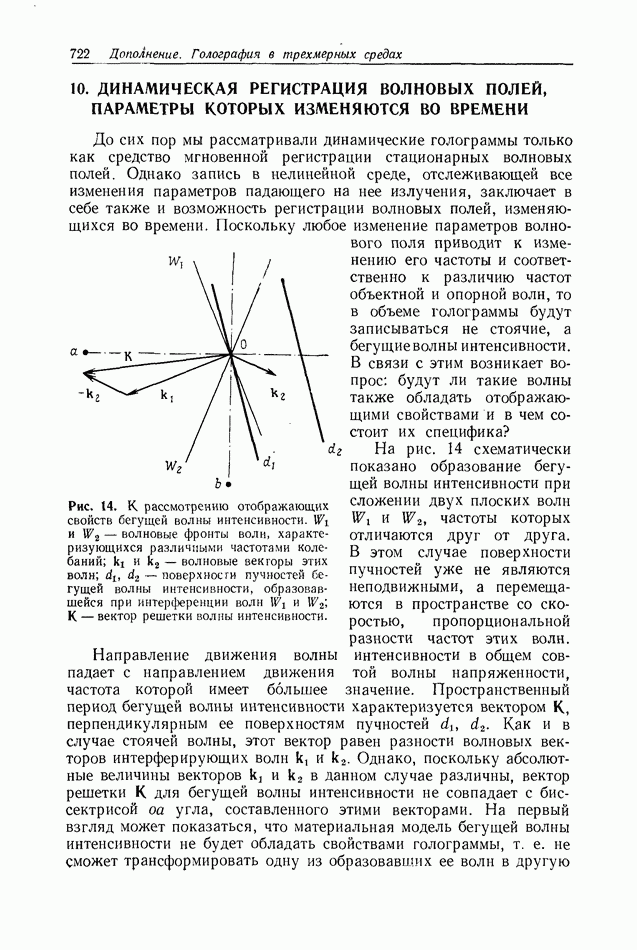
Рис. 3. К рассмотрению пространственного варианта кинематической теории трехмерной голограммы. V — объем трехмерной голограммы;  элемент объема; h - точка наблюдения;
элемент объема; h - точка наблюдения;  -радиус-вектор, связывающий точку наблюдения с элементом объема
-радиус-вектор, связывающий точку наблюдения с элементом объема  один из плоских слоев, на которые можно разбить объем голограммы при интегрировании с использованием формулы Кирхгофа — Зоммерфельда;
один из плоских слоев, на которые можно разбить объем голограммы при интегрировании с использованием формулы Кирхгофа — Зоммерфельда;  волновая функция излучения объекта, восстановленная в точках объема голограммы; — созданная излучением всех точек объема волновая функция, которая совпадает со значением объектной волны в точке А.
волновая функция излучения объекта, восстановленная в точках объема голограммы; — созданная излучением всех точек объема волновая функция, которая совпадает со значением объектной волны в точке А.
Подставляя сюда значение  найденное из выражений (12) и (6), и ограничиваясь одним слагаемым
найденное из выражений (12) и (6), и ограничиваясь одним слагаемым  соответствующим оператору
соответствующим оператору  определяемому формулой (7), в соответствии со свойством этого оператора (8) находим
определяемому формулой (7), в соответствии со свойством этого оператора (8) находим

Это выражение по существу определяет значение, которое имеет в некоторой точке наблюдения  волна, созданная источниками, колеблющимися в каждой точке объема голограммы V сиифазно с волной
волна, созданная источниками, колеблющимися в каждой точке объема голограммы V сиифазно с волной  излучения, рассеянного объектом. Действительно, как это видно из выражения (18) (см. также рис. 3), каждый элементарный объем голограммы
излучения, рассеянного объектом. Действительно, как это видно из выражения (18) (см. также рис. 3), каждый элементарный объем голограммы  испускает колебания с амплитудой
испускает колебания с амплитудой  Распространяясь от объема
Распространяясь от объема  точки наблюдения
точки наблюдения  удаленной от него на расстояние
удаленной от него на расстояние  амплитуда испущенной этим объемом волны уменьшается обрагло пропорционально пройденному волной пути
амплитуда испущенной этим объемом волны уменьшается обрагло пропорционально пройденному волной пути  а набег фазы
а набег фазы  этом пути равен
этом пути равен 
Нетрудно понять, что имеющая такой смысл функция определяет волну, совпадающую по существу с объектной волной  Убедиться в этом можно несколькими способами. В частности, можно заметить, что выражение (18) формально совпадает с выражением, описывающим объектную волну, которая пересекла на своем пути объем V, заполненный усиливающей средой
Убедиться в этом можно несколькими способами. В частности, можно заметить, что выражение (18) формально совпадает с выражением, описывающим объектную волну, которая пересекла на своем пути объем V, заполненный усиливающей средой  Очевидно, что в результате такого усиления увеличится лишь амплитуда объектной волны, а форма ее волнового фронта останется без изменения. Другой вариант отождествления волновой функции основан на выполнении интегрирования по объему V посредством разбиения этого объема на плоские слои толщиной
Очевидно, что в результате такого усиления увеличится лишь амплитуда объектной волны, а форма ее волнового фронта останется без изменения. Другой вариант отождествления волновой функции основан на выполнении интегрирования по объему V посредством разбиения этого объема на плоские слои толщиной  В соответствии с известной формулой Кирхгофа — Зоммерфельда интеграл по каждому такому слою с точностью до несущественного (в данном случае косинусного члена) будет равен значению волновой функции
В соответствии с известной формулой Кирхгофа — Зоммерфельда интеграл по каждому такому слою с точностью до несущественного (в данном случае косинусного члена) будет равен значению волновой функции  в точке наблюдения
в точке наблюдения  Суммирование по всем слоям приводит лишь к увеличению амплитуды восстановленной объектной волны.
Суммирование по всем слоям приводит лишь к увеличению амплитуды восстановленной объектной волны.
Перейдем теперь к рассмотрению частотного представления [5, 6]. В этом случае процесс записи и восстановления трехмерной голограммы рассматривается в пространстве Фурье. Запишем волновые функции падающего на голограмму и восстановленного ею излучения в виде разложения по плоским волнам, а структуру голограммы представим в виде разложения по трехмерным гармоникам. Тогда процесс восстановления голограммы можно рассматривать как преобразование каждой плоской волны в компоненты восстановленной волны посредством отражения от соответствующих гармоник голограммы. Таким образом, основным элементом разложения структуры голограммы является пространственная гармоника. Рассмотрим свойства таких гармоник более подробно.
Предположим, что волновые функции падающего на голограмму излучения и излучения, рассеянного объектом, представлены в виде разложения по плоским волнам, и выделим по одной компоненте  из этих разложений:
из этих разложений:

и

где  волновые векторы, нормальные фронтам интерферирующих плоских волн. При этом имеет место очевидное в данном случае соотношение
волновые векторы, нормальные фронтам интерферирующих плоских волн. При этом имеет место очевидное в данном случае соотношение

где  длина волны в среде, в которой происходит интерференция. Складывая величины
длина волны в среде, в которой происходит интерференция. Складывая величины  и умножая результат на
и умножая результат на
сопряженную величину, находим интенсивность стоячей волны, образующейся при интерференции рассматриваемых плоских волн:

Нетрудно заметить, что это выражение описывает пространственную гармонику, пространственная частота и ориентация которой характеризуются вектором решетки К, аналогичным по физическому смыслу волновому вектору к:

Пространственный период гармоники  связан с величиной вектора решетки К соотношением, аналогичным (21):
связан с величиной вектора решетки К соотношением, аналогичным (21):


Рис. 4. К рассмотрению частотного варианта кинематической теории трехмерной голограммы. V — объем трехмерной голограммы;  волновые векторы плоских волн, интерферирующих в объеме голограммы;
волновые векторы плоских волн, интерферирующих в объеме голограммы;  поверхности пучностей гармоники, образовавшейся при интерференции плоских волн; К — вектор решетки этой гармоники;
поверхности пучностей гармоники, образовавшейся при интерференции плоских волн; К — вектор решетки этой гармоники;  ее пространственный период;
ее пространственный период;  поверхность сферы Эвальда.
поверхность сферы Эвальда.
На рис. 4 представлена схема образования пространственной гармоники. Из рисунка следует, что волновые векторы интерферирующих плоских волн связаны с век тором решетки соотношением

Подставив в это выражение значения  и
и  из (24) и (21), получим зависимость длины волны от угла между интерферирующими плоскими волнами и от пространственного периода образованной этими волнами гармоники:
из (24) и (21), получим зависимость длины волны от угла между интерферирующими плоскими волнами и от пространственного периода образованной этими волнами гармоники:

Предположим, что образованная при интерференции плоских волн гармоника интенсивности записана на голограмме, в результате чего мы получили структуру, диэлектрическая проницаемость которой также изменяется по гармоническому закону. Как известно, в соответствии с условием Брэгга такая пространственная решетка отражает только те плоские волны, угол падения которых  и длина волны К удовлетворяют соотношению, совпадающему в точности с выражением (26). Остальные плоские волны проходят черег эту структуру беспрепятственно.
и длина волны К удовлетворяют соотношению, совпадающему в точности с выражением (26). Остальные плоские волны проходят черег эту структуру беспрепятственно.
Таким образом, условие отражения излучения от пространственной гармоники имеет тот же вид, что и условие ее образования. Очевидно, что при этих обстоятельствах каждая из гармоник, взаимодействуя с излучением, выберет из него именно ту составляющую, которая участвовала в образовании этой гармоники при записи, и преобразует ее в соответствующую составляющую волновой функции излучения, рассеянного объектом. Рассматривая интерференцию всех плоских волн, из которых составлено падающее излучение, с плоскими волнами излучения, отраженного объектом, и используя упомянутое свойство пространственной гармоники, образованной при интерференции двух плоских волн, можно показать, что волновые функции излучения, отраженного трехмерной голограммой и объектом, совпадают.
При использовании частотного варианта теории весьма полезно опираться на понятие «сферы взаимодействия», или «сферы Эваль-да». Этот геометрический образ непосредственно следует из выражения (23), которое связывает вектор решетки К с волновыми векторами взаимодействующих с этой решеткой волн, а также из неявно сопровождающего это выражение условия равенства абсолютных значений этих волновых векторов.
Очевидно, что в частотном пространстве условие равенства длин волн полей излучения, интерферирующих при записи голограммы, а также полей излучения, падающего на голограмму и отраженного ею при восстановлении, сводится к тому, что концы волновых векторов, описывающих это излучение плоских волн, должны находиться на поверхности сферы о, радиус которой равен волновому числу  (рис. 4). При этом из выражения (23) следует, что концы векторов всех решеток, которые можно записать в объеме голограммы или считать излучением на данной длине волны, также должны касаться поверхности указанной сферы.
(рис. 4). При этом из выражения (23) следует, что концы векторов всех решеток, которые можно записать в объеме голограммы или считать излучением на данной длине волны, также должны касаться поверхности указанной сферы.
Наиболее существенные следствия частотного варианта теории трехмерной голограммы получил ван Хирден, который предложил так называемую запись трехмерных голограмм без использования опорной волны. Он показал, что процесс считывания трехмерной голограммы обладает свойством ассоциативности, похожим на ассоциативную память мозга, а также предложил использовать трехмерную голограмму для сверхплотной записи информации [6].
| << Предыдущий параграф | Следующий параграф >> |
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
- 10.9. СПЕКТРОСКОПИЯ
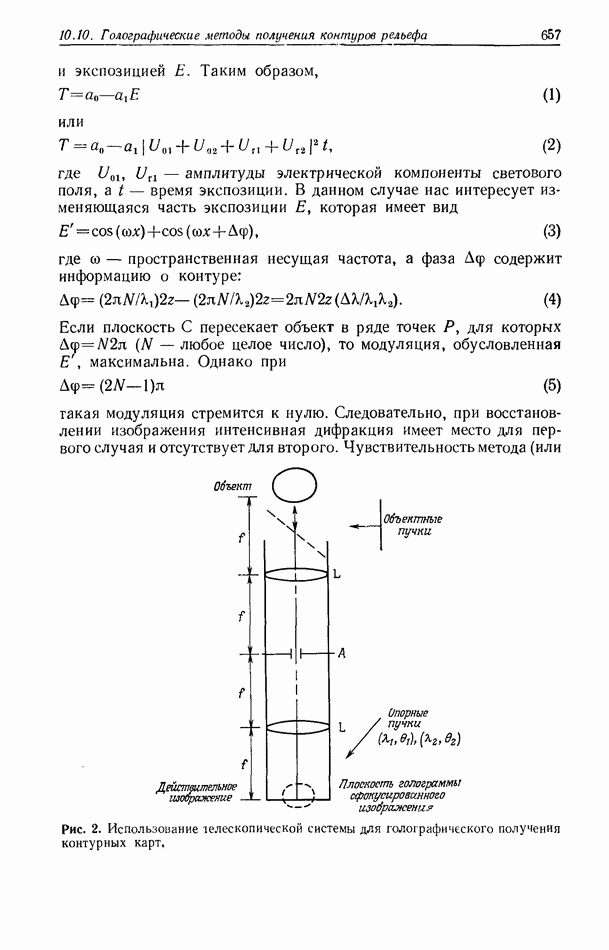
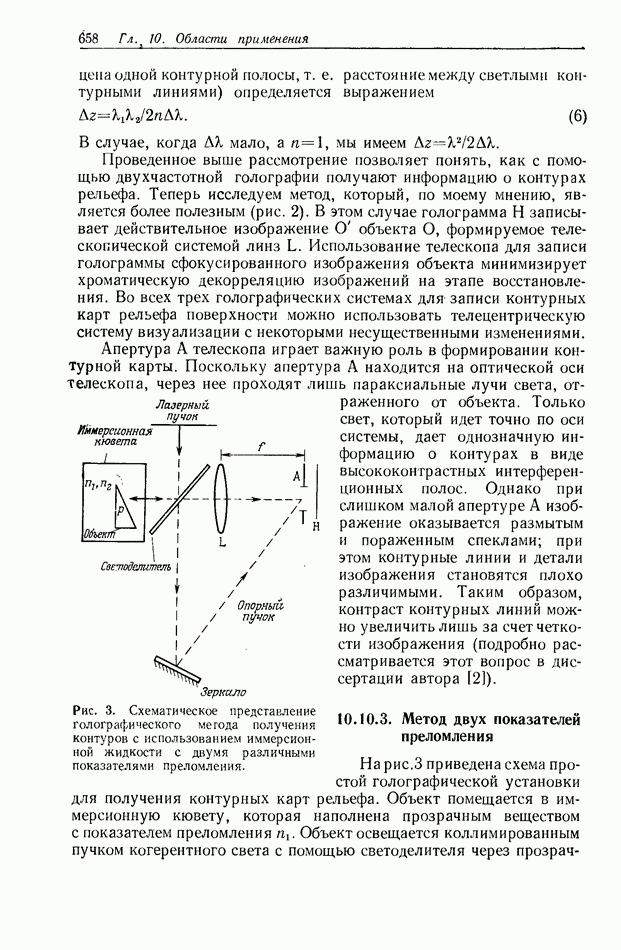
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
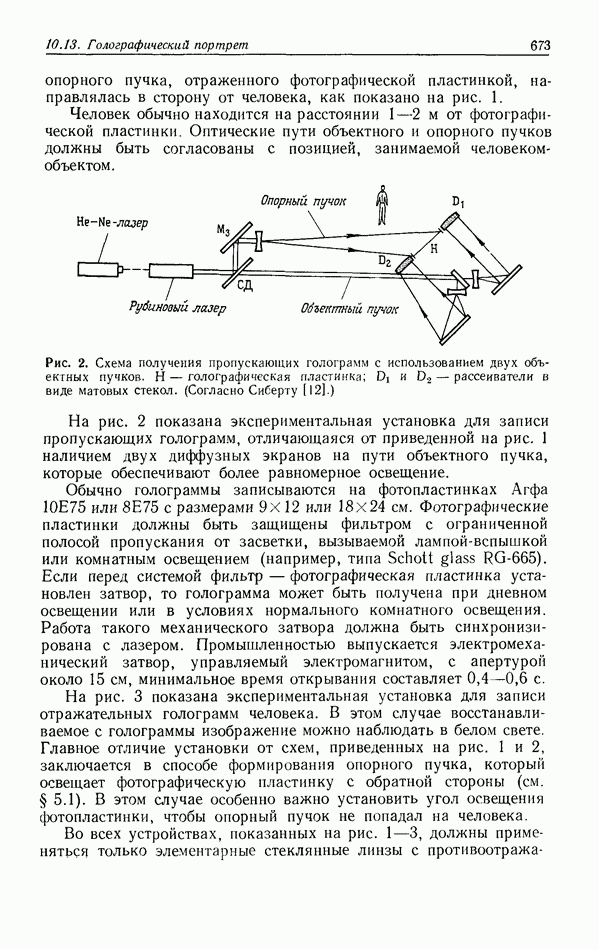
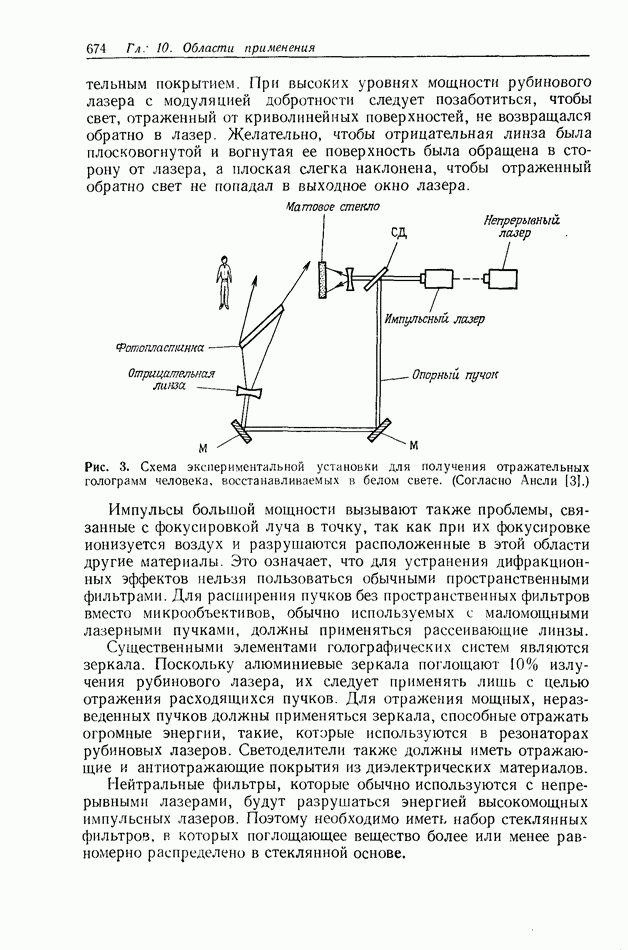
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ