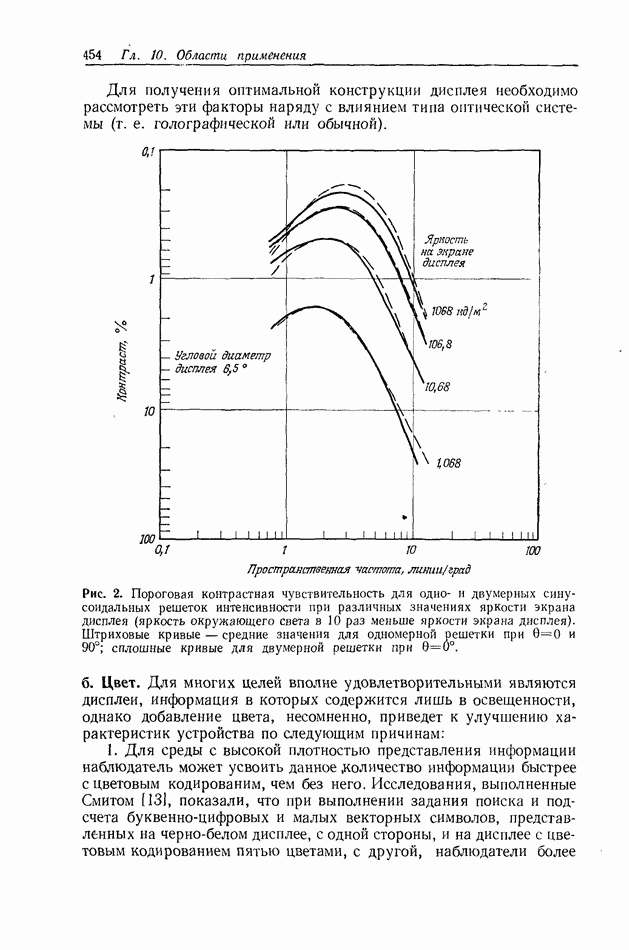
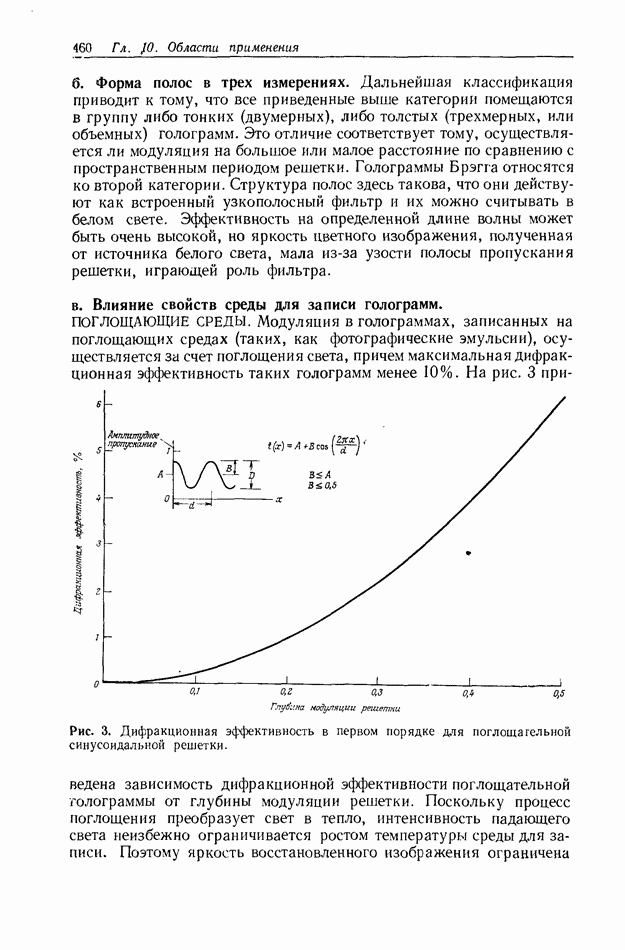
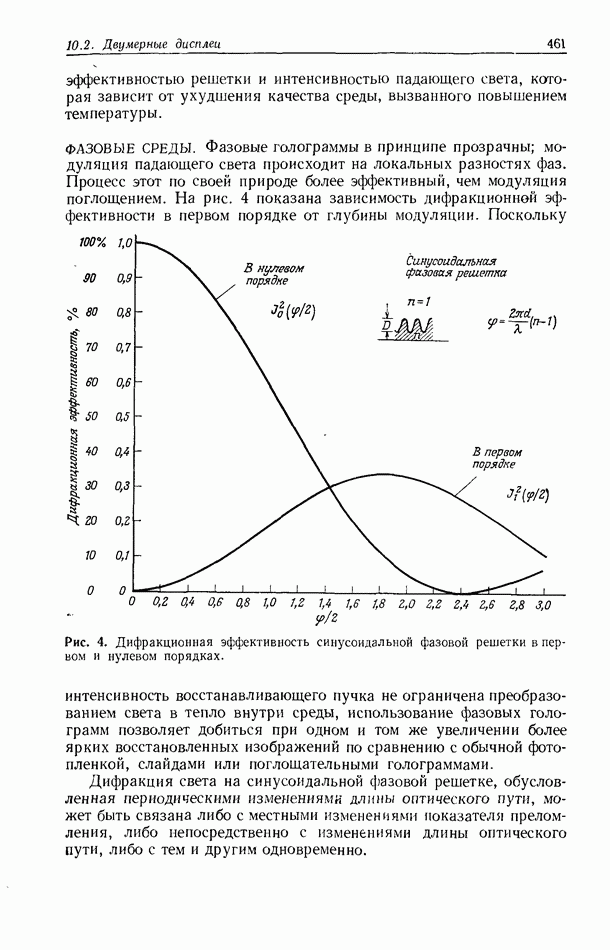
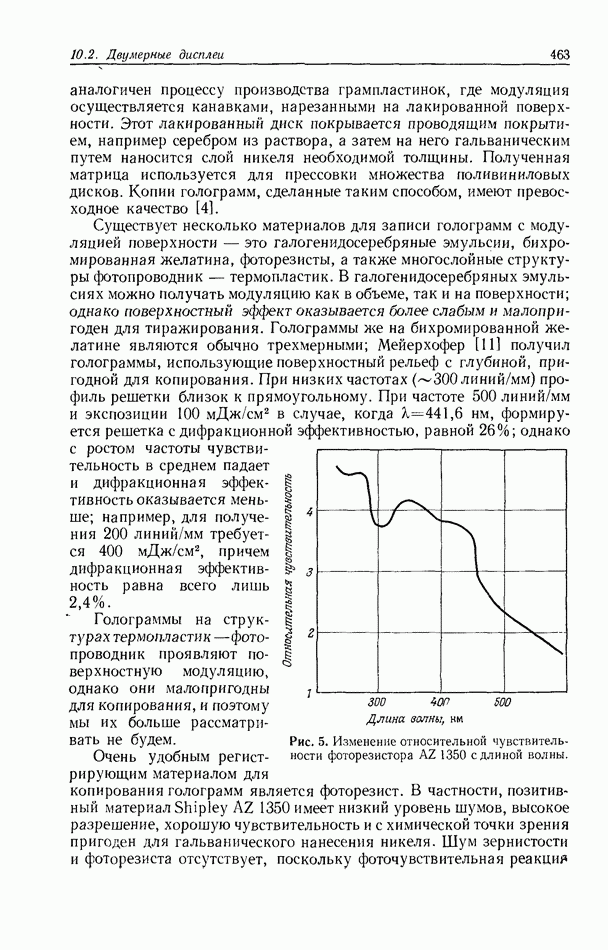
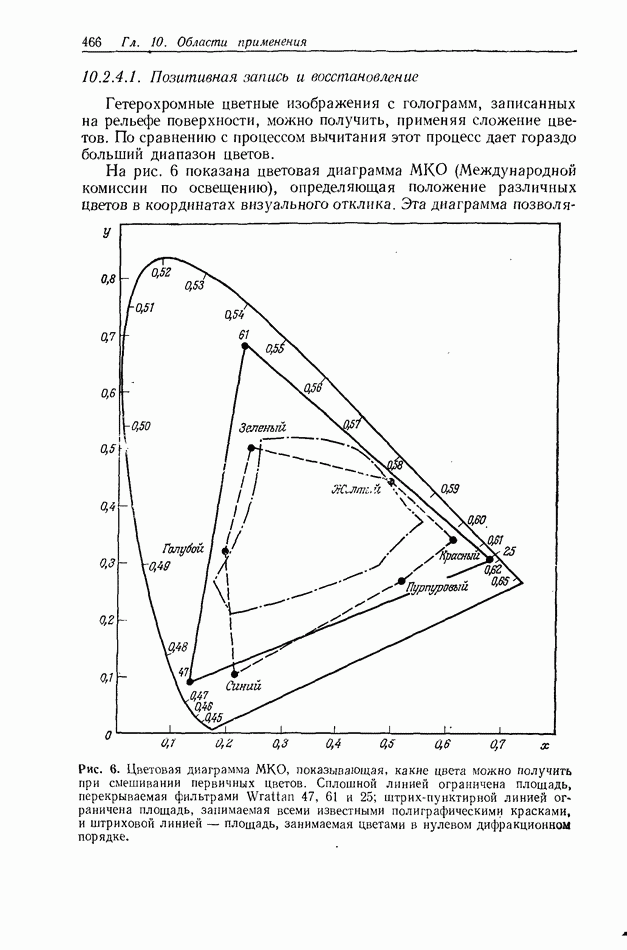
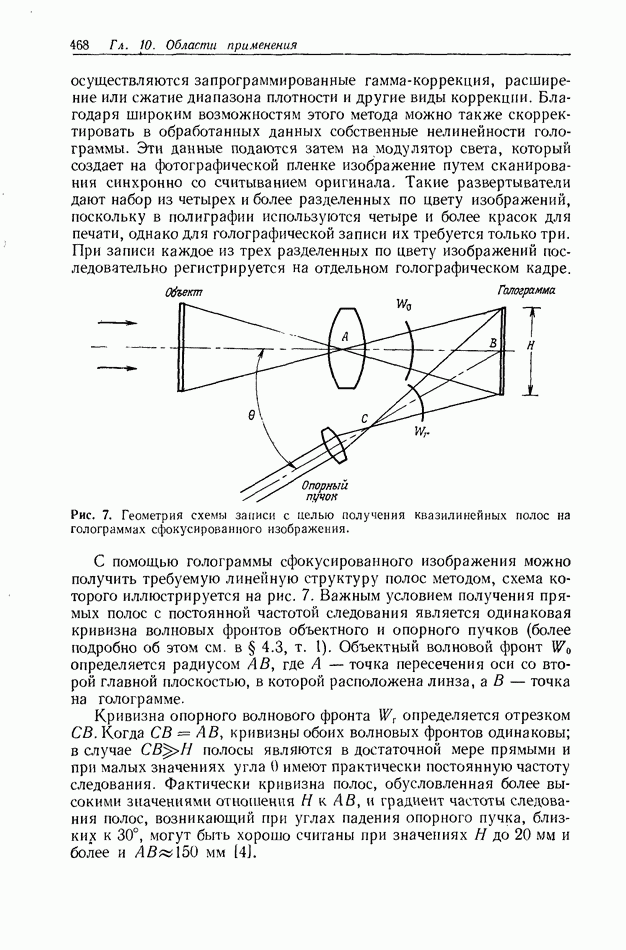
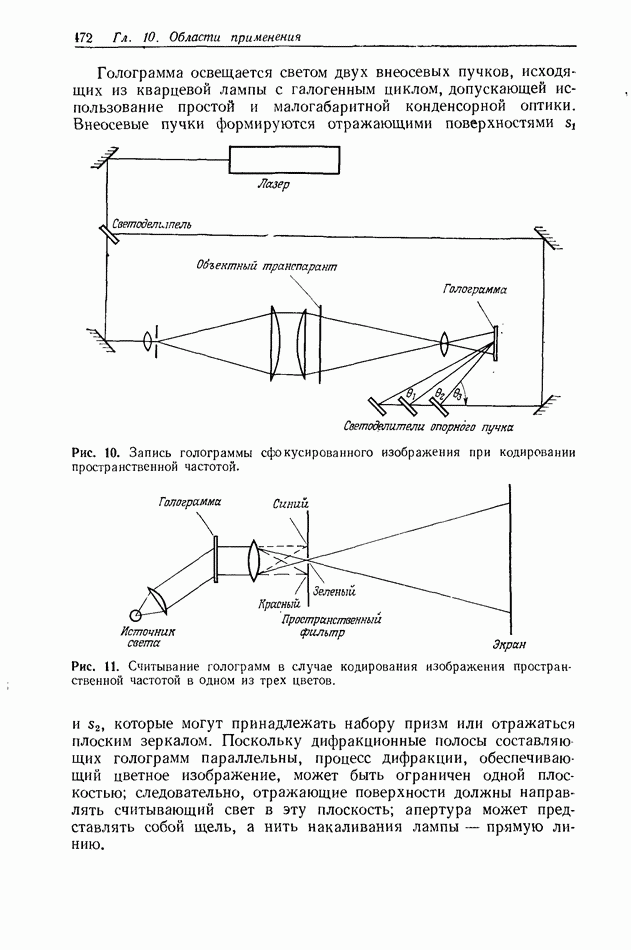
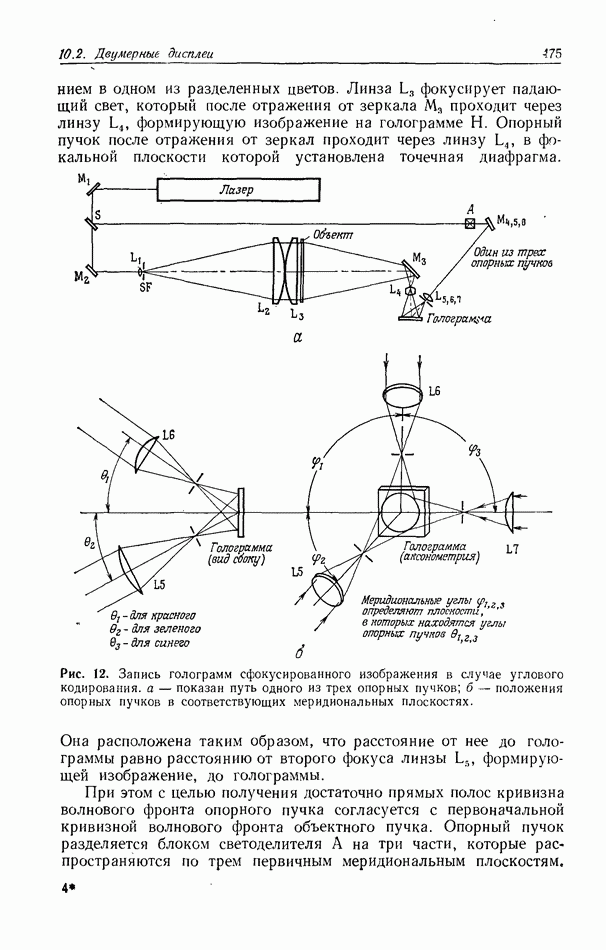
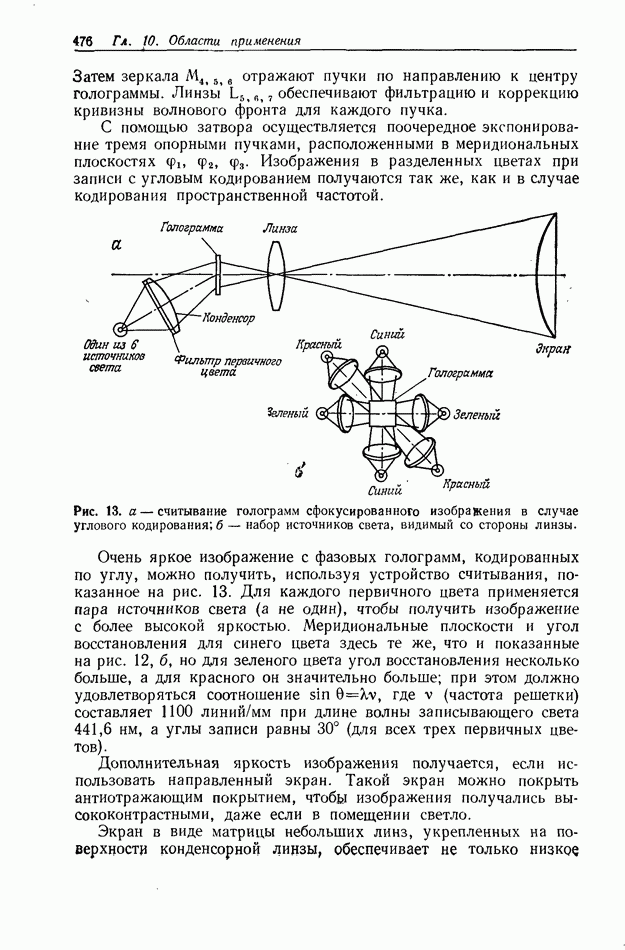
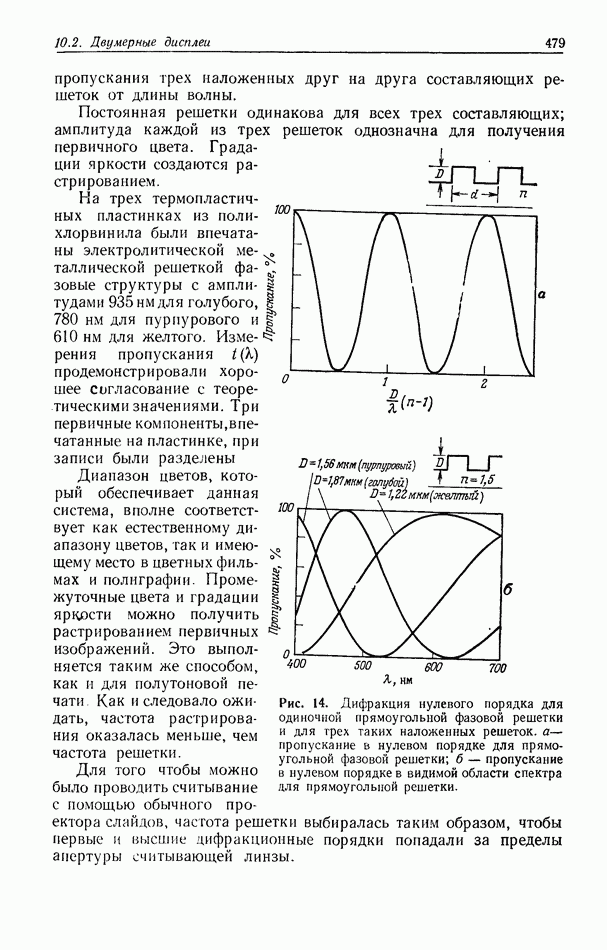
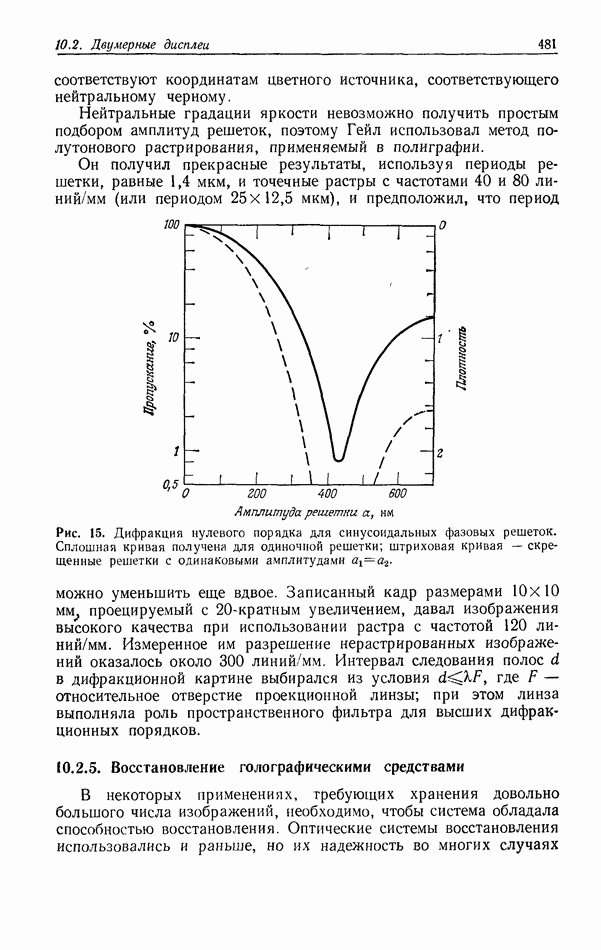
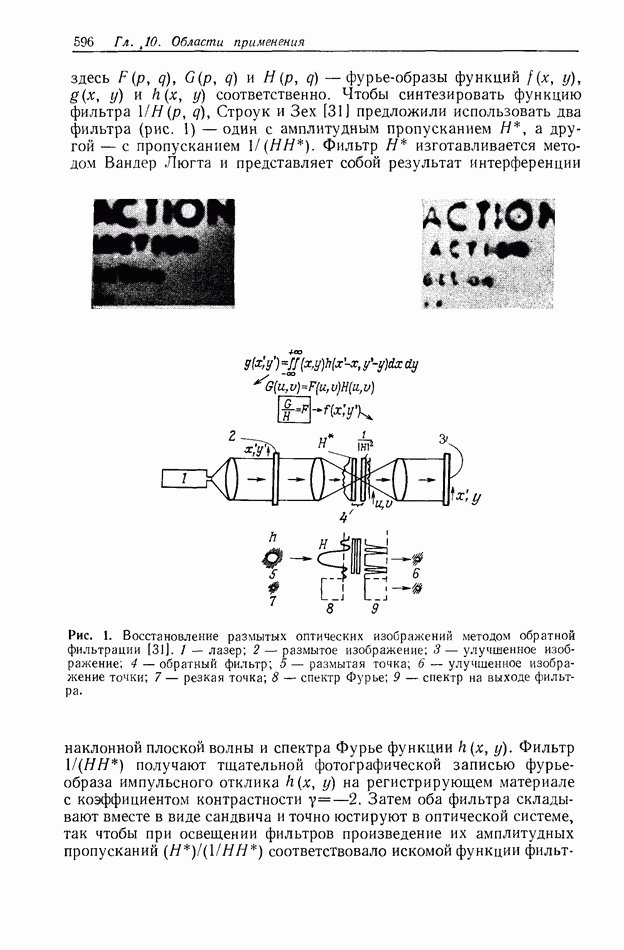
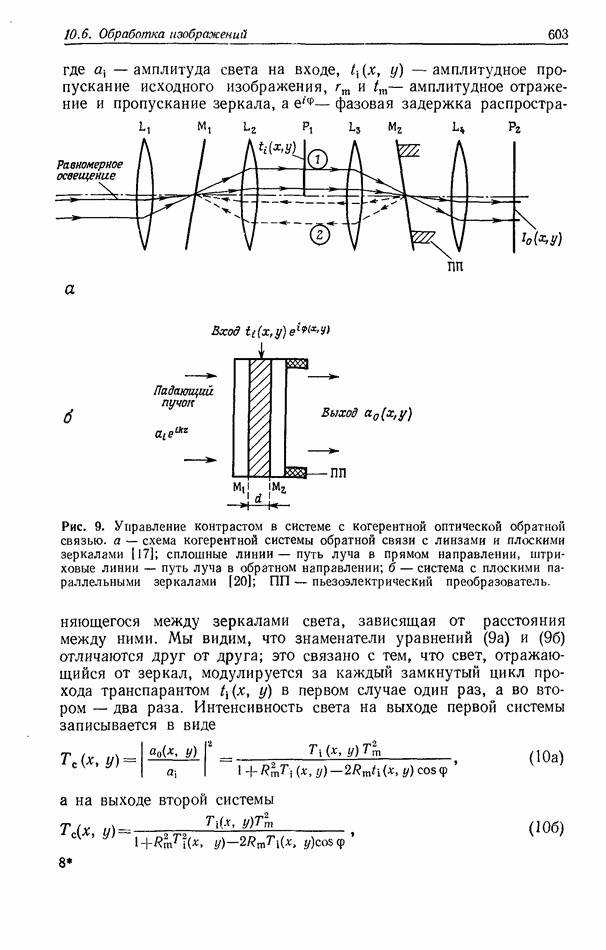
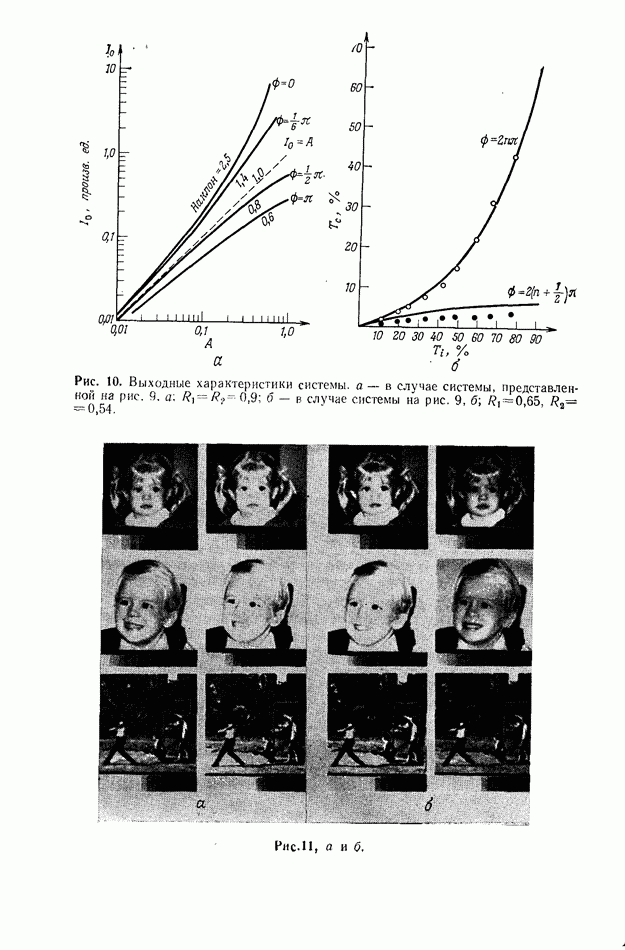
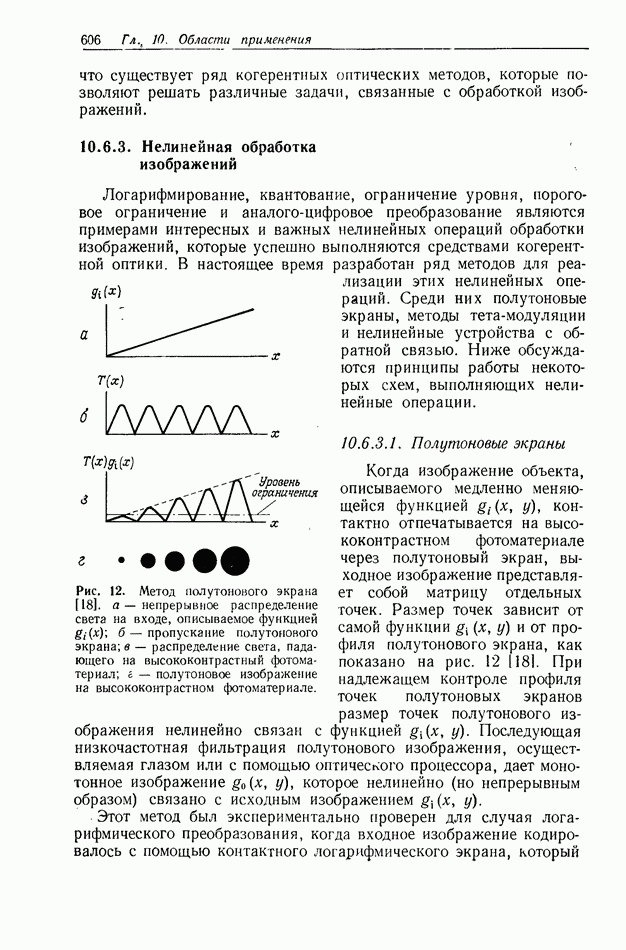
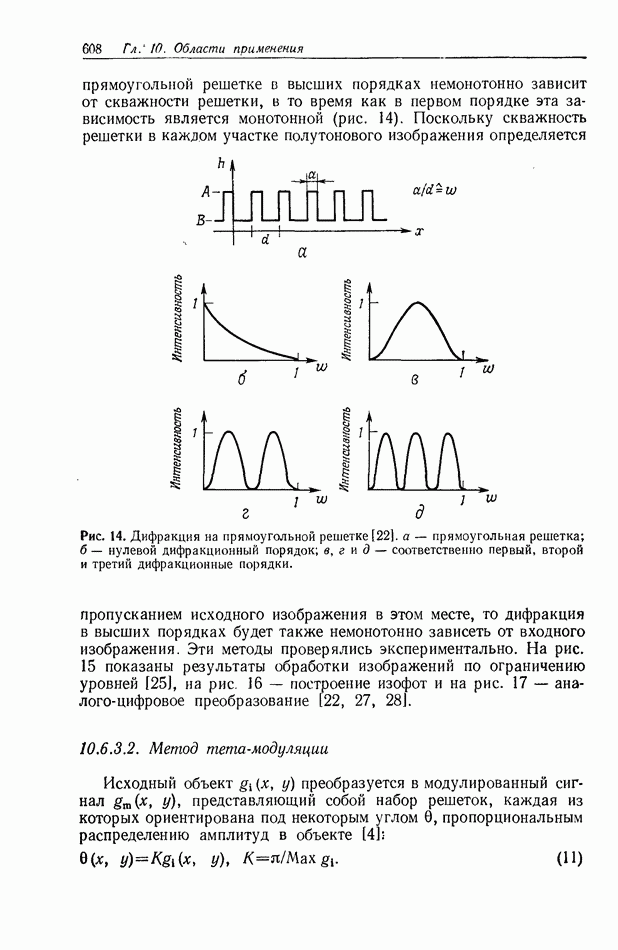
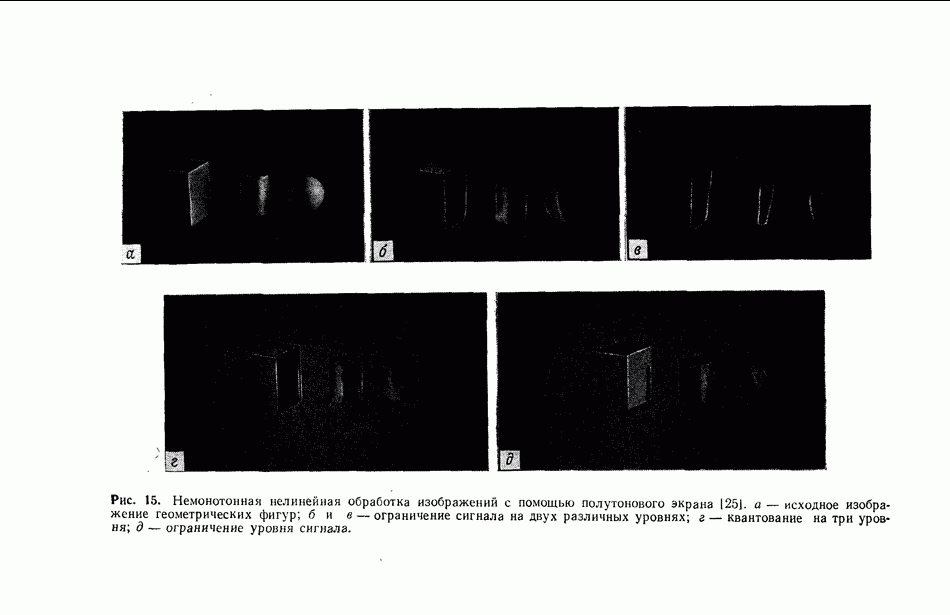
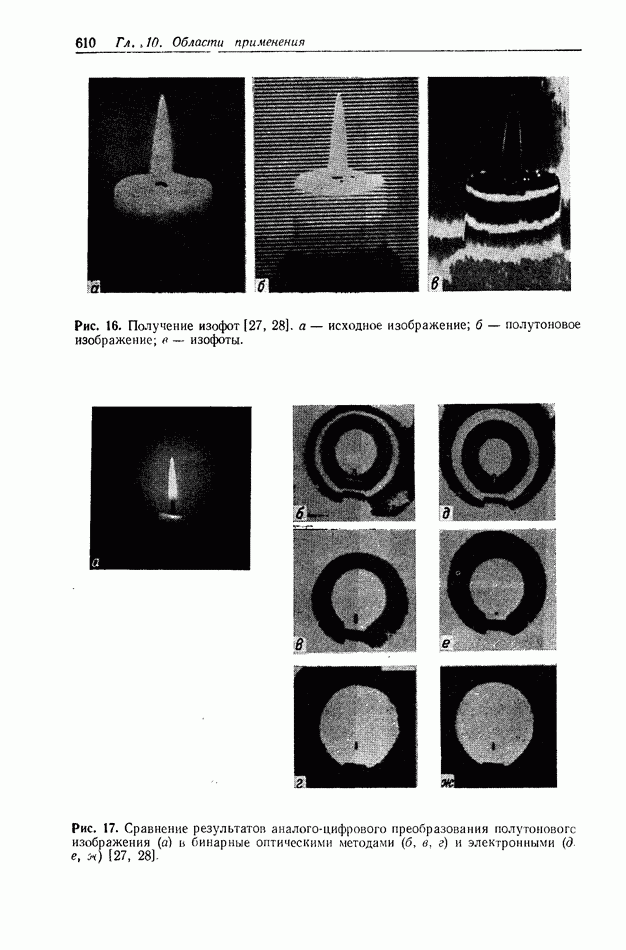
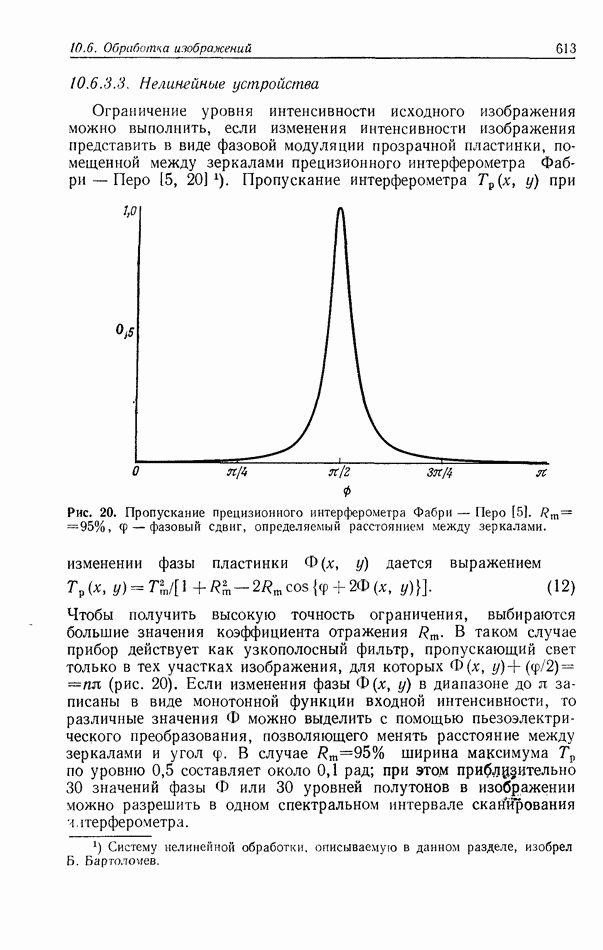
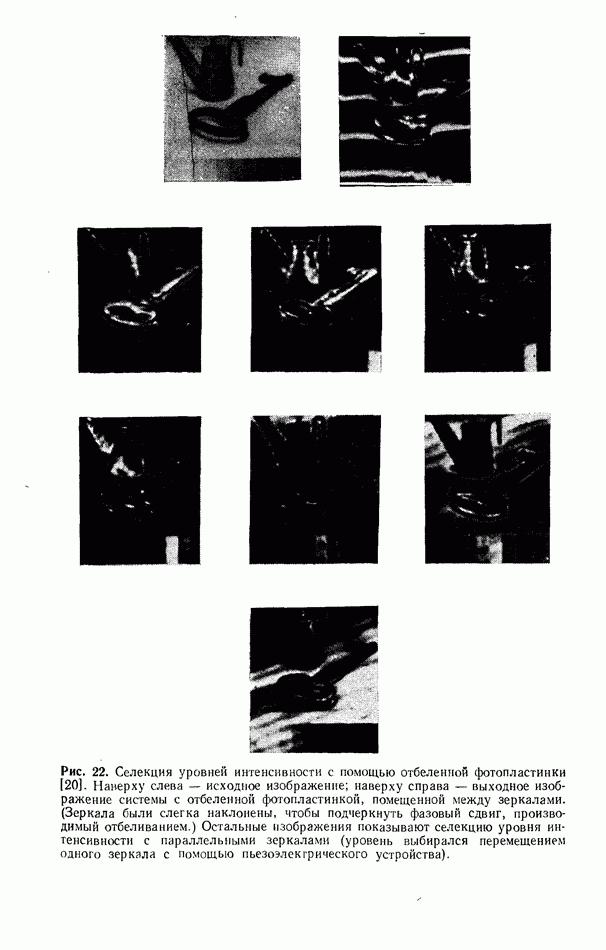
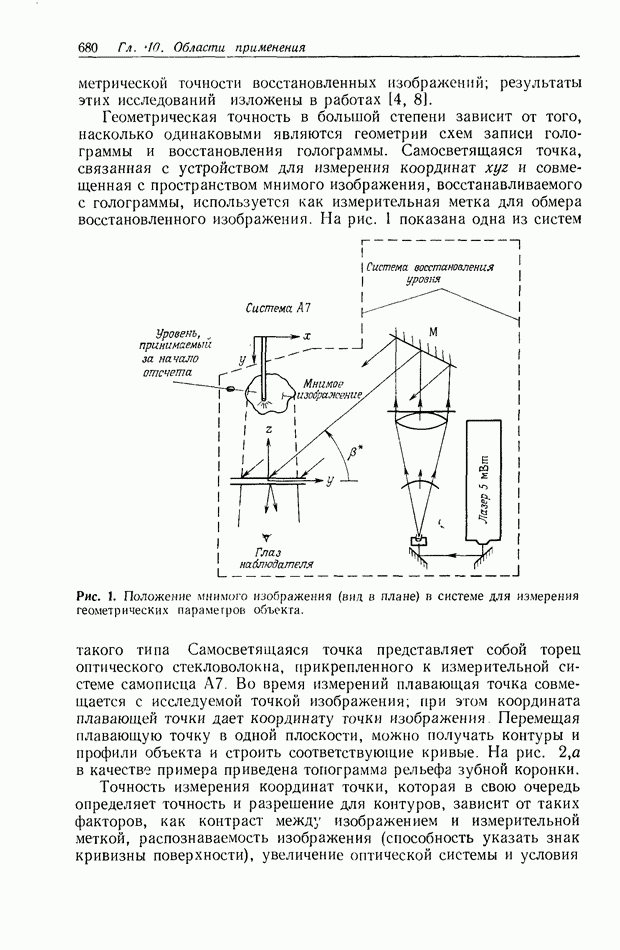
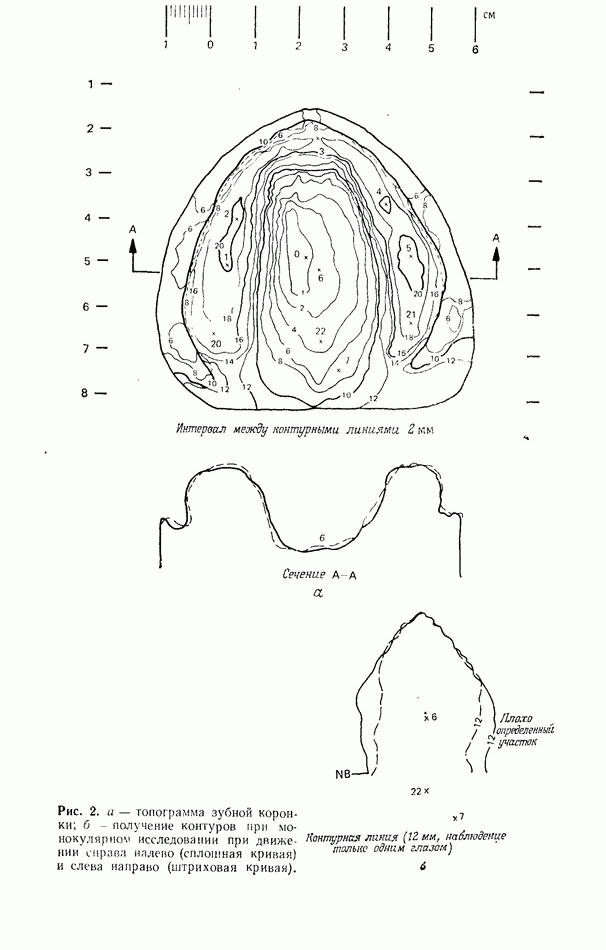
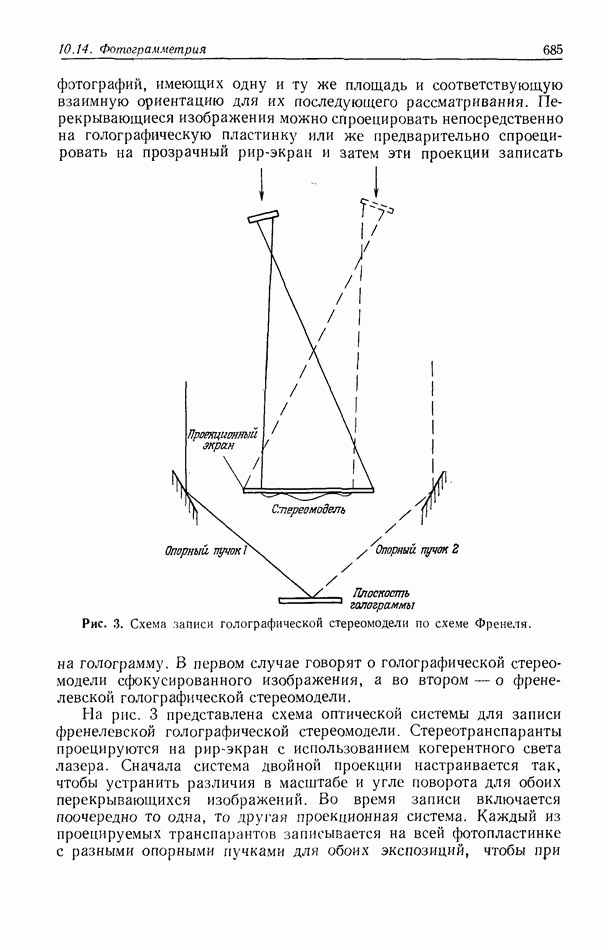
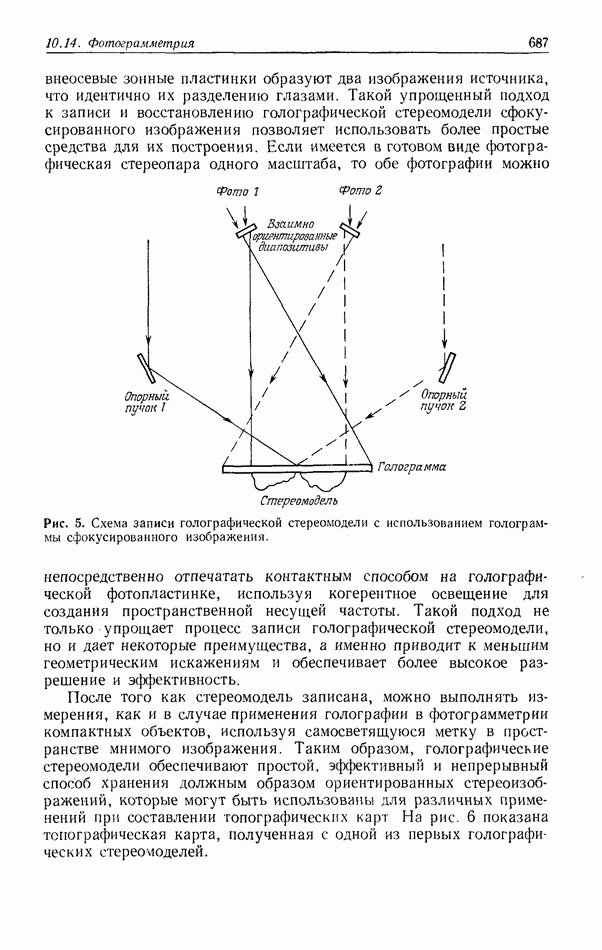
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.5.15. Оптимизация параметров согласованного пространственного фильтра
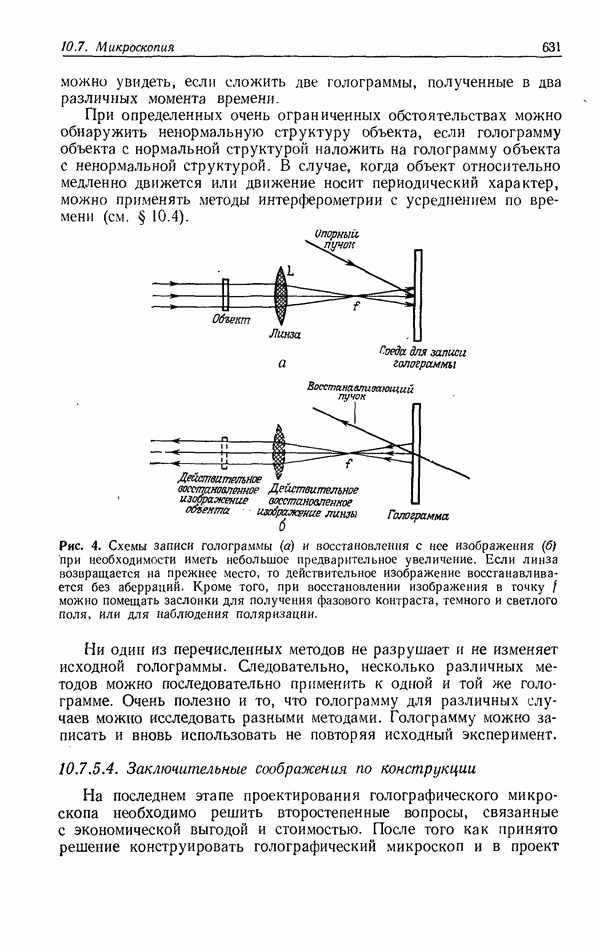
Рассмотрим теперь проблему синтеза согласованных пространственных фильтров, которые необходимы для корреляторов с частотной плоскостью. В частности, мы обсудим вопросы выбора следующих трех параметров СПФ: экспозиции смещения  отношения интенсивностей опорного и сигнального пучков К и полосы пространственных частот
отношения интенсивностей опорного и сигнального пучков К и полосы пространственных частот  в пределах которой величина К равна выбранному значению. В качестве критериев оценки оптимальной корреляции мы используем интенсивность
в пределах которой величина К равна выбранному значению. В качестве критериев оценки оптимальной корреляции мы используем интенсивность  пика корреляции и отношение сигнал/шум на выходе коррелятора. Из выражения (5) следует, что экспозиция при записи СПФ имеет вид
пика корреляции и отношение сигнал/шум на выходе коррелятора. Из выражения (5) следует, что экспозиция при записи СПФ имеет вид

где  время экспозиции,
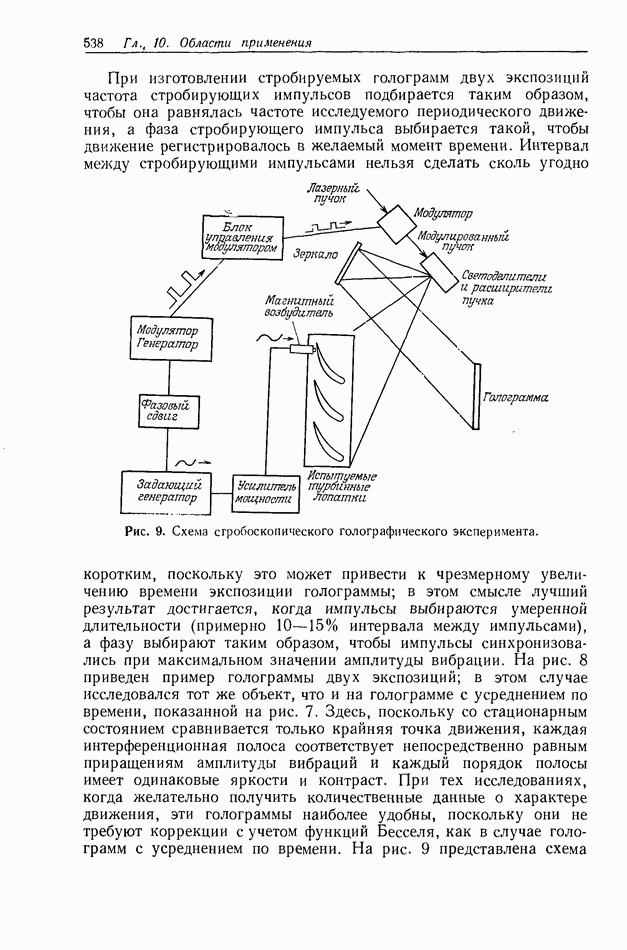
время экспозиции,  средняя экспозиция,
средняя экспозиция,  отношение интенсивностей опорного и объектного пучков,
отношение интенсивностей опорного и объектного пучков,  Следовательно, амплитудное пропускание полученного СПФ зависит от
Следовательно, амплитудное пропускание полученного СПФ зависит от  а и вида кривой
а и вида кривой  для фотопленки. Таким образом,
для фотопленки. Таким образом,

здесь  среднее пропускание, А — члены более высоких порядков,
среднее пропускание, А — члены более высоких порядков,  наибольший размах переменной составляющей амплитудного пропускания (от максимального значения до минимального) или наибольшая модуляция косинусоидальной волны,
наибольший размах переменной составляющей амплитудного пропускания (от максимального значения до минимального) или наибольшая модуляция косинусоидальной волны,  амплитудная дифракционная эффективность. Тогда интенсивность в пике автокорреляции функции
амплитудная дифракционная эффективность. Тогда интенсивность в пике автокорреляции функции  принимает вид
принимает вид

Проанализируем полученные результаты. Передаточная функция фильтра  является функцией пространственных частот и, следовательно, так же как и
является функцией пространственных частот и, следовательно, так же как и  зависит от вида кривой
зависит от вида кривой  фотопленки и выбранных значений
фотопленки и выбранных значений  Поскольку
Поскольку  и К изменяются с пространственной частотой, должна быть обеспечена полоса пространственных частот
и К изменяются с пространственной частотой, должна быть обеспечена полоса пространственных частот  в пределах которой измеряется величина К. Такие данные, к сожалению, редко включаются в публикации по оптическому распознаванию образов. После того как стала известна зависимость
в пределах которой измеряется величина К. Такие данные, к сожалению, редко включаются в публикации по оптическому распознаванию образов. После того как стала известна зависимость  и выбрана величина
и выбрана величина  можно найти и зависимость
можно найти и зависимость  Поскольку К, так же как
Поскольку К, так же как
и  зависит от пространственной частоты, ее можно определить, если известен пространственно-частотный спектр
зависит от пространственной частоты, ее можно определить, если известен пространственно-частотный спектр  входной функции
входной функции 
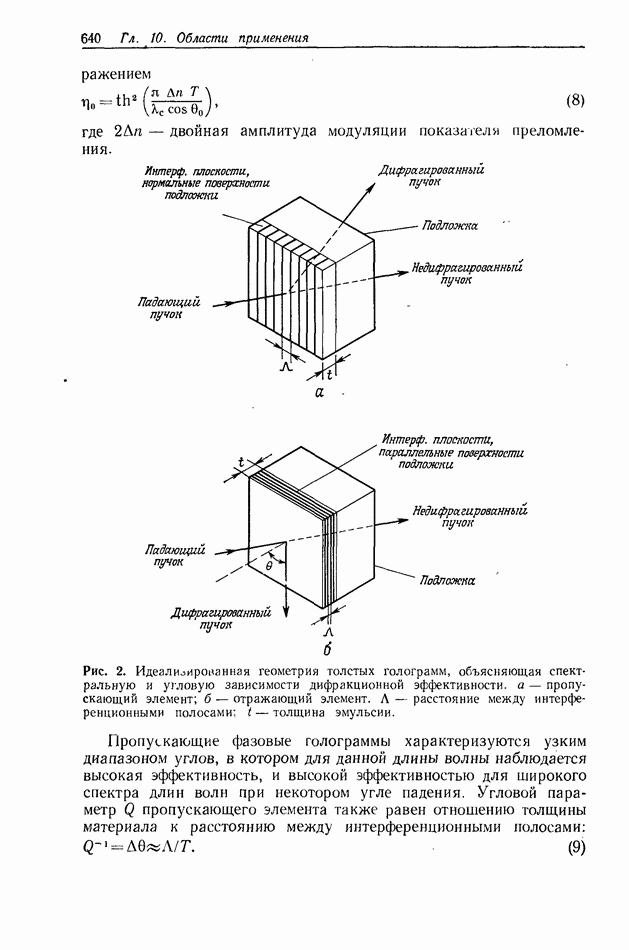
Для большинства материалов, используемых для изготовления СПФ, имеются кривые зависимости контраста интерференционных полос от дифракционной эффективности  , по которым можно определить зависимости амплитудной дифракционной эффективности
, по которым можно определить зависимости амплитудной дифракционной эффективности  от К при разных средних экспозициях, а также построить кривую зависимости
от К при разных средних экспозициях, а также построить кривую зависимости  от экспозиции
от экспозиции  Обычно используется линейный участок этой кривой. Линейная запись требует выполнения условия
Обычно используется линейный участок этой кривой. Линейная запись требует выполнения условия  (где величина
(где величина  соответствует значению
соответствует значению  что эквивалентно условию 5,8. Это хорошо согласуется с тем, что для обеспечения линейной записи данных мы должны использовать большие значения
что эквивалентно условию 5,8. Это хорошо согласуется с тем, что для обеспечения линейной записи данных мы должны использовать большие значения  При записи СПФ имеет место насыщение, если
При записи СПФ имеет место насыщение, если  и наблюдается ограничение при
и наблюдается ограничение при  Поэтому выбирают
Поэтому выбирают  и вопрос состоит в том, в какой полосе пространственных частот
и вопрос состоит в том, в какой полосе пространственных частот  установить
установить  Как видно из этих кратких замечаний, синтез СПФ отличается от обычной голографической записи, в которой нас интересует высокое качество восстановленного изображения, а не высокое качество корреляции на выходе.
Как видно из этих кратких замечаний, синтез СПФ отличается от обычной голографической записи, в которой нас интересует высокое качество восстановленного изображения, а не высокое качество корреляции на выходе.
Приведем теперь результаты некоторых экспериментов, чтобы лучше показать влияние рассматриваемых параметров СПФ на корреляционные параметры. При линейной записи средняя экспозиция соответствует амплитудному пропусканию 70% и значения К оказываются оптимальными. В результате выполнения большой серии экспериментов были получены графики зависимости интенсивности пика корреляции  и отношения сигнал/шум на выходе от величины
и отношения сигнал/шум на выходе от величины  для различных входных изображений, использованных пленок и линз. Во всех случаях значения
для различных входных изображений, использованных пленок и линз. Во всех случаях значения  соответствующие максимумам
соответствующие максимумам  составляли всего 10% от всей величины
составляли всего 10% от всей величины  Наблюдалось уменьшение
Наблюдалось уменьшение  в 100 раз при уменьшении
в 100 раз при уменьшении  всего на 50%. Было найдено, что наклон кривой зависимости
всего на 50%. Было найдено, что наклон кривой зависимости  от отношения сигнал/шум равен
от отношения сигнал/шум равен  Это указывает на то, что шумы увеличиваются при отклонении величины
Это указывает на то, что шумы увеличиваются при отклонении величины  от своего оптимального значения и что правильный выбор величины
от своего оптимального значения и что правильный выбор величины  очень важен для обеспечения хорошей корреляции. Так как небольшие изменения амплитудного пропускания
очень важен для обеспечения хорошей корреляции. Так как небольшие изменения амплитудного пропускания  приводят к большим изменениям величины
приводят к большим изменениям величины  то более чувствительным и более практичным параметром для управления характеристиками СПФ является величина
то более чувствительным и более практичным параметром для управления характеристиками СПФ является величина  а не
а не 
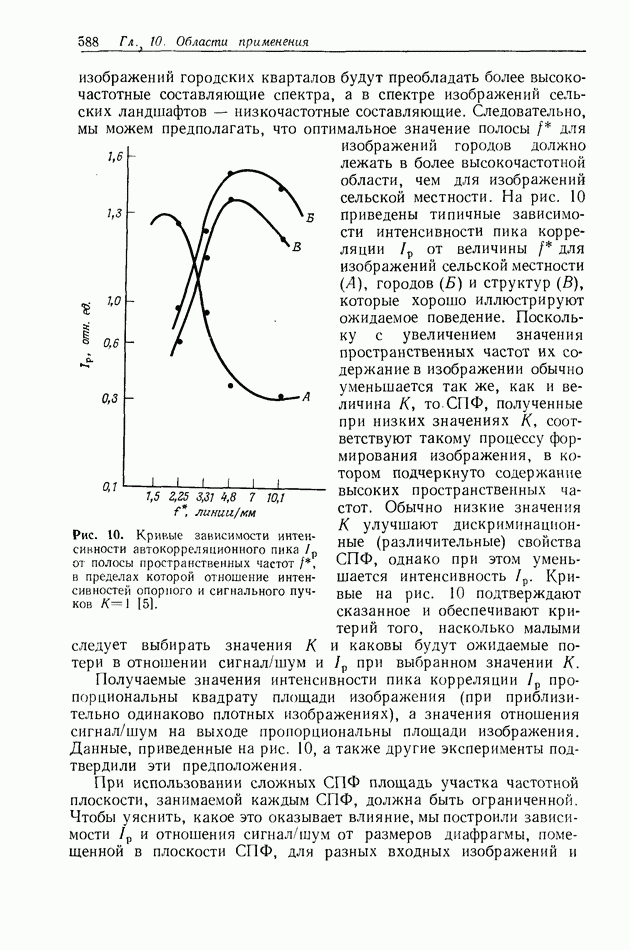
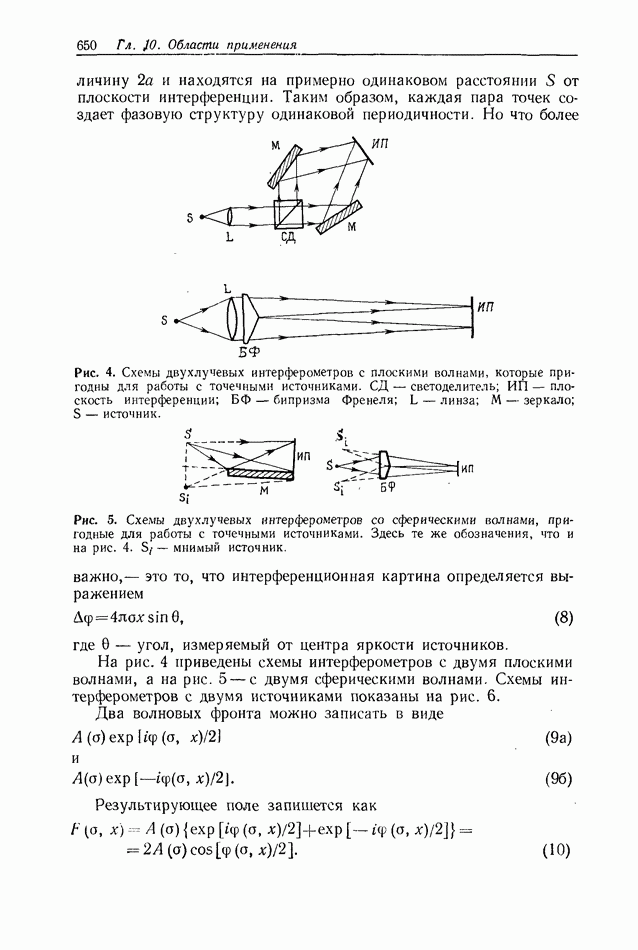
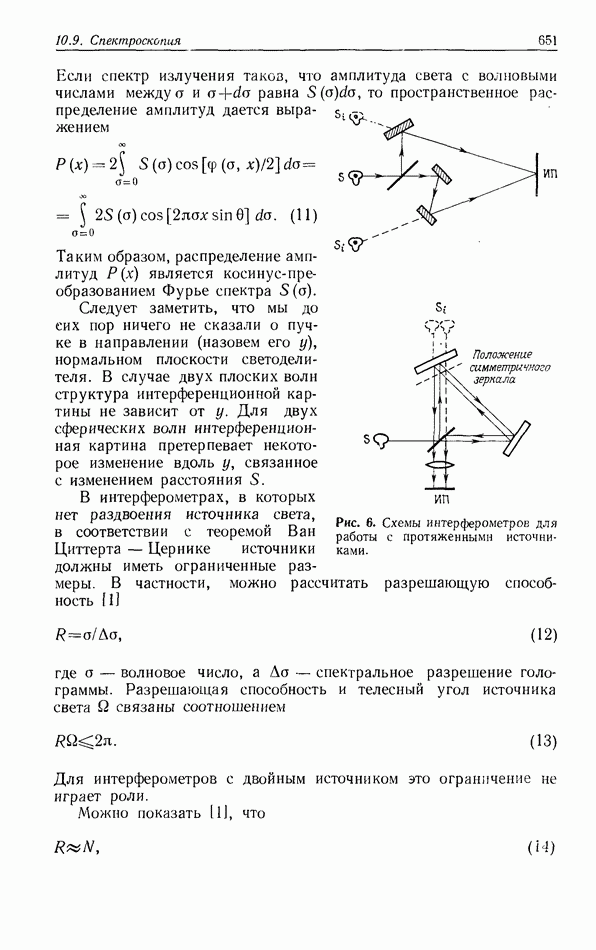
При решении задач распознавания обычно используются изображения разного характера (аэрофотоснимки сельской местности и городов, изображения структур). Пространственно-частотные спектры этих изображений будут различными. Так, в спектре
изображений городских кварталов будут преобладать более высокочастотные составляющие спектра, а в спектре изображений сельских ландшафтов — низкочастотные составляющие. Следовательно, мы можем предполагать, что оптимальное значение полосы  для изображений городов должно лежать в более высокочастотной области, чем для изображений сельской местности. На рис. 10 приведены типичные зависимости интенсивности пика корреляции
для изображений городов должно лежать в более высокочастотной области, чем для изображений сельской местности. На рис. 10 приведены типичные зависимости интенсивности пика корреляции  от величины
от величины  для изображений сельской местности (А), городов (Б) и структур (В), которые хорошо иллюстрируют ожидаемое поведение. Поскольку с увеличением значения пространственных частот их содержание в изображении обычно уменьшается так же, как и величина К, то. СПФ, полученные при низких значениях К, соответствуют такому процессу формирования изображения, в котором подчеркнуто содержание высоких пространственных частот. Обычно низкие значения К улучшают дискриминационные (различительные) свойства СПФ, однако при этом уменьшается интенсивность
для изображений сельской местности (А), городов (Б) и структур (В), которые хорошо иллюстрируют ожидаемое поведение. Поскольку с увеличением значения пространственных частот их содержание в изображении обычно уменьшается так же, как и величина К, то. СПФ, полученные при низких значениях К, соответствуют такому процессу формирования изображения, в котором подчеркнуто содержание высоких пространственных частот. Обычно низкие значения К улучшают дискриминационные (различительные) свойства СПФ, однако при этом уменьшается интенсивность  Кривые на рис. 10 подтверждают сказанное и обеспечивают критерий того, насколько малыми следует выбирать значения К и каковы будут ожидаемые потери в отношении сигнал/шум и
Кривые на рис. 10 подтверждают сказанное и обеспечивают критерий того, насколько малыми следует выбирать значения К и каковы будут ожидаемые потери в отношении сигнал/шум и  при выбранном значении К.
при выбранном значении К.
Получаемые значения интенсивности пика корреляции  пропорциональны квадрату площади изображения (при приблизительно одинаково плотных изображениях), а значения отношения сигнал/шум на выходе пропорциональны площади изображения. Данные, приведенные на рис. 10, а также другие эксперименты подтвердили эти предположения.
пропорциональны квадрату площади изображения (при приблизительно одинаково плотных изображениях), а значения отношения сигнал/шум на выходе пропорциональны площади изображения. Данные, приведенные на рис. 10, а также другие эксперименты подтвердили эти предположения.

Рис. 10. Кривые зависимости интенсивности автокорреляционного пика  от полосы пространственных частот
от полосы пространственных частот  в пределах которой отношение интенсивностей опорного и сигнального пучков
в пределах которой отношение интенсивностей опорного и сигнального пучков  [5].
[5].
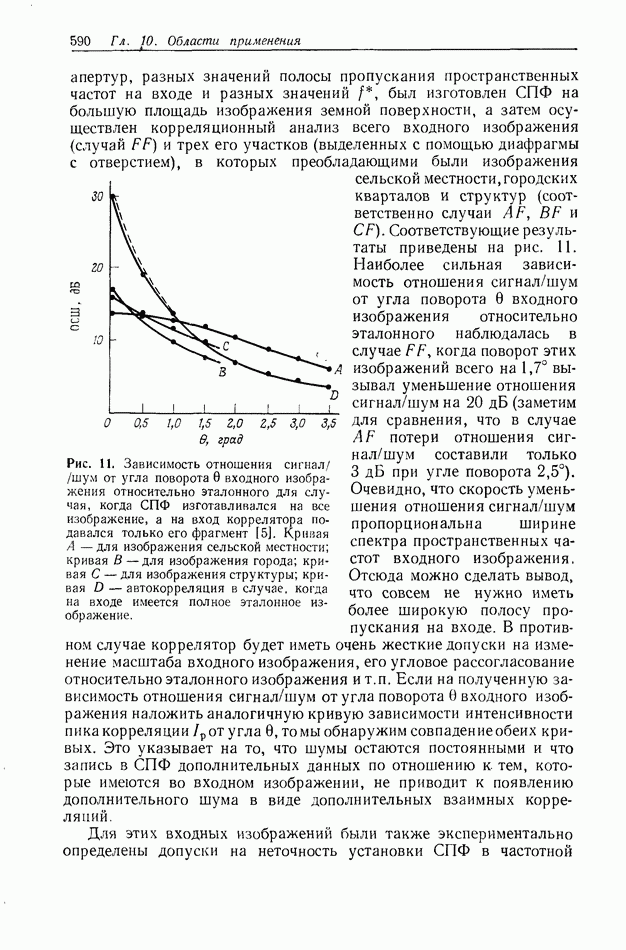
При использовании сложных СПФ площадь участка частотной плоскости, занимаемой каждым СПФ, должна быть ограниченной. Чтобы уяснить, какое это оказывает влияние, мы построили зависимости  и отношения сигнал/шум от размеров диафрагмы, помещенной в плоскости СПФ, для разных входных изображений и
и отношения сигнал/шум от размеров диафрагмы, помещенной в плоскости СПФ, для разных входных изображений и
разных значении  В результате мы нашли, что интенсивность пика корреляции
В результате мы нашли, что интенсивность пика корреляции  и отношение сигнал/шум СПФ, записанных с более высокими значениями
и отношение сигнал/шум СПФ, записанных с более высокими значениями  резко снижаются, как только уменьшается диаметр диафрагмы, в то время как для СПФ, записанных при более низких значениях
резко снижаются, как только уменьшается диаметр диафрагмы, в то время как для СПФ, записанных при более низких значениях  это уменьшение
это уменьшение  и отношения сигнал/шум проявлялось в значительно меньшей степени, пока диаметр диафрагмы не уменьшался до величины
и отношения сигнал/шум проявлялось в значительно меньшей степени, пока диаметр диафрагмы не уменьшался до величины  при которой был записан фильтр.
при которой был записан фильтр.
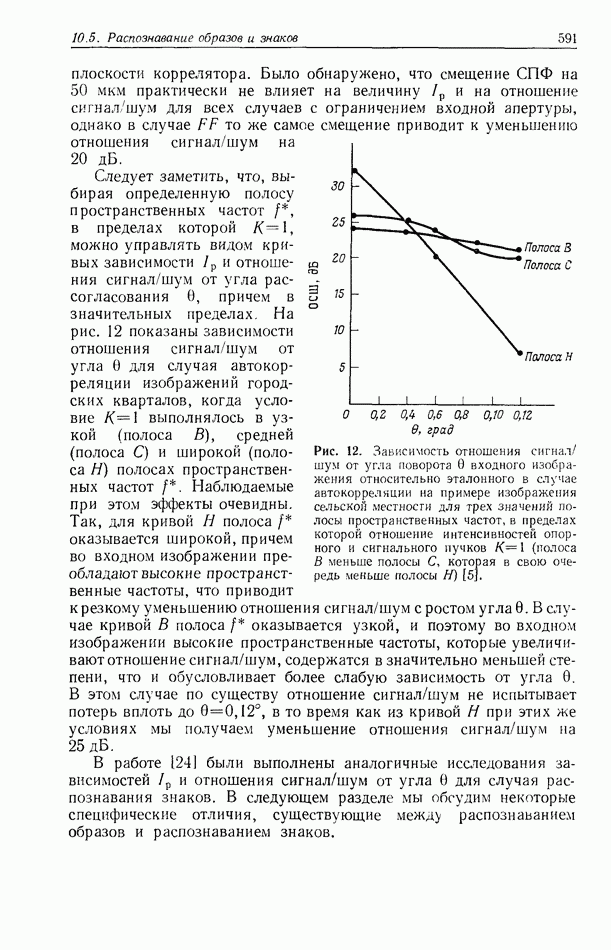
Исходя из этих и других случаев (см. разд. 10.5.16), мы пришли к выводу, что для уменьшения степени изменения  и отношения сигнал/шум предпочтительнее иметь более низкие значения
и отношения сигнал/шум предпочтительнее иметь более низкие значения  а на практике предпочтительнее выбирать более низкие значения
а на практике предпочтительнее выбирать более низкие значения  и отношения сигнал/шум путем выбора более низких значений
и отношения сигнал/шум путем выбора более низких значений  по сравнению с теми, которые обеспечили бы максимальные значения интенсивности
по сравнению с теми, которые обеспечили бы максимальные значения интенсивности  и отношения сигнал/шум.
и отношения сигнал/шум.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
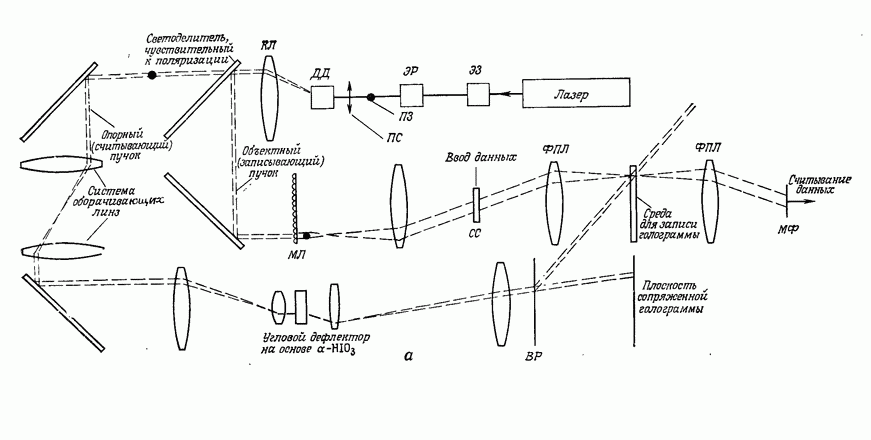
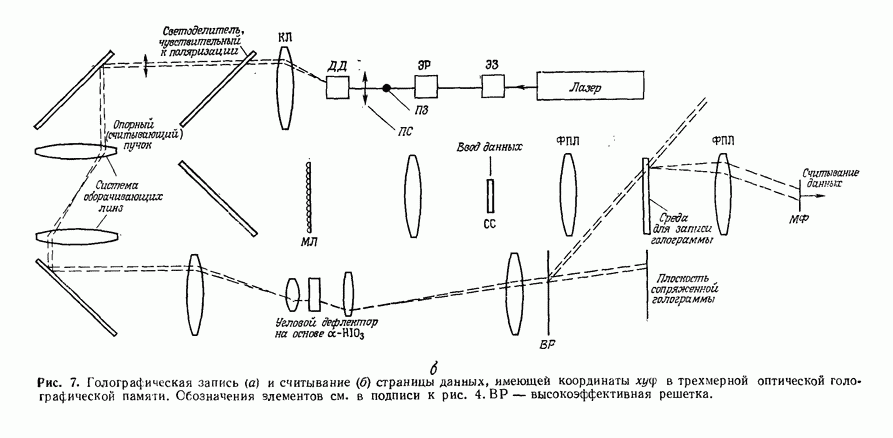
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
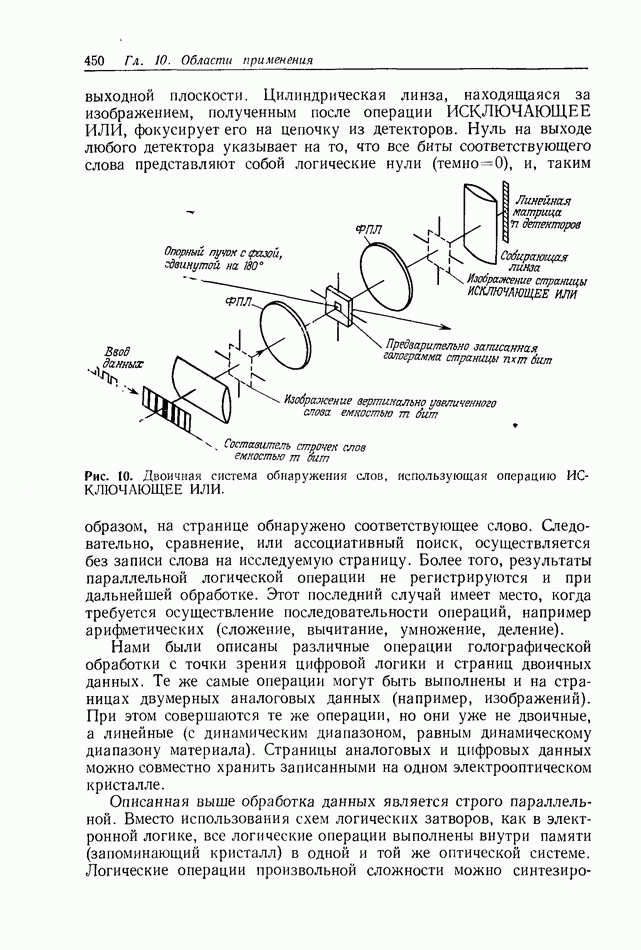
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
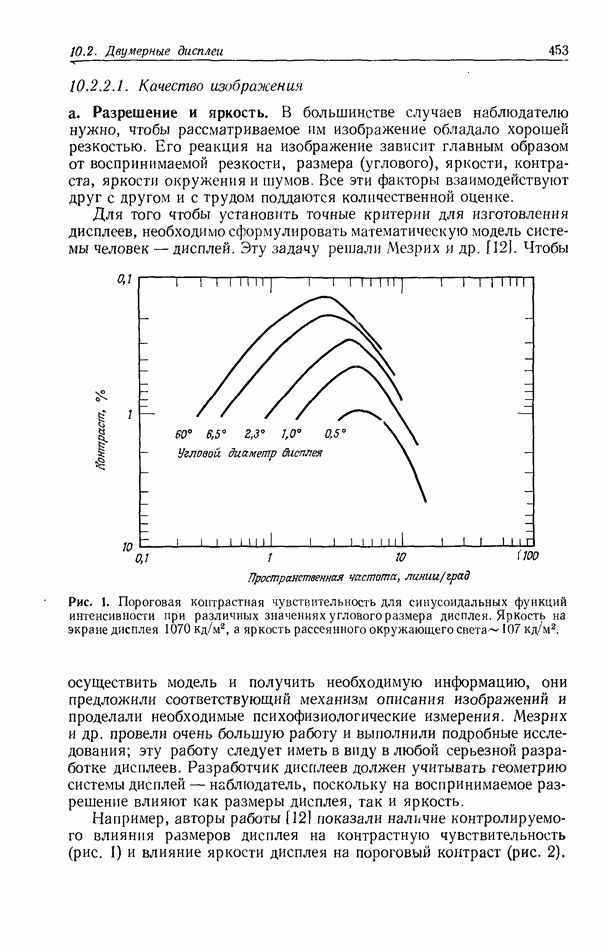
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
- 10.9. СПЕКТРОСКОПИЯ
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
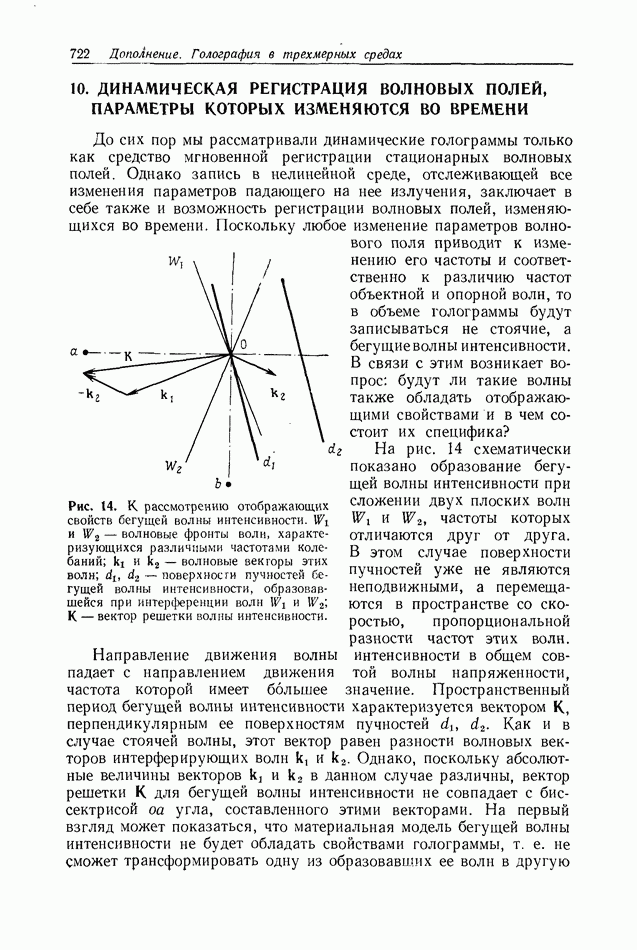
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ