| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
Г Колфилд
10.11.1. Введение
По многим причинам желательно уметь преобразовывать отдельное изображение в большое число идентичных изображений, и существует большое число методов, позволяющих это сделать. Мы перечислим четыре основных типа систем мультиплицирования изображений:
1) шаговые фотокамеры с последовательным экспонированием,
2) некогерентные оптические,
3) когерентные неголографические и
4) когерентные голографические системы.
Хотя темой настоящего параграфа является рассмотрение последней системы, мы дадим краткий обзор других, более ранних способов, поскольку они позволяют установить критерии для оценки успехов, достигнутых в мультиплицировании изображений.
На сегодняшний день лучшим прибором для систем мультиплицирования является шаговая фотокамера с последовательным экспонированием. Она очень проста и не формирует сразу множество изображений, а создает последовательно одно изображение за другим, причем их местоположением можно управлять. Преимущества такого прибора заключаются в доступности, легкости программирования, идентичности качества каждого изображения и разнообразии вариантов (они могут производить контактные отпечатки или проекционные снимки).

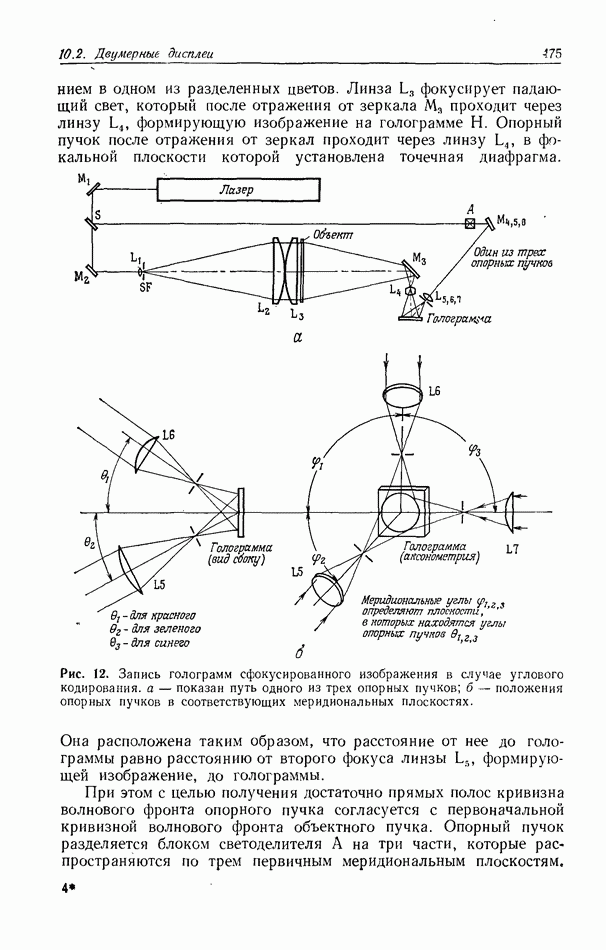
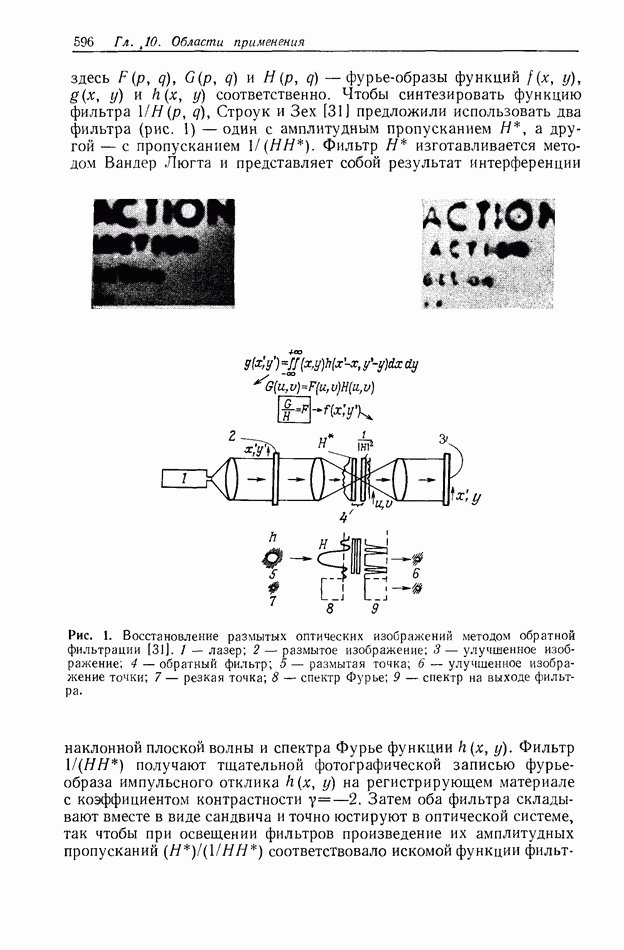
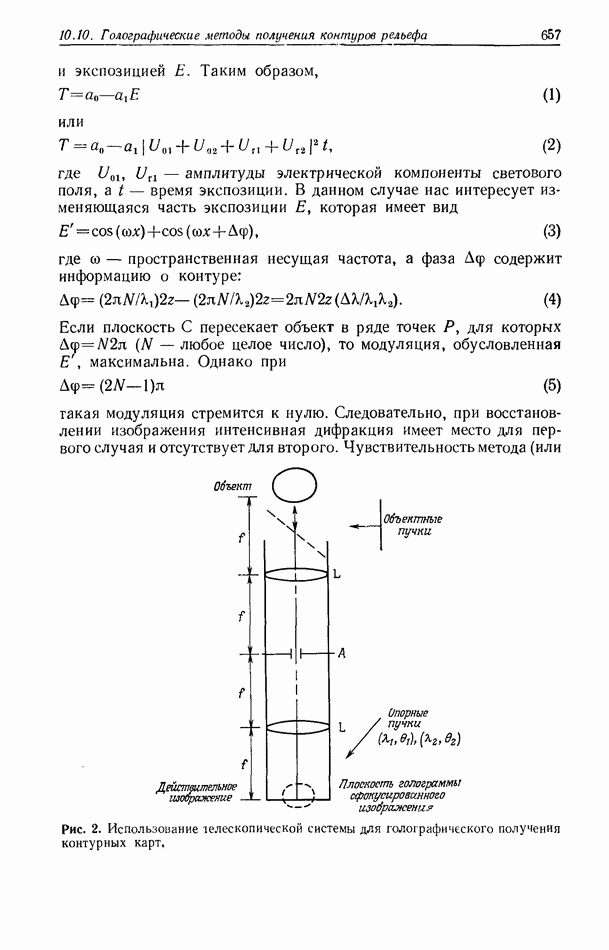
Рис. 1. Падающий на периодическую маску свет от некогерентно излучающего объекта образует в плоскости изображения множество изображений этого объекта.
Основной их недостаток — низкая скорость. Чтобы записать  изображений, необходимо в
изображений, необходимо в  раз больше времени, чем требуется для записи одного изображения. Отсюда очевидно стремление к мультиплицированию изображений. Основная цель ясна: нужно послать одно изображение в «черный ящик» и получить на выходе матрицу идентичных изображений.
раз больше времени, чем требуется для записи одного изображения. Отсюда очевидно стремление к мультиплицированию изображений. Основная цель ясна: нужно послать одно изображение в «черный ящик» и получить на выходе матрицу идентичных изображений.
На рис. 1 приведена схема, иллюстрирующая основную идею некогерентных методов мультиплицирования изображений. При точечном освещающем источнике в выходной плоскости формируется изображение периодической маски (ПМ). Если освещающим источником является входное изображение, то на выходе наблюдается множество копий входного изображения — по одному изображению для каждой точки периодической маски. Читатель понимает, что слово «некогерентный» в действительности вводит в заблуждение, поскольку метод требует пространственной когерентности света на периодической маске. Этот метод подробно обсуждается Томпсоном [6].
Строго когерентный вариант такой системы рассматривал Томпсон [5], а позднее (в несколько другом виде) Калестинский [3]. Периодическая структура осуществляет выборку дифракционной картины Фраунгофера входного изображения, так что выходное изображение представляет собой свертку входного изображения с периодической функцией.
Этим двум методам присущи два основных недостатка. Во-первых, в выходном изображении имеет место конкуренция между яркостью и разрешением. Чтобы получить хорошее разрешение, маска должна иметь очень маленькие отверстия, а чтобы иметь хорошее пропускание, отверстия должны быть большие. Во-вторых, очень трудно получить  изображений с одинаковой яркостью. Эти проблемы голографического мультиплицирования изображений требуют своего решения.
изображений с одинаковой яркостью. Эти проблемы голографического мультиплицирования изображений требуют своего решения.
10.11.2. Некоторые проблемы, рассмотренные в других разделах
Метод голографического мультиплицирования изображений, предложенный независимо  предлагает создание специального голограммного оптического элемента. Оптические элементы и их аберрации обсуждаются в § 2.4 и в разд. 10.11.7, поэтому здесь мы только заостряем внимание читателя на этих вопросах. Кроме того, качество изображений в большой степени зависит от условий восстановления (разд. 10.11.6). И наконец, серьезную проблему, которая характерна для всех когерентных изображений, представляют спеклы (см. § 9.2).
предлагает создание специального голограммного оптического элемента. Оптические элементы и их аберрации обсуждаются в § 2.4 и в разд. 10.11.7, поэтому здесь мы только заостряем внимание читателя на этих вопросах. Кроме того, качество изображений в большой степени зависит от условий восстановления (разд. 10.11.6). И наконец, серьезную проблему, которая характерна для всех когерентных изображений, представляют спеклы (см. § 9.2).
10.11.3. Мультиплицирование изображений с помощью голограмм Фурье
Пусть на входе системы имеем изображение с амплитудным пропусканием  Обозначим его фурье-образ через
Обозначим его фурье-образ через  Изготовим голограмму с пропусканием
Изготовим голограмму с пропусканием

где  целые числа. Волновой фронт непосредственно за голограммой можно записать в виде
целые числа. Волновой фронт непосредственно за голограммой можно записать в виде

Оптическое преобразование Фурье этого распределения создает изображение

В действительности, конечно, мы получаем изображение  , но в большинстве случаев это не имеет значения, и можно ввести коррективы, представив входное изображение в виде
, но в большинстве случаев это не имеет значения, и можно ввести коррективы, представив входное изображение в виде  , а не в виде
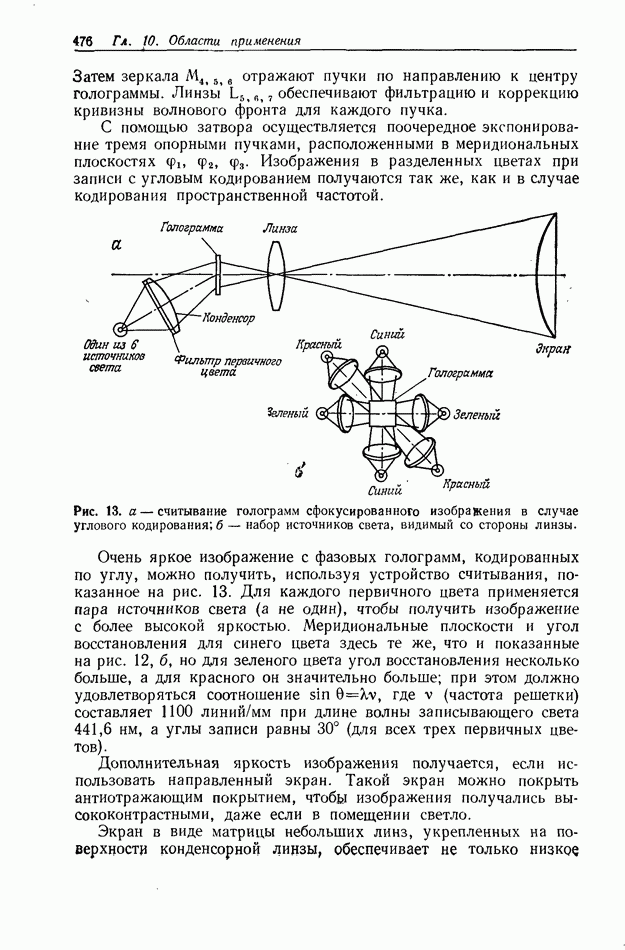
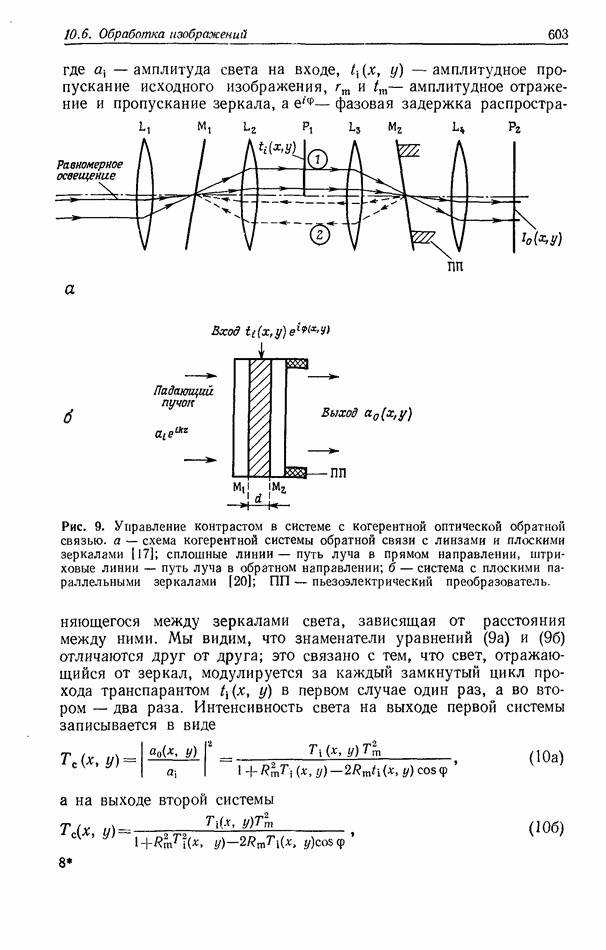
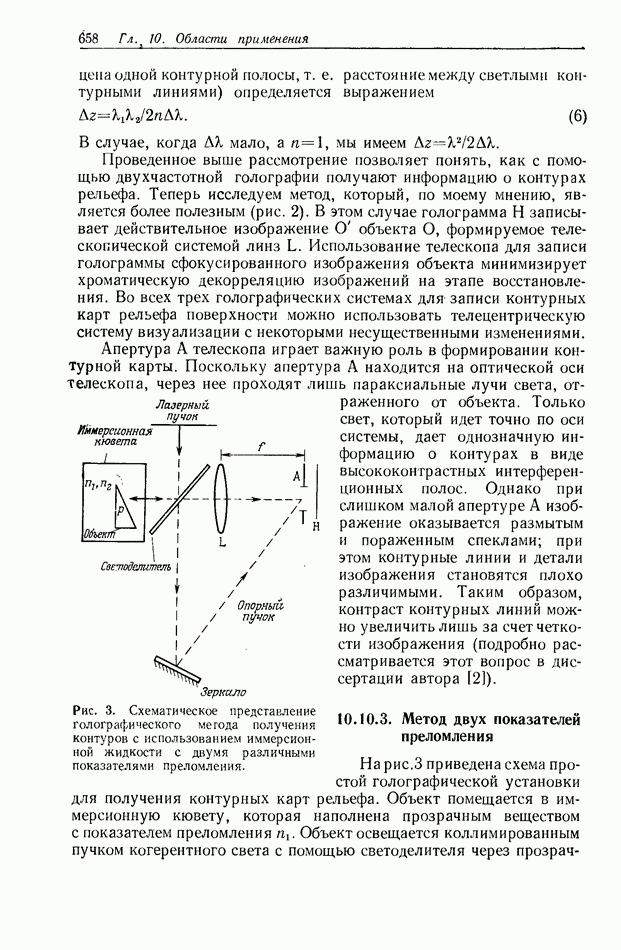
, а не в виде  Такой метод мультиплицирования рассматривал Лю [4]. На рис. 2 приведено схематическое представление этого метода.
Такой метод мультиплицирования рассматривал Лю [4]. На рис. 2 приведено схематическое представление этого метода.
Исследуем вопрос о том, как записать голограмму, необходимую для реализации данного метода. Голограмма восстанавливает плоские волны, распространяющиеся в нескольких направлениях (по числу  мультиплицируемых изображений). Единственная возможность получить соотношение интенсивностей объектного и опорного пучков
мультиплицируемых изображений). Единственная возможность получить соотношение интенсивностей объектного и опорного пучков  по всей площади голограммы — это использование плоских волн; при этом достигается наивысшая возможная дифракционная эффективность.
по всей площади голограммы — это использование плоских волн; при этом достигается наивысшая возможная дифракционная эффективность.

Рис. 2. Падающий на специальную голограмму  свет от когерентно излучающего объекта
свет от когерентно излучающего объекта  формирует множество изображений этого объекта.
формирует множество изображений этого объекта.
Более того, в этом случае каждая плоская волна освещает всю апертуру голограммы равномерно и однородными оказываются восстановленные волны. Остаются три основные проблемы:
1. Как избежать перекрестных искажений?
2. Как достичь максимальной дифракционной эффективности?
3. Как получить одну и ту же дифракционную эффективность для всех плоских волн?
Явление перекрестных искажений связано с нелинейной записью (см. § 8.3), при которой свет, вместо того чтобы попасть в точку с координатами  попадает в другие положения. В случае строго периодического мультиплицирования, который рассматривается только из соображений простоты, свет будет наблюдаться в точках с координатами
попадает в другие положения. В случае строго периодического мультиплицирования, который рассматривается только из соображений простоты, свет будет наблюдаться в точках с координатами  Для иллюстрации представим, что мы хотим записать голограмму
Для иллюстрации представим, что мы хотим записать голограмму  объектных волновых фронтов
объектных волновых фронтов  с одной опорной волной
с одной опорной волной  При этом экспозиция будет пропорциональна
При этом экспозиция будет пропорциональна

где  перекрестная информация:
перекрестная информация:

В конкретном случае одномерной структуры, т. е.

имеем

Группируя члены, получаем по одному члену  по два
по два  и по
и по  членов
членов  Освещая такую голограмму волной света
Освещая такую голограмму волной света  можно записать следующие члены:
можно записать следующие члены:  а также
а также  Эти члены описывают пучки, которые появляются вокруг восстанавливающего пучка и не перекрываются с объектным пучком. Однако при нелинейной записи голограммы
Эти члены описывают пучки, которые появляются вокруг восстанавливающего пучка и не перекрываются с объектным пучком. Однако при нелинейной записи голограммы  имеется некоторое взаимодействие между этими пучками и объектным пучком, причем картина выглядит так, как если бы линейная голограмма освещалась несколькими восстанавливающими пучками. Это приводит к тому, что входное изображение представляет собой свертку не с матрицей дельта-функций, а а дельта-функциями, свернутыми с периодической функцией, имеющей максимум в начале координат и простирающейся
имеется некоторое взаимодействие между этими пучками и объектным пучком, причем картина выглядит так, как если бы линейная голограмма освещалась несколькими восстанавливающими пучками. Это приводит к тому, что входное изображение представляет собой свертку не с матрицей дельта-функций, а а дельта-функциями, свернутыми с периодической функцией, имеющей максимум в начале координат и простирающейся  Ясно, что при линейной записи
Ясно, что при линейной записи  перекрестные искажения отсутствуют. Однако осуществить линейную запись очень трудно, а иногда и невозможно. Проблема состоит в том, чтобы все же
перекрестные искажения отсутствуют. Однако осуществить линейную запись очень трудно, а иногда и невозможно. Проблема состоит в том, чтобы все же
предотвратить перекрестные искажения. Достичь этого можно только одним путем. Мы можем использовать при записи мультиплицирующей голограммы последовательную запись элементарных голограмм. (Вопрос о мультиплицировании голограмм обсуждается в § 5.2.) Как показано в § 5.2, дифракционная эффективность отдельной голограммы составляет  дифракционной эффективности, достигаемой при записи одной голограммы с
дифракционной эффективности, достигаемой при записи одной голограммы с  и
и  эффективности, получаемой при
эффективности, получаемой при  -точечном объекте. С другой стороны, при этом перекрестные искажения уменьшаются и легко достигается равномерная яркость изображений. При наличии перекрестных искажений и
-точечном объекте. С другой стороны, при этом перекрестные искажения уменьшаются и легко достигается равномерная яркость изображений. При наличии перекрестных искажений и  в принципе нельзя добиться равномерности изображений.
в принципе нельзя добиться равномерности изображений.
Характерный для неголографических методов обмен между разрешением и яркостью изображения (что связано с выбором размера отверстия) в случае голографии не имеет значения. Отверстия в решетке могут иметь дифракционно-ограниченные размеры или меньше (как они воспроизводятся линзой, осуществляющей преобразование Фурье) без потери дифракционной эффективности голограммы.
10.11.4. Метод мультиплицирования изображений с помощью безлинзовых голограмм Фурье
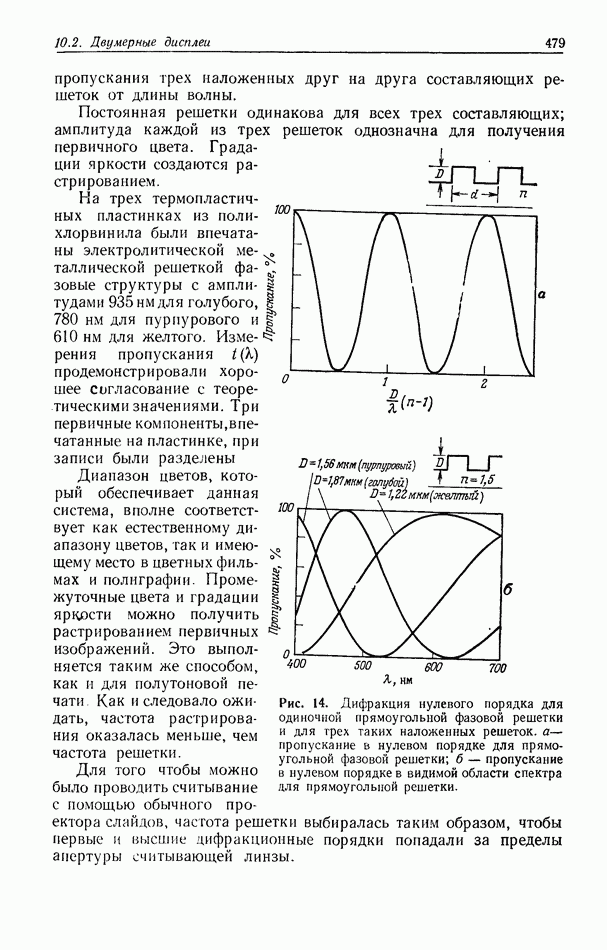
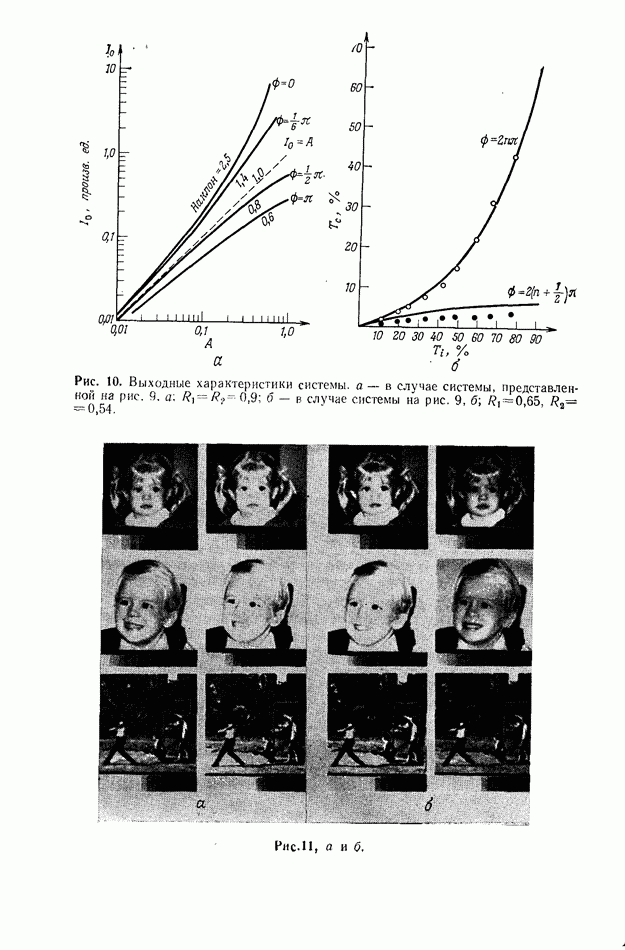
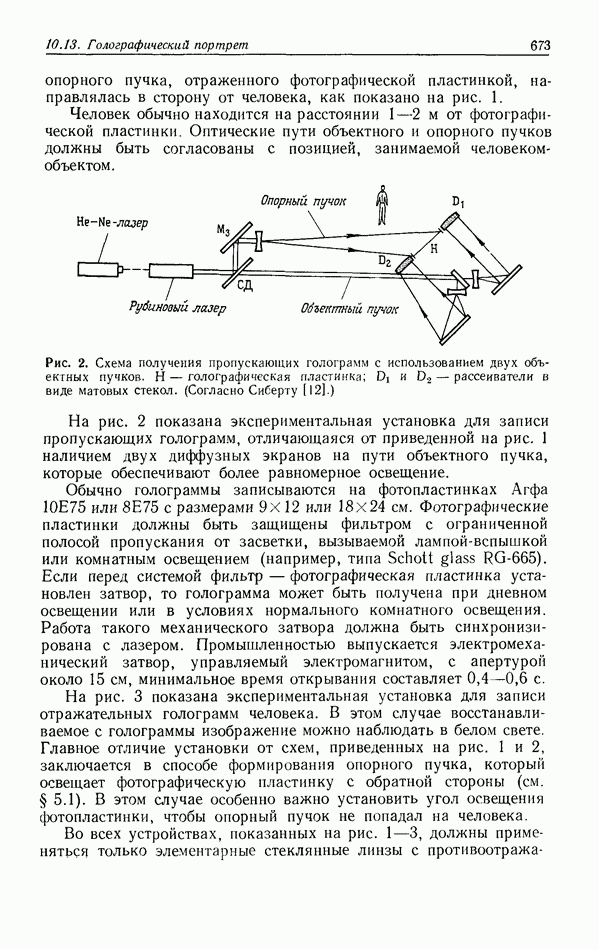
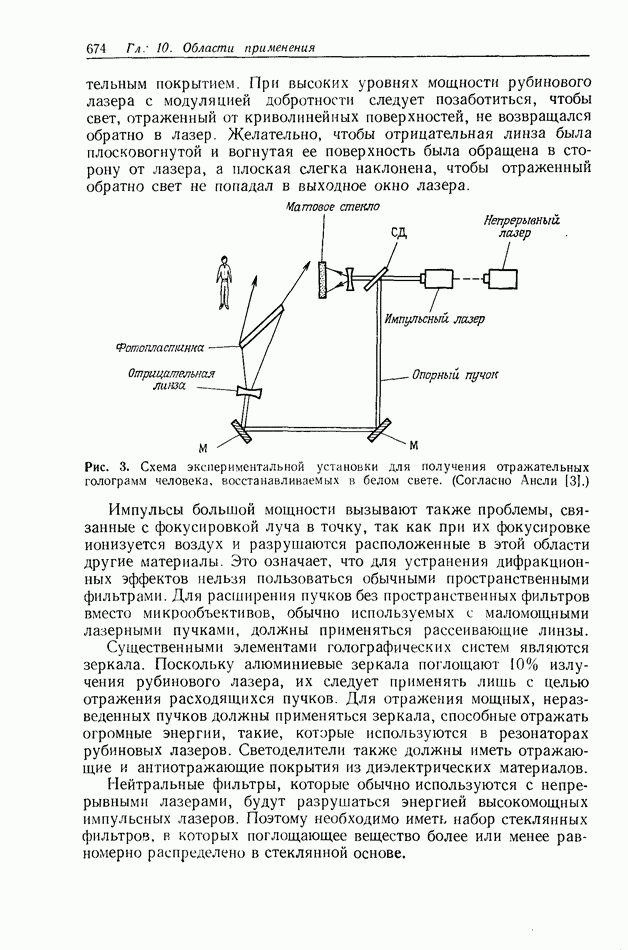
Предположим, что мы не используем линзы ни при записи голограмм, ни при проецировании мультиплицированных изображений, а вместо них применяем голограмму, которая сама выполняет их функции. На рис. 3, а показано, как можно записать такую голограмму, а на рис. 3,б — как ее использовать для размножения изображений. Этот метод был предложен  в 1968 г. [1].
в 1968 г. [1].

Рис. 3а — формирование голограммы с использованием многих точечных объектов; 6 — при освещении полученной голограммы объектной волной (в нашем случае объектом является буква  в месте восстановления каждого исходного точечного объекта будет формироваться изображение буквы х.
в месте восстановления каждого исходного точечного объекта будет формироваться изображение буквы х.
При записи такой голограммы необходимо, чтобы опорная и объектная точки находились на одинаковых расстояниях от голограммы с целью устранения квадратичных составляющих их волновых фронтов и получения однородной голограммы (см. § 4.3).
Как обсуждалось выше, точки можно записать последовательно или одновременно с присущими для каждого из этих подходов преимуществами и недостатками.
10.11.5. Голограммы, мультиплицирующие изображения
Калестинский [2] предложил свой вариант метода  который с таким же успехом можно считать вариантом метода
который с таким же успехом можно считать вариантом метода  Идея предложения заключается в записи мультиплицируемого изображения с несколькими опорными пучками. При восстановлении мультиплицированных изображений используется один восстанавливающий пучок. Калестинский не видит каких-либо преимуществ в изготовлении голограммы, предназначенной для мультиплицирования только одного изображения, в то время как при таких же усилиях можно изготовить голограмму, которая мультиплицирует любое входное изображение.
Идея предложения заключается в записи мультиплицируемого изображения с несколькими опорными пучками. При восстановлении мультиплицированных изображений используется один восстанавливающий пучок. Калестинский не видит каких-либо преимуществ в изготовлении голограммы, предназначенной для мультиплицирования только одного изображения, в то время как при таких же усилиях можно изготовить голограмму, которая мультиплицирует любое входное изображение.
10.11.6. Общие замечания
Голографические методы мультиплицирования имеют очевидные преимущества в скорости по сравнению с шаговой фотокамерой. Однако не ясно, имеет ли этот метод абсолютное преимущество. Для каждого из  изображений величина сигнала и отношение сигнал/шум изменяются как
изображений величина сигнала и отношение сигнал/шум изменяются как  или
или  в зависимости от способа записи голограмм. Необходимость достаточно хорошего отношения сигнал/шум ограничивает число мультиплицированных изображений. Имеются сообщения, что наилучшие голограммы позволяют получить до
в зависимости от способа записи голограмм. Необходимость достаточно хорошего отношения сигнал/шум ограничивает число мультиплицированных изображений. Имеются сообщения, что наилучшие голограммы позволяют получить до  хороших изображений. Из-за внеосевых аберраций голограммы (таких, как астигматизм) качество выходных изображений меняется от изображения к изображению. Налицо остаются все трудности, связанные с формированием изображения в когерентном свете. В некоторых случаях этими проблемами можно пренебречь, в других нельзя. С другой стороны, голографии свойственна универсальность, что позволяет делать некоторые вещи исключительно хорошо. Например, операция юстировки каждого изображения, необходимая при последовательной процедуре мультиплицирования, в голографическом методе не нужна, поскольку для этого достаточно настроить одно-единственное изображение. Когда одно изображение отъюстировано, все выходные изображения оказываются настроенными.
хороших изображений. Из-за внеосевых аберраций голограммы (таких, как астигматизм) качество выходных изображений меняется от изображения к изображению. Налицо остаются все трудности, связанные с формированием изображения в когерентном свете. В некоторых случаях этими проблемами можно пренебречь, в других нельзя. С другой стороны, голографии свойственна универсальность, что позволяет делать некоторые вещи исключительно хорошо. Например, операция юстировки каждого изображения, необходимая при последовательной процедуре мультиплицирования, в голографическом методе не нужна, поскольку для этого достаточно настроить одно-единственное изображение. Когда одно изображение отъюстировано, все выходные изображения оказываются настроенными.
Еще одно преимущество голографического мультиплицирования изображений по сравнению с неголографическим состоит в том, что в нем не существует проблемы, связанной с обменом между яркостью и разрешением в изображении, и, кроме того, можнб улучшить равномерность освещения изображения.
10.11.7. Применения
Нам известно, что голограммы мультиплицированных изображений нашли применение в четырех случаях, а именно:
1) для записи изображений, например в фотолитографии при производстве полупроводниковых приборов,
2) для осуществления многоканальной параллельной оптической обработки одного входного изображения,
3) для реализации поэлементной пространственно-неинвариантной обработки изображений и
4) для различных целей в качестве согласующих элементов оптических волоконных систем.
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
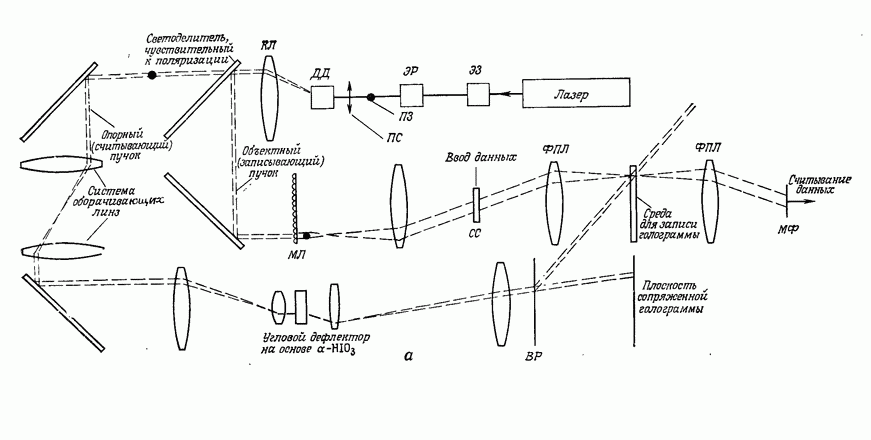
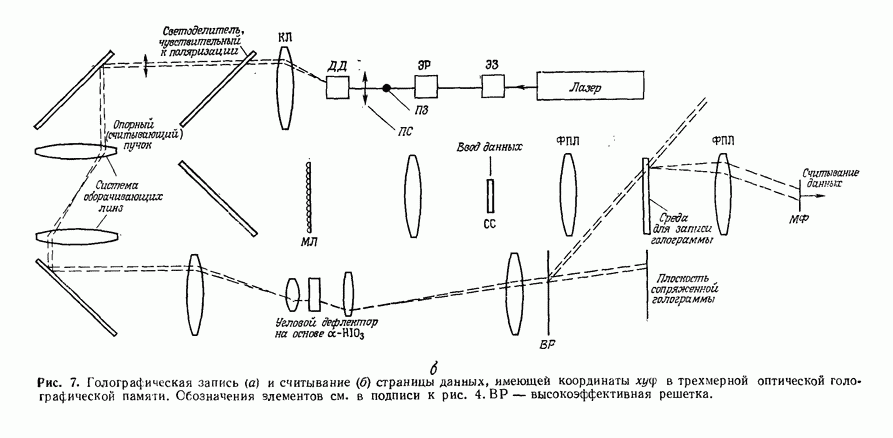
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
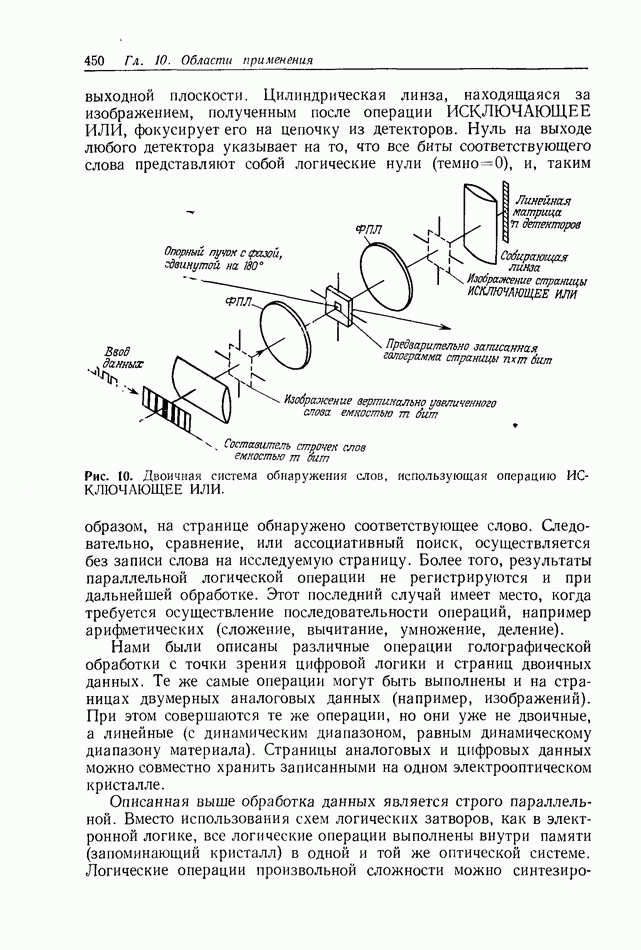
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
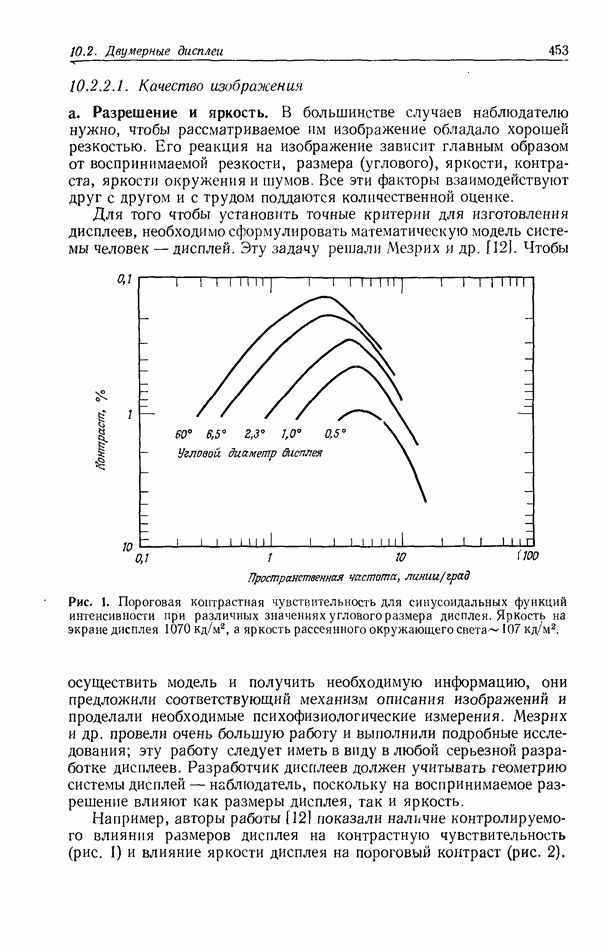
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
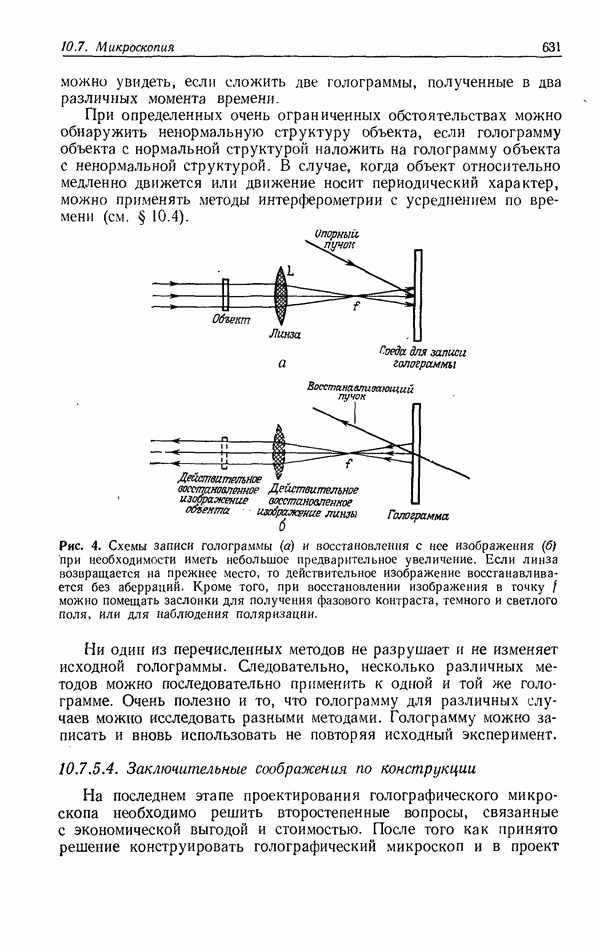
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
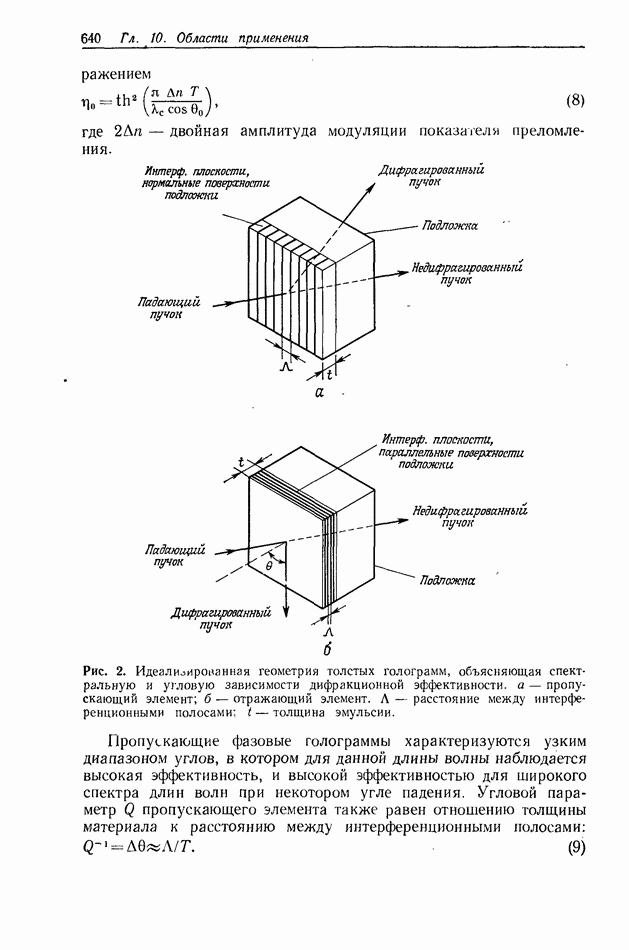
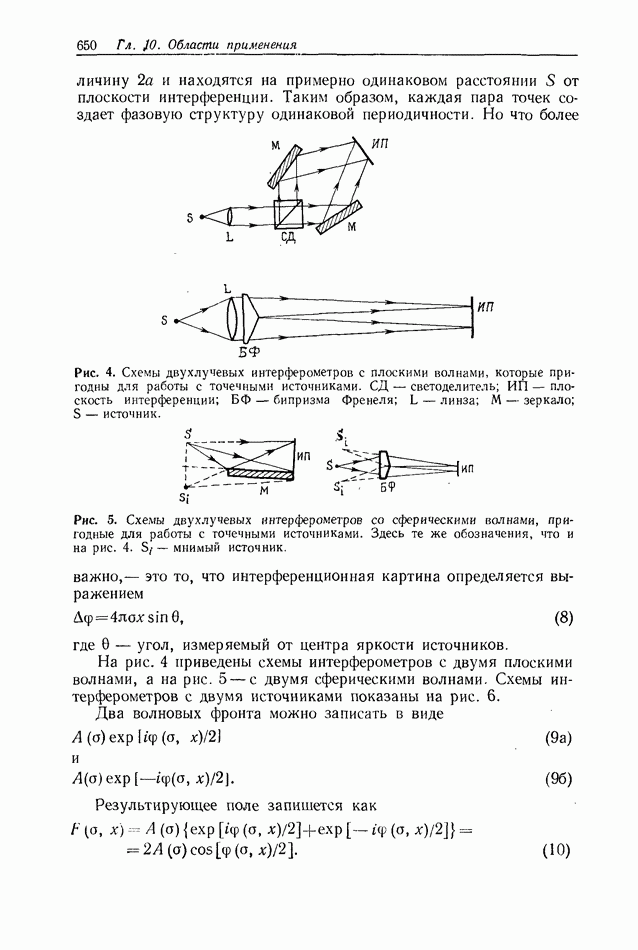
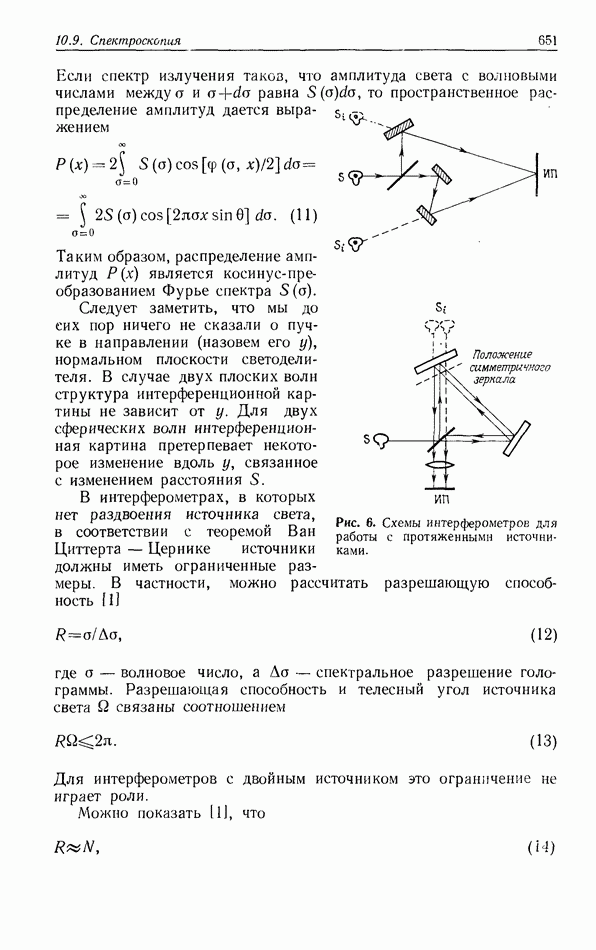
- 10.9. СПЕКТРОСКОПИЯ
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
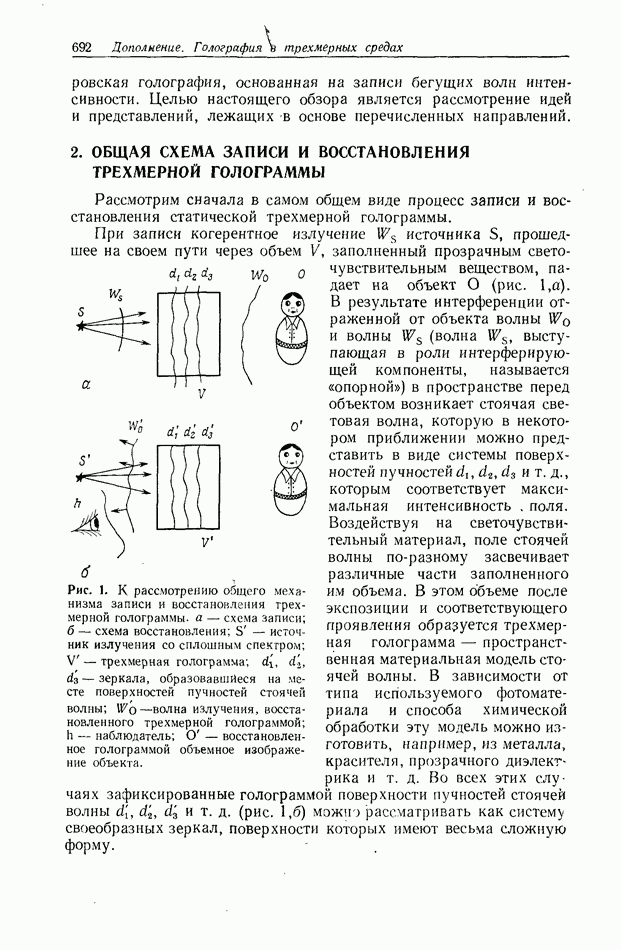
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
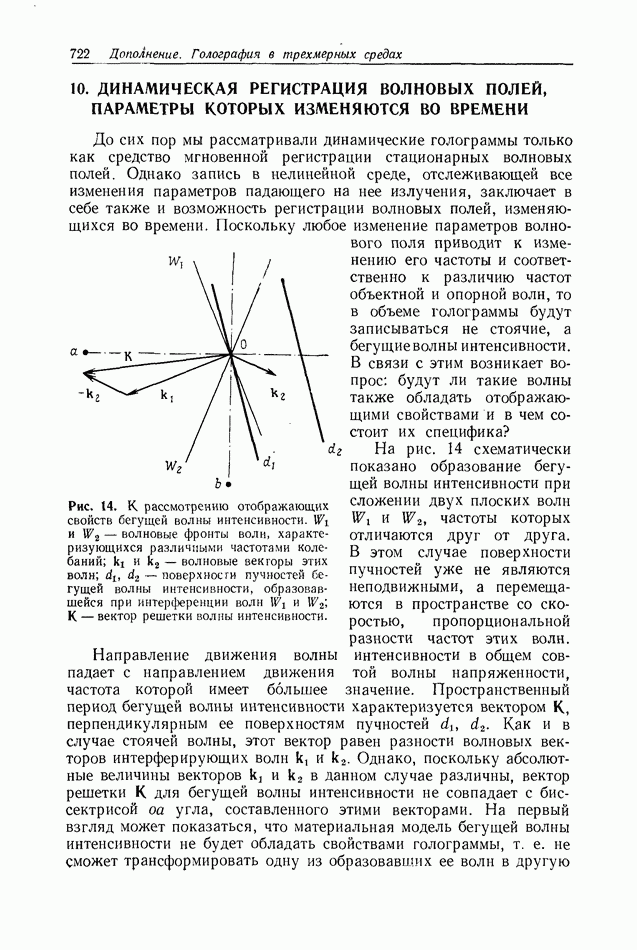
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ