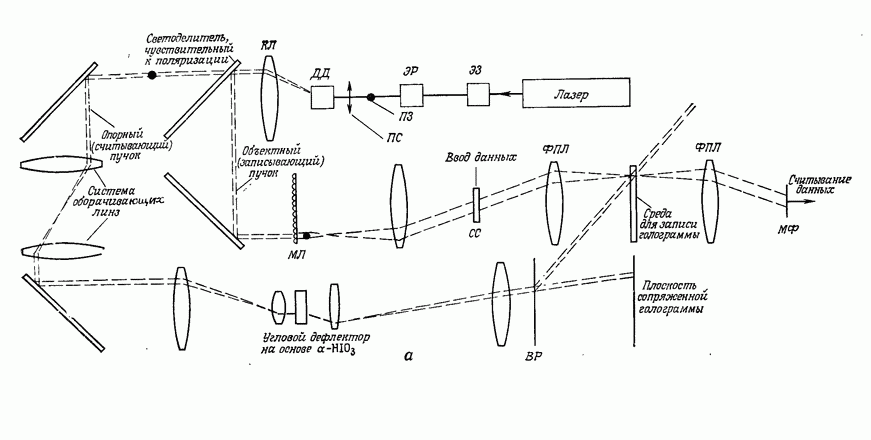
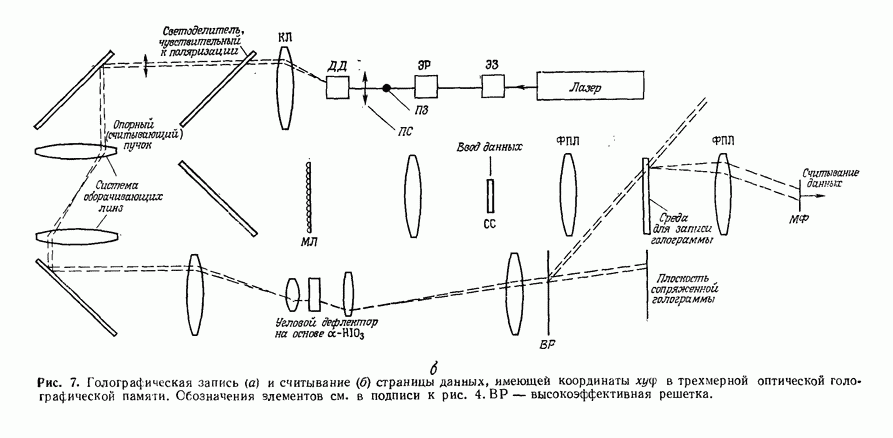
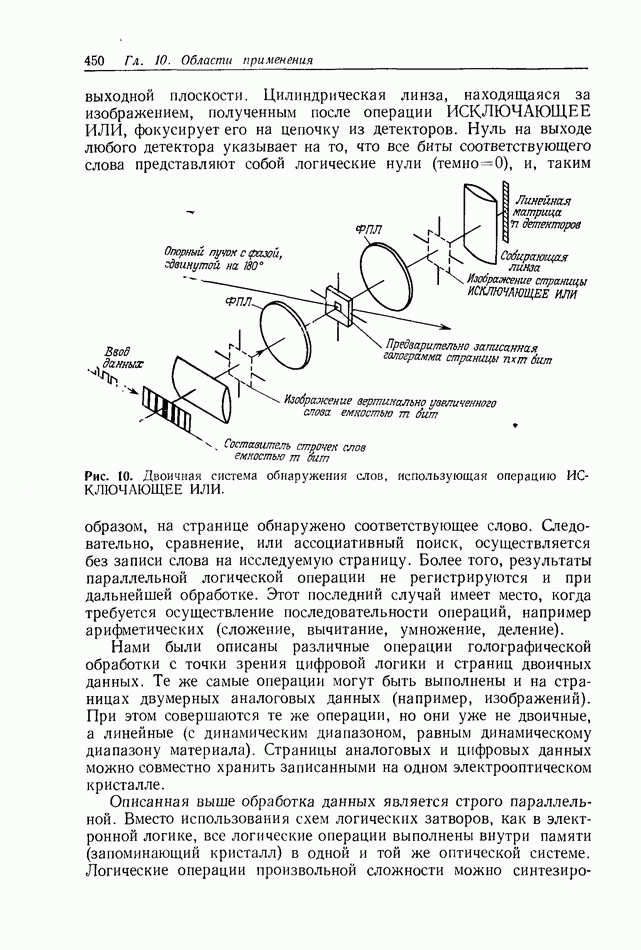
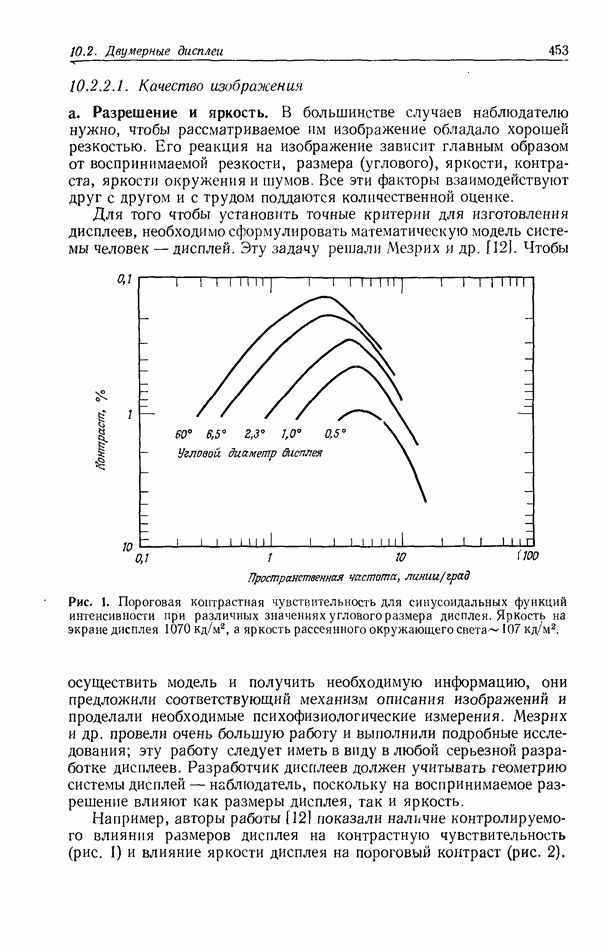
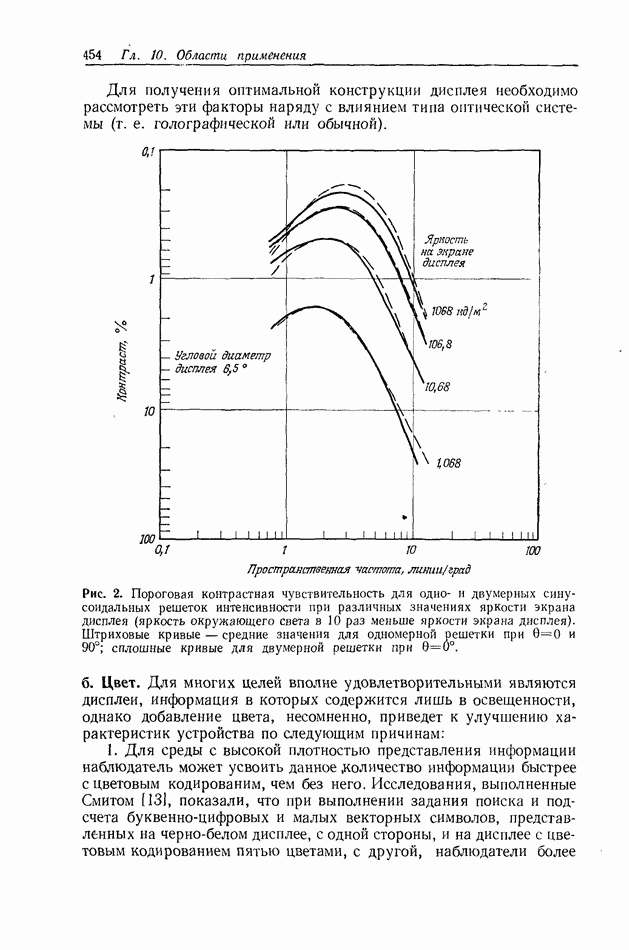
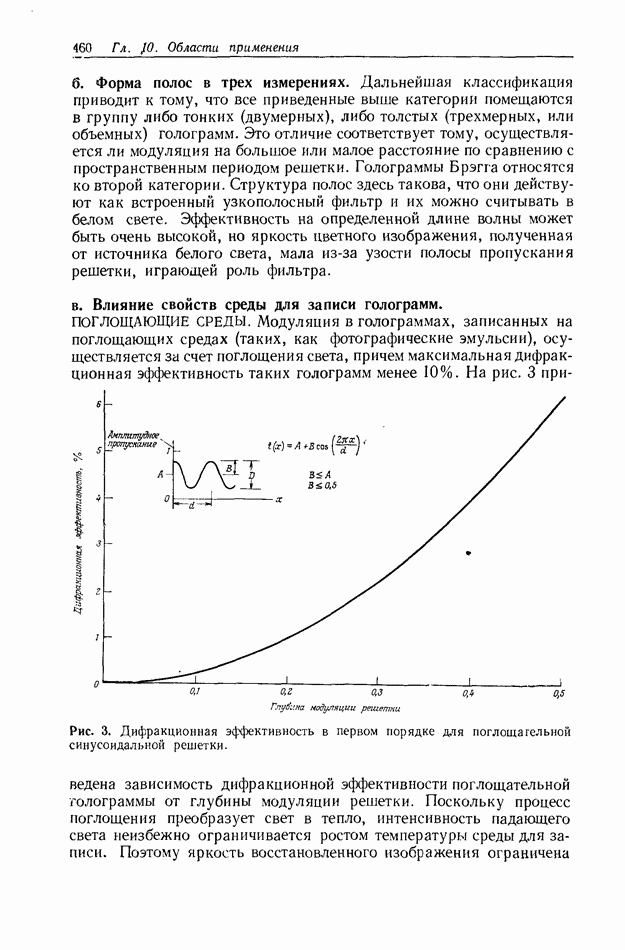
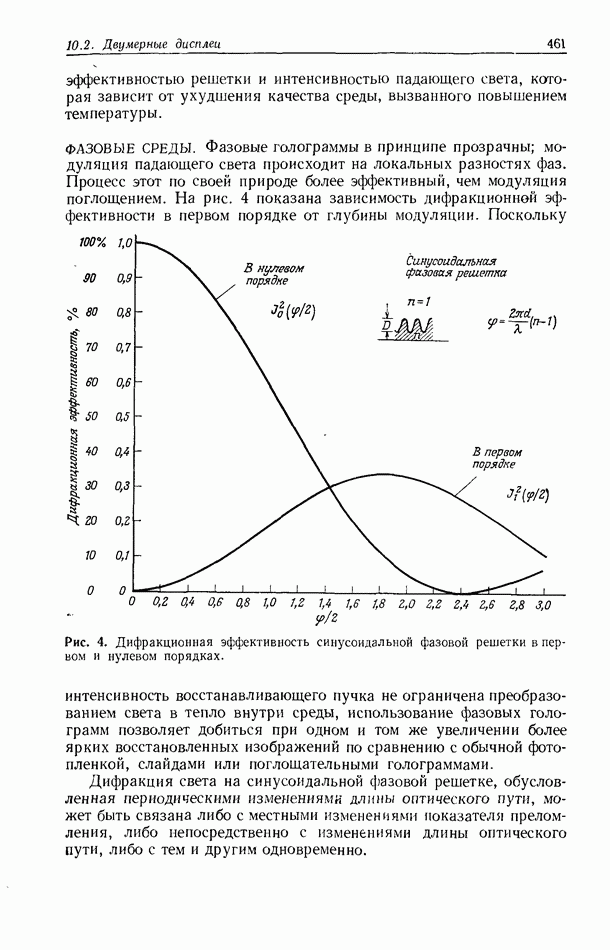
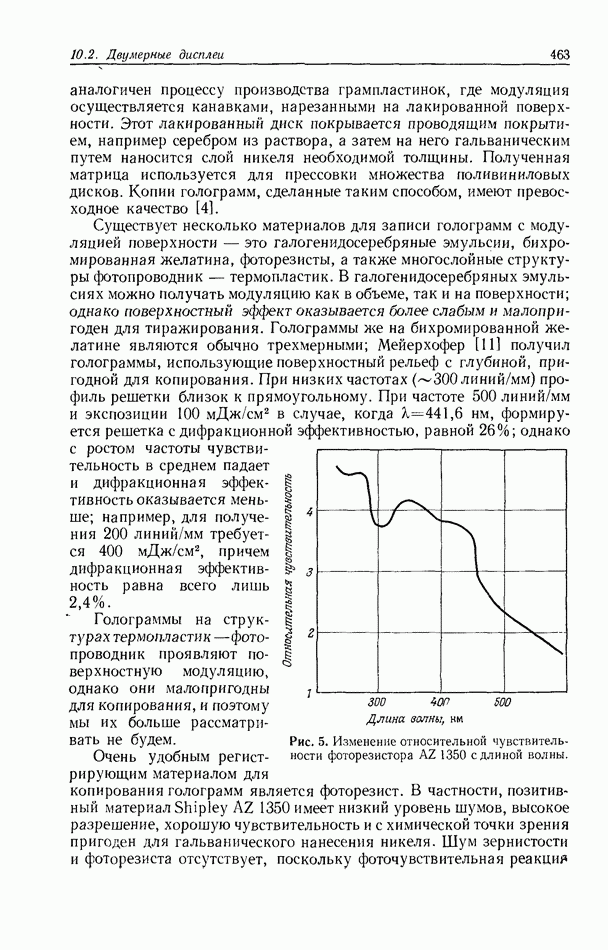
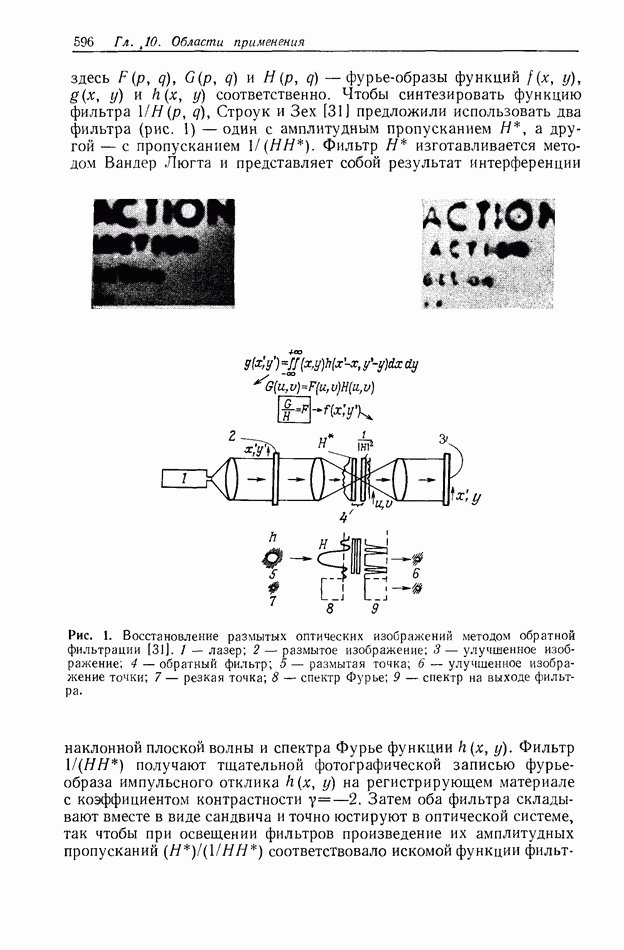
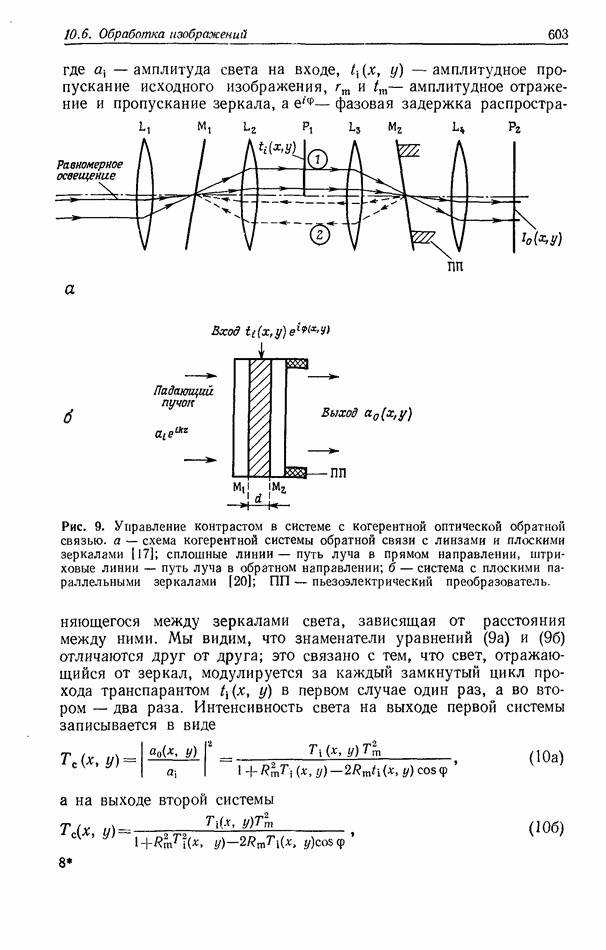
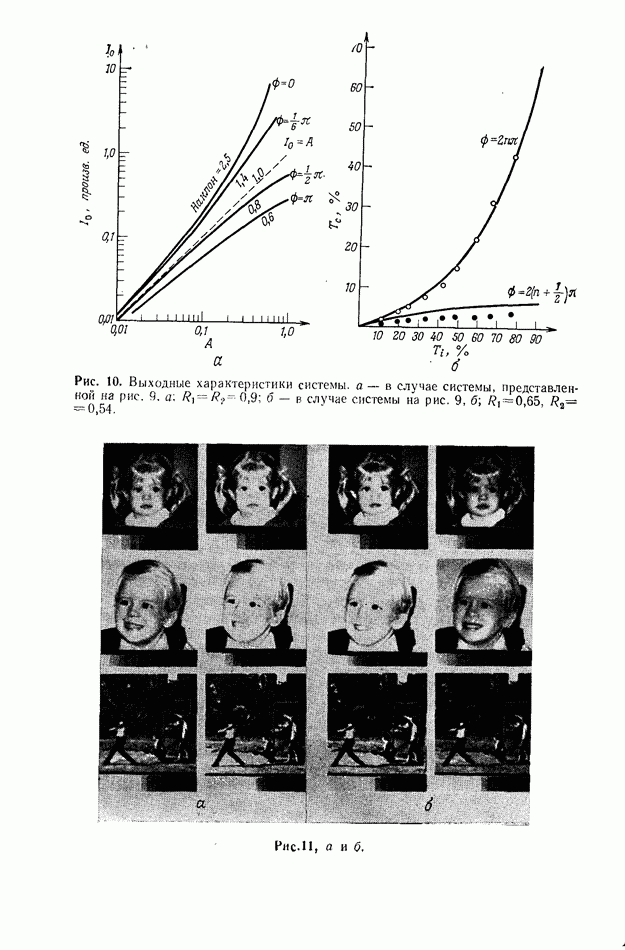
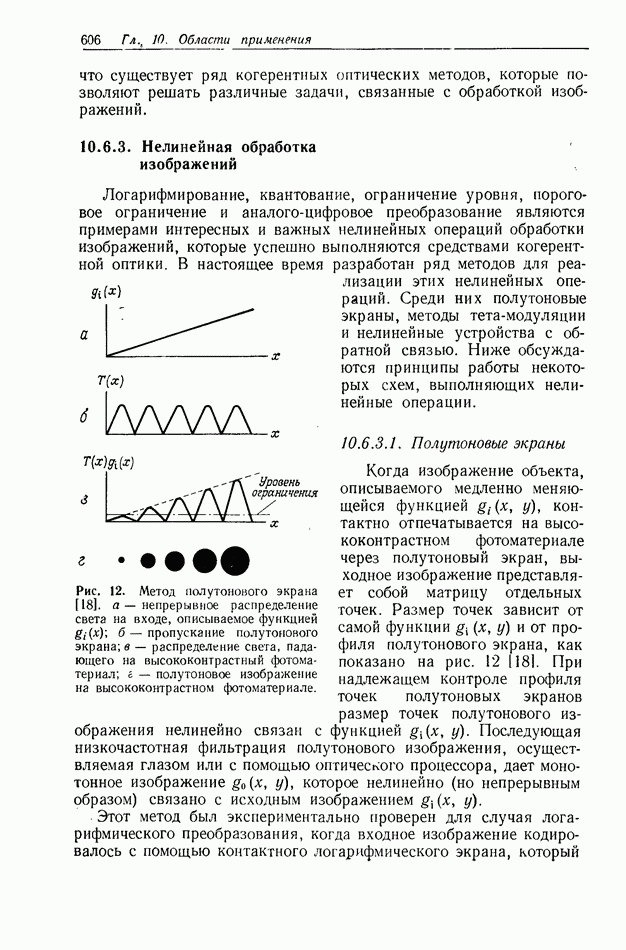
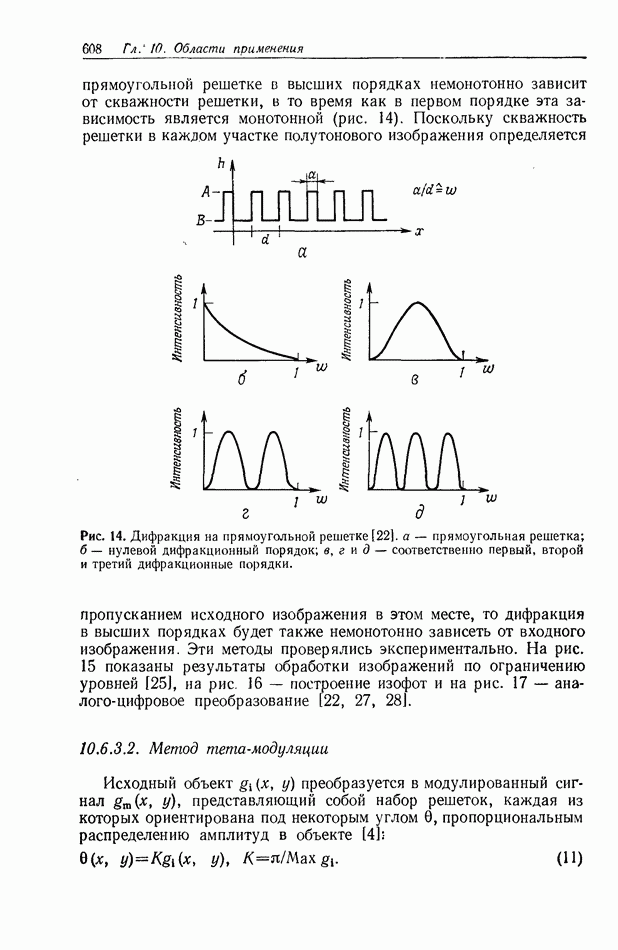
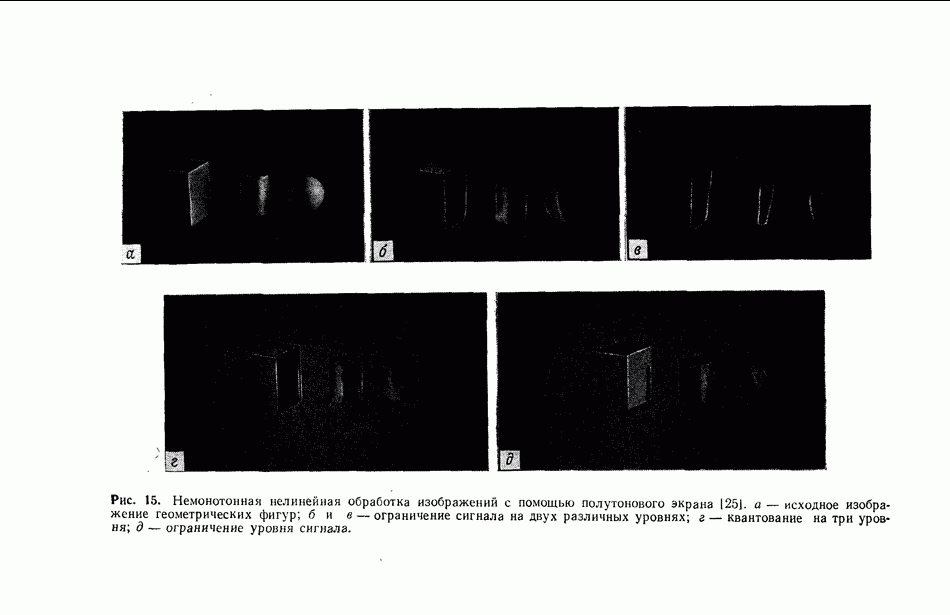
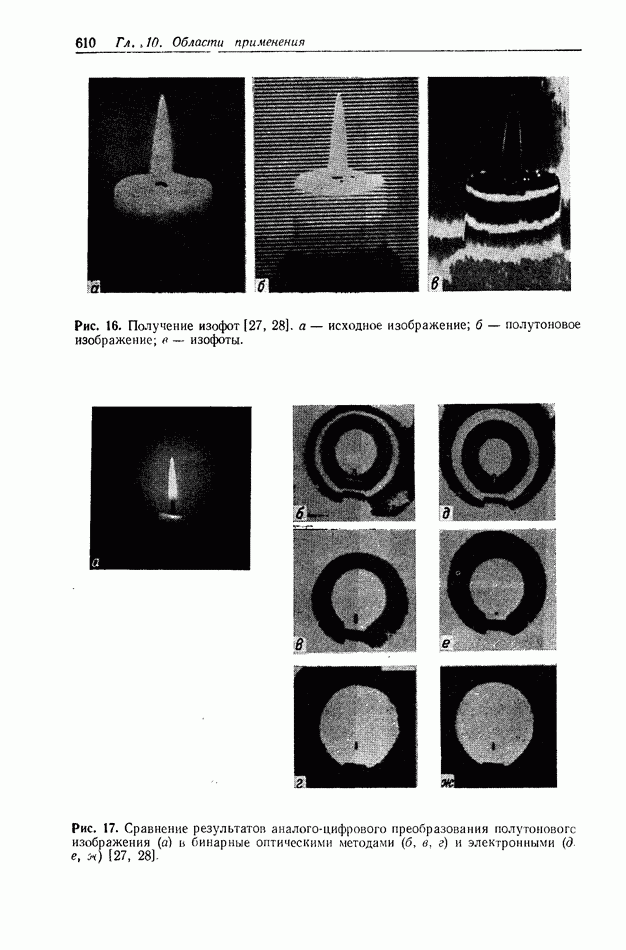
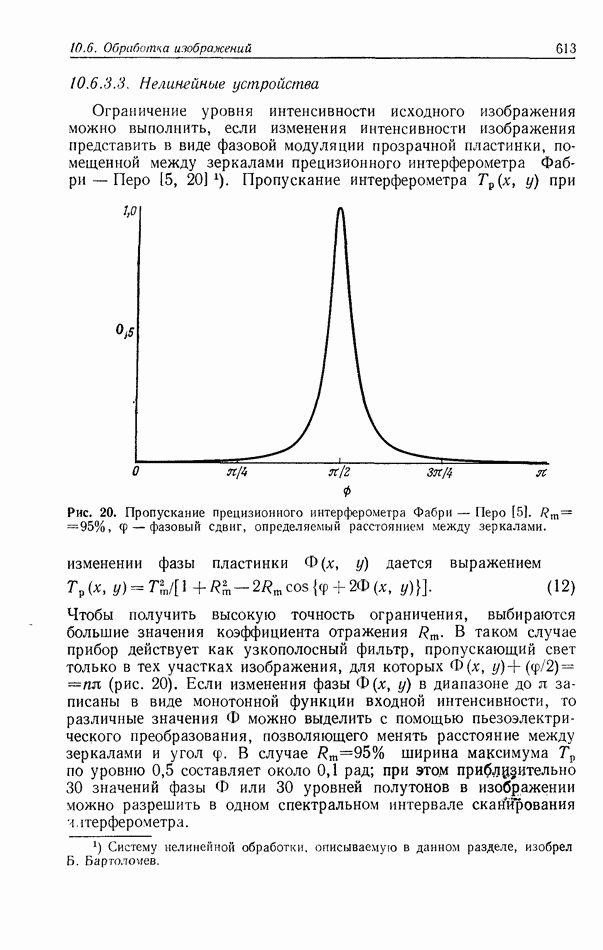
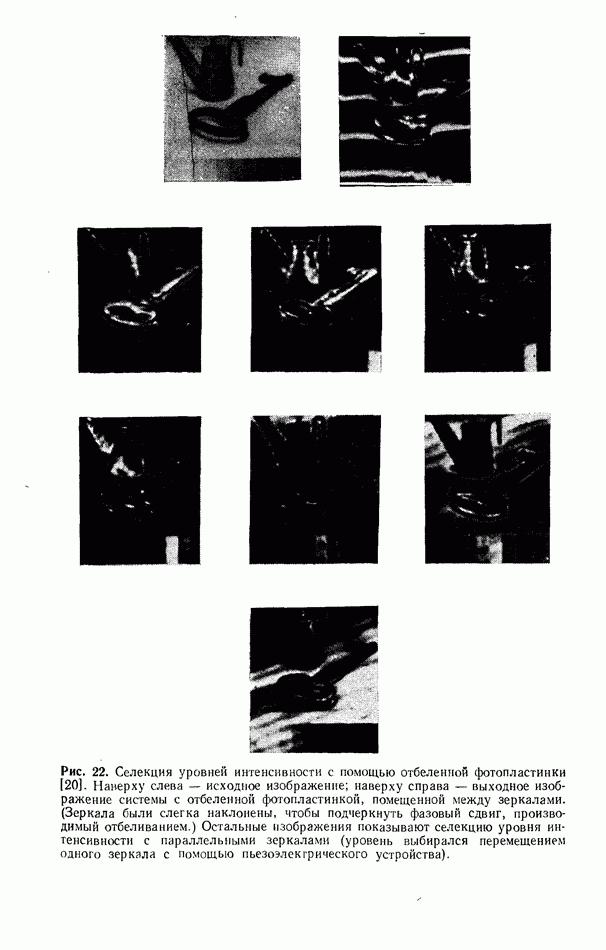
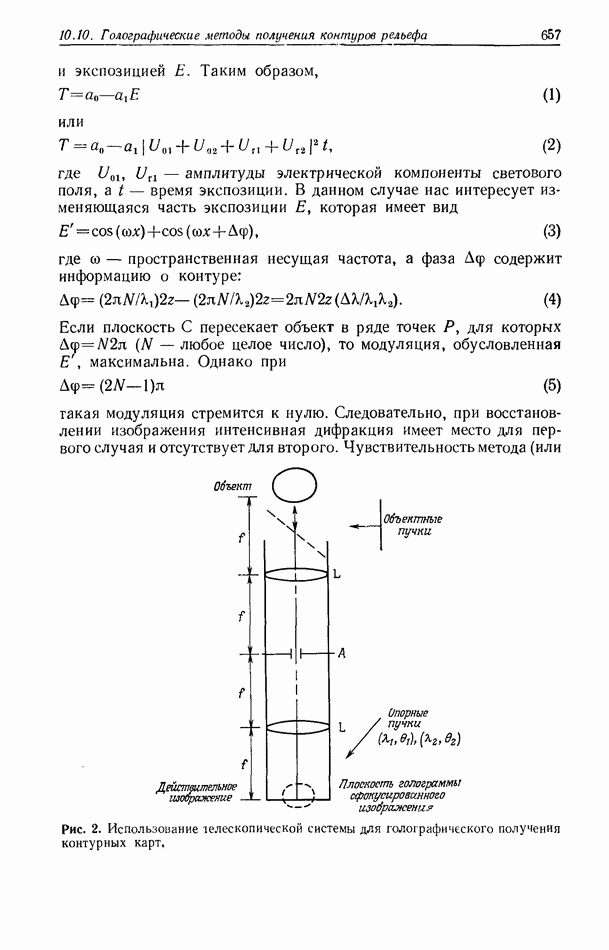
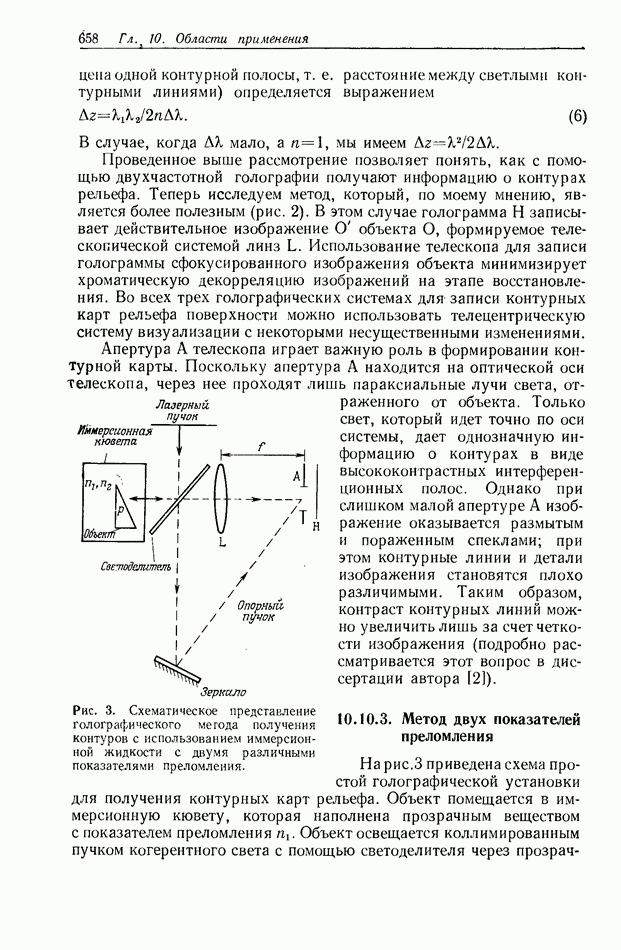
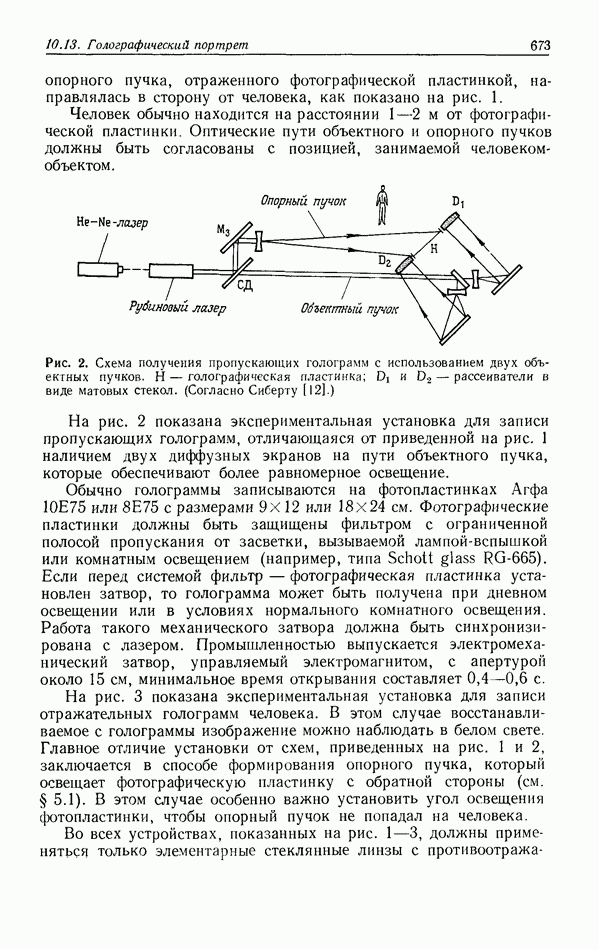
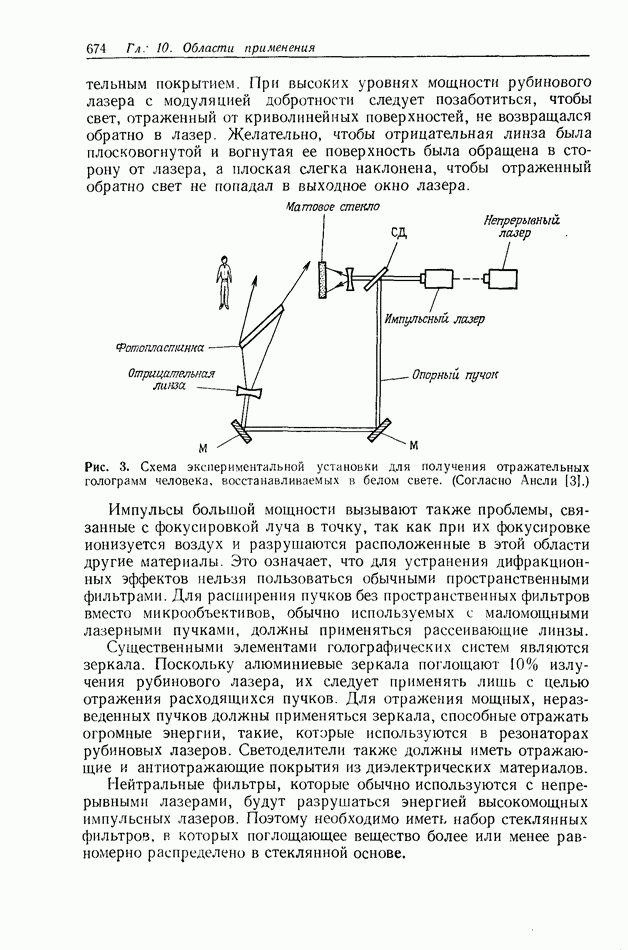
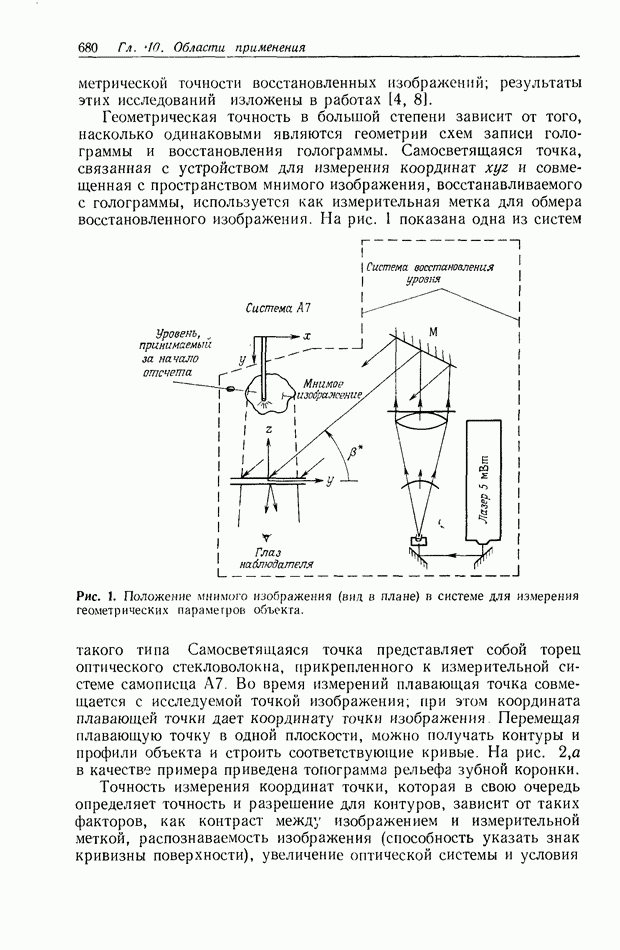
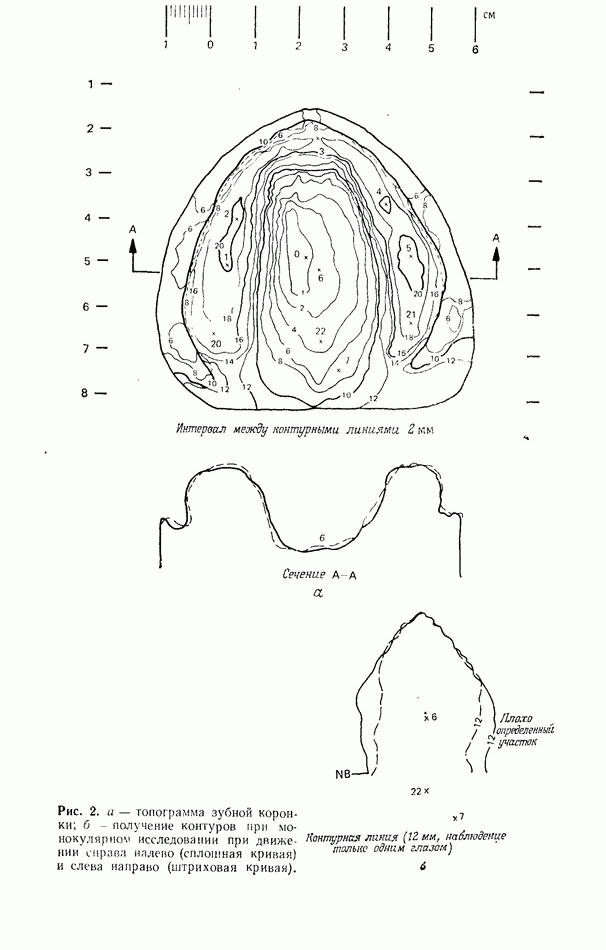
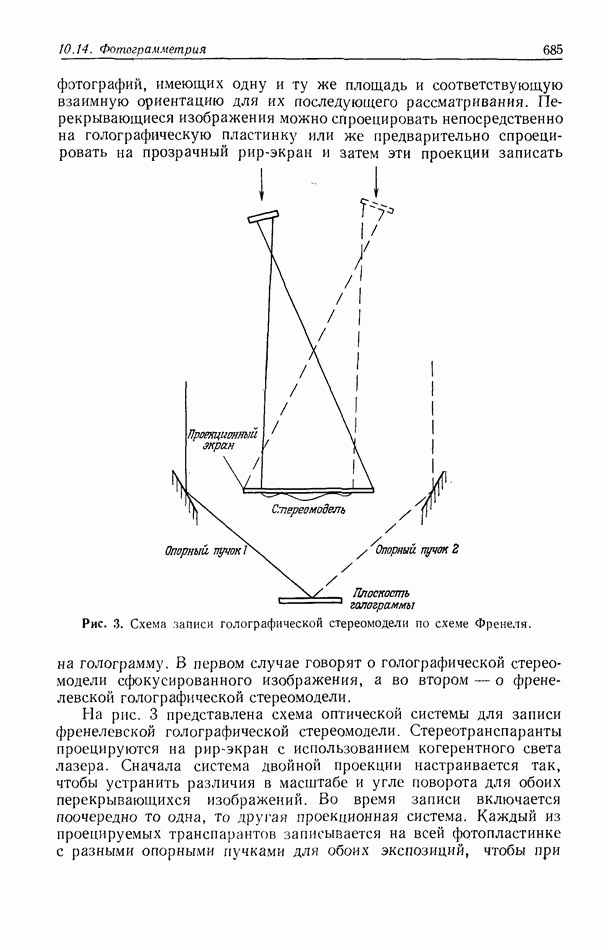
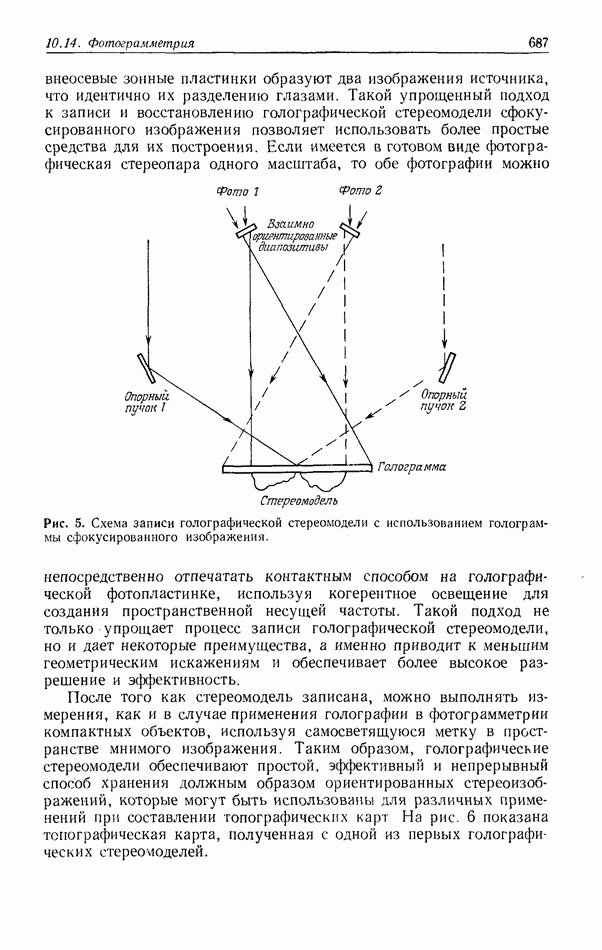
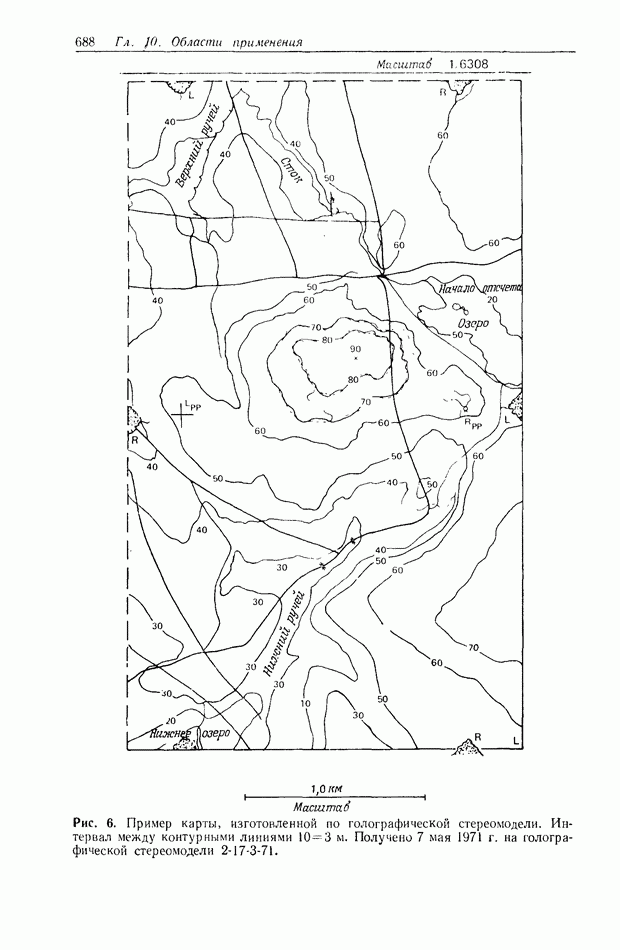
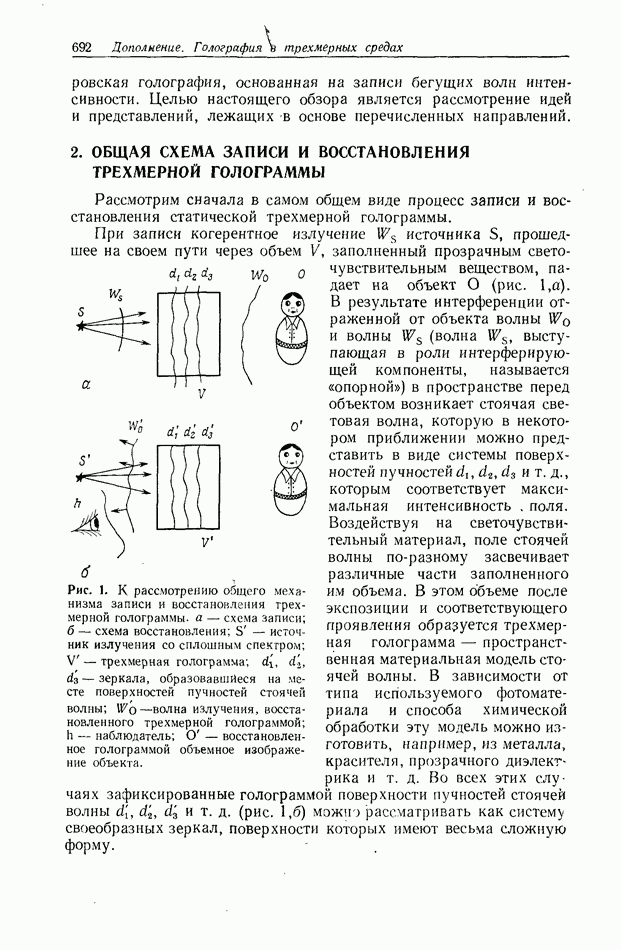
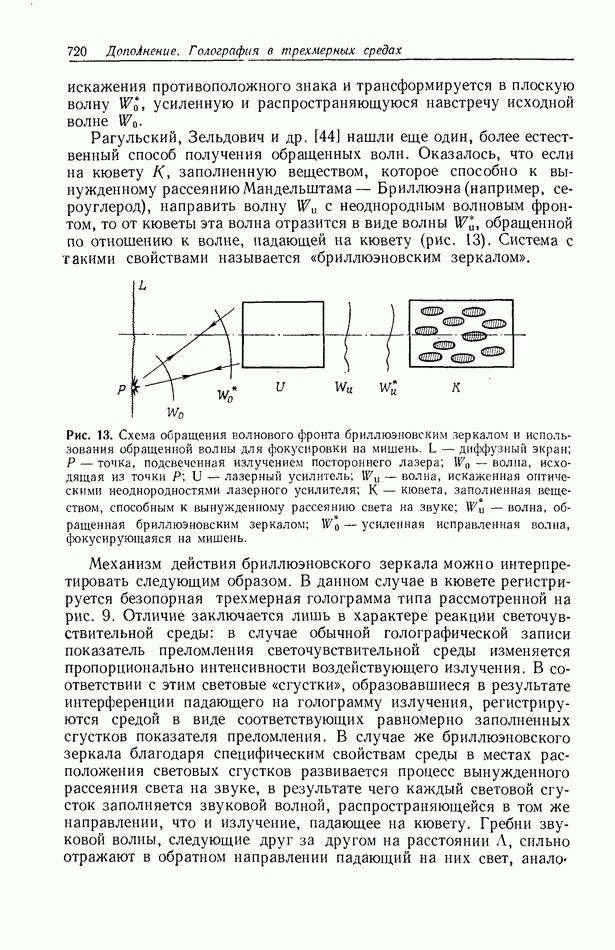
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
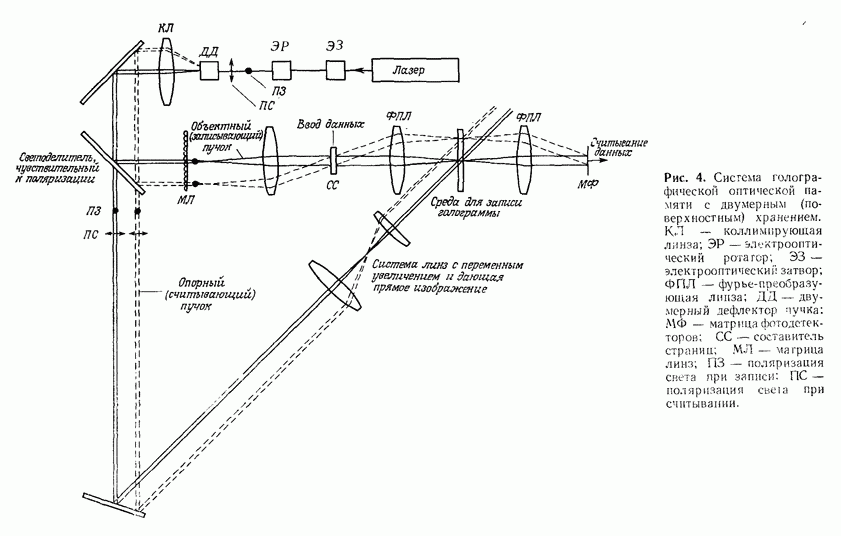
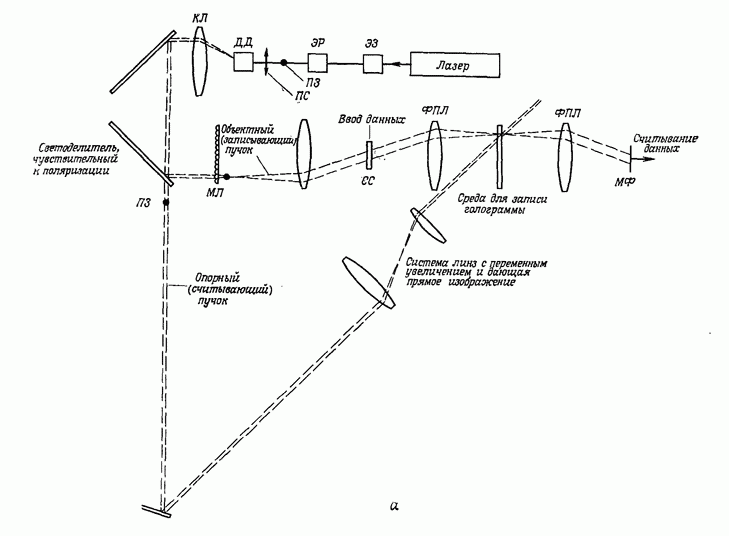
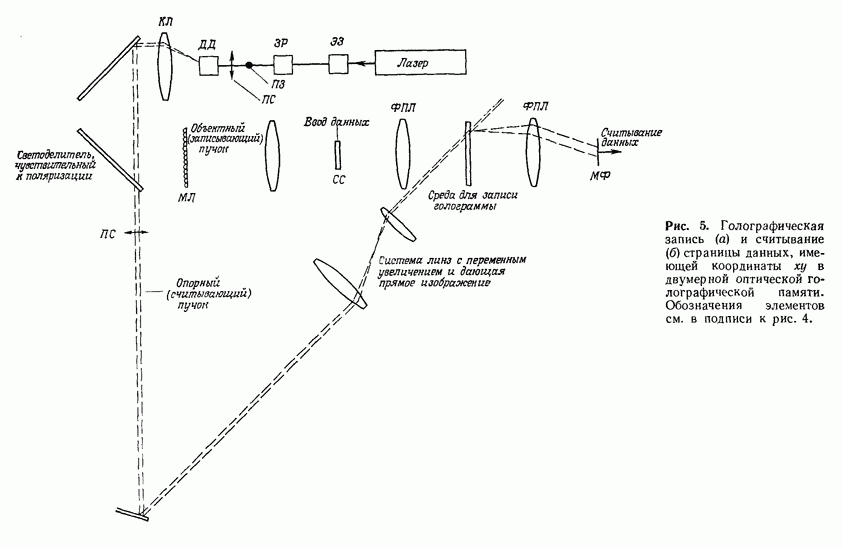
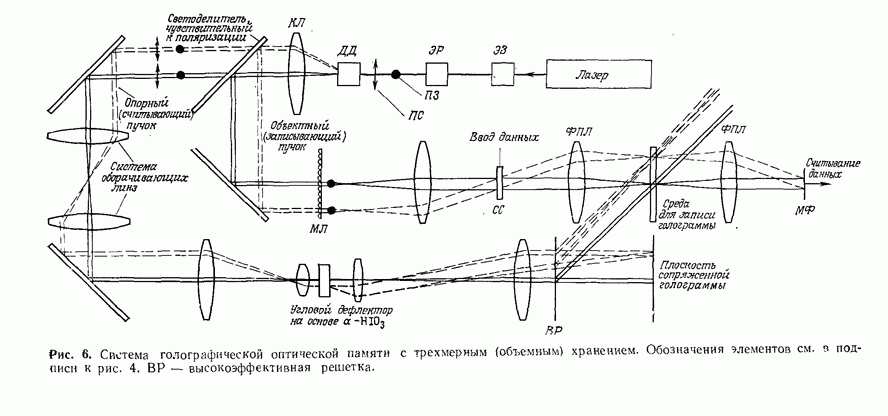
5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
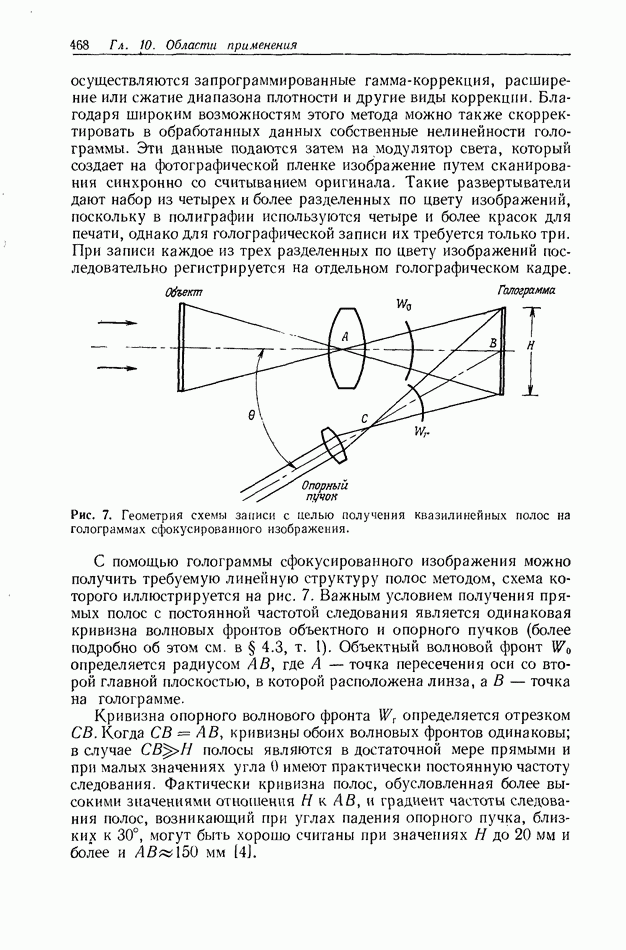
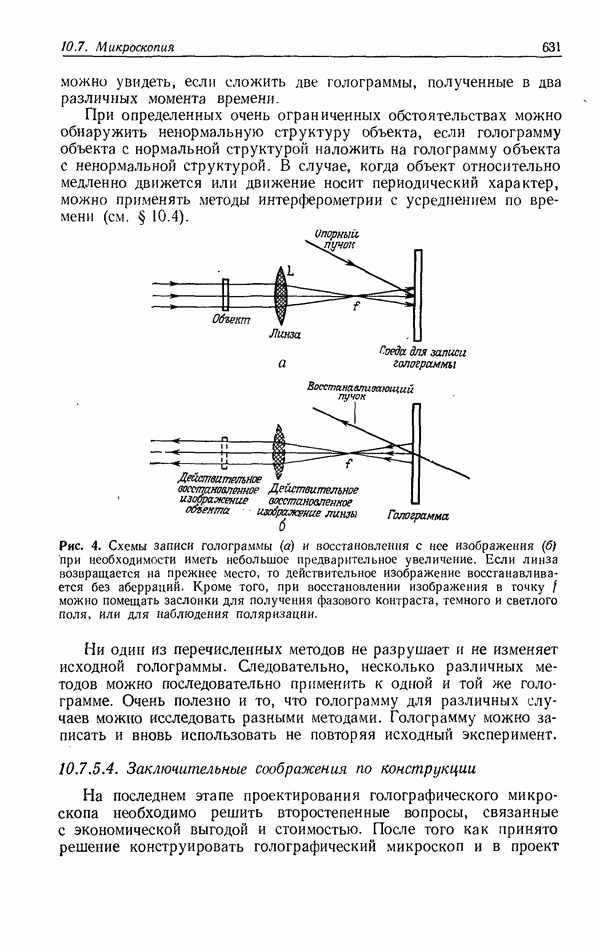
Как уже отмечалось, кинематическая теория, правильно описывая основной механизм трехмерной голограммы, не дает количественных соотношений; в частности, с ее помощью нельзя рассчитать дифракционную эффективность. Вместе с тем знание закономерностей, которые определяют эту весьма важную величину,
и параметров, от которых она зависит, играют определяющую роль при разработке технологии изготовления фотоматериалов, предназначенных для записи тех или иных типов трехмерных голограмм. При этом для оценки качества фотоматериала, как правило, используют некоторую условную величину — дифракционную эффективность простейшей объемной решетки, полученной в результате регистрации картины интерференции двух плоских волн.

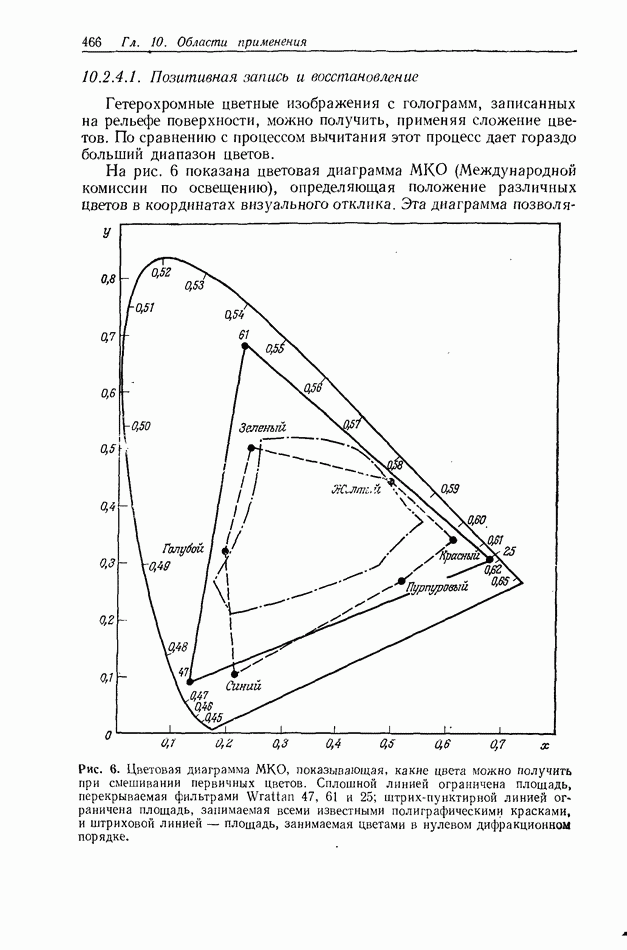
Рис. 5. К рассмотрению теории связанных волн. V — объем голограммы;  лучевые векторы плоских волн, экспонировавших голограмму при записи;
лучевые векторы плоских волн, экспонировавших голограмму при записи;  слои диэлектрика, образовавшиеся на месте поверхностей пучностей стоячей волны. Голограмма при освещении ее волной
слои диэлектрика, образовавшиеся на месте поверхностей пучностей стоячей волны. Голограмма при освещении ее волной  восстанавливает волну с лучевым вектором параллельным
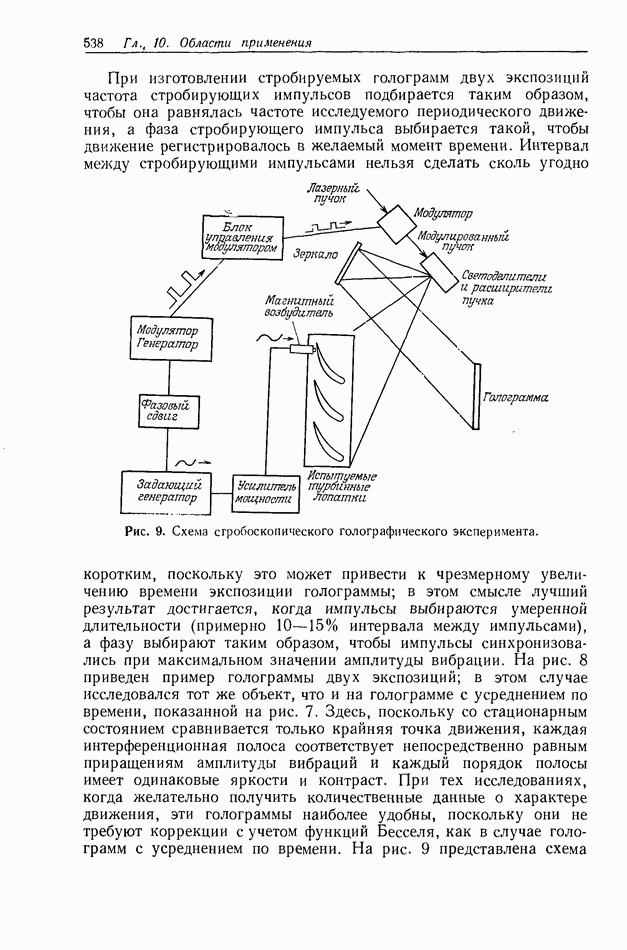
восстанавливает волну с лучевым вектором параллельным  в свою очередь волна восстанавливает волну
в свою очередь волна восстанавливает волну  волна
волна  волну и т. д. Интенсивность восстановленной голограммой волны определяется посредством суммирования всех составляющих
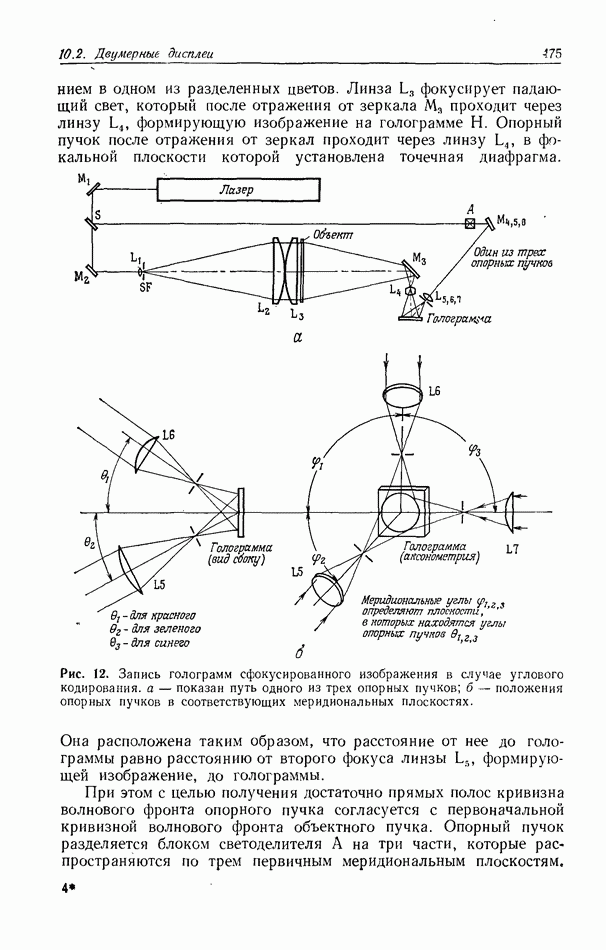
волну и т. д. Интенсивность восстановленной голограммой волны определяется посредством суммирования всех составляющих  с учетом их фаз. Справа приведен график зависимости дифракционной эффективности от толщины голограммы.
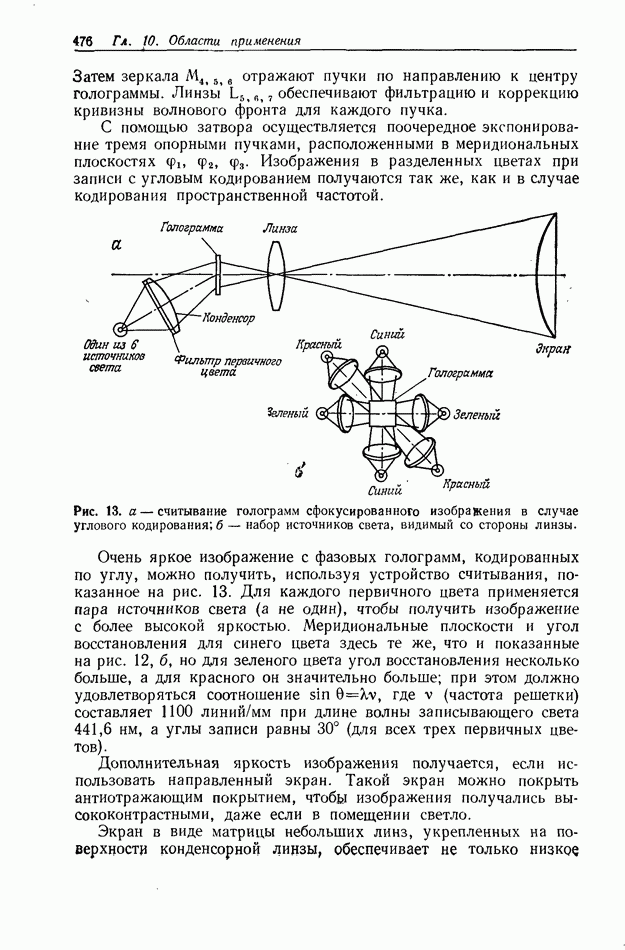
с учетом их фаз. Справа приведен график зависимости дифракционной эффективности от толщины голограммы.
Именно в применении к решению этой весьма важной задачи и используется в основном теория связанных волн, предложенная американским, исследователем Когельником [7]. Рассмотрим соответствующий этой теории механизм взаимодействия света с решеткой несколько подробнее.
Предположим, что на голограмме записаны две плоские волны о лучевыми векторами  и что после проявления в ее объеме Образовалась гармоническая фазовая решетка — система плоских слоев
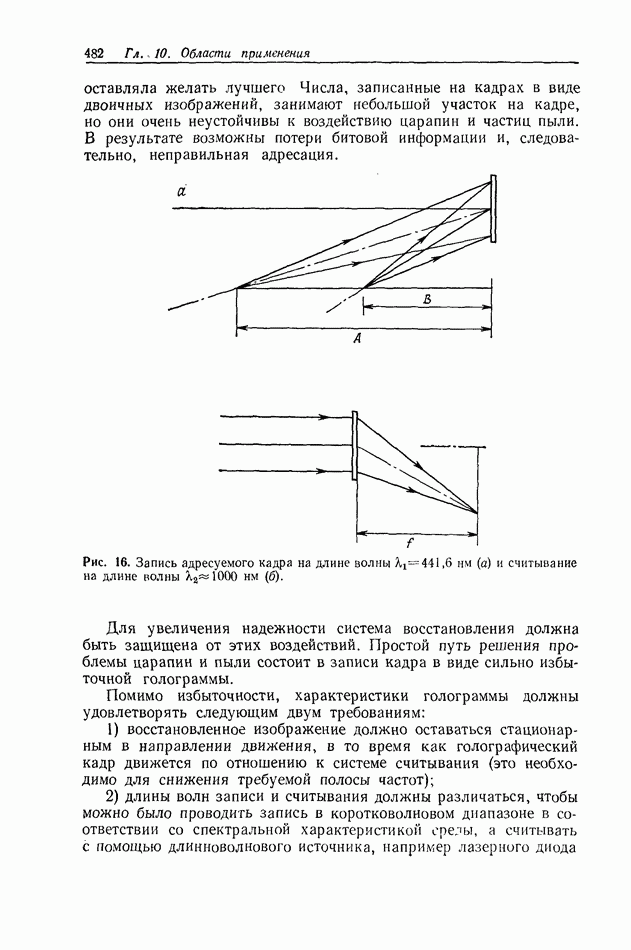
и что после проявления в ее объеме Образовалась гармоническая фазовая решетка — система плоских слоев  отличающихся значением показателя преломления (рис. 5). Пусть при восстановлении на такую структуру падает одна из образовавших ее плоских волн, например 10. В соответствии с представлениями кинематической теории восстанавливающая волна
отличающихся значением показателя преломления (рис. 5). Пусть при восстановлении на такую структуру падает одна из образовавших ее плоских волн, например 10. В соответствии с представлениями кинематической теории восстанавливающая волна  проходя без затухания через объем
проходя без затухания через объем
голограммы, преобразуется во всех точках этого объема в волну  которая выходит из голограммы, не взаимодействуя с ее структурой.
которая выходит из голограммы, не взаимодействуя с ее структурой.
Теория связанных волн внесла в эти представления уточнения. Очевидно, что восстановленная волна  прежде чем покинуть объем голограммы, испытает взаимодействие с ее структурой и в результате частично преобразуется в волну
прежде чем покинуть объем голограммы, испытает взаимодействие с ее структурой и в результате частично преобразуется в волну  совпадающую по направлению с волной 10 — второй из волн, записанных на голограмме. Волна
совпадающую по направлению с волной 10 — второй из волн, записанных на голограмме. Волна  в свою очередь снова трансформируется в волну
в свою очередь снова трансформируется в волну  совпадающую по направлению с волной
совпадающую по направлению с волной 
Таким образом, на первоначальные падающую и восстановленные волны накладываются вторичные волны, совпадающие с ними по направлению, но отличающиеся по фазе. Результат сложения этих волн не является тривиальным. Например, в рассматриваемом случае при некоторой толщине голограммы  вся энергия перекачивается в волну
вся энергия перекачивается в волну  т. е. дифракционная эффективность становится равной 100%. При дальнейшем увеличении толщины голограммы до значения
т. е. дифракционная эффективность становится равной 100%. При дальнейшем увеличении толщины голограммы до значения  вся энергия переходит в волну
вся энергия переходит в волну  и дифракционная эффективность голограммы становится равной нулю и т. д.
и дифракционная эффективность голограммы становится равной нулю и т. д.
Последовательность преобразований теории связанных волн сначала формально совпадает с соответствующей последовательностью теории первого приближения [см. выражения (13) — (15)]. Отличие состоит лишь в том, что в выражении (14) волны  считают равноправными и в выражении (15) поэтому нельзя пренебречь третьим членом. Учет связи падающей и восстановленной голограммой волн основан на рассмотренном ранее свойстве структуры голограммы преобразовывать в каждой своей точке одну из интерферирующих компонент в другую [см. выражение
считают равноправными и в выражении (15) поэтому нельзя пренебречь третьим членом. Учет связи падающей и восстановленной голограммой волн основан на рассмотренном ранее свойстве структуры голограммы преобразовывать в каждой своей точке одну из интерферирующих компонент в другую [см. выражение  В частном случае, когда на голограмме записана пара плоских волн, амплитуда которых не зависит от пространственных координат, указанное свойство действительно как при преобразовании
В частном случае, когда на голограмме записана пара плоских волн, амплитуда которых не зависит от пространственных координат, указанное свойство действительно как при преобразовании  так и наоборот. Учитывая это, а также опуская члены, соответствующие преобразованиям типа
так и наоборот. Учитывая это, а также опуская члены, соответствующие преобразованиям типа  выражение (15) можно записать следующим образом:
выражение (15) можно записать следующим образом:

Поскольку это уравнение выполняется при произвольном выборе пары плоских волн и записываемых на голограмме, то суммы членов, одна из которых содержит только  а другая — должны обращаться в нуль по отдельности. Следовательно, мы получаем систему двух уравнений:
а другая — должны обращаться в нуль по отдельности. Следовательно, мы получаем систему двух уравнений:

Нетрудно заметить, что эти уравнения связаны друг с другом: в уравнение для волновой функции входит амплитуда волновой функции  и наоборот. Подставляя в (28) и (29) вместо
и наоборот. Подставляя в (28) и (29) вместо  и
и
выражения для плоских волн, аналогичные (19) и (20), получаем два уравнения для амплитуд  с помощью которых можно найти зависимость этих амплитуд от толщины голограммы.
с помощью которых можно найти зависимость этих амплитуд от толщины голограммы.
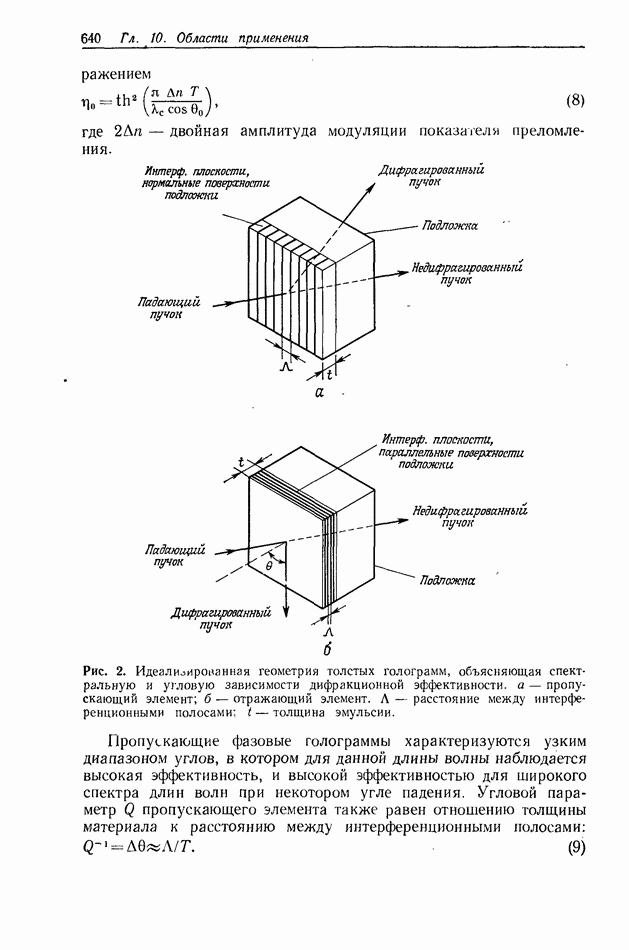
Используя такой подход, Когельник рассмотрел наиболее характерные случаи записи. В частности, он показал, что дифракционная эффективность фазовой отражательной решетки при некоторой достаточно большой толщине стремится к 100%. Дифракционная эффективность такой же амплитудной решетки не превышает 7,2%.
Однако следует заметить, что теорию связанных волн нельзя рассматривать как теорию трехмерной голограммы во втором приближении. Действительно, голограмма по своему физическому смыслу представляет собой запись информации о сложном волновом поле, которое можно представить в виде суммы множества плоских волн. Поэтому решетку, образованную в результате записи картины интерференции двух плоских волн, свойства которой рассматриваются в теории Когельника, можно назвать голограммой только условно.
Теорию Когельника нельзя считать теорией даже элементарного механизма голограммы — процесса записи и восстановления двух плоских волн, на основе которого можно было бы разработать общую теорию, учитывающую закономерности записи и воспроизведения произвольного волнового фронта, составленного из множества плоских волн. Трудность здесь обусловлена тем, что одна и та же плоская волна, как правило, участвует в создании множества решеток. В таких условиях практически все решетки оказываются связанными друг с другом, и поле излучения, восстановленное голограммой, в отличие от первого приближения уже нельзя представить в виде простой суммы полей, соответствующих отдельным решеткам. При этом теория Когельника не дает ответа на основной вопрос о том, как учесть все эти связи.
Более плодотворным путем развития теории трехмерной голограммы оказался подход, предложенный Эвальдом [8] и основанный на идеях динамической теории дифракции рентгеновских лучей. Первоначально эта теория применялась для изучения простой объемной голографической решетки [9]. Впервые для анализа собственно объемной голограммы, т. е. структуры, составленной из множества решеток, ее использовали Аристов и Шехтман (см., например, [10]) В этих работах, в частности, было показано, что, в случае когда голограмма получена с участием мощной опорной ролны, а также когда записанная на голограммах волна имеет сложную структуру, для определения интенсивности восстановленной волны можно пользоваться формулами Когельника.
Представления, основанные на динамической теории дифракции, нашли наибольшее выражение в так называемой модовой теории трехмерной голограммы, предложенной Сидоровичем [11].
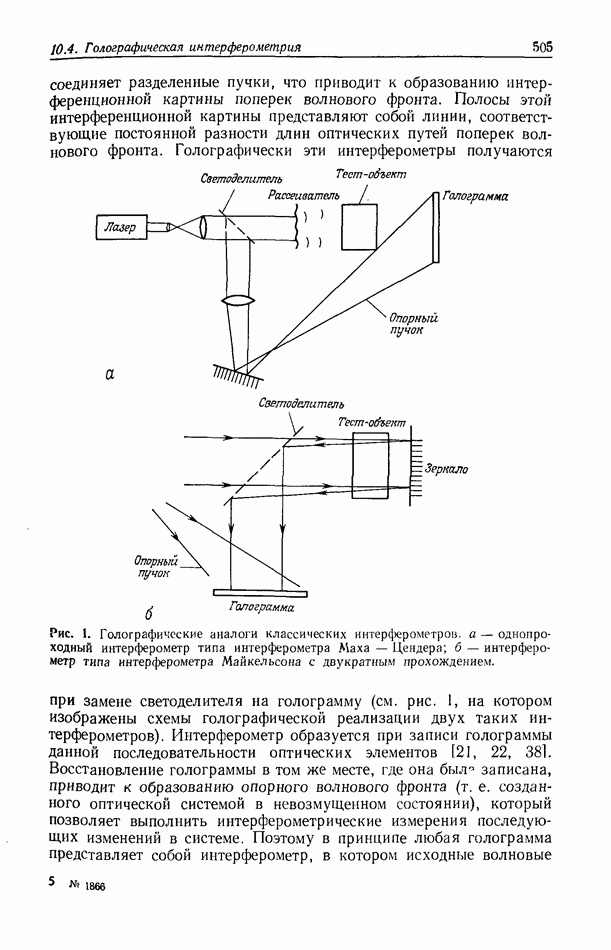
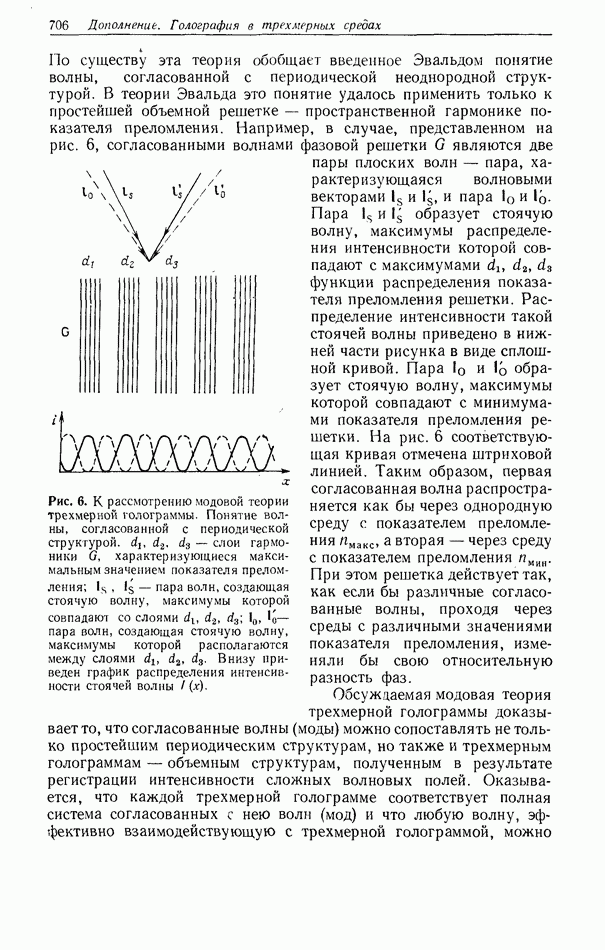
По существу эта теория обобщает введенное Эвальдом понятие волны, согласованной с периодической неоднородной структурой. В теории Эвальда это понятие удалось применить только к простейшей объемной решетке — пространственной гармонике показателя преломления. Например, в случае, представленном на рис. 6, согласованными волнами фазовой решетки  являются две пары плоских волн — пара, характеризующаяся волновыми векторами
являются две пары плоских волн — пара, характеризующаяся волновыми векторами  и пара
и пара  Пара
Пара  и 1д образует стоячую волну, максимумы распределения интенсивности которой совпадают с максимумами
и 1д образует стоячую волну, максимумы распределения интенсивности которой совпадают с максимумами  функции распределения показателя преломления решетки. Распределение интенсивности такой стоячей волны приведено в нижней части рисунка в виде сплошной кривой. Пара
функции распределения показателя преломления решетки. Распределение интенсивности такой стоячей волны приведено в нижней части рисунка в виде сплошной кривой. Пара  образует стоячую волну, максимумы которой совпадают с минимумами показателя преломления решетки. На рис. 6 соответствующая кривая отмечена штриховой линией. Таким образом, первая согласованная волна распространяется как бы через однородную среду с показателем преломления ямакс. а вторая — через среду с показателем преломления пмин. При этом решетка действует так, как если бы различные согласованные волны, проходя через среды с различными значениями показателя преломления, изменяли бы свою относительную разность фаз.
образует стоячую волну, максимумы которой совпадают с минимумами показателя преломления решетки. На рис. 6 соответствующая кривая отмечена штриховой линией. Таким образом, первая согласованная волна распространяется как бы через однородную среду с показателем преломления ямакс. а вторая — через среду с показателем преломления пмин. При этом решетка действует так, как если бы различные согласованные волны, проходя через среды с различными значениями показателя преломления, изменяли бы свою относительную разность фаз.

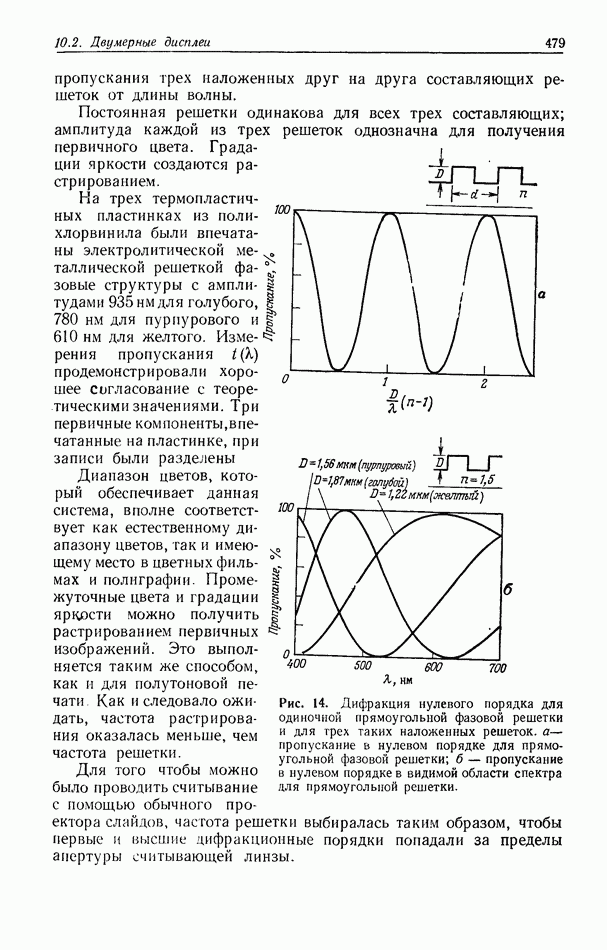
Рис. 6. К рассмотрению модовой теории трехмерной голограммы. Понятие волны, согласованной с периодической структурой,  слои гармоники
слои гармоники  характеризующиеся максимальным значением показателя преломления;
характеризующиеся максимальным значением показателя преломления;  пара волн, создающая стоячую волну, максимумы которой совпадают со слоями
пара волн, создающая стоячую волну, максимумы которой совпадают со слоями  — пара волн, создающая стоячую волну, максимумы которой располагаются между слоями
— пара волн, создающая стоячую волну, максимумы которой располагаются между слоями  Внизу приведен график распределения интенсивности стоячей волны
Внизу приведен график распределения интенсивности стоячей волны 
Обсуждаемая модовая теория трехмерной голограммы доказывает то, что согласованные волны (моды) можно сопоставлять не только простейшим периодическим структурам, но также и трехмерным голограммам — объемным структурам, полученным в результате регистрации интенсивности сложных волновых полей. Оказывается, что каждой трехмерной голограмме соответствует полная система согласованных с нею волн (мод) и что любую волну, эффективно взаимодействующую с трехмерной голограммой, можно
разложить по этим модам. В частности, применительно к фазовой голограмме теория предполагает, что каждая мода проходит через голограмму как через однородную среду с определенным показателем преломления. В этом случае действие голограммы состоит в том, что она сдвигает относительную разность фаз между модами.
В общих чертах рассмотрение проводится следующим образом. Волну, записанную на голограмме, представляют в виде суммы  плоских волн:
плоских волн:

Подставив это значение  в выражение (6), найдем с помощью соотношения (12) функцию распределения диэлектрической проницаемости голограммы:
в выражение (6), найдем с помощью соотношения (12) функцию распределения диэлектрической проницаемости голограммы:

Будем считать, что условиям распространения света через данную среду удовлетворяют специальные волновые функции (моды)

Относительно этих функций предполагается, что они составлены из тех же плоских волн, которые участвовали в записи голограммы, однако их направления распространения вследствие изменения диэлектрической проницаемости среды после экспозиции стали несколько другими. Кроме того, будем считать, что для любых компонент данной моды это изменение диэлектрической проницаемости одинаково. Все эти условия имеют вид специальных соотношений между волновыми векторами моды к и волновыми векторами  излучения, записанного на голограмме.
излучения, записанного на голограмме.
Подставляя в уравнение Гельмгольца (13) выражение (32) для  и учитывая упомянутые соотношения между
и учитывая упомянутые соотношения между  можно получить систему
можно получить систему  уравнений, связывающих амплитуды компонент моды с амплитудами составляющих поля, записанного на голограмме. В матричной форме эти уравнения имеют вид
уравнений, связывающих амплитуды компонент моды с амплитудами составляющих поля, записанного на голограмме. В матричной форме эти уравнения имеют вид

где  матрица голограммы, составленная из коэффициентов,
матрица голограммы, составленная из коэффициентов,  линейная матрица амплитуд 1-й моды, бег — значение диэлектрической проницаемости, соответствующее 1-й моде. Таким образом, задача сводится к нахождению собственных функций и собственных значений оператора
линейная матрица амплитуд 1-й моды, бег — значение диэлектрической проницаемости, соответствующее 1-й моде. Таким образом, задача сводится к нахождению собственных функций и собственных значений оператора  характеризующего структуру голограммы. Поскольку этот оператор является самосопряженным, система его собственных функций (мод)
характеризующего структуру голограммы. Поскольку этот оператор является самосопряженным, система его собственных функций (мод)
составляет полный ортогональный базис, по которому можно разложить любую волновую функцию, составленную из плоских волн, экспонировавших голограмму.
Модовая теория существенно упрощает рассмотрение процессов, протекающих в трехмерной голограмме, благодаря тому, что она автоматически учитывает очень сложные взаимные связи между рассеянием света на множестве решеток, из которых составлена голограмма, а также и потому, что аналогично теориям первого приближения представляет результат в виде суперпозиции независимых функций. Конкретно модовая теория была развита в применении к фазовым пропускающим [11, 12], амплитудным усиливающим [13] и трехмерным отражательным голограммам [14]. В настоящее время наиболее актуальным является применение модовой теории к описанию отражения света «бриллюэновским зеркалом» [15]. В данном случае модовая теория правильно предсказывает значение полного коэффициента усиления в среде, которое необходимо, чтобы амплитуда обращенной волны превышала шумы. Модовая теория позволяет также сформулировать условия устойчивости обращенной волны при ее распространении сквозь усиливающую голограмму. Все это нашло подтверждение в большом числе экспериментов.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
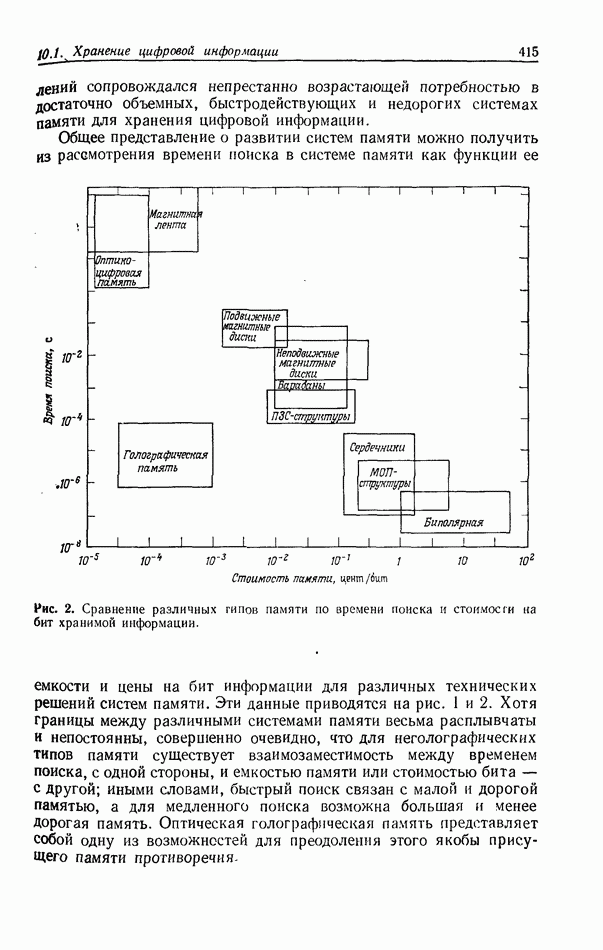
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
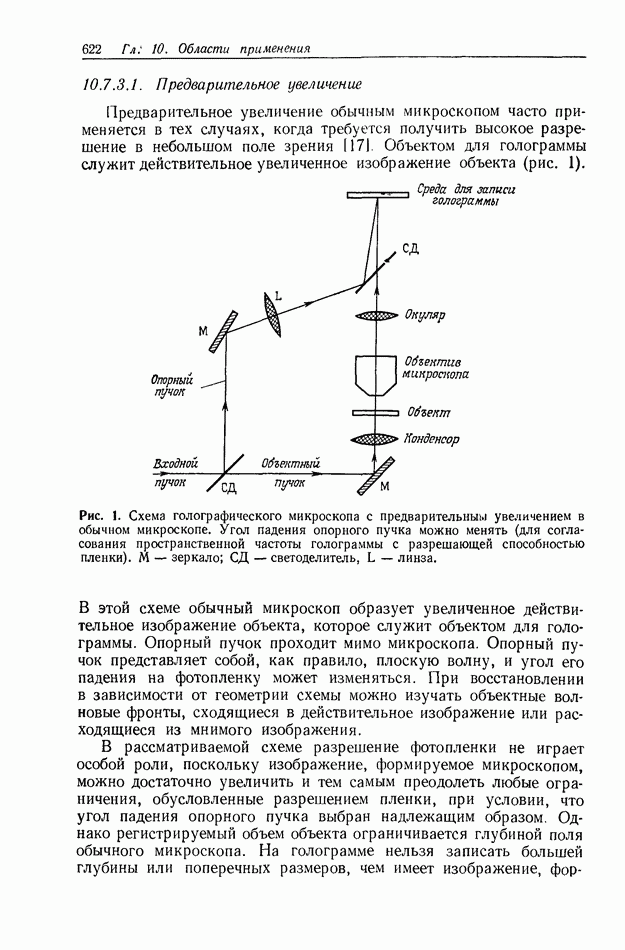
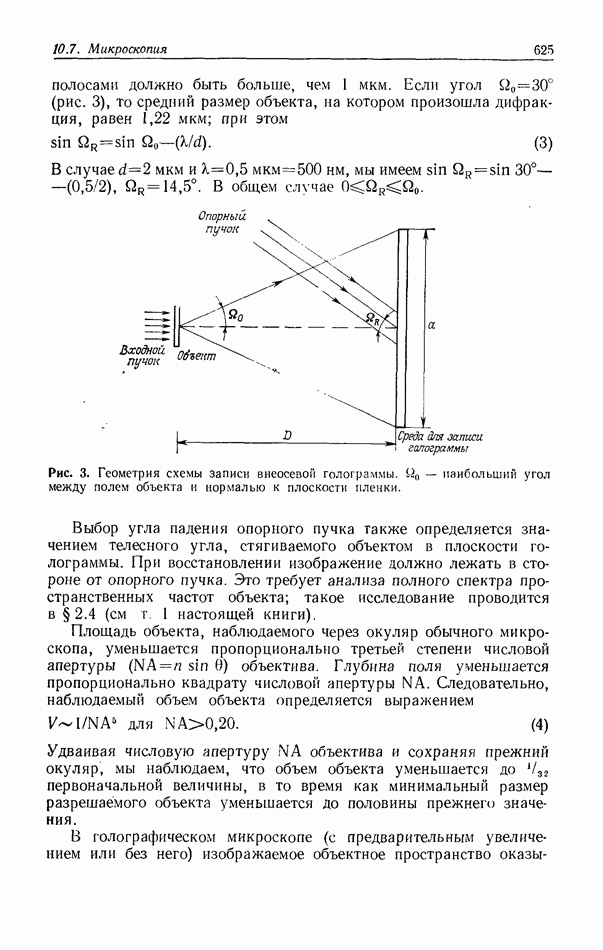
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
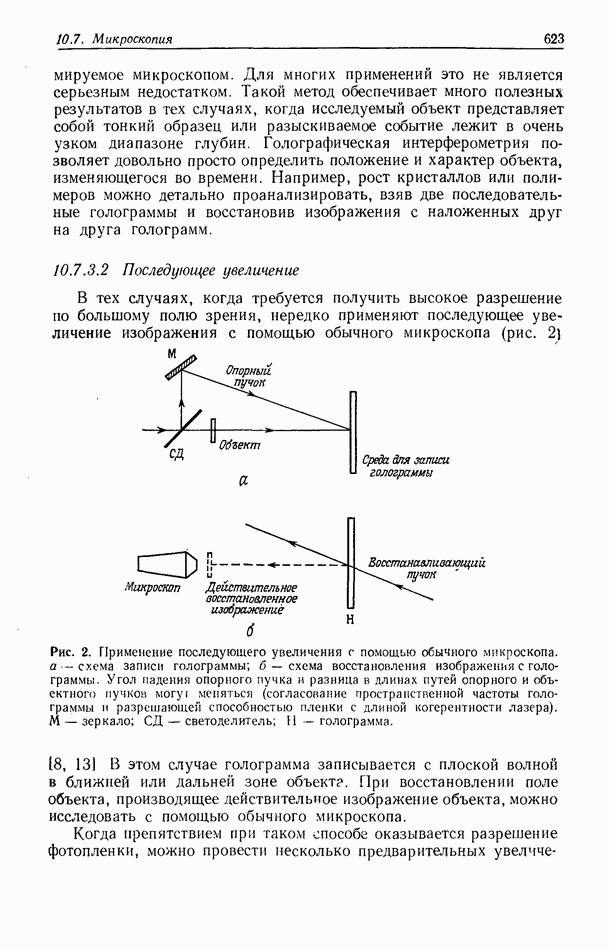
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
- 10.9. СПЕКТРОСКОПИЯ
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
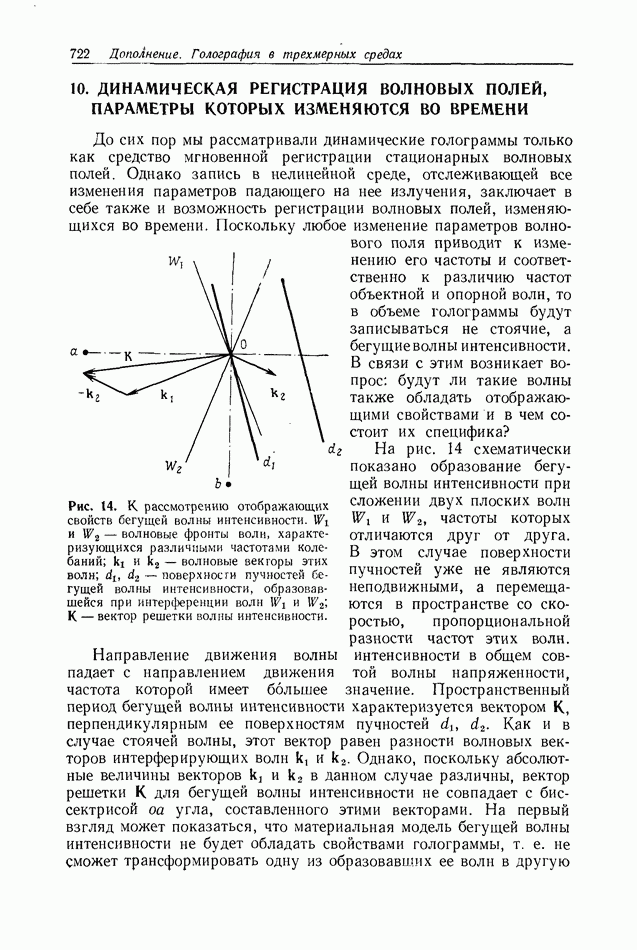
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ