| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
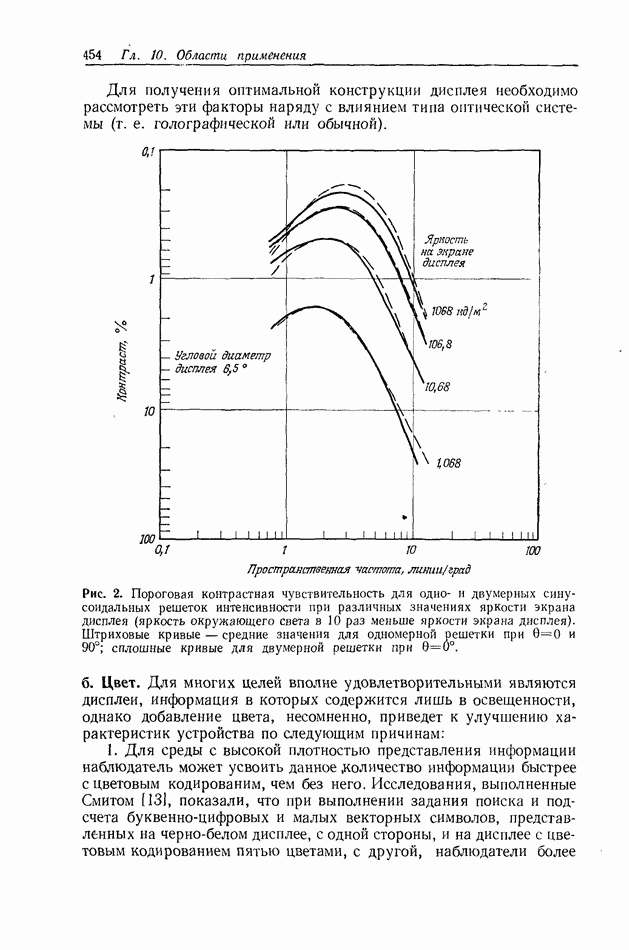
10.6.2. Линейная обработка изображений
Обработка называется линейной, когда обработанное (выходное) изображение линейно связано с исходным. Примерами линейных операций обработки являются полосовая фильтрация, вычитание, свертка и корреляция. Улучшение изображений методами полосовой или высокочастотной фильтрации легко осуществить с помощью линз, которые при использовании когерентного света [1, 3, 161 формируют фурье-образ изображения. В этом разделе мы лишь опишем и прокомментируем методы пространственной фильтрации  некоторые другие, более сложные методы (например, обработку с использованием оптической обратной связи).
некоторые другие, более сложные методы (например, обработку с использованием оптической обратной связи).
10.6.2.1. Улучшение изображений методами обратной фильтрации
Фотографические изображения, искаженные случайно (из-за перемещений, плохой фокусировки, турбулентности и т. п.) или намеренно (например, кодирование изображений при специальной обработке или синтезирование изображений), можно подвергнуть обработке и улучшить их качество. Обозначая функцию размытия, или импульсный отклик, через  искаженное изображение
искаженное изображение  можно записать в виде
можно записать в виде

Качество изображения можно улучшить, если подвергнуть исходное изображение операции обратной свертки. Для осуществления такой операции необходим пространственный фильтр с функцией пропускания  поскольку фурье-образ функции
поскольку фурье-образ функции  дается выражением
дается выражением

откуда

здесь  и
и  фурье-образы функций
фурье-образы функций  соответственно. Чтобы синтезировать функцию фильтра
соответственно. Чтобы синтезировать функцию фильтра  Строук и
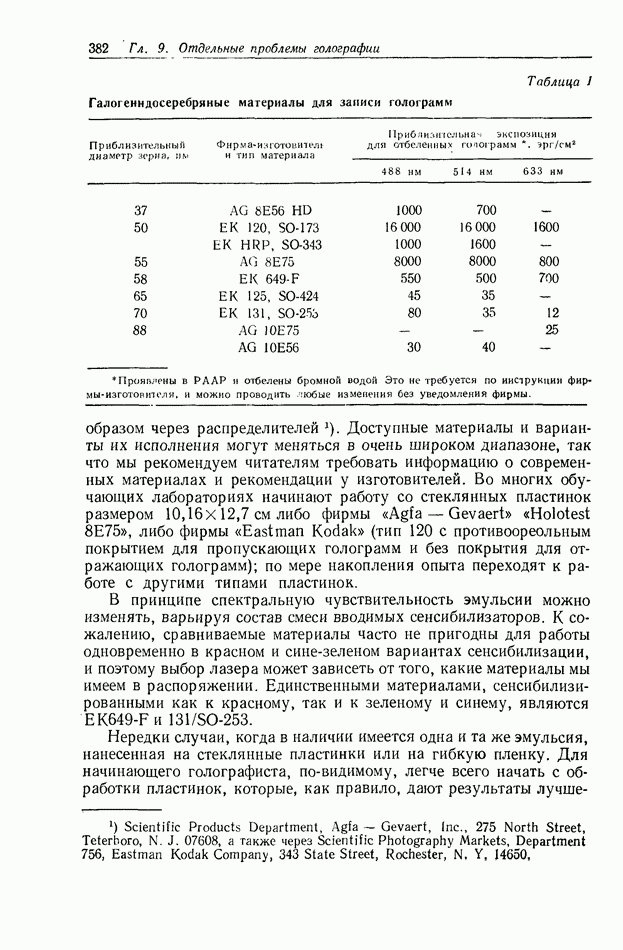
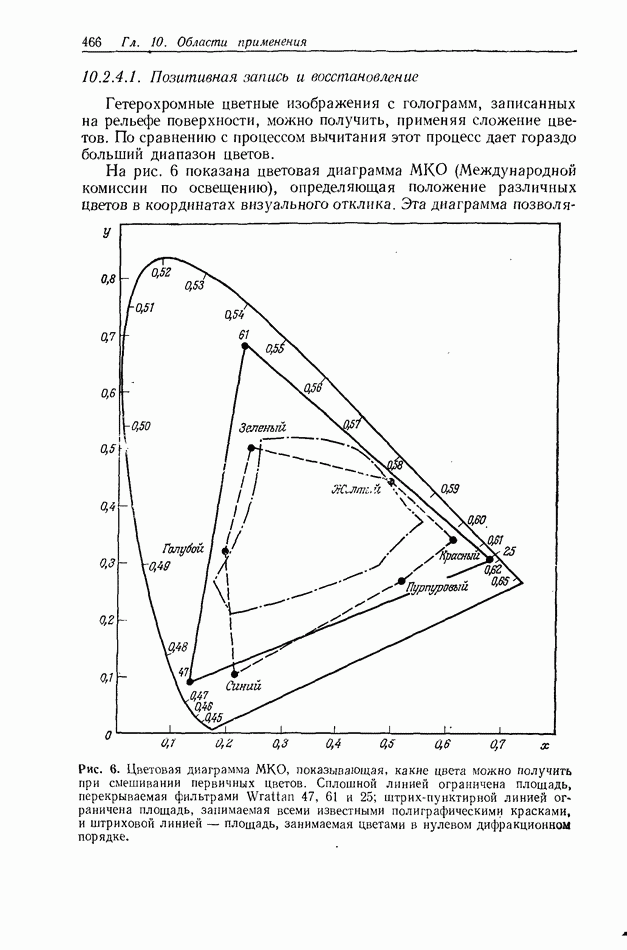
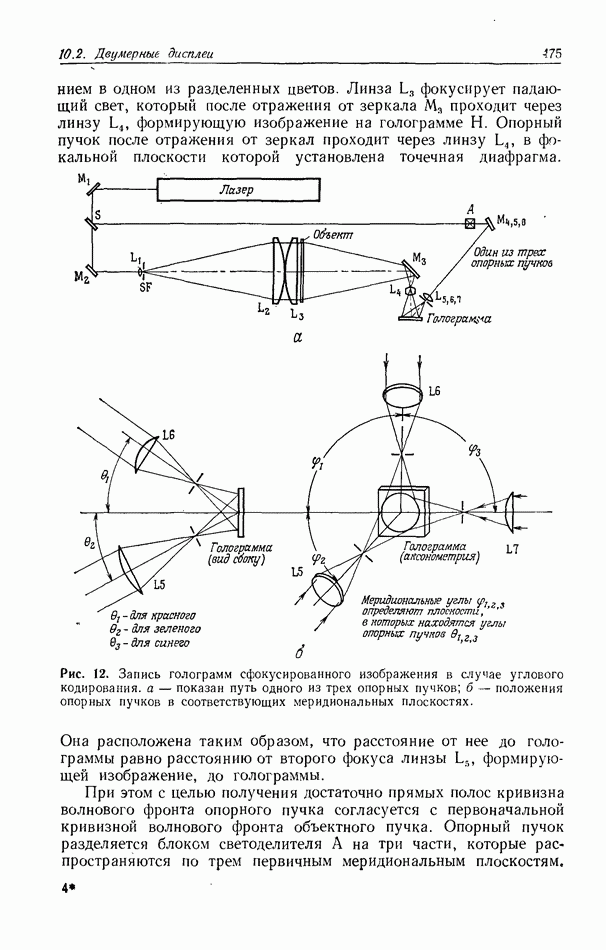
Строук и  предложили использовать два фильтра (рис. 1) — один с амплитудным пропусканием
предложили использовать два фильтра (рис. 1) — один с амплитудным пропусканием  а другой — с пропусканием
а другой — с пропусканием  Фильтр
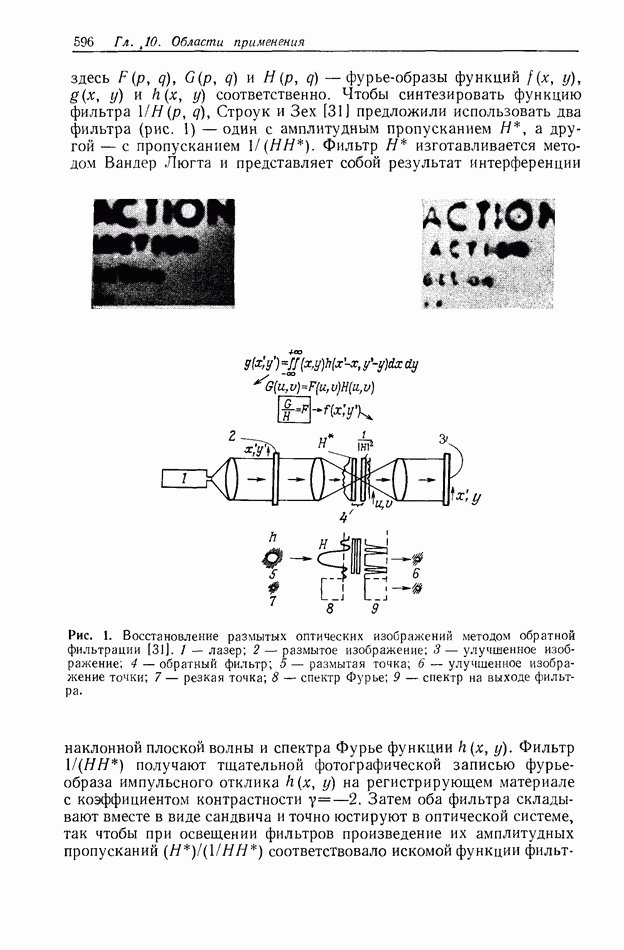
Фильтр  изготавливается методом Вандер Люгта и представляет собой результат интерференции наклонной плоской волны и спектра Фурье функции
изготавливается методом Вандер Люгта и представляет собой результат интерференции наклонной плоской волны и спектра Фурье функции 

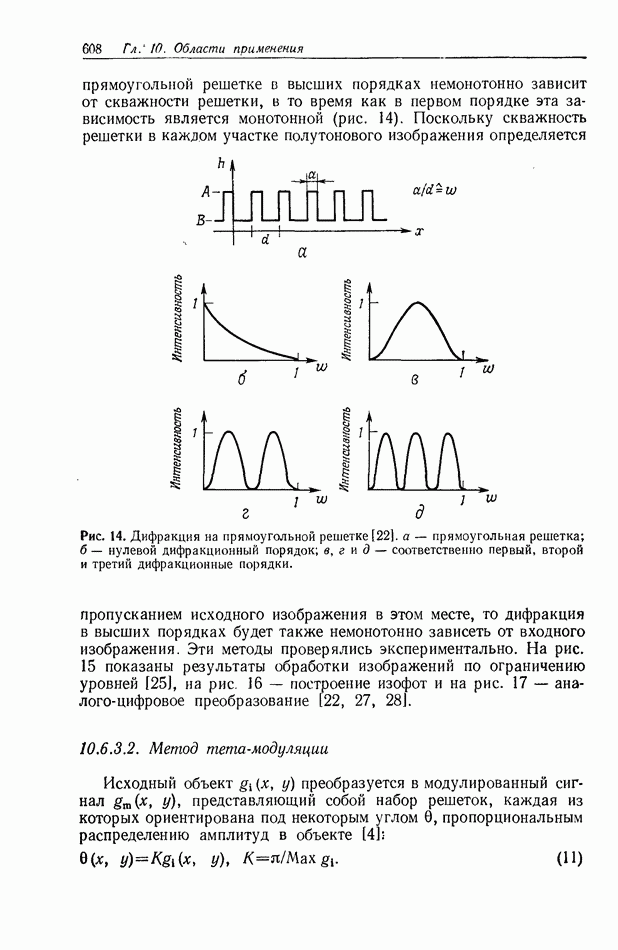
Рис. 1. Восстановление размытых оптических изображений методом обратной фильтрации [31]. 1 - лазер; 2 — размытое изображение; 3 — улучшенное изображение; 4 — обратный фильтр;  -размытая точка; 6 — улучшенное изображение точки; 7— резкая точка; 8 — спектр Фурье; 9 — спектр на выходе фильтра.
-размытая точка; 6 — улучшенное изображение точки; 7— резкая точка; 8 — спектр Фурье; 9 — спектр на выходе фильтра.
Фильтр  получают тщательной фотографической записью фурье-образа импульсного отклика
получают тщательной фотографической записью фурье-образа импульсного отклика  на регистрирующем материале с коэффициентом контрастности
на регистрирующем материале с коэффициентом контрастности  Затем оба фильтра складывают вместе в виде сандвича и точно юстируют в оптической системе, так чтобы при освещении фильтров произведение их амплитудных пропусканий
Затем оба фильтра складывают вместе в виде сандвича и точно юстируют в оптической системе, так чтобы при освещении фильтров произведение их амплитудных пропусканий  соответствовало искомой функции
соответствовало искомой функции

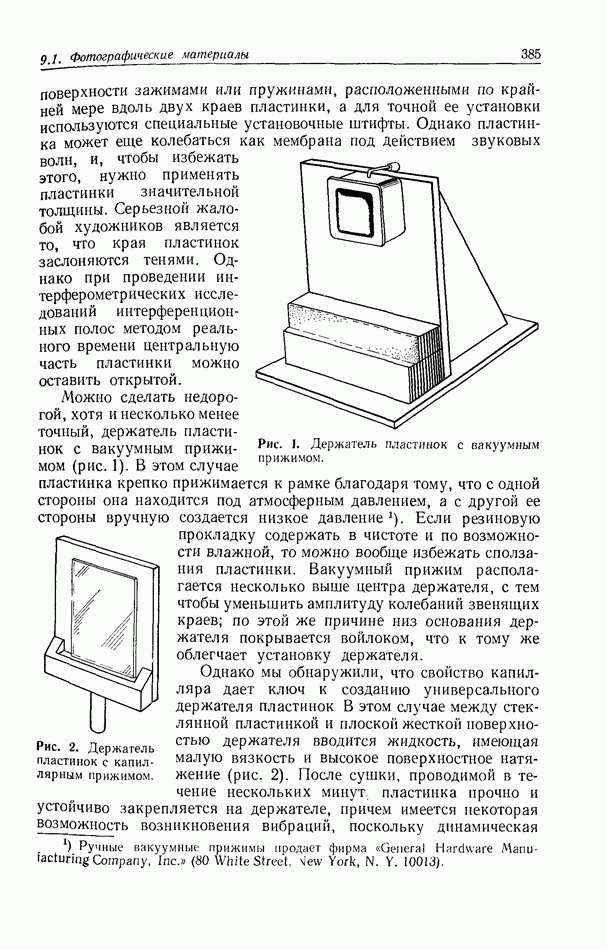
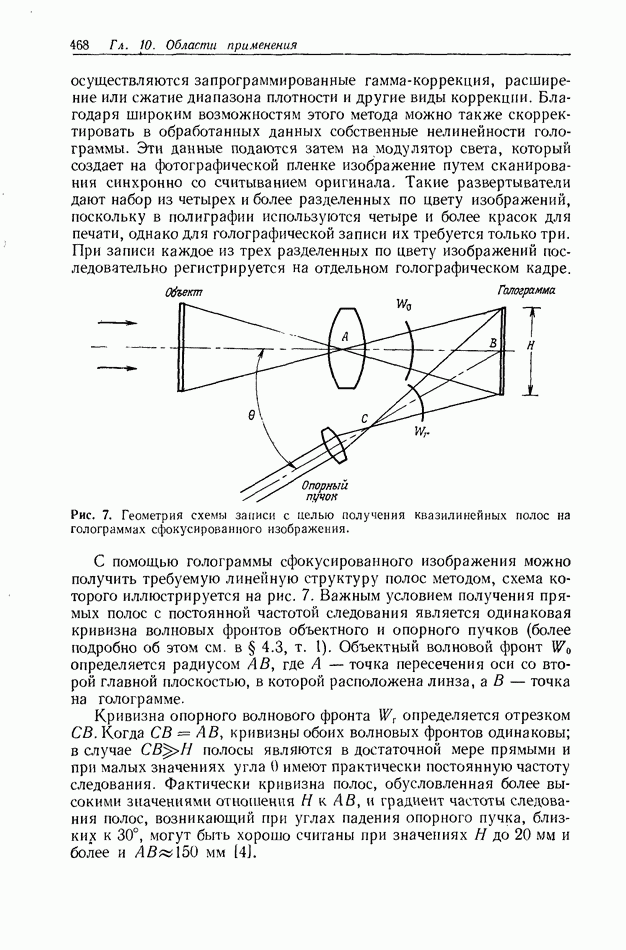
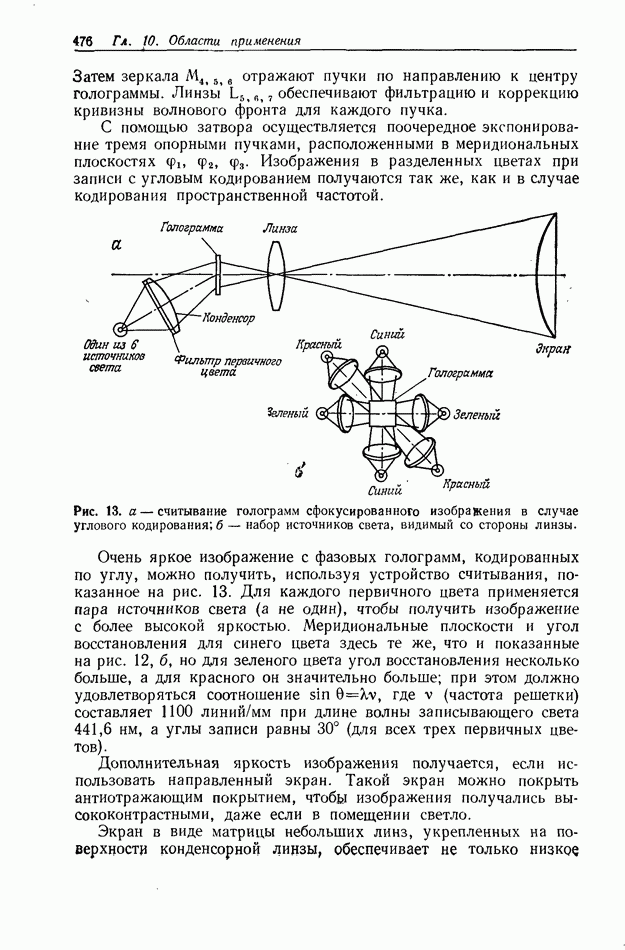
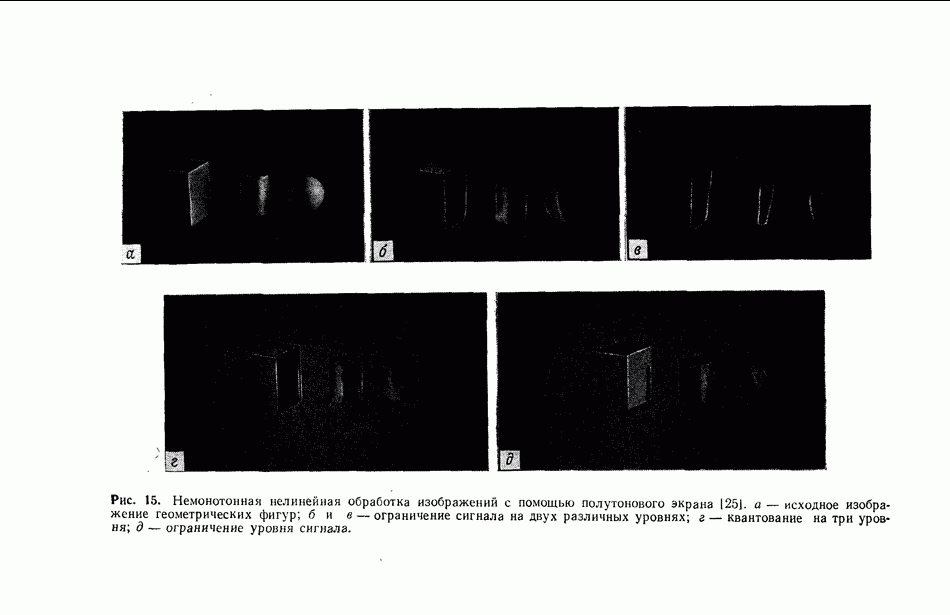
Рис. 2, Рентгеновская фотография Солнца, полученная с помощью камеры-обскуры в мае 1968 г., была улучшена Строуком и Зехом летом 1969 г. [29].
фильтрации  На рис. 2 показана рентгеновская фотография Солнца, полученная камерой обскурой и улучшенная благодаря применению этого метода [29]. На рис. 3 иллюстрируется улучшение изображения в сканирующем электронном микроскопе [30].
На рис. 2 показана рентгеновская фотография Солнца, полученная камерой обскурой и улучшенная благодаря применению этого метода [29]. На рис. 3 иллюстрируется улучшение изображения в сканирующем электронном микроскопе [30].

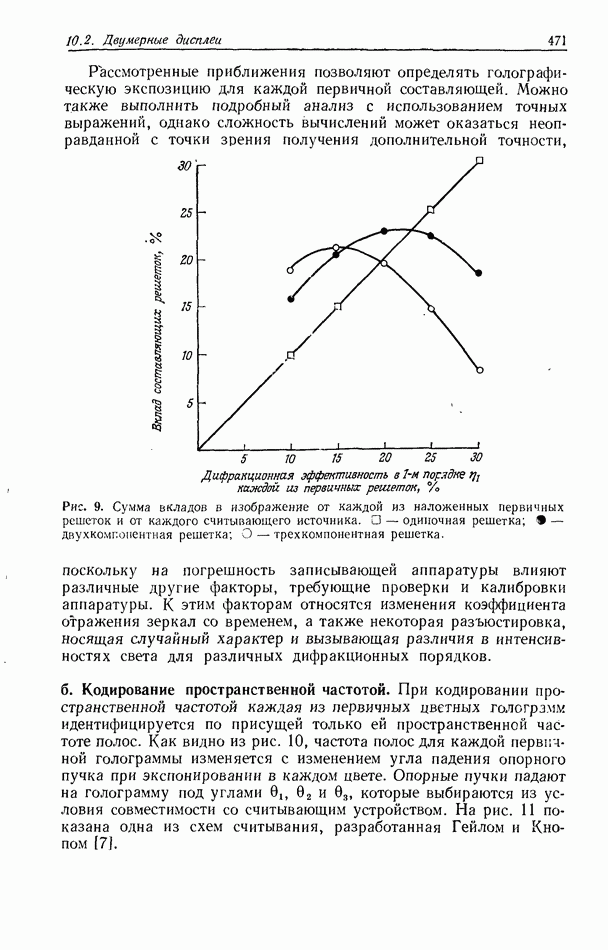
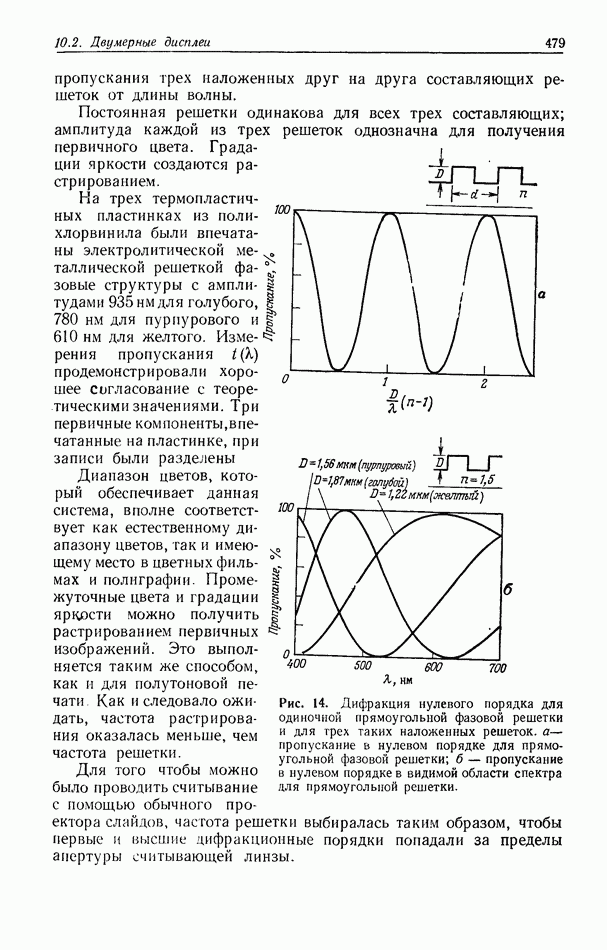
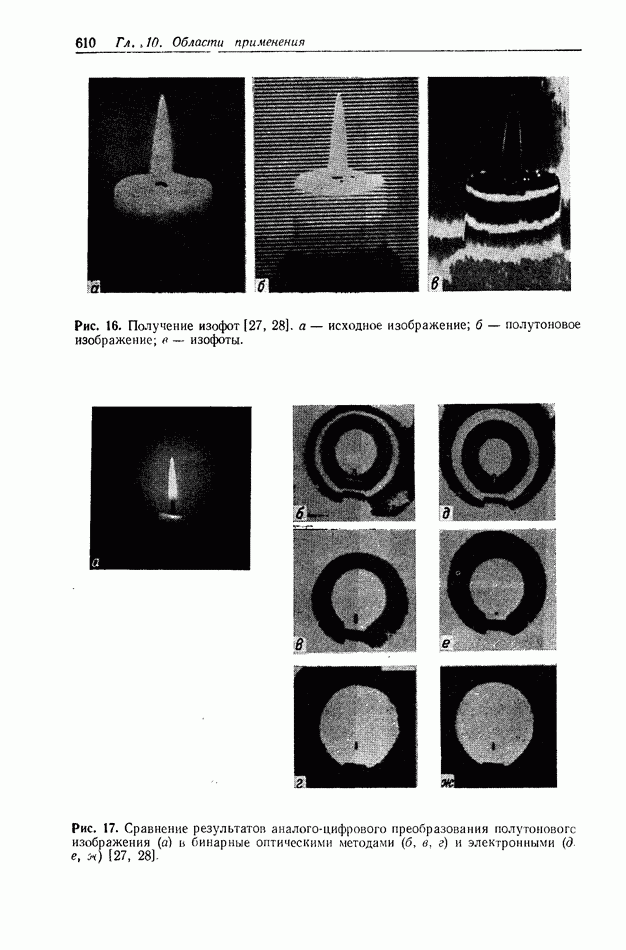
Рис. 3. а — исходное изображение, полученное в сканирующем электронном микроскопе при оптимальных условиях (разрешение — 200 А, увеличение —  напряжение —
напряжение —  и в — изображения, обработанные голографическим способом; разрешение стало лучше 70 А, и соответственно вырос контраст [30].
и в — изображения, обработанные голографическим способом; разрешение стало лучше 70 А, и соответственно вырос контраст [30].
10.6.2.2. Кодирование и декодирование изображений с пространственными фильтрами, вычисляемыми на ЭВМ
Кодирование и декодирование изображений представляет собой имеющую большое значение и интересную область оптической обработки изображений. Если изображение  необходимо закодировать в виде
необходимо закодировать в виде  методом пространственной фильтрации, то фильтр, используемый для этой цели, должен иметь пропускание
методом пространственной фильтрации, то фильтр, используемый для этой цели, должен иметь пропускание  поскольку эта величина описывается отношением двух комплексных функций: такой фильтр легче синтезировать с помощью ЭВМ, чем построить обычными голографическими методами.
поскольку эта величина описывается отношением двух комплексных функций: такой фильтр легче синтезировать с помощью ЭВМ, чем построить обычными голографическими методами.

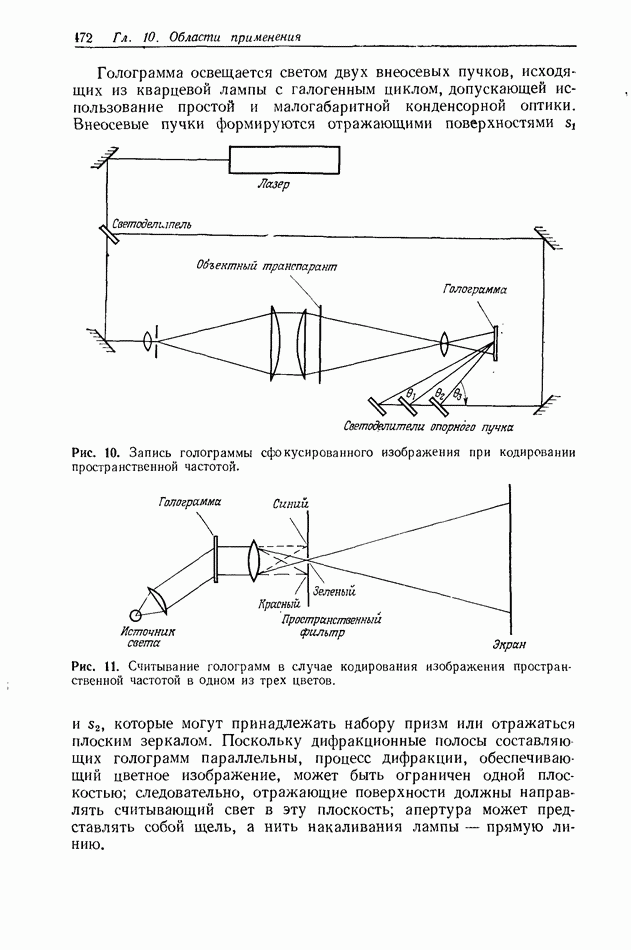
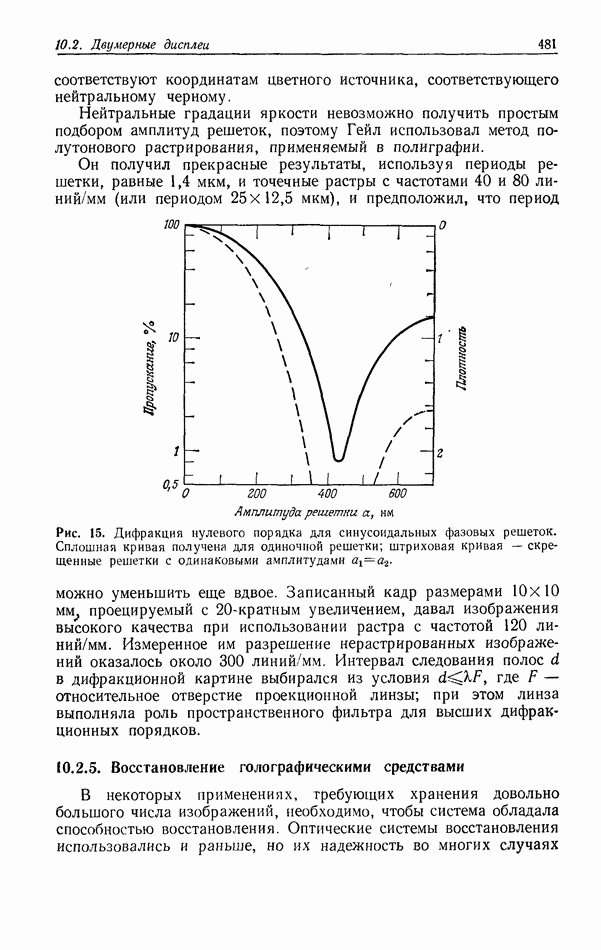
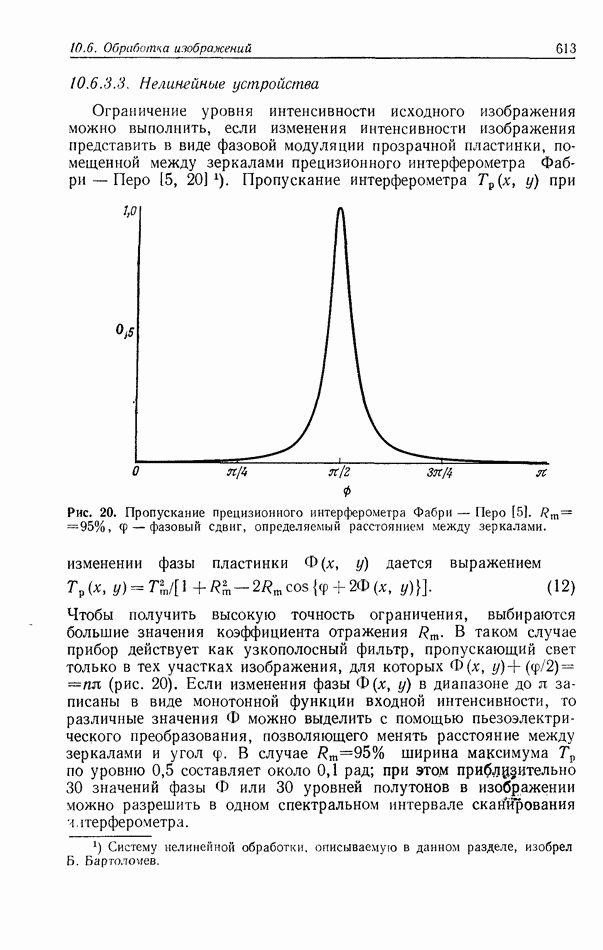
Рис. 4. Синтезированные на ЭВМ пространственные фильтры, использующие косвенные фазовые эффекты для синтеза комплексных функций фильтра.
Впервые синтезированную на ЭВМ голограмму произвольной комплексной функции фильтра создали Ломан с сотр. [7, 211. Чтобы получить такую голограмму, прежде всего необходимо сделать выборку комплексного поля. В каждой точке выборки комплексное поле представляется прямоугольной щелью, ширина которой пропорциональна амплитуде, а ее смещение в поперечном направлении (от точки выборки) пропорционально фазе. Синтезированную на ЭВМ голограмму можно рассматривать как дифракционную решетку с целенаправленно введенными дефектами Желаемое комплексное поле получается в результате косвенных фазовых эффектов в одном из дифракционных порядков (рис. 4). На рис. 5 показана такая голограмма-фильтр, преобразующая букву  в знак
в знак  Экспериментальные результаты применения этого фильтра были получены Ломаном и сотр. 123] (рис. 6).
Экспериментальные результаты применения этого фильтра были получены Ломаном и сотр. 123] (рис. 6).
10.6.2.3. Вычитание и дифференцирование изображений с помощью дифракционных решеток
Операции вычитания и дифференцирования изображений полезны, когда надо обнаружить различия между двумя сценами пли подчеркнуть скорость изменения информации в пределах одной сцены. Пространственные фильтры для этих операций могут быть

Рис. 5. Бинарный пространственный фильтр для преобразования буквы  в знак
в знак 

Рис. 6. Иллюстрация процесса трансляции. Слева — изображение объекта [23]; справа — выходное изображение, в котором вместо буквы  виден знак
виден знак 
изготовлены голографическими методами или с помощью ЭВМ [6, 21]. Было показано также, что для этих целей пригодны и простые дифракционные решетки или комбинация нескольких решеток [19, 32]. Обсудим теперь теорию фильтрации с использованием
Рис. 7. (см. скан) Комплексное амплитудное сложение и вычитание с помощью дифракционных решеток, а — оптическая схема;  два входных изображения; в и
два входных изображения; в и  сумма и разность изображений буквы О и слова HOLOGRAM в центральной области выходной плоскости.
сумма и разность изображений буквы О и слова HOLOGRAM в центральной области выходной плоскости.
дифракционных решеток, поскольку они широко распространены и их нетрудно изготовить.
Как показано на рис. 7, синусоидальная решетка, максимальное пропускание которой смещено на четверть ширины штриха от оптической оси, производит вычитание изображений в центральной части выходной плоскости, когда оба неперекрывающихся изображения симметрично расположены во входной плоскости на расстояниях  от оптической оси (здесь
от оптической оси (здесь  соответственно частота решетки, длина волны света и фокусное расстояние линзы). Чтобы проанализировать этот процесс, запишем функцию пропускания синусоидальной решетки в виде
соответственно частота решетки, длина волны света и фокусное расстояние линзы). Чтобы проанализировать этот процесс, запишем функцию пропускания синусоидальной решетки в виде


Рис. 8. Оптическое дифференцирование (экспериментальные результаты) с помощью составных решеток [32]. а— объекты; 
Амплитуду света, падающего на эту решетку, можно представить следующей функцией;

где  и
и  фурье-образы входных функций
фурье-образы входных функций  в верхней и нижней частях входной плоскости. При этом амплитуда света за решеткой дается выражением
в верхней и нижней частях входной плоскости. При этом амплитуда света за решеткой дается выражением

Таким образом, на выходе мы получаем

Для дифференцирования изображений необходимы две синусоидальные решетки со слегка отличающимися пространственными частотами, причем максимальное пропускание одной решетки должно быть смещено на половину светлой полосы относительно другой решетки. Передаточная характеристика такой составной
решетки имеет вид

импульсный отклик равен

Результат дифференцирования входного изображения, полученный с помощью двух синусоидальных решеток, наблюдается в выходной плоскости в одном из дифракционных порядков (рис. 8), поскольку

здесь обозначает операцию корреляции.
10.6.2.4. Когерентная обратная связь и управление контрастом
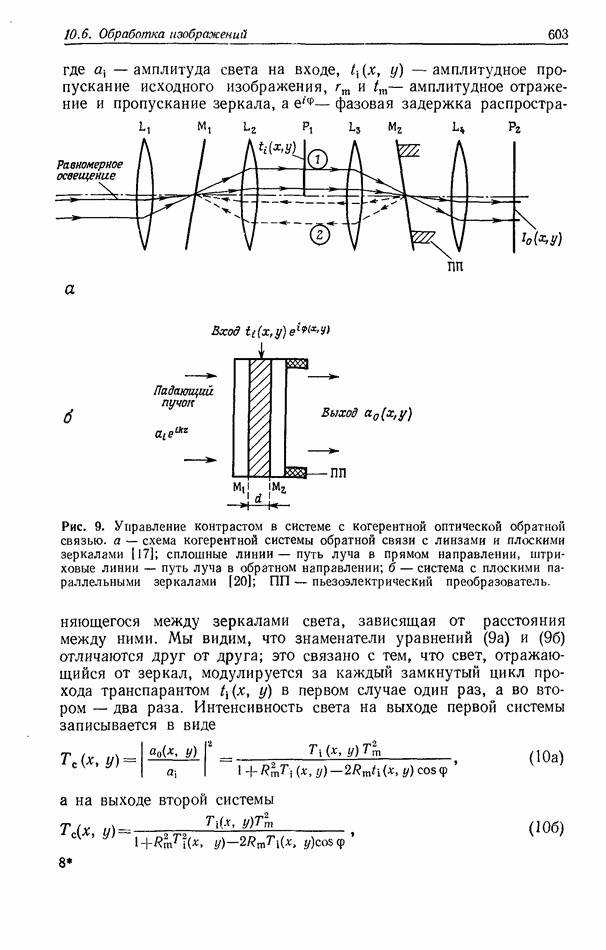
Визуальное качество изображения в большой степени зависит от контраста или относительных интенсивностей фона изображения и участков, несущих информацию. В определенных случаях контраст фотографических (обработанных) транспарантов должен быть изменен. Например, контраст аэроснимков во многих случаях необходимо уменьшать, а контраст рентгеновских изображений — усиливать. Для управления контрастом можно использовать когерентные оптические системы с обратной связью (рис. 9). В таких системах входной транспарант модулирует свет, многократно отраженный от зеркал обратной связи, прежде чем информация выводится из системы 117, 20]. С изменением расстояния между зеркалами контраст изображения усиливается или ослабляется в зависимости от того, конструктивная или деструктивная интерференция имеет место между многократно отраженными сигналами.
Амплитуды выходных сигналов в системах с когерентной обратной связью, схематически показанных на рис. 9, а и б, соответственно определяются следующими уравнениями:

где  амплитуда света на входе,
амплитуда света на входе,  амплитудное пропускание исходного изображения,
амплитудное пропускание исходного изображения,  амплитудное отражение и пропускание зеркала, а
амплитудное отражение и пропускание зеркала, а  фазовая задержка распространяющегося между зеркалами света, зависящая от расстояния между ними.
фазовая задержка распространяющегося между зеркалами света, зависящая от расстояния между ними.

Рис. 9. Управление контрастом в системе с когерентной оптической обратной связью, а — схема когерентной системы обратной связи с линзами и плоскими зеркалами [17]; сплошные линии—путь луча в прямом направлении, штриховые линии — путь луча в обратном направлении; б - система с плоскими параллельными зеркалами [20];  пьезоэлектрический преобразователь.
пьезоэлектрический преобразователь.
Мы видим, что знаменатели уравнений (9а) и (96) отличаются друг от друга; это связано с тем, что свет, отражающийся от зеркал, модулируется за каждый замкнутый цикл прохода транспарантом  в первом случае один раз, а во втором — два раза. Интенсивность света на выходе первой системы записывается в виде
в первом случае один раз, а во втором — два раза. Интенсивность света на выходе первой системы записывается в виде

а на выходе второй системы


(кликните для просмотра скана)
где  коэффициенты пропускания, а
коэффициенты пропускания, а  -коэффициент отражения по интенсивности. Таким образом, меняя расстояния между зеркалами, которыми определяется задержка
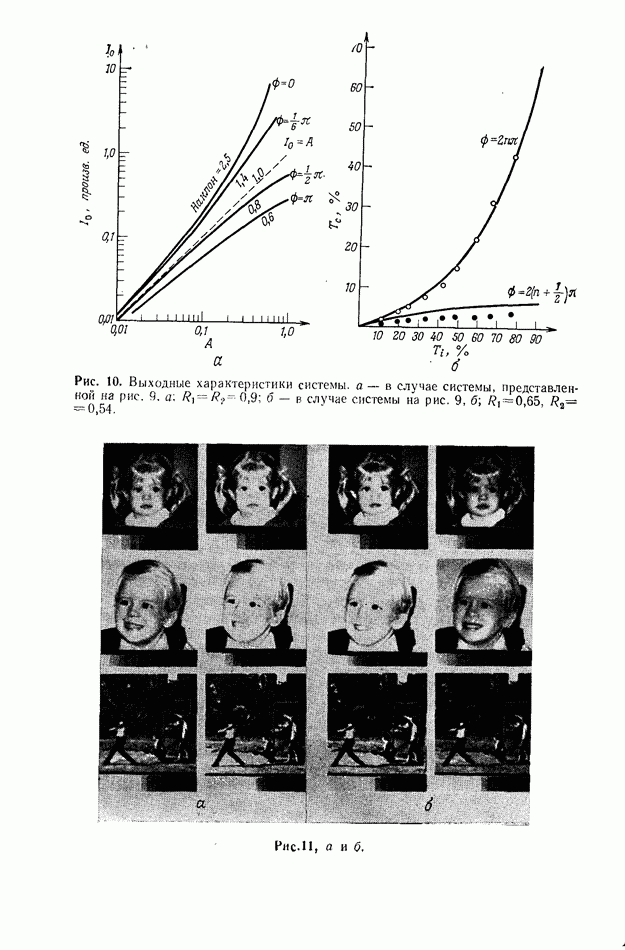
-коэффициент отражения по интенсивности. Таким образом, меняя расстояния между зеркалами, которыми определяется задержка  можно управлять контрастом выходного изображения (рис. 10, а и б). На рис. 11 приведена иллюстрация экспериментальных результатов.
можно управлять контрастом выходного изображения (рис. 10, а и б). На рис. 11 приведена иллюстрация экспериментальных результатов.
Системы с когерентной оптической обратной связью полезны не только для управления контрастом изображений, но также и для улучшения качества изображений и решения дифференциальных уравнений в частных производных [11,17]; кроме кодирования и декодирования изображений, пространственные фильтры, синтезированные на ЭВМ, можно также применять для восстановления размытых изображений и их дифференцирования [21]. В этом разделе мы не пытались дать исчерпывающее изложение вопросов линейной обработки изображений, а лишь показали на примерах,
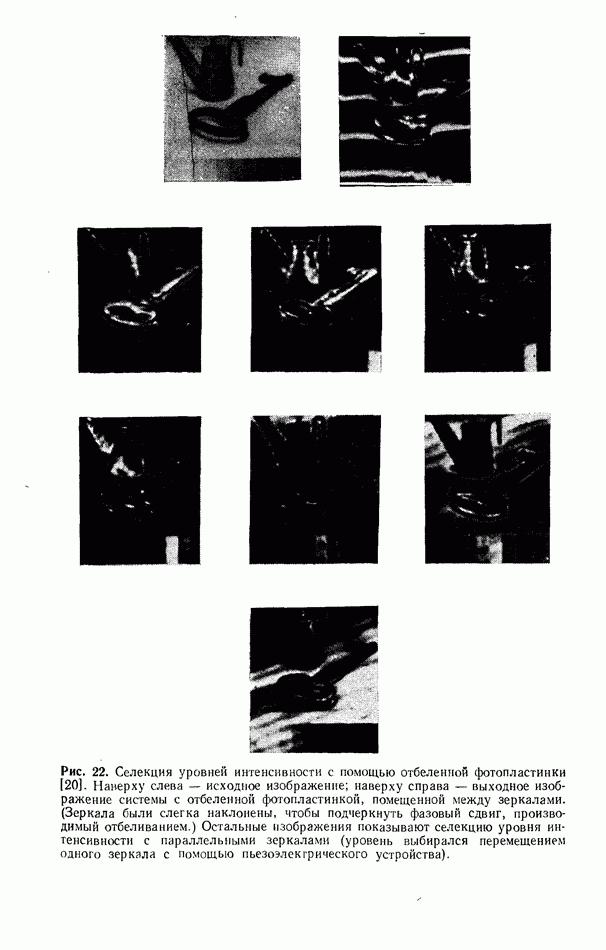
Рис. 11. (см. скан) Экспериментальные результаты управления контрастом, полученные для двух когерентных систем, представленных на рис. 9, а и б; в левых колонках показаны исходные изображения, а в правых — изображения на выходе системы обратной связи, а — усиление контраста, полученное в системе, приведенной на рис. 9, а [17]; б - ослабление контраста в той же системе [17]; в — управление контрастом в системе, показанной на рис. 9, б; в этом случае исходное изображение приведено в центре картины [20],
что существует ряд когерентных оптических методов, которые позволяют решать различные задачи, связанные с обработкой изображений.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 9. ОТДЕЛЬНЫЕ ПРОБЛЕМЫ ГОЛОГРАФИИ
- 9.2. СПЕКЛЫ
- 9.3. КОПИРОВАНИЕ ГОЛОГРАММ
- Глава 10. ОБЛАСТИ ПРИМЕНЕНИЯ
- 10.1. ХРАНЕНИЕ ЦИФРОВОЙ ИНФОРМАЦИИ
- 10.1.2. Виды голографической памяти
- 10.1.3. Компоненты оптической памяти
- 10.1.4. Соотношения между конструктивными параметрами устройства голографической памяти и его информационной емкостью
- 10.1.5. Некоторые системы оптической памяти, выпускаемые промышленностью
- 10.1.6. Параллельная цифровая обработка в системах памяти [10]
- 10.2. ДВУМЕРНЫЕ ДИСПЛЕИ
- 10.2.3. Типы голограмм, используемых в дисплеях
- 10.2.4. Применение голограмм сфокусированного изображения, записанных на рельефе поверхности
- 10.2.5. Восстановление голографическими средствами
- 10.3. ТРЕХМЕРНЫЕ ДИСПЛЕИ
- 10.3.2. Голографические системы, работающие на просвет
- 10.3.3. Отражательные голографические системы
- 10.3.4. Радужная голография
- 10.3.5. Мультиплексная голография
- 10.3.6. Голографическое кино
- 10.3.7. Голография с диффузным опорным излучением
- 10.3.8. Когерентность и стабильность
- 10.3.9. Источники света для восстановления
- 10.3.10. Цветная голография
- 10.3.11. Голографические системы отображения
- 10.3.12. Изобразительная голография
- 10.3.13. Применения трехмерных дисплеев
- 10.3.14. Будущее изобразительной голографии
- 10.4. ГОЛОГРАФИЧЕСКАЯ ИНТЕРФЕРОМЕТРИЯ
- 10.4.2. Интерферометры для прозрачных сред
- 10.4.3. Интерферометрия трехмерных диффузных объектов
- 10.4.4. Специальные методы и технические приемы
- 10.4.5. Заключение
- 10.5. РАСПОЗНАВАНИЕ ОБРАЗОВ И ЗНАКОВ
- 10.5.2. Коррелятор с частотной плоскостью
- 10.5.3. Коррелятор с переменным масштабом
- 10.5.4. Коррелятор с одновременным преобразованием [20]
- 10.5.5 Многоканальный одномерный коррелятор [9]
- 10.5.6. Коррелятор сложных кодированных сигналов
- 10.5.7. Коррелятор с плоскостью изображения
- 10.5.8. Акустооптические корреляторы
- 10.5.9. Коррелятор скрещенных сигналов
- 10.5.10. Коррелятор с преобразованием Меллина
- 10.5.11. Коррелятор, инвариантный к вращению [12]
- 10.5.12. Транспонированный коррелятор [25]
- 10.5.13. Корреляторы со сложными согласованными пространственными фильтрами
- 10.5.14. Некогерентные корреляторы
- 10.5.15. Оптимизация параметров согласованного пространственного фильтра
- 10.5.16. Источники уменьшения корреляции
- 10.5.17. Различия в распознавании образов и знаков
- 10.5.18. Резюме, выводы и предстоящие исследования
- 10.6. ОБРАБОТКА ИЗОБРАЖЕНИЙ
- 10.6.2. Линейная обработка изображений
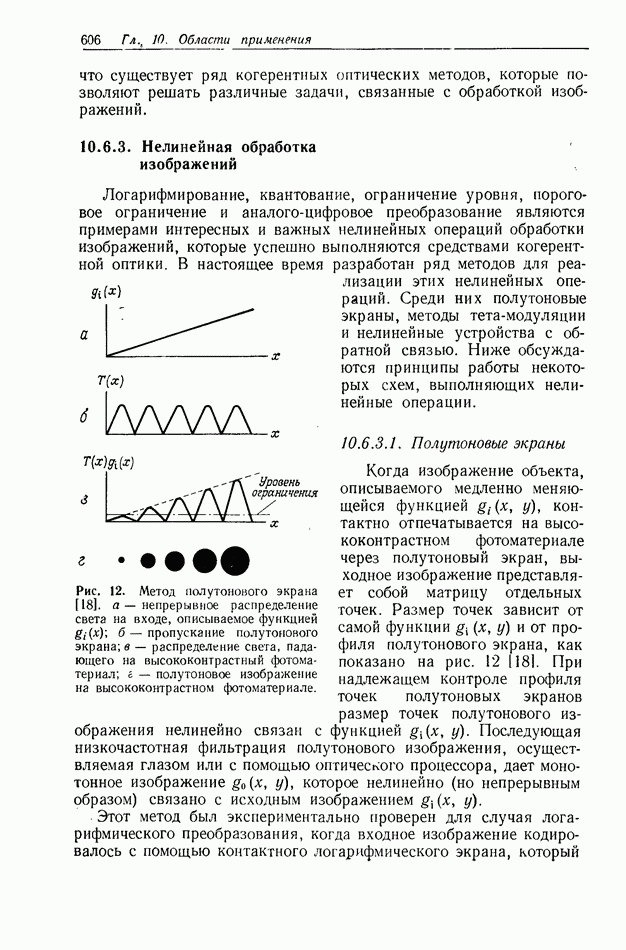
- 10.6.3. Нелинейная обработка изображений
- 10.6.4. Пространственно-неинвариантная обработка изображений
- 10.6.5. Заключительные замечания
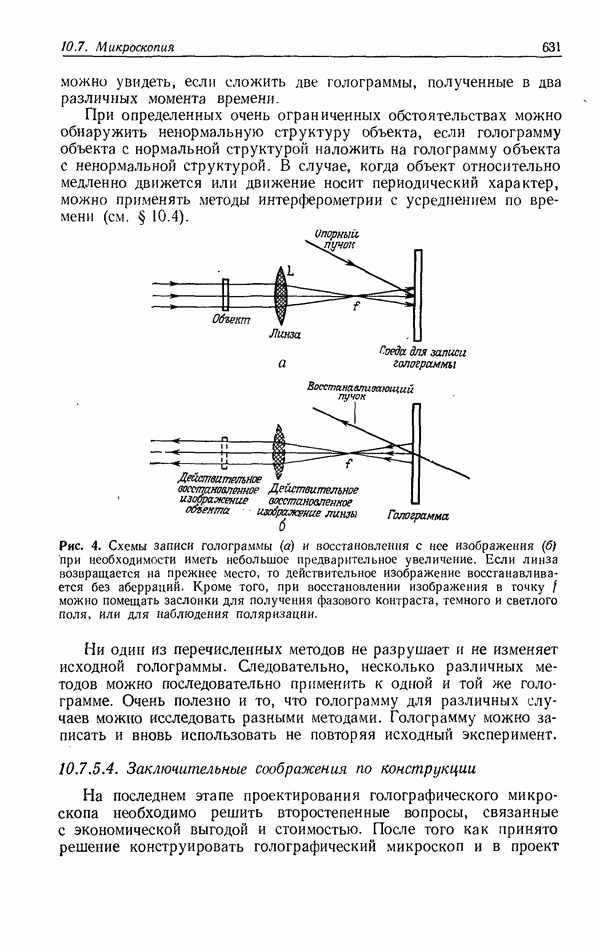
- 10.7. МИКРОСКОПИЯ
- 10.7.2. Голографическое увеличение и изменение масштаба
- 10.7.3. Голографирование изображений, увеличенных микроскопом
- 10.7.4. Уравнения голографической микроскопии
- 10.7.5. Конструктивные решения
- 10.7.6. Заключение
- 10.8. ГОЛОГРАММНЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ
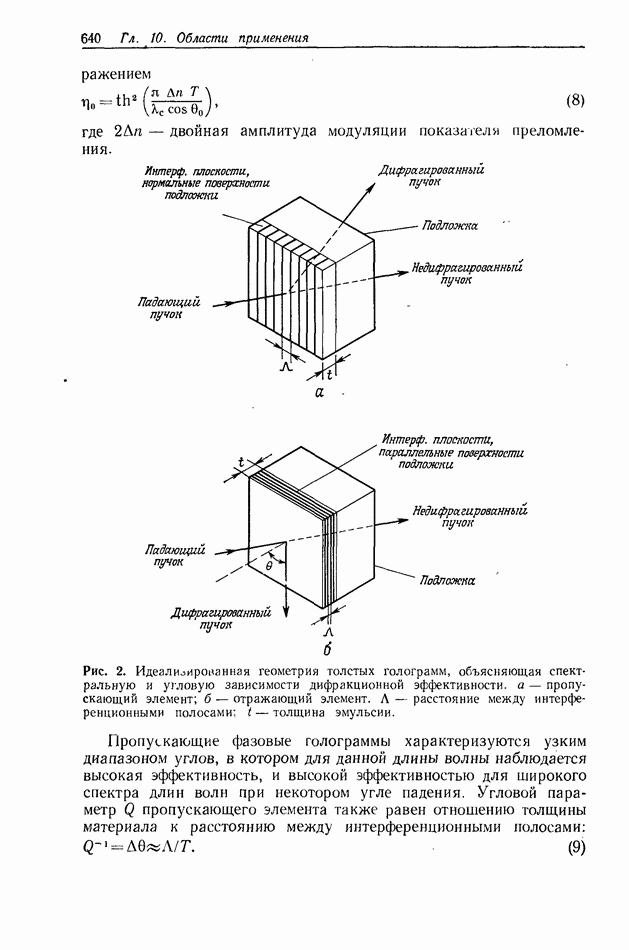
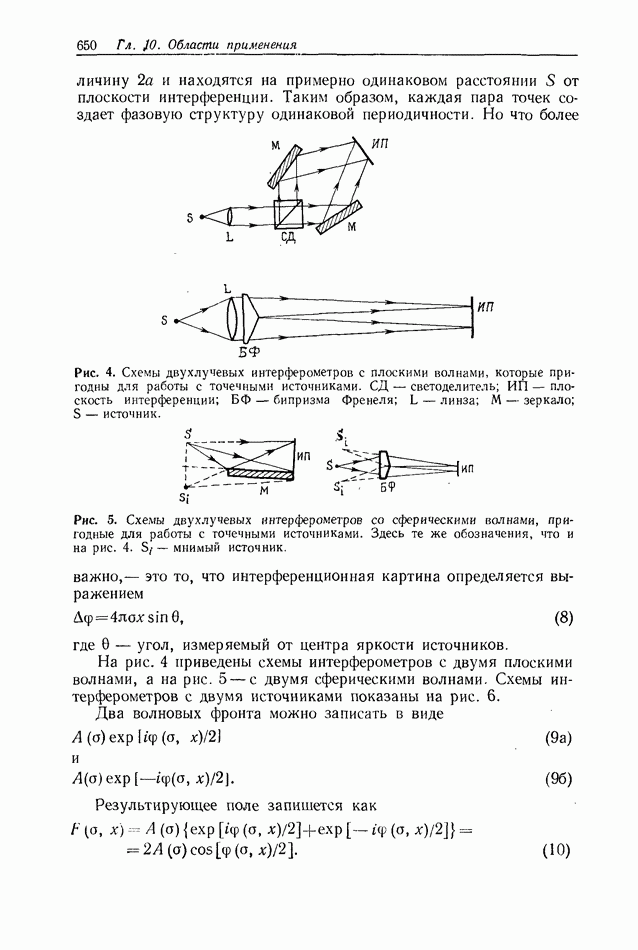
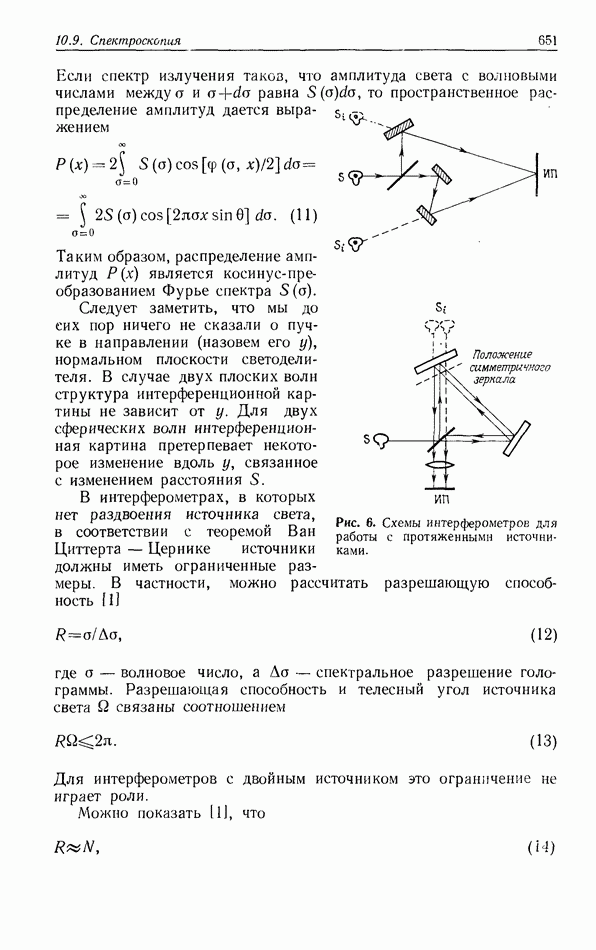
- 10.9. СПЕКТРОСКОПИЯ
- 10.10. ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ КОНТУРОВ РЕЛЬЕФА
- 10.11. МУЛЬТИПЛИЦИРОВАНИЕ ИЗОБРАЖЕНИЙ
- 10.12. ИЗМЕРЕНИЕ РАЗМЕРА ЧАСТИЦ
- 10.13. ГОЛОГРАФИЧЕСКИЙ ПОРТРЕТ
- 10.14. ФОТОГРАММЕТРИЯ
- Дополнение. НЕКОТОРЫЕ ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ ГОЛОГРАФИИ В ТРЕХМЕРНЫХ СРЕДАХ
- 2. ОБЩАЯ СХЕМА ЗАПИСИ И ВОССТАНОВЛЕНИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 3. КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 4. ПРОСТРАНСТВЕННЫЙ И ЧАСТОТНЫЙ ВАРИАНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 5. ТЕОРИЯ СВЯЗАННЫХ ВОЛН И МОДОВАЯ ТЕОРИЯ ТРЕХМЕРНОЙ ГОЛОГРАММЫ
- 6. НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ТРЕХМЕРНЫХ ГОЛОГРАММ, ЗАПИСАННЫХ В АНИЗОТРОПНЫХ СРЕДАХ
- 7. ПРИМЕНЕНИЕ ТОНКОСЛОЙНЫХ ТРЕХМЕРНЫХ ГОЛОГРАММ В ИЗОБРАЗИТЕЛЬНОЙ И ПРОЕКЦИОННОЙ ТЕХНИКЕ
- 8. СВЕРХПЛОТНАЯ И АССОЦИАТИВНАЯ ПАМЯТЬ НА ОСНОВЕ ТРЕХМЕРНЫХ ГОЛОГРАММ С ГЛУБОКОЙ ЗАПИСЬЮ
- 9. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ СТАЦИОНАРНЫХ ВОЛНОВЫХ ПОЛЕЙ
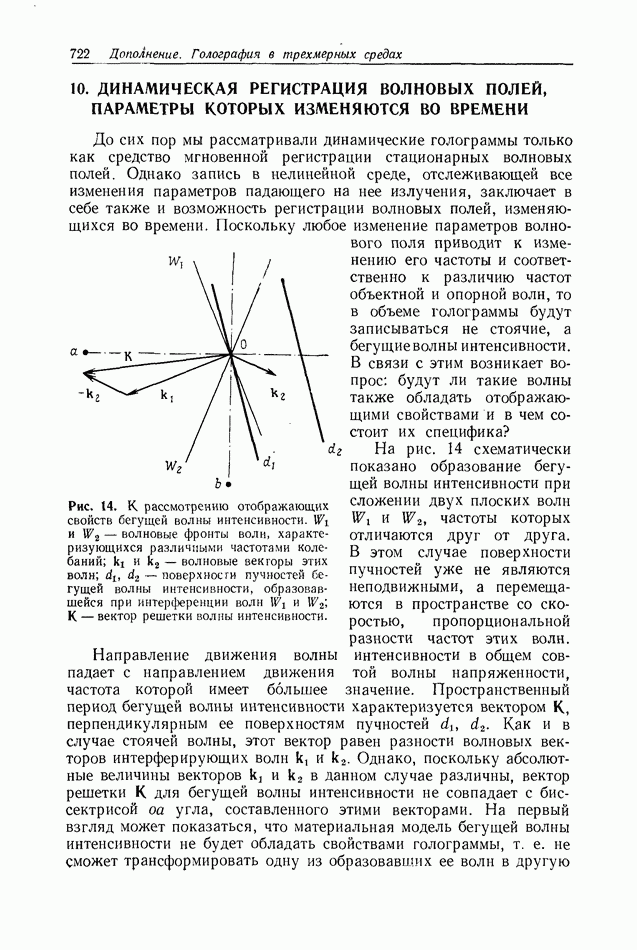
- 10. ДИНАМИЧЕСКАЯ РЕГИСТРАЦИЯ ВОЛНОВЫХ ПОЛЕЙ, ПАРАМЕТРЫ КОТОРЫХ ИЗМЕНЯЮТСЯ ВО ВРЕМЕНИ
- 11. ЗАКЛЮЧЕНИЕ