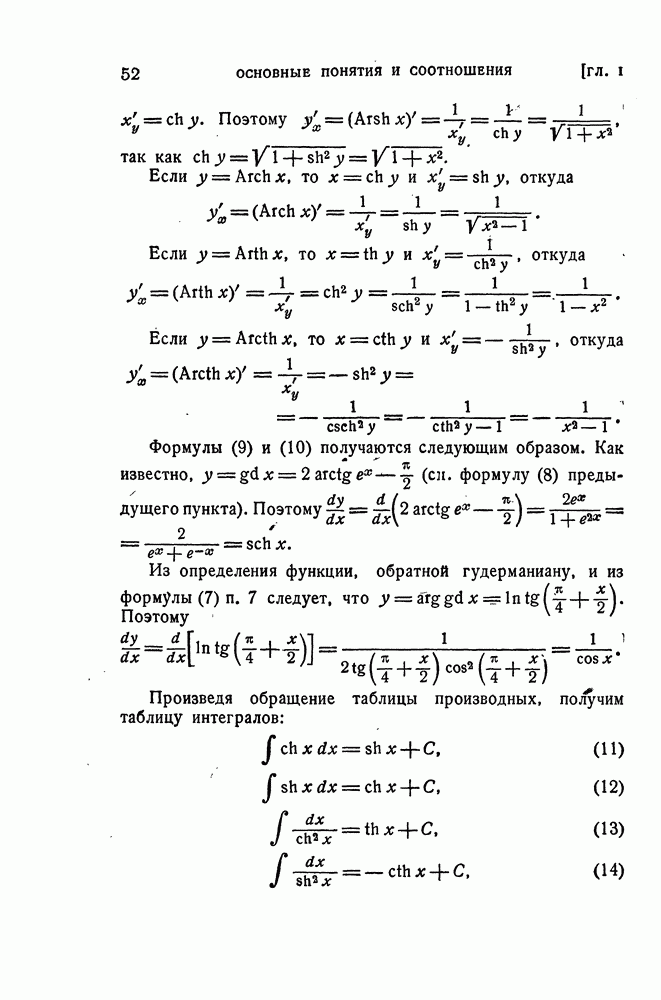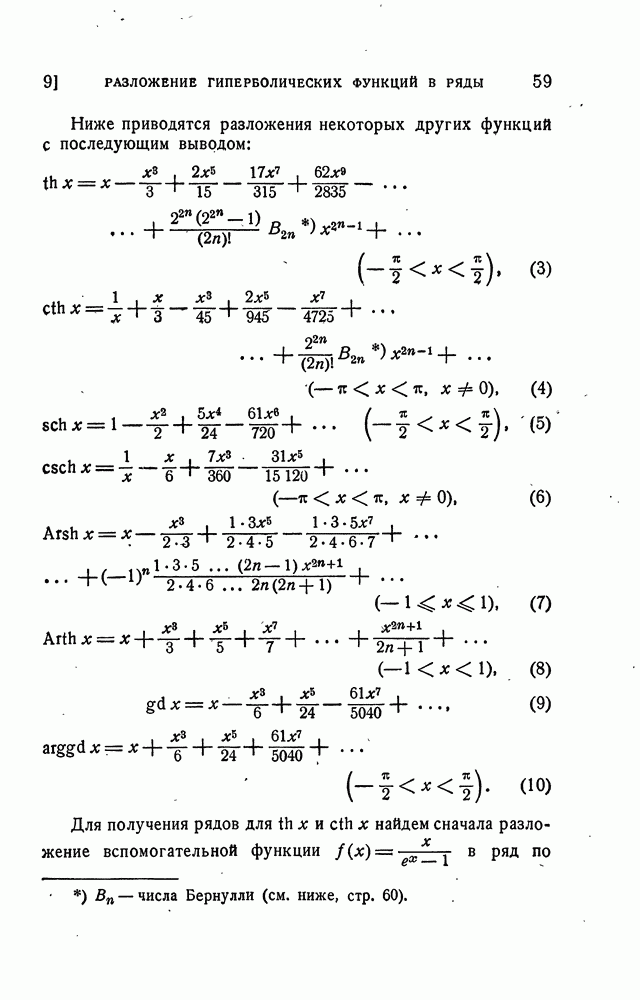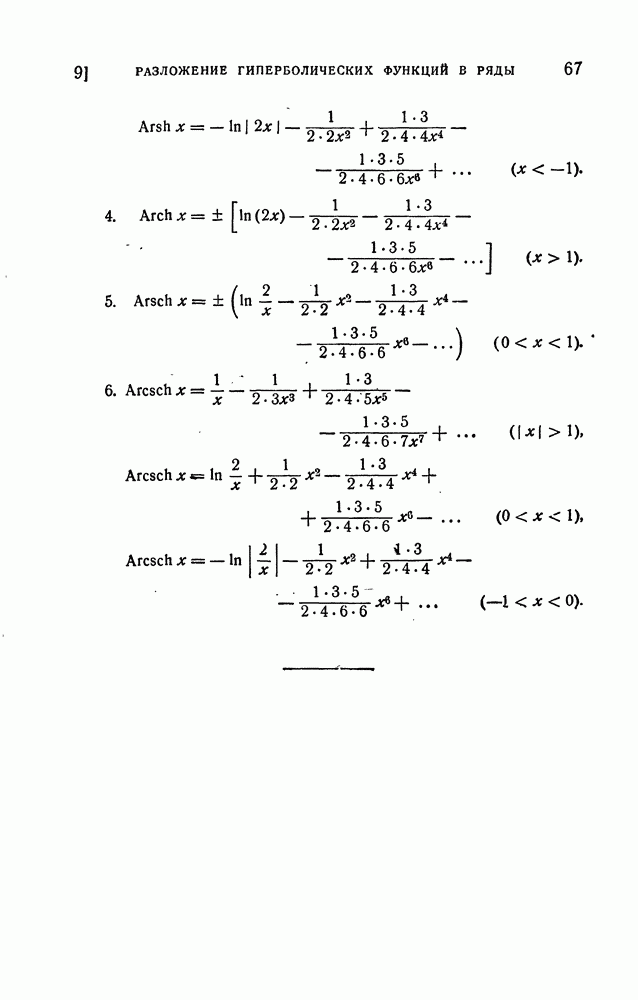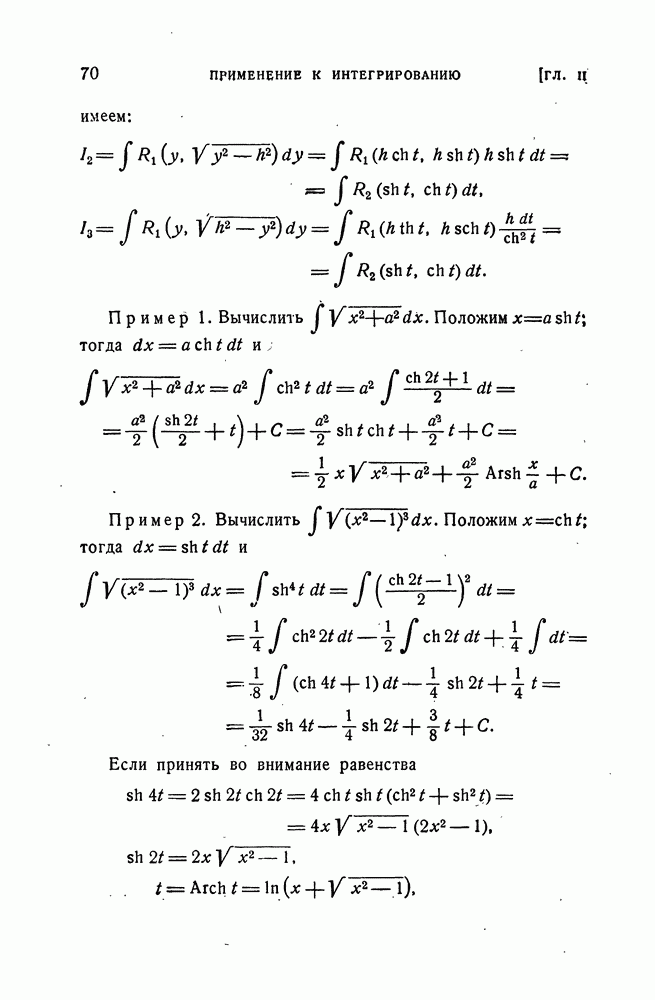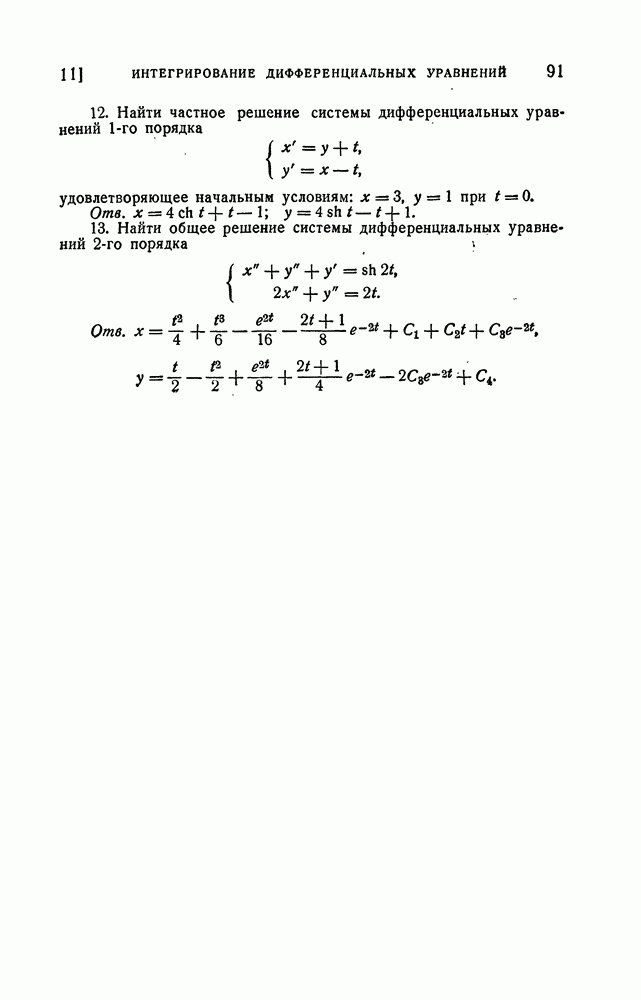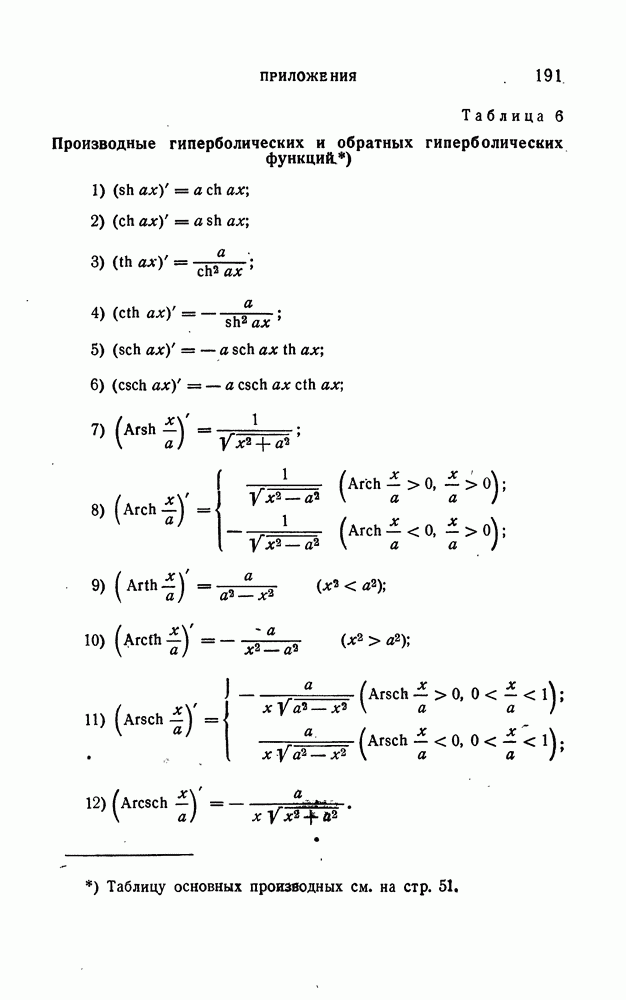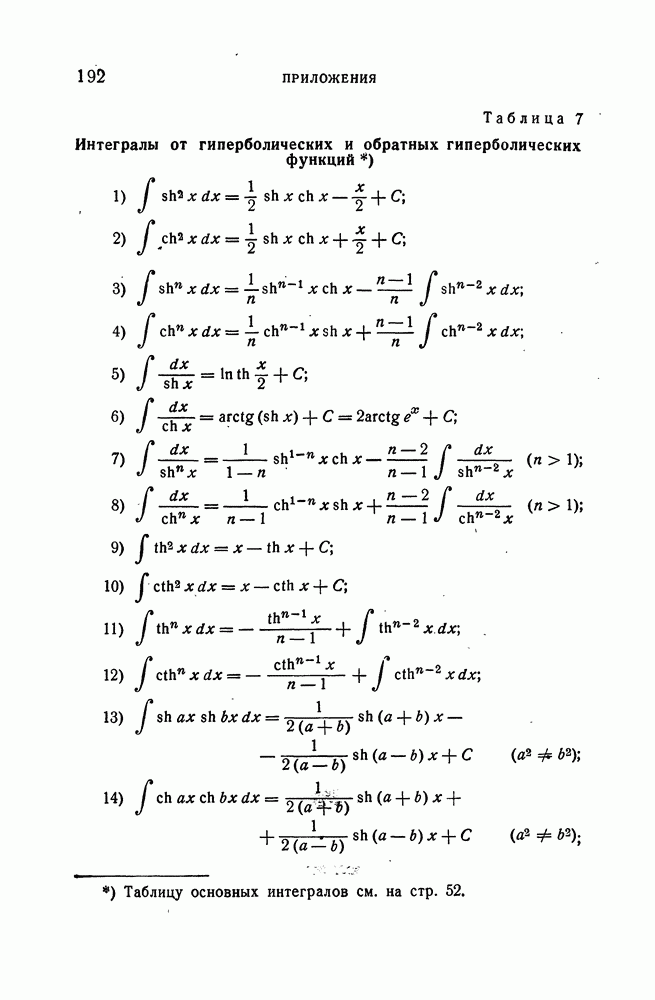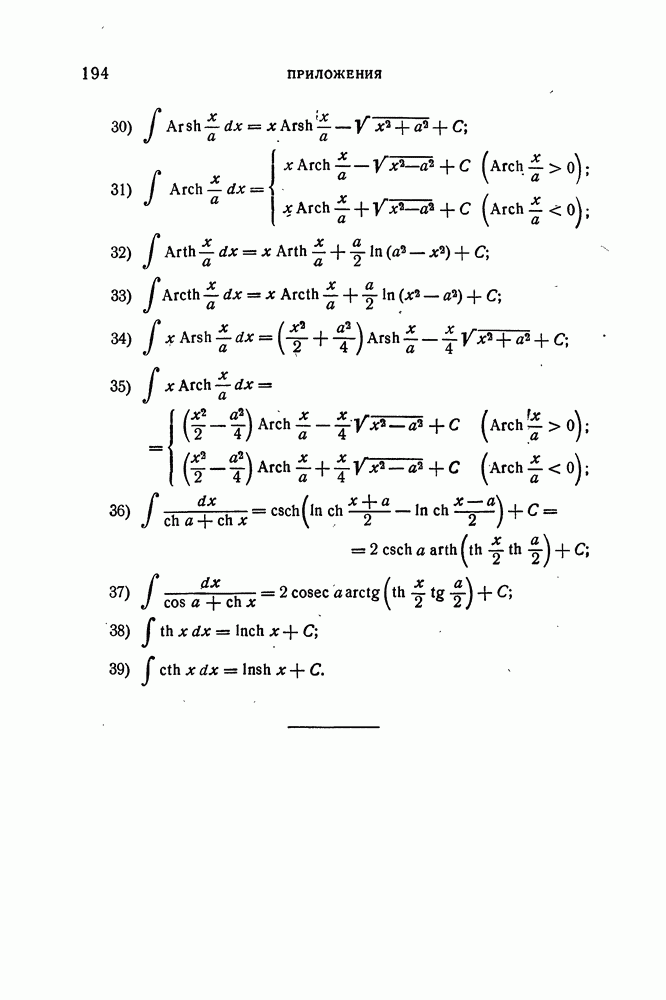| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11. Интегрирование некоторых дифференциальных уравнений
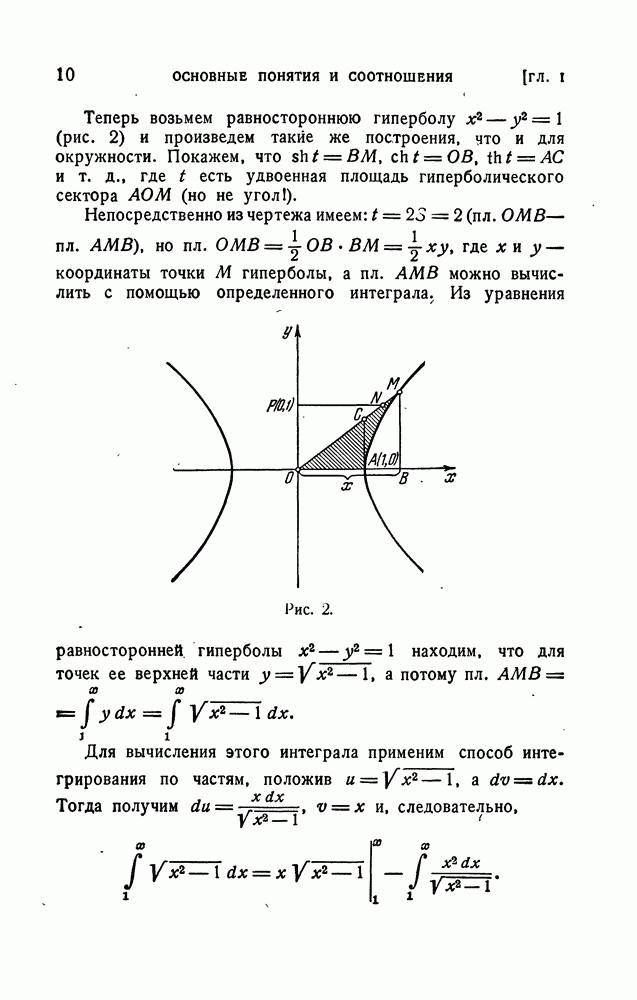
Гиперболические функции находят применение при интегрировании некоторых дифференциальных уравнений. Не говоря о том, что в процессе интегрирования уравнений можно получить квадратуры, которые сравнительно легко вычисляются при помощи гиперболических подстановок, решения многих дифференциальных уравнений, в частности линейных, удобно выражать через гиперболические функции. При этом значительно сокращаются выкладки и сами решения
получаются в более компактной форме. Кроме того, гиперболические подстановки позволяют иногда упростить дифференциальные уравнения, сводя их к легко интегрируемым видам.
Рассмотрим несколько примеров на отыскание решений дифференциальных уравнений, в первую очередь линейных однородных и неоднородных уравнений 2-го и 4-го порядков с постоянными коэффициентами, наиболее часто встречающихся на практике.
Пример 1.  Это однородное линейное уравнение
Это однородное линейное уравнение  порядка с постоянными коэффициентами. Его характеристическое уравнение
порядка с постоянными коэффициентами. Его характеристическое уравнение  имеет корни
имеет корни  а. Поэтому частными решениями будут показательные функции
а. Поэтому частными решениями будут показательные функции  а также их линейные комбинации. Примем в качестве частных решений полусумму и полуразность показательных функций
а также их линейные комбинации. Примем в качестве частных решений полусумму и полуразность показательных функций  Легко убедиться в линейной независимости этих частных решений. Для этого составим и вычислим определитель Вронского:
Легко убедиться в линейной независимости этих частных решений. Для этого составим и вычислим определитель Вронского:

Так как  , то наши частные решения образуют фундаментальную систему и общее решение запишется в виде
, то наши частные решения образуют фундаментальную систему и общее решение запишется в виде

Если задать начальные условия  и
и  при
при  то, подставив сначала значения х и у в общее решение, получим
то, подставив сначала значения х и у в общее решение, получим  а вычислив производную
а вычислив производную  и подставив в нее значения х и у, получим
и подставив в нее значения х и у, получим  и таким образом частное решение выражается через гиперболический косинус
и таким образом частное решение выражается через гиперболический косинус 
Если изменить начальные условия, задав  и
и  при
при  то в качестве частного решения получим гиперболический синус
то в качестве частного решения получим гиперболический синус 
Пример 2.  Это неоднородное линейное уравнение
Это неоднородное линейное уравнение  порядка с постоянными коэффициентами. Для отыскания его общего решения применим метод вариации постоянных. С этой целью возьмем общее решение соответствующего однородного уравнения (пример 1)
порядка с постоянными коэффициентами. Для отыскания его общего решения применим метод вариации постоянных. С этой целью возьмем общее решение соответствующего однородного уравнения (пример 1)
 , полагая
, полагая  подберем эти функции таким образом, чтобы функция
подберем эти функции таким образом, чтобы функция

удовлетворяла нашему неоднородному уравнению. Поскольку мы варьируем обе произвольные постоянные, а накладываем только одно это условие, то мы вправе ввести еще одно условие, например, потребовать, чтобы выражение первой производной, вычисленное при переменных  имело такой же вид, как и при постоянных
имело такой же вид, как и при постоянных  Так как
Так как  то это условие сводится к следующему уравнению относительно
то это условие сводится к следующему уравнению относительно 

и, таким образом,

Вычислим вторую производную; имем:

Выражения функции у и производной у" через х подставим в исходное уравнение. После несложных алгебраических преобразований получим:

Итак, мы имеем систему из двух линейных алгебраических уравнений относительно неизвестных 

Система совместна и имеет единственное решение, так как определитель системы  отличен от нуля:
отличен от нуля:

Решая эту систему, получим выражения производных искомых произвольных «постоянных»:

а с помощью квадратур запишем и самые произвольные «постоянные»:

Здесь  — любая постоянная,
— любая постоянная,  — новые произвольные постоянные (без кавычек), а переменная интегрирования во избежание путаницы в дальнейшем обозначается через
— новые произвольные постоянные (без кавычек), а переменная интегрирования во избежание путаницы в дальнейшем обозначается через 
Подставив выражения  в функцию
в функцию  получим общее решение неоднородного уравнения
получим общее решение неоднородного уравнения  в виде.
в виде.

или в окончательной компактной форме

Легко заметить, что сумма последних двух членов полностью соответствует общему решению однородного уравнения  что же касается первого члена, то он представляет собой частное решение неоднородного уравнения, которое в сумме с общим решением однородного уравнения составляет, согласно теории лицейных уравнений,
что же касается первого члена, то он представляет собой частное решение неоднородного уравнения, которое в сумме с общим решением однородного уравнения составляет, согласно теории лицейных уравнений,
общее решение неоднородного уравнения. Так, если дано, в частности,  где
где  то частное решение этого конкретного неоднородного уравнения будет
то частное решение этого конкретного неоднородного уравнения будет 

следовательно, общее решение имеет вид

Пример  Это однородное линейное уравнение
Это однородное линейное уравнение  порядка с постоянными коэффициентами. Его характеристическое уравнение имеет корни
порядка с постоянными коэффициентами. Его характеристическое уравнение имеет корни

Рассмотрим только случай

когда корни вещественные и разные.
Положим

Тогда  и частьыми решениями уравнения будут функции и а также их линейные комбинации. Примем в качестве частных решений полусумму и полуразность этих функций:
и частьыми решениями уравнения будут функции и а также их линейные комбинации. Примем в качестве частных решений полусумму и полуразность этих функций:

и

Легко убедиться в том, что эти решения образуют фундаментальную систему, и, следовательно, общее решение уравнения имеет вид

Пример  Это неоднородное линейное уравнение
Это неоднородное линейное уравнение  порядка с постоянными коэффициентами. Его общее решение будем искать, как в примере 2, методом вариации постоянных, входящих в общее решение соответствующего однородного уравнения (см. пример 3), причем, как в примере 3, ограничимся случаем, когда
порядка с постоянными коэффициентами. Его общее решение будем искать, как в примере 2, методом вариации постоянных, входящих в общее решение соответствующего однородного уравнения (см. пример 3), причем, как в примере 3, ограничимся случаем, когда  имеем:
имеем:

Как в примере 2, потребуем, чтобы выражение, стоящее в последних квадратных скобках, обратилось в нуль. Это дает нам первое уравнение относительно 

Запишем первую производную в виде

и вычислим вторую производную

Теперь умножим у на  на
на  и подставим эти произведения вместе с У в исходное уравнение; после приведения
и подставим эти произведения вместе с У в исходное уравнение; после приведения
подобных членов получим:

Так как  то выражение, стоящее в фигурных скобках, обращается в нуль, и мы приходим ко второму уравнению относительно
то выражение, стоящее в фигурных скобках, обращается в нуль, и мы приходим ко второму уравнению относительно 

которое вместе с первым уравнением образует систему из двух алгебраических линейных уравнений с неизвестными  Составим определитель системы А и вычислим его:
Составим определитель системы А и вычислим его:

Следовательно, система совместна и имеет единственнох решение. Корни ее дают производные искомых произвольные «постоянных»

С помощью квадратур запишем и сами произвольные «постоянные»:

Здесь, как в примере 2,  - любая постоянная,
- любая постоянная,  и
и  -новые произвольные постоянные (без кавычек),
-новые произвольные постоянные (без кавычек),  переменная интегрирования.
переменная интегрирования.
Подставляя функции  в выражение
в выражение  получим общее решение неоднородного уравнения
получим общее решение неоднородного уравнения  в виде
в виде

Как и в примере 2, первый член представляет частное решение  неоднородного уравнения, а второй — общее решение соответствующего однородного уравнения.
неоднородного уравнения, а второй — общее решение соответствующего однородного уравнения.
Заметим, не производя выкладок, что в случае  частное решение
частное решение

где  в случае —
в случае —  частное решение
частное решение

Пример  Это однородное линейное уравнение
Это однородное линейное уравнение  порядка с постоянными коэффициентами. Его характеристическое уравнение
порядка с постоянными коэффициентами. Его характеристическое уравнение  имеет корни
имеет корни  где
где  решение
решение  Если заменить
Если заменить  через
через  через
через  то будем иметь:
то будем иметь:  где положено
где положено  и
и 
Пример  Это тоже однородное линейное уравнение
Это тоже однородное линейное уравнение  порядка с постоянными коэффициентами. Характеристическое уравнение
порядка с постоянными коэффициентами. Характеристическое уравнение  Для
Для
нахождения его корней разложим левую часть на множители следующим образом:

Приравнивая нулю выражения, стоящие в скобках, каждое в отдельности, получим два квадратных уравнения. Решая их, будем иметь корни характеристического уравнения  Поэтому общим решением будет функция
Поэтому общим решением будет функция 

Если, как и в предыдущем примере, произвести замену  то после несложных алгебраическах преобразований получим общее решение в виде
то после несложных алгебраическах преобразований получим общее решение в виде

 где положено
где положено 
Рассмотрим несколько примеров на нелинейные дифференциальные уравнения 1-го и 2-го порядков.
Пример 7.  . Это уравнение с разделяющимися переменными. После разделения переменных получим:
. Это уравнение с разделяющимися переменными. После разделения переменных получим:

откуда, беря квадратуры, будем иметь общий интеграл

или общее решение

Если задать начальное условие  при
при  то, подставив в общее решение вместо х и у их значения, получим
то, подставив в общее решение вместо х и у их значения, получим
 откуда следует, что произвольное постоянное С равно нулю, и потому частным решением уравнения будет гиперболический синус
откуда следует, что произвольное постоянное С равно нулю, и потому частным решением уравнения будет гиперболический синус

Пример 8.  Это нелинейное уравнение
Это нелинейное уравнение  порядка, которое подстановкой
порядка, которое подстановкой  и соответственно
и соответственно  сводится к уравнению
сводится к уравнению  порядка
порядка  После разделения переменных получим
После разделения переменных получим  откуда, беря квадратуры, придем к уравнению
откуда, беря квадратуры, придем к уравнению  потенцируя которое, будем иметь
потенцируя которое, будем иметь  — или
— или 
Взяв квадратуры, получим  откуда
откуда  (знак минус перед аргументом под знаком гиперболического косинуса опускаем, ибо косинус является четной функцией).
(знак минус перед аргументом под знаком гиперболического косинуса опускаем, ибо косинус является четной функцией).
Пример  Это нелинейное уравнение
Это нелинейное уравнение  порядка, которое, как и в предыдущем примере, подстановкой
порядка, которое, как и в предыдущем примере, подстановкой  сводится к уравнению
сводится к уравнению  порядка
порядка  откуда, сократив на
откуда, сократив на  (полагаем
(полагаем  , случай
, случай  дает тривиальное решение
дает тривиальное решение  и взяв квадратуру, получим
и взяв квадратуру, получим  или
или  . Разделив переменные, будем иметь
. Разделив переменные, будем иметь

При интегрировании левой части полученного уравнения могут представиться две возможности:
1) если принять  и положить
и положить  то получим
то получим  или
или  откуда
откуда  где положено
где положено 
2) если принять  и положить
и положить  то получим —
то получим —  или
или  откуда
откуда  где, как и выше, положено
где, как и выше, положено  причём предполагается, что
причём предполагается, что  имеем
имеем 
Во всех разобранных примерах гиперболические функции возникали в процессе интегрирования уравнений. Разберем несколько примеров на применение гиперболических подстановок для упрощения дифференциальных уравнений до их интегрирования.
Пример 10.  Положим
Положим  Тогда уравнение преобразуется к виду
Тогда уравнение преобразуется к виду  откуда дифференцированием находим, что
откуда дифференцированием находим, что  или заменяя у через
или заменяя у через  Сокращая на
Сокращая на  получим
получим  откуда
откуда  а следовательно,
а следовательно, 
Пример  Положим
Положим  Тогда
Тогда  и уравнение преобразуется к виду
и уравнение преобразуется к виду  откуда
откуда  Поэтому
Поэтому  и окончательно
и окончательно

Пример  Положим
Положим  Тогда
Тогда  и уравнение принимает вид
и уравнение принимает вид  После упрощения получим
После упрощения получим  откуда
откуда  и, следовательно,
и, следовательно, 
Пример  Положим, как и в предыдущем примере,
Положим, как и в предыдущем примере,  Вычислив у и перейдя
Вычислив у и перейдя
к переменным  преобразуем уравнение к виду
преобразуем уравнение к виду  откуда
откуда  , и, следовательно,
, и, следовательно, 
Рассмотрим более сложный пример на интегрирование дифференциального уравнения, содержащего гиперболические функции.
Пример 14.  Это линейное уравнение
Это линейное уравнение  порядка с переменными коэффициентами. Преобразуем его к более простому виду. Для этого подберем соответствующую функцию
порядка с переменными коэффициентами. Преобразуем его к более простому виду. Для этого подберем соответствующую функцию  и произведем замену переменной, положив
и произведем замену переменной, положив  Имеем:
Имеем:

следовательно,

Выберем функцию  так, чтобы выражение, стоящее в квадратных скобках, обратилось в нуль, т. е. потребуем, чтобы
так, чтобы выражение, стоящее в квадратных скобках, обратилось в нуль, т. е. потребуем, чтобы

Это нелинейное дифференциальное уравнение, допускающее понижение порядка, так как в нем отсутствует аргумент 
Чтобы проинтегрировать его, положим  тогда
тогда  и уравнение примет вид
и уравнение примет вид

Взяв квадратуры, получим:

(здесь положено  ибо нам достаточно иметь одну какую-нибудь функцию
ибо нам достаточно иметь одну какую-нибудь функцию  Взяв квадратуры в последнем уравнении, будем иметь:
Взяв квадратуры в последнем уравнении, будем иметь:

Выбрав  мы преобразуем исходное уравнение к виду
мы преобразуем исходное уравнение к виду

Общее решение этого уравнения

и окончательно

Рассмотрим пример на интегрирование дифференциального уравнения в частных производных.
Пример 15. Найти частное решение дифференциального уравнения Лапласа

удовлетворяющее граничным условиям:

Решение. Используя первое граничное условие, будем искать частное решение в виде произведения

где  — неизвестная функция, зависящая только от у и обращающаяся в а при
— неизвестная функция, зависящая только от у и обращающаяся в а при 
Вычислив частные производные  порядка
порядка 

и подставив их в уравнение Лапласа, мы получаем тождество

откуда, так как  , имеем обыкновенное линейное однородное дифференциальное уравнение с постоянными коэффициентами
, имеем обыкновенное линейное однородное дифференциальное уравнение с постоянными коэффициентами

Его общее решение (см. пример 1)  .
.
Для нахождения частного решения, удовлетворяющего условию  подставим в общее решение а вместо
подставим в общее решение а вместо  и 0 вместо у, что дает
и 0 вместо у, что дает  , следовательно,
, следовательно,  . Поэтому
. Поэтому

Используем второе граничное условие. Найдем  подставим 0 вместо
подставим 0 вместо  и
и  вместо у. Имеем:
вместо у. Имеем:

а после подстановки

откуда, поскольку  ,
,

Из этого уравнения находим отношение

и подставляем его в  Имеем:
Имеем:

или, заметив, что

получим ответ:

где положено 
Эта задача встречается в гидродинамике при отыскании потенциала скоростей волн в канале глубины  с вертикальными стенками.
с вертикальными стенками.
Рассмотрим пример на решение функционального уравнения, т. е. уравнения, из которого требуется определить общий вид функции.
Пример 16. Найти такую дважды дифференцируемую функцию  , чтобы соотношение
, чтобы соотношение

оставалось справедливым для всех значений 
Решение. Продифференцируем заданное равенство по х, а затем по у; получим:

Второе равенство перепишем так:

откуда заключаем, что функция  не должна изменяться от замены
не должна изменяться от замены  на
на  Так как
Так как  могут иметь любые значения и не зависят друг от друга, то
могут иметь любые значения и не зависят друг от друга, то

где
Рассмотрим два случая.
1)  ; Получаем дифференциальное уравнение
; Получаем дифференциальное уравнение

Его общее решение (см. пример 1)

Если в исходном равенстве положить  то получим:
то получим:

Так как  то мы имеем условие
то мы имеем условие  которое позволяет определить одну из произвольных постоянных. Для этого подставим значение
которое позволяет определить одну из произвольных постоянных. Для этого подставим значение  в общее решение; тогда
в общее решение; тогда

откуда  , следовательно,
, следовательно,  где вместо
где вместо  взято С.
взято С.
2)  . Получаем дифференциальное уравнение
. Получаем дифференциальное уравнение

Его общее решение 
Дополнительное условие  приводит к соотношению
приводит к соотношению  откуда
откуда  , следовательно,
, следовательно,  где, как и в предыдущем случае, произведена замена
где, как и в предыдущем случае, произведена замена  на С.
на С.
В заключение рассмотрим одну геометрическую задачу. Пример 17. Найти кривую, у которой величина отрезка, отсекаемого касательной в любой точке кривой на оси  пропорциональна секансу угла
пропорциональна секансу угла  образованного радиус-вектором этой точки с осью
образованного радиус-вектором этой точки с осью 
Решение. Величина отрезка, отсекаемого касательной на оси  равна
равна  Так как
Так как  то
то 
Составляем дифференциальное уравнение

и преобразуем его к виду

Его общее решение (см. пример 13)

(знак минус в правой части отсутствует потому, что в нашем уравнении, в отличие от примера 13, коэффициент а входит со знаком минус, который можно вынести за знак гиперболического синуса как нечетной функции).
Упражнения
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ
- 1. Введение. Определение гиперболических функций
- 2. Соотношения между гиперболическими функциями
- 3. Обратные гиперболические функции
- 4. Показательные, тригонометрические и гиперболические функции от комплексного аргумента. Формулы Эйлера
- 5. Соотношения между тригонометрическими и гиперболическими функциями
- 6. Соотношения между логарифмическими, обратными тригонометрическими и обратными гиперболическими функциями
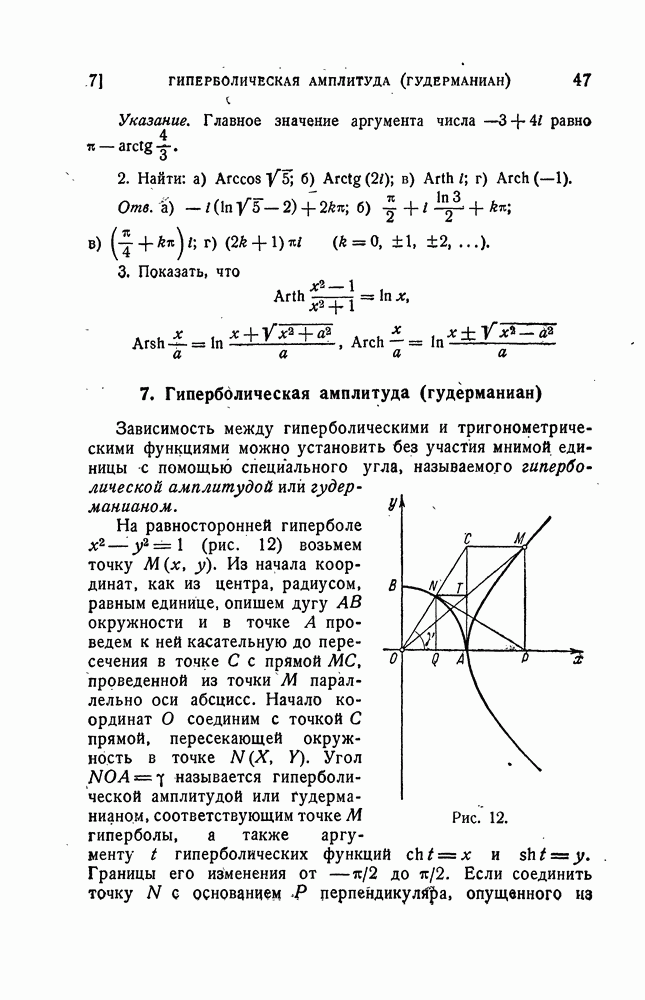
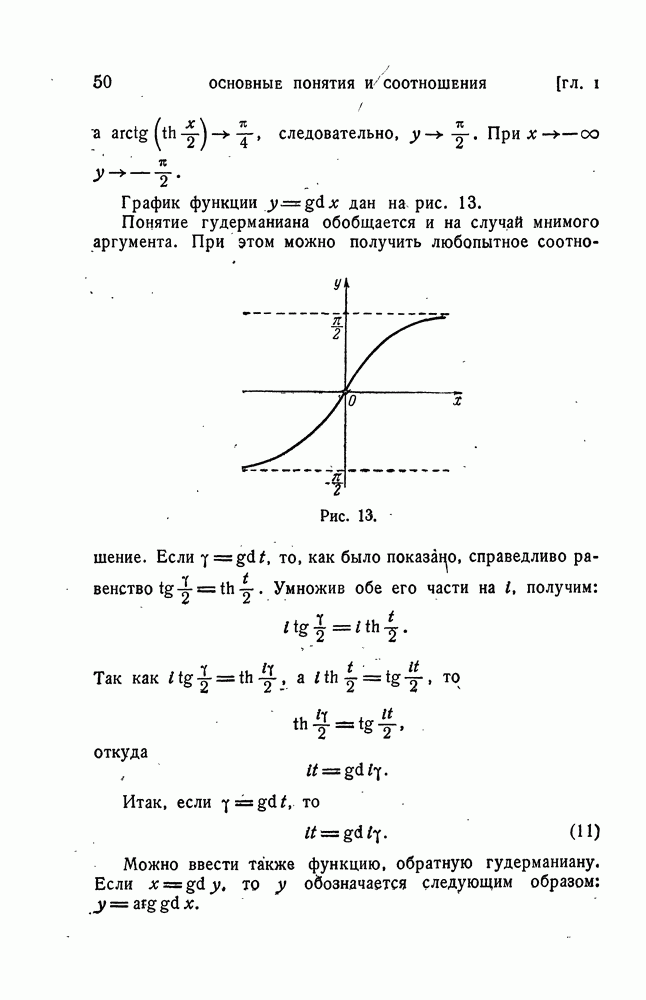
- 7. Гиперболическая амплитуда (гудерманиан)
- 8. Дифференцирование и интегрирование гиперболических и обратных гиперболических функций
- 9. Разложение гиперболических функций в степенные ряды и в тригонометрические ряды Фурье
- ГЛАВА II. ПРИМЕНЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ К ИНТЕГРИРОВАНИЮ
- 10. Интегрирование функций (гиперболические подстановки)
- 11. Интегрирование некоторых дифференциальных уравнений
- ГЛАВА III. ПРИМЕНЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ В ГЕОМЕТРИИ, МЕХАНИКЕ И ФИЗИКЕ
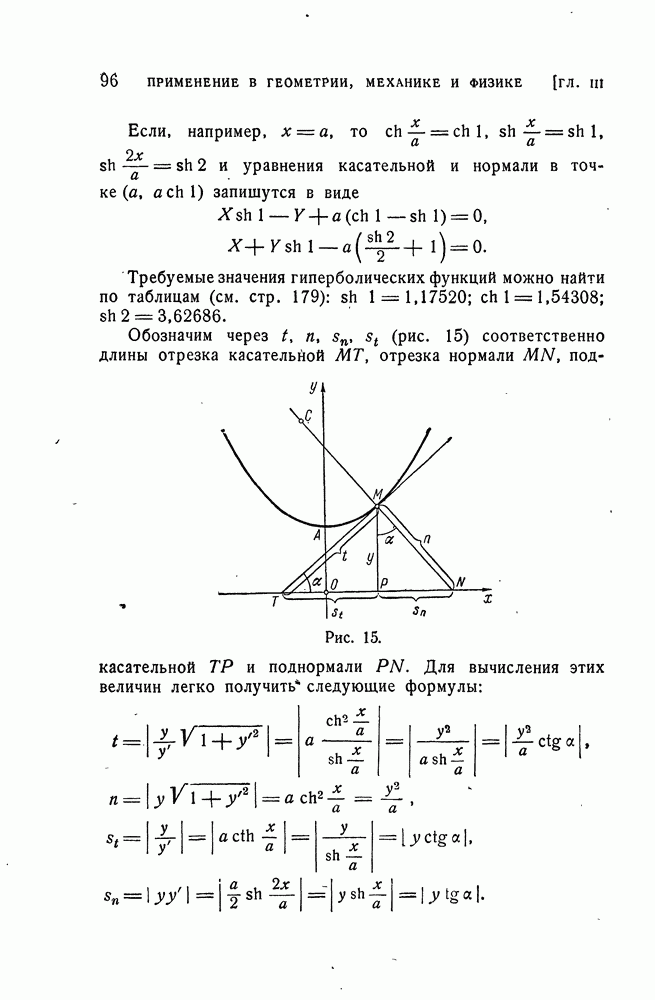
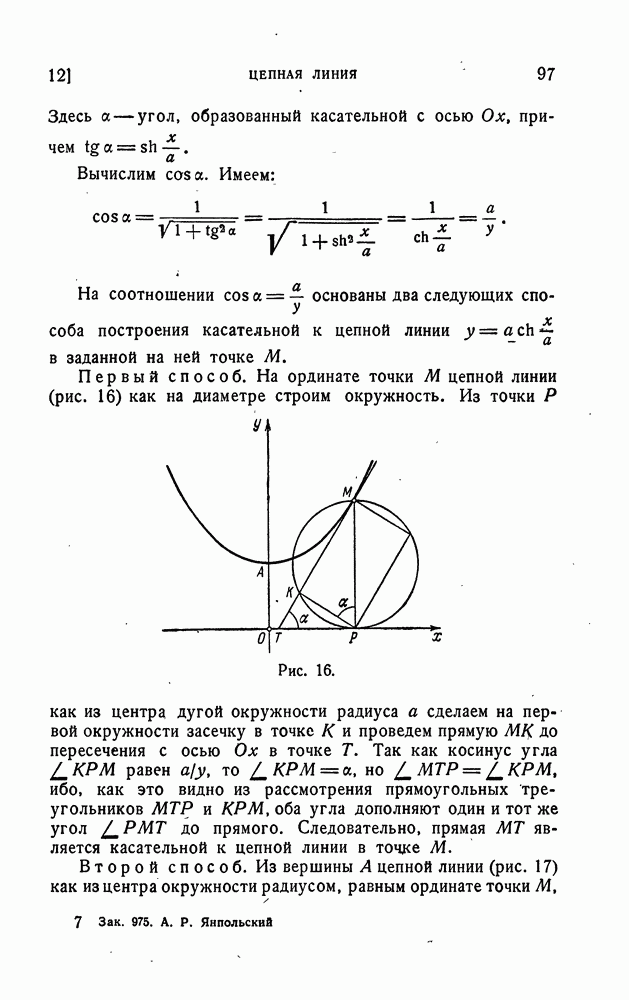
- Касательная и нормаль.
- Параметрические уравнения цепной линии.
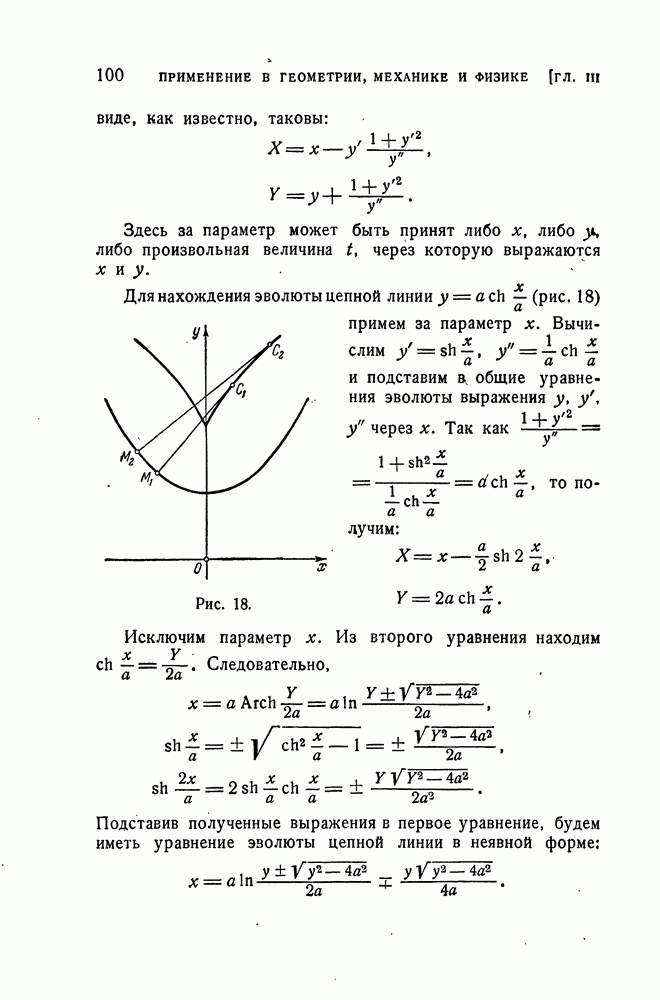
- Кривизна и радиус кривизны.
- Эвольвента цепной линии (трактриса).
- Натуральное уравнение линии.
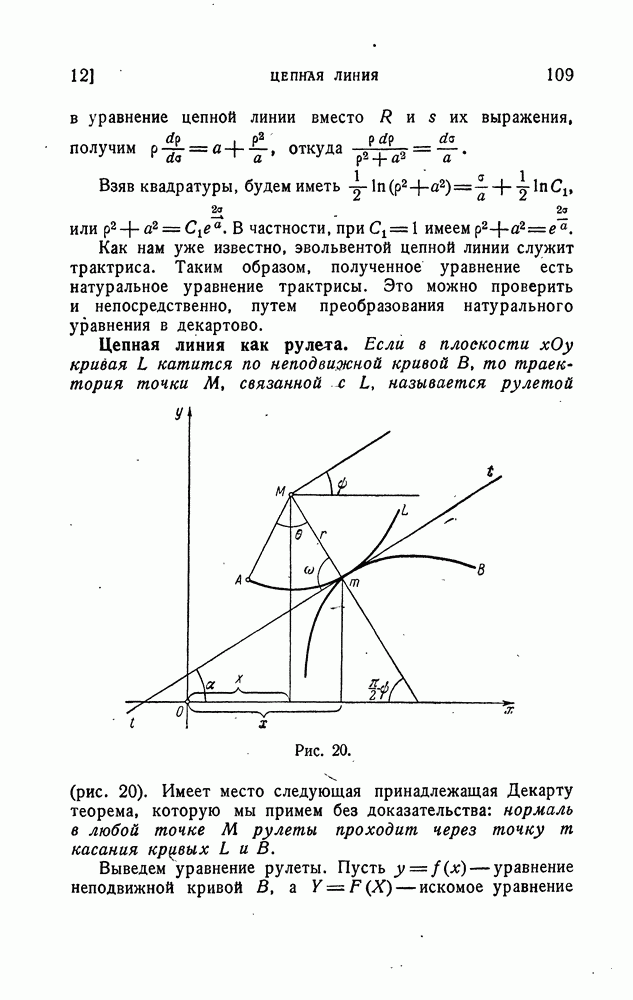
- Цепная линия как рулета.
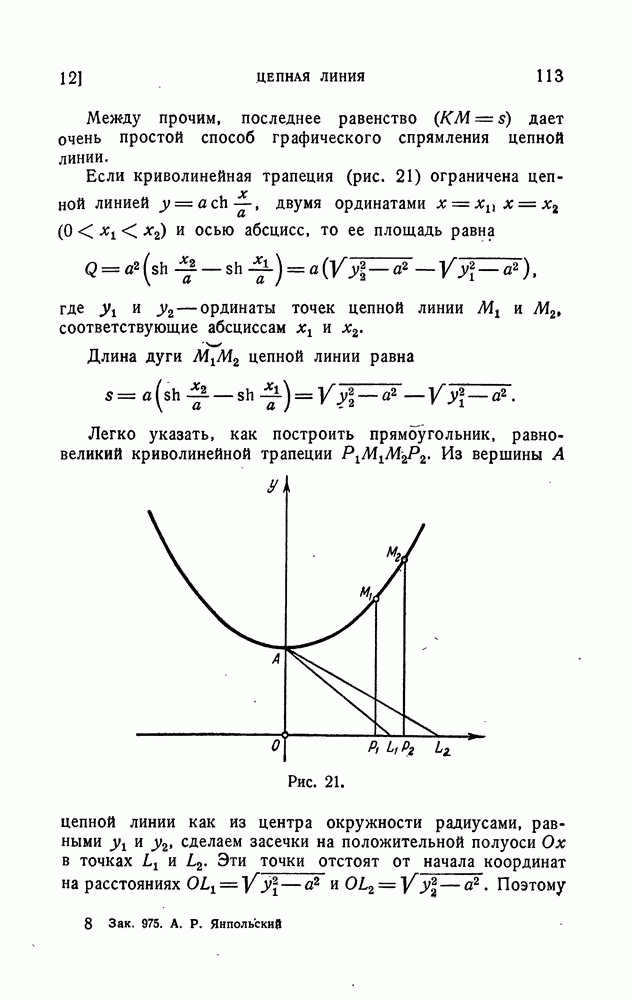
- Площадь криволинейной трапеции и длина дуги.
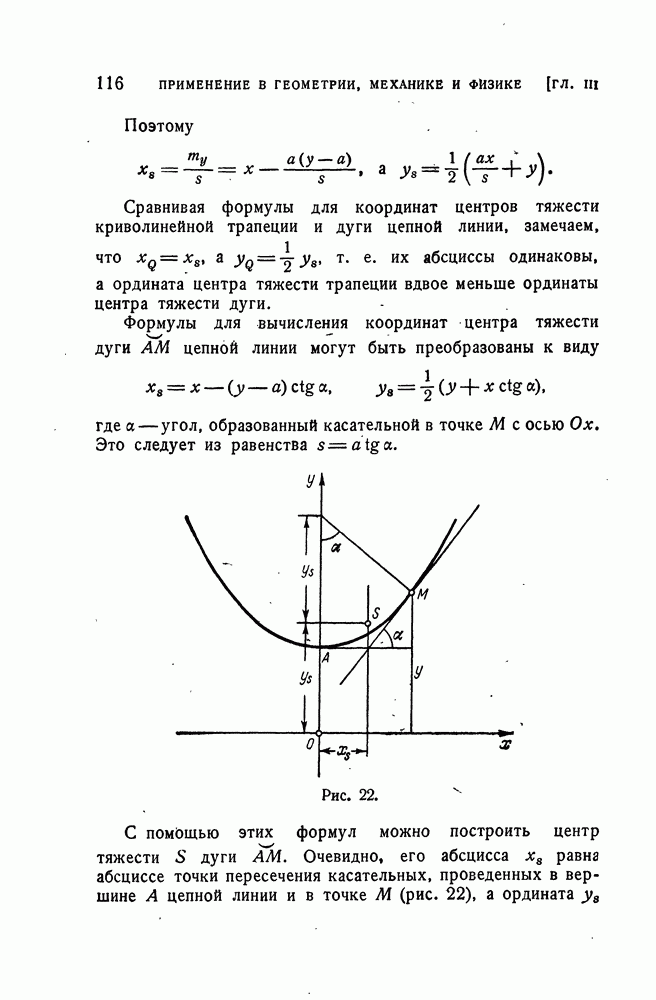
- Центр тяжести криволинейной трапеции и дуги.
- Катеноид.
- Минимальные свойства цепной линии.
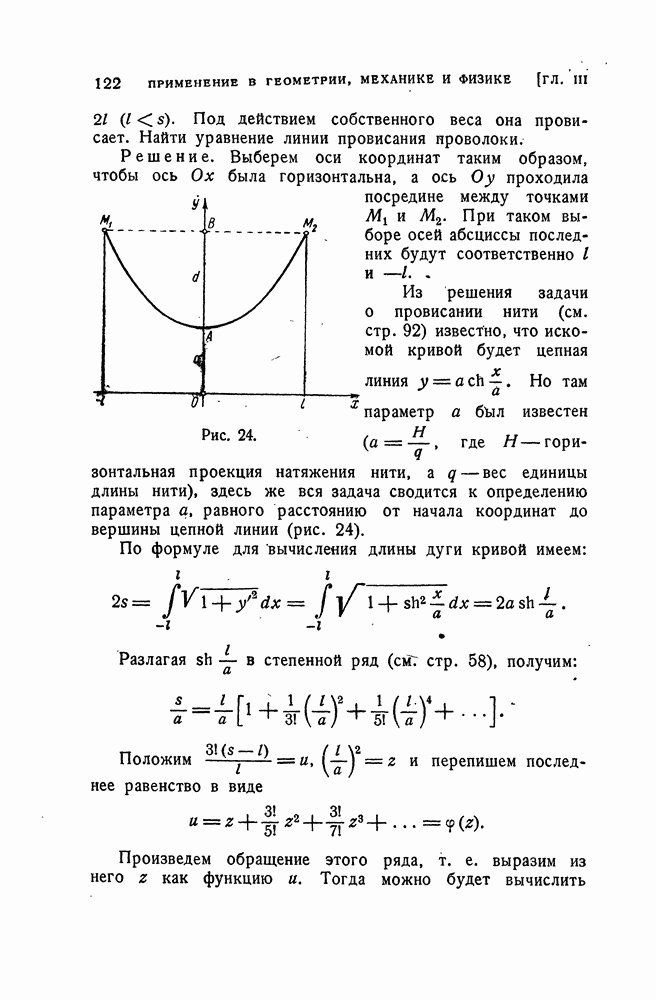
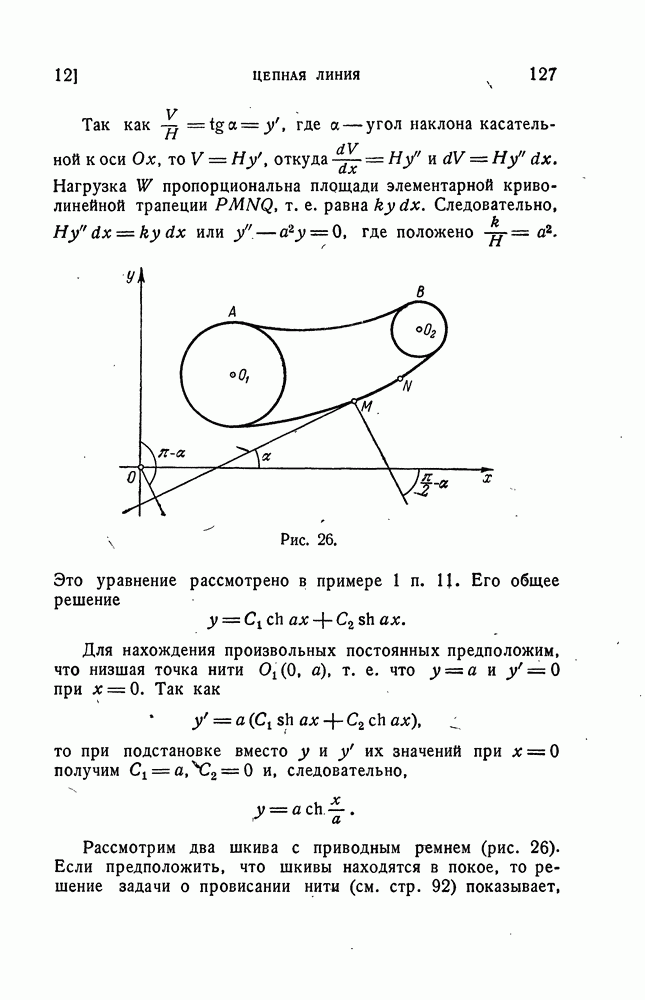
- Задачи, связанные с цепной линией.
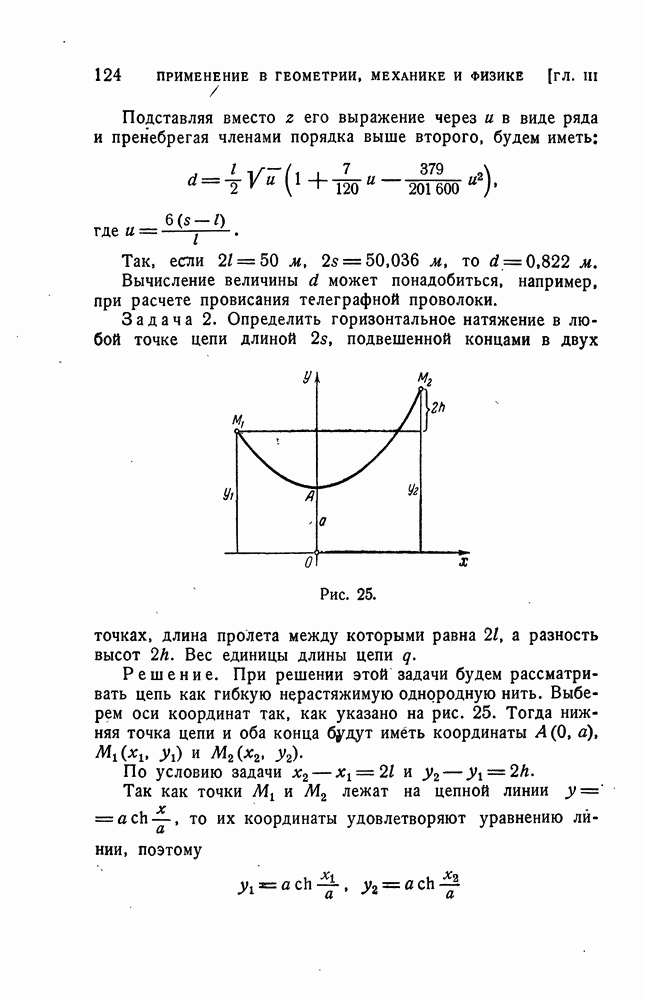
- 13. Некоторые прикладные задачи
- Движение материальной точки.
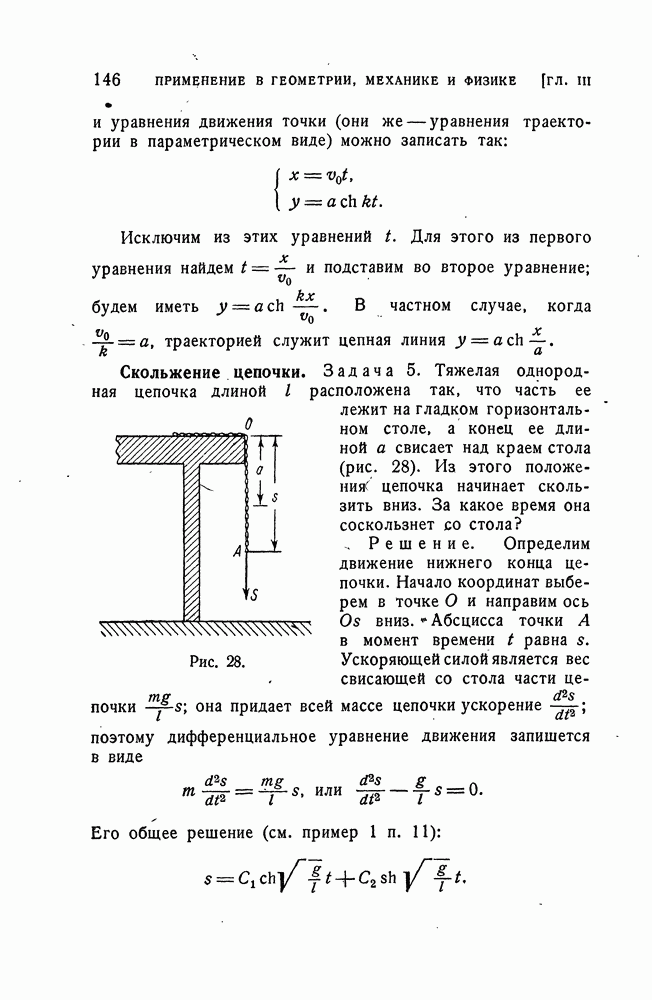
- Скольжение цепочки.
- Движение шарика во вращающейся трубке.
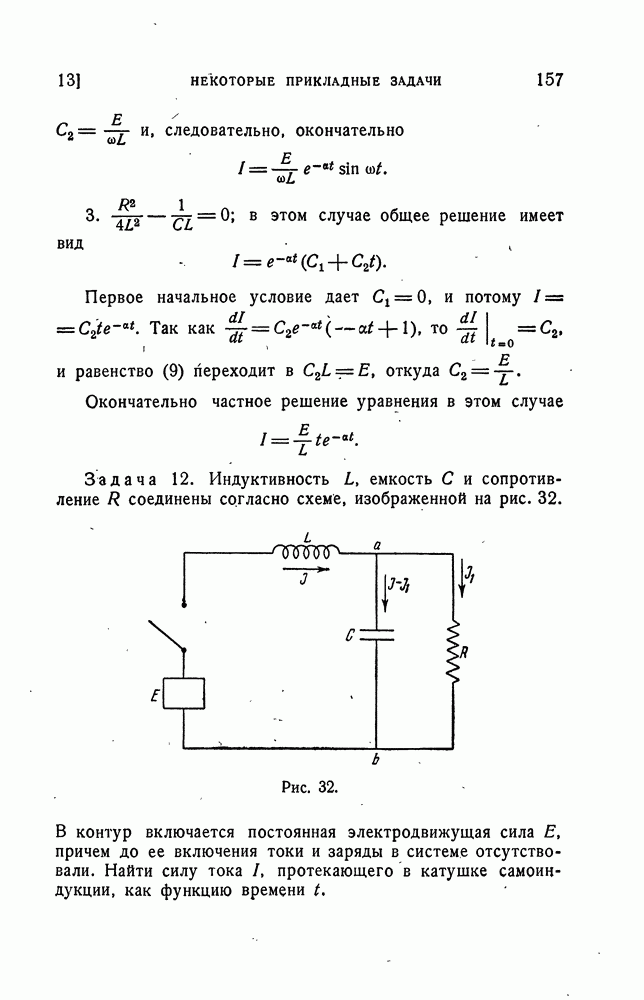
- Включение электродвижущей силы в контур.
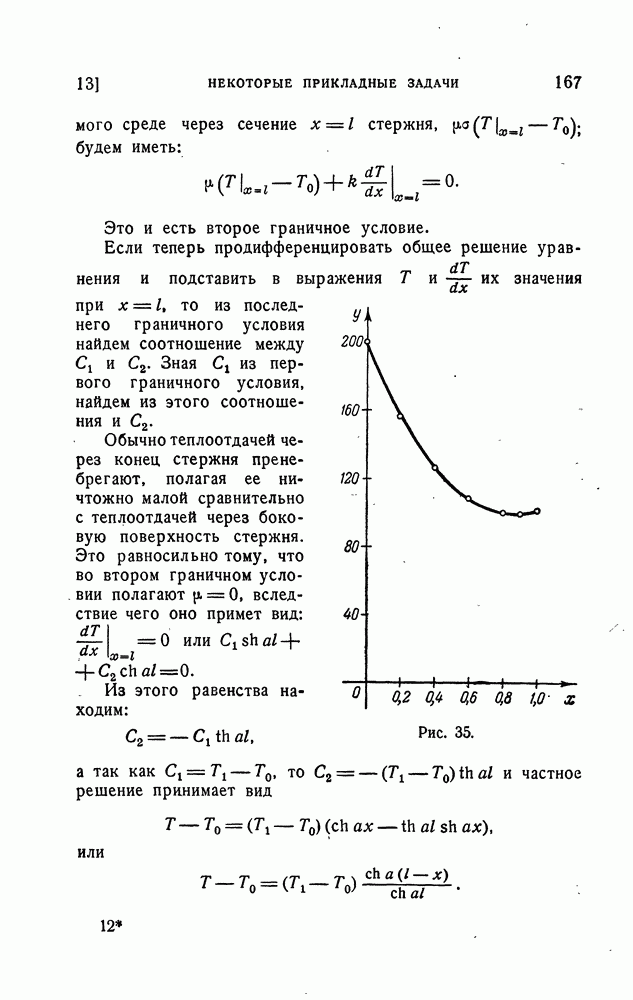
- Установившееся распределение температуры в стержне.
- Ионизация газа.
- Диффузия, сопровождаемая химической реакцией.
- Размножение бактерий.
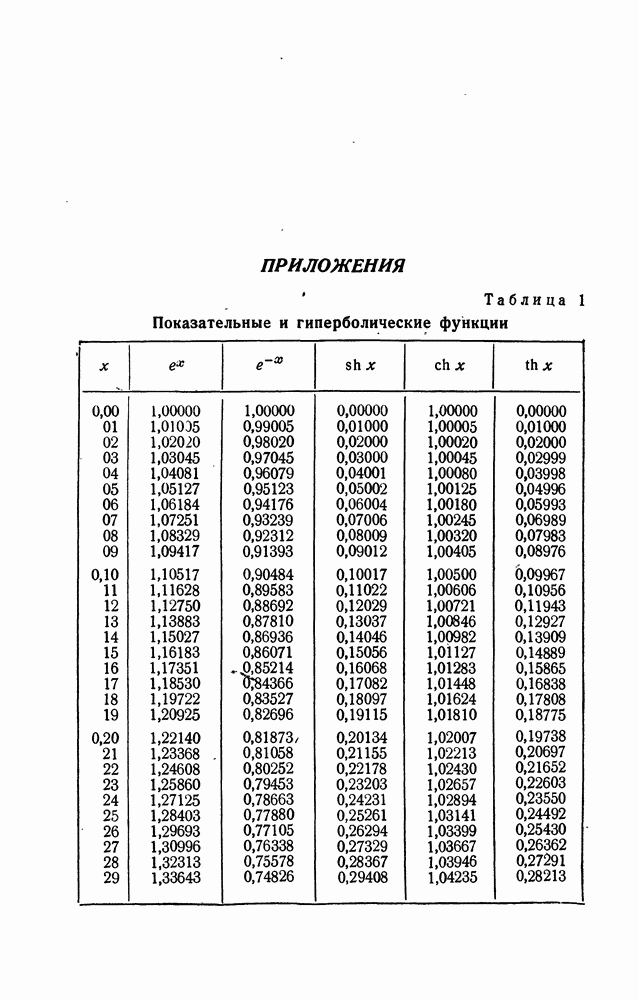
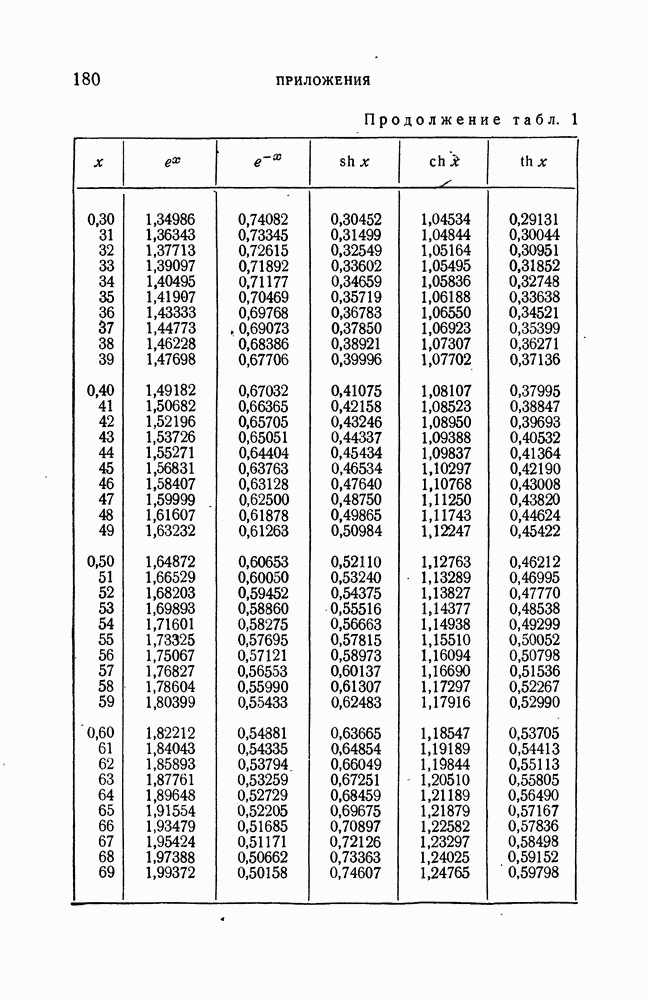
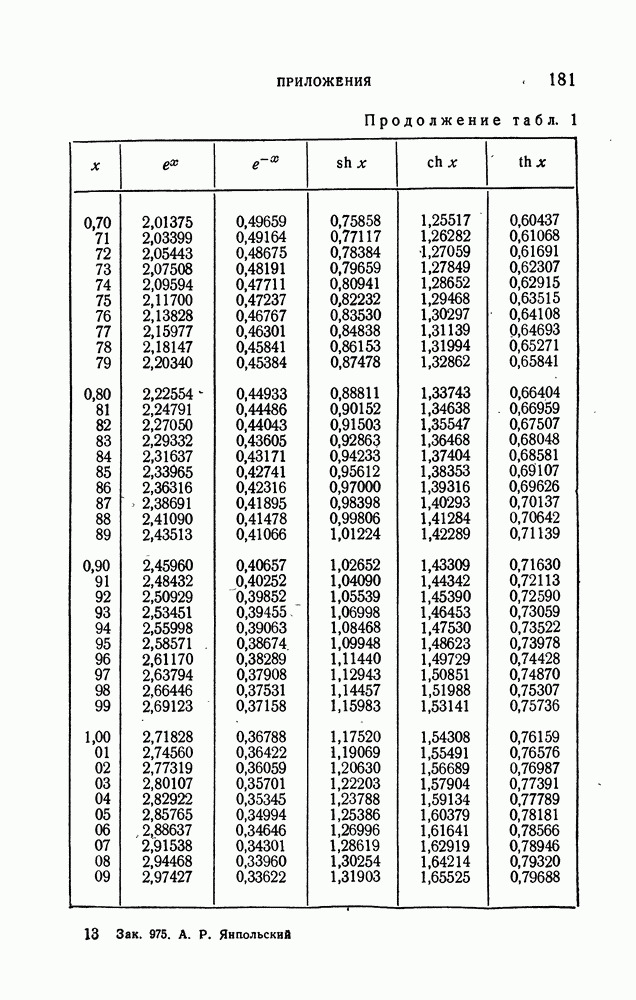
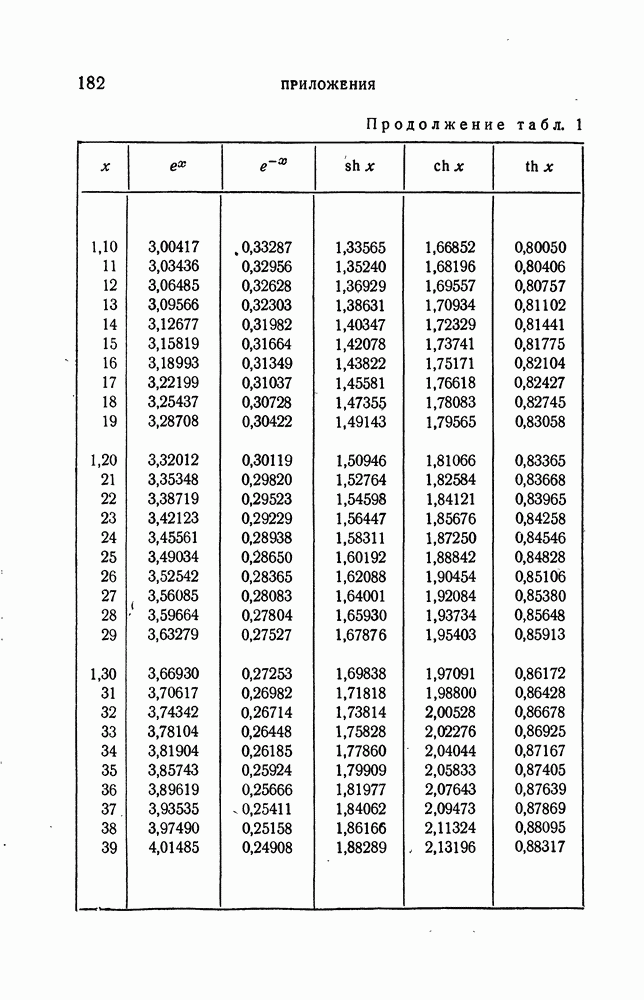
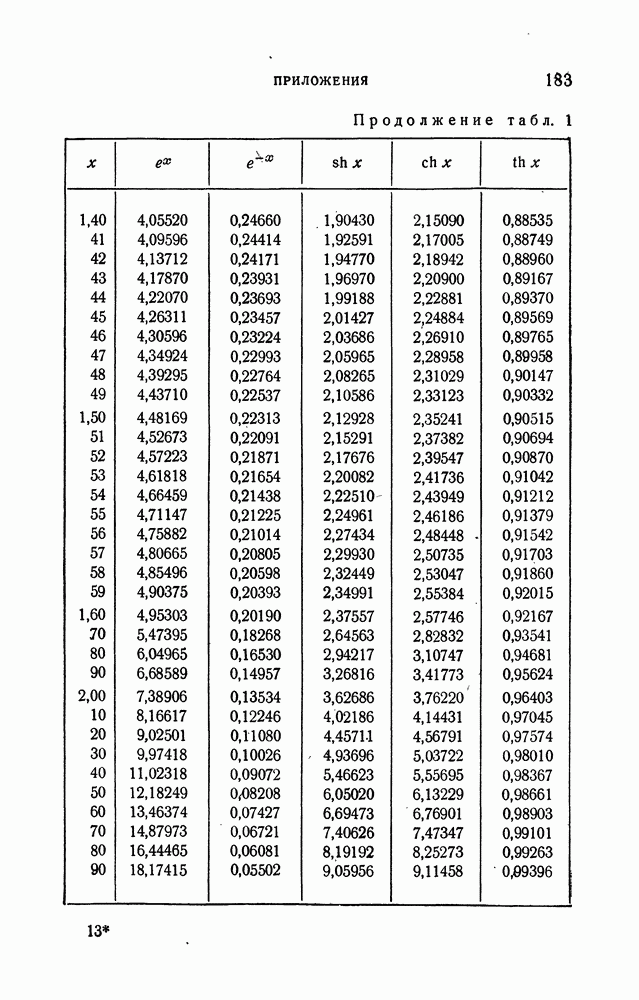
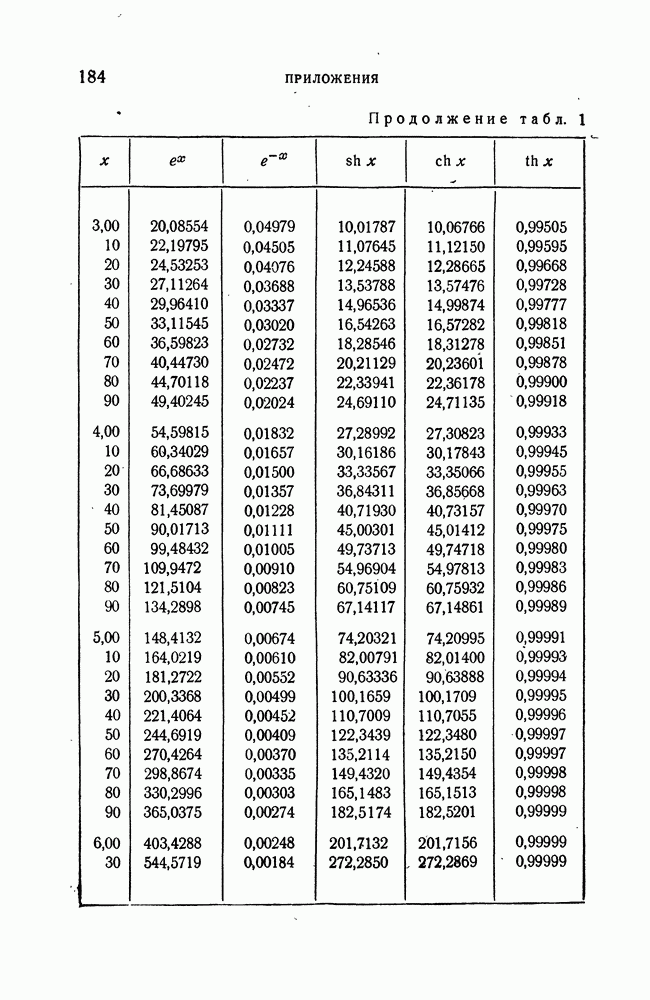
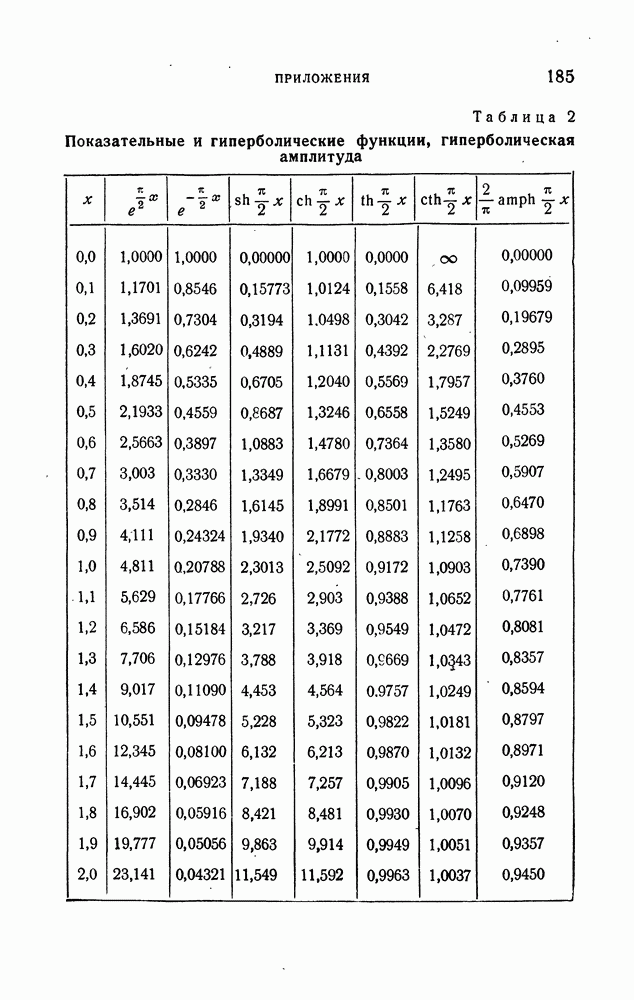
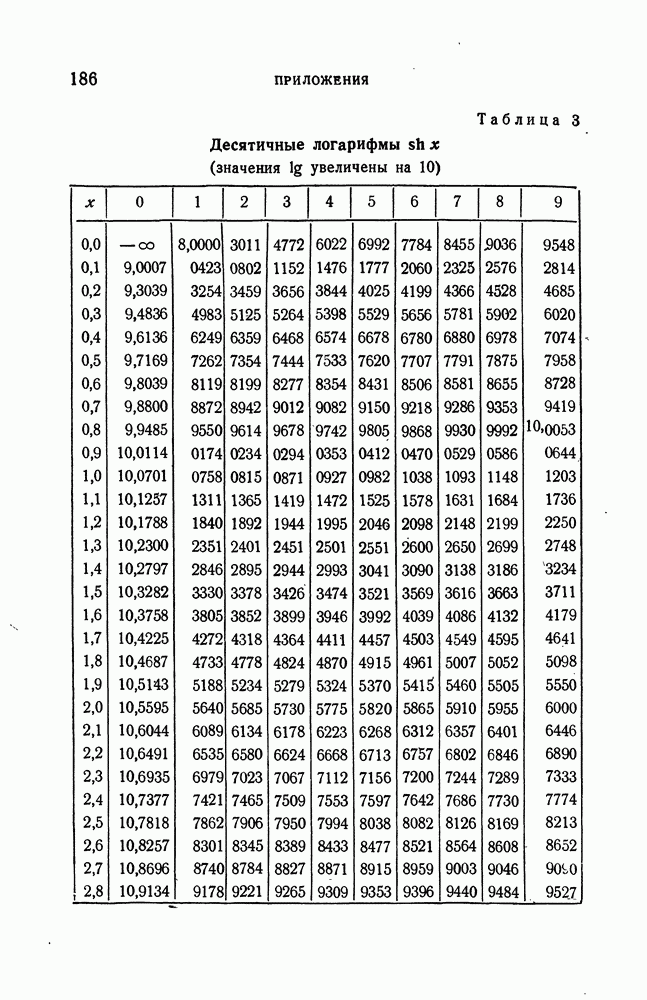
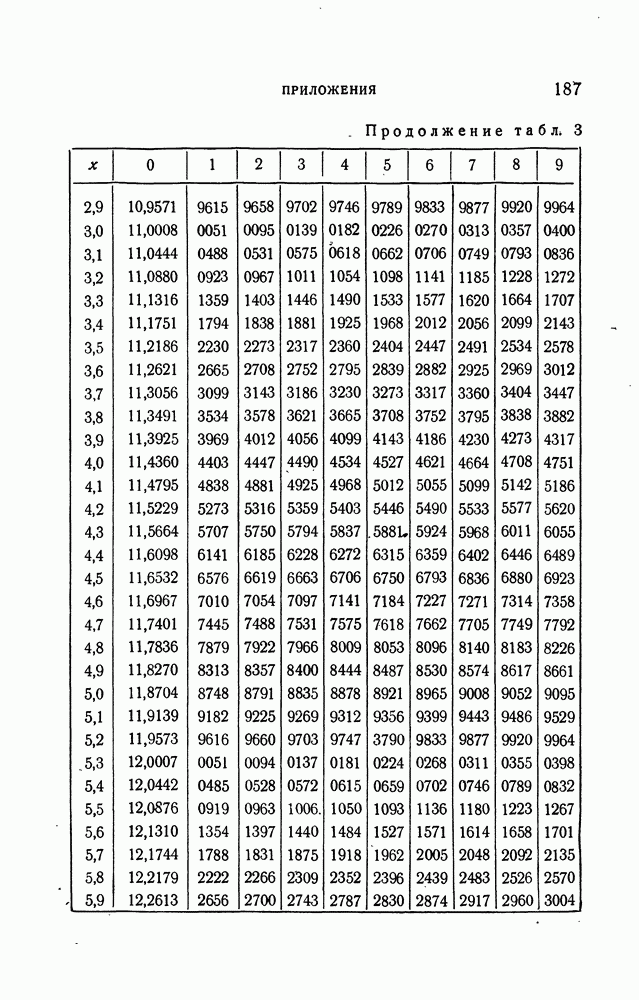
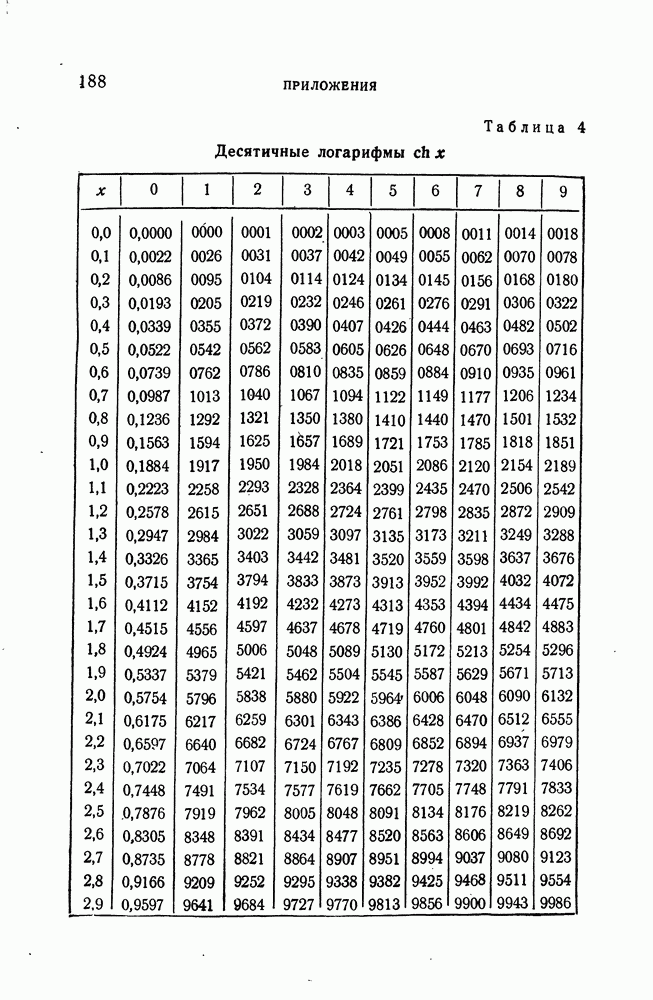
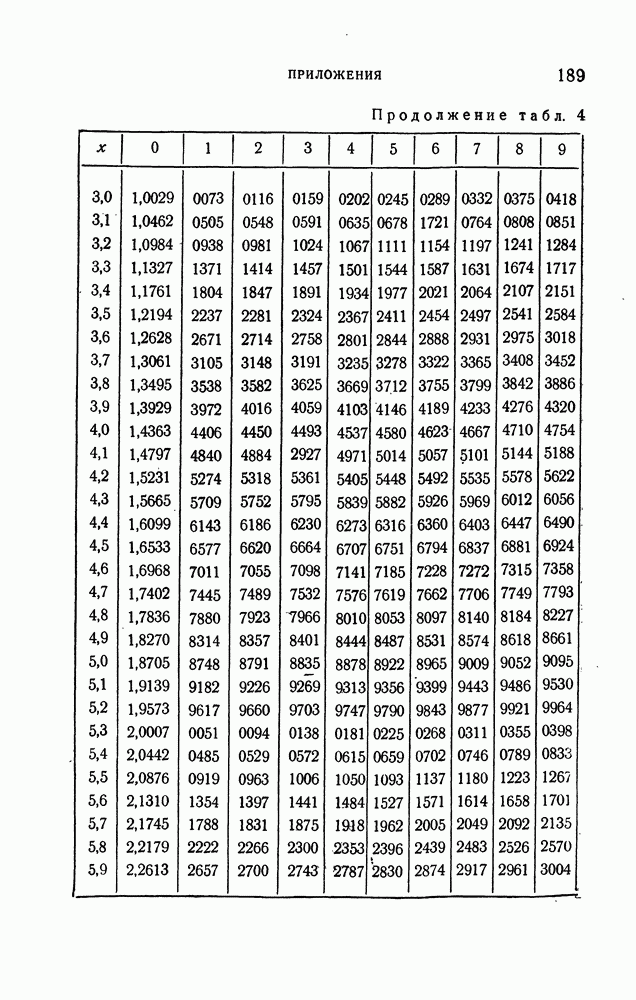
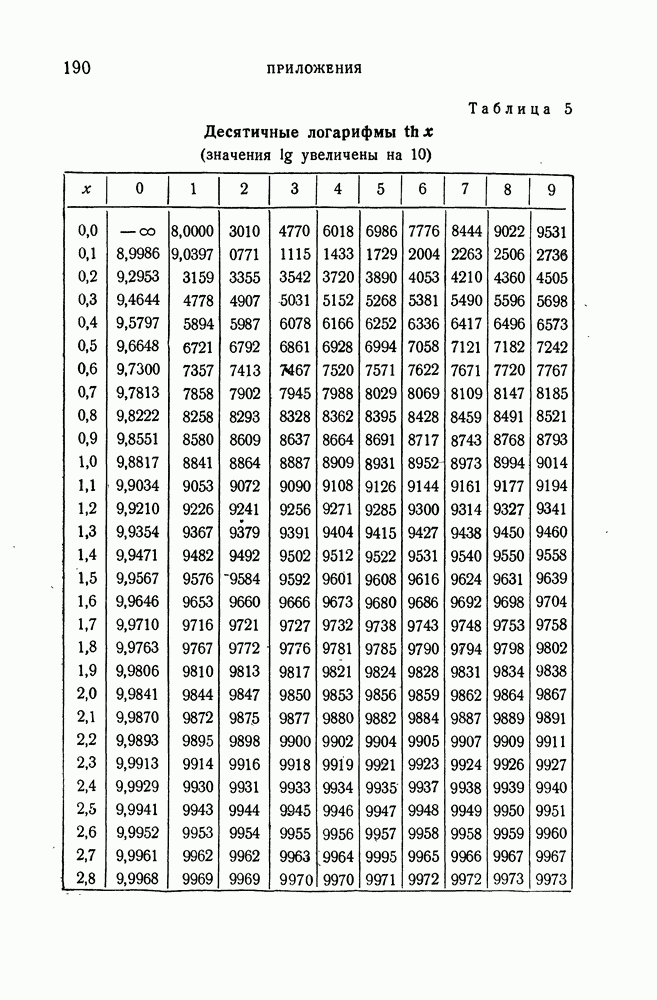
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА